东华大学大物A2作业解答
大学物理A2习题答案2011-2012.1
班级 学号 姓名第10章 静电场10-1关于点电荷的电场有下列说法，其中正确的是[Ｄ ](A)公式30π4r rq E ερρ=中的q 也是试探电荷； (B)由30π4r rq E ερρ=知r → 0时E →∞; (C)对正点电荷由30π4r rq E ερρ=知，r 越小电场越强，对负点电荷由30π4r rq E ερρ=知， r 越小电场越弱；(D) 利用点电荷的场强公式与叠加原理，原则上可求各种带电体的场强。
10-2在空间有一非均匀电场，其电场线分布如图所示．在电场中作一半径为R 的闭合球面S ，已知通过球面上某一面元S ∆的电场强度通量为,e Φ∆则通过该球面其余部分的电场强度ρ通量为e Φ∆-．10-3一个点电荷放在球形高斯面的中心, 如图所示．下列哪种情况通过该高斯面的电通量有变化? [ B ] (A) 将另一点电荷放在高斯面外； (B) 将另一点电荷放在高斯面内；(C) 将中心处的点电荷在高斯面内移动； (D) 缩小高斯面的半径。
10-4 电量都是q 的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?解: 如图示(1) 以A 处点电荷为研究对象，由力平衡知：q '为负电荷20220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-='10-5 一个半径为R 的均匀带电半圆环，电荷线密度为λ,求环心处O 点的场强。
S q解: 如图，在圆环上取微元ϕRd dl =，其带电ϕλλd d d R l q ==，它在O 点产生场强大小为20π4d d RR E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0R E E x ==ϕϕελϕπd cos π4)cos(d d 0R E E y -=-=积分R R E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπRE y∴ R E E x 0π2ελ==，方向沿x 轴正向．10-6 长l=15.0cm 的直导线AB 上均匀地分布着线密度λ=5.0x10-9C·m-1的正电荷．试求：(1)在导线的延长线上与导线B 端相距a =5.0cm 处P 点的场强； (2)在导线的垂直平分线上与导线中点相距d =5.0cm 处Q点的场强。
大学物理A2的重要习题
1．如计算题7-1图所示，一根铜棒长为L=0.05m ，水平放置于一竖直向上的匀强磁场中，绕位于距a 端L/5处的竖直轴OO /在水平面内旋转，每秒钟转两圈。
已知该磁场的磁感应强度B=0.50×10-4T 。
求铜棒两端a 、b 的电位差。
计算题7-1图 1. 解:建立坐标系如图所示在ab 上任取线元dx,如图。
当铜棒旋转时产生的动生电动势xdx B i dx B v d ωε=⋅⨯=)(动整根铜棒产生的动生电动势⎰--⨯===545(1071.410382L L L B xdx B 伏）动ωωε 2．如计算题7-2图所示，无限长直导线，通以电流I ，有一与之共面的直角三角形线圈ABC ，已知AC 边长为b ，与长直导线平行，BC 边长为a 若线圈以垂直于导线方向的速度向右平移，当B 点与长直导线的距离为d 时，求线圈ABC 内的感应电动势的大小和感应电动势的方向。
计算题7-2图解：建立坐标系，长直导线为Y 轴，BC 边为X 轴，原点长直导线上，则斜边的方程为abr a bx y -= 式中r 是t 时刻B 点与长直导线的距离，三角形中的磁通量⎰⎰+++-=-==r a r r a rrr a a br b I dx ax br a b I dxxyI )ln (2)(22000πμπμπμφ td r d r a a r r a a b I dt d )(ln 20+-+=-=πμφε 当r = d 时，vr a a r r a a b I )(ln 20+-+=πμε 方向：ACBA （顺时针）3．两根平行无限长直导线相距为d ，载有大小相等方向相反的电流I ，电流变化率dI/dt=α>0。
一个边长为d 的正方形线圈位于导线平面内与一根导线相距d ，如计算题7-3图所示。
求线圈中的感应电动势ε，并说明线圈中的感应电动势是顺时针还是逆时针方向。
计算题7-3图 解：（1）载流为I 的无限长直导线在与其相距为r 处产生的磁感应强度为： r I B πμ20=以顺时针绕向为线圈的正方向，与线圈相距较远的导线在线圈中产生的磁通量为： 23ln22034241πμπμφId r d rI d =⋅=⎰与线圈相距较近的导线在线圈中产生的磁通量为： 2ln 2202442πμπμφIdr d rI d -=⋅-=⎰ 总磁通量34ln2021πμφφφId -=+=感应电动势为：34ln234ln 200παμπμφεd t d I d d dt d ==-=由ε>0和回路正方向为顺时针，所以ε的绕向为顺时针方向，线圈中的感应电动势亦为顺时针方向。
大学物理学第二版 习题解答
大学物理学习题答案习题一答案 习题一1.1 简要回答下列问题：(1) 位移和路程有何区别在什么情况下二者的量值相等在什么情况下二者的量值不相等 (2) 平均速度和平均速率有何区别在什么情况下二者的量值相等(3) 瞬时速度和平均速度的关系和区别是什么瞬时速率和平均速率的关系和区别又是什么 (4) 质点的位矢方向不变，它是否一定做直线运动质点做直线运动，其位矢的方向是否一定保持不变(5) r ∆v 和r ∆v 有区别吗v ∆v 和v ∆v有区别吗0dv dt =v 和0d v dt=v 各代表什么运动 (6) 设质点的运动方程为：()x x t =，()y y t =，在计算质点的速度和加速度时，有人先求出r =drv dt= 及 22d r a dt =而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即v = 及 a =你认为两种方法哪一种正确两者区别何在(7) 如果一质点的加速度与时间的关系是线性的，那么，该质点的速度和位矢与时间的关系是否也是线性的(8) “物体做曲线运动时，速度方向一定在运动轨道的切线方向，法向分速度恒为零，因此其法向加速度也一定为零.”这种说法正确吗(9) 任意平面曲线运动的加速度的方向总指向曲线凹进那一侧，为什么(10) 质点沿圆周运动，且速率随时间均匀增大，n a 、t a 、a 三者的大小是否随时间改变 (11) 一个人在以恒定速度运动的火车上竖直向上抛出一石子，此石子能否落回他的手中如果石子抛出后，火车以恒定加速度前进，结果又如何1.2 一质点沿x 轴运动，坐标与时间的变化关系为224t t x -=，式中t x ,分别以m 、s 为单位，试计算：(1)在最初s 2内的位移、平均速度和s 2末的瞬时速度；(2)s 1末到s 3末的平均加速度；(3)s 3末的瞬时加速度。
解：(1) 最初s 2内的位移为为： (2)(0)000(/)x x x m s ∆=-=-=最初s 2内的平均速度为： 00(/)2ave x v m s t ∆===∆ t 时刻的瞬时速度为：()44dxv t t dt==- s 2末的瞬时速度为：(2)4424/v m s =-⨯=-(2) s 1末到s 3末的平均加速度为：2(3)(1)804/22ave v v v a m s t ∆---====-∆ (3) s 3末的瞬时加速度为：2(44)4(/)dv d t a m s dt dt-===-。
大学物理A2-总复习
（1）相位差
∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0 ， 1， ) ± L
A = A1 + A2
（2）相位差
相互加强
∆ϕ = ϕ 2 − ϕ1 = (2k + 1) π (k = 0 ， 1， ) ± L
A = A1 − A2
相互削弱
大学物理A2-总复习 大学物理A2A2
不同频率简谐振动的合成 拍现象（了解） （2）同方向不同频率简谐振动的合成 拍现象（了解） ）同方向不同频率
波腹 波节
λ
1 (k + ) 2 2
相邻两波腹（节）之间的距离：xk +1 − xk = 之间的距离： 相邻两波腹（
λ
2
长的许多段， 所有波节点将媒质划分为 λ 长的许多段，每段中 2 各质点的振动振幅不同， 相位皆相同； 各质点的振动振幅不同，但相位皆相同；而相邻段 间各质点的振动相位相反; 间各质点的振动相位相反; 即驻波中不存在相位的 传播。 传播。
x1(t) = A cos(ω t +ϕ1) 1 1
x2 (t) = A cos(ω2t +ϕ2 ) 2
频率相近的两个同方向不同频率的合振动： 频率相近的两个同方向不同频率的合振动：
ν = (ν 1 + ν 2 ) 2
ν拍 =ν 2 −ν1
——拍频 拍频
大学物理A2-总复习 大学物理A2A2
第12章 12章
x
x
大学物理A2-总复习 大学物理A2A2
5、 简谐振动的能量 、 6、简谐振动的合成 、 （1）同方向、同频率的简谐振动的合成 ）同方向、同频率的简谐振动的合成
x1 = A1 cos(ω t + ϕ 1 ) x2 = A2 cos(ω t + ϕ 2 )
大学物理A2总复习资料(修改版)(DOC)
元培学院大学物理学A2复习题一．选择题36．根据电介质中的高斯定律，下列说法正确的是（A ）若电位移矢量沿一闭合曲面的通量等于零，则这个曲面内一定没有自由电荷；（B ）若闭合曲面内没有自由电荷，则电位移矢量沿该闭合曲面的通量等于零；（C ）若闭合曲面内没有自由电荷，则曲面上的电位移矢量一定等于零；（D ）电位移矢量只与自由电荷的分布有关37．极化电荷与自由电荷的最大区别是（A ）自由电荷能激发电场，而极化电荷则不会；（B ）自由电荷能激发静电场，而极化电荷则只能产生涡旋电场；（C ）自由电荷有正负两种电荷，而极化电荷则没有正负之分；（D ）自由电荷能单独地自由运动，而极化电荷则不能脱离电介质中原子核而单独移动38．一个带电量为q ，半径为R 的薄金属壳外充满了相对电容率为r ε的均匀介质，球壳内为真空，则球壳的电势为（A ）R q 04πε （B ）R qr επε04 (C)０ (D))(40R r r qr >επε39．两个半径相同的金属球，一为空心，一为实心，把两者各自孤立时的电容值加以比较，则()A 空心球电容值大 ()B 实心球电容值大()C 两球电容值相等 ()D 大小关系无法确定40．如图所示，先接通开关K ，使电容器充电，然后断开K ；当电容器板间的距离增大时，假定电容器处于干燥的空气中，则()A 电容器上的电量减小 ()B 电容器两板间的场强减小 ()C 电容器两板间的电压变小 ()D 以上说法均不正确41．在感应电场中电磁感应定律可写成t l E LK d d d Φ-=⎰⋅ ，式中K E 为感应电场的电场强度．此式表明(A) 闭合曲线L 上K E 处处相等(B) 感应电场是保守力场(C) 感应电场的电场强度线不是闭合曲线(D) 在感应电场中不能像对静电场那样引入电势的概念42．关于产生感应电流的条件，下面说法正确的是（A ）任何导体在磁场中运动都产生感应电流（B ）只要导体在磁场中做切割磁感线运动时，导体中都能产生感应电流（C ）闭合电路的一部分导体，在磁场里做切割磁感线运动时，导体中就会产生感应电流（D ）闭合电路的一部分导体，在磁场里沿磁感线方向运动时，导体中就会产生感应电流43．由导体组成的一矩形线框，以匀速率v从无磁场的空间进入一个均匀磁场中，然后从磁场中出来，又在无磁场空间中运动。
大学物理A2稳恒磁场习题解答PPT课件
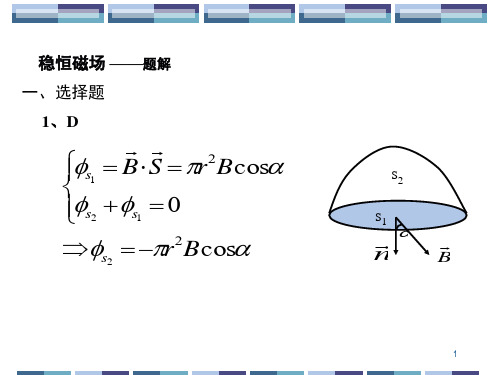
7、D
B
0 Ir , 2R 2 0I ,r 2r
rR R
8、B
3
2
1
45 6
6
9、C 10、C 11、B
12、D
Rm ,T2m ,m 4,Q 2
qB qB m H Q H
R m P
eB eB
Sin D eBD
RP
R BO•
-e
D
MP mB0
7
13、C
123 F3
F1
F2
1A 2A 3A
Ｌ３、Ｌ４在Ｏ点产生的磁感应强度的大小相 等，方向相反，总值为０。即
B3B4 0
ቤተ መጻሕፍቲ ባይዱ19
Ｏ点的磁感应强度：
B0
B1B2 B3 B4
0I 4R
方向垂直图面向外。
20
3、带电粒子在均匀磁场中由静止开始下降，磁场方 向与与重力方向（ X轴方向）垂直，求粒子下落 距离为 X 时的速率 V， 并叙述求解方法的理论依据。
16
2、用两根彼此平行的半无限长的直导线 L、1 L 2
把半径为 R的均匀导体圆环连到电源上，如图所
示，已知直导线上的电流为 I，求圆环中心 O
点的磁感应强度。
O
a
L1
R
b
L2
17
解：L1在O点产生的磁感应强度： 由于L1与O点在一条直线，由毕奥—萨伐定律可求出
B1=0
L2在Ｏ点产生的磁感应强度： Ｌ２为半无限长直电流，它在Ｏ处产生的场是无限长直 电流的一半，由安培环路定律和叠加原理有
0
I1
3
4、D I
a1 O1
I
O2
a2
B12a01I;B222a20I(见2题）
大学物理2习题参考答案
题1-3图第一章 流体力学1.概念（3）理想流体：完全不可压缩又无黏性的流体。
（4）连续性原理：理想流体在管道中定常流动时，根据质量守恒定律，流体在管道内既不能增 多，也不能减少，因此单位时间内流入管道的质量应恒等于流出管道的质量。
（6）伯努利方程：C gh v P =++ρρ221（7）泊肃叶公式：LPR Q ηπ84∆=2、从水龙头徐徐流出的水流，下落时逐渐变细，其原因是（ A ）。
A. 压强不变，速度变大； B. 压强不变，速度变小；C. 压强变小，流速变大；D. 压强变大，速度变大。
3、 如图所示，土壤中的悬着水，其上下两个液面都与大气相同，如果两个页面的曲率半径分别为R A 和R B (R A <R B )，水的表面张力系数为α，密度为ρ，则悬着水的高度h 为___)11(2BA R R g -ρα__。
(解题：BB A A A B R P P R P P gh P P ααρ2,2,00-=-==-) 4、已知动物的某根动脉的半径为R, 血管中通过的血液流量为Q ， 单位长度血管两端的压强差为ΔP ，则在单位长度的血管中维持上述流量需要的功率为____ΔPQ ___。
5、城市自来水管网的供水方式为：自来水从主管道到片区支管道再到居民家的进户管道。
一般说来，进户管道的总横截面积大于片区支管的总横截面积，主水管道的横截面积最小。
不考虑各类管道的海拔高差（即假设所有管道处于同水平面），假设所有管道均有水流，则主水管道中的水流速度 大 ，进户管道中的水流速度 小 。
10、如图所示，虹吸管的粗细均匀，略去水的粘滞性，求水流速度及A 、B 、C 三处的压强。
221.2 理想流体的定常流动'2gh v C =∴222121'CC D D v P v gh P ρρρ+=++0,0≈==D C D v P P P 练习5：如图，虹吸管粗细均匀，略去水的粘滞性，求管中水流流速及A 、B 、C 三处的压强。
大学物理A2 作业答案
10 静电场（1）习题解10-1 （A ）由即得 ,0dq dF ,r4)q Q (q F 20=-=πε 10-2 （C ）10-3 （C ） 0x4Q214Q ,0i r 4Q 2i 14Q E 20202020=-=-=πεπεπεπε即可得. 10-4 （A ）2220(1)2Qq k k Q ⋅⋅=⇒=- 10-5 （A ） 10-6 0 ，214S a λπε∆⋅⋅； 由圆心指向S ∆方向 10-7011()4a L aλπε-+ 10-8 解：2204()dxdq dx dE a x λλπε=⇒=+1222220cos 4()()x dxxdE dE a x a x λθπε=-=⋅++ 1222220sin 4()()y dxadE dE a x a x λθπε=-=⋅++积分后得到：04x E a λπε=-；04y E a λπε=；0()4E i j aλπε=-+ 10-9 解：取宽为dx 的细长条dx λσ=该细长条在P 处产生的电场强度为002()2()dxdE a b x a b x λσππεππε==+-+- ，则P 处的电场强度为：000ln 2()2b dx a bE dE a b x aσσπεπε+===+-⎰⎰ 指向+X 方向10-10 解：θθλλd sin R dl dq 0==， 200R4d sin R dE πεθθλ=， 三11 静电场（2）习题解11-1 （A ） 通过半球面的电通量与以R 为半径的圆平面的电通量等. 11-2 （C ）穿进高斯面的电通量与穿出高斯面的电通量相等。
11-3 （D ）把点电荷用空间立体面包围,则电通量为q/ε0,所给平面面积为空间立体面面积的1/6, ∴电通量也为过空间立体面的1/6.11-4 （D ）作一半径为r 的高斯面(球面),包围电荷为Q a , 即可得. 11-5 q/24ε0 ;若要把A 点全部包围,需要如图的8个立方体,封闭曲面表面积为24个abcd 面.11-6 Q ΔS/16π2ε0R 4; 由球心指向ΔS. 用补偿法: 球面看成完整带正电的, 球心场强为0;ΔS 带负电,所带电量q=σΔS=Q ΔS/(4πR 2), 场强由球心指向ΔS ，即可得叠加结果.11-7 4.43×10-13（C ·m -3）.⎰⎰⎰=-=-==ππθθπελθθθπελ02000200x x 0)2(d 2sin 41R 4Rd sin cos R 4RdE E R8 d sin R 4RdE E 0002200y y ελθθπελπ-=-==⎰⎰jR8j E i E E 00y xελ-=+=∴0dE E Ry Ry ==⎰θπεθθλθsin R 4d sin R sin dE dE 200y -=-=θπεθθλθcos R4d sin R cos dE dE 200x -=-=由高斯定理 012SSh S E S E S d E ε∆ρ∆∆=-=⋅⎰h)E E (120-=ερ11-8 解：分别在r a <，a r b <<，b r <建立高斯面r a <时，110Q E d S ε⋅=⎰ ；1100Q E =⇒=a rb <<时，22222004Q Q E d S E r πεε⋅=⇒⋅=⎰；3324()3Q r a ρπ=⋅-33332204()()343r a r a E r rρπρπεε⋅--== b r <时，23333004Q Q E d S E r πεε⋅=⇒⋅=⎰，3334()3Q b a ρπ=⋅-33333204()()343b a b a E r rρπρπεε⋅--== 11-9解：空腔内可看成电荷体密度大小相等的带异号电荷的球体叠加而成. 整个大球带正电, 作高斯面过P 点,场强32Sr 34r 4'E S d 'E επρπ==⋅⎰, 00233434'ερεππρrr r E ==,OP33r 'E 00ερερ==小球带负电, 同样作过P 点高斯面,场强32'34'4''''επρπr r E S d E S-==⋅⎰,P O r E '33'''00ερερ-=-=b P O OP E E E03)'(3'''ερερ=-=+=11-10 解：因为电荷分布以纵轴对称，电场线只能沿x 轴，作柱形高斯面，在平板内（小柱面）:0SS x 2Q ES 2S d E ερε===⋅⎰ ,2dx 2d -, x E 0<<=ερ ; 在平板外（大柱面）: , dS Q ES 2S d E0Sρε===⋅⎰ 2dx 2d , d 2E 0-≤≤=ερ 12 静电场（3）习题解12-1 （D ） a 8q )a 21a 1(4q r d e r 4qV l d E V 00a a 2r20p pM M πεπεπε-=--=⋅=+⋅=⎰⎰ 12-2 （E ）12-3 （C ） 均匀电场场强处处相等；电势梯度 常矢量=∂∂-=n e nV E(相等).12-4 （D ） 20202422R q r d e r q l d E V R rpMπεπε⎰⎰∞=⋅=⋅= 12-5 (1)U=0；（2）E 0=0 .电势和场强分别在点叠加 0r4q (2r4q 2V 2V 2V 00=-+=+=-+πεπε）设顶角分别为a 、b 、c 、d, 中点场强： d c b a E E E E E+++=因为对角线顶点为等量同号电荷，场强相等而反向，所以0E =12-6 45(V); -15(V) . 由电势定义 B Bp p V l d E V +⋅=⎰计算即得.12-7 E x =-2Ax/(x 2+y 2) ; E y =-2Ay/(x 2+y 2) .按场强与电势梯度关系 yV E x V E y x ∂∂-=∂∂-= , 12-8 (q A -q B )d/2ε0S .12-9 解：（1）由于D ，C 在1q ，2q 产生的电场中具有对称性，故D C U U =即0DC U ∆=。
东华大学大物A2作业解答
25-24（58） (a)如图，导线在下方时要受到引力作用，受力平衡为
（b）当导线向上移动时，引力大于重力，向上运动，不会回到原来位置， 是非稳定平衡。
(c)导线在上方时要受到斥力作用，仍然和重力平衡， 通电电流也为360A。 （d）当导线向上移动时，斥力小于重力，向下运动，回到原来位置，是 稳定平衡。
东华大学大物A2作业解答
27-10（9）
东华大学大物A2作业解答
第28章麦克斯韦方程组和电磁波
28-1 根据位移电流的公式可得
28-5 电场沿着Z轴负方向传输,因此传播方向为 方向
传播方向为
,磁场沿着 方向.
东华大学大物A2作业解答
28-8
28-10
东华大学大物A2作业解答
28-13
28-14
东华大学大物A2作业解答
24-18（39）
东华大学大物A2作业解答
第25章磁场的源（原28章）
25-6（18）
方向指向线圈
25-12（28）
东华大学大物A2作业解答
25-13（31） 如图做安培环路，通电部分的电流密度分别为：
东华大学大物A2作业解答
25-15（34）由图可知，C点磁场由两段圆弧产生，在圆弧上取dl 得 25-16（35）
29-31
东华大学大物A2作业解答
29-33 29-36
东华大学大物A2作业解答
第30章衍射和偏振
30-1
东华大学大物A2作业解答
30-5
条纹级次最大为
缺级级次为
因此级次为3的倍数的条纹看不见,m取3、6、 9……..198共66条。 一共能产生的条纹为（198-66）*2+1=265条
大学物理A2半期考试试题以与答案
大学物理A2半期考试试题以与答案2011-2012-2 《大学物理A1》半期考试试卷一、判断题 (回答正确或错误，每小题 2 分，共 8 分 )1、一对作用力与反作用力作功之和一定为零。
（）2、用r表示质点位置矢量，dr ds。
（）s 表示离开原点的路程，有dtdt3、两个同方向、不同频率的简谐振动的合振动仍是简谐振动。
（）4、由同时的相对性知道：在一个参照系中同时发生的两个事件，在另在一个参照系中一定不同时。
（）二、选择题(每小题 3 分，共39 分)1、一质点沿 x 轴运动的规律是x t 24t 5 （SI）。
前三秒内它的()A 、位移和路程都是 3 mB 、位移和路程都是 -3mC、位移是 -3m，路程是 3m D 、位移是 -3m，路程是 5m2、某物体的运动规律为 d v /d t k v t ，式中的k为大于零的常量．当t0 时，初速为v0，则速度 v 与时间t的函数关系是()v0 e kt v0 e kt 2v k v0 e t k v0 et 2(A)v, (B)v 2 ,(C),(D)v23、一绕定轴旋转的刚体，其转动惯量为I，转动角速度为0 。
现受一与转动角速度的成正比的阻力距M f k的作用，比例系数为 k(k0) 。
试求此刚体转动的角速度及刚体从0 到0 /2所需的时间是 ()。
(A)t I(B)tk(C)tI(D)k ln 2ln 2k ln 2tk I I ln 24、地球绕太阳作椭圆轨道运动，地球的动量和角动量是否守恒正确的说法是()A、动量不守恒，角动量不守恒 B 、动量守恒，角动量不守恒C、动量不守恒，角动量守恒 D 、动量守恒，角动量守恒5、花样滑冰运动员绕通过自身的竖直轴转动，开始时两臂伸开，转动惯量为I，角速度为0 ；然后将两手臂合拢，使其转动惯量为2I 3，则转动角速度变为()A、203B、203C、302D、3026．如图所示的弹簧振子，当振动到最大位移处恰好有一质量为m 的泥块从正上方落到质量为 m 的物体上，并与物体粘在一起运动，则下述结论正确的是()A 、振幅变小，周期变小B、振幅变小，周期不变m0C、振幅不变，周期变小kD、振幅不变，周期变大m7、质量为0.04kg 的质点在力F的作用下，由静止开始沿平面曲线x29 y 从点P（0，0）运动到点Q (3,1)，若力F 的两个分量为F x2xy, F y 3x 2，式中 F 以牛顿、 x 和y 以米计，那么质点运动到Q 点的速度的大小为 ()-1B -1-1-1A 、40m s、 30m s C、 20m s D 、 10m s8l、质量为 m 的均匀细杆置于光滑水平面上。
大学物理A2-A卷-3-选择题答案
（本科）试卷（A 卷）《大学物理A2》期末考试试卷开课单位：大学物理教研室，考试形式：闭卷，允许带 计算器 入场一、选择题（共20分，每题2分）（1）点电荷Q 被曲面S 所包围 ， 从无穷远处引入另一点电荷q 至曲面外一点，如图所示，则引入前后：( D ) （A ）曲面S 上的电通量不变，曲面上各点场强不变． （B ）曲面S 上的电通量变化，曲面上各点场强不变． （C ）曲面S 上的电通量变化，曲面上各点场强变化． （D ）曲面S 上的电通量不变，曲面上各点场强变化．（2）真空中一“无限大”均匀带负电荷的平面如图所示，其电场的场强分布图线应是（设场强方向向右为正、向左为负）( D )（3）关于高斯定理，下列说法中哪一个是正确的？( C )（A ）高斯面内不包围自由电荷，则面上各点电位移矢量D为零．（B ）高斯面上处处D 为零，则面内必不存在自由电荷． （C ）高斯面的D 通量仅与面内自由电荷有关．（D ）以上说法都不正确．（4）把轻的导线圈用线挂在磁铁Ｎ极附近，磁铁的轴线穿过线圈中心，且与线圈在同一平面内，如图所示．当线圈内通以如图所示方向的电流时，线圈将( B ) （A ）不动．（B ）发生转动，同时靠近磁铁． （C ）发生转动，同时离开磁铁． （D ）不发生转动，只靠近磁铁． （E ）不发生转动，只离开磁铁． （5）一个圆形线环，它的一半放在一分布在方形区域的匀强磁场B中，另一半位于磁场之外，如图所示．磁场B的方向垂直指向纸内．欲使圆线环中产生逆时针方向的感应电流，应使 ( C )（A ）线环向右平移．（B ）线环向上平移． （C ）线环向左平移． （D ）磁场强度减弱．（6）在真空中波长为λ的单色光，在折射率为ｎ的透明介质中从A 沿某路径传播到B ，若A 、B 两点位相差为3π，则此路径AB 的光程为 ( A )（A ）1.5λ． （B ）1.5ｎλ． （C ）3λ． （D ）1.5λ／ｎ．（7）一衍射光栅对某一定波长的垂直入射光，在屏幕上只能出现零级和一级主极大，欲使屏幕上出现更高级次的主极大，应该 ( B ) （A ）换一个光栅常数较小的光栅． （B ）换一个光栅常数较大的光栅． （C ）将光栅向靠近屏幕的方向移动．（D ）将光栅向远离屏幕的方向移动．（8）如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，假设二者对光无吸收，光强为I 0的自然光垂直入射在偏振片上，则出射光强为 ( A )（A ）I 0／8． （B ）3I 0／8． （C ）I 0／4． （D ）3I 0／4．（9）质量为m =0.02Kg ，速率为300m/s 子弹的德布罗意波长为 ( D ) m. (h =6.63⨯10-34) （A ）2.21⨯10-34． （B ）2.21⨯10-33． （C ）4.42⨯10-34． （D ）1.11⨯10-34．（10）已知一单色光照射在钠表面上，测得光电子的最大动能是 1.2 eV ，而钠的红限波长是5400Å，那么入射光的波长是 ( D )（A ）5350 Å． （B ）5000 Å． （C ）4350 Å． （D ）3550 Å． 二、计算题（共80分，每题10分）1、如图2-1所示，直线上有A 、B 、C 三点，A-B 点、B-C 点的距离均+Q 的正电荷，B 点放置电量为+q 的检验电荷。
大学物理2A卷附答案
大学物理2A卷附答案A 卷一、选择题（每题3分，共30分）1、轻弹簧上端固定，下系一质量为m 1的物体，稳定后在m 1下边又系一质量为m 2的物体，于是弹簧又伸长了?x ．若将m 2移去，并令其振动，则振动周期为(A) g m xm T 122?π= ． (B) g m x m T 212?π=．(C) g m x m T 2121?π=． (D) gm m xm T )(2212+π=?．［］2、一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［］-3、图中画出一平面简谐波在t = 2 s 时刻的波形图，则平衡位置在P 点的质点的振动方程是 (A) ]31)2(cos[01.0π+-π=t y P (SI)． (B) ]31)2(cos[01.0π++π=t y P (SI)． (C) ]31)2(2cos[01.0π+-π=t y P (SI)． (D) ]31)2(2cos[01.0π--π=t y P (SI)．［］ 4\一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：(A) 它的动能转换成势能． (B) 它的势能转换成动能．(C) 它从相邻的一段质元获得能量其能量逐渐增大． (D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小．［］5、在单缝夫琅禾费衍射实验中波长为λ的单色光垂直入射到单缝上．对应于衍射角为y (m)30°的方向上，若单缝处波面可分成 3个半波带，则缝宽度a 等于(A) λ．(B) 1.5 λ．(C) 2 λ．(D) 3 λ．［］ 6、自然光以60°的入射角照射到某两介质交界面时，反射光为完全线偏振光，则知折射光为(A) 完全线偏振光且折射角是30°．(B) 部分偏振光且只是在该光由真空入射到折射率为3的介质时，折射角是30°． (C) 部分偏振光，但须知两种介质的折射率才能确定折射角． (D) 部分偏振光且折射角是30°．［］7、(1)对某观察者来说，发生在某惯性系中同一地点、同一时刻的两个事件，对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说，它们是否同时发生？(2)在某惯性系中发生于同一时刻、不同地点的两个事件，它们在其它惯性系中是否同时发生？关于上述两个问题的正确答案是：(A) (1)同时，(2)不同时．(B)(1)不同时，(2)同时． (C) (1)同时，(2)同时．(D) (1)不同时，(2)不同时．［］8、在康普顿效应实验中，若散射光波长是入射光波长的1.2倍，则散射光光子能量ε与反冲电子动能E K 之比ε / E K 为(A) 2． (B) 3． (C) 4． (D) 5．［］9、根据玻尔的理论，氢原子在n =5轨道上的动量矩与在第一激发态的轨道动量矩之比为(A) 5/4． (B) 5/3．(C) 5/2． (D) 5．［］10、已知粒子在一维矩形无限深势阱中运动，其波函数为：a x ax 23cos 1)(π?=ψ, ( - a ≤x ≤a )那么粒子在x = 5a /6处出现的概率密度为(A) 1/(2a )．(B) 1/a ． (C) a 2/1． (D) a /1 ［］1、图中用旋转矢量法表示了一个简谐振动．旋转矢量的长度为0.04 m ，旋转角速度ω = 4π rad/s ．此简谐振动以余弦函数表示的振动方程为x =__________________________(SI)．2、在截面积为S 的圆管中，有一列平面简谐波在传播，其波的表达式为)]/(2cos[λωx t A y π-=，管中波的平均能量密度是w ，则通过截面积S 的平均能流是____________________________________．3、如图所示，波源S 1和S 2发出的波在P 点相遇，P 点距波源S 1和S 2的距离分别为3λ 和10 λ / 3 ，λ 为两列波在介质中的波长，若P 点的合振幅总是极大值，波源S 1 的相位比S 2 的相位领先_________________．4、用波长为λ的单色光垂直照射到空气劈形膜上，从反射光中观察干涉条纹，距顶点为L 处是暗条纹．使劈尖角θ 连续变大，直到该点处再次出现暗条纹为止．劈尖角的改变量?θ是_____________．5、一个平凸透镜的顶点和一平板玻璃接触，用单色光垂直照射，观察反射光形成的牛顿环，测得中央暗斑外第k 个暗环半径为r 1．现将透镜和玻璃板之间的空气换成某种液体(其折射率小于玻璃的折射率)，第k 个暗环的半径变为r 2，由此可知该液体的折射率为___ _____．6、用迈克耳孙干涉仪测微小的位移．若入射光波波长λ＝628.9nm ，当动臂反射镜移动时，干涉条纹移动了2048条，反射镜移动的距离d ＝________．7、波长为λ=550 nm (1nm=10-9m )的单色光垂直入射于光栅常数d =2310-4 cm 的平面衍射光栅上，可能观察到光谱线的最高级次为第________________级．8、两个偏振片叠放在一起，强度为I 0的自然光垂直入射其上，若通过两个偏振片后的光强为I 0 /8。
大学物理A2复习资料分解
波动光学1． 在真空中波长为λ的单色光，在折射率为n 的透明介质中从A 沿某路径传播到B ，若A 、B 两点相位差为3π，则此路径AB 的光程为 (A) 1.5 λ． (B) 1.5 λ/ n ．(C) 1.5 n λ． (D) 3 λ．2． 单色平行光垂直照射在薄膜上，经上下两表面反射的两束光发生干涉，如图所示，若薄膜的厚度为e ，且n 1＜n 2＞n 3，λ1为入射光在n 1中的波长，则两束反射光的光程差为 (A) 2n 2e ． (B) 2n 2 e - λ1 / (2n 1)．(C) 2n 2 e - n 1 λ1 / 2． (D) 2n 2 e - n 2 λ1 / 2．3． 在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等，走过的光程相等． (B) 传播的路程相等，走过的光程不相等． (C) 传播的路程不相等，走过的光程相等．(D) 传播的路程不相等，走过的光程不相等．4． 在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹．5． 在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是(A) 使屏靠近双缝．(B) 使两缝的间距变小． (C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．6． 在双缝干涉实验中，屏幕E 上的P 点处是明条纹．若将缝S 2盖住，并在S 1 S 2连线的垂直平分面处放一高折射率介质反射面M ，如图所示，则此时(A) P 点处仍为明条纹． (B) P 点处为暗条纹． (C) 不能确定P 点处是明条纹还是暗条纹．(D) 无干涉条纹．7． 在双缝干涉实验中，光的波长为600 nm (1 nm ＝10－9 m )，双缝间距为2 mm ，双缝与屏的间距为300 cm ．在屏上形成的干涉图样的明条纹间距为 (A) 0.45 mm ． (B) 0.9 mm ．(C) 1.2 mm (D) 3.1 mm ．8． 在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处n 1n 2n 3入射光反射光1反射光2eP EM S 1 S 2 S(A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹． 9． 在图示三种透明材料构成的牛顿环装置中，用单色光垂直照射，在反射光中看到干涉条纹，则在接触点P 处形成的圆斑为(A) 全明． (B) 全暗．(C) 右半部明，左半部暗．(D) 右半部暗，左半部明．10． 一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为 (A) λ / 4 ． (B) λ / (4n )．(C) λ / 2 ． (D) λ / (2n )． 11． 若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹(A) 中心暗斑变成亮斑． (B) 变疏．(C) 变密． (D) 间距不变．12． 用劈尖干涉法可检测工件表面缺陷，当波长为λ的单色平行光垂直入射时，若观察到的干涉条纹如图所示，每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切，则工件表面与条纹弯曲处对应的部分(A) 凸起，且高度为λ / 4． (B) 凸起，且高度为λ / 2．(C) 凹陷，且深度为λ / 2． (D) 凹陷，且深度为λ / 4．13． 如图，用单色光垂直照射在观察牛顿环的装置上．当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹(A) 向右平移． (B) 向中心收缩．(C) 向外扩张． (D) 静止不动．(E) 向左平移．14． 在迈克耳孙干涉仪的一条光路中，放入一折射率为n ，厚度为d 的透明薄片，放入后，这条光路的光程改变了(A) 2 ( n -1 ) d ． (B) 2nd ． (C) 2 ( n -1 ) d +λ / 2． (D) nd ．(F) ( n -1 ) d ．15． 在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a ＝4 λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为 (A) 2 个． (B) 4 个．(C) 6 个． (D) 8 个．P 1.521.75 1.52 图中数字为各处的折射λ 1.62 1.62平玻璃 工件 空气劈尖空气单色光16． 一束波长为λ的平行单色光垂直入射到一单缝AB 上，装置如图．在屏幕D 上形成衍射图样，如果P 是中央亮纹一侧第一个暗纹所在的位置，则BC 的长度为 (A) λ / 2．(B) λ．(C) 3λ / 2 ． (D) 2λ ．17． 根据惠更斯－菲涅耳原理，若已知光在某时刻的波阵面为S ，则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的(A) 振动振幅之和． (B) 光强之和．(C) 振动振幅之和的平方． (D) 振动的相干叠加．18． 波长为λ的单色平行光垂直入射到一狭缝上，若第一级暗纹的位置对应的衍射角为θ=±π / 6，则缝宽的大小为(A) λ / 2． (B) λ．(C) 2λ． (D) 3 λ ．19． 在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小． (B) 对应的衍射角变大．(A) 对应的衍射角也不变． (D) 光强也不变．20．在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹(A) 宽度变小； (B) 宽度变大；(C) 宽度不变，且中心强度也不变； （D ）宽度不变，但中心强度变小．21． 在如图所示的单缝夫琅禾费衍射实验装置中，S 为单缝，L 为透镜，C 为放在L 的焦面处的屏幕，当把单缝S 垂直于透镜光轴稍微向上平移时，屏幕上的衍射图样(A)向上平移． (B)向下平移． (C)不动． (D)消失．22． 测量单色光的波长时，下列方法中哪一种方法最为准确？(A) 双缝干涉． (B) 牛顿环 ．(C) 单缝衍射． (D) 光栅衍射．23． 一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是 (A) 紫光． (B) 绿光． (C) 黄光． (D) 红光．24． 对某一定波长的垂直入射光，衍射光栅的屏幕上只能出现零级和一级主极大，欲使屏幕上出现更高级次的主极大，应该(A) 换一个光栅常数较小的光栅． (B) 换一个光栅常数较大的光栅．C屏f PD LABλSCL(C) 将光栅向靠近屏幕的方向移动．(B) 将光栅向远离屏幕的方向移动．25． 一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片．若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的5倍，那么入射光束中自然光与线偏振光的光强比值为(A) 1 / 2． (B) 1 / 3．(C) 1 / 4． (D) 1 / 5． 26． 一束光强为I 0的自然光，相继通过三个偏振片P 1、P 2、P 3后，出射光的光强为I ＝I 0 / 8．已知P 1和P 2的偏振化方向相互垂直，若以入射光线为轴，旋转P 2，要使出射光的光强为零，P 2最少要转过的角度是(A) 30°． (B) 45°．(C) 60°． (D) 90°．27．一束光强为I 0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I 为 (A) 4/0I 2 ． (B) I 0 / 4．(C) I 0 / 2． (D) 2I 0 / 2．28． 三个偏振片P 1，P 2与P 3堆叠在一起，P 1与P 3的偏振化方向相互垂直，P 2与P 1的偏振化方向间的夹角为30°．强度为I 0的自然光垂直入射于偏振片P 1，并依次透过偏振片P 1、P 2与P 3，则通过三个偏振片后的光强为 (A) I 0 / 4． (B) 3 I 0 / 8．(C) 3I 0 / 32．(D) I 0 / 16．29． 两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过．当其中一偏振片慢慢转动180°时透射光强度发生的变化为： (A) 光强单调增加．(B) 光强先增加，后又减小至零． (C) 光强先增加，后减小，再增加．(C) 光强先增加，然后减小，再增加，再减小至零．30． 如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，光强为I 0的自然光垂直入射在偏振片上，则出射光强为 (A) I 0 / 8． (B) I 0 / 4．(C) 3 I 0 / 8． (D) 3 I 0 / 4．31． 一束自然光自空气射向一块平板玻璃(如图)，设入射角等于布儒斯特角i 0，则在界面2的反射光 (A) 是自然光．(B) 是线偏振光且光矢量的振动方向垂直于入射面．(C) 是线偏振光且光矢量的振动方向平行于入射面．(E) 是部分偏振光．32． 自然光以60°的入射角照射到某两介质交界面时，反射光为完全线偏振光，则知折射光为(A) 完全线偏振光且折射角是30°．i 012(B) 部分偏振光且只是在该光由真空入射到折射率为3的介质时，折射角是30°．(C) 部分偏振光，但须知两种介质的折射率才能确定折射角．(D) 部分偏振光且折射角是30°．33．自然光以布儒斯特角由空气入射到一玻璃表面上，反射光是(A) 在入射面内振动的完全线偏振光．(B) 平行于入射面的振动占优势的部分偏振光．(C) 垂直于入射面振动的完全线偏振光．(D) 垂直于入射面的振动占优势的部分偏振光．1A 2 C 3 C 4B 5B 6B 7B 8B 9D 10B11C 12C 13B 14A 15B 16B 17D 18C 19B 20B21C 22D 23D 24B 25A 26B 27B 28C 29B 30A31B 32D 33C8、在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹；(B) 变为暗条纹；(C) 既非明纹也非暗纹；(D) 无法确定是明纹，还是暗纹．9、在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变大．(B) 对应的衍射角变小．(C) 对应的衍射角也不变．(D) 光强也不变．10、三个偏振片P1，P2与P3堆叠在一起，P1与P3的偏振化方向相互垂直，P2与P1的偏振化方向间的夹角为30°．强度为I0的自然光垂直入射于偏振片P1，并依次透过偏振片P1、P2与P3，则通过三个偏振片后的光强为(A) I0 / 16．(B) 3I0 / 32．(C) 3 I0 / 8．(D) I0 / 4．5、一双缝干涉装置，在空气中观察时干涉条纹间距为1.0 mm．若整个装置放在水中，干涉条纹的间距将为____________________mm．(设水的折射率为4/3)6、在单缝夫琅禾费衍射实验中，设第一级暗纹的衍射角很小，若钠黄光(λ1≈589 nm) 中央明纹宽度为4.0 mm，则λ2=442 nm (1 nm = 10-9 m)的蓝紫色光的中央明纹宽度为____________________．7、一束平行的自然光，以60°角入射到平玻璃表面上．若反射光束是完全偏振的，则透射光束的折射角是____________________________。
大学物理_下A2 期末练习题含解答汇编
xyoa∙∙∙a-(0,)P y qq-大学物理（下A2）练习题第八章 真空中的静电场1．如图所示，在点((,0)a 处放置一个点电荷q +，在点(,0)a -处放置另一点电荷q -。
P 点在y 轴上，其坐标为(0,)y ，当y a 时，该点场强的大小为(A) 204q y πε； (B) 202q y πε；(C)302qa y πε； (D)304qa y πε.[ ]2．将一细玻璃棒弯成半径为R 的半圆形，其上半部均匀分布有电量Q +, 下半部均匀分布有电量Q -，如图所示。
求圆心o 处的电场强度。
3．带电圆环的半径为R ,电荷线密度0cos λλφ=,式中00λ>，且为常数。
求圆心O 处的电场强度。
4．一均匀带电圆环的半径为R ，带电量为Q ，其轴线上任一点P 到圆心的距离为a 。
求P 点的场强。
5．关于高斯定理有下面几种说法，正确的是(A) 如果高斯面上E 处处为零，那么则该面内必无电荷； (B) 如果高斯面内无电荷，那么高斯面上E 处处为零； (C) 如果高斯面上E 处处不为零，那么高斯面内必有电荷；(D) 如果高斯面内有净电荷，那么通过高斯面的电通量必不为零； (E) 高斯定理仅适用于具有高度对称性的电场。
[ ]6．点电荷Q 被闭合曲面S 所包围，从无穷远处引入另一点电荷q 至曲面S 外一点,如图所示，则引入前后(A) 通过曲面S 的电通量不变，曲面上各点场强不变；(B) 通过曲面S 的电通量变化，曲面上各点场强不变；(C) 通过曲面S 的电通量变化，曲面上各点场强变化；(D) 通过曲面S 的电通量不变，曲面上各点场强变化。
[ ]7．如果将带电量为q 的点电荷置于立方体的一个顶角上，则通过与它不相邻的每个侧面的电场强度通量为(A) 06q ε； (B) 012q ε； (C) 024q ε； (D) 048q ε. [ ]xq S Q8．如图所示，A 、B 为真空中两个平行的“无限大”均匀带电平面，A 面上的电荷面密度721.7718A C m σ--=-⨯⋅，B 面上的电荷面密度723.5418B C m σ--=⨯⋅。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
30-10
30-17
反方向入射
30-18
第三十一章狭义相对论 必做题 : 2，3，8，10，14，19
31-2
31-3
31-8 沿着运动方向长度收缩，则观察者看到底边变为：
静止时飞船的底角为： 三角形高为：
则观察者看到的飞船的腰为：
31-10
31-14
31-19
第32章 原子物理
32-7
28-17
第29章光的干涉 29-5
29-8
29-12
在可见光范围的是
29-14
29-16
29-26
29-27 A点：空气和油膜反射时有半波损失，2条光 线的相干为暗纹。
29-31
29-33
29-36
第30章衍射和偏振
30-1
30-5
条纹级次最大为
缺级级次为
因此级次为3的倍数的条纹看不见,m取3、6、 9……..198共66条。 一共能产生的条纹为（198-66）*2+1=265条
(c)导线在上方时要受到斥力作用，仍然和重力平衡， 通电电流也为360A。 （d）当导线向上移动时，斥力小于重力，向下运动，回到原来位置，是 稳定平衡。
第26章电磁感应（原29章）
26-2（6）
26-3（7）
26-15（22）
26-16（29）
第27章互感自感和磁场能量
27-3（3）
27-5（9）
第23章电势
23-4（14）
23-10（34）
23-12（35）
半径为R处取dR宽的圆环带，所带电量为
则x处电势为：
23-19（61）
质子和电子的电量大小相等，带正电，则质子从B点静止出发到 A点获得的动能与电子反向运动获得的动能相等，为1.33kev。
速度比值为
23-22（71）
b点到两个电荷的距离为
32-11
32-13
32-25
第33章 量子力学
33-4
33-5
24-5（10）第24章磁场（原27章）
l (2.0i)m 时， F （-2.5j ）N
l (2.0 j )m 时， F （2.5j-5.0k ）N
可求得
24-7（19）
被电场加速后获得的速度为：
洛伦兹力为
24-9（22）
24-11（25）
24-18（39）
由于自感的存在，可看做电阻和电感的 串联，电流增加，自感电流方向与原来 方向相反，则电势方向如图。
27-10（9）
第28章麦克斯韦方程组和电磁波
28-1 根据位移电流的公式可得
28-5 电场沿着Z轴负方向传输,因此传播方向为 方向
传播方向为 ,磁场沿着 方向.
28-8
28-10
28-13
28-14
第25章磁场的源（原28章）
25-6（18）
方向指向线圈
25-12（28）
25-13（31）
如图做安培环路，通电部分的电流密度分别为：
25-15（34）由图可知，C点磁场由两段圆弧产生，在圆弧上取dl 得
25-16（35）
25-24（58）
(a)如图，导线在下方时要受到引力作用，受力平衡为
（b）当导线向上移动时，引力大于重力，向上运动，不会回到原来位置， 是非稳定平衡。