高中立体几何定理及性质讲课讲稿
高中数学立体几何讲义

高中数学立体几何讲义(一)(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--平面与空间直线(Ⅰ)、平面的基本性质及其推论1、空间图形是由点、线、面组成的。
点、线、面的基本位置关系如下表所示:图形符号语言文字语言(读法) AaA a ∈ 点A 在直线a 上。
AaA a ∉点A 不在直线a 上。
AαA α∈点A 在平面α内。
AαA α∉点A 不在平面α内。
b a Aa b A =直线a 、b 交于A 点。
aαa α直线a 在平面α内。
aαa α=∅直线a 与平面α无公共点。
aAαa A α=直线a 与平面α交于点A 。
l αβ=平面α、β相交于直线l 。
α⊄a (平面α外的直线a )表示a α=∅或a A α=。
2、平面的基本性质公理1: 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内推理模式:A AB B ααα∈⎫⇒⎬∈⎭。
如图示:应用:是判定直线是否在平面内的依据,也是检验平面的方法。
BA α公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
推理模式:A l A ααββ∈⎫⇒=⎬∈⎭且A l ∈且l 唯一如图示:应用:①确定两相交平面的交线位置;②判定点在直线上。
例1.如图,在四边形ABCD 中,已知AB ∥CD ,直线AB ,BC ,AD ,DC 分别与平面α相交于点E ,G ,H ,F .求证:E ,F ,G ,H 四点必定共线. 解:∵AB ∥CD ,∴AB ,CD 确定一个平面β.又∵AB α=E ,AB ⊂β,∴E ∈α,E ∈β, 即E 为平面α与β的一个公共点.同理可证F ,G ,H 均为平面α与β的公共点.∵两个平面有公共点,它们有且只有一条通过公共点的公共直线, ∴E ,F ,G ,H 四点必定共线.说明:在立体几何的问题中,证明若干点共线时,常运用公理2,即先证明这些点都是某二平面的公共点,而后得出这些点都在二平面的交线上的结论.例2.如图,已知平面α,β,且α β=l .设梯形ABCD 中,AD ∥BC ,且AB ⊂α,CD ⊂β,求证:AB ,CD ,l 共点(相交于一点).α D C B A EFHGA证明∵梯形ABCD中,AD∥BC,∴AB,CD是梯形ABCD的两条腰.∴AB,CD必定相交于一点,设AB CD=M.又∵AB⊂α,CD⊂β,∴M∈α,且M∈β.∴M∈α β.又∵α β=l,∴M∈l,即AB,CD,l共点.说明:证明多条直线共点时,一般要应用公理2,这与证明多点共线是一样的.公理3:经过不在同一条直线上的三点,有且只有一个平面。
高中数学教学备课教案立体几何的基本概念和性质

高中数学教学备课教案立体几何的基本概念和性质高中数学教学备课教案立体几何的基本概念和性质导言:立体几何是数学中的一个重要分支,它研究了三维空间中的几何形体及其属性。
本教案旨在通过教师备课,系统地介绍立体几何的基本概念和性质,并提供一些教学策略和资源。
一、基本概念在开始讲解立体几何之前,我们首先要了解一些基本概念。
下面将介绍几个常用的基本概念。
1. 空间和立体空间是三维几何学的基本对象,我们生活的世界就是一个三维空间。
而立体是空间中的一个特殊对象,它具有长度、宽度和高度三个维度。
常见的立体包括立方体、圆柱体、圆锥体、球体等。
2. 面面是指立体几何中的二维表面,它由一组相互连接的线段组成。
在立体几何中,常见的面有底面、侧面和顶面等。
3. 边和顶点边是指立体几何中连接两个点的线段,它是立体的构造要素之一。
而顶点是指立体几何中的一个尖点,它是多条边的交汇点。
4. 直线、射线和线段直线是由无数个点连成的,它没有起点和终点。
射线是由一个起点出发,并延伸至无穷远的线段。
线段是由两个端点和之间的所有点组成。
5. 平行和垂直平行是指在同一个平面中,两条直线或线段永远不会相交。
垂直是指两条直线或线段在相交处的夹角为90度。
二、基本性质除了基本概念外,了解立体几何的基本性质也是非常重要的。
下面将介绍几个与立体几何相关的基本性质。
1. 体积和表面积体积是指立体几何中所包含的三维空间的大小。
通常用单位立方米(m³)来表示。
而表面积是指立体几何的外部各个面的总面积。
常见的计量单位有平方米(m²)。
2. 图形的投影立体几何中,当一个立体体块投影到一个平面上时,得到的图形被称为该立体体块在该平面上的投影。
常见的投影有俯视图、侧视图和正视图等。
3. 空间角空间角是指由两个非平行线段所夹的角度。
例如,两条直线的夹角就是一个空间角。
空间角的大小可以通过角度或弧度来表示。
4. 空间位置关系在立体几何中,各个面、边和顶点之间有着特定的位置关系。
(完整word版)高中数学立体几何讲义(二)

空间中的垂直关系I、直线与平面垂直1线面垂直定义:如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面互相垂直.其中直线叫做平面的垂线,平面叫做直线的垂面。
交点叫做垂足。
直线与平面垂直简称线面垂直,记作:a丄a。
2、直线与平面垂直的判定方法:①利用定义。
②判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
③其它方法:(I)、如果两条平行直线中的一条垂直于一个平面,那么另一条直线也垂直于这个平面。
(n)、如果一条直线垂直于两个平行平面中的一个,那么也垂直于另一个面。
(川)、如果两个平面互相垂直,那么在一个平面内垂直于他们交线的直线垂直于另一个平面。
(W)、如果两个相交平面都和第三个平面垂直,那么相交平面的交线也垂直于第三个方面。
3、直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
4、三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的投影垂直,那么它也和这条斜线垂直。
说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;PO ,OPAI A a PAa , a OA5、三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的投影垂直。
aAPO ,O PAI A a AOa , a AP练习:1若a,b,c 表示直线,表示平面,下列条件中,能使 a 的是 (D )(A) a b, a c,b , c (B)a b,b//(C)aI b A, b, a b(D) a//b,b2 .已知 l 与m 是两条不同的直线,若直线 1平面,①若直线m l ,则m 〃;②若m,则m//l ;③若m,则m l:④ m//l ,则 m。
上述判断正确的是 (B)(A)①②③(B)②③④(C)①③④ (D)②④3.设三棱锥P ABC 的顶点P 在平面ABC 上的射影是H ,给出以下命题:① 若PA BC ,PB AC ,则H 是 ABC 的垂心② 若PA, PB,PC 两两互相垂直,则 H 是 ABC 的垂心 ③ 若 ABC 90°,H 是AC 的中点,贝U PA PB PC ④ 若PA PB PC ,则H 是 ABC 的外心其中正确命题的命题是 _①②③④ ________________例1、 已知PA ^O O 所在的平面,AB 是O O 的直径,C 是O O 上任意一点,过 A 点作AE ± PC 于点E ,求证:AE ±平面PBC证明:••• PAL 平面 ABC 二PA !BG 又T AB 是O O 的直径,二BC 丄AG 而PC A AC=C ••• BC 丄平面 PAC 又T AE 在平面 PAC 内,二BC 丄AE= •/ PC 丄 AE,且 PC n BC=C • AE!平面 PBC[反思归纳]证明直线与平面垂直的常用方法有:利用线面垂直的定义; 利用线面垂直的判定定理;利用"若直线a //直线b ,直线a 丄平面a,则直线 b 丄平面a”P KC例2、在直三棱柱ABC-A i BQ 中,BC =A C, A B± AC,求证:A i B±B G证明:取A i B 的中点D,连结C i D。
高一数学立体几何讲义

I. 基础知识要点一、 平面.1. 经过不在同一条直线上的三点确定一个面.注:两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将空间分成3或4部分.(①两个平面平行,②两个平面相交)3. 过三条互相平行的直线可以确定1或3个平面.(①三条直线在一个平面内平行,②三条直线不在一个平面内平行)[注]:三条直线可以确定三个平面,三条直线的公共点有0或1个.4. 三个平面最多可把空间分成 8 部分.(X 、Y 、Z 三个方向)二、 空间直线.1. 空间直线位置分三种:相交、平行、异面. 相交直线——共面有且仅有一个公共点;平行直线——共面没有公共点;异面直线——不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行,也可能是点和直线等)②直线在平面外,指的位置关系:平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形) ⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段)⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图).(二面角的取值范围[) 180,0∈θ) (直线与直线所成角(] 90,0∈θ)(斜线与平面成角() 90,0∈θ)(直线与平面所成角[] 90,0∈θ) 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.5. 两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线)②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线) 12方向相同12方向不相同③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交)⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面)⑦直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理), 得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA .● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.[注]:①垂直于同一平面....的两个平面平行.(×)(可能相交,垂直于同一条直线.....的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上四、 平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.P OA a P αβ推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.证明:如图,找O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形......②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×)(直棱柱不能保证底面是钜形可如图)②(直棱柱定义)棱柱有一条侧棱和底面垂直.[注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形) ④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)2. 棱锥: [注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V Sh V ==.⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)3. 球:⑴球的截面是一个圆面.①球的表面积公式:24R S π=. ②球的体积公式:334R V π=. 附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥形体积:Sh V 31=(S 为底面积,h 为高) 侧面积公式S 直棱柱侧=ch ( c -底面周长,h -高 )S 正棱锥侧=1/2 ch ( c -底面周长,h -斜高 )S 正棱台侧=1/2 (c +c')h (c ,c'-上、下底面周长,h -斜高)S 圆柱侧=cl =2πrl (c -底面周长,l -母线长 ,r -底面半径) S 圆锥侧=1/2cl =πrl (c -底面周长,l -母线长 ,r -底面半径) S 圆台侧=1/2(c +c')l =π(r +r')l(c ,c' -上、下底面周长,r ,r -上、下底面半径)体积公式V 柱体=Sh ( S -底面积,h -高 )V 椎体=1/3Sh ( S -底面积,h -高 )()h ss s s V '31'++=台体 (S ,S -上下底面积,h -高 ) 3R 34π=球V (R 为球的半径) 24R S π=球。
数学课教案立体几何的基本概念和性质

数学课教案立体几何的基本概念和性质教案:数学课教案立体几何的基本概念和性质引言:数学是一门抽象而严谨的学科,它不仅可以培养学生的逻辑思维和分析问题的能力,还可以增强学生的空间想象力。
而立体几何作为数学的一个分支,对于学生来说,既具有理论性又具有实践性。
本节课主要介绍立体几何的基本概念和性质,通过学习,让学生了解立体几何的基本知识和应用。
一、了解立体几何的基本概念在开始学习立体几何之前,我们首先要了解一些基本概念,这样才能更好地理解立体几何的内容。
1. 点、线、面的概念和关系点是几何学的基本要素,没有大小和方向的概念。
线是由无数个点组成,有长度和方向的概念。
而面则是由无数个线段组成,有长度、宽度和方向的概念。
点、线、面是立体几何的基本构成要素,它们之间有着密切的联系和关系。
2. 立体几何的基本体立体几何的基本体主要包括球体、圆锥、圆柱、棱锥、棱柱等。
每个基本体都有其独特的性质和特点,我们需要通过实例来了解它们。
3. 立体几何的基本要素立体几何的基本要素主要包括面积、体积、表面积和侧面积等。
不同的基本要素有着不同的计算方式和应用场景。
二、探索立体几何的性质1. 球体的性质球体是立体几何中的一种基本体,它具有许多特殊的性质和规律。
通过观察实例和推理分析,学生将会发现球体的表面积和体积的计算公式,并且学会在实际问题中应用。
2. 圆锥的性质圆锥也是常见的一种基本体,它由一个圆锥顶点和一个底面组成。
通过观察不同形状的圆锥,学生可以总结出圆锥的性质和特点,并学会应用圆锥的计算公式。
3. 圆柱的性质圆柱是立体几何中最有代表性的基本体之一,它具有许多重要的性质和应用。
通过观察不同形状的圆柱,学生可以总结出圆柱的性质和特点,并学会应用圆柱的计算公式。
4. 棱锥和棱柱的性质棱锥和棱柱是由平面多边形组成的立体体,它们有着丰富的性质和特点。
通过观察不同形状的棱锥和棱柱,学生可以总结出它们的性质和特点,并学会应用相应的计算公式。
高中立体几何八大定理知识讲解
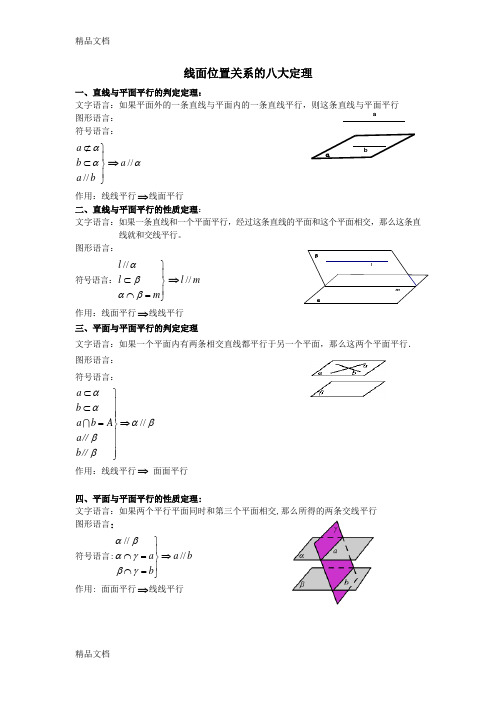
五、直线与平面垂直的判定定理:
文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面
图形语言:
符号语言:
现在是个飞速发展的时代,与时俱进的大学生当然也不会闲着,在装扮上也不俱一格,那么对作为必备道具的饰品多样性的要求也就可想而知了。作用:线线垂直 线面垂直
符号语言:
作用:线面平行 线线平行
三、平面与平面平行的判定定理
文字语言:如果一个平面内有平行.
图形语言:
符号语言:
作用:线线平行 面面平行
四、平面与平面平行的性质定理:
文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行
图形语言:
符号语言:
秘诀:好市口+个性经营
六、直线与平面垂直的性质定理:
文字语言:若两条直线垂直于同一个平面,则这两条直线平行
3、你是否购买过DIY手工艺制品?图形语言:
十字绣□编制类□银饰制品类□串珠首饰类□符号语言:
6、你购买DIY手工艺制品的目的有那些?作用:线面垂直 线线平行
七、平面与平面垂直的判定定理:
(2)缺乏经营经验文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
(四)DIY手工艺品的“个性化”图形语言:
而手工艺制品是一种价格适中,不仅能锻炼同学们的动手能力,同时在制作过程中也能体会一下我国传统工艺的文化。无论是送给朋友还是亲人都能让人体会到一份浓厚的情谊。它的价值是不用金钱去估价而是用你一颗真诚而又温暖的心去体会的。更能让学生家长所接受。符号语言:
作用:面面垂直 线面垂直
十字绣□编制类□银饰制品类□串珠首饰类□ 图形语言:
符号表示:
开了连锁店,最大的好处是让别人记住你。“漂亮女生”一律采用湖蓝底色的装修风格,简洁、时尚、醒目。“品牌效应”是商家梦寐以求的制胜法宝。注:线面垂直 面面垂直
高中数学讲义 第七章 立体几何初步(超级详细)
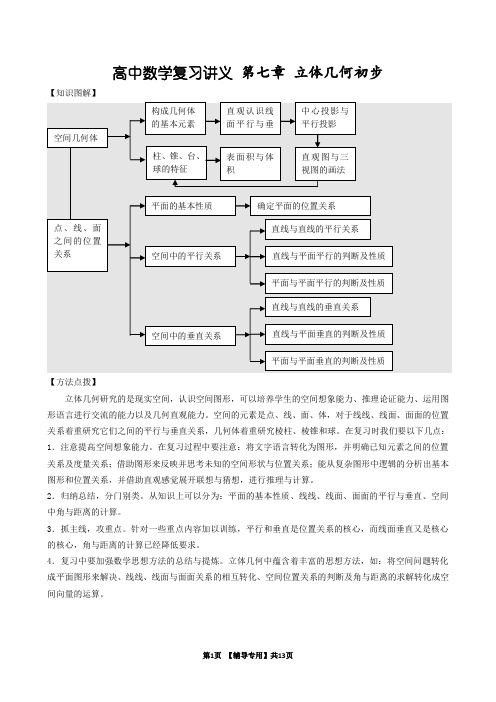
分析:证明两条直线异面通常采用反证法。
证明:(1)(反证法)假设AC与BD不是异面直线,则AC与BD共面,
所以A、B、C、D四点共面
这与空间四边形ABCD的定义矛盾
所以对角线AC与BD是异面直线
(2)解:∵E,F分别为AB,BC的中点,∴EF//AC,且EF= AC.
(1)求圆锥的母线与底面所成的角;
(2)求圆锥的全面积.
解: (1)设圆锥的底面半径为R,母线长为l,
由题意得: ,
即 ,
所以母线和底面所成的角为
(2)设截面与圆锥侧面的交线为MON,
其中O为截面与AC的交点,则OO1//AB且
在截面MON内,以OO1所在有向直线为y轴,O为原点,建立坐标系,
则O为抛物线的顶点,所以抛物线方程为x2=-2py,
同理HG//AC,且HG= AC.∴EF平行且相等HG,∴EFGH是平行四边形.
又∵F,G分别为BC,CD的中点,∴FG//BD,∴∠EFG是异面直线AC与BD所成的角.
∵AC⊥BD,∴∠EFG=90o.∴EFGH是矩形.
(3)作法取BD中点E,AC中点F,连EF,则EF即为所求.
点评:在空间四边形中我们通常会遇到上述类似的问题,取中点往往是很有效的方法,特别是遇到等腰三角形的时候。
3.抓主线,攻重点。针对一些重点内容加以训练,平行和垂直是位置关系的核心,而线面垂直又是核心的核心,角与距离的计算已经降低要求。
4.复习中要加强数学思想方法的总结与提炼。立体几何中蕴含着丰富的思想方法,如:将空间问题转化成平面图形来解决、线线、线面与面面关系的相互转化、空间位置关系的判断及角与距离的求解转化成空间向量的运算。
高中数学教案立体几何的基本概念和性质

高中数学教案立体几何的基本概念和性质高中数学教案:立体几何的基本概念和性质导语:立体几何是数学中的一个重要分支,涉及到空间中的各种图形和体形。
本教案旨在介绍立体几何的基本概念和性质,帮助学生全面理解并掌握相关知识。
一、点、线、面的区别和联系在几何中,点、线、面是构成立体的基本要素。
点是没有长度、宽度和高度的,线是由无数个点连在一起形成,面是由无数条线相互平行或相交组成的。
点、线和面之间有着密切的联系,点可以确定一条线,线可以确定一个面,而面可以包含无数个点和线。
二、立体几何的基本概念1. 多面体多面体是指由平面多边形围成的立体图形。
常见的多面体有正方体、长方体、正六面体等。
多面体由若干个面、边和顶点组成。
2. 面的种类在立体几何中,面分为底面、侧面和顶面。
底面是多面体的一个平面,通常用于支撑整个多面体。
侧面是由底面和顶面的边所组成,可以理解为多面体的侧边。
顶面则是多面体的最上方的一个面。
3. 棱的种类棱是由多面体的两个顶点所确定的线段,不同多面体中的棱有不同的名称。
常见的棱有边棱、对棱和斜棱等。
4. 顶点与对顶点多面体的顶点是多条棱相交的地方,一个多面体通常有多个顶点。
对顶点是指多面体中,关于某条线段对称的两个顶点。
三、立体几何的基本性质1. 和等在立体几何中,相同形状和大小的多面体可以做加法。
即两个相同形状和大小的多面体放在一起时,它们的体积等于两个多面体的体积之和。
2. 是等角当两个多面体的相应对面之间的夹角相等时,它们是等角的。
等角的多面体,虽然形状可能不同,但是它们的面之间的夹角是相等的。
3. 是等积当两个多面体的相应面积相等时,它们是等积的。
等积的多面体,虽然形状可能不同,但是它们的面积是相等的。
4. 是全等当两个多面体的相应面积和相应夹角都相等时,它们是全等的。
全等的多面体,不仅形状相同,而且各个对应部分的大小相等。
5. 是轴对称轴对称是指多面体中存在一个直线,使得直线两侧的图形关于该直线完全对称,即一个图形可以通过旋转180度绕着直线得到另一个图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中立体几何定理及
性质
高中立体几何定理及性质
一、公理及其推论
文字语言符号语言图像语言作用公理1
如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
α
α
α
⊂
⇒
∈
∈
∈
∈
l
B
A
l
B
l
A,
,
,①用来验证直
线在平面内;
②用来说明平
面是无限延展
的
公理2
如果两个平面有
一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)
l
l
P
∈
=
⋂
⇒
⋂
∈
P
且
β
α
β
α
①用来证明两
个平面是相交
关系;
②用来证明多
点共线,多线
共点。
公理3
经过不在同一条直线上的三点,有且只有一个平面
确定一个平面
不共线
C
B
A
C
B
A
,
,
,
,
⇒
用来证明多点
共面,多线共
面
推论1
经过一条直线和
这条直线外的一点,有且只有一个平面
α
α
α
α
⊂
∈
⇒
∉
a
A
A
,
使
,有且只有一个平面
推论2
经过两条相交直
线,有且只有一个平面
α
α
α
⊂
⊂
⇒
=
⋂
b
a
P
b
a
,
使
,有且只有一个平面
推论3
经过两条平行直
线,有且只有一个平面
α
α
α
⊂
⊂
⇒
b
a
b
a
,
使
,有且只有一个平面
∥
公理4 (平行公理)
平行于同一条直线的两条直线平行
c
a
c
b
b
a
∥
∥
∥
⇒
⎭
⎬
⎫用来证明线线
平行
二、平行关系
文字语言符号语言图像语言作用
(1)公理4 (平行公理)平行于同一条直线的两条直线平行
c
a
c
b
b
a
∥∥
∥
⇒
⎭
⎬
⎫
(2)线面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
αα
α∥∥
a
b
a
b
a
⇒
⎪
⎭
⎪
⎬
⎫
⊂
⊄
(3)线面平行
的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
b
a
a
b
b
∥∥
⇒
⎪
⎭
⎪
⎬
⎫
⊂
=
⋂
β
β
α
β
(4)面面平行的判定定理
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
β
α
α
α
β
β
∥∥
∥
⇒
⎪
⎪
⎪
⎭
⎪⎪
⎪
⎬
⎫
⊂
⊂
=
⋂
b
a
O
b
a
b
a
(5)面面平行的判定如果两个
β
α
β
α
∥
⇒
⎭
⎬
⎫
⊥
'
⊥
'
O
O
O
O
平面垂直于同一条直线,那么这两个平面平行。
(6)面面平行
的性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
b
a
b
a∥∥
⇒
⎪
⎭
⎪
⎬
⎫
=
⋂
=
⋂
γ
β
γ
α
β
α
(7)面面平行的性质如果两个平面平行,那么其中一个平面内的直线平行于另一个平面。
βα
β
α
∥∥
a
a
⇒
⎭
⎬
⎫
⊂
(8)面面平行
的性质如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面。
βα
β
α
⊥
⇒
⎭
⎬
⎫
⊥
l
l
∥
(9)面面平行的性质
平行于同一个平面的两个平面平行。
γ
α
γ
β
β
α
∥∥
∥
⇒
⎭
⎬
⎫
三、垂直关系
文字语言符号语言图像语言作用(10)三垂线定理
在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直
PO
a
a
AO
a
O
PO
PA
⊥
⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⊂
⊥
=
⋂
⊥
α
α
α
(11)三垂线定理的
逆定理
在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂
AO
a
a
PO
a
O
PO
PA
⊥
⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⊂
⊥
=
⋂
⊥
α
α
α
直.
(12)线面垂直的判定定理
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
αα
α
⊥
⇒
⎪
⎪
⎪
⎭
⎪⎪
⎪
⎬
⎫
⊂
⊂
=
⋂
⊥
⊥
l
n
m
B
n
m
n
l
m
l
(13)线面垂直的判定
如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面
αα
⊥
⇒
⎭
⎬
⎫
⊥
b
a
b
a∥
(14)线面垂直的性质定理如果两条直线同垂直于一个平面,那么这两条直线平行。
b
a
b
a
∥
⇒
⎭
⎬
⎫
⊥
⊥
α
α
(15)线面垂直的性
质
如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线
b
a
b
a∥∥
⇒
⎪
⎭
⎪
⎬
⎫
=
⋂
=
⋂
γ
β
γ
α
β
α
(16)面面垂直的判定定理
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
β
α
β
α
⊥
⇒
⎭
⎬
⎫
⊂
⊥
AB
AB
(17)面面垂直的性
质定理
如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
α
β
β
α
β
α
⊥
⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⊂
⊥
=
⋂
⊥
AB
AB
CD
AB
CD
最小角定理
斜线和平面所成的角,是这条斜线和这个平面内的直线
所成的一切角中最小的角,且有21cos cos cos θθθ⋅= (其中21,,θθθ如图中所示)。
