高中数学《立体几何》重要公式、定理
立体几何基本定理与公式
立几基本公式空间直线.1. 空间直线位置分三种：相交、平行、异面.相交直线—共面有且有一个公共点；平行直线—共面没有公共点；异面直线—不同在任一平面内2. 异面直线判定定理：过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）3. 平行公理：平行于同一条直线的两条直线互相平行.4. 等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等（如下图）.（二面角的取值范围[)οο180,0∈θ） （直线与直线所成角(]οο90,0∈θ） （斜线与平面成角()οο90,0∈θ）（直线与平面所成角[]οο90,0∈θ）（向量与向量所成角])180,0[οο∈θ推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角（或直角）相等.5. 两异面直线的距离：公垂线的长度. 一、直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种：相交、平行、在平面内.2. 直线与平面平行判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和这个平面平行.（“线线平行，线面平行”）3. 直线和平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行，线线平行”）4. 直线与平面垂直是指直线与平面任何一条直线垂直，过一点有且只有一条直线和一个平面12方向相同12方向不相同POAa垂直，过一点有且只有一个平面和一条直线垂直.若PA⊥α，a⊥AO，得a⊥PO（三垂线定理），得不出α⊥PO. 因为a⊥PO，但PO不垂直OA.三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一：如果一条直线和一个平面内的两条相交直线都垂直，那么这两条直线垂直于这个平面.（“线线垂直，线面垂直”）直线与平面垂直的判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.推论：如果两条直线同垂直于一个平面，那么这两条直线平行.5. ⑴垂线段和斜线段长定理：从平面外一点．．向这个平面所引的垂线段和斜线段中，①射影相等的两条斜线段相等，射影较长的斜线段较长；②相等的斜线段的射影相等，较长的斜线段射影较长；③垂线段比任何一条斜线段短.⑵射影定理推论：如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上一、平面平行与平面垂直.1. 空间两个平面的位置关系：相交、平行.2. 平面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行.（“线面平行，面面平行”）推论：垂直于同一条直线的两个平面互相平行；平行于同一平面的两个平面平行.[注]：一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理：如果两个平面平行同时和第三个平面相交，那么它们交线平行.（“面面平行，线线平行”）4. 两个平面垂直性质判定一：两个平面所成的二面角是直二面角，则两个平面垂直.两个平面垂直性质判定二：如果一个平面与一条直线垂直，那么经过这条直线的平面垂直于这个平面.（“线面垂直，面面垂直”）注：如果两个二面角的平面对应平面互相垂直，则两个二面角没有什么关系.5. 两个平面垂直性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论：如果两个相交平面都垂直于第三平面，则它们交线垂直于第三平面.五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积：Ch S =（C 为底面周长，h 是高）②斜棱住侧面积：l C S 1=（1C 是斜棱柱直截面周长，l 是斜棱柱的侧棱长） ⑵{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱柱}⊃{正方体}. {直四棱柱}⋂{平行六面体}={直平行六面体}.⑶棱柱具有的性质：①棱柱的各个侧面都是平行四边形，所有的侧棱都相等；直棱柱的各个侧面都是矩形．．．．．．．．；正棱柱的各个侧面都是全等的矩形．．．．．. ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等．．多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形. （直棱柱定义）：棱柱有一条侧棱和底面垂直. ⑷平行六面体：定理一：平行六面体的对角线交于一点．．．．．．．．．．．．．，并且在交点处互相平分. [注]：四棱柱的对角线不一定相交于一点.定理二：长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和. [注]：①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥；所以棱柱棱柱3V S h V ==.正棱锥定义：底面是正多边形；顶点在底面的射影为底面的中心.[注]：i. 正四棱锥的各个侧面都是全等的等腰三角形.（不是等边三角形）PαβθM AB Oii. 正四面体是各棱相等，而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论：若一个棱锥的各个侧面都是全等的等腰三角形（即侧棱相等）；底面为正多边形. 正棱锥的侧面积：'Ch 21S =（底面周长为C ，斜高为'h ） ⑵棱锥具有的性质：①正棱锥各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高相等（它叫做正棱锥的斜高）.②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形，正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.3. 球：⑴球的截面是一个圆面.①球的表面积公式：24R S π=. ②球的体积公式：334R V π=.②圆锥体积：h r V 231π=（r 为半径，h 为高）③锥形体积：Sh V 31=（S 为底面积，h 为高）六. 空间向量.1（1）共线向量：共线向量亦称平行向量，指空间向量的有向线段所在直线互相平行或重合. （2）共线向量定理：对空间任意两个向量)0(,≠b b a ，a ∥b 的充要条件是存在实数λ（具有唯一性），使λ=.（3）共面向量：若向量a 使之平行于平面α或a 在α内，则a 与α的关系是平行，记作a ∥α. （4）①共面向量定理：如果两个向量b a ,不共线，则向量与向量b a ,共面的充要条件是存在实数对x 、y 使y x +=.②空间任一点．．．O ．和不共线三点．．．．．．A ．、．B ．、．C ．，则)1(=++++=z y x OC z OB y OA x OP 是PABC 四点共面的充要条件.（简证：→+==++--=AC z AB y AP OC z OB y OA z y OP )1(P 、A 、B 、C 四点共面）注： 是证明四点共面的常用方法.2. 空间向量基本定理：如果三个向量．．．．c b a ,,不共面．．．，那么对空间任一向量P ，存在一个唯一的有序实数组x 、y 、z ，使c z b y a x p ++=.推论：设O 、A 、B 、C 是不共面的四点，则对空间任一点P , 都存在唯一的有序实数组x 、y 、z使 z y x ++=(这里隐含x +y+z≠1).注：设四面体ABCD 的三条棱，,,,d AD c AC b AB ===其中Q 是△BCD 的重心，则向量)(31c b a AQ ++=用MQ AM AQ +=即证.3. （1）空间向量的坐标：空间直角坐标系的x 轴是横轴（对应为横坐标），y 轴是纵轴（对应为纵轴），z 轴是竖轴（对应为竖坐标）. ①令a =(a 1,a 2,a 3),),,(321b b b =，则),,(332211b a b a b a b a ±±±=+))(,,(321R a a a a ∈=λλλλλ332211b a b a b a b a ++=⋅a ∥)(,,332211Rb a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔ 0332211=++⇔⊥b a b a b a b a222321a a a ++==(a a =⇒⋅=) 232221232221332211||||,cos b b b a a a b a b a b a b a ba b a ++⋅++++=⋅⋅>=<ρρρρρρ②空间两点的距离公式：212212212)()()(z z y y x x d -+-+-=.（2）法向量：若向量a 所在直线垂直于平面α，则称这个向量垂直于平面α，记作α⊥a ，如果α⊥那么向量叫做平面α的法向量. （3）用向量的常用方法：①利用法向量求点到面的距离定理：如图，设n 是平面α的法向量，AB 是平面α的一条射线，其中α∈A ，则点B 到平面α②利用法向量求二面角的平面角定理：设21,n n 分别是二面角βα--l 中平面βα,的法向量，DCBAB则21,n n 所成的角就是所求二面角的平面角或其补角大小（21,n n 方向相同，则为补角，21,n n 反方，则为其夹角）.③证直线和平面平行定理：已知直线≠⊄a 平面α，α∈⋅∈⋅D C a B A ,，且CDE 三点不共线，则a ∥α的充要条件是存在有序实数对μλ⋅使CE CD AB μλ+=.（常设CE CD AB μλ+=求解μλ,若μλ,存在即证毕，若μλ,不存在，则直线AB 与平面相交）.。
立体几何所有的定理大总结（绝对全）
⽴体⼏何所有的定理⼤总结（绝对全）（⼆）异⾯直线所成⾓1.定义：不同在任何⼀个平⾯内的两条直线或既不平⾏也不相交的两条直线叫异⾯直线。
2.画法：借助辅助平⾯。
1.定义：对于异⾯直线a 和b ，在空间任取⼀点P ，过P 分别作a 和b 的平⾏线1a 和1b ，我们把1a 和1b 所成的锐⾓或者叫做异⾯直线a 和b 所成的⾓。
2.范围：(0°，90°】(★空间两条直线所成⾓范围：【0°，90°】)（三）线⾯⾓1.定义：当直线l 与平⾯α相交且不垂直时，叫做直线l 与平⾯α斜交，直线l 叫做平⾯α的斜线。
设直线l 与平⾯α斜交与点M ，过l 上任意点A ，做平⾯α的垂线，垂⾜为O ，把点O 叫做点A 在平⾯α上的射影，直线OM 叫做直线l 在平⾯α上的射影。
1.定义：把直线l 与其在平⾯α上的射影所成的锐⾓叫做直线l 和平⾯α所成的⾓。
2.范围【0°，90°】（★斜线与平⾯所成⾓范围：【0°，90°】）（三）⼆⾯⾓1.定义：（1）半平⾯：平⾯内的⼀条直线把这个平⾯分成两个部分，其中每⼀个部分叫做半平⾯。
（3）⼆⾯⾓的棱：这⼀条直线叫做⼆⾯⾓的棱。
（4）⼆⾯⾓的⾯：这两个半平⾯叫做⼆⾯⾓的⾯。
（5）⼆⾯⾓的平⾯⾓：以⼆⾯⾓的棱上任意⼀点为端点，在两个⾯内分别作垂直于棱的两条射线，这两条射线所成的⾓叫做⼆⾯⾓的平⾯⾓。
（6）直⼆⾯⾓：平⾯⾓是直⾓的⼆⾯⾓叫做直⼆⾯⾓。
1.定义：从⼀条直线出发的两个半平⾯所组成的图形叫做⼆⾯⾓。
2.表⽰：如下图，可记作α-AB-β或P-AB-Q3.范围为【0°，180°】（五）六种距离1.点到点的距离：两点之间的线段PQ 的长。
2.点到线的距离：过P 点作1PP ⊥l ，交l 于1P ，线段1PP 的长。
3.点到⾯的距离：过P 点作1PP ⊥α，交α于1P ，线段1PP 的长。
高中数学必背公式——立体几何与空间向量
〔1〕求点 到直线 的距离；〔2〕求点 到平面 的距离。
例14：如图，正方形 与 成 的二面角，且正方形的边长为 ， 、 分别为 ， 的中点，求异面直线 与 的距离。
例15：如图，四棱锥P-ABCD的底面是正方形，
，求异面直线AB与PC的距离。
例16：已知 是底面边长为 的正四棱柱， 为 与 的交点．
底面 为梯形， ， ． ，
点 在棱 上，且 ．
〔1〕求证：平面 ⊥平面 ；
〔2〕求证： ∥平面 ；
〔3〕求平面 和平面 所成锐二面角的余弦值．
例10：已知四棱锥 的底面为直角梯形， ， 底面 ，
且 ， 是 的中点。
〔1〕证明：面 ⊥面 所成二面角的余弦值。
高中数学必背公式——立体几何与空间向量
知识点复习：
1.空间几何体的三视图“长对正、高平齐、宽相等〞的规律。
2.在计算空间几何体体积时注意割补法的应用。
3.空间平行与垂直关系的关系的证明要注意转化：
线线平行 线面平行 面面平行，线线垂直 线面垂直 面面垂直。
4．求角：〔1〕异面直线所成的角：
可平移至同一平面；也可利用空间向量： =
方法二：向量法：二面角 的平面角 或
〔 ， 为平面 ， 的法向量〕.
5. 求空间距离：
〔1〕点与点的距离、点到直线的距离，一般用三垂线定理“定性〞；
〔2〕两条异面直线的距离： 〔 同时垂直于两直线， 、 分别在两直线上〕；
〔3〕求点面距： 〔 为平面 的法向量， 是经过面 的一条斜线， 〕；
〔3〕线面距、面面距都转化为点面距。
A． B． C． D．
题型二：空间点、线、面位置关系的判断
例4：已知 、 是不重合的直线， 和 是不重合的平面，有下列命题：
高一数学必修2立体几何知识点详细总结
立体几何一、立体几何网络图：（1）线线平行的判断：⑴平行于同一直线的两直线平行。
⑶如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。
⑹如果两个平行平面同时和第三个平面相交，那么它们的交线平行。
⑿垂直于同一平面的两直线平行。
（2）线线垂直的判断：⑺在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。
⑻在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直。
⑽若一直线垂直于一平面，这条直线垂直于平面内所有直线。
补充：一条直线和两条平行直线中的一条垂直，也必垂直平行线中的另一条。
（3）线面平行的判断：⑵如果平面外的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。
⑸两个平面平行，其中一个平面内的直线必平行于另一个平面。
（4）线面垂直的判断：⑼如果一直线和平面内的两相交直线垂直，这条直线就垂直于这个平面。
⑾如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面。
⒁一直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。
⒃如果两个平面垂直，那么在—个平面内垂直于交线的直线必垂直于另—个平面。
（5）面面平行的判断：⑷一个平面内的两条相交直线分别平行于另一个平面，这两个平面平行。
⒀垂直于同一条直线的两个平面平行。
（6）面面垂直的判断：⒂一个平面经过另一个平面的垂线，这两个平面互相垂直。
二、其他定理：（1）确定平面的条件：①不公线的三点；②直线和直线外一点；③相交直线；（2）直线与直线的位置关系：相交；平行；异面；直线与平面的位置关系：在平面内；平行；相交（垂直是它的特殊情况）；平面与平面的位置关系：相交；；平行；（3）等角定理：如果两个角的两边分别平行且方向相同，那么这两个角相等；如果两条相交直线和另外两条相交直线分别平行，那么这两组直线所成的锐角(或直角)相等；（4）射影定理（斜线长、射影长定理）：从平面外一点向这个平面所引的垂线段和斜线段中，射影相等的两条斜线段相等；射影较长的斜线段也较长；反之，斜线段相等的射影相等；斜线段较长的射影也较长；垂线段比任何一条斜线段都短。
立体几何常考定理的总结(八大定理)
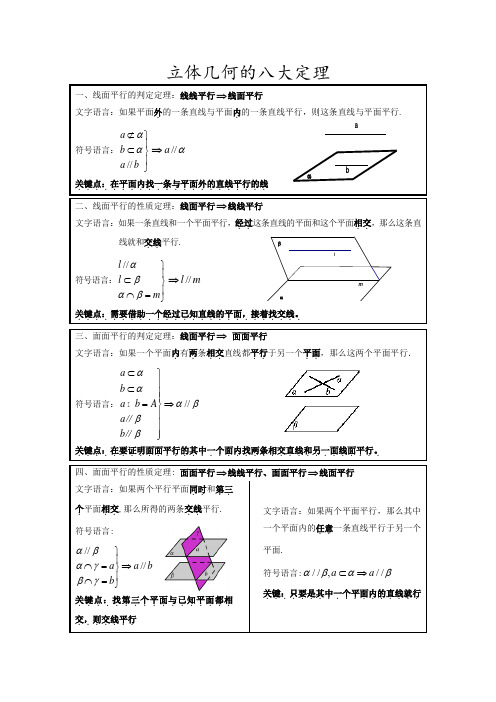
lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点：在平面内找一条与平面外的直线平行的线．．．．．．．．．．．．．．．．．．．．．． 二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要借助一个经过已知直线的平面，接着找交线。
．．．．．．．．．．．．．．．．．．．．．．．．．． 三、面面平行的判定定理：线面平行⇒ 面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行． 符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点：找第三个平面与已知平面都相．．．．．．．．．．．．．．．．．交，则交线平行．．．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．nmAαaBA l βαaβα五、线面垂直的判定定理：线线垂直⇒线面垂直文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面. 符号语言：,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．． 六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．． 七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点：．．．．在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。
高中数学立体几何知识点归纳总结
③正棱锥中六个元素,即侧棱、高、斜高、侧棱在底面内的射影、斜高在底面的射影、底面边
长一半,构成四个直角三角形;如上图： SOB, SOH, SBH, OBH 为直角三角形
3.3 侧面展开图：正 n 棱锥的侧面展开图是有 n 个全等的等腰三角形组成的;
3.4
面积、体积公式：S
正棱锥侧=
1 2
ch
,S
正棱锥全=
推论 2：两条相交直线确定一个平面. 图形语言：
推论 3：两条平行直线确定一个平面. 图形语言：
用途：用于确定平面;
公理 3：如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线两个
平面的交线.
用途：常用于证明线在面内,证明点在线上.
图形语言：
符号语言：
形语言,文字语言,符号语言的转化：
2.3 侧面展开图：圆柱的侧面展开图是以底面周长和 母线长为邻边的矩形.
A
O
B
2.4 面积、体积公式：
C'
轴
轴截面
C
侧面
底面
S = 圆柱侧 2 rh ；S = 圆柱全 2 rh 2 r2 ,V 圆柱=S 底 h= r2h 其中 r 为底面半径,h 为圆柱高
3.棱锥
3.1 棱锥——有一个面是多边形,其余各 面是有一个公共顶点的三角形,由这些
母线 l
轴
h
侧面
轴截面
A
r O
B 底面
S
我们把截面与底面之间的部分称为棱台.
5.2 正棱台的性质： ①各侧棱相等,各侧面都是全等的等腰梯形； ②正棱台的两个底面以及平行于底面的截面是 正多边形； ③ 如右图：四边形 O`MNO,O`B`BO 都是直角梯 形
高中数学立体几何公式大全
立体几何公式大全向量式cos a b a b θ⋅=⋅ a b ⊥0a b ⋅=//a b （0b ≠）a b λ=（0,λ>方向相同0,λ<方向相反）模a2a a =夹角θ（0a ≠，0b ≠）cos a b a bθ⋅=⋅二、求角和距离公式： 求异面直线a 与b ： 12222111cos a b x x y a bx y z θ⋅+==⋅++与平面αa n a n⋅⋅（n 表示平面为平面α的法向量1n 与平面2n 的夹角：则12112cos n n n n θ⋅=⋅：求二面角步骤：一、瞄：瞄一下看二面角θ是锐角还是钝角；二、的法向量1n 与平面的法向2n ，而后用12112cos n n n n θ⋅=⋅ 求出1n 与2n 的夹角1θ；三、定：同锐相等：若θ是锐角，也是锐角，；同钝相等：若θ是锐角，θ也是锐角，则1θ=；锐钝互补：若θJP69/KP127/AP n n⋅A 为平面α上的任意n 为平面α的法向量三、求法向量步骤：（1） 设法向量(,,)n x y z =，利用法向量n 与平面上的两相交直线方向向量垂直数量积为0建立两个方程；（2） 求出x 等于多少z, y 等于多少z;并令z=1进而求出x,y,从而得到法向量n ；或者求出x 等于多少y, z 等于多少y;并令y=1进而求出x,z,从而得到法向量n ； 或者求出y 等于多少x, z 等于多少x;并令x=1进而求出y,z,从而得到法向量n ；（3） 把所求的法向量n 代入方程组检验！ 四、法向量n 的在证明题中用处:(1) 线面平行：l l n α⊄⊥平面且⇔//l α平面：参见JP65/例2 （证明线面平行问题只要转成去求线的向量与法向量数量积为0即可） (2) 面面平行：12//n n ⇔//αβ平面平面：参见JP65/例2（证明面面平行问题只要转成去证两个法向量存在一个倍数关系问题即可） (3) 线面垂直：//l n l α⇔⊥平面：（证明线面垂直问题只要转成求证线的向量与法向量存在一个倍数关系即可） (4) 面面垂直：12n n ⊥⇔αβ⊥平面平面：参见JP65/例3 （证明面面垂直问题只要转成去求两法向量数量积为0即可）。
高中数学立体几何知识点归纳总结
高中数学立体几何知识点归纳总结一、立体几何知识点归纳 第一章 空间几何体（一）空间几何体的结构特征（1）多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中，这条定直线称为旋转体的轴。
（2）柱，锥，台，球的结构特征 1.棱柱1.1棱柱——有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列（棱柱、斜棱柱、直棱柱、正棱柱）的关系：①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱底面为矩形1.3①侧棱都相等，侧面是平行四边形；②两个底面与平行于底面的截面是全等的多边形；③过不相邻的两条侧棱的截面是平行四边形； ④直棱柱的侧棱长与高相等，侧面与对角面是矩形。
1.4长方体的性质：①长方体一条对角线长的平方等于一个顶点上三条棱的平方和；【如图】222211AC AB AD AA =++②（了解）长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ，，，那么222c o s c o sc o s 1αβγ++=，222sin sin sin 2αβγ++=；③（了解）长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ，，，则222co s co s co s 2αβγ++=，222sin sin sin 1αβγ++=.1.5侧面展开图：正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形. 1.6面积、体积公式：2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底，V （其中c 为底面周长，h 为棱柱的高）2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫圆柱.2.2圆柱的性质：上、下底及平行于底面的截面都是等圆；过轴的截面（轴截面）是全等的矩形.2.3侧面展开图：圆柱的侧面展开图是以底面周长和母线长为邻边的矩形.2.4面积、体积公式：S =2rh π；S=222rh r ππ+，V=Sh=2r h π（其中r 为底面半径，h 为圆柱高） 3.棱锥3.1棱锥——有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。
高考数学：立体几何需熟透四公理八定理
⾼考数学：⽴体⼏何需熟透四公理⼋定理 海南华侨中学⾼三数学备课组长邓建书为⽹友解疑答惑。
(南海⽹记者陈望摄) 南海⽹海⼝4⽉17⽇消息(南海⽹记者刘嘉珮)⾼考数学中⼏何是难点重点，有什么复习技巧?每次能听懂，但是轮到⾃⼰答题时却发蒙该怎么办?遇上难题该如何化解恐惧⼼理?4⽉17⽇，海南华侨中学⾼三数学备课组长邓建书参加南海⽹“2012⾼考名校名师全媒体辅导”时⼀⼀为⽹友们进⾏解答。
⽴体⼏何需熟透四公理⼋定理 针对⽹友提出⼏何复习办法的疑问，邓建书⽼师表⽰，⼏何分为⽴体⼏何和解析⼏何。
⽴体⼏何⼜分为四个公理⼋个定理，考⽣⾸先需要把这⽅⾯的教材都通读⼀遍，如果还不能理解的话，就拿出笔和纸把这些定理公理都抄下来，再把相应的图形画出来，必须记住这些内容，能做到脱⼝⽽出，只有熟悉基础知识，做题才能找到思路。
⽴体⼏何是基本的概念，解析⼏何则是最原始的定义，⾼考时做解析⼏何却让很多考⽣头痛不已，邓建书对解析⼏何计算的技巧给出了⾃⼰的建议。
“在计算这⽅⾯我们最⾸要的是相信⾃⼰，很多同学拿铅笔做题就是还不相信⾃⼰。
我认为在做题的时候可以先把⾃⼰知道的都在卷⾯上写下来，然后再在稿纸上算⼀下，算⼀步写⼀步。
免得这道题⽬不会做，在稿纸上算很久都没有算出来，⼜没有时间写在试卷上。
先在试卷上把知道的写下来这样能节省很多时间，即使没有做出来前⾯步骤分还在。
” 做不来题还是基础知识不牢固 有⽹友表⽰，学习数学时⽼师讲的时候⼤家很清楚，⾃⼰做的时候感觉却很难，邓建书⽼师认为这个同学还是基础知识不牢固。
“学习分为⼏个层次，第⼀个叫做⽣中成熟，第⼆熟中⽣巧，第三巧中⽣变，我觉得这个实际上就是知识熟练的过程，题⽬更多的就是考知识点，知识点不熟悉，题就做不好。
”他建议这位同学对⾼中的教材再进⾏梳理⼀遍，这样知识点可以慢慢熟悉起来，也可以找两、三位同学在⼀块互相提问，拿着书⼀本⼀本问，这个⽅法⽐较好。
时间不够，是很多考⽣都会遇到的苦恼，该如何保证考试正确率的同时⼜能提⾼速度?邓建书表⽰，如果⼤题没有时间做，肯定是因为考⽣在选择题和填空题上消耗了太多时间。
立体几何公式定理大全
立体几何公式定理大全、公理定理（一）平面基本性质公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有的点都在这个平面内。
公理2：过不在同一条直线上的三个点，有且只有一个平面。
推论1：经过一条直线和这条直线外一点，有且只有一个平面。
推论2：经过两条相交直线，有且只有一个平面。
推论3：经过两条平行直线，有且只有一个平面。
公理3：如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。
公理4：平行于同一条直线的两条直线互相平行。
等角定理：如果一个角的两边和另一个角的两边分别平行，那么这两个角相等或互补。
（二）空间中两条直线的位置关系空间两直线的位置关系：空间两条直线只有三种位置关系：平行、相交、异面1、按是否共面可分为两类：（1）共面：平行、相交（2）异面：异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理：过平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。
两异面直线所成的角：过空间任意一点引两条直线分别平行于两条异面直线，它们所成的锐角（或直角）就是异面直线所成的角。
范围为0 , 90两异面直线间距离: 公垂线段（有且只有一条） 2、若从有无公共点的角度看可分为两类：（1）有且仅有一个公共点——相交直线；（2）没有公共点——平行或异面三）平行关系1．线面平行定义：直线和平面没有公共点判定定理：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。
2．面面平行定义：空间两平面没有公共点判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。
性质定理引理：两个平面互相平行则其中一个平面内的直线平行于另一个平面。
性质定理：如果两个平行平面同时和第三个平面相交，那么交线平行。
（四）垂直关系1线面垂直定义：如果一条直线a和一个平面内的任意一条直线都垂直，我们就说直线a和平面互相垂直.直线a叫做平面的垂线，平面叫做直线a的垂面。
立体几何公式大全
立体几何公式大全一、空间向量的基础公式：向量式坐标式数量积cos a b a b q×=×=121212x x y y z z ++a b^ 0a b ×= =121212x x y y z z ++=0 //a b （0b ¹ ）a b l =（0,l >方向相同；0,l <方向相反）=111(,,)x y z =l 222(,,)x y z 即：12x x l =，12y y l =，12z z l =模a2a a= =222111x y z ++夹角q （0a ¹，0b ¹）cos ab a b q ×=×=121212222222111222x x y y z z x y z x y z ++++++二、求角和距离公式：求异面直线a 与b 所成角q：121212222222111222cos a bx x y y z z a b x y z x y z q ×++==×++++ KP115/例1 JP60/例3 求直线a 与平面a 所成角q ：sin a n a nq ×=× （n表示平面a 的法向量）KP125/例1 二面角l a b --的大小q : 设1q 为平面a 的法向量1n 与平面b 的法向量2n的夹角：则12112cos n n n n q ×=× ：求二面角q 步骤：一、瞄：瞄一下看二面角q 是锐角还是钝角；二、求：先求平面a 的法向量1n与平面b 的法向量2n ，而后用12112cos n n n n q ×=×求出1n 与2n 的夹角1q；三、定：同锐相等：若；三、定：同锐相等：若q是锐角，1q 也是锐角，则1q q =；同钝相等：若q 是锐角，1q 也是锐角，则1q q =；锐钝互补：若q 是锐角，1q 也是锐角，则1180q q =-JP69/例3(2) KP127/例2（2）点P 到平面a 的距离d: 注：注：1、直线l //平面a ，求直线l 与平面a 的距离的距离 d:只要在l 上取一点P 仍然用此公式；仍然用此公式；2、平面b //平面a ，求平面a 与平面b 的距离的距离 d:只要在平面b 上取一点P 仍然用此公式；式；APn d n×=注：点A 为平面a 上的任意一点，n为平面a 的法向量的法向量JP71/例2 三、求法向量步骤：三、求法向量步骤：（1） 设法向量(,,)n x y z = ，利用法向量n与平面上的两相交直线方向向量垂直数量积为0建立两个方程；建立两个方程；（2） 求出x 等于多少z, y 等于多少z;并令z=1进而求出x,y,从而得到法向量n；或者求出x 等于多少y, z 等于多少y;并令y=1进而求出x,z,从而得到法向量n；或者求出y 等于多少x, z 等于多少x;并令x=1进而求出y,z,从而得到法向量n；（3） 把所求的法向量n代入方程组检验！代入方程组检验！ 四、法向量n的在证明题中用处: (1) 线面平行：l l n a Ë^ 平面且Û//l a 平面：参见JP65/例2 （证明线面平行问题只要转成去求线的向量与法向量数量积为0即可）即可）(2) 面面平行：12//n nÛ//a b 平面平面：参见JP65/例2 （证明面面平行问题只要转成去证两个法向量存在一个倍数关系问题即可）（证明面面平行问题只要转成去证两个法向量存在一个倍数关系问题即可） (3) 线面垂直：//l n l a Û^平面：（证明线面垂直问题只要转成求证线的向量与法向量存在一个倍数关系即可） (4) 面面垂直：12n n ^Ûa b ^平面平面：参见JP65/例3 （证明面面垂直问题只要转成去求两法向量数量积为0即可）即可）（整理不易，望同学们好好珍惜利用！）。
立体几何经典定理概述(八大定理)
立体几何经典定理概述(八大定理)立体几何经典定理概述（八大定理）本文将概述立体几何中的八大经典定理。
立体几何是研究三维空间中的图形和形体的数学学科，定理是在研究过程中得出的具有重要意义的数学命题。
1. 欧拉定理欧拉定理是立体几何中最著名的定理之一。
它规定了三维物体的面、顶点和边的关系。
具体来说，如果一个多面体满足面+顶点-边=2的关系，那么它就是一个封闭的多面体。
欧拉定理形象地描述了三维世界中多面体的特性。
2. 柯西定理柯西定理是关于立体几何中平行四边形的定理。
它指出，对于一个平行四边形，其对角线互相平分彼此。
这个定理在解决平行四边形的性质和关系时非常有用，能够帮助我们更好地理解平面几何的性质。
3. 形心定理形心定理是关于多边形形心的定理。
形心是多边形中所有顶点的连线的交点，该定理指出，任意多边形的形心一定在多边形的重心和质心连线的上面。
形心定理可以帮助我们确定多边形的形心位置，从而研究多边形的性质和变形。
4. 二等分线定理二等分线定理是关于立体几何中等分线的定理。
它规定了等分线在多面体中的特性，即等分线和相应的两个面以及它们的交点构成的平面垂直。
这个定理在解决多面体的等分线问题时非常有用，能够帮助我们进一步理解多面体的性质。
5. 范恩艾克线定理范恩艾克线定理是关于球面上切线和交角的定理。
它指出，在球面上，任意切线与相应交角的正弦值等于球心到交点的距离和切线长的比值。
这个定理在解决球面上的切线和交角问题时非常有用，能够帮助我们研究球面的性质和切线关系。
6. 斯坦纳定理斯坦纳定理是关于三维空间中图的生成树的定理。
生成树是一个无圈连通图的子图，其中包含了所有顶点并且边的数量最少。
斯坦纳定理指出，在三维空间中的图中，生成树的条数等于顶点数减去连通分量的数量。
这个定理在解决三维空间图的生成树问题时非常有用。
7. 勾股定理勾股定理是立体几何中最基础的定理之一。
它规定了直角三角形边长之间的关系，即直角三角形的两个直角边的平方和等于斜边的平方。
立体几何公理、定理一览表(新)
立体几何公理、定理一览表
用“平移法”作异面直线所成的角，关键是选择适当的点，一般选在一对异面直线的一条线段的端点或中点；用“射影法”作斜线与平面所成的角，关键是垂足位置的确定；作二面角的平面角有三种方法，一是“定义法”，二是“垂线法”，三是作棱的“垂面法”。
求距离，找垂足或转换（利用平行间距离相等或三棱锥的顶点转换）；
即：遇到求“距离、线面所成角、面面所成角”等，都要设法找到图中存在或隐藏的“线面垂直、面面垂直”关系。
且要一作（找）、二证（说理）、三计算（平面分离）。
高中数学立体几何总结
高中数学立体几何总结立体几何是高中数学中一个重要的内容，大致内容包括立体几何基本概念、体积、体积计算公式、侧棱、正三棱柱、正四棱锥、正八棱锷、台面等等。
（一）立体几何基本概念1、三视图：即从三个不同的视角把物体有条不紊的绘出来的文字图形，可以根据它来确定物体的三维形状。
2、几何体：是由把平面图形几何关系组合而成的任何在空间中由一致点构成的物体。
3、棱：即立体几何中各几何体的侧面所围成的线段或面称为棱，如正三棱柱的侧棱。
（二）体积1、体积的定义：体积是立体图形的面积之和，反映物体内部空间的容积大小。
2、体积的计算公式：几何体的体积可用面积的乘积公式计算，比如正三棱柱的体积的表示公式：V=ah；正四棱锥的体积的表示公式：V=1/3bh；正八棱锷的表示公式为：V=1/3πr²h。
（三）正三棱柱1、正三棱柱，是一种方形底面，面积相同的三角柱体，它有三个直角，等边的三个棱，以及一个正方形的底部。
2、侧棱：正三棱柱的侧棱可以分别表示为a，b，c三条线段，表示a=b=c，它们在同一平面且互相垂直。
3、体积计算：正三棱柱的体积可以用面积乘积公式来计算：V=ah；其中，a表示正三棱柱的侧棱，h表示高度。
（四）正四棱锥1、正四棱锥是由正方形底面、顶面和棱构成的三角锥体，它有四个直角棱，棱之间相互垂直，底面和顶面也相互垂直。
2、侧棱：正四棱锥的侧棱只有一条，用a表示，它的四条边都要等于。
（五）正八棱锷1、正八棱锷是一种八个棱组成的几何体，其四条边中有三条边为互相垂直的折线，其余五条边为圆形弧线。
2、侧棱：正八棱锷有八个侧棱，用a1，a2，a3…a8表示，但它们互相之间不相等，作用上也不是等距的。
（六）台面1、台面，又称台体，是由一个小三角形共同构成的平面图形。
当该平面图形在三维空间中展开时，可以形成一个台体，它由三个等高的并列棱构成。
2、台体体积计算：台体的体积可以由其三角面积和三边长共同确定，台体的体积公式为：V=1/3(A1+A2+A3)H；其中，A1，A2，A3表示三个三角面积，H表示高度。
第八章 立体几何初步(公式、定理、结论图表)--2023年高考数学必背知识手册(新教材)
第八章立体几何初步（公式、定理、结论图表）1．多面体的结构特征名称棱柱棱锥棱台图形底面互相平行且全等多边形互相平行且相似侧棱互相平行且相等相交于一点，但不一定相等延长线交于一点侧面形状平行四边形三角形梯形2.正棱柱、正棱锥的结构特征(1)正棱柱：侧棱垂直于底面的棱柱叫做直棱柱，底面是正多边形的直棱柱叫做正棱柱．反之，正棱柱的底面是正多边形，侧棱垂直于底面，侧面是矩形．(2)正棱锥：底面是正多边形，顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥．特别地，各棱均相等的正三棱锥叫正四面体．3．旋转体的结构特征(1)几何体的三视图包括正视图、侧视图、俯视图，分别是从几何体的正前方、正左方和正上方观察几何体画出的轮廓线．(2)在画三视图时，重叠的线只画一条，挡住的线要画成虚线．(3)三视图的长度特征：“长对正、高平齐、宽相等”，即正俯同长、正侧同高、俯侧同宽．5．空间几何体的直观图空间几何体的直观图常用斜二测画法来画，其规则是：(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴，y′轴的夹角为45°或135°，z′轴与x′轴和y′轴所在平面垂直．(2)原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴；平行于x轴和z轴的线段在直观图中保持原长度不变；平行于y轴的线段在直观图中长度为原来的一半．6．多面体的表(侧)面积因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．7．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧＝2πrl S圆锥侧＝πrl S圆台侧＝π(r1＋r2)l三者关系S圆柱侧＝2πrl――→r′＝rS圆台侧＝π(r＋r′)l――→r′＝0S圆锥侧＝πrl8.柱、锥、台和球的表面积和体积(1)公理1：如果一条直线上的两点在一个平面内，那么这条直线在这个平面内．(2)公理2：过不在一条直线上的三点，有且只有一个平面．(3)公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．(4)公理2的三个推论推论1：经过一条直线和这条直线外的一点，有且只有一个平面．推论2：经过两条相交直线，有且只有一个平面．推论3：经过两条平行直线，有且只有一个平面．10．空间直线的位置关系(1)位置关系的分类异面直线：不同在任何一个平面内，没有公共点(2)异面直线所成的角①定义：设a，b是两条异面直线，经过空间任一点O作直线a′∥a，b′∥b，把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)．(3)平行公理(公理4)和等角定理平行公理：平行于同一条直线的两条直线互相平行．等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．11．空间中直线与平面、平面与平面的位置关系(1)空间中直线与平面的位置关系空间中两个平面的位置关系位置关系图形表示符号表示公共点两平面平行α∥β没有公共点两平面相交斜交α∩β＝l有一条公共直线垂直α⊥β且α∩β＝a12．线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为“线面平行⇒面面平行”)∵a ∥β，b ∥β，a ∩b ＝P ，a ⊂α，b ⊂α，∴α∥β性质定理如果两个平行平面同时和第三个平面相交，那么它们的交线平行∵α∥β，α∩γ＝a ，β∩γ＝b ，∴a ∥b14．直线与平面垂直(1)定义：如果直线l与平面α内的任意一条直线都垂直，则直线l与平面α垂直．(2)判定定理：如果一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．(3)推论：如果在两条平行直线中，有一条垂直于一个平面，那么另一条也垂直于这个平面．(4)直线和平面垂直的性质：①垂直于同一个平面的两条直线平行．②直线垂直于平面，则垂直于这个平面内的任一直线．③垂直于同一条直线的两平面平行．15．直线和平面所成的角(1)平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角．(2)当直线与平面垂直和平行(或直线在平面内)时，规定直线和平面所成的角分别为90°和0°.(3)直线和平面所成角的范围是0°≤θ≤90°.16．二面角的有关概念(1)二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．(2)二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角．(3)二面角的范围是0°≤θ≤180°.17．平面与平面垂直(1)定义：如果两个平面所成的二面角是直二面角，就说这两个平面互相垂直．(2)平面与平面垂直的判定定理与性质定理l⊥α<常用结论>1．特殊的四棱柱2．球的截面的性质3．按照斜二测画法得到的平面图形的直观图，其面积与原图形面积的关系如下：5．几个与球有关的切、接常用结论(1)正方体的棱长为a，球的半径为R，6．异面直线的判定定理7．等角定理的引申(1)在等角定理中，若两角的两边平行且方向相同或相反，则这两个角相等．(2)在等角定理中，若两角的两边平行且方向一个边相同，一个边相反，则这两个角互补．8．唯一性定理(1)过直线外一点有且只有一条直线与已知直线平行．(2)过直线外一点有且只有一个平面与已知直线垂直．(3)过平面外一点有且只有一个平面与已知平面平行．(4)过平面外一点有且只有一条直线与已知平面垂直．9.线、面平行的性质(1)两个平面平行，其中一个平面内的任意一条直线平行于另一个平面．(4)两条直线被三个平行平面所截，截得的对应线段成比例．(5)如果两个平面分别和第三个平面平行，那么这两个平面互相平行．(6)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线，那么这两个平面平行．12．两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．<解题方法与技巧>一、空间几何体概念辨析题的常用方法A．各个面都是三角形的几何体是三棱锥B．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥C．棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥D．圆锥的顶点与底面圆周上的任意一点的连线都是母线D[A错误．如图1所示，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不是棱锥．图1图2B错误．如图2，若△ABC不是直角三角形或是直角三角形，但旋转轴不是直角边所在直线，所得的几何体都不是圆锥．C错误．由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长．D正确．]二、识别三视图的步骤(2)根据三视图的有关定义和规则先确定正视图，再确定俯视图，最后确定侧视图；(3)被遮住的轮廓线应为虚线，若相邻两个物体的表面相交，表面的交线是它们的分界线；对于简单的组合体，要注意它们的组合方式，特别是它们的交线位置．典例2：(1)如图是一个正方体，A，B，C为三个顶点，D是棱的中点，则三棱锥ABCD 的正视图、俯视图是(注：选项中的上图为正视图，下图为俯视图)()A B C D(2)中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是()(1)A(2)A[(1)正视图和俯视图中棱AD和BD均看不见，故为虚线，易知选A.(2)由题意可知，咬合时带卯眼的木构件如图所示，其俯视图为选项A中的图形．]三、由三视图确定几何体的步骤典例3:(1)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为()A．1B．2C．3D．4(2)某圆柱的高为2，底面周长为16，其三视图如图所示．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N 的路径中，最短路径的长度为()A．217B．25C．3D．2(1)C(2)B[(1)在正方体中作出该几何体的直观图，记为四棱锥PABCD，如图，由图可知在此四棱锥的侧面中，直角三角形的个数为3，故选C.(2)先画出圆柱的直观图，根据题图的三视图可知点M，N的位置如图1所示．图1图2圆柱的侧面展开图及M，N的位置(N为OP的四等分点)如图2所示，连接MN，则图中MN即为M到N的最短路径．ON＝14×16＝4，OM＝2，∴MN＝OM2＋ON22 5.故选B.]四、由几何体的部分视图确定剩余视图的方法解决此类问题，可先根据已知的一部分视图，还原、推测直观图的可能形式，然后再找其剩下部分视图的可能形式．当然作为选择题，也可将选项逐项代入检验．典例4：如图是一个空间几何体的正视图和俯视图，则它的侧视图为()A B C DA [由正视图和俯视图可知，该几何体是由一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径可知侧视图应为A ，故选A.]五、空间几何体的直观图1．用斜二测画法画直观图的技巧在原图形中与x 轴或y 轴平行的线段在直观图中与x ′轴或y ′轴平行，原图中不与坐标轴平行的直线段可以先画出线段的端点再连线．2．原图形与直观图面积的关系典例5：(1)已知等腰梯形ABCD ，CD ＝1，AD ＝CB ＝2，AB ＝3，以AB 所在直线为x 轴，则由斜二测画法画出的直观图A ′B ′C ′D ′的面积为()A.2B.24C.22D ．22(2)如图，矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图，其中O ′A ′＝6cm ，O ′C ′＝2cm ，则原图形是()A ．正方形B ．矩形C ．菱形D ．一般的平行四边形(1)C (2)C [(1)法一(作图求解)：如图，取AB 的中点O 为坐标原点，建立平面直角坐标系，y 轴交DC 于点E ，O ，E 在斜二测画法中的对应点为O ′，E ′，过E ′作E ′F ′⊥x ′轴，垂足为F ′，因为OE ＝(2)2－12＝1，所以O′E′＝12，E′F′＝24.所以直观图A′B′C′D′的面积为S′＝12×(1＋3)×24＝22，故选C.法二(公式法)：由题中数据得等腰梯形ABCD的面积S＝12×(1＋3)×1＝2.由S直观图＝24S原图形，得S直观图＝24×2＝22，故选C.(2)如图，在原图形OABC中，应有OD＝2O′D′＝2×22＝42(cm)，CD＝C′D′＝2cm.所以OC＝OD2＋CD2＝(42)2＋22＝6(cm)，所以OA＝OC，由题意得OA綊BC，故四边形OABC是菱形，故选C.]六、求解几何体表面积的类型及求法A．48＋πB．48－πC．48＋2πD．48－2π(2)已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为()A．122πB．12πC．82πD．10π(1)A(2)B[(1)该几何体是正四棱柱挖去了一个半球，正四棱柱的底面是正方形(边长为2)，高为5，半球的半径是1，那么该几何体的表面积为S＝2×2×2＋4×2×5－π×12＋2π×12＝48＋π，故选A.(2)因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为22，底面圆的直径为22，所以该圆柱的表面积为2×π×(2)2＋2π×2×22＝12π.]七、求体积的常用方法典例7：(1)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是()A.π2＋1B.π2＋3C.3π2＋1 D.3π2＋3(2)如图，已知正方体ABCD A 1B 1C 1D 1的棱长为1，则四棱锥A 1BB 1D 1D 的体积为．(1)A (2)13[(1)由三视图可知该几何体是由底面半径为1，高为3的半个圆锥和三棱锥SABC 组成的，如图，三棱锥的高为3，底面△ABC 中，AB ＝2，OC ＝1，AB ⊥OC .故其体积V ＝13×12×π×12×3＋13×12×2×1×3＝π2＋1.故选A.(2)四棱锥A 1BB 1D 1D 的底面BB 1D 1D 为矩形，其面积S ＝1×2＝2，又四棱锥的高为点A 1到平面BB 1D 1D 的距离，即h ＝12A 1C 1＝22，所以四棱锥的体积V ＝13×2×22＝13.]八、空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．(2)若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，利用4R2＝a2＋b2＋c2求解．典例8：(1)设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为93，则三棱锥DABC体积的最大值为()A．123B．183C．243D．543(2)已知直三棱柱ABCA1B1C1的6个顶点都在球O的球面上，若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为()A.3172B．210C.132D．310(1)B(2)C[(1)如图，E是AC中点，M是△ABC的重心，O为球心，连接BE，OM，OD，BO.因为S△ABC＝34AB2＝93，所以AB＝6，BM＝23BE＝23AB2－AE2＝2 3.易知OM⊥平面ABC，所以在Rt△OBM中，OM＝OB2－BM2＝2，所以当D，O，M三点共线且DM＝OD＋OM时，三棱锥DABC的体积取得最大值，且最大值V ma x＝13S△ABC×(4＋OM)＝13×93×6＝18 3.故选B.(2)如图所示，由球心作平面ABC的垂线，则垂足为BC 的中点M .因为AB ＝3，AC ＝4，AB ⊥AC ，所以BC ＝5.又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA＝132，故选C.]九、共点、共线、共面问题的证明方法(1)证明点共线问题：①公理法：先找出两个平面，然后证明这些点都是这两个平面的公共点，再根据基本公理3证明这些点都在交线上；②同一法：选择其中两点确定一条直线，然后证明其余点也在该直线上．(2)证明线共点问题：先证两条直线交于一点，再证明第三条直线经过该点．(3)证明点、直线共面问题：①纳入平面法：先确定一个平面，再证明有关点、线在此平面内；②辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合．典例9：(1)以下命题中，正确命题的个数是()①不共面的四点中，其中任意三点不共线；②若点A ，B ，C ，D 共面，点A ，B ，C ，E 共面，则A ，B ，C ，D ，E 共面；③若直线a ，b 共面，直线a ，c 共面，则直线b ，c 共面；④依次首尾相接的四条线段必共面．A ．0B ．1C ．2D ．3(2)如图，正方体ABCD A 1B 1C 1D 1中，E ，F 分别是AB 和AA 1的中点．求证：①E ，C ，D 1，F 四点共面；②CE，D1F，DA三线共点．(1)B[①正确，可以用反证法证明，假设任意三点共线，则四个点必共面，与不共面的四点矛盾；②中若点A，B，C在同一条直线上，则A，B，C，D，E不一定共面，故②错误；③中，直线b，c可能是异面直线，故③错误；④中，当四条线段构成空间四边形时，四条线段不共面，故④错误．](2)[证明]①如图，连接EF，CD1，A1B.∵E，F分别是AB，AA1的中点，∴EF∥BA1.又∵A1B∥D1C，∴EF∥CD1，∴E，C，D1，F四点共面．②∵EF∥CD1，EF<CD1，∴CE与D1F必相交，设交点为P，则由P∈直线CE，CE⊂平面ABCD，得P∈平面ABCD.同理P∈平面ADD1A1.又平面ABCD∩平面ADD1A1＝DA，∴P∈直线DA，∴CE，D1F，DA三线共点．十、空间两条直线的位置关系典例10：(1)已知a，b，c为三条不同的直线，且a⊂平面α，b⊂平面β，α∩β＝c，给出下列命题：①若a与b是异面直线，则c至少与a，b中的一条相交；②若a不垂直于c，则a与b一定不垂直；③若a∥b，则必有a∥c.其中真命题有．(填序号)(2)如图，G，H，M，N分别是正三棱柱的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有(填上所有正确答案的序号)．①②③④(1)①③(2)②④[(1)对于①，若c与a，b都不相交，则c∥a，c∥b，从而a∥b，这与a与b是异面直线矛盾，故①正确．对于②，a与b可能异面垂直，故②错误．对于③，由a∥b可知a∥β，又α∩β＝c，从而a∥c，故③正确．(2)图①中，直线GH∥MN；图②中，G，H，N三点共面，但M∉平面GHN，因此直线GH与MN异面；图③中，连接MG(图略)，GM∥HN，因此GH与MN共面；图④中，G，M，N共面，但H∉平面GMN，因此GH与MN异面，所以在图②④中，GH与MN异面．]十一、平移法求异面直线所成角的步骤典例11：(1)在正方体ABCDA1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD 所成角的正切值为()A.2 2B.32C.52D.72(2)在我国古代数学名著《九章算术》中，将四个面都为直角三角形的四面体称为鳖臑．如图，在鳖臑ABCD 中，AB ⊥平面BCD ，且AB ＝BC ＝CD ，则异面直线AC 与BD 所成角的余弦值为()A.12B ．－12C.32D ．－32(1)C (2)A [(1)如图，连接BE ，因为AB ∥CD ，所以异面直线AE 与CD 所成的角等于相交直线AE 与AB 所成的角，即∠EAB .不妨设正方体的棱长为2，则CE ＝1，BC ＝2，由勾股定理得BE ＝ 5.又由AB ⊥平面BCC 1B 1可得AB ⊥BE ，所以tan ∠EAB ＝BE AB ＝52.故选C.(2)如图，分别取AB ，AD ，BC ，BD 的中点E ，F ，G ，O ，连接EF ，EG ，OG ，FO ，FG ，则EF ∥BD ，EG ∥AC ，所以∠FEG 为异面直线AC 与BD 所成的角．易知FO ∥AB ，因为AB ⊥平面BCD ，所以FO ⊥平面BCD ，所以FO ⊥OG ，设AB ＝2a ，则EG ＝EF ＝2a ，FG ＝a 2＋a 2＝2a ，所以∠FEG ＝60°，所以异面直线AC 与BD 所成角的余弦值为12，故选A.]十二、判定线面平行的四种方法(1)利用线面平行的定义(无公共点)；(2)利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)；(3)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)；(4)利用面面平行的性质(α∥β，a ⊄α，a ⊄β，a ∥α⇒a ∥β)．典例12：如图，在四棱锥P ABCD 中，AD ∥BC ，AB ＝BC ＝12AD ，E ，F ，H 分别为线段AD ，PC ，CD 的中点，AC 与BE 交于O 点，G 是线段OF 上一点．(1)求证：AP ∥平面BEF ；(2)求证：GH ∥平面P AD .[证明](1)连接EC ，因为AD ∥BC ，BC ＝12AD ，E 为AD 中点，所以BC AE ，所以四边形ABCE 是平行四边形，所以O 为AC 的中点．又因为F 是PC 的中点，所以FO ∥AP ，因为FO ⊂平面BEF ，AP ⊄平面BEF ，所以AP ∥平面BEF .(2)连接FH ，OH ，因为F ，H 分别是PC ，CD 的中点，所以FH ∥PD ，因为FH ⊄平面PAD ，PD ⊂平面PAD ，所以FH ∥平面PAD .又因为O 是BE 的中点，H 是CD 的中点，所以OH ∥AD ，因为OH ⊄平面PAD ，AD ⊂平面PAD .所以OH ∥平面P AD .又FH ∩OH ＝H ，所以平面OHF ∥平面PAD .又因为GH ⊂平面OHF ，所以GH∥平面PAD.十三、判定平面与平面平行的四种方法(1)面面平行的定义，即证两个平面没有公共点(不常用)；(2)面面平行的判定定理(主要方法)；(3)利用垂直于同一条直线的两个平面平行(客观题可用)；(4)利用平面平行的传递性，两个平面同时平行于第三个平面，那么这两个平面平行(客观题可用)．注意：谨记空间平行关系之间的转化典例13：已知空间几何体ABCDE中，△BCD与△CDE均为边长为2的等边三角形，△ABC 为腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD，M，N分别为DB，DC的中点．(1)求证：平面EMN∥平面ABC；(2)求三棱锥AECB的体积．[解](1)证明：取BC中点H，连接AH，∵△ABC为等腰三角形，∴AH⊥BC，又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，∴AH⊥平面BCD，同理可证EN⊥平面BCD，∴EN ∥AH ，∵EN ⊄平面ABC ，AH ⊂平面ABC ，∴EN ∥平面ABC ，又M ，N 分别为BD ，DC 中点，∴MN ∥BC ，∵MN ⊄平面ABC ，BC ⊂平面ABC ，∴MN ∥平面ABC ，又MN ∩EN ＝N ，∴平面EMN ∥平面ABC .(2)连接DH ，取CH 中点G ，连接NG ，则NG ∥DH ，由(1)知EN ∥平面ABC ，所以点E 到平面ABC 的距离与点N 到平面ABC 的距离相等，又△BCD 是边长为2的等边三角形，∴DH ⊥BC ，又平面ABC ⊥平面BCD ，平面ABC ∩平面BCD ＝BC ，DH ⊂平面BCD ，∴DH ⊥平面ABC ，∴NG ⊥平面ABC ，∴DH ＝3，又N 为CD 中点，∴NG 又AC ＝AB ＝3，BC ＝2，∴S △ABC ＝12·|BC |·|AH |＝22，∴V E ABC ＝V N ABC ＝13·S △ABC ·|NG |＝63.十四、证明直线与平面垂直的常用方法(1)利用线面垂直的判定定理．(2)利用“两平行线中的一条与平面垂直，则另一条也与这个平面垂直”．(3)利用“一条直线垂直于两个平行平面中的一个，则与另一个也垂直”．(4)利用面面垂直的性质定理．典例14：如图，在斜三棱柱ABC A 1B 1C 1中，底面ABC 是边长为2的正三角形，M 为棱BC 的中点，BB 1＝3，AB 1＝10，∠CBB 1＝60°.(1)求证：AM ⊥平面BCC 1B 1；(2)求斜三棱柱ABC A 1B 1C 1的体积．[解](1)证明：如图，连接B 1M ，因为底面ABC 是边长为2的正三角形，且M 为棱BC 的中点，所以AM ⊥BC ，且AM ＝3，因为BB 1＝3，∠CBB 1＝60°，BM ＝1，所以B 1M 2＝12＋32－2×1×3×cos 60°＝7，所以B 1M ＝7.又因为AB 1＝10，所以AM 2＋B 1M 2＝10＝AB 21，所以AM ⊥B 1M .又因为B 1M ∩BC ＝M ，所以AM ⊥平面BCC 1B 1.(2)设斜三棱柱ABC A 1B 1C 1的体积为V ，则V ＝3VB 1ABC ＝3VA B 1BC＝3×13S △B 1BC ·|AM |＝12×2×3×sin 60°×3＝92.所以斜三棱柱ABCA1B1C1的体积为9 2 .十五、证明面面垂直的两种方法(1)定义法：利用面面垂直的定义，即判定两平面所成的二面角为直二面角，将证明面面垂直问题转化为证明平面角为直角的问题．(2)定理法：利用面面垂直的判定定理，即证明其中一个平面经过另一个平面的一条垂线，把问题转化成证明线线垂直加以解决，注意：三种垂直关系的转化典例15：(1)如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则()A．BM＝EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM＝EN，且直线，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线B[取CD的中点F，DF的中点G，连接EF，FN，MG，GB，BD，BE.∵点N为正方形ABCD的中心，∴点N在BD上，且为BD的中点．∵△ECD是正三角形，∴EF⊥CD.∵平面ECD⊥平面ABCD，∴EF⊥平面ABCD.∴EF⊥FN.不妨设AB＝2，则FN＝1，EF＝3，∴EN＝FN2＋EF2＝2.∵EM＝MD，DG＝GF，∴MG∥EF，∴MG⊥平面ABCD，∴MG⊥BG.∵MG＝12EF＝32，BG＝CG2＋BC2＝52，∴BM＝MG2＋BG2＝7.∴BM≠EN.∵BM，EN是△DBE的中线，∴BM，EN必相交．故选B.](2)如图，四棱锥PABCD中，△PCD为等边三角形，CD＝AD＝2AB，E，S，T，Q为CD，P A，PB，AD的中点，∠ABC＝∠BCD＝∠PEA＝90°，平面STRQ∩平面ABCD＝RQ.①证明：平面P AE⊥平面STRQ；②若AB＝1，求三棱锥QBCT的体积．[解]①证明：因为E为CD的中点，CD＝2AB，∠ABC＝∠BCD＝90°，所以四边形ABCE 为矩形，所以AE⊥CD.由已知易得RQ∥CD，所以RQ⊥AE.因为∠PEA＝90°，PE∩CD＝E，故AE⊥平面PCD，又因为AE⊂平面ABCD.故平面PCD⊥平面ABCD.因为PE⊥CD，所以PE⊥平面ABCD.因为RQ⊂平面ABCD，所以RQ⊥PE.又PE ∩AE ＝E ，所以RQ ⊥平面PAE .所以平面P AE ⊥平面STRQ .②由①可知，PE ⊥平面ABCD ，又T 是PB 的中点，∴点T 到平面BCQ 的距离为12PE ＝32，易知S △BCQ ＝12S 梯形ABCD ＝12×12×(1＋2)×3＝334.故三棱锥Q BCT 的体积V ＝13×334×32＝38.十六、求点到平面的距离(高)的两种方法(1)定义法：求几何体的高或点到面的距离，经常根据高或距离的定义在几何体中作出高或点到面的距离．其步骤为：一作、二证、三求．如何作出点到面的距离是关键，一般的方法是利用辅助面法，所作的辅助面，一是要经过该点，二是要与所求点到面的距离的面垂直，这样在辅助面内过该点作交线的垂线，点到垂足的距离即为点到面的距离．(2)等体积法：求棱锥的高或点到平面的距离常常利用同一个三棱锥变换顶点及底面的位置，其体积相等的方法求解．典例16:(1)已知∠ACB ＝90°，P 为平面ABC 外一点，PC ＝2，点P 到∠ACB 两边AC ，BC 的距离均为3，那么P 到平面ABC 的距离为．2[如图，过点P 作⊥平面ABC 于O ，则PO 为P 到平面ABC 的距离．再过O 作OE ⊥AC 于E ，OF ⊥BC 于F ，连接PC ，PE ，PF ，则PE ⊥AC ，PF ⊥BC .又PE ＝PF ＝3，所以OE ＝OF ，所以CO 为∠ACB 的平分线，即∠ACO ＝45°.在Rt △PEC 中，PC ＝2，PE ＝3，所以CE ＝1，所以OE ＝1，所以PO ＝PE 2－OE 2＝(3)2－12＝ 2.](2)如图，在三棱锥P ABC 中，AB ＝BC ＝22，PA ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．①证明：PO ⊥平面ABC ；②若点M 在棱BC 上，且MC ＝2MB ，求点C 到平面POM 的距离．[解]①证明：因为AP ＝CP ＝AC ＝4，O 为AC 的中点，所以OP ⊥AC ，且OP ＝2 3.连接OB .因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.由OP 2＋OB 2＝PB 2知，OP ⊥OB .由OP ⊥OB ，OP ⊥AC ，OB ⊂平面ABC ，AC ⊂平面ABC ，OB ∩AC ＝O ，知PO ⊥平面ABC .②作CH ⊥OM ，垂足为H .又由①可得OP ⊥CH ，OP ⊂平面POM ，OM ⊂平面POM ，OP ∩OM ＝O ，所以CH ⊥平面POM .故CH 的长为点C 到平面POM 的距离．由题设可知OC ＝12AC ＝2，CM ＝23BC ＝423，∠ACB ＝45°，所以OM ＝253，CH ＝OC ·MC ·sin ∠ACB OM ＝455.所以点C 到平面POM 的距离为455.十七、求直线和平面所成角的步骤(1)寻找过斜线上一点与平面垂直的直线；(2)连接垂足和斜足得到斜线在平面上的射影，斜线与其射影所成的锐角或直角即为所求的角；(3)把该角归结在某个三角形中，通过解三角形，求出该角．典例17:(1)在长方体ABCDA1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为()A．8B．62C．82D．83C[如图，连接AC1，BC1，AC.∵AB⊥平面BB1C1C，∴∠AC1B为直线AC1与平面BB1C1C所成的角，∴∠AC1B＝30°.又AB＝BC＝2，在Rt△ABC1中，AC1＝2sin30°＝4.在Rt△ACC1中，CC1＝42－(22＋22)＝22，∴V长方体＝AB×BC×CC1＝2×2×22＝82.](2)如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB＝2，AD＝23，∠BAD＝90°.①求证：AD⊥BC；②求异面直线BC与MD所成角的余弦值；③求直线CD与平面ABD所成角的正弦值．[解]①证明：由平面ABC⊥平面ABD，平面ABC∩平面ABD＝AB，AD⊥AB，可得AD⊥平面ABC，故AD⊥BC.②如图，取棱AC 的中点N ，连接MN ，ND .又因为M 为棱AB 的中点，所以MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角．在Rt △DAM 中，AM ＝1，故DM ＝AD 2＋AM 2＝13.因为AD ⊥平面ABC ，所以AD ⊥AC .在Rt △DAN 中，AN ＝1，故DN ＝AD 2＋AN 2＝13.在等腰三角形DMN 中，MN ＝1，可得cos ∠DMN ＝12MN DM＝1326.所以，异面直线BC 与MD 所成角的余弦值为1326.③如图，连接CM .因为△ABC 为等边三角形，M 为边AB 的中点，所以CM ⊥AB ，CM ＝ 3.又因为平面ABC ⊥平面，平面ABC ∩平面ABD ＝AB ，而CM ⊂平面ABC ，故CM ⊥平面ABD ，所以∠CDM 为直线CD 与平面ABD 所成的角．在Rt △CAD 中，CD ＝AC 2＋AD 2＝4.在Rt △CMD 中，sin ∠CDM ＝CM CD ＝34.所以，直线CD 与平面ABD 所成角的正弦值为34.十八、转化思想的应用(1)证明线面平行、面面平行可转化为证明线线平行；证明线线平行可以转化为证明线面平行或面面平行．(2)从解题方法上讲，由于线线垂直、线面垂直、面面垂直之间可以相互转化，因此整个解题过程始终沿着线线垂直、线面垂直、面面垂直的转化途径进行．(3)求几何体的体积也常用转化法．如三棱锥顶点和底面的转化，几何体的高利用平行、中点，比例关系的转化等．典例18:如图，在四棱锥P ABCD 中，△PAD 是等腰直角三角形，且∠APD ＝90°，∠ABC ＝90°，AB ∥CD ，AB ＝2CD ＝2BC ＝8，平面PAD ⊥平面ABCD ，M 是PC 的三等分点(靠近C 点处)．(1)求证：平面MBD ⊥平面P AD ；(2)求三棱锥D MAB 的体积．[解](1)证明：由题易得BD ＝AD ＝42，∴AB 2＝AD 2＋BD 2，∴BD ⊥AD .∵平面P AD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，BD ⊂平面ABCD ，∴BD ⊥平面P AD .又∵BD ⊂平面MBD ，∴平面MBD ⊥平面PAD .(2)过点P 作PO ⊥AD 交AD 于点O (图略)，∵平面PAD ⊥平面DAB ，平面PAD ∩平面DAB ＝AD ，∴PO ⊥平面DAB ，∴点P 到平面DAB 的距离为PO ＝2 2.∴V D MAB ＝V M DAB ＝13S △DAB ·13PO ＝13×12×(42)2×13×22＝3229.十九、解决平面图形翻折问题的步骤典例19：图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB ＝1，BE ＝BF ＝2，∠FBC ＝60°.将其沿AB ，BC 折起使得BE 与BF 重合，连接DG ，如图2.图1图2(1)证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；(2)求图2中的四边形ACGD的面积．[解](1)证明：由已知得AD∥BE，CG∥BE，所以AD∥CG，故AD，CG确定一个平面，从而A，C，G，D四点共面．由已知得AB⊥BE，AB⊥BC，故AB⊥平面BCGE.又因为AB⊂平面ABC，所以平面ABC⊥平面BCGE.(2)取CG的中点M，连接EM，DM.因为AB∥DE，AB⊥平面BCGE，所以DE⊥平面BCGE，故DE⊥CG.由已知，四边形BCGE是菱形，且∠EBC＝60°，得EM⊥CG，故CG⊥平面DEM.因此DM⊥CG.在Rt△DEM中，DE＝1＝3，故DM＝2.所以四边形ACGD的面积为4.二十、存在性问题的一般解题方法先假设其存在，然后把这个假设作为已知条件，和题目的其他已知条件一起进行推理论证和计算．在推理论证和计算无误的前提下，如果得到了一个合理的结论，则说明存在；如果得到了一个不合理的结论，则说明不存在．而对于探求点的问题，一般是先探求点的位置，多为线段的中点或某个三等分点，然后给出符合要求的证明．典例20：如图，在四棱锥PABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点．。
数学立体几何八大定理
数学立体几何八大定理
1. 柿子定理：一个作为平面多边形底面的凸多面体的侧面积等
于这个凸多面体表面积的一半加上这个多面体面数目乘以它的底面积。
2. 欧拉定理：一个简单凸多面体的面数、顶点数和边数满足公式：面
数+顶点数=边数+2。
3. 狄利克雷定理：如果一个立体角的每个边界面都可以划分成互不相
交有限个平凡的平面角，则这个立体角为平凡的。
一个立体角被称为
平凡的，当且仅当它可以被划分成三角形。
4. 菲赫斯定理：一个多面体的每条棱所在的平面相交于一点（称为多
面体的菲赫斯点）。
5. 球冠切割定理：一个球的表面可以被三个平面分割成球冠。
6. 萨公定理：任何一个超过120度的立体角可以被切割成平凡的立体角。
7. 凸多面体的交角定理：凸多面体中任意两个面交角的余角的总和等
于360度。
8. 柯西・切比雪夫定理：如果两个凸多面体的交集不为空，则它们的
交界面至少有一点。
立体几何定理公理公式归纳总结
立体几何定理公理公式归纳总结好嘞，以下是为您生成的关于立体几何定理公理公式的归纳总结：在我们学习数学的漫漫长路中，立体几何就像是一座神秘而又充满魅力的城堡。
想要在这座城堡里自由穿梭，那就得把那些关键的定理、公理和公式牢记于心。
咱们先来说说线面平行的判定定理。
如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。
这就好比你在操场上跑步，跑道是个平面，你沿着跑道旁边的直线跑，只要和跑道里的某条线一直保持平行，那你就和整个跑道处于平行的状态。
再看看面面平行的判定定理，如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行。
想象一下，有两个教室的地面，一个教室里地面上有两条相交的线，它们和另一个教室地面的线都平行，那这两个教室的地面就是平行的啦。
线面垂直的判定定理也很重要，一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。
这就好像你在攀岩，你抓住的那根绳子要和岩石上两条相交的棱都垂直，你才能稳稳地攀上去。
面面垂直的判定定理也别落下，如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。
就像两堵墙，一堵墙靠着另一堵墙立着，只要有一根杆子垂直于其中一堵墙并且穿过另一堵墙，那这两堵墙就是垂直的关系。
接下来看看体积公式。
长方体的体积等于长乘宽乘高，这太好理解了，就像一个大盒子，量一量它的长宽高，乘起来就是能装多少东西的量。
圆柱的体积等于底面积乘高，想象一下，一个大柱子，底面积多大，再乘以高度，就是它的体积。
圆锥的体积是三分之一底面积乘高，这就像是个尖顶的帽子，体积只有圆柱的三分之一。
还有球的体积公式，那可是个神奇的存在。
在学习立体几何的过程中，我记得有一次做练习题。
那是一道关于三棱锥体积计算的题目，我一开始怎么都找不到头绪，看着那些线条和角度，脑子都乱成了一团麻。
我不停地在草稿纸上画图，尝试各种方法，可就是算不出来。
后来我静下心来，重新梳理了一遍学过的定理和公式，突然想到可以通过转换顶点来计算体积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学《立体几何》重要公式、定理1．证明直线与平面的平行的思考途径（1）转化为直线与平面无公共点；（2）转化为线线平行；（3）转化为面面平行.2．证明直线与直线的平行的思考途径（1）转化为判定共面二直线无交点；（2）转化为二直线同与第三条直线平行；（3）转化为线面平行；（4）转化为线面垂直；（5）转化为面面平行.3．证明直线与直线的垂直的思考途径（1）转化为相交垂直；（2）转化为线面垂直；（3）转化为线与另一线的射影垂直；（4）转化为线与形成射影的斜线垂直.4．证明直线与平面垂直的思考途径（1）转化为该直线与平面内任一直线垂直；（2）转化为该直线与平面内相交二直线垂直；（3）转化为该直线与平面的一条垂线平行；（4）转化为该直线垂直于另一个平行平面；（5）转化为该直线与两个垂直平面的交线垂直.5．证明平面与平面平行的思考途径（1）转化为判定二平面无公共点；（2）转化为线面平行；（3）转化为线面垂直.6．证明平面与平面的垂直的思考途径（1）转化为判断二面角是直二面角；（2）转化为线面垂直.7.空间向量的加法与数乘向量运算的运算律(1)加法交换律：a ＋b=b ＋a ．(2)加法结合律：(a ＋b)＋c=a ＋(b ＋c)．(3)数乘分配律：λ(a ＋b)=λa ＋λb ．8.共线向量定理对空间任意两个向量a 、b(b ≠0 )，a ∥b ⇔存在实数λ使a=λb ．P A B 、、三点共线⇔||AP AB ⇔AP t AB =⇔(1)OP t OA tOB =-+. ||AB CD ⇔AB 、CD 共线且AB CD 、不共线⇔AB tCD =且AB CD 、不共线.9.共面向量定理向量p 与两个不共线的向量a 、b 共面的⇔存在实数对,x y ,使p ax by =+．推论 空间一点P 位于平面MAB 内的⇔存在有序实数对,x y ,使MP xMA yMB =+， 或对空间任一定点O ，有序实数对,x y ，使OP OM xMA yMB =++.10.平面向量加法的平行四边形法则向空间的推广始点相同且不在同一个平面内的三个向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所表示的向量.11.对空间任一点O 和不共线的三点A 、B 、C ，满足OP xOA yOB zOC =++（x y z k ++=），则当1k =时，对于空间任一点O ，总有P 、A 、B 、C 四点共面；当1k ≠时，若O ∈平面ABC ，则P 、A 、B 、C 四点共面；若O ∉平面ABC ，则P 、A 、B 、C 四点不共面．C A B 、、、D 四点共面⇔AD 与AB 、AC 共面⇔AD xAB yAC =+⇔(1)OD x y OA xOB yOC =--++（O ∉平面ABC ）.12.空间向量基本定理如果三个向量a 、b 、c 不共面，那么对空间任一向量p ，存在一个唯一的有序实数组x ，y ，z ，使p ＝xa ＋yb ＋zc ．推论 设O 、A 、B 、C 是不共面的四点，则对空间任一点P ，都存在唯一的三个有序实数x ，y ，z ，使OP xOA yOB zOC =++.13．空间的线线平行或垂直设111(,,)a x y z =，222(,,)b x y z =，则a b ⇔(0)a b b λ=≠⇔121212x x y y z z λλλ=⎧⎪=⎨⎪=⎩；a b ⊥⇔0a b ⋅=⇔1212120x x y y z z ++=.14.夹角公式设a ＝123(,,)a a a ，b ＝123(,,)b b b ，则cos 〈a ，b 〉.推论 2222222112233123123()()()a b a b a b a a a b b b ++≤++++，此即三维柯西不等式. 15. 四面体的对棱所成的角四面体ABCD 中, AC 与BD 所成的角为θ,则2222|()()|cos 2AB CD BC DA AC BDθ+-+=⋅. 16．异面直线所成角cos |cos ,|a b θ= =21||||||a b a b x ⋅=⋅+（其中θ（090θ<≤）为异面直线a b ,所成角，,a b 分别表示异面直线a b ,的方向向量）17.直线AB 与平面所成角sin ||||AB m arc AB m β⋅=(m 为平面α的法向量). 18.射影公式 已知向量AB =a 和轴l ，e 是l 上与l 同方向的单位向量.作A 点在l 上的射影'A ，作B点在l 上的射影'B ，则''||cos AB AB =〈a ，e 〉=a ·e 19.向量的直角坐标运算设a ＝123(,,)a a a ，b ＝123(,,)b b b 则(1)a ＋b ＝112233(,,)a b a b a b +++；(2)a －b ＝112233(,,)a b a b a b ---；(3)λa ＝123(,,)a a a λλλ (λ∈R)；(4)a ·b ＝112233a b a b a b ++；20.设A 111(,,)x y z ，B 222(,,)x y z ，则AB OB OA =-= 212121(,,)x x y y z z ---.21.若ABC ∆所在平面若β与过若AB 的平面α成的角θ,另两边AC ,BC 与平面α成的角分别是1θ、2θ,A B 、为ABC ∆的两个内角，则2222212sin sin (sin sin )sin A B θθθ+=+.特别地,当90ACB ∠=时,有22212sin sin sin θθθ+=.22.若ABC ∆所在平面若β与过若AB 的平面α成的角θ,另两边AC ,BC 与平面α成的角分别是1θ、2θ,''A B 、为ABO ∆的两个内角，则 222'2'212tan tan (sin sin )tan A B θθθ+=+.特别地,当90AOB ∠=时,有22212sin sin sin θθθ+=.23.二面角l αβ--的平面角cos ||||m n arc m n θ⋅=或cos ||||m n arc m n π⋅-（m ，n 为平面α，β的法向量）. 24. 三射线定理若夹在平面角为ϕ的二面角间的线段与二面角的两个半平面所成的角是1θ,2θ,与二面角的棱所成的角是θ，则有22221212sin sin sin sin 2sin sin cos ϕθθθθθϕ=+- ;1212||180()θθϕθθ-≤≤-+(当且仅当90θ=时等号成立).25.三余弦定理设AC 是α内的任一条直线，且BC ⊥AC ，垂足为C ，又设AO 与AB 所成的角为1θ，AB 与AC 所成的角为2θ，AO 与AC 所成的角为θ．则12cos cos cos θθθ=.26.空间两点间的距离公式若A 111(,,)x y z ，B 222(,,)x y z ，则,A B d =||AB AB AB =⋅=27.点B 到平面α的距离||||AB n d n ⋅=（n 为平面α的法向量，AB 是经过面α的一条斜线，A α∈）. 28.点Q 到直线l 距离h =(点P 在直线l 上，直线l 的方向向量a=PA ，向量b=PQ ).29.异面直线间的距离||||CD n d n ⋅=(12,l l 是两异面直线，其公垂向量为n ，C D 、分别是12,l l 上任一点，d 为12,l l 间的距离).30.异面直线上两点距离公式22cos d mn θ.',d EA AF =.d ='E AA F ϕ=--）.(两条异面直线a 、b 所成的角为θ，其公垂线段'AA 的长度为h.在直线a 、b 上分别取两点E 、F ，'A E m =,AF n =,EF d =).31.三个向量和的平方公式2222()222a b c a b c a b b c c a ++=+++⋅+⋅+⋅ 2222||||cos ,2||||cos ,2||||cos ,a b c a b a b b c b c c a c a =+++⋅+⋅+⋅32. 长度为l 的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、，夹角分别为123θθθ、、,则有2222123l l l l =++222123cos cos cos 1θθθ⇔++=222123sin sin sin 2θθθ⇔++=.（立体几何中长方体对角线长的公式是其特例）.33. 斜棱柱的直截面已知斜棱柱的侧棱长是l ,侧面积和体积分别是S 斜棱柱侧和V 斜棱柱,它的直截面的周长和面积分别是1c 和1S ,则①1S c l =斜棱柱侧.②1V S l =斜棱柱.34．作截面的依据三个平面两两相交，有三条交线，则这三条交线交于一点或互相平行.35．棱锥的平行截面的性质如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比（对应角相等，对应边对应成比例的多边形是相似多边形，相似多边形面积的比等于对应边的比的平方）；相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比．36. 面积射影定理'cos S S θ=. (平面多边形及其射影的面积分别是S 、'S ，它们所在平面所成锐二面角的为θ).37.欧拉定理(欧拉公式)2V F E +-=(简单多面体的顶点数V 、棱数E 和面数F).（1）E =各面多边形边数和的一半.特别地,若每个面的边数为n 的多边形，则面数F 与棱数E 的关系：12E nF =； （2）若每个顶点引出的棱数为m ，则顶点数V 与棱数E 的关系：12E mV =. 38.球的半径是R ，则其体积343V R π=, 其表面积24S R π=． 147.球的组合体(1)球与长方体的组合体:长方体的外接球的直径是长方体的体对角线长.(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.(3) 球与正四面体的组合体:棱长为a 的正四面体的内切球的半径为12a ,外接球的半径为4a . 148．柱体、锥体的体积 13V Sh =柱体（S 是柱体的底面积、h 是柱体的高）. 13V Sh =锥体（S 是锥体的底面积、h 是锥体的高）.。