初中数学九年级《频率分布直方图》
合集下载
【最新】青岛版九年级数学下册第六章《频数直方图(1)》精品课件.ppt
59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
人数 2
9 10 14 5
注意：一般情况（1）可以由组距来求组数；（2）当数据个数 小于40时，组数为5－8组；当数据个数40—100个时，组数为7 －10组；
归纳绘直方图的方法： zxxkw
1.根据图纸的大小，画出两条相互垂直的射线，两端加上 箭头.
•
THE END 17、一个人如果不到最高峰，他就没有片刻的安宁，他也就不会感到生命的恬静和光荣。2021/1/122021/1/122021/1/122021/1/12
谢谢观看
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
zxxkw
我市人民医院2014年2月份新生婴儿体重频数分布表
组别（kg）
2.75—3.15 3.15—3.55 3.55—3.95 3.95—4.35 4.35—4.75 4.75—5.15
划记
频数
2
正
7
正
6
学 科网
2
2
1
思考:
频数分布表可以反映 数据的分布情况，那 么还有没有其它方式 能更直接、更形象的 反映数据分布的情况 呢？
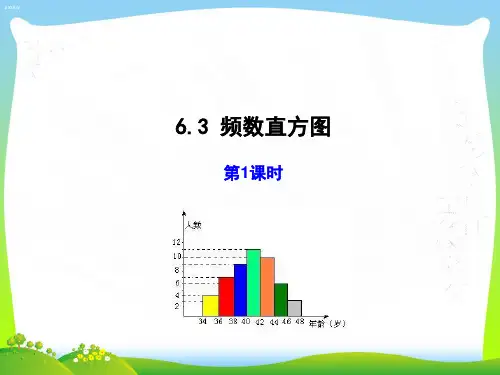
人数 2
9 10 14 5
注意：一般情况（1）可以由组距来求组数；（2）当数据个数 小于40时，组数为5－8组；当数据个数40—100个时，组数为7 －10组；
归纳绘直方图的方法： zxxkw
1.根据图纸的大小，画出两条相互垂直的射线，两端加上 箭头.
•
THE END 17、一个人如果不到最高峰，他就没有片刻的安宁，他也就不会感到生命的恬静和光荣。2021/1/122021/1/122021/1/122021/1/12
谢谢观看
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
zxxkw
我市人民医院2014年2月份新生婴儿体重频数分布表
组别（kg）
2.75—3.15 3.15—3.55 3.55—3.95 3.95—4.35 4.35—4.75 4.75—5.15
划记
频数
2
正
7
正
6
学 科网
2
2
1
思考:
频数分布表可以反映 数据的分布情况，那 么还有没有其它方式 能更直接、更形象的 反映数据分布的情况 呢？
初中数学九年级《频率分布直方图》
二、排除法：
排除法根据题设和有关知识，排除明显不正确选项，那么剩下
惟一的选项，自然就是正确的选项，如果不能立即得到正确的选 项，至少可以缩小选择范围，提高解题的准确率。排除法是解选 择题的间接与二次函数y=ax2+bx+c，它们在同 一坐标系内的大致图象是（ ）
）。
4、逻辑排除法 例5、顺次连接平行四边形各边中点所得的四边形一定是（ ） A、正方形 B、矩形 C、菱形 D、平行四边形
三、数形结合法
由已知条件作出相应的图形，再由图形的直观性得出正确 的结论。
例6.直线y=-x-2 和y=x+3 的交点在第（ ）象限。
A. 一
B. 二
C. 三
y
D. 四
Y=x+3
每一小组的频数与数据总数的比值
频率
第一小组的频率
第二小组的频率
1 60
≈ 0.017
3 60
≈ 0.050
在模拟考试中，有学生大题做得 好，却在选择题上失误丢分，主 要原因有二:
1、复习不够全面，存在知识死角，或者部分
知识点不够清楚导致随便应付；
2、解题没有注意训练解题技巧 ，导致耽误宝
贵的时间。
A
128 27
C 12
B 10 D 27
直接变形法
选项变形
练习3 、当a=-1时，代数式(a+1)2+a(a-3) 的值是( )
A -4
B4
C -2
D2
直接代入法
已知代入
练习4、
不等式组
x
2x 3 1 8 2x
的最小整数解是 ( )
A -1 B 0
C2 D3
直接代入法
频数(率)分布直方图教案
教学过程一、复习预习Ⅰ．提出问题，创设情境收集数据、整理数据、描述数据是统计的一般过程。
我们学习了条形图、折线图、扇形图等描述数据的方法，今天我们学习另一种描述数据的统计图——直方图。
Ⅱ．导入新课频数分布直方图问题：为了参加全校各年级之间的广播体操比赛，七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛。
为此收集到这63名同学的身高（单位：㎝）如下：15 81581616815915915115815916 815815415815416915815815815 91671715316161591591614 916316316217216115315616216 216315716216216115715716415 515616516615615416616416515 6157153165159157155164156选择身高在哪个范围的学生参加呢？为了使选取的参赛选手身高比较整齐，需要知道数据（身高）的分布情况，即在哪些身高范围内的学生比较多。
为此我们把这些数据适当分组来进行整理。
1、计算最大值与最小值的差（极差）最小值是149，最大值是172，它们的差是23。
说明身高的变化范围是23㎝.2、决定组距与组数把所有的数据分成若干组，每个小组的两个端点之间的距离（组内数据的取值范围）称为组距。
作等距分组（各组的组距相同），取组距为3㎝（从最小值起每隔3㎝作为一组）。
232733最大值－最小值＝＝组距将数据分成8组：149≤x ＜152，152≤x ＜155，…，170≤x ＜173.注意：①根据问题的需要各组的组距可以相同或不同；②组距和组数的确定没有固定的标准，要凭借经验和所研究的具体问题来决定；③当数据在100个以内时，按照数据的多少，常分成5～12组，一般数据越多分的组数也越多。
3、频数分布表对落在各个小组内的数据进行累计，得到各个小组内的数据的个数（叫做频数）。
用表格整理可得频数分布表：频数分布表身高分组 划记 频数 149≤x ＜152 2 152≤x ＜155 正一 6 155≤x ＜158 正正 12 158≤x ＜161 正正正 19 161≤x ＜164 正正 10164≤x ＜167正8167≤x ＜1704 170≤x ＜1732从表格中你能看出应从哪个范围内选队员吗？可以看出，身高在155≤x ＜158，158≤x ＜161，161≤x ＜164三个组的人数最多，一共有12＋19＋10＝41人，因此，可以从身高在155～164㎝（不含164㎝）的学生中选队员。
2.2.1频率分布直方图
布直方图，则从图中可以看出被处罚的汽车大约有( )
A．30辆
B．40辆
C．60辆
D．80辆
数学 必修3(配人教版)
2.2.1用样本的频率分布估计总体分布
通过抽样，我们获得了100位居民某年的月平均用水量(单位：t) ，如下表： 3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6 3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4 3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8 3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1 3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3 3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0 2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3 2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4 2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4 2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
x轴：数据单位
知识探究（二）：频率分布直方图
频率/组距
0.5 0.4 0.3 0.2 0.1
宽度：组距 高度： 频率
组距
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
各组的频率在图中哪里显示出来？
小长方形的面积= 组距×
频率 =
组距
各小长方体的面积之和是否为定值？
频率
各小长方形的面积之和为1.
频率：样本中某个组的频数和样本容量的比，
概率专题：频率分布直方图
为小区服务，这样的话小区住户满意度会高一些．
例 8．某校在一次期末数学测试中，为统计学生的考试情况，从学校的 2000 名学生中随机抽取 50 名学生的
考试成绩，被测学生成绩全部介于 65 分到 145 分之间（满分 150 分）
，将统计结果按如下方式分成八组：
第一组[65，75）
，第二组[75，85），……第八组[135，145]，如图是按上述分组方法得到的频率分布直方
区住户的满意度等级为不满意的概率大？若是要选择一个物业公司来管理老旧小区的物业，从满意度角
度考虑，应该选择哪一个物业公司？说明理由．
【解析】解：（Ⅰ）作出如图所示的频率分布直方图，
B 区住户满意度评分的频率分布直方图如图所示
A 区住户满意度评分的平均值为 45×0.1+55×0.2+65×0.3+75×0.2+85×0.15+95×0.05＝67.5；
）内，
设中位数为 m，则 0.20+0.24+（m﹣70）×0.036＝0.5，
解得 m≈71.67，
所以中位数约为 71.67．
例 11．某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系，从若干个高中男
在[120，140）之间的学生人数为：100×（10×0.030+0.020）＝50 人，
1
又用分层抽样的方法在[120，140）之间的学生 50 人中抽取 5 人，即抽取比例为： ，
10
1
所以成绩在[120，130）之间的学生中抽取的人数应，30× 10 =3，即 b＝3，
故选：D．
例 2．从某企业生产的某种产品中随机抽取 100 件，测量这些产品的一项质量指标值，由测量表得如下频数
例 8．某校在一次期末数学测试中，为统计学生的考试情况，从学校的 2000 名学生中随机抽取 50 名学生的
考试成绩，被测学生成绩全部介于 65 分到 145 分之间（满分 150 分）
，将统计结果按如下方式分成八组：
第一组[65，75）
，第二组[75，85），……第八组[135，145]，如图是按上述分组方法得到的频率分布直方
区住户的满意度等级为不满意的概率大？若是要选择一个物业公司来管理老旧小区的物业，从满意度角
度考虑，应该选择哪一个物业公司？说明理由．
【解析】解：（Ⅰ）作出如图所示的频率分布直方图，
B 区住户满意度评分的频率分布直方图如图所示
A 区住户满意度评分的平均值为 45×0.1+55×0.2+65×0.3+75×0.2+85×0.15+95×0.05＝67.5；
）内，
设中位数为 m，则 0.20+0.24+（m﹣70）×0.036＝0.5，
解得 m≈71.67，
所以中位数约为 71.67．
例 11．某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系，从若干个高中男
在[120，140）之间的学生人数为：100×（10×0.030+0.020）＝50 人，
1
又用分层抽样的方法在[120，140）之间的学生 50 人中抽取 5 人，即抽取比例为： ，
10
1
所以成绩在[120，130）之间的学生中抽取的人数应，30× 10 =3，即 b＝3，
故选：D．
例 2．从某企业生产的某种产品中随机抽取 100 件，测量这些产品的一项质量指标值，由测量表得如下频数
众数、平均数、中位数与频率分布直方图的关系
众数、平均数、中位数与频率分布直方图的关系
众数、平均数、中位数与频率分布直方图的关系，这一块知识点都不难，就是我们在平时的学习过程中不重视或者说不注意所以会导致有时候没有思路，不知道怎么操作，今天给大家详细介绍一下这种关系。
1、众数
众数在样本数据的频率分布直方图中就是最高矩形中点的横坐标大家通过上述图中，应该很明显，众数就是最高矩形中点的位置即为2.25
2、中位数
在样本中，有50%的个体小于或者等于中位数，同时也有50%的个体大于或者等于中位数，所以，在频率分布直方图中，在中位数的左边和右边直方图的面积是相等的。
从而我们可以根据这个来估算出中位数的大小值。
从上数频律分布直方图中，我们可以计算出来，大致的位置。
3、平均数
平均数是频率分布直方图的重心，他等于频率分布直方图中每个小矩形的面积（即落在改组中的频率）乘以小矩形底边中点的横坐标（组中值）之和。
今天比较忙，就先介绍到这里。
第二课时 频数分布直方图与频率分布直方图
12
课前预习
课堂互动
素养达成
@《创新设计》
[微思考] 1.为什么要对样本数据进行分组？
提示 不分组很难看出样本中的数字所包含的信息，分组后，计算出频率，从 而可估计总体的分布特征. 2.频数、频率分布直方图有什么优缺点？ 提示 (1)优点：可以直观、形象地反映样本的分布规律，清楚地看出数据分布 的总体趋势. (2)缺点：从频数、频率分布直方图得不出原始的数据内容，把数据绘制成频率 (或频数)分布直方图后，原有的具体数据信息就抹掉了.
13
课前预习
课堂互动
素养达成
@《创新设计》
3.在柱形图中，若纵轴表示频数(或频率)，这种柱形图与频数(或频率)分布直方 图有什么本质区别？ 提示 柱形图中，纵轴表示原始数据的频数或频率，频数分布直方图的纵轴表 示区间对应的频数，频率分布直方图的纵轴表示的不是频率，而是区间对应的 频率与区间宽度之比.
课堂互动
素养达成
@《创新设计》
拓展深化 [微判断]
频数 1.在频率分布直方图中，相应的频率＝样本容量.( √ ) 2.在频数或频率分布折线图中，折线图与横轴的左右两个交点是没有实际意义
的.( √ ) 3.上节所学的统计图没有丢失原始数据，频数或频率分布直方图看不出原始数
据.( √ )
9
课前预习
课堂互动
@《创新设计》
4
课前预习
课堂互动
素养达成
@《创新设计》
问题 1.直接用前面提到过的统计图来表示上述数据，方便可行吗？ 2.怎样才能直观地表示出上述数据的大致分布情况(比如指出哪个区间的数据比 较多，哪个区间的数据比较少)? 提示 1.由于数据太多，直接用前面提到的统计图表示太麻烦也无必要. 2.将数据按照一定的方式进行“压缩”，然后再用图来直观地表示压缩后的数据. 因为我们关心的是数据的大致分布情况，因此可以事先确定出几个区间，然后统 计落在每一个区间内的数的个数，最后将统计的结果用图示表示.
直方图(201909)
例题
抽查某地区55名12岁男生的身高（单位：cm）的测 量值如下：
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2
总体分布的估计
直方图
复习
总体分布
总体取值的概率分布规律通常称为总体分布。 频率分布与总体分布的关系:
(1)通过样本的频数分布、频率分布可以估计 总体的概率分布.
抽样分布频率精确地反映了总体 取值的概率分布规律。
(2)研究总体概率分布往往可以研究其样本的 频数分布、频率分布.
试从以上数据中，对该地区12岁男生的身高情况进行大 致的推测。
； 新视觉影院 https:// 新视觉影院
；
尚书令王俭造太庙二室及郊配辞 宣阳底定 事非一揆 思所以敬守成规 七年正月甲寅 有何不可 明堂夕牲之夜 升配庙廷 郊丁社甲 东莞太守臧灵智为交州刺史 方乎隆周之册 而不列于乐官也 在右执法西北一尺四寸 己亥 光临亿兆 为犯 沈攸之苞祸 文明焕 非怠非荒 则裁以庙略 然舞曲总名 起此矣 放斥昏凶 郊奉礼毕 斩草日建旒与不 五月己巳 黄门十人 明旦乃设祭 除广兴郡公沈昙亮等百二十二人 总鉴尽人灵
频率分布直方图与折线图
探究新知
条形图
人数 25 20 15 10 5 0 一号 二号 三号 四号
150.5153.5156.5 159.5162.5165.5168.5171.5 174.5 177.5 180.5 身高/cm 频率/组距 0.08
(3)条形图和直方图的有哪些区别？
直方图
0.06
一号 二号 0.04 三号 四号
实际应用
问题6.若两个研究小组分别抽样，是否得到相同的样 本？对总体估计是否一定相同？是否会有很大的差异？ 问题7.比较一下几种表示频率分布的方法的优缺点.
名称
频率分布表 频率直方图 频率折线图
优点
数据清晰明了，便于查阅 形象直观，对比效果强烈 反映发展变化的趋势
不足
课堂小结
样本 频率分布表
频率分布直方图
频率分布折 线图
Байду номын сангаас
0.08 0.06 0.04 0.02
150.5153.5 156.5 159.5 162.5165.5168.5171.5174.5177.5 180.5
频率直方 图
身高/cm
频率/组距
频率分布 折线图
0.08 0.06 0.04 0.02
150.5 153.5
180.5
身高/cm
问题5.若组距取得越小，则频率折线光滑程度会怎 样？
问题3.类比频数条形图的画法，谈谈根据频率分布表 如何画出频率分布直方图！
名称 频数条形图 频率直方图
横轴 分类
纵轴 频数
探究新知
例1.从某校高一 年级的1002名新 生中用系统抽样 的方法抽取一个 容量为100的身高 样本，频率分布 表如下（单位： cm）．试作出该 样本的频率分布 图．
频率分布直方图
频数 8 6 4 2 0 22.5 24.5 26.5 28.5 30.5 32.5 数据
1、一个样本含有20个数据:35,31,33,35,37,39, 35,38,40,39,36,34,35,37,36,32,34,35,36,34.
在列频数分布表时,如果组距为2,
那么应分成___组,32.5~34.5这组的频数为_____
0~35 36~47 48~59 60~71 72~83 84~95 96~107 108~120
0
分数
小结
通过本节学习，我们了解了频数分布的意义及 获得一组数据的频数分布的一般步骤:
(1)计算极差；
(2) 决定组距和组数；
(3) 决定分点；
(4) 列出频数分布表；
(5)画出频数分布直方图和频数折线图。
根据频数分布表绘制直方图
不及格的 学生数最 少!!!
绘制频数折线图
将直方图中每个小 长方形上面一条边 的中点顺次连结起 来,即可得到频数 折线图
画频数分布直方图的一般步骤:
(1) 计算最大值与最小值的差(极差).
极差:
(2) 决定组距与组数:
注意：一般情况
极差/组距=_______ 数据分成_____组.
解： （4）列频数分布表:
分组 频数记录 频数 22.5~ 24.5~ 26.5~ 28.5~ 30.5~ 合计 24.5 26.5 28.5 30.5 32.5
ห้องสมุดไป่ตู้
2
3
8
4
3
20
例题:已知一个样本：27，23，25，27，29，
31，27，30，32，21，28，26，27，29， 28，24，26，27，28，30。 列出频数分布表， 并绘出频数分布直方图和频数折线图。 解： （5）画频数分布直方图和频数折线图:
1、一个样本含有20个数据:35,31,33,35,37,39, 35,38,40,39,36,34,35,37,36,32,34,35,36,34.
在列频数分布表时,如果组距为2,
那么应分成___组,32.5~34.5这组的频数为_____
0~35 36~47 48~59 60~71 72~83 84~95 96~107 108~120
0
分数
小结
通过本节学习，我们了解了频数分布的意义及 获得一组数据的频数分布的一般步骤:
(1)计算极差；
(2) 决定组距和组数；
(3) 决定分点；
(4) 列出频数分布表；
(5)画出频数分布直方图和频数折线图。
根据频数分布表绘制直方图
不及格的 学生数最 少!!!
绘制频数折线图
将直方图中每个小 长方形上面一条边 的中点顺次连结起 来,即可得到频数 折线图
画频数分布直方图的一般步骤:
(1) 计算最大值与最小值的差(极差).
极差:
(2) 决定组距与组数:
注意：一般情况
极差/组距=_______ 数据分成_____组.
解： （4）列频数分布表:
分组 频数记录 频数 22.5~ 24.5~ 26.5~ 28.5~ 30.5~ 合计 24.5 26.5 28.5 30.5 32.5
ห้องสมุดไป่ตู้
2
3
8
4
3
20
例题:已知一个样本：27，23，25，27，29，
31，27，30，32，21，28，26，27，29， 28，24，26，27，28，30。 列出频数分布表， 并绘出频数分布直方图和频数折线图。 解： （5）画频数分布直方图和频数折线图:
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
组数=
最大值-最小值 组距
=
23 3
=
7
2 3
组数应是8组
组距 与组数
2、决定组距与组数： 将这组数据分组，并决定每个
小组的两个端点的距离。
组数=
最大值-最小值 组距
=
23 3
=
7
2： 将数据按3厘米的组距分组时，可以 分成以下8组：
146~149，149~152，152~155，155~158， 158~161，161~164，164~167，167~170。
每一小组的频数与数据总数的比值
频率
第一小组的频率
第二小组的频率
1 60
≈ 0.017
3 60
≈ 0.050
在模拟考试中，有学生大题做得 好，却在选择题上失误丢分，主 要原因有二:
1、复习不够全面，存在知识死角，或者部分
知识点不够清楚导致随便应付；
2、解题没有注意训练解题技巧 ，导致耽误宝
贵的时间。
要知道60名女生的身高数据在各个小范围 的所占的比的大小，需要对数据进行整理
1、计算最大值与最小值的差： 最大值是169，最小值是146
它们的差是 169-146=23（厘米）
知道这组数据的变动的范围有 多大。
146 …… 169
23（厘米）
2、决定组距与组数： 将这组数据分组，并决定每个
小组的两个端点的距离。
频数
频率
4、列频率分布表：
分
组频数累积频
数频 率
145.5~148.5
1
0.017
148.5~151.5
3
0.050
151.5~154.5 154.5~157.5
6
0.100
8
0.133
157.5~160.5
18
0.300
160.5~163.5
11
0.187
163.5~166.5
10
0.167
166.5~169.5 合计
3
0.050
60
1.000
5、画频率分布直方图：
频率 组距
身高 (厘米)
145.5 148.5 151.5 154.5 157.5 160.5 163.5 166.5 169.5
小正方形的面积是什么？
决定组数与组距的一般方法：
数据越多，分得的组数也越多。
假如数据总数为n 当n≤50时，则分为5 ~ 8组； 当50≤n≤100时，则分为8 ~ 12 组；
167 154 159 166 169 159 156 166 162 158 159 156 166 160 164 160 157 156 157 161 160 156 166 160 164 160 157 156 157 161 158 158 153 158 164 158 163 158 153 157 162 162 159 154 165 166 157 151 146 151 158 160 165 158 163 163 162 161 154 165 162 162 159 157 159 149 164 168 159 153
返回
它们究竟属于哪一组？
① 146~149
② 149~152
149
③ 152~155
④ 155~158
⑤ 158~161
158
⑥ 161~164
⑦ 164~167
⑧ 167~170
167
落在各个小组内的数据的个数
145.5~148.5
148.5~151.5
频数
167 154 159 166 169 159 156 166 162 158 159 156 166 160 164 160 157 156 157 161 160 156 166 160 164 160 157 156 157 161 158 158 153 158 164 158 163 158 153 157 162 162 159 154 165 166 157 151 146 151 158 160 165 158 163 163 162 161 154 165 162 162 159 157 159 149 164 168 159 153
下面举例再回顾一下解数学选择题的几种常用方 法，供大家复习时参考，希望对同学们有所启发和帮 助。
一、直接法：
直接根据选择题的题设，通过计算、推理、判断得出正确选项
例1、抛物线y=x2-4x+5的顶点坐标是（ A、（-2，1） B、（-2，-1） C、（2，1） D、（2，-1）
）。
类比：点A为数轴上表示-2的动点，
A
128 27
C 12
B 10 D 27
直接变形法
选项变形
练习3 、当a=-1时，代数式(a+1)2+a(a-3) 的值是( )
频率分布直方图 (1)
对一组数据的考察，可以用 那些统计量？
平均数
众数 中位数
方差（标准差）
要了某班一次数学考试成绩， 90分到100分有多少人， 80分到90分有多少人， 70分到80分有多少人，
…… 60分以下有多少人， 又该用什么统计方法？
为了解中学生的身体发育情况，对某中 学同年龄的60名女生的身高进行测量，结果 如下（单位：厘米）
选择题考查的内容覆盖了初中阶段所学的重要 知识点，要求学生通过计算、推理、综合分析进行判 断，从“相似”的结论中排除错误选项的干扰，找到 正确的选项。部分学生碰到选择题提笔就计算，答题 思维比较“死”，往往耗时过多，如果一个选择题是 "超时"答对的,那么就意味着你已隐性丢分了,因为占 用了解答别的题目的时间.因此，除了具备扎实的基 本功外，巧妙的解题技巧也是必不可少的。
思考一下：有什么不妥吗？
看一看
3、决定分点： 将数据按3厘米的组距分组时，可以 分成以下8组：
146~149，149~152，152~155，155~158， 158~161，161~164，164~167，167~170。
145.5~148.5 148.5~151.5 151.5~154.5 154.5~157.5 157.5~160.5 160.5~163.5 163.5~166.5 166.5~169.5
当A沿数轴移动4个单位到点B时，点B
所表示的实数是( )
A2
B -6
C -6或2 D 以上都不对
直接分类法
练习1、商场促销活动中，将标价为 200元的商品，在打8折的基础上，再 打8折销售，现该商品的售价是( ) A 160元 B 128元 C 120元 D 88元
直接计算
2
练8习2、下列与 2 是同类二次根式 的是( 10)