福建省福州市2013届高三5月质检试题(word版)数学理
2013福州5月份质检理数(word版)

2013年福州市5月高中毕业班质量检查数学(理科)试卷第Ⅰ卷 (选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题所给的四个答案中有且只有一个答案是正确的,把正确选项涂在答题卡的相应位置上.) 1.i 是虚数单位,复数(2)(1)z x i i =++,R ∈x .若z 的虚部为4,则x 等于A .2B .-2C .1D .-12. 要得到函数tan(2)3y x π=+的图象,只须将x y 2tan =的图象上的所有的点 A.向左平移3π个单位长度 B.向右平移3π个单位长度C.向左平移6π个单位长度D.向右平移6π个单位长度3. 根据某市环境保护局公布2007-2012这六年每年的空气质量优良的天数,绘制折线图如图.根据图中信息可知,这六年的每年空气质量优良天数的中位数是 A.300 B. 305C.315D. 3204.已知函数()af x x x=+,则“4a =”是“函数()f x 在(2,)+∞上为增函数”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件 5.已知命题“直线l 与平面α有公共点”是真命题,那么下列命题:①直线l 上的点都在平面α内;②直线l 上有些点不在平面α内; ③平面α内任意一条直线都不与直线l 平行. 其中真命题的个数是 A.3 B.2 C.1 D.06.已知等比数列{}n a 的公比2=q ,且462,,48a a 成等差数列,则{}n a 的前8项和为 A.127B.255C.511D.10237.设88018(1),x a a x a x +=+++ 则0,18,,a a a 中奇数的个数为 A .2B .3C .4D .58.已知点P 是△ABC 所在平面内的一点,边AB 的中点为D ,若2(1)PD PA CB λ=-+,其中R ∈λ,则点P 一定在A .AB 边所在的直线上 B .BC 边所在的直线上 C .AC 边所在的直线上D .△ABC 的内部天数年份3503403303203103002902007 2008 2009 2010 2011 2012第3题图9.对于任意给定的实数m ,直线03=+-m y x 与双曲线0(12222>=-a by a x ,)0>b 最多有一个交点,则双曲线的离心率等于 A .2B .2C .3D .1010.对于函数()f x 与()g x 和区间D ,如果存在0x D ∈,使00()()1f x g x -≤,则称0x 是函数()f x 与()g x 在区间D 上的“友好点”.现给出两个函数: ①2()f x x =,22)(-=x x g ; ②()f x x =,()2g x x =+;③xx f -=e )(,1()g x x=-; ④()f x ln x =,x x g =)(,则在区间()0,+∞上的存在唯一“友好点”的是A .①②B .③④C . ②③D .①④二、填空题11.一个三棱锥的正视图和侧视图及其尺寸如图所示,则该三棱锥的俯视图的面积为 .12.已知函数()f x cos ,0,1,0,x x x ≥⎧=⎨<⎩,则22()d f x x π-⎰的值等于 .13. 已知程序框图如右图所示,执行该程序,如果输入10=x ,输出4=y ,则在图中“?”处可填入的算法语句是 (写出以下所有满足条件的序号).①1-=x x ; ②2-=x x ; ③3-=x x ; ④4-=x x . 14.在区间]2,0[上任取两个数a ,b ,能使函数()f x 1ax b =++在区间]1,1[-内有零点的概率等于________.15.设数列}{n a 是由集合t s ts<≤+0|33{,且s ,}Z ∈t 中所有的数从小到大排列成的数列,即41=a ,102=a ,123=a ,284=a ,a 5=30,a 6=36,…,若2013a =nm33+(0m n ≤<,且m ,}n ∈Z ,则n m +的值等于____________. 三、解答题16已知平面向量a (sin ,3)3x π=错误!未找到引用源。
福建省福州市2013届高三5月质检试题(word版)英语

2013年福州市高中毕业班质量检查英语试卷(完卷时间:120分钟;满分:150分)本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷1至11页,第二卷12页。
注意事项:1 答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2. 考生作答时,请将答案答在答题卡上,请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
在草稿纸、试卷上答题无效。
3. 选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4. 保持答题卡卡面清洁,不折叠,不破损。
考试结束后,将本试卷和答题卡一并交回。
第一卷(选择题共115分)第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1 What does the woman want to do?A. Read today’s newspaper.B. Read yesterday’s newspaper.C. Buy a new copy of China Daily,2. Where are the speakers?A. On a plane.B. In an office.C. In a restaurant.3. What is the relationship between the speakers?A. Boss and employee.B. Hairdresser and customer.C. Doctor and patient.4. How does the man feel?A. Regretful.B. Excited.C. Disappointed.5. What does the man do on his microblog (微博)A. He writes about his fashion designs.B. He predicts what is going to be in fashionC. He writes about the fashion shows he attended.第二节(共15小题;每小题1.5分,满分22.5分}请听下面5段对话或独白。
福建省福州市2014届高三质检数学理试题 Word版含解析

2014年福州市高中毕业班质量检测理科数学试卷第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{(,)lg },{(,)}A x y y x B x y x a ====,若A B =∅,则是实数a 的取值范围是( )A. 1a <B. 1a ≤C. 0a <D. 0a≤2.“实数1a =”是“复数(1)ai i +(,a R i ∈”的 ( )A.充分非必要条件B.必要非充分条件C.充要条件D.既不是充分条件又不是必要条件3.执行如图所示的程序框图,输出的M 值是 ( )A .2B .1-C .12D .2- 【答案】B4.命题“x R ∃∈,使得()f x x =”的否定是 ( ) A. x R ∀∈,都有()f x x = B.不存在x R ∈,使()f x x ≠ C. x R ∀∈都有()f x x ≠ D. x R ∃∈使()f x x ≠5.已知等比数列{}n a 的前n 项积记为n ∏,若3488a a a =,则 9∏= ( ) A.512 B.256 C.81 D.166.如图,设向量(3,1),(1,3)OA OB ==,若OC OA OB λμ=+,且1λμ≥≥,则用阴影表示C 点所有可能的位置区域正确的是 ( )BAxxx7.函数()f x 的部分图像如图所示,则()f x 的解析式可以是 ( ) A. ()sin f x x x =+ B. cos ()xf x x=C.()cosf x x x = D. 3()()()22f x x x x ππ=--x考点:1.函数的图像.2.分类讨论.3.列举排除的数学思想.4.归纳化归的数学思想.8.已知1F 、2F 是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,若双曲线左支上存在一点一点P 与点2F 关于直线bxy a=对称,则该双曲线的离心率为 ( ) A.2B.C.D. 29.若定义在R 上的函数f (x )满足f (-x )=f (x ), f (2-x )=f (x ),且当x ∈[0,1]时,其图象是四分之一圆(如图所示),则函数H (x )= |x e x|-f (x )在区间[-3,1]上的零点个数为 ( )A.5B.4C.3D.2x【答案】B 【解析】试题分析:因为定义在R 上的函数f(x)满足f(-x)=f(x),所以函数()f x 为偶函数,又因为f(2-x)=f(x),所以函数()f x 关于直线1x =对称.因为函数H(x)= |xe x|-f(x)在区间[-3,1]上的零点即等价求方程()x f x xe =的解的个数.等价于函数x y xe =和函数()y f x =的图像的交点个数,由图象可得共有4个交点.故选B.考点:1.函数的性质.2.数形结合的思想.3.函数图像的正确表示及绘制.10.已知函数32()f x x bx cx d =+++(b 、c 、d 为常数),当(0,1)x ∈时取极大值,当(1,2)x ∈时取极小值,则221()(3)2b c ++-的取值范围是( ) A.(2B. C. 37(,25)4D. (5,25)第Ⅱ卷(共100分)二、填空题:本大题共5小题,每小题4分,共20分.11.5名同学站成一排,其中甲同学不站排头,则不同的排法种数是______________(用数字作答).12.如图所示,在边长为1的正方形OABC 中任取一点M ,则点M 恰好取自阴影部分的概率为________.14.已知某几何体的三视图(单位:cm)如图所示,则该几何体的表面积为____________.俯视图侧视图正视图15.已知函数1(1)sin 2,[2,21)2(),()(1)sin 22,[21,22)2nn x n x n n f x n N x n x n n ππ+⎧-+∈+⎪⎪=∈⎨⎪-++∈++⎪⎩,若数列{}m a 满足*()()2m ma f m N =∈,且{}m a 的前m 项和为m S ,则20142006S S -=_____________. 【答案】8042 【解析】试题分析:20142006S S -=20072008200920102011201220132014a a a a a a a a +++++++.因为20072007()250122a f ==⨯+,2008(1004)2502a f ==⨯,20092009()250222a f ==+⨯,2010(1005)125022a f ==-+⨯+,2011250222a =-+⨯+,20122503a =⨯,201325032a =+⨯,2014125032a =-+⨯+.所以20142006S S -=8042.考点:1.分段函数的问题.2.数列的思想.3.三角函数的周期性.4.分类列举的数学思想.三、解答题 (本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)16.(本小题满分13分)在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:21006542098874286438210乙地甲地规定:当产品中的此种元素含量15≥毫克时为优质品.(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数); (Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望()E ξ.(II)ξ的取值为1,2,3. 12823101(1),15C C P C ξ⋅===21823107(2),15C C P C ξ⋅===157)3(3100238=⋅==C C C P ξ 所以ξ的分布列为故的数学期望为123.1515155E ξ=⨯+⨯+⨯=() 考点:1.茎叶图的知识.2.列举对比的数学思想.3.数学期望的计算.4.概率知识.17.(本小题满分13分)已知函数2()2cos cos ().f x x x x x R =+∈.(Ⅰ)当[0,]2x π∈时,求函数)(x f 的单调递增区间;(Ⅱ)设ABC ∆的内角C B A ,,的对应边分别为c b a ,,,且3,()2,c f C ==若向量)sin ,1(A m =与向量)sin ,2(B n =共线,求b a ,的值.令-222,262k x k k Z πππππ+≤+≤+∈,18.(本小题满分13分) 如图,直角梯形ABCD 中,090,24ABC AB BC AD ∠====,点,E F 分别是,AB CD 的中点,点G 在EF 上,沿EF 将梯形ABCD 翻折,使平面AEFD ⊥平面EBCF .(Ⅰ)当AG GC +最小时,求证:BD CG ⊥;(Ⅱ)当2B ADGE D GBCF V V --=时,求二面角D BG C --平面角的余弦值.EB【答案】(Ⅰ)参考解析;(Ⅱ)6【解析】试题分析:(Ⅰ)因为当AG GC +最小时,及连结AC 与EF 的交点即为G 点,通过三角形的相似可得到EG 的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相(Ⅱ)解法一:设EG=k ,AD ∥平面EFCB ,∴点D 到平面EFCB 的距离为即为点A 到平面EFCB 的距离.S 四形GBCF =12[(3- k )+4]×2=7-k D GBCF V S AE 四形GBCF -\=鬃13=2(7)3k -又B ADGE ADGE V S BE 四形-=?13=2(2)3k +,B ADGE D GBCF V V --=2,∴4(2)3k +=2(7)3k -,1k ∴=即EG =1设平面DBG 的法向量为1(,,)n x y z =,∵G (0,1,0),∴(2,1,0),BG =-BD =(-2,2,2),则 1100n BD n BG ⎧⋅=⎪⎨⋅=⎪⎩,即222020x y z x y -++=⎧⎨-+=⎩19.(本小题满分13分) 已知动圆C 过定点(1,0),且与直线1x =-相切. (Ⅰ)求动圆圆心C 的轨迹方程;(Ⅱ)设,A B 是轨迹C 上异于原点O 的两个不同点,直线OA 和OB 的倾斜角分别为α和β,①当2παβ+=时,求证直线AB 恒过一定点M ;②若αβ+为定值(0)θθπ<<,直线AB 是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.20.(本小题满分14分)已知函数1()ln()f x x axa=+-,其中a R∈且0a≠(Ⅰ)讨论()f x 的单调区间;(Ⅱ)若直线y ax =的图像恒在函数()f x 图像的上方,求a 的取值范围;(Ⅲ)若存在1210,0x x a-<<>,使得12()()0f x f x ==,求证:120x x +>. 【答案】(Ⅰ)参考解析;(Ⅱ)2ea >;(Ⅲ)参考解析【解析】()h x ∴的最小值为1()2h a -,所以只需1()02h a -> 即1112()ln()022a a a a ⋅---+>,1ln 12a ∴<-,2ea ∴>(Ⅲ)由于当0a <时函数在),1(+∞-a上是增函数,不满足题意,所以0a >21.本小题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则安所做的前两题计分.作答时,先用2B 铅笔在答题卡上把所选题目对应提好右边的方框涂黑,并将所选题号填入括号中. (1)(本小题满分7分)选修4-2:矩阵与变换. 已知矩阵3A c ⎛= ⎝3d ⎫⎪⎭,若矩阵A 属于特征值6的一个特征向量为111α⎛⎫= ⎪⎭⎝,属于特征值1的一个特征向量232α⎛⎫= ⎪-⎭⎝.(Ⅰ)求矩阵A 的逆矩阵; (Ⅱ)计算314A ⎛-⎫⎪⎭⎝ 【答案】(Ⅰ)⎪⎪⎪⎪⎭⎫ ⎝⎛--=-213121321A;(Ⅱ)429434⎛⎫ ⎪⎝⎭【解析】试题分析:(Ⅰ)因为已知矩阵3A c ⎛= ⎝ 3d ⎫⎪⎭,若矩阵A 属于特征值6的一个特征向量为111α⎛⎫= ⎪⎭⎝,属于特征值1的一个特征向量232α⎛⎫= ⎪-⎭⎝.通过特征向量与特征值的关系,可求矩阵A 中的相应参数的值,再通过逆矩阵的含义可求出矩阵A 的逆矩阵.同样可以从通过特征根的方程方面入手,求的结论.(2)(本小题满分7分)选修4-4:坐标与参数方程.在平面直角坐标系xoy 中,以O 为极点,x 轴非负半轴为极轴建立坐标系,已知曲线C 的极坐标方程为2sin 4cos ρθθ=,直线l 的参数方程为:2242x y ⎧=-+⎪⎪⎨⎪=-+⎪⎩(t 为参数),两曲线相交于,M N 两点.(Ⅰ)写出曲线C 的直角坐标方程和直线l 的普通方程; (Ⅱ)若(2,4)P --求PM PN +的值.(3)(本小题满分7分)选修4-5:不等式选讲 设函数()43f x x x =-+-, (Ⅰ)求()f x 的最小值m ;(Ⅱ)当23(,,)a b c m a b c R ++=∈时,求222a b c ++的最小值. 【答案】(Ⅰ)1;(Ⅱ)114【解析】试题分析:(Ⅰ)因为()43f x x x =-+-,所以通过绝对值的基本不等式a b a b +≥-,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.亿折网一折网。
【2013福建省质检】福建省2013届高三毕业班质量检测数学理试题Word版含答案

2013年福建普通高中毕业班质量检查理科数学本试卷分第I 卷(选择题)和第II卷(非选择题),第II 卷第21题为选考题,其他题为必考题.本试卷共5页.满分150分.考试时间120分钟. 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照題号在各题的答题区域(黑色线框)内作答, 超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效. 3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选 择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚. 4. 做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号 涂黑.5. 保持答题卡卡面清洁,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回 参考公式:样本数据n x x x ,21,的标准差 锥体体积公式])()()[(122221x x x x x x n s n -++-+-=Sh V 31=, 其中x 为样本的平均数 其中S 为底面面积,h 为高 柱体体积公式 球的表面积、体积公式 V Sh = 24R S π=,334R V π= 其中S 为底面面积,h 为高 其中R 表示球的半径 第I 卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是 符合题目要求的.1. 已知复数z=1+i,A. z =-1-iB. | =2 D. 2.已知向量a= (m 2,4),b=(1,1)则“m= -2”是“a//b”的 A. 充分而不必要条件B.必要而不充分条件C. 充要条件D.既不充分也不必要条件 3. 函数)22(cos log )(21ππ<<-=x x x f 的图象大致是4. 执行如图所示的程序框图,若输入的x 值为2,则输出的x 值为A. 3B. 126C. 127D. 1285. 设M ,N 是两条不同的直线,A ,β是两个不同的平面.下列命题正确的是A. 若m//n, m 丄β,则n 丄βB. 若m//n ,m //β,则 n //βC. 若m //a ,m//β,则 a //βD. 若n 丄a, n 丄β,则a 丄β6. 已知函数1cos sin 32sin 2)(2-+=x x x x f 的图象关于点(ϕ,0)对称,则 ϕ的值可以是A. -6πC.12π 7. 设抛物线y 2=6x 的焦点为F ,准线为L ,P 为抛物线上一点,PA 丄l,垂足为A,如果ΔAPF 为 正三角形,那么|P F |等于A , 34B . 36C 6D . 128. 在矩形ABCD 中,AB = 1 ,AD),(R ∈+=μλμλ,则μλ3+的最大值为A.4236+ 9. 若函数⎪⎩⎪⎨⎧>≤--=0,ln 0,1)(2x x x kx x x x f 有且只有2个不同的零点,则实数k 的取值范围是A. (-4,0) B, ( -∞ ,0] C. ( -4,0] D, ( - ∞ ,0)10. 设数集S={a,b,c,d}满足下列两个条件:(1)S xy S y x ∈∈∀,,;(2) yz xz y x S z y x ≠≠∈∀则或,,, 现给出如下论断:①A ,B ,C ,D 中必有一个为0; ②A 、b,c ,d 中必有一个为1;③若x∈S且xy =1.,则y ∈S; ④存在互不相等的x,y,z∈S,使得x 2=y,y 2=z. 其中正确论断的个数是A 1 B.2 C. 3 D.4第II 卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡相应位置.11.(x+2)4展开式中含x 2项的系数等于________.12.若变量x,y 满足约束条件⎪⎩⎪⎨⎧≥≤-+≥--20113013y y x y x ,则z =2x +y 的最大值为_____.点A,则ΔMOA的面积等于______.14.如图.A1,A2,…A m-1(m≥2)将区间[0,l] m等分,直线x=0,x=1, y=0和曲线y=e x所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2.在Ω1中任取一点,则该点取自Ω2的概率等于______.15.定义两个实数间的一种新运算“*”:x*y=lg(10x+10y),x,y∈R 当.x①(a*b) * c=a* (b* c); ②(a * b)+c=(a+c) * (b+c);其e正确的结论是_____.(写出所有正确结论的序号)三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16. (本小题满分13分)某几何体ABC-A1B1C1的三视图和直观图如图所示.(I)求证:A1C丄平面AB1C1(II)求二面角C1-AB1 -C的余弦值.17 (本小题满分13分)国IV标准规定:轻型汽车的氮氧化物排放量不得超过80mg/km.根据这个标准,检测单位 从某出租车公司运营的A,B 两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量 进行检测,检测结果记录如下(单位:mg/km)由于表格被污损,数据x ,y 看不清,统计员只记得A 、B 两种出租车的氮氧化物排放量的平均值相等,方差也相等.(I)求表格中x 与y 的值;(II )从被检测的5辆B 种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km” 的车辆数为ξ求ξ的分布列和数学期望.18. (本小题满分13分)如图,我海监船在D 岛海域例行维权巡航,某时刻航行至A 处,此时测得其东北方向与它相距16海里的B 处有一外国船只,且D 岛位于海监船正东(I)求此时该外国船只与D 岛的距离;(II)观测中发现,此外国船只正以每小时4海里的速度 沿正南方向航行.为了将该船拦截在离D 岛12海 里处,不让其进入D 岛12海里内的海域,试确定海 监船的航向,并求其速度的最小值.(参考数据:)19. (本小题满分13分))0(122>>=+b a by 的左、右焦点分别为F 1 F 2 ,(I)求椭圆E 的方程; (II)给出命题:“已知P 是椭圆E 上异于A 1,A 2的一点,直线 A 1P,A 2P 分别交直线l:x=t(t为常数)于不同两点M ,N, 点Q 在直线L 上.若直线PQ 与椭圆E 有且只有一个公共 点P,则Q 为线段MN 的中点”,写出此命题的逆命题,判 断你所写出的命题的真假,并加以证明;(III)试研究(II)的结论,根据你的研究心得,在图2中作出与该双 曲线有且只有一个公共点S 的直线m ,并写出作图步骤. 注意:所作的直线不能与双曲线的渐近线平行.20. (本小题满分14分)已知函数x f =)((I )求a,b 的值及f(x)的单调区间;x 且与曲线y=f(x)没有公共点的直线?证明你的结论; (III )设数列{a n }满足a 1=λ(λ≠l),a n + 1 =f(a n ),若{a n }是单调数列,求实数λ的取值 范围.21. 本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做, 则按所做的前两题记分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑.并 将所选题号填人括号中.(1) (本小题满分7分)选修4-2:矩阵与变换已知矩阵⎪⎪⎭⎫ ⎝⎛--=1234 M ,向量,a=⎪⎪⎭⎫ ⎝⎛= 57a (I)求矩阵M 的特征值及属于每个特征值的一个特征向量;(II)求M 3a(2) (本小题满分7分)选修4-4:极坐标与参数方程如图,在极坐标系中,圆C 的圆心坐标为(1,0),半径为1.(I )求圆C 的极坐标方程;(II)若以极点0为原点,极轴所在直线为x 轴建立平面直角坐标系.已知直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+-=6sin 1πt y t x (3)(本小题满分7分)选修4一5 :不等式选讲 已知函数x x x f -+=52)((I)求证:5)(≤x f ,并说明等号成立的条件;(II)若关于x 的不等式. |2|)(-≤m x f 恒成立,求实数m 的取值范围,。
福建省福州市5月市质检试题及答案电子版
2013年福州市高中毕业班质量检查理科综合能力测试2013年05月19日周日(完卷时间150分钟;满分:300分)解题可能用到的相对原子质量:H - 1、C 一 12、N - 14、0 - 16、Na -23第I卷(必考)本题共18小题,每小题6分,共108分。
选择题(本题共18小题。
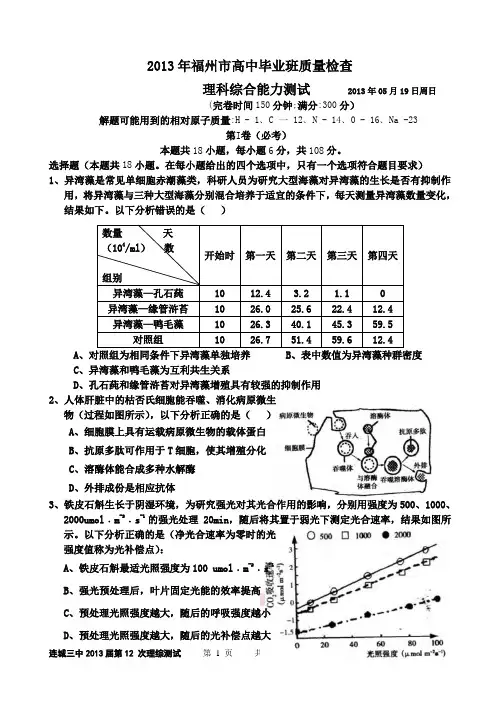
在每小题给出的四个选项中,只有一个选项符合题目要求)1、异湾藻是常见单细胞赤潮藻类,科研人员为研究大型海藻对异湾藻的生长是否有抑制作用,将异湾藻与三种大型海藻分别混合培养于适宜的条件下,每天测量异湾藻数量变化,结果如下。
以下分析错误的是()数量天(104/ml)数开始时第一天第二天第三天第四天组别异湾藻—孔石莼10 12.4 3.2 1.1 0异湾藻—缘管浒苔10 26.0 25.6 22.4 12.4异湾藻—鸭毛藻10 26.3 40.1 45.3 59.5对照组10 26.7 51.4 59.6 12.4 AC、异湾藻和鸭毛藻为互利共生关系D、孔石莼和缘管浒苔对异湾藻增殖具有较强的抑制作用2、人体肝脏中的枯否氏细胞能吞噬、消化病原微生物(过程如图所示),以下分析正确的是()A、细胞膜上具有运载病原微生物的载体蛋白B、抗原多肽可作用于T细胞,使其增殖分化C、溶酶体能合成多种水解酶D、外排成份是相应抗体3、铁皮石斛生长于阴湿环境,为研究强光对其光合作用的影响,分别用强度为500、1000、2000umol﹒m-2﹒s-1的强光处理20min,随后将其置于弱光下测定光合速率,结果如图所示。
以下分析正确的是(净光合速率为零时的光强度值称为光补偿点):A、铁皮石斛最适光照强度为100 umol﹒m-2﹒s-1B、强光预处理后,叶片固定光能的效率提高C、预处理光照强度越大,随后的呼吸强度越小D、预处理光照强度越大,随后的光补偿点越大4、下列实验设计能达到实验目的的是()实验目的A 验证植物顶端优势产生的原因是侧芽生长素浓度过高实验组植物切除顶芽,对照组不切除顶芽B 证明DNA是遗传物质将被35S和31P同时标记的噬菌体侵染细菌,培养一定时间后搅拌离心,分虽测定上清液和沉淀物的放射性强度。
2013年福州市高中毕业班5月质量检查理科综合试题及答案

[来源:学科网ZXXK]第11 页共19 页第12 页共19 页第 13 页 共 19 页2013年福州市高中毕业班质量检查 理科综合试卷参考答案及评分标准评分说明:1.本答案供阅卷评分时使用,考生若写出其它正确答案,可参照评分标准给分。
2.物理计算题只有最后答案而无演算过程的,不得分;只写出一般公式,但未能与试题所给具体条件联系的,不得分。
3.化学方程式、离子方程式未配平,不给分;热化学方程式状态、数据、单位等有误都不给分。
第Ⅰ卷选择题共18题,共108分。
选对的给6分,选错或未选的给0分。
1.C 2.B 3.D 4.D 5.C 6.B 7.A 8.D 9.C 10.C 11.D 12.B 13.B 14.C 15.A 16.C 17.D 18.B 第Ⅱ卷必考部分共10题,共157分。
19.(18分)(1)(6分)AC ;漏选得3分,错选不给分。
(2)(12分)①B (2分);画出的IR 1-图线是一条直线,容易求出电池的电动势和内电阻(3分) ②0.05V (2分,答案在0.045~0.055V 之间均给2分。
);880Ω(2分,答案在850~900Ω之间均给2分。
)③电池内阻过大(3分) 20.(15分)解:(1)沿斜面向上为正方向滑块上滑过程中加速度 22m/s 15m/s 16.06.32.1-=-=∆∆=t v a (4分) 加速度方向沿斜面向下。
(2分) (2)设F 沿斜面向上,则第 14 页 共 19 页ma mg mg F =--θμθcos sin (5分) ma mg mg F ++=θμθcos sin代入数据解得:N 10-=F (2分)力F 的方向平行于斜面向下。
(2分) 21.(19分)解:⑴未挂物体B 时,设弹簧压缩量为1x ,对于物体A 由平衡条件有:030sin 1=︒-mg kx (2分)解得:kmg x 21= (1分)挂上B ,整体平衡时,设弹簧伸长量为2x ,由平衡条件有:︒+=30sin 2mg kx mg (2分)kmgx 22=(1分) 振幅为kmgx x A =+=21 (2分) (2)因1x 与2x 相等,故在此过程中弹簧弹性势能改变量0=∆P E (1分)设最大速度为v ,对于A 、B 及弹簧组成的系统由机械能守恒定律得[来源:学科网]2212122130sin )()(mv x x mg x x mg ⨯=︒+-+ (3分) 将1x 、2x 代入得 kmgk mg v 222== (1分) (3)A 运动到最高点时弹簧的伸长量122x x x += (1分) 设此时细绳对B 的拉力为T 'A 在最高点时,由牛顿第二定律 ma T kx mg ='-+︒30sin (2分)B 在最低点时,由牛顿第二定律 ma mg T =-' (2分)第 15 页 共 19 页联立解得mg T 23=' (1分)22.(20分)解:(1)小球在无电场区,只受重力作用,做加速度等于重力加速度g 的匀加速直线运动,小球在电场区,所受电场力等于重力,做匀速直线运动。
福建省福州市2013届高三上学期期末质检数学理试题
福建省福州市2013届高三上学期期末质量检查数学(理)试题(满分:150分;完卷时间:120分钟)参考公式:用最小二乘法求线性回归方程系数公式1221,ni ii nii x y nx yb a y bx xnx==-==--∑∑第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题所给的四个答案中有且只有一个答案是正确的.把正确选项涂在答题卡的相应位置上.) 1.i 是虚数单位,复数21ii-+在复平面上的对应点所在直线的方程是 A .x+y -2 =0 B .x -y+2 =0 C .x+y+1 =0D .x -y -1=02.如图设全集U 为整数集,集合{|18},{0,1,2}A x N x B =∈≤≤=则下图中阴影部分表示的集合的真子集的个数为 A .3 B .4 C .7 D .8 3.在2012年第30届伦敦奥运会上,中国队教练想从5名女运动员中选出3名参加乒乓球女子团体比赛,不同选法有A .35种B .53种C .35A 种D .35C 种4根据上表,利用最小二乘法得它们的回归直线方程为10.5y x a ∧∧=+,据此模型来预测当x= 20时,y 的估计值为A . 210B .210.5C .211.5D .212.55.函数21,0()2,0xog x x f x a x >⎧⎨-+≤⎩有且只有一个零点的充分不必要条件是A .0a <B .102a <<C .112a << D .01a a ≤>或6.若运行如右图所示的程序,则输出S 的值是A .20122011 B .20112012 C .20122013D .201320127.已知函数()sin()(0,0,||2f x M x M πωϕωϕ=+>><半个周期内的图象如图所示,则函数()f x 的解析式为A .()2sin()6f x x π=+B . ()2sin(2)6f x x π=-C .()2sin()6f x x π=-D .()2sin(2)6f x x π=+8.若函数2(),()1||(0,1),x f x a g x og x a a -==>≠且(3)f ·(3)0g -<则函数()f x 、()g x 在同一坐标系内的大致图象是9.设向量a ,b 是非零向量,若函数()()f x xa b =+ ·()()a xb x R -∈的图象不是直线,且在x=0处取得最值,则必有 A .a ⊥bB .a ∥bC .a ,b 苫不垂直且||||a b =D .a ,b ,不垂直且||||a b ≠10.能够把圆O :x 2 +y 2= 16的周长和面积同时分为相等的两部分的函数称为圆O 的 “和谐函数”,下列函数不是圆O 的“和谐函数”的是 A .3()4f x x x =+ B .5()15xf x nx-=+C .()tan2x f x =D .()xxf x e e-=+第Ⅱ卷(非选择题共100分)二、填空题(本大题共5小题,每小题4分,共20分,把答案填在答题卡的相应位置上。
新课标全国统考区2013届最新高三名校理科数学试题精选分类汇编13:统计
新课标全国统考区(吉林、河南、黑龙江、内蒙古、山西、云南)2013届最新高三名校理科数学试题精选分类汇编13:统计一、选择题1 .(河南省郑州市2013届高三第三次测验预测数学(理)试题)已知实数:x ,y 取值如下表:从所得的散点图分析可知::y 与:r 线性相关,且yˆ==0. 95x+a ,则a 的值是 ( )A .1.30B .1. 45C .1. 65D .1. 80【答案】B2 .(河南省商丘市2013届高三第三次模拟考试数学(理)试题)为防止某种疾病,今研制一种新的预防药,2K 的观测值为3.2079,则在犯错误的概率不超过( )的前提下认为“药物对防止某种疾病有效”参考数据:( )A .0.025B .0.05C .0.010D .0.10【答案】D3 .(河南省六市2013届高三第二次联考数学(理)试题)某公司对下属员工在蛇年春节期间收到的祝福短信数量进行了统计,得到了如图所示的频率分布直方图,如果该公司共有员工200人,则收到125条以上的大约有( )A .6人B .7人C .8人D .9人【答案】C4 .(河北省石家庄市2013届高中毕业班第二次模拟考试数学理试题(word 版) )给定一组数据x 1,x 2,,x 20若这组数据的方差为3,则 数据2x 1+3,2x 2+3,,2x 20+3的方差为( )A .6B .9C .12D .15【答案】C二、填空题5 .(云南省2013年第二次高中毕业生复习统一检测数学理试题(word 版) )一个射击训练,某小组的成绩只有7环、8环、9环三种情况,且该小组的平均成绩为8.15环,设该小组成绩为7环的有x 人,成绩为8环、9环的人数情况见下表:那么=_________________.【答案】56 .(吉林省吉林市2013届高三三模(期末)试题 数学理 )在一次考试中,5名学生的数学和物理成绩如下表:(已知学生的数学和物理成绩具有线性相关关系)现已知其线性回归方程为∧∧+=a x y 36.0,则根据此线性回归方程估计数学 得90分的同学的物理成绩为_______________.(四舍五入到整数)【答案】737 .(河南省豫东、豫北十所名校2013届高三阶段性测试(四) 数学(理)试题(word 版))已知某化妆品的广告费用x(万元)与销售额y(百万元)的统计数据如下表所示:从散点图分析,y 与x 有较强的线性相关性,且a x yˆ95.0ˆ+=,若投入广告费用5万元,预计销售额为_________百万元.【答案】7.358 .(2013年长春市高中毕业班第四次调研测试理科数学)给出下列5种说法:①在频率分布直方图中,众数左边和右边的直方图的面积相等;②标准差越小, 样本数据的波动也越小;③回归分析就是研究两个相关事件的独立性;④在回归分 析中,预报变量是由解释变量和随机误差共同确定的;⑤相关指数2R 是用来刻画回归效果的,2R 的值越大,说明残差平方和越小,回归模型的拟合效果越好.其中说法正确的是____________(请将正确说法的序号写在横线上). 【答案】【命题意图】本小题通过统计学基本定义问题考查学生的统计学的思想,是一道中档难度的综合试题.【试题解析】由统计学的相关定义可知,②④⑤的说法正确.三、解答题 9 .(2013年长春市高中毕业班第四次调研测试理科数学)为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000 株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:(1) 再从这10株玉米中随机 选出3株,求选到的3株之中既有圆粒玉米又有皱粒玉米的概率;(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下 认为玉米的2()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)【答案】【命题意图】本小题通过统计与概率的相关知识,具体涉及到随机变量的分布列、数学期望的求法和统计案例中独立性检验等知识内容,考查学生对数据处理的能力,对考生的运算求解能力、推理论证能力都有较高要求. 本题属于统计概率部分综合题,对考生的统计学的知识考查比较全面,是一道的统计学知识应用的基础试题.【试题解析】解:(1) 现采用分层抽样的方法,从样本中取出的10株玉米中圆粒的有6株,皱粒的有4株,所以从中再次选出3株时,既有圆粒又有皱粒的概率为1221646431045C C C C P C +==.(2) 根据已知列联表:所以2250(1171319)3.860 3.84130202426K⨯⨯-⨯=≈>⨯⨯⨯.又2( 3.841)0.050p K=≥,因此能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关.。
2014-2015年福州市第一学期高三期末理科数学质量检查(word版)
福州市2014-2015学年度第一学期高三质量检查理科数学试卷(满分:150分;完卷时间:120分钟)注意事项:1.本科考试分试题卷和答题卷,考生须在答题卷上作答,答题前,请在答题卷的密封线内填写学校、班级、准考证号、姓名;2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题所给的四个选项中有且只有一个选项是正确的.把正确选项涂在答题卡的相应位置上.) 1. 如图,复平面上的点1234,,,Z Z Z Z 到原点的距离都相等.若复数z所对应的点为1Z ,则复数z 的共轭复数所对应的点为( ). A .1Z B .2Z C .3ZD .4Z2. 已知πtan()34+=α,则tan α的值是( ).A .2B .12C .1-D .3-3. 已知A ⊂≠B ,则“x A ∈”是“x B ∈”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4. 某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a 为座位号),并以输出的值作为下一个输入的值. 若第一次输入的值为8,则第三次输出的值为( ). A .8 B .15 C .29D .365. 如图,若在矩形OABC 中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( ). A .1π B .2π C .3πD .12第4题图第5题图6. 已知函数()lg(1)=-f x x 的值域为(,1]-∞,则函数()f x 的定义域为( ).A .[9,)-+∞B .[0,)+∞C .(9,1)-D .[9,1)-7. 已知抛掷一枚质地均匀的硬币,正面朝上的概率为0.5.现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:101 111 010 101 010 100 100 011 111 110 000 011 010 001 111 011 100 000 101 101 据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率为( ). A .0.30B .0.35C .0.40D .0.658. ABC △的三个内角,,A B C 所对的边分别为,,a b c .若cos cos A bB a==C 的大小为( ). A .60︒B . 75︒C .90︒D .120︒9. 若双曲线2222:1x y a bΓ-=(0,0a b >>)的右焦点()4,0到其渐近线的距离为,则双曲线Γ的离心率为( ). ABC .2D .410.定义运算“*”为:,0,2,0a b ab a a b a +<⎧⎪*=⎨⎪⎩≥.若函数()(1)f x x x =+*,则该函数的图象大致是( ).AC11.已知ABC ∆的三个顶点,,A B C 的坐标分别为())()0,1,,0,2-,O 为坐标原点,动点P 满足1CP =,则OA OB OP ++的最小值是( ).A .4-B 1C 1D 12.已知直线:l y ax b =+与曲线:Γ1x y y=+没有公共点.若平行于l 的直线与曲线Γ有且只有一个公共点,则符合条件的直线l ( ). A .不存在B .恰有一条C .恰有两条D .有无数条第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置上.) 13.若变量,x y 满足约束条件0,0,2x y y x ⎧⎪⎨⎪-⎩≤≥≤,则z x y =+的最小值为 ★★★ .14.已知6234560123456(1)x a a x a x a x a x a x a x +=++++++,则016,,,a a a ⋅⋅⋅中的所有偶数..的和等于 ★★★ .15.已知椭圆2239x y +=的左焦点为1F ,点P 是椭圆上异于顶点的任意一点,O 为坐标原点.若点D 是线段1PF 的中点,则1FOD ∆的周长为 ★★★ . 16. 若数列{}n a 满足112n n n a a a +-+≥(2n ≥),则称数列{}n a 为凹数列.已知等差数 列{}n b 的公差为d ,12b =,且数列n b n ⎧⎫⎨⎬⎩⎭是凹数列,则d 的取值范围为 ★★★ .三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)已知等比数列{}n a 的公比1q >,1a ,2a 是方程2320x x -+=的两根. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列{}2n n a ⋅的前n 项和n S .18.(本小题满分12分)“ALS 冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.(Ⅰ)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?(Ⅱ)假定(Ⅰ)中被邀请到的3个人中恰有两人接受挑战.根据活动规定,现记X 为接下来被邀请到的6个人中接受挑战的人数,求X 的分布列和均值(数学期望).19.(本小题满分12分)已知函数()4f x x π⎛⎫= ⎪⎝⎭在同一半周期内的图象过点,,O P Q ,其中O 为坐标原点,P 为函数()f x 图象的最高点,Q 为函数()f x 的图象与x的正半轴的交点.(Ⅰ)试判断OPQ ∆的形状,并说明理由.(Ⅱ)若将O P Q ∆绕原点O 按逆时针方向旋转02ααπ⎛⎫<< ⎪⎝⎭时,顶点,P Q ''恰好同时落在曲线k y x =()0x >(如图所示),求实数k 的值.20.(本小题满分12分)一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用.已知每服用m (14m ≤≤且m ∈R )个单位的药剂,药剂在血液中的含量y (克)随着时间x (小时)变化的函数关系式近似为)(x f m y ⋅=,其中()10,06,4.4,682x xf x x x ⎧<⎪⎪+=⎨⎪-⎪⎩≤≤≤(Ⅰ)若病人一次服用3个单位的药剂,则有效治疗时间可达多少小时?(Ⅱ)若病人第一次服用2个单位的药剂,6个小时后再服用m 个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求m 的最小值.21.(本小题满分12分)已知抛物线Γ的顶点为坐标原点,焦点为(0,1)F . (Ⅰ)求抛物线Γ的方程;(Ⅱ)若点P 为抛物线Γ的准线上的任意一点,过点P 作抛物线Γ的切线PA 与PB ,切点分别为,A B ,求证:直线AB 恒过某一定点;(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题...,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分). 22.(本小题满分14分)已知函数()()e sin cos ,cos x x f x x x g x x x =-=,其中e 是自然对数的底数.(Ⅰ)判断函数()y f x =在π(0,)2内的零点的个数,并说明理由;(Ⅱ)12ππ0,,0,22x x ⎡⎤⎡⎤∀∈∃∈⎢⎥⎢⎥⎣⎦⎣⎦,使得不等式12()()f x g x m +≥成立,试求实数m 的取值范围;(Ⅲ)若1x >-,求证:()()0f x g x ->.第19题图福州市2014-2015学年度第一学期高三质量检查理科数学试卷参考答案及评分细则一、选择题:本大题共12小题,每小题5分,共60分. 1.C 2.B 3.A 4.A 5.B 6.D 7.B 8.C 9.C 10.D 11.B 12.C二、填空题:本大题共4小题,每小题4分,共16分,13.2- 14.32 15.316.(,2]-∞ 三、解答题:本大题共6小题,共74分.17. 本题主要考查一元二次方程的根、等比数列的通项公式、错位相减法求数列的和等基础知识,考查应用能力、运算求解能力,考查函数与方程思想. 解:(Ⅰ)方程2320x x -+=的两根分别为1,2, ·························································· 1分 依题意得11a =,22a =. ································································································ 2分 所以2q =,······················································································································· 3分 所以数列{}n a 的通项公式为12n n a -=. ·········································································· 4分 (Ⅱ)由(Ⅰ)知22n n n a n ⋅=⋅, ··················································································· 5分 所以212222n n S n =⨯+⨯+⋅⋅⋅+⨯, ············································ ①23121222(1)22n n n S n n +⋅=⨯+⨯+⋅⋅⋅+-⋅+⨯, ························· ② 由①-②得23222n S -=+++⋅⋅⋅122n n n ++-⨯, ··············································································· 8分 即 1222212nn n S n +-⋅-=-⨯-, ······················································································· 11分 所以12(1)2n n S n +=+-⋅. ····························································································· 12分 18.本题主要考查离散型随机变量的概率、分布列、数学期望等基础知识,考查运算求解能力以及应用意识,考查必然与或然思想等.解法一:(Ⅰ)这3个人接受挑战分别记为A 、B 、C ,则,,A B C 分别表示这3个人不接受挑战.这3个人参与该项活动的可能结果为:{},,A B C ,{},,A B C ,{},,A B C ,{},,A B C ,{},,A B C ,{},,A B C ,{},,A B C ,{},,A B C .共有8种; ································································ 2分 其中,至少有2个人接受挑战的可能结果有:{},,A B C ,{},,A B C ,{},,A B C ,{},,A B C ,共有4种. ······················································································································ 3分根据古典概型的概率公式,所求的概率为4182P ==. ·················································· 4分(说明:若学生先设“用(),,x y z 中的,,x y z 依次表示甲、乙、丙三人接受或不接受挑战的情况”,再将所有结果写成(),,A B C ,(),,A B C ,(),,A B C ,(),,A B C ,(),,A B C ,(),,A B C ,(),,A B C ,(),,A B C ,不扣分.) (Ⅱ)因为每个人接受挑战与不接受挑战是等可能的,所以每个人接受挑战的概率为12,不接受挑战的概率也为12. ···································· 5分所以()060611102264P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,()51611631226432P X C ⎛⎫⎛⎫==⋅== ⎪ ⎪⎝⎭⎝⎭, ()2426111522264P X C ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭,()3336112053226416P X C ⎛⎫⎛⎫==⋅== ⎪ ⎪⎝⎭⎝⎭, ()4246111542264P X C ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭,()515611635226432P X C ⎛⎫⎛⎫==⋅== ⎪ ⎪⎝⎭⎝⎭, ()6661116.2264P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭······················································································· 9分 故X10分所以()1315515310123456364326416643264E X =⨯+⨯+⨯+⨯+⨯+⨯+⨯=.故所求的期望为3. ········································································································ 12分 解法二:因为每个人接受挑战与不接受挑战是等可能的,所以每个人接受挑战的概率为12,不接受挑战的概率也为12. ···································· 1分 (Ⅰ)设事件M 为“这3个人中至少有2个人接受挑战”,则2323331111()2222P M C C ⎛⎫⎛⎫⎛⎫=⋅+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. ·········································································· 4分 (Ⅱ)因为X 为接下来被邀请的6个人中接受挑战的人数,所以1~6,2X B ⎛⎫⎪⎝⎭.··········································································································· 5分 所以()060611102264P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,()51611631226432P X C ⎛⎫⎛⎫==⋅== ⎪ ⎪⎝⎭⎝⎭, ()2426111522264P X C ⎛⎫⎛⎫==⋅= ⎪ ⎪⎝⎭⎝⎭,()3336112053226416P X C ⎛⎫⎛⎫==⋅== ⎪ ⎪⎝⎭⎝⎭, ()4246111542264P X C ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭,()515611635226432P X C ⎛⎫⎛⎫==⋅== ⎪ ⎪⎝⎭⎝⎭, ()6661116.2264P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭······················································································· 9分故X10分所以()1632E X =⨯=.故所求的期望为3. ······································································································ 12分 19.本题主要考查反比例函数、三角函数的图象与性质、三角函数的定义、同角三角函数的基本关系式、二倍角公式、两角和的正弦公式等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想. 解法一:(Ⅰ)OPQ ∆为等边三角形. ············································································ 1分 理由如下:因为函数()4f x x π⎛⎫= ⎪⎝⎭,所以2π84T ==π,所以函数()f x 的半周期为4, 所以4OQ =. ·················································································································· 2分 又因为P 为函数()f x 图象的最高点,所以点P坐标为(2,,所以4OP =, ···································································· 4分 又因为Q 坐标为(4,0),所以4PQ =,所以OPQ ∆为等边三角形. ··························································································· 6分 (Ⅱ)由(Ⅰ)知,4OP OQ ==,所以点P ',Q '的坐标分别为4cos 4sin 33αα⎛⎫ππ⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,(4cos 4sin )αα,, ················ 7分代入k y x =,得216cos sin 8sin(2π)333k αααππ⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭,且16sin cos 8sin 2k ααα==, ························································································· 9分所以2sin 2sin(2π)3αα=+,结合22sin (2)cos (2)1αα+=,02απ<<,解得1sin 22α=,············································································································· 11分所以4k =,所以所求的实数k 的值为4. ····································································· 12分 解法二:(Ⅰ)OPQ ∆为等边三角形. ·········································································· 1分 理由如下:因为函数()4f x x π⎛⎫= ⎪⎝⎭,所以2π84T ==,所以函数()f x 的半周期为4,所以4OQ =, ··································· 2分 因为P 为函数()f x 的图象的最高点,所以点P坐标为(2,,所以4OP =,所以OP OQ =. ······································ 4分 又因为直线OP的斜率k ==60POQ ∠=︒, 所以OPQ ∆为等边三角形. ··························································································· 6分(Ⅱ)由(Ⅰ)知,4OP OQ ==,所以点P ',Q '的坐标分别为4cos 4sin 33αα⎛⎫ππ⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,(4cos 4sin )αα,, ·················· 7分 因为点P ',Q '在函数(0)ky x x=>的图象上,所以16cos sin ,3316sin cos k k ⎧ππ⎛⎫⎛⎫=++⎪ ⎪ ⎪⎝⎭⎝⎭⎨⎪=⎩αααα, ················································································ 8分 所以28sin(2π),38sin 2k k ⎧=+⎪⎨⎪=⎩αα, ·································································································· 9分 消去k 得, 2sin 2sin(2π)3αα=+,所以22sin 2sin 2cos πcos2sin π33ααα=+,所以3sin 222αα=,所以tan 2α=,····························································· 10分又因为 02απ<<,所以26απ=,所以1sin 22α=, ···················································· 11分所以4k =.所以所求的实数k 的值为4. ····································································· 12分 解法三:(Ⅰ)同解法一或同解法二;(Ⅱ)由(Ⅰ)知,OPQ ∆为等边三角形.因为函数(0)ky x x=>的图象关于直线y x =对称, ························································ 8分由图象可知,当12απ=时,点P ',Q '恰在函数(0)ky x x =>的图象上. ······················ 10分此时点Q '的坐标为(4cos 4sin )1212ππ,, ········································································· 11分 所以16sin cos 8sin 412126k πππ===,所以所求的实数k 的值为4. ···························· 12分20. 本题主要考查分段函数模型的应用问题、一元二次函数的最值、解不等式等基础知识,考查应用意识、运算求解能力,考查化归与转化思想、分类讨论思想等.解:(I )因为3m =,所以30,06,4312,682x xy x x ⎧<⎪⎪+=⎨⎪-⎪⎩≤≤≤. ······················································ 1分当06x <≤时,由3024x+≥,解得x ≤11,此时06x <≤; ······································· 3分 当68x ≤≤时,由31222x -≥,解得203x ≤,此时2063x ≤≤. ····························· 5分综上所述,2003x ≤≤.故若一次服用3个单位的药剂,则有效治疗的时间可达203小时. ······························ 6分 (Ⅱ)当6x ≤≤8时,110102(4)[]824(6)2my x m x x x =⨯-+=-++--, ······················· 8分因为10822mx x -+-≥对6x ≤≤8恒成立,即281210x x m -+≥对6x ≤≤8恒成立,等价于2max 812)10x x m -+≥(,6x ≤≤8.······································································ 9分 令2812()10x x g x -+=,则函数2(4)4()10x g x --=在[6,8]是单调递增函数, ·············· 10分当x =8时,函数2812()10x x g x -+=取得最大值为65, ················································ 11分所以65m ≥,所以所求的m 的最小值为65. ································································ 12分解法二:(Ⅰ)同解法一;(Ⅱ)当6x ≤≤8时,110102(4)[]824(6)2my x m x x x =⨯-+=-++--, ······················· 8分注意到18y x =-及2102my x =-(14m ≤≤且m ∈R )均关于x 在[6,8]上单调递减,则1082my x x =-+-关于x 在[6,8]上单调递减, ····························································· 10分故10588823m m y -+=-≥,由523m≥,得65m ≥, ······················································· 11分 所以所求的m 的最小值为65. ······················································································· 12分21. 本题主要考查抛物线的标准方程与性质、直线与抛物线的位置关系、归纳推理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等. 解:(Ⅰ)依题意可设抛物线Γ的方程为:22x py =(0p >). ··································· 1分由焦点为(0,1)F 可知12p=,所以2p =.······································································· 2分所以所求的抛物线方程为24x y =. ················································································ 3分 (Ⅱ)方法一:设切点A 、B 坐标分别为221212,,,44x x x x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,由(Ⅰ)知,12y x '=.则切线PA PB 、的斜率分别为12112211,22x x x x k y x k y x ==''====, 故切线PA PB 、的方程分别为211111()42y x x x x -=-,222211()42y x x x x -=-, ············· 4分。
高三数学上学期第二次月考试卷 理(含解析)-人教版高三全册数学试题
2015-2016学年某某省马某某市红星中学高三(上)第二次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集U是实数集R,M={x|y=ln(x2﹣2x) },N={y|y=},则图中阴影部分表示的集合是( )A.{x|﹣2≤x<2} B.{x|1<x≤2}C.{x|1≤x≤2}D.{x|x<1}2.已知函数f(x)=且f(a)=﹣3,则f(6﹣a)=( ) A.﹣B.﹣C.﹣D.﹣3.给出如下命题,正确的序号是( )A.命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠xB.命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5C.若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件D.命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>04.已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.5.设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,•的值等于( )A.0 B.2 C.4 D.﹣26.设a=log37,b=21.1,c=0.83.1,则( )A.b<a<c B.c<a<b C.c<b<a D.a<c<b7.执行如图所示的程序框图,如果输入P=153,Q=63,则输出的P的值是( )A.2 B.3 C.9 D.278.若点(16,tanθ)在函数y=log2x的图象上,则=( ) A.B.C.4 D.49.已知函数f(x)=()x﹣log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值( )A.恒为负B.等于零C.恒为正D.不大于零10.已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,则a2+a4+a5+a9的值等于( )A.52 B.40 C.26 D.2011.函数y=e|lnx|﹣|x﹣1|的图象大致是( )A.B. C.D.12.已知定义在R上的奇函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>2f(﹣x),若g(x)=x2f(x),则不等式g(x)<g(1﹣3x)的解集是( )A.(,+∞)B.(﹣∞,)C.(0,)D.(﹣∞,)∪(,+∞)二、填空题:本大题共4小题,每小题5分.13.计算:()+lg+lg70+=__________.14.设变量x,y满足约束条件,则z=x﹣3y的最小值是__________.15.已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=__________.16.关于函数f(x)=(x≠0),有下列命题:①f(x)的最小值是lg2;②其图象关于y轴对称;③当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;④f(x)在区间(﹣1,0)和(1,+∞)上是增函数,其中所有正确结论的序号是__________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知p:|1﹣|≤2;q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要不充分条件,某某数m的取值X围.18.已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+(x>0).(1)若y=g(x)﹣m有零点,求m的取值X围;(2)确定m的取值X围,使得g(x)﹣f(x)=0有两个相异实根.19.已知函数f(x)=log a(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.(1)写出函数g(x)的解析式;(2)当x∈[0,1)时,总有f(x)+g(x)≥m成立,求m的取值X围.20.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利?(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.21.已知函数f(x)=+xlnx,g(x)=x3﹣x2﹣3.(1)讨论函数h(x)=的单调性;(2)如果对任意的s,t∈[,2],都有f(s)≥g(t)成立,某某数a的取值X围.四、选做题:请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.已知曲线C1的参数方程是(θ为参数)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=﹣4cosθ.(1)求曲线C1与C2交点的极坐标;(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).23.已知不等式|2x+2|﹣|x﹣1|>a.(1)当a=0时,求不等式的解集(2)若不等式在区间[﹣4,2]内无解.某某数a的取值X围.2015-2016学年某某省马某某市红星中学高三(上)第二次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集U是实数集R,M={x|y=ln(x2﹣2x) },N={y|y=},则图中阴影部分表示的集合是( )A.{x|﹣2≤x<2} B.{x|1<x≤2}C.{x|1≤x≤2}D.{x|x<1}【考点】Venn图表达集合的关系及运算.【专题】应用题;集合思想;定义法;集合.【分析】由图知,阴影部分表示的集合中的元素是在集合N中的元素但不在集合M中的元素组成的,即N∩C U M.【解答】解:由韦恩图知阴影部分表示的集合为N∩(C U M)M={x|y=ln(x2﹣2x) }∴x2﹣2x>0,解得x<0,或x>2,∴M={x|x<0,或x>2},∴C U M={x|0≤x≤2}=[0,2],N={y|y=}={y|y≥1}=[1,+∞),∴N∩(C U M)=[1,2],故选:C【点评】本小题主要考查Venn图表达集合的关系及运算、二次不等式的解法等基础知识,属于基础题2.已知函数f(x)=且f(a)=﹣3,则f(6﹣a)=( ) A.﹣B.﹣C.﹣D.﹣【考点】分段函数的应用;函数的零点.【专题】函数的性质及应用.【分析】由f(a)=﹣3,结合指数和对数的运算性质,求得a=7,再由分段函数求得f(6﹣a)的值.【解答】解:函数f(x)=且f(a)=﹣3,若a≤1,则2a﹣1﹣2=﹣3,即有2a﹣1=﹣1<0,方程无解;若a>1,则﹣log2(a+1)=﹣3,解得a=7,则f(6﹣a)=f(﹣1)=2﹣1﹣1﹣2=﹣.故选:A.【点评】本题考查分段函数的运用:求函数值,主要考查指数和对数的运算性质,属于中档题.3.给出如下命题,正确的序号是( )A.命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠xB.命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5C.若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件D.命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>0【考点】命题的真假判断与应用.【专题】计算题;规律型;简易逻辑.【分析】利用命题的否定判断A的正误;四种命题的逆否关系判断B的正误;充要条件判断C 的正误;命题的真假判断D的正误;【解答】解:对于A,命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠x0,不满足命题的否定形式,所以不正确;对于B,命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5,不满足否命题的形式,所以不正确;对于C,若ω=1是函数f(x)=cosx在区间[0,π]上单调递减的,而函数f(x)=cosωx在区间[0,π]上单调递减的,ω≤1,所以ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件,正确.对于D,命题:∃x0∈R,x02+a<0为假命题,则命题:a≥0,∀x∈R,x2+a≥0是真命题;所以,命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>0,不正确;故选:C.【点评】本题考查命题的真假的判断与应用,基本知识的考查.4.已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.【考点】由三视图求面积、体积.【专题】图表型.【分析】先由三视图还原成原来的几何体,再根据三视图中的长度关系,找到几何体中的长度关系,进而可以求几何体的体积.【解答】解:由三视图可得该几何体的上部分是一个三棱锥,下部分是半球,所以根据三视图中的数据可得:V=××=,故选C.【点评】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是组合体的体积,一般组合体的体积要分部分来求.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.5.设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,•的值等于( )A.0 B.2 C.4 D.﹣2【考点】椭圆的简单性质.【专题】计算题.【分析】通过题意可推断出当P、Q分别在椭圆短轴端点时,四边形PF1QF2面积最大.进而可根据椭圆的方程求得焦点的坐标和P的坐标,进而求得和,则•的值可求得.【解答】解:根据题意可知当P、Q分别在椭圆短轴端点时,四边形PF1QF2面积最大.这时,F1(﹣,0),F2(,0),P(0,1),∴=(﹣,﹣1),=(,﹣1),∴•=﹣2.故选D【点评】本题主要考查了椭圆的简单性质.考查了学生数形结合的思想和分析问题的能力.6.设a=log37,b=21.1,c=0.83.1,则( )A.b<a<c B.c<a<b C.c<b<a D.a<c<b【考点】对数值大小的比较.【专题】函数的性质及应用.【分析】分别讨论a,b,c的取值X围,即可比较大小.【解答】解:1<log37<2,b=21.1>2,c=0.83.1<1,则c<a<b,故选:B.【点评】本题主要考查函数值的大小比较,根据指数和对数的性质即可得到结论.7.执行如图所示的程序框图,如果输入P=153,Q=63,则输出的P的值是( )A.2 B.3 C.9 D.27【考点】程序框图.【专题】图表型;算法和程序框图.【分析】模拟执行程序,依次写出每次循环得到的R,P,Q的值,当Q=0时,满足条件Q=0,退出循环,输出P的值为3.【解答】解:模拟执行程序,可得P=153,Q=63不满足条件Q=0,R=27,P=63,Q=27不满足条件Q=0,R=9,P=27,Q=9不满足条件Q=0,R=0,P=9,Q=0满足条件Q=0,退出循环,输出P的值为9.故选:C.【点评】本题主要考查了程序框图和算法,依次写出每次循环得到的R,P,Q的值是解题的关键,属于基本知识的考查.8.若点(16,tanθ)在函数y=log2x的图象上,则=( ) A.B.C.4 D.4【考点】三角函数的化简求值.【专题】计算题;转化思想;转化法;三角函数的求值.【分析】先根据对数的运算性质求出tanθ,再化简代值计算即可.【解答】解:点(16,tanθ)在函数y=log2x的图象上,∴tanθ=log216=4,∴====,故选:B.【点评】本题考查了二倍角公式,函数值的求法,以及对数的运算性质,属于基础题.9.已知函数f(x)=()x﹣log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值( )A.恒为负B.等于零C.恒为正D.不大于零【考点】函数的零点与方程根的关系.【专题】函数的性质及应用.【分析】由函数的性质可知,f(x)=()x﹣log3x在(0,+∞)上是减函数,且可得f(x0)=0,由0<x0<x1,可得f(x1)<f(x0)=0,即可判断【解答】解:∵实数x0是方程f(x)=0的解,∴f(x0)=0.∵函数y()x,y=log3x在(0,+∞)上分别具有单调递减、单调递增,∴函数f(x)在(0,+∞)上是减函数.又∵0<x0<x1,∴f(x1)<f(x0)=0.∴f(x1)的值恒为负.故选A.【点评】本题主要考查了函数的单调性的简单应用,解题的关键是准确判断函数f(x)的单调性并能灵活应用.10.已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,则a2+a4+a5+a9的值等于( )A.52 B.40 C.26 D.20【考点】数列的求和.【专题】等差数列与等比数列.【分析】首先根据题中的已知条件已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,进一步求出数列的通项公式,然后根据通项公式求出各项的值,最后确定结果.【解答】解:已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2则:∴a n=3n﹣5a2+a4+a5+a9=40故选:B【点评】本题考查的知识点:根据点的斜率求出数列的通项公式,由通项公式求数列的项.11.函数y=e|lnx|﹣|x﹣1|的图象大致是( )A.B. C.D.【考点】对数的运算性质;函数的图象与图象变化.【分析】根据函数y=e|lnx|﹣|x﹣1|知必过点(1,1),再对函数进行求导观察其导数的符号进而知原函数的单调性,得到答案.【解答】解:由y=e|lnx|﹣|x﹣1|可知:函数过点(1,1),当0<x<1时,y=e﹣lnx﹣1+x=+x﹣1,y′=﹣+1<0.∴y=e﹣lnx﹣1+x为减函数;若当x>1时,y=e lnx﹣x+1=1,故选D.【点评】本题主要考查函数的求导与函数单调性的关系.12.已知定义在R上的奇函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>2f(﹣x),若g(x)=x2f(x),则不等式g(x)<g(1﹣3x)的解集是( )A.(,+∞)B.(﹣∞,)C.(0,)D.(﹣∞,)∪(,+∞)【考点】函数奇偶性的性质.【专题】转化思想;数学模型法;函数的性质及应用;导数的综合应用.【分析】f(x)是定义在R上的奇函数,可得:f(﹣x)=﹣f(x).对任意正实数x满足xf′(x)>2f(﹣x),可得:xf′(x)+2f(x)>0,由g(x)=x2f(x),可得g′(x)>0.可得函数g(x)在(0,+∞)上单调递增.即可得出.【解答】解:∵f(x)是定义在R上的奇函数,∴f(﹣x)=﹣f(x).对任意正实数x满足xf′(x)>2f(﹣x),∴xf′(x)+2f(x)>0,∵g(x)=x2f(x),∴g′(x)=2xf(x)+x2f′(x)>0.∴函数g(x)在(0,+∞)上单调递增.又g(0)=0,g(﹣x)=x2f(﹣x)=﹣g(x),∴函数g(x)是R上的奇函数,∴g(x)是R上的增函数.由不等式g(x)<g(1﹣3x),∴x<1﹣3x,解得.∴不等式g(x)<g(1﹣3x)的解集为:.故选:B.【点评】本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.二、填空题:本大题共4小题,每小题5分.13.计算:()+lg+lg70+=.【考点】对数的运算性质;有理数指数幂的化简求值.【专题】计算题;函数思想;定义法;函数的性质及应用.【分析】根据对数和幂的运算性质计算即可.【解答】解:()+lg+lg70+=+lg()+1﹣lg3=+lg+1=+1+1=,故答案为:.【点评】本题考查了对数和幂的运算性质,关键是掌握性质,属于基础题.14.设变量x,y满足约束条件,则z=x﹣3y的最小值是﹣8.【考点】简单线性规划.【专题】不等式的解法及应用.【分析】将z=x﹣3y变形为,此式可看作是斜率为,纵截距为的一系列平行直线,当最大时,z最小.作出原不等式组表示的平面区域,让直线向此平面区域平移,可探求纵截距的最大值.【解答】解:由z=x﹣3y,得,此式可看作是斜率为,纵截距为的直线,当最大时,z最小.画出直线y=x,x+2y=2,x=﹣2,从而可标出不等式组表示的平面区域,如右图所示.由图知,当动直线经过点P时,z最小,此时由,得P(﹣2,2),从而z min=﹣2﹣3×2=﹣8,即z=x﹣3y的最小值是﹣8.故答案为:﹣8.【点评】本题考查了线性规划的应用,为高考常考的题型,求解此类问题的一般步骤是:(1)作出已知不等式组表示的平面区域;(2)运用化归思想及数形结合思想,将目标函数的最值问题转化为平面中几何量的最值问题处理.15.已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=﹣8.【考点】奇偶性与单调性的综合;函数的周期性.【专题】数形结合.【分析】由条件“f(x﹣4)=﹣f(x)”得f(x+8)=f(x),说明此函数是周期函数,又是奇函数,且在[0,2]上为增函数,由这些画出示意图,由图可解决问题.【解答】解:此函数是周期函数,又是奇函数,且在[0,2]上为增函数,综合条件得函数的示意图,由图看出,四个交点中两个交点的横坐标之和为2×(﹣6),另两个交点的横坐标之和为2×2,所以x1+x2+x3+x4=﹣8.故答案为﹣8.【点评】数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.16.关于函数f(x)=(x≠0),有下列命题:①f(x)的最小值是lg2;②其图象关于y轴对称;③当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;④f(x)在区间(﹣1,0)和(1,+∞)上是增函数,其中所有正确结论的序号是①②④.【考点】命题的真假判断与应用;奇偶性与单调性的综合.【专题】函数思想;定义法;函数的性质及应用.【分析】是结合复合函数单调性的关系进行判断.②根据基本由函数奇偶性的定义判断函数为偶函数判断;③利用对勾函数的单调性判断;④由对勾函数的最值及函数奇偶性的性质进行判断即可.【解答】解:①函数f(x)=lg,(x∈R且x≠0).∵=2,∴f(x)=lg≥2,即f(x)的最小值是lg2,故①正确,②∵f(﹣x)==f(x),∴函数f(x)为偶函数,图象关于y轴对称,故②正确;③当x>0时,t(x)=,在(0,1)上单调递减,在(1,+∞)上得到递增,∴f(x)=lg在(0,1)上单调递减,在(1,+∞)上得到递增,故③错误;④∵函数f(x)是偶函数,由③知f(x)在(0,1)上单调递减,在(1,+∞)上得到递增,∴在(﹣1,0)上单调递增,在(﹣∞,﹣1)上得到递减,故④正确,故答案为:①②④【点评】本题考查了命题的真假判断与应用,考查了函数奇偶性的性质,考查了复合函数的单调性,是中档题.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知p:|1﹣|≤2;q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要不充分条件,某某数m的取值X围.【考点】必要条件;绝对值不等式的解法.【专题】规律型.【分析】先求出命题p,q的等价条件,利用¬p是¬q的必要不充分条件转化为q是p的必要不充分条件,建立条件关系即可求出m的取值X围.【解答】解:由||=,得|x﹣4|≤6,即﹣6≤x﹣4≤6,∴﹣2≤x≤10,即p:﹣2≤x≤10,由x2+2x+1﹣m2≤0得[x+(1﹣m)][x+(1+m)]≤0,即1﹣m≤x≤1+m,(m>0),∴q:1﹣m≤x≤1+m,(m>0),∵¬p是¬q的必要不充分条件,∴q是p的必要不充分条件.即,且等号不能同时取,∴,解得m≥9.【点评】本题主要考查充分条件和必要条件的应用,将¬p是¬q的必要不充分条件转化为q 是p的必要不充分条件是解决本题的关键.18.已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+(x>0).(1)若y=g(x)﹣m有零点,求m的取值X围;(2)确定m的取值X围,使得g(x)﹣f(x)=0有两个相异实根.【考点】函数零点的判定定理;根的存在性及根的个数判断.【专题】计算题;函数的性质及应用;导数的综合应用;不等式的解法及应用.【分析】(1)由基本不等式可得g(x)=x+≥2=2e,从而求m的取值X围;(2)令F(x)=g(x)﹣f(x)=x++x2﹣2ex﹣m+1,求导F′(x)=1﹣+2x﹣2e=(x﹣e)(+2);从而判断函数的单调性及最值,从而确定m的取值X围.【解答】解:(1)∵g(x)=x+≥2=2e;(当且仅当x=,即x=e时,等号成立)∴若使函数y=g(x)﹣m有零点,则m≥2e;故m的取值X围为[2e,+∞);(2)令F(x)=g(x)﹣f(x)=x++x2﹣2ex﹣m+1,F′(x)=1﹣+2x﹣2e=(x﹣e)(+2);故当x∈(0,e)时,F′(x)<0,x∈(e,+∞)时,F′(x)>0;故F(x)在(0,e)上是减函数,在(e,+∞)上是增函数,故只需使F(e)<0,即e+e+e2﹣2e2﹣m+1<0;故m>2e﹣e2+1.【点评】本题考查了基本不等式的应用及导数的综合应用,同时考查了函数零点的判断与应用,属于中档题.19.已知函数f(x)=log a(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.(1)写出函数g(x)的解析式;(2)当x∈[0,1)时,总有f(x)+g(x)≥m成立,求m的取值X围.【考点】求对数函数解析式;函数解析式的求解及常用方法;函数最值的应用.【专题】计算题;转化思想.【分析】(1)由已知条件可知函数g(x)的图象上的任意一点P(x,y)关于原点对称的点Q (﹣x,﹣y)在函数f(x)图象上,把Q(﹣x,﹣y)代入f(x),整理可得g(x)(2)由(1)可令h(x)=f(x)+g(x),先判断函数h(x)在[0,1)的单调性,进而求得函数的最小值h(x)min,使得m≤h(x)min【解答】解:(1)设点P(x,y)是g(x)的图象上的任意一点,则Q(﹣x,﹣y)在函数f (x)的图象上,即﹣y=log a(﹣x+1),则∴(2)f(x)+g(x)≥m 即,也就是在[0,1)上恒成立.设,则由函数的单调性易知,h(x)在[0,1)上递增,若使f(x)+g(x)≥m在[0,1)上恒成立,只需h(x)min≥m在[0,1)上成立,即m≤0.m的取值X围是(﹣∞,0]【点评】本题(1)主要考查了函数的中心对称问题:若函数y=f(x)与y=g(x)关于点M (a,b)对称,则y=f(x)上的任意一点(x,y)关于M(a,b)对称的点(2a﹣x,2b﹣y)在函数y=g(x)的图象上.(2)主要考查了函数的恒成立问题,往往转化为求最值问题:m≥h(x)恒成立,则m≥h(x)m≤h(x)恒成立,max则m≤h(x)min20.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利?(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.【考点】基本不等式在最值问题中的应用.【专题】计算题.【分析】(1)赢利总额y元即x年中的收入50x减去购进机床的成本与这x年中维修、保养的费用,维修、保养的费用历年成等差数增长,,(2)由(1)的结论解出结果进行判断得出何年开始赢利.(3)算出每一种方案的总盈利,比较大小选择方案.【解答】解:(1)y=﹣2x2+40x﹣98,x∈N*.(2)由﹣2x2+40x﹣98>0解得,,且x∈N*,所以x=3,4,,17,故从第三年开始盈利.(3)由,当且仅当x=7时“=”号成立,所以按第一方案处理总利润为﹣2×72+40×7﹣98+30=114(万元).由y=﹣2x2+40x﹣98=﹣2(x﹣10)2+102≤102,所以按第二方案处理总利润为102+12=114(万元).∴由于第一方案使用时间短,则选第一方案较合理.【点评】考查审题及将题中关系转化为数学符号的能力,其中第二问中考查了一元二次不等式的解法,第三问中考查到了基本不等式求最值,本题是一个函数基本不等式相结合的题.属应用题中盈利最大化的问题.21.已知函数f(x)=+xlnx,g(x)=x3﹣x2﹣3.(1)讨论函数h(x)=的单调性;(2)如果对任意的s,t∈[,2],都有f(s)≥g(t)成立,某某数a的取值X围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【专题】综合题;导数的综合应用.【分析】(1)求导数,利用导数的正负,即可讨论函数h(x)=的单调性;(2)求出g(x)max=g(2)=1,当x∈[,2]时,f(x)=+xlnx恒成立,等价于a≥x﹣x2lnx 恒成立,然后利用导数求函数u(x)=x﹣x2lnx在区间[,2]上取得最大值,则实数a的取值X围可求.【解答】解:(1)h(x)==+lnx,h′(x)=,①a≤0,h′(x)≥0,函数h(x)在(0,+∞)上单调递增②a>0时,h'(x)>0,则x∈(,+∞),函数h(x)的单调递增区间为(,+∞),h'(x)<0,则x∈(0,),函数h(x)的单调递减区间为(0,),.(2)g(x)=x3﹣x2﹣3,g′(x)=3x(x﹣),x 2g′(x)0 ﹣0 +g(x)﹣递减极小值递增 13由上表可知,g(x)在x=2处取得最大值,即g(x)max=g(2)=1所以当x∈[,2]时,f(x)=+xlnx≥1恒成立,等价于a≥x﹣x 2lnx恒成立,记u(x)=x﹣x2lnx,所以a≥u(x)max,u′(x)=1﹣x﹣2xlnx,可知u′(1)=0,当x∈(,1)时,1﹣x>0,2xlnx<0,则u′(x)>0,∴u(x)在x∈(,2)上单调递增;当x∈(1,2)时,1﹣x<0,2xlnx>0,则u′(x)<0,∴u(x)在(1,2)上单调递减;故当x=1时,函数u(x)在区间[,2],上取得最大值u(1)=1,所以a≥1,故实数a的取值X围是[1,+∞).【点评】本题考查了利用导数研究函数的单调性,考查了导数在最大值、最小值问题中的应用,考查了数学转化思想方法和函数构造法,训练了利用分离变量法求参数的取值X围,属于中档题.四、选做题:请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.已知曲线C1的参数方程是(θ为参数)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=﹣4cosθ.(1)求曲线C1与C2交点的极坐标;(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).【考点】参数的意义;简单曲线的极坐标方程.【专题】选作题;转化思想;综合法;坐标系和参数方程.【分析】(1)把参数方程和极坐标方程化为直角坐标方程,联立方程组求出交点的坐标,再把交点的直角坐标化为极坐标;(2)画出图象,由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.【解答】解:(1)由(θ为参数),消去参数得:x2+(y﹣2)2=4,即x2+y2﹣4y=0;由ρ=﹣4cosθ,得ρ2=﹣4ρcosθ,即x2+y2=﹣4x.两式作差得:x+y=0,代入C1得交点为(0,0),(﹣2,2).其极坐标为(0,0),(2,);(2)如图,由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.此时|AB|=2+4,O到AB的距离为.∴△OAB的面积为S=×(2+4)×=2+2.【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程,考查了推理能力与计算能力,属于基础题.23.已知不等式|2x+2|﹣|x﹣1|>a.(1)当a=0时,求不等式的解集(2)若不等式在区间[﹣4,2]内无解.某某数a的取值X围.【考点】绝对值不等式的解法.【专题】不等式的解法及应用.【分析】(1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(2)求得f(x)=|2x+2|﹣|x﹣1|=在区间[﹣4,2]内的值域,结合|2x+2|﹣|x﹣1|>a无解,求得a的X围.【解答】解:(1)当a=0时,不等式即|2x+2|﹣|x﹣1|>0,可得①,或②,或③.解①求得 x<﹣3,解②求得﹣<x<1,解③求得x≥1.综上可得,原不等式的解集为{x|x<﹣3,或x>﹣}.(2)当x∈[﹣4,2],f(x)=|2x+2|﹣|x﹣1|=的值域为[﹣2,3],而不等式|2x+2|﹣|x﹣1|>a无解,故有a≤3.【点评】本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想;还考查了分段函数的应用,求函数的值域,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年福州市高中毕业班质量检查数学(理科)试卷(完卷时间120分钟;满分150分)注意事项:1.本科考试分试题卷和答题卷,考生须在答题卷上作答,答题前,请在答题卷内填写学校、班级、准考证号、姓名;2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟. 参考公式:第Ⅰ卷 (选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题所给的四个答案中有且只有一个答案是正确的,把正确选项涂在答题卡的相应位置上.) 1.i 是虚数单位,复数(2)(1)z x i i =++,R ∈x .若z 的虚部为4,则x 等于A .2B .-2C .1D .-12. 要得到函数tan(2)3y x π=+的图象,只须将x y 2tan =的图象上的所有的点 A.向左平移3π个单位长度 B.向右平移3π个单位长度C.向左平移6π个单位长度D.向右平移6π个单位长度3. 根据某市环境保护局公布2007-2012这六年每年的空气质量优良的天数,绘制折线图如图.根据图中信息可知,这六年的每年空气质量优良天数的中位数是 A.300B. 305C.315D. 320 4.已知函数()af x x x=+,则“4a =”是“函数()f x 在(2,)+∞上为增函数”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 5.已知命题“直线l 与平面α有公共点”是真命题,那么下列命题:第3题图①直线l 上的点都在平面α内; ②直线l 上有些点不在平面α内;③平面α内任意一条直线都不与直线l 平行. 其中真命题的个数是 A.3 B.2 C.1D.06.已知等比数列{}n a 的公比2=q ,且462,,48a a 成等差数列,则{}n a 的前8项和为 A.127B.255C.511D.10237.设88018(1),x a a x a x +=+++ 则0,18,,a a a 中奇数的个数为 A .2B .3C .4D .58.已知点P 是△ABC 所在平面内的一点,边AB 的中点为D ,若2(1)PD PA CB λ=-+ ,其中R ∈λ,则点P 一定在 A .AB 边所在的直线上 B .BC 边所在的直线上 C .AC 边所在的直线上D .△ABC 的内部9.对于任意给定的实数m ,直线03=+-m y x 与双曲线0(12222>=-a by a x ,)0>b 最多有一个交点,则双曲线的离心率等于 A .2B .2C .3D .1010.对于函数()f x 与()g x 和区间D ,如果存在0x D ∈,使00()()1f x g x -≤,则称0x 是函数()f x 与()g x 在区间D 上的“友好点”.现给出两个函数:①2()f x x =,22)(-=x x g ; ②()f x =()2g x x =+;③x x f -=e )(,1()g x x=-; ④()f x ln x =,x x g =)(,则在区间()0,+∞上的存在唯一“友好点”的是A .①②B .③④C . ②③D .①④第Ⅱ卷 (非选择题 共100分)二、填空题(本大题共5小题,每小题4分,共20分,把答案填在答题卡的相应位置上.)11.一个三棱锥的正视图和侧视图及其尺寸如图所示,则该三棱锥的俯视图的面积为 .12.已知函数()f x cos ,0,1,0,x x x ≥⎧=⎨<⎩,则22()d f x x π-⎰的值等于 .13. 已知程序框图如右图所示,执行该程序,如果输入10=x ,输出4=y ,则在图中“?”处可填入的算法语句是 (写出以下所有满足条件的序号).①1-=x x ; ②2-=x x ; ③3-=x x ; ④4-=x x .14.在区间]2,0[上任取两个数a ,b ,能使函数()f x 1a x b =++在区间]1,1[-内有零点的概率等于________.15.设数列}{n a 是由集合t s ts<≤+0|33{,且s ,}Z ∈t 中所有的数从小到大排列成的数列,即41=a ,102=a ,123=a ,284=a ,a 5=30,a 6=36,…,若2013a =n m 33+(0m n ≤<,且m ,}n ∈Z ,则n m +的值等于____________.三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.) 16.(本小题满分13分) 已知平面向量a (sin3x π=,b =)3cos,1(x π,定义函数=)(x f a ⋅b(Ⅰ)求函数()f x 的值域;(Ⅱ)若函数()f x 图象上的两点M 、N 的横坐标分别为1和3,O 为坐标原点,求△MON 的面积.17.(本小题满分13分)某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:第13题图(Ⅰ)从甲.抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X ,求X 的分布列和数学期望; (Ⅱ)请你根据乙.抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.下面的临界值表供参考:(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)18.(本小题满分13分) 如图,已知多面体EABCDF 的底面ABCD 是边长为2的正方形,⊥EA 底面ABCD ,EA FD //,且121==EA FD . (Ⅰ)求多面体EABCDF 的体积; (Ⅱ)求直线EB 与平面ECF 所成角的正弦值;(Ⅲ)记线段BC 的中点为K ,在平面ABCD 内过点K 作一条直线与平面ECF 平行,要求保留作图痕迹,但不要求证明.19. (本小题满分13分)已知>a 0>b ,曲线C 上任意一点P 分别与点)0,(a A -、)0,(a B 连线的斜率的乘积为22ab -. (Ⅰ)求曲线C 的方程;(Ⅱ)设直线)0,0(:≠≠+=h k h kx y l 与x 轴、y 轴分别交于M 、N 两点,若曲线C 与直线l 没有公共点,求证:||MN a b >+.20.(本小题满分14分) 已知函数2)1ln()(+-+=x axx x f . (Ⅰ)当0=a 时,求曲线)(x f y =在原点处的切线方程; (Ⅱ)当0>a 时,讨论函数)(x f 在区间),0(+∞上的单调性; (Ⅲ)证明不等式1ln 1215131+<++++n n 对任意*N ∈n 成立.14.本题有(1).(2).(3)三个选做题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中. (1)(本小题满分7分)选修4-2:矩阵与变换已知线性变换τ:⎩⎨⎧+='+='y x y y x x 22,3对应的矩阵为T ,向量β⎪⎪⎭⎫ ⎝⎛=65. (Ⅰ )求矩阵T 的逆矩阵1-T;(Ⅱ )若向量α在τ作用下变为向量β,求向量α.(2)(本小题满分7分)选修4-4:坐标系与参数方程在极坐标系中,圆C 的极坐标方程为θθρsin 8cos 6+=.现以极点O 为原点,极轴为x 轴的非负半轴建立平面直角坐标系. (Ⅰ)求圆C 的直角坐标方程;(Ⅱ)若圆C 上的动点P 的直角坐标为),(y x ,求x y +的最大值,并写出y x +取得最大值时点P 的直角坐标. (3)(本小题满分7分)选修4-5:不等式选讲已知不等式3|||2|≤-++m x x 的解集为}12|{≤≤-x x . (Ⅰ )求m 的值;(Ⅱ )若m c b a =++22232,求c b a 32++的取值范围.2013年福州市高中毕业班质量检查 数学(理科)试卷参考答案及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.选择题和填空题不给中间分.一、选择题:本大题考查基础知识和基本运算.每小题5分,共50分. 1.A 2.C 3.C 4.A 5.D 6.B 7.A 8.C 9.D 10.D 二、填空题:本大题考查基础知识和基本运算.每小题4分,共20分. 11.112.313.②③④14.8115.122三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.本题考查平面向量的数量积、三角函数的图象与性质、诱导公式、解三角形等基础知识,考查运算求解能力及数形结合思想、化归与转化思想等,满分13分.解:(Ⅰ)依题意得()sin33f x x x ππ=+………………………………1分2sin()33x ππ=+…………………………………………………………………3分所以函数()f x 的值域为[2,2]-.………………………………………………………5分(Ⅱ)方法一 由(Ⅰ)知,()2sin()33f x x ππ=+(1)2sin 33f ππ⎛⎫=+= ⎪⎝⎭(3)2sin 3f π=-=………………………………6分从而 (3),3,3)M N .………………………………………………7分∴2,OM ON ====4,MN ==……………………………………………9分根据余弦定理得222cos 02OM ON MN MON OM ON +-∠===.∴90MON ∠=,…………………………………………………………………10分△MON 的面积为11222S OM ON ==⨯⨯=分方法二 同方法一得:(1(3,M N .…………………………………………7分则 (1(3,OM ON ==. ………………………………………………8分13(0OM ON ⋅=⨯=.……………………………………………10分 所以90MON ∠=, OM ON ⊥即△MON 的面积为11222S OM ON ==⨯⨯=分方法三 同方法一得:(1(3,M N .…………………………………………7分直线OM 的方程为y =0y -=. …………… …………………8分点N 到直线OM 的距离为d ==分又因为2,OM =,………………………………………………………11分所以△MON 的面积为11222S OM d =⋅=⨯⨯=分17.本题考查抽样、独立性检验、离散型随机变量的分布列与期望等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等,满分13分. 解:(Ⅰ)由甲抽取的样本数据可知,投篮成绩优秀的有7人,投篮成绩不优秀的有5人. X 的所有可能取值为0,1,2.……………………………………………………1分所以25212C 5(0)C 33P X ===,1175212C C 35(1)C 66P X ===,27212C 217(2)C 6622P X ====.…4分故X分∴53577()0123366226E X =⨯+⨯+⨯=. ……6分(Ⅱ…………7分2K 的观测值212(6411) 5.1827557k ⨯-⨯=≈⨯⨯⨯>3.841,……………………………9分所以有95%以上的把握认为投篮成绩与性别有关. ……………………10分 (Ⅲ)甲用的是系统抽样,乙用的是分层抽样. ……………………11分 由(Ⅱ)的结论知,投篮成绩与性别有关,并且从样本数据能看出投篮成绩与性别有明显差异,因此采用分层抽样方法比系统抽样方法更优. ……………………13分18.本小题主要考查直线与直线,直线与平面,平面与平面位置关系等基础知识;考查空间想象能力,推理论证能力和运算求解能力.满分13分. (Ⅰ)如图,连接ED ,∵⊥EA 底面ABCD 且EA FD //,∴⊥FD 底面ABCD , ∴AD FD ⊥,∵D CD FD AD DC =⋂⊥,,∴⊥AD 面FDC , ----------------1分∴32221213131=⨯⨯⨯⨯=⋅=∆-FDC FCD E S AD V , --------2分 E ABCD V -=13EA ⋅ ABCD S 1822233=⨯⨯⨯= , -------------3分∴多面体EABCDF 的体积310=+=--ABCD E FCD E V V V 多面体.--------------5分(Ⅱ)以点A 为原点,AB 所在的直线为x 轴,AD 所在的直线为y轴,建立空间直角坐标系,如图.由已知可得A (0,0,0),E (0,0,2),B (2,0,0),C (2,2,0),F (0,2,1),所以)1,2,0(,),2,0,2(),222(-=-=-=,, ------7分 设平面ECF 的法向量为),,(z y x =n,则⎪⎩⎪⎨⎧=⋅=⋅00EF n n 得:⎩⎨⎧=-=-+,02,0222z y z y x取y =1,得平面ECF 的一个法向量为(1,1,2)=n ------9分设直线EB 与平面ECF 所成角为θ,所以sin |cos ,|EB θ= n ||||||EBEB ⋅=⋅nn 6==----11分(Ⅲ)取线段CD 的中点Q ;连接KQ ,直线KQ 即为所求. ---------------12分图上有正确的作图痕迹………………………………13分19.本题主要考查直线、椭圆等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想和化归与转化思想等,满分13分. 解:(Ⅰ)设曲线C 上任意一点P 的坐标为),(y x .依题意22ab a x y a x y k k PBPA -=-⋅+=⋅,且a x ±≠,………………3分 整理得12222=+b y a x .所以,曲线C 的方程为:12222=+b y a x ,a x ±≠.………5分(Ⅱ)由⎪⎩⎪⎨⎧+==+,,12222h kx y b y a x 得0)(2)(22222222=-+++b h a hkx a x k a b ,()422222222222244()0,a h k b a k a h b b a k h ∴∆=-+-<+<即,……7分由已知条件可知)0,-(khM ,),0(h N ,所以ab b a k a kb b a k a b k k a b h k h MN 2||2222222222222222222++≥+++=+++>+=, 从而22)(||b a MN +>, 即b a MN +>||.………………13分20.(本小题满分14分)本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想.满分14分.解:2)2(211)(+-+='x a x x f 22)2)(1()24()24(++-+-+=x x a x a x . (Ⅰ)当0=a 时,0)0(=f ,切线的斜率1)0(='=f k ,所以切线方程为x y =,即0=-y x .……3分(Ⅱ)当0>a 时,因为0>x ,所以只要考查)24()24()(2a x a x x g -+-+=的符号. 由0)24(4)24(2≤---=∆a a ,得20≤<a ,当20≤<a 时,0)(>x g ,从而0)(>'x f ,)(x f 在区间),0(+∞上单调递增; 当2>a 时,由0)(=x g 解得a a a x 222-+-=. ……6分 当x 变化时,)(x f '与)(x f 的变化情况如下表:函数)(x f 在区间)22,0(2a a a -+-单调递减,在区间),22(2+∞-+-a a a 上单调递增.……9分(Ⅲ)由(Ⅱ)知,当2=a 时,)(x f 在区间),0(+∞上单调递增; 所以0)0(22)1ln()(=>+-+=f x xx x f , 即)1ln(22x x x+<+对任意),0(+∞∈x 成立. ……11分 取k x 1=,n k ,,3,2,1 =,得121ln(1)12k k k<++,即k k k ln )1ln(122-+<+,n k ,,3,2,1 =.……13分 将上述n 个不等式求和,得到:∑∑==-+<+nk nk k k k 11]ln )1[ln(122,即不等式1ln 1215131+<++++n n 对任意*N ∈n 成立. ……14分21.(1)选修4-2:矩阵与变换本小题主要考查矩阵与变换、矩阵的特征值与特征向量等基础知识,考查运算求解能力.满分7分.解:(Ⅰ)依题意⎥⎦⎤⎢⎣⎡=2213T ,所以42213det ==T ,本卷第11页(共11页) 所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-432141211T . ----------3分 (Ⅱ)由βα=T ,得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==-2165432141211βαT . ----------7分 (2)选修4-4:坐标系与参数方程本小题主要考查参数方程、极坐标方程等基础知识,考查运算求解能力,满分7分. 解:(Ⅰ)由θθρsin 8cos 6+=,得θρθρρsin 8cos 62+=,所以圆C 的直角坐标方程为08622=--+y x y x ,即2225)4()3(=-+-y x .………………………………………………3分 (Ⅱ)由(Ⅰ)得圆C 的参数方程为⎩⎨⎧+=+=θθsin 54,cos 53y x (θ为参数). 所以)4sin(257πθ++=+y x , ………………………5分 因此当ππθk 24+=,Z ∈k 时,y x +取得最大值为257+,且当y x +取得最大值时点P 的直角坐标为)2254,2253(++.……………7分(3)选修4-5:不等式选讲本小题主要考查绝对值不等式、柯西不等式等基础知识,考查运算求解能力,满分7分. 解:(Ⅰ)依题意,当1=x 时不等式成立,所以3|1|3≤-+m ,解得1=m , 经检验,1=m 符合题意. ---------------------3分(Ⅱ)由(Ⅰ)知132222=++c b a .根据柯西不等式, 得6])3()2()[321()32(2222222=++++≤++c b a c b a ,-----------------5分 所以6326≤++≤-c b a , 当且仅当66===c b a 时,取得最大值6,66-===c b a 时,取得最小值6-, 因此c b a 32++的取值范围是]6,6[-. -------------7分。
