2013年中环杯青少年科技报思维训练营五年级试题9月10月1-5期
第十三届中环杯五年级初赛试题附答案分析 2
第十三届“中环杯”小学生思维能力训练活动五年级选拔赛1.计算:31.3×7.7+11×8.85+0.368×230=()。
2.宠物商店有狃狸犬和西施犬共2012只,其中母犬1110只,狐狸犬1506 只,公西施犬202只。
那么母狐狸犬有_( )只。
3.一个数A为质数,并且A+14, A+18, A+32, A+36也是质数。
那A的值是( )4.一个口袋中有50个编上号码的相同的小球,其中编号为1,2,3,4,5的小球分别有2,6,10,12,20个。
任意从口袋中取球,至少要取出()个小球,才能保证其中至少有7个号码相同的小球。
5.表格中定义了关于“*”的运算,如3*4=2。
(1*2)*(1*2)*……(1*2)=()。
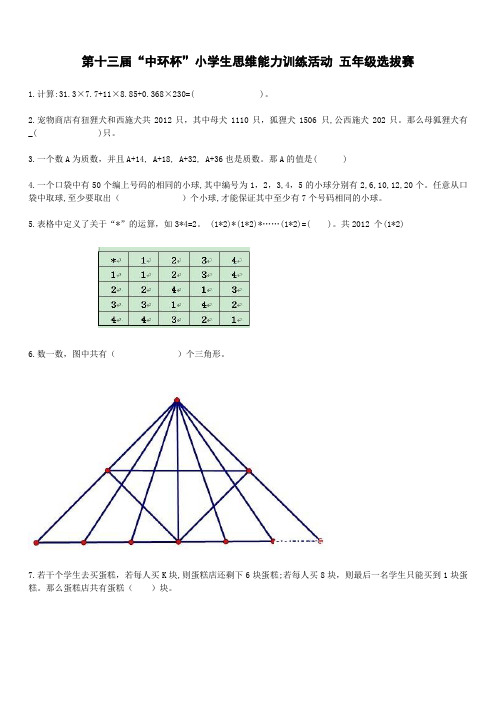
共2012 个(1*2)6.数一数,图中共有()个三角形。
7.若干个学生去买蛋糕,若每人买K块,则蛋糕店还剩下6块蛋糕;若每人买8块,则最后一名学生只能买到1块蛋糕。
那么蛋糕店共有蛋糕()块。
8.—张正方形纸,如图所示折叠后,构成的图形中,角x的度数是()。
9.A、B两地相距66千米,甲、丙两人从A地向B地行走,乙从B地向AI地行走。
甲每小时行12千米,乙每小时行10千米,丙每小时行8千米。
三人同时出发()小时后, 乙刚好走到甲、丙两人距离的中点。
10.有()个形如abcdabcd的数能被18769 整除。
11.小明带24个自制的纪念品去伦敦奥运会卖。
早上每个纪念品卖7英镑,卖出的纪念品不到总数的一半。
下午他对每个纪念品的价格进行打折,折后的价格仍是—个整数。
下午他卖完了剩下的纪念品。
全天共收入120英镑。
那么早上他卖出了()个纪念品。
12.如图,在一个四边形ABCD中,AC,BD相交于点O。
作三角形DBC的高DE,联结AE。
若三角形ABO的面积与三角形DCO的面积相等,且DC=17厘米,DE=15厘米,则阴影部分的面积为( )平方厘米。
13.五名选手在一次数学竞赛中共得414分;毎人得分互不相等且都是整数,并且其中得分最高的选手得了92分,那么得分最低的选手至少得()分,最多得()分。
十三届五年级中环杯选拔赛答案

7. 【答案】 97 块
3 能被 8 K 整除。 先用盈亏问题思考, 人数 6 7 8 K , 即1 所以 K 7 ,
即学生人数是 13 人。所以蛋糕共有 13 8 7 97 块 8. 【答案】 75 9. 【答案】 3.3
66 12 8 2 10 3.3 (小时)
所以 a3 28 。所以 a2 a3 8 。 17. 【答案】 623
2012 y 6 x y 2012 y x y 6 。 6 x 7 y 2012 7 x y 2012 x x y 2012 x 7
1 1 DE EC 15 8 60cm 2 。 2 2
13. 【答案】52,79 如果要考虑最低的得分,那么其余几人的得分要尽量高,则为 91、90、89, 则得解为 52。 如要考虑最多得分, 那要用平均思想解答。 414-92=322, 322 ÷4=80.5,则其余四人的分数分别为 82、81、80、79。 14. 【答案】 C 由 D 与 E 所讲的话可判断出 D 与 E 两人间至少有一人是说谎者;若 C 说实 话,则 AB 两人均说谎,说谎人数超过两人,矛盾,故 C 是说谎者,因此 AB 两人都说实话,可推知写字的人是 C 。 15. 【答案】18.75 或 6.25 此题两解。第二次相遇,可能在中点的左面,也可能在中点的右面。 首先求出 AB 两地的距离:300×2÷(60-40)=30 分钟,(60+40)×30 =3000 米。 再求第二次相遇两人分别走的时间之差,得到两个结果:18.75 分钟或 6.25 分钟。 16. 【答案】 8 首先当 m 2 时,要使得
(1)根据 x y
第十六届“中环杯”中小学生思维能力训练活动五年级决赛试题答案

⎝ ⎭ 第 16 届中环杯五年级决赛
一、填空题 A (本大题共 8 小题,每题 6 分,共 48 分):
1. 计算: 2016 ⨯ ⎛ 1 + 1 - 1 - 1 ⎫ = .
21 42 27 54 ⎪
【答案】32
2. 若 E 、U 、L 、S 、R 、T 分别表示 1、2、3、4、5、6(不同的字母表示不同的数 字),且满足:
(1) E + U + L = 6 ;
(2) S + R + U + T = 18 ;
(3)U ⨯ T = 15 ;
(4) S ⨯ L = 8 ;
则六位数 EULSRT = .
【答案】132465
3. 一个超过 20 的自然数 N ,在14 进制与 20 进制中都可以表示为回文数(回文数就是指 正读与倒读都一样的数,比如12321 、 3443 都是回文数,而12331 不是回文数)。
N 的 最小值为 (答案用10 进制表示)
【答案】105
4. 一位父亲要将他的财产分给他的孩子:首先将 1000 元以及剩余财产的 1 10
给老大,其
次将 2000 元以及剩余财产的 1 10 给老二,再次将 3000 元以及剩余财产的 1 10
给老三,
依次类推。
结果发现每个孩子都分到了相同的数量的财产,这位父亲一共有 个
孩子
【答案】9。
2013年中环杯青少年科技报思维训练营五年级试题10月11月6-10期

2013年“中环杯”中小学生思维能力训练活动思维训练营6-10期五年级试题第6期:多次相遇问题例、甲、乙两车同时从相距55千米的A、B两地相向开出,匀速行驶,甲行驶23千米后与乙相遇,之后两车继续前进,到达对方出发地后立即返回。
(1)第2次相遇,甲距B地多少千米?(2)第3次相遇,甲距A地多少千米?(3)第4次相遇,甲距A地多少千米?第7期:时钟问题例、泡泡的手表比家里的闹钟走得快一些。
这天中午12点时,泡泡把手表和闹钟校准。
但是闹钟显示为下午1点时,手表显示的时间是下午1点5分。
(1)当闹钟显示为下午5点的时候,手表显示的时间是多少?(2)当手表显示为下午6点30分的时候,闹钟显示的时间是多少?第8期:反序数问题我们把类似于102和201,35和53,11和11的数称为“互为反序的数”。
不过需要注意的是,120和021并不构成反序数。
求反序数时,如果涉及的是数的成绩,我们可以运用分解质因数和猜数字谜的方法进行解答。
例1、已知两个互为反序的自然数的乘积为30492,求这两个自然数。
例2、已知两个互为反序的自然数的成绩为92565,求这两个自然数。
第9期:立体图形表面积变化例、在一个边长为4的立方体的角上、棱上、面上分别挖去一个边长为1的立方体,求剩下的部分的表面积是多少?第10期:工程问题基本目标:由两个或两个以上的单位或人,共同去完成一项工作或一项工程,要求计算完成任务需要的时间。
题型特点:1、题目中没有给出具体的总工程量,通常用“1”表示。
2、基本数量关系与一般工作问题完全相同。
总工程量÷工作效率=工作时间;总工程量÷工作时间=工作效率;工作效率×工作时间=总工程量。
例、现铺设一条公路,由甲队单独完成需要20天,由乙队单独完成需要30天。
如果让甲、乙两队一起铺设,则需要几天?“中环杯”网站内容精选例、计算:3333333339.08.07.06.05.04.03.02.01.0++++++++。
五年级中环杯竞赛试题

第九届“中环杯”小学生思维能力训练活动区 学校 班姓名 准考证号 907999.99799.9979.997.998.9989.99899.998999.99()+++++++=201020102008200820082010⨯-⨯=( )。
将自然数按下图从1开始,2处拐弯,4处拐弯,7、11、16 处拐弯。
第20次拐弯的数是( )。
161514131222222221234520052006+++++++ 的和的末位数是( )。
如果32347;454567830∆=+=∆=++++=,按此规律计算:①74=( )∆② 321,x x ∆==()。
一艘客船在两个码头之间航行,顺水5小时行完全程,逆水7小时行完全程。
水速每小时5千米,那么两码头之间的距离是()千米。
一只魔袋里装有30种不同颜色的魔球各30只,现在请你闭上眼睛到袋中去摸球,每次限摸3只。
要使摸出的球至少有三种颜色是不少于3只的,那么至少要摸( )次。
将从8开始的11个连续自然数填入下图中的圆圈内,要使每边上的三个数字和都相等,共有( )种填法。
三角形ABC和三角形D EF是两个完全一样的直角三角形,如下图,把它们重叠在一起,那么阴影部分的面积为()2cm。
F2005年小明家养了一只大母羊,第二年春天它生了2只小公羊和3只小母羊。
每只小母羊从出生的第三年起也生了2只小公羊和3只小母羊。
那么到2010年,小明家共有()只羊。
下图两个完全一样的图形都是由5个小正方形组成的,请把它们分成四块,拼成一个大正方形,在原图上画出划分方法,并在空白处画出所拼的大正方形。
下图是由五个同样的正方形组成的图形,请你将它平均分成3份,要使每份的形状、大小完全一样。
下图是边长为2的三个完全一样的正方形,将它分成形状大小完全一样的四块,再拼成一个长方形,在下图上作图表示如何分法,并在空白处画出所拼的长方形。
并求这个长方形的周长。
第十五届“中环杯”初赛五年级 试题解析

第十五届“中环杯”小学生思维能力训练活动五年级选拔赛1、已知2468135713572468m n++++++-=++++++,其中 m,,n 是两个互质的正整数,则10______m n +=。
【考点】分数计算【答案】110 分析:2016910920110162020=-=⨯+=原式。
2、D 老师家里有五个烟囱,这五个烟囱正好从矮到高排成一排,相邻两个烟囱之间的高度差为 2 厘米,其中最高的烟囱又正好等于最矮的两个烟囱的高度之和,则五个烟囱的高度之和是________厘米。
【考点】等差数列,方程【答案】50分析:设这五个烟囱分别为 x-4,x-2,x ,x+2,x+4,则 x+4=x-2+x-4,x=10, 和为 5x=50。
3、已知()()22332014a b c d =+⨯-,其中 a 、b 、c 、d 是四个正整数,请你写出满足条件的一个乘法算式:___________。
【考点】数的拆分,分解质因数【答案】答案不唯一 分析:2014=1×2014=2×1007=19×106=38×53()()22335932+⨯-4、一个长方体的长、宽分别为 20 厘米、15 厘米,其体积的数值与表面积的数值相等,则它的高为______厘米(答案写为假分数)。
【考点】立体几何,方程 【答案】6023分析:设高为 h ,则 ()60201520152015223h h h h ⨯⨯=⨯++⨯=,则。
5、一次中环杯比赛,满分为 100 分,参赛学生中,最高分为 83 分,最低分为 30 分(所有的分数都是整数),一共有 8000 个学生参加,那么至少有_____个学生的分数相同。
【考点】抽屉原理【答案】149分析:833015480005414881481149-+=÷=+=,…,。
6、对 35个蛋黄月饼进行打包,一共有两种打包规格:大包袋里每包有9 个月饼,小包装里每包有 4个月饼。
五年级中环杯历届试题

五年级中环杯历届试题五年级中环杯历届试题导语:在所有好的,不好的情绪里,毫无预兆地想念你,是我不可告人的隐疾。
以下小编为大家介绍五年级中环杯历届试题文章,欢迎大家阅读参考!五年级中环杯历届试题一、单项选择题(在下列每题的四个选项中,只有一个选项是符合试题要求的。
请把答案填入答题框中相应的题号下。
每小题1分,共23分)1. 健康牛的体温为( )。
A. 38~39.5°CB. 37~39°CC. 39~41°CD. 37.5~39.5°C2. 动物充血性疾病时,可视黏膜呈现( )。
A. 黄染B. 潮红C. 苍白D. 发绀3. 心肌细胞脂肪变性是指( )。
A. 心肌间质脂肪浸润B. 心肌脂肪组织变性C. 心外膜脂肪细胞堆积D. 心肌细胞胞质中出现脂滴4. 化脓菌入血、生长繁殖、产生毒素、形成多发性脓肿,该病是( )。
A. 脓毒血症B. 毒血症C. 败血症D. 菌血症5. 细胞坏死过程中,核变小、染色质浓聚,被称之为( )。
A. 核溶解B. 核分裂C. 核固缩D. 核碎裂6. 在慢性炎症组织中,最多见的炎症细胞是( )。
A.中性粒细胞 B.嗜酸性粒细胞C.淋巴细胞 D.肥大细胞7. 商品蛋鸡中暑时的胸肌颜色( )。
A.暗红色 B.鲜红色 C.浅白色 D.基本正常8. 甲硝唑主要用于下列哪种情况( )。
A. 大肠杆菌病B. 抗滴虫和厌氧菌C. 需氧菌感染D. 真菌感染9. 下列动物专用抗菌药是( )。
A.环丙沙星 B.氧氟沙星 C.强力霉素 D.泰乐菌素10.被病毒污染的场地,进行消毒时,首选的消毒药是( )。
A.烧碱 B.双氧水 C.来苏儿 D.新洁尔灭11.解救弱酸性药物中毒时加用NaHCO3的目的是( )。
A. 加快药物排泄B. 加快药物代谢C. 中和药物作用D. 减少药物吸收12.国家强制免疫的动物疫病不含( )。
A.禽流感 B.蓝耳病 C.猪瘟 D.新城疫13.鸭传染性浆膜炎的病原为( )。
青少年科技报-五年级(1-9期)解析版

n n 大的约数 ) , 考虑到它一共有 10 个约数, 所以必须为 2 34 或 24 3 , 显然 2 34 3 2 =162 比较大。
【点评】 难度: ☆☆☆ 本题考查整数的约数个数定理:若
an a2 a3 n p1a1 p2 p3 ... pn ,则 n 的约数个数:
d (n) (a1 1)(a2 1)( a3 1)...( a4 1) 。在本题中,由第
b a 2 ,而且 1 号、10 号不能同时选出。 c b 2
b a 2 (b 1) a 1 ,考虑到 c b 2 (c 2) (b 1) 1
3
我们先不考虑 1 号、 10 号的问题。由于
1 a<b<c 10 ,所以 1 a<b-1<c-2 8 ,一共有 C8 =56 (种)选法,其中 1 号、10 号被
2 3
2
3
【点评】 难度: ☆☆☆ 本题是一道排列组合的综合问题,结合了特殊元素、分类分步等方法。位置与气球作为 两个不同维度应分步讨论, 每个维度内再根据特殊要求作分类讨论, 承接上一期分类分步思 想,进一步深化练习。
同时选出的选法有 6 种,所以答案为 56 6 50 (种) 。 【点评】 难度: ☆☆☆ 本题考查环型排列中的不相邻问题。插空法是解决直线型排列中不相邻问题最常用的 方法,本题需先将环型排列转化为直线型排列,即可轻松求出答案。 官方解答中对不等式的应用超越了大多数五年级考生的能力范围, 因此用插空法来解题 可能更易理解,在此提出以下两种解法供大家参考: (1) 插空法: 先将环型排列转化成直线型排列,即将 10 个站台编号为 1、2、…、10,按直线型插空 法来做,再去掉 1 号和 10 号同时被选出的情况。 在 1 10 号中选出三个不相邻的站台,即相当于将选出的三个站台插入另 7 个站台所形 成的 8 个空隙中(不能插入同一个空隙) ,总共有 C8 =56 (种)情况。其中同时选出 1 号跟 10 号的情况里,还需再选出一个站台,只能在 3 案为 56 6 50 (种) 。 (2) 排除法:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 2 页 共 4 页
上海-智康 1 对 1
王洪福老师 数学
例 3、一个四位数满足下列条件:它的各位数字都是奇数;它的各位数字互不相同;它的每个数字都能整除 它本身。请问这样的四位数共有多少个?
例 4、若一个班级中共有 10 人,现需要派人去开会。可以去也可以不去,可以去任意人数,那么共有多少种 不同的情况?
王洪福老师 数学
例 2、如图,∆ABC 的每边长都是 96cm,用折线把这个三角形分割成面积相等的四个三角形,求线段 CE 和
CF 的长度之和。
定价问题
例、某超市在一所学校开设连锁店。每月租金、员工工资、设备损耗等固定成本 2 万元,每进价值 1 千元的
商品,从进货到上架销售需 25 元额外费用。经过一段时间试营业后,公司发现学校内消费群体比较固定, 且 每天在超市有总量不低于 2 千元、不超过 3 千元的消费,每月平均可以保证有 22 个正常营业日。现在超市打 算每月赚得 1 万元的利润, 那么进价价值 1 千元的商品, 应以多少元的零售价出售?该超市一种纸盒装 1000ml 的牛奶零售价为 6.9 元,那么进价约为多少元?
第 1 页 共 4 页
上海-智康 1 对 1
王洪福老师 数学
例 2、现有甲、乙、丙三人,甲每分钟走 40 米,乙每分钟走 50 米,丙每分钟走 60 米。A、B 两地相距 2700 米,甲、乙分别从 A、B 两地同时出发,相向而行,他们出发 15 分钟后,丙从 B 地出发追赶乙。请问:甲在 与乙相遇之后多少分钟又与丙相遇?又过了多少分钟,丙才追上乙?
2013 年“中环杯”中小学生思维能力训练活动 思维训练营 1-5 期 五年级试题 学而思智康 王洪福老师出品 2013.12.9
第 4 页 共 4 页
上海-智康 年“中环杯”中小学生思维能力训练活动 思维训练营 1-5 期 五年级试题
----学而思智康 王洪福老师出品 比例类行程问题
例 1、甲、乙两车分别从 A、B 两站同时出发相向而行,已知甲车与乙车的速度比是 3:2。C 站在 A、B 两站 之间,甲乙两车到达 C 站的时间分别是上午 5 时和下午 3 时。那么,甲、乙两车在几时相遇?
例 2、甲、乙两车分别从 A、B 两地同时出发相向而行,经过 2 小时相遇。相遇后各自继续前进,又经过 1.5 小时,甲车到达 B 地,这时乙车距 A 地还有 35 千米。求 A、B 两地的距离。
多人相遇问题
例 1、泡泡每分钟走 30 米,朵朵每分钟走 40 米,当当每分钟走 50 米。泡泡、朵朵从欢乐谷,当当从图书馆, 同时相向出发,当当遇到朵朵 5 分钟后又遇到了泡泡,求欢乐谷到图书馆的距离。
三角形的等级变形
例 1、分别延长四边形 ABCD 的四个边,使得 AB BA ' , BC CB ' , CD DC ' , DA AD ' 如果四边形 ABCD 的面积是 1 平方厘米,试求四边形 A ' B ' C ' D ' 的面积? (如图所示)。
第 3 页 共 4 页
上海-智康 1 对 1
计数问题
例 1、如图所示,水按照箭头方向在管道内流动。管道网一共有 5 个阀门,阀门可以是开也可以是关。也就是 说可以让水流通过也可以不让水流通过。5 个阀门的开活关一共有 25 32 (种)不同组合。那么这 32 种不 同组合中有几种组合可以让水从 A 流到 B?
例 2、若一个自然数中至少有两个数字,且每个数字小于其右边的所有数字,则称这个数是“上升数” 。问一 共有多少这样的自然数?
