2015年广东省揭阳市高三二模考试数学(理科)试题含答案
2015年高考数学广东卷(理科)试卷及答案(word完整版)

绝密★启用前 试卷类型:A2015年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一个选项是符合题目要求的。
{}}{|(4)(1)0,|(4)(1)0M x x x N x x x =++==--=,则M N ⋂=}{A.1,4}{B.1,4--}{C.D.∅(32)z i i =-(i 是虚数单位),则z = A.23i -B.23i +C.32i +D.32i -3. 下列函数中,既不是奇函数,也不是偶函数的是A.y 1B.y x x=+1C.22x xy =+D.x y x e =+4. 袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球,从袋中任取2个球,所取的2个球中恰好有1个白球,1个红球的概率为5A.2110B.2111C.21D.15. 平行于直线2++1=0x y 且与圆225x y +=相切的直线的方程是A.250250x y x y ++=+-=或B.2020x y x y +=+=或C.250250x y x y -+=--=或D.2020x y x y -=-=或6. 若变量,x y 满足约束条件4581302x y x y +≥⎧⎪≤≤⎨⎪≤≤⎩,则32z x y =+的最小值为A.4 23B.5C.6 31D.57. 已知双曲线2222:1x y C a b -=的离心率54e =,且其右焦点为2(5,0)F ,则双曲线C 的方程为22A.143x y -= 22B.1916x y -= 22C.1169x y -= 22D.134x y -= 8. 若空间中n 个不同的点两两距离都相等,则正整数n 的取值A.3至多等于B.4至多等于C.5等于D.5大于二、填空题:本大题 共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9-13题)9.在4)的展开式中,x 的系数为 .10. 在等差数列{}n a 中,若3456725a a a a a ++++=,则28a a += .11. 设ABC∆的内角A,B,C的对边分别为a,b,c,若a=1sin2B=,6Cπ=,则b= .12. 某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了条毕业留言。
广二模理数答案
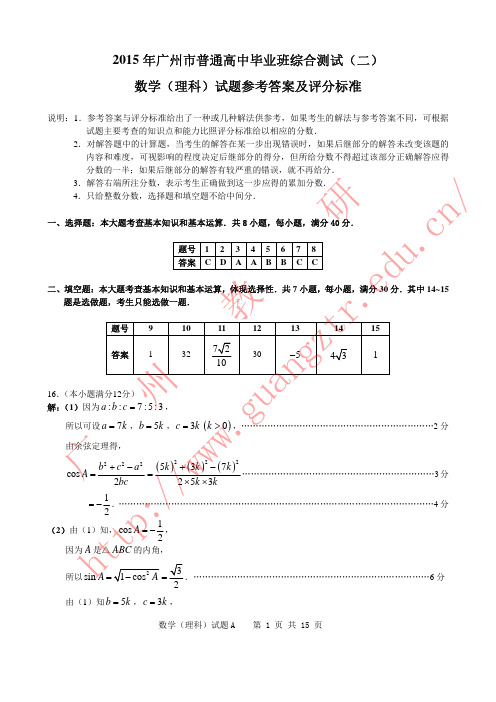
A
M
第 5 页 共 15 页
ed u. c
B
n/
ì ï-3 y + 3 z = 0, ï î3 3 x - 2 y = 0.
在△ ABA1 中, AM = AN = 1 , AB = AA1 = 3 , 所以
AM AN = , AB AA1
所以 MN P BA1 .…………………………………………………………………………………………4分 所以 MN P DE1 . 所以 M , N , E1 , D 四点共面.………………………………………………………………………6分
取 y = 3 3 ,则 x = 2 , z = 3 3 . 所以 n = 2,3 3,3 3 是平面 MNE1 D 的一个法向量.………………………………………………12分 设直线 BC 与平面 MNE1 D 所成的角为 q ,
(
)
=
2
æ 3 3ö 3 2´ç ÷+ 3 3´ +3 3´0 2 è 2 ø
F
(
)
ed u. c
B D1 C1 B1 D C
ht t
r uuu r æ 3 3 3 ö uuuu 则 BC = ç , DE1 = ( 0, -3,3) , , , 0 ÷ B ç 2 2 ÷ A M è ø x uuuu r DM = 3 3, -2, 0 .……………………………………………………………………………………10分
教
第(1) (2)问均用向量法:
州
(1)证明:以点 E 为坐标原点, EA , ED , EE1 所在的直线 分别为 x 轴, y 轴, z 轴,建立如图的空间直角坐标系,
gu
an gz
F1 A1
2015年广东高考理科数学试题及答案(完整版)

2015年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、若集合()(){}410M x x x =++=,()(){}410N x x x =--=,则M N =( )A .{}1,4B .{}1,4--C .{}0D .∅2、若复数()32z i i =-(i 是虚数单位),则z =( )A .23i -B .23i +C .32i +D .32i -3、下列函数中,既不是奇函数,也不是偶函数的是( )A.y = B .1y x x =+ C .122x x y =+ D .x y x e =+ 4、袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )A .521B .1021C .1121D .1 5、平行于直线210x y ++=且与圆225x y +=相切的直线的方程是( )A .250x y ++=或250x y +-= B.20x y ++=或20x y +=C .250x y -+=或250x y --= D.20x y -+=或20x y -=6、若变量x ,y 满足约束条件4581302x y x y +≥⎧⎪≤≤⎨⎪≤≤⎩,则32z x y =+的最小值为( )A .4B .235C .6D .3157、已知双曲线C:22221x y a b -=的离心率54e =,且其右焦点为()2F 5,0,则双曲线C 的方程为( ) A .22143x y -= B .221916x y -= C .221169x y -= D .22134x y -= 8、若空间中n 个不同的点两两距离都相等,则正整数n 的取值( )A .至多等于3B .至多等于4C .等于5D .大于5二、填空题(本大题共7小题,考生作答6小题,每小题5分,满分30分.)(一)必做题(11~13题)9、在)41的展开式中,x 的系数为 . 10、在等差数列{}n a 中,若3456725a a a a a ++++=,则28a a += .11、设C ∆AB 的内角A ,B ,C 的对边分别为a ,b ,c .若3a =,1sin 2B =,C 6π=,则b = .12、某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答)13、已知随机变量X 服从二项分布(),n p B ,若()30E X =,()D 20X =,则p = .(二)选做题(14、15题,考生只能从中选作一题)14、(坐标系与参数方程选做题)已知直线l 的极坐标方程为2sin 24πρθ⎛⎫-= ⎪⎝⎭,点A 的极坐标为722,4π⎛⎫A ⎪⎝⎭,则点A 到直线l 的距离为 . 15、(几何证明选讲选做题)如图1,已知AB 是圆O 的直径,4AB =,C E 是圆O 的切线,切点为C ,C 1B =.过圆心O 作C B 的平行线,分别交C E 和C A 于点D 和点P ,则D O = .三、解答题16.(本小题满分12分)在平面直角坐标系xOy 中,已知向量(1) 若m n ⊥,求tan x 的值;(2) 若m 与n 的夹角为3π,求x 的值. 17. (本小题满分12分)某工厂36名工人年龄数据如下表(1) 用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;(2) 计算(1)中样本的均值x 和方差2s ;(3) 36名工人中年龄在x s -和x s +之间有多少人?所占百分比是多少(精确到0.01%)?18.(本小题满分14分)如图2,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,4,6,3PD PC AB BC ====,点E 是CD 的中点,点、F G 分别在线段、AB BC 上,且2,2AF FB CG GB ==.(1) 证明:PE FG ⊥; (2) 求二面角P AD C --的正切值;(3) 求直线PA 与直线FG 所成角的余弦值.19. (本小题满分14分)设1a >,函数2()(1)x f x x e a =+-(1) 求()f x 的单调区间; (2) 证明()f x 在(,)-∞+∞上仅有一个零点;(3) 若曲线()y f x =在点P 处的切线与x 轴平行,且在点M (m,n )处的切线与直线OP 平行,(O 是坐标原点),证明:1m ≤-.20. (本小题满分14分)已知过原点的动直线l 与圆221:650C x y x +-+=相交于不同的两点A 、B.(1) 求圆1C 的圆心坐标;(2) 求线段AB 的中点M 的轨迹C 的方程;(3) 是否存在实数k,使得直线:(4)l y k x =-与曲线C 只有一个交点?若存在,求出k 的取值范围;若不存在,说明理由.21. (本小题满分14分) 数列{a }n 满足:*12122......3,2n n n a a na n N -+++=-∈. (1) 求3a 的值;(2) 求数列{a }n 的前 n 项和n T ;(3) 令111111,(1......)(2),23n n n T b a b a n n n-==+++++≥证明:数列{}n b 的前n 项和S n 满足22ln n S n <+2015年普通高等学校招生全国统一考试(广东卷)数学(理科)参考答案。
2015年广东省高考数学试卷(理科)含解析

A.{1,4}
B.{﹣1,﹣4}
C.[0}
D∅
.
2.(5 分)(2015•广东)若复数 z=i(3﹣2i)(i 是虚数单位),则 =( )
A.2﹣3i
B.2+3i
C.3+2i
D 3﹣2i
.
3.(5 分)(2015•广东)下列函数中,既不是奇函数,也不是偶函数的是( )
A.y=
B.y=x+
C.y=2x+
21.(14 分)(2015•广东)数列{an}满足:a1+2a2+…nan=4﹣
,n∈N+.
(1)求 a3 的值; (2)求数列{an}的前 n 项和 Tn;
(3)令 b1=a1,bn=
+(1+ + +…+ )an(n≥2),证明:数列{bn}的前 n 项和 Sn 满足
a2+a8=
.
11.(5 分)(2015•广东)设△ABC 的内角 A,B,C 的对边分别为 a,b,c.若 a= ,
sinB= ,C= ,则 b=
.
12.(5 分)(2015•广东)某高三毕业班有 40 人,同学之间两两彼此给对方仅写一条毕业
留言,那么全班共写了
条毕业留言.(用数字作答)
13.(5 分)(2015•广东)已知随机变量 X 服从二项分布 B(n,p),若 E(X)=30,D
Colin291210657
2015 年广东省高考数学试卷(理科)
一、选择题(本大题共 8 小题,每小题 5 分,满分 40 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.) 1.(5 分)(2015•广东)若集合 M={x|(x+4)(x+1)=0},N={x|(x﹣4)(x﹣1)=0},则 M∩N=( )
高三数学第二次模拟试题理揭阳二模,扫描版新人教A版

广东省揭阳市高三数学第二次模拟试题理(揭阳二模,扫描版)揭阳市 高中毕业班高考第二次模拟考数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数.一.选择题:BCDA DACC解析:1.由210x -≥得0x ≥,[0,)A ∴=+∞,故选B .2.由(12)1ai i bi +=-得1,12a b ⇒=-=-||a bi ⇒+==选C .3.设(,)B x y ,由3AB a =u u u r r 得1659x y +=⎧⎨-=⎩,所以选D .4.由129m a a a a =+++L 得5(1)93637m d a d m -==⇒=,选A .5.依题意可知该几何体的直观图如右上图,其体积为.3112322111323-⨯⨯⨯⨯⨯=,故选D.6.令()ln(1)g x x x =-+,则1'()111x g x x x =-=++,由'()0,g x >得0,x >即函数()g x 在(0,)+∞上单调递增,由'()0g x <得10x -<<,即函数()g x 在(1,0)-上单调递减,所以当0x =时,函数()g x 有最小值,min ()(0)0g x g ==,于是对任意的(1,0)(0,)x ∈-+∞U ,有()0g x ≥,故排除B 、D,因函数()g x 在(1,0)-上单调递减,则函数()f x 在(1,0)-上递增,故排除C,所以答案选A.7.四名学生中有两名分在一所学校的种数是24C ,顺序有33A 种,而甲乙被分在同一所学校的有33A 种,所以不同的安排方法种数是23343330C A A -=.故选C. 8. 因21(3)(2)()55(3)(2)1n n n a f f n n n n ⎛⎫+-+== ⎪++++-⎝⎭11()()23f f n n =-++,故81ii a =∑128111111()()()()()()34451011a a a f f f f f f =+++=-+-++-L L 111131()()()()31111314f f f f -=-==⨯-,故选C.二.填空题:;10. 43200x y --=;11.34;12. 12a >(或1(,)2a ∈+∞);13.2; 14. cos sin 20ρθρθ+-=(或cos()4πρθ-=;. 解析:9.依题意得3a =,则4tan a π=4tan 3π= 10.双曲线221916x y -=的右焦点为(5,0),渐近线的方程为43y x =±,所以所求直线方程为4(5),3y x =-即43200x y --=. 11.两个电子元件的使用寿命均服从正态分布2(1000,50)N 得:两个电子元件的使用寿命超过1000小时的概率均为12p =,则该部件使用寿命超过1000小时的概率为:2131(1)4P p =--=12.由“∃)1,0(0∈x ,使得0)(0=x f ”是真命题,得(0)(1)0f f ⋅<⇒(12)(4||21)0a a a --+<0(21)(21)0a a a ≥⎧⇔⎨+->⎩或0(61)(21)0a a a <⎧⎨--<⎩⇒12a >13.令,x y u y v +==,则点(,)Q u v 满足01,0 2.u v u ≤-≤⎧⎨≤≤⎩,在uov 平面内画出点(,)Q u v 所构成的平面区域如图,易得其面积为2.14.把)4πρθ=-化为直角坐标系的方程为2222x y x y +=+,圆心C 的坐标为(1,1),与直线OC 垂直的直线方程为20,x y +-=化为极坐标系的方程为cos sin 20ρθρθ+-=或cos()4πρθ-=15.依题意知30DBA ∠=o ,则AD=2,过点D 作DG AB ⊥于G ,则AG=BE=1,所以3BF =. 三.解答题:16.解:(1)函数()f x 要有意义,需满足:cos 0x ≠, 解得,2x k k Z ππ≠+∈,------------2分 即()f x 的定义域为{|,}2x x k k Z ππ≠+∈-------------------------------------4分(2)∵1)4()cos x f x xπ-=122)22cos x x x =1cos 2sin 2cos x x x +-=--------6分22cos 2sin cos cos x x x x -=2(cos sin )x x =--------------------------------------------------8分 由4tan 3α=-,得4sin cos 3αα=-, 又22sin cos 1αα+= ∴29cos 25α=,∵α是第四象限的角∴3cos 5α=,4sin 5α=----------------------10分 ∴14()2(cos sin )5f ααα=-=.-----------------------------------------------------------12分 17. 解:(1)设A 表示事件“从第三箱中有放回地抽取3次(每次一件),恰有两次取到二等品”,依题意知,每次抽到二等品的概率为25,------------------------------2分 故2232336()()55125P A C =⨯=. ------------------------------------------5分 (2)ξ可能的取值为0,1,2,3.----------------------------------6分P (ξ=0)=C 24C 25·C 23C 25=18100=950, P (ξ=1)=C 14C 25·C 23C 25+C 24C 25·C 13·C 12C 25=1225, P (ξ=2)=C 14C 25·C 13·C 12C 25+C 24C 25·C 22C 25=1550, P (ξ=3)=C 14C 25·C22C 25=125.-----------------------------10分 ξ的分布列为--------------------------------11数学期望为E ξ=1×1225+2×1550+3×125=1.2.-------------------------------------------------------12分N 1M 1E A B C D FN M18.解:(1)13a =,23a c =+,333a c =+, --------------------------------1分∵1a ,2a ,3a 成等比数列,∴2(3)3(33)c c +=+, --------------------------------2分解得0c =或3c =. --------------------------------3分当0c =时,123a a a ==,不符合题意舍去,故3c =.-------------------------------4分(2)当2n ≥时,由21a a c -=,322a a c -=,……1(1)n n a a n c --=-, 得1(1)[12(1)]2n n n a a n c c --=+++-=L .--------------------------------6分 又13a =,3c =,∴2333(1)(2)(23)22n a n n n n n =+-=-+=L ,,.-------------------------8分 当1n =时,上式也成立,∴23(2)()2n a n n n N *=-+∈.--------------------------------9分 (3)由2013n a ≥得23(2)20132n n -+≥,即213400n n --≥--------------------------10分∵n N ∈*,∴12n +≥141813622+⨯>=--------------------------------11分 令37n =,得3720012013a =<,令38n =得3821122013a =>----------------------13分∴使2013n a ≥成立的最小自然数38n =.--------------------------------14分19.解:(1)依题意得,,EF DE EF AE EF ⊥⊥∴⊥平面ADE ,DEA ∠=θ-------2分由45θ=o得,1sin 4524ADE S DE EA ∆=⋅=o ,∴4BCF ADE ADE V S EF -∆=⋅=----------------------------------------------------------------------4分 (2)证法一:过点M 作1MM BF ⊥交BF 于1M ,G E AB CD F N M QE A B C D FN M过点N 作1NN CF ⊥交BF 于1N ,连结11M N ,------------5分∵11//,//MM AB NN EF ∴11//MM NN又∵11MM NN FM CN AB FA CE EF === ∴11MM NN =--------------------------------7分∴四边形11MNN M 为平行四边形,--------------------------------------------------------8分11//MN N M ∴,11,,MN BCF N M BCF ⊄⊂又面面//.MN BCF ∴面--------------------10分【法二:过点M 作MG EF ⊥交EF 于G ,连结NG ,则,CN FM FG NE MA GE== //NG CF ∴--------------------------------------------------------------6分 ,,//NG BCF CF BCF NG BCF ⊄⊂∴又面面面,------------7分 同理可证得//MG BCF 面,又MG NG G =I , ∴平面MNG//平面BCF-------------9分∵MN ⊂平面MNG,//MN BCF ∴面.----------------------------------------------------10分】(3)法一:取CF 的中点为Q ,连结MQ 、NQ ,则MQ//AC ,∴NMQ ∠或其补角为异面直线MN 与AC 所成的角,--------11分 ∵090θ=且2a =∴12NQ =,2MQ ==2MN ∴=---------------------------------------------------------------------12分222cos 2QM MN NQ NMQ MN QM +-∴∠==⋅ 即MN 与AC所成角的余弦值为3--------------------------------14分 【法二:∵090θ=且2a = 分别以FE 、FB 、FC 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系. --------------11分则111111(1,1,0),(0,0,1),(,,0),(,0,),(1,1,1),(0,,),222222A C M N AC MN =--=-u u u r u u u u r 得----12分cos ,AC MN ∴<>==u u u r u u u u r 13分 所以与AC所成角的余弦值为14分】 20. 解:(1)∵1cos602122p OA ==⨯=o ,即2p =, ∴所求抛物线的方程为24y x = --------------------------------2分∴设圆的半径为r ,则122cos 60OB r =⋅=o ,∴圆的方程为22(2)4x y -+=.--------------4分(2) 设()()1122,,,G x y H x y ,由0OG OH ⋅=u u u r u u u r 得02121=+y y x x∵2211224,4y x y x ==,∴1216x x =, --------------------------------6分 ∵12GOH S OG OH ∆=u u u r u u u r ,∴()()222222*********GOH S OG OH x y x y ∆==++u u u r u u u r =()()2211221444x x x x ++ =()()21212121214164x x x x x x x x ⎡⎤+++⎣⎦≥()212121214164x x x x x x ⎡⎤+⋅⎣⎦=256 ∴16GOH S ∆≥,当且仅当122x x ==时取等号,∴GOH ∆面积最小值为16.-------------------------------------------9分(3) 设()()4433,,,y x Q y x P 关于直线m 对称,且PQ 中点()00,y x D∵ ()()4433,,,y x Q y x P 在抛物线C 上,∴2233444,4y x y x ==两式相减得:()()()3434344y y y y x x -+=---------------------------------11分 ∴343434444PQx x y y k y y k -+=⋅==--,∴02y k =- ∵()00,y x D 在()():10m y k x k =-≠上∴010x =-<,点()00,y x D 在抛物线外--------------------------------13分∴在抛物线C 上不存在两点Q P ,关于直线m 对称. --------------------------14分 21.解:(1)解法1:∵121'()(1)2(1)(1)[(1)2]n n n n f x nx x x x x x n x x --=---=----------1分当1n =时,1'()(1)(13)f x x x =--当1[,1]2x ∈时,1'()0f x ≤,即函数1()f x 在1[,1]2上单调递减, ∴1111()28a f ==,--------------------------------------------------3分当2n =时,2'()f x 2(1)(12)x x x =--当1[,1]2x ∈时,2'()0f x ≤,即函数2()f x 在1[,1]2上单调递减, ∴2211()216a f ==---------------------------------------------------5分【解法2:当1n =时,21()(1)f x x x =-,则21'()(1)2(1)(1)(13)f x x x x x x =---=--当1[,1]2x ∈时,1'()0f x ≤,即函数1()f x 在1[,1]2上单调递减,∴1111()28a f ==, 当2n =时,222()(1)f x x x =-,则222'()2(1)2(1)f x x x x x =---2(1)(12)x x x =--当1[,1]2x ∈时,2'()0f x ≤,即函数2()f x 在1[,1]2上单调递减,∴2211()216a f ==】(2)令'()0n f x =得1x =或2n x n =+,∵当3n ≥时,1[,1]22n n ∈+且当1[,)22nx n ∈+时'()0n f x >,当(,1]2nx n ∈+时'()0n f x <,-----------------------7分故()n f x 在2nx n =+处取得最大值,即当3n ≥时,22()()()222n n n n n a f n n n ==+++24(2)n n n n +=+,------(*)------------------9分当2n =时(*)仍然成立,综上得21,184.2(2)n nn n a n n n +⎧=⎪⎪=⎨⎪≥⎪+⎩-------------------------------------10分 (3)当2n ≥时,要证2241(2)(2)n n n n n +≤++,只需证明2(1)4n n +≥-------------------11分∵01222(1)()()n nnn n n C C C nnn+=+++L 2(1)41212142n n n-≥++⋅≥++= ∴对任意*n N ∈(2n ≥),都有21(2)n a n ≤+成立.--------------------------------14分。
广东省揭阳市高三数学学业水平考试试题理

揭阳市2015-2016学年度高中三年级学业水平考试数学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效。
3.答案第Ⅱ卷时,将答案写在答题卡上,答在本试卷上无效。
4.考试结束后,将本试题和答题卡一并交回。
第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}{}2=1,2,1,0,1,2M x x N >=--,则MN =(A ) {}0 (B ) {}2 (C ){}2,1,1,2-- (D ){}2,2- 2.复数112i i i -+的实部与虚部的和为 (A )12- (B ) 1 (C )12 (D )323.在等差数列{}n a 中,已知35710132,9a a a a a +=++=,则此数列的公差为 (A )13 (B )3 (C )12 (D )164.如果双曲线经过点p ,且它的一条渐近线方程为y x =,那么该双曲线的方程式(A )22312y x -= (B ) 22122x y -= (C )22136x y -= (D )22122y x -= 5.利用计算机在区间(0,1)上产生随机数a,则不等式ln(31)0a -<成立的概率是 (A )13 (B )23 (C )12 (D )146.设,a b 是两个非零向量,则“222()a b a b +=+”是 “a b ⊥”的 (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分又不必要条件7.已知奇函数()y f x =的图像关于直线2x =对称,且()3f m =, 则(4)f m -的值为(A )3 (B )0 (C )-3 (D )138.函数24()cos cos f x x x =-的最大值和最小正周期分别为 (A )1,4π (B )1,42π (C )1,2π (D )1,22π9.某人以15万元买了一辆汽车,此汽车将以每年20%的速度 折旧,图1是描述汽车价值变化的算法流程图,则当n=4时, 最后输出的S 的值为 (A )9.6 (B )7.68 (C )6.144 (D )4.915210.如图2,网格纸上小正方形是边长为1,粗线画出的是一正方 体被截去一部分后所得几何体的三视图,则该几何体的表面积为 (A )54 (B )162(C )54+(D )162+11.已知直线0x y a -+=与圆心为C 的圆2270x y ++-+=相交于A ,B 两点,且4AC BC ⋅=,则实数a 的值为(A (B(C (D )12.若函数32()21f x x ax =-++存在唯一的零点,则实数a 的取值范围为 (A )[0,)+∞ (B )[0,3] (C )(3,0]- (D )(3,)-+∞第Ⅱ卷本卷包括必答题和选考题两部分,第13题~第21题为必答题,每个试题考生都必须作答,第22题~第24题为选考题,考生根据要求作答。
揭阳市届高三第二次模拟数学试题及答案(理)

2015年广东省揭阳市高考数学二模试卷(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知A={x|x=3k﹣1,k∈Z},则下列表示正确的是()A.﹣1∉A B.﹣11∈A C.3k+2∉A D.3k2﹣1∈A【考点】元素与集合关系的判断.【专题】集合.【分析】判断一个元素是不是集合A的元素,只要看这个元素是否满足条件x=3k﹣1,k ∈Z,即可:若判断一个具体的整数是否为A的元素,只需令这个数等于3k﹣1,解出k,判断k是否满足k∈Z即可;而若这个元素是含字母的式子时,需要看这个式子能否写成x=3k ﹣1,k∈Z,的形式,按照这个方法判断每个选项的正误即可.【解析】解:A.k=0时,x=﹣1,∴﹣1∈A,∴该选项错误;B.令﹣11=3k﹣1,k=,∴﹣11∉A,∴该选项错误;C.3k+2=3(k﹣1)﹣1,k﹣1∈Z,∴3k+2∈A,∴该选项错误;D.对于3k2﹣1,k2∈Z,∴3k2﹣1∈A,∴该选项正确.故选D.【点评】考查描述法表示集合,集合、元素的概念,以及元素与集合的关系,元素与集合关系的判断方法.2.(5分)已知复数z=1+i,则=()A.2 B.﹣2 C.2i D.﹣2i【考点】复数代数形式的乘除运算.【专题】数系的扩充和复数.【分析】利用复数的运算法则即可得出.【解析】解:∵复数z=1+i,∴==﹣=﹣2,故选:B.【点评】本题考查了复数的运算法则,属于基础题.3.(5分)命题P:“∃x∈R,x2+1<2x”的否定¬P为()A.∃x∈R,x2+1>2x B.∃x∈R,x2+1≥2x C.∀x∈R,x2+1≥2x D.∀x∈R,x2+1<2x【考点】命题的否定.【专题】简易逻辑.【分析】直接利用特称命题的否定是全称命题写出结果即可.【解析】解:因为特称命题的否定是全称命题,所以,命题P:“∃x∈R,x2+1<2x”的否定¬P为:∀x∈R,x2+1≥2x.故选:C.【点评】本题考查命题的否定特称命题与全称命题的否定关系.4.(5分)已知,则cos2α=()A.B.C.D.【考点】二倍角的余弦.【专题】计算题;三角函数的求值.【分析】由已知及诱导公式可求sinα,由二倍角的余弦函数公式即可得解.【解析】解:∵,∴可得sinα=﹣,∴cos2α=1﹣2sin2α=1﹣2×=.故选:A.【点评】本题主要考查了诱导公式,二倍角的余弦函数公式的应用,属于基础题.5.(5分)设向量=(1,2),=(2,3),若向量与向量=(﹣5,﹣6)共线,则λ的值为()A.B.C.D.4【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算、向量共线定理即可得出.【解析】解:∵=(1,2)﹣λ(2,3)=(1﹣2λ,2﹣3λ),与共线,∴﹣5(2﹣3λ)﹣(﹣6)(1﹣2λ)=0,化为﹣4+3λ=0,解得.故选:A.【点评】本题考查了向量的坐标运算、向量共线定理,属于基础题.6.(5分)已知变量x,y满足约束条件,则的最小值是()A.1 B. 4 C.D.0【考点】简单线性规划.【专题】不等式的解法及应用.【分析】作出不等式组对应的平面区域,利用直线的斜率的几何意义进行求解即可.【解析】解:作出不等式组对应的平面区域如图:则z=,则z的几何意义为区域内的点到原点的斜率,由图象知OB的斜率最小,由,解得,即B(3,2),则z==,故选:C【点评】本题主要考查线性规划以及直线斜率公式的应用,利用数形结合是解决本题的关键.7.(5分)已知点P在抛物线x2=4y上,那么点P到点M(﹣1,2)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.B.C.(﹣1,2)D.(1,2)【考点】抛物线的简单性质.【专题】计算题;圆锥曲线的定义、性质与方程.【分析】过点P作PQ⊥l,垂足为Q,连接FP,利用抛物线的定义可得|PQ|=|FP|.可知当PQ∥x轴时,点P、Q、M三点共线,因此|PM|+|PF|取得最小值|QM|,求出即可.【解析】解:抛物线x2=4y的焦点F的坐标为F(0,1),准线方程为y=﹣1,过点P作PQ⊥l,垂足为Q,连接FP,则|PQ|=|FP|.故当PQ∥y轴时,|PM|+|PF|取得最小值|QM|=2﹣(﹣1)=3.设点P(﹣1,y),代入抛物线方程(﹣1)2=4y,解得y=,∴P(﹣1,).故选:B.【点评】本题考查抛物线的简单性质,着重考查抛物线的定义的应用,突出转化思想的运用,属于中档题.8.(5分)连续掷一正方体骰子(各面的点数分别为1,2,3,4,5,6)两次得到的点数分别为m、n,作向量,若,则与的夹角成为直角三角形内角的概率是()A.B.C.D.【考点】列举法计算基本事件数及事件发生的概率.【专题】概率与统计.【分析】总的基本事件共36种,而符合题意的共21个,由概率公式可得.【解析】解:由题意可得m、n均取自1到6,故向量有6×6=36种取法,由知,则m≥n,列举可得这样的(m,n)为(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),(5,3),(5,4),(5,5),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)共有1+2+3+4+5+6=21(个),故所求的概率故选:B.【点评】本题考查古典概型及其概率公式,属基础题.二、填空题:本大题共5小题,考生作答6小题,每小题5分,满分25分.(一)必做题(9-13题)9.(5分)已知幂函数y=f(x)的图象过点,则的值为1.【考点】幂函数的概念、解析式、定义域、值域.【专题】函数的性质及应用.【分析】利用待定系数法求出f(x)的表达式即可.【解析】解:设f(x)=xα,则f(3)=3α=,解得α=﹣1,则f(x)=x﹣1,f(2)=,则log f(2)=log=1,故答案为:1;【点评】本题主要考查函数值的计算以及幂函数解析式的求解,利用待定系数法是解决本题的关键.10.(5分)展开式中的常数项为﹣160.【考点】二项式系数的性质.【专题】二项式定理.【分析】写出二项式的通项,直接由x得系数为0求得r的值,再代入通项求得答案.【解析】解:由,得=•x r﹣3.由r﹣3=0,得r=3.∴展开式中的常数项为=﹣160.故答案为:﹣160.【点评】本题考查了二项式定理,考查了二项式的展开式,是基础的计算题.11.(5分)图中的三个直角三角形是一个体积为30cm3的几何体的三视图,则侧视图中的h=6cm.【考点】简单空间图形的三视图.【专题】空间位置关系与距离.【分析】根据三视图得出几何体是一个三棱锥,存在两两垂直的棱,画出图形运用体积公式判断即可.【解析】解:根据三识图判断得出:∵PA,AB,AC两两垂直,∴PA⊥面ABC,且PA=h,AB=6,AC=6,∴V==5h=30,即h=6,故答案为:6.【点评】本题考查了空间几何体的三视图,根据给出的数据恢复空间几何体,判断几何体的性质,难度不大,属于中档题.12.(5分)下表记录了某学生进入高三以来各次数学考试的成绩将第1次到第12次的考试成绩依次记为a1,a2,…,a12.图2是统计上表中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.【考点】程序框图.【专题】图表型;算法和程序框图.【分析】模拟执行程序框图,可得程序框图的功能是统计12次考试中成绩大于等于90的次数,根据成绩表即可得解.【解析】解:模拟执行程序框图,可得程序框图的功能是统计12次考试中成绩大于等于90的次数,根据成绩表可知,成绩大于等于90的次数n=7.故答案为:7.【点评】本题主要考查了循环结构的程序框图,解题的关键是弄清算法流程图的含义,属于基础题.13.(5分)在△ABC中,已知角A,B,C所对的边分别为a,b,c,且c(acosB﹣bcosA)=b2,则=.【考点】余弦定理;正弦定理.【专题】解三角形.【分析】由条件利用正弦定理和余弦定理求得要求式子的值.【解析】解:△ABC中,∵c(acosB﹣bcosA)=b2,故由余弦定理可得ac•﹣bc•=b2,化简可得=2,∴=.再利用正弦定理可得=,故答案为:.【点评】本题主要考查正弦定理和余弦定理的应用,属于基础题.(二)选做题(14-15题,考生只能从中选做一题)【坐标系与参数方程选做题】14.(5分)在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ(2cosθ﹣sinθ)=3与ρ(cosθ+2sinθ)=﹣1的交点的极坐标为.【考点】简单曲线的极坐标方程.【专题】坐标系和参数方程.【分析】首先把极坐标方程转化成直角坐标方程,进一步建立方程组,求出交点的坐标,最后把交点的直角坐标转化为极坐标.【解析】解:在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ(2cosθ﹣sinθ)=3,转化为直角坐标方程为:2x﹣y﹣3=0.曲线ρ(cosθ+2sinθ)=﹣1,转化为直角坐标方程为:x+2y+1=0.建立方程组为:,解得:所以交点的直角坐标为:(1,﹣1),转化为极坐标为:(,).故答案为:.【点评】本题考查的知识要点:极坐标方程与直角坐标方程之间的转化,解二元一次方程组,直角坐标与极坐标之间的相互转化.主要考查学生的应用能力.【几何证明选讲选做题】15.如图,点P在圆O的直径AB的延长线上,且PB=OB=3,PC切圆O于C点,CD⊥AB于D点,则CD的长为.【考点】与圆有关的比例线段.【专题】选作题;推理和证明.【分析】由切割线定理得PC2=PB•PA=12,由此能求出CD长.【解析】解:∵AB是⊙O的直径,点P在AB的延长线上,且PB=OB=3,PC切⊙O于点C,CD⊥AB于点D,∴由切割线定理得PC2=PB•PA=27,∴PC=3,连结OC,则OC=OP,∴∠P=30°,∴CD=PC=.故答案为:.【点评】此题综合运用了切割线定理、切线的性质定理以及解直角三角形的知识,属于基础题.三.解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(12分)已知函数(A>0,ω>0)的部分图象如图所示,其中M为图象与x轴的交点,为图象的最高点.(1)求A、ω的值;(2)若,,求的值.【考点】正弦函数的图象.【专题】三角函数的求值;三角函数的图像与性质.【分析】(1)直接利用函数的图象确定函数的A和周期.(2)利用函数的关系式,进一步利用函数的恒等变换求出结果.【解析】解:(1)由为图象的最高点知A=2,又点M知函数f(x)的最小正周期,∵∴ω=π,(2)由(1)知,由得,∵∴∴,∵=∴=【点评】本题考查的知识要点:利用函数的图象求函数的解析式,及函数的周期,利用函数的关系变换求函数的值,主要考查学生的应用能力.17.(12分)某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)甲:132,108,112,121,113,121,118,127,118,129;乙:133,107,120,113,122,114,125,118,129,127.(1)以百位和十位为茎,个位为叶,在图5中作出甲、乙两班学生数学成绩的茎叶图,并判断哪个班的平均水平较高;(2)若数学成绩不低于128分,称为“优秀”,求从甲班这10名学生中随机选取3名,至多有1名“优秀”的概率;(3)以这20人的样本数据来估计整个学校的总体成绩,若从该校(人数很多)任选3人,记X表示抽到“优秀”学生的人数,求X的数学期望.【考点】离散型随机变量的期望与方差;茎叶图;离散型随机变量及其分布列.【专题】概率与统计.【分析】(1)直接利用茎叶图的作法画出茎叶图即可.(2)直接利用古典概型概率个数求解即可.(3)求出概率判断概率类型X~B(3,0.2),求出期望即可.【解析】解:(1)甲、乙两班学生数学成绩的茎叶图如图示:………..(3分)乙班的平均水平较高;…………………………………(4分)(2)由上数据知:甲班这10人中“优秀”的学生有2名,则从这10名学生中随机选取3人,至多有1人“优秀”的概率.………………….(8分)(3)因样本20名学生中,“优秀”的有4名,故从这20名学生中任选1名,恰好抽到“优秀”的概率为,……………………..(10分)据此可估计从该校中任选1名学生,其为“优秀”的概率为0.2,因X~B(3,0.2),所以EX=3×0.2=0.6.……………………….(12分)【点评】本题考查茎叶图以及古典概型,考查期望的求法,考查计算能力.18.(14分)已知等比数列f'(x)满足:a n>0,a1=5,S n为其前n项和,且20S1,S3,7S2成等差数列.(1)求数列{a n}的通项公式;(2)设b n=log5a2+log5a4+…+log5a2n+2,求数列{}的前n项和T n.【考点】数列的求和.【专题】等差数列与等比数列.【分析】(1)利用等差数列与等比数列的通项公式即可得出;(2)利用对数的运算性质、“裂项求和”即可得出.【解析】解:(1)设数列{a n}的公比为q,∵20S1,S3,7S2成等差数列,∴2S3=20S1+7S2.即,化简得2q2﹣5q﹣25=0,解得:q=5或∵a n>0,∴不合舍去,∴.(2)∵b n=log5a2+log5a4+…+log5a2n+2=,=,∴=,∴==.【点评】本题考查了等差数列与等比数列的通项公式、对数的运算性质、“裂项求和”,考查了推理能力与计算能力,属于中档题.19.(14分)如图,已知四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,AB∥CD,AD⊥CD,PA=PD=CD=2AB=2.(1)求证:AB⊥PD;(2)记AD=x,V(x)表示四棱锥P﹣ABCD的体积,当V(x)取得最大值时,求二面角A﹣PD﹣B的余弦值.【考点】二面角的平面角及求法;空间中直线与直线之间的位置关系.【专题】空间位置关系与距离;空间角.【分析】(1)通过线面垂直的判定定理及性质定理即得结论;(2)解:取AD中点E,连结PE,通过题意易得当V(x)取得最大值时,利用常用法或坐标法即可得结果.【解析】(1)证明:∵AB∥CD,AD⊥CD,∴AB⊥AD,∵侧面PAD⊥底面ABCD,且平面PAD∩平面ABCD=AD,∴AB⊥平面PAD,又∵PD⊂平面PAD,∴AB⊥PD;(2)解:取AD中点E,连结PE,∵PA=PD,∴PE⊥AD,又侧面PAD⊥底面ABCD,且平面PAD∩平面ABCD=AD,∴PE⊥底面ABCD,在Rt△PEA中,,∴==(0<x<4),∵V(x),当且仅当,即时“=”成立,即当V(x)取得最大值时,解法1:∵,PA2+PD2=8=AD2,∴PD⊥PA,又由(1)知AB⊥PD,PA∩AB=A,∴PD⊥平面PAB,又PB⊂平面PAB,∴PD⊥PB,∴∠APB为二面角A﹣PD﹣B的平面角,在Rt△PAB中,,即当V(x)取得最大值时,二面角A﹣PD﹣B的余弦值为;解法2:以点E为坐标原点,EA所在的直线为x轴、PE所在的直线为z轴建立空间直角坐标系如图示:则E(0,0,0),A(,0,0),D(,0,0),P(0,0,),,∴,,设平面PDB的法向量为,由得,,令c=1,则a=﹣1,∴,又是平面PAD的一个法向量,设二面角二面角A﹣PD﹣B的大小为θ,则,即所求二面角A﹣PD﹣B的余弦值为.【点评】本题主要考查线面关系及面面角,考查学生分析解决问题的能力,考查空间想象能力和逻辑推理能力,属于中档题.20.(14分)已知椭圆C:的焦点分别为、,P为椭圆C上任一点,的最大值为1.(1)求椭圆C的方程;(2)已知点A(1,0),试探究是否存在直线l:y=kx+m与椭圆C交于D、E两点,且使得|AD|=|AE|?若存在,求出k的取值范围;若不存在,请说明理由.【考点】椭圆的简单性质.【专题】平面向量及应用;直线与圆;圆锥曲线的定义、性质与方程.【分析】(1)设P(x,y),运用向量的数量积的坐标表示,结合点满足椭圆方程,运用椭圆的性质,即可得到最大值1,可得a=2,b=1,进而得到椭圆方程;(2)假设存在直线l满足题设,设D(x1,y1),E(x2,y2),将y=kx+m代入,运用韦达定理和判别式大于0,结合两点的距离公式,可得k,m的关系式,消去m,解不等式即可得到k的范围.【解析】解:(1)设P(x,y),由、,得,.∴=x2+y2﹣3,由得,∴=,∵0≤x2≤a2,∴当x2=a2,即x=±a时,有最大值,即,∴b2=1,a2=c2+b2=4,∴所求椭圆C的方程为;(2)假设存在直线l满足题设,设D(x1,y1),E(x2,y2),将y=kx+m代入并整理得(1+4k2)x2+8kmx+4m2﹣4=0,由△=64k2m2﹣4(1+4k2)(4m2﹣4)=﹣16(m2﹣4k2﹣1)>0,得4k2+1>m2①又,由|AD|=|AE|可得,⇒(1+k2)(x1+x2)+2km﹣2=0,化简得②将②代入①得,,化简得20k4+k2﹣1>0⇒(4k2+1)(5k2﹣1)>0,解得或.所以存在直线l,使得|AD|=|AE|,此时k的取值范围为.【点评】本题考查椭圆的方程和性质,主要考查椭圆方程的运用,联立直线方程,运用韦达定理,同时考查两点的距离公式的运用和化简整理的能力,属于中档题和易错题.21.(14分)已知函数(1)当a=1时,解不等式f(x)<x﹣1;(2)当a>0时,求函数f(x)的单调区间;(3)若在区间(0,1]上,函数f(x)的图象总在直线y=m(m∈R,m是常数)的下方,求a的取值范围.【考点】分段函数的应用;其他不等式的解法.【专题】函数的性质及应用;不等式的解法及应用.【分析】(1)讨论x>0,x<0,去绝对值,运用绝对值不等式的解集即可得到所求;(2)通过讨论x的范围,去绝对值,再由二次函数的对称轴和区间的关系,即可得到所求单调区间;(3)运用不等式恒成立思想,在区间(0,1]上,函数f(x)的图象总在直线y=m(m∈R,m是常数)的下方,即对∀x∈(0,1]都有f(x)<m,⇔对∀x∈(0,1]都有x|x﹣a|<m+1,显然m>﹣1,运用导数判断单调性,求得最值,即可得到a的范围.【解析】解:(1)当a=1时,不等式f(x)<x﹣1即x|x﹣1|<x,显然x≠0,当x>0时,原不等式可化为:|x﹣1|<1⇒﹣1<x﹣1<1⇒0<x<2;当x<0时,原不等式可化为:|x﹣1|>1⇒x﹣1>1或x﹣1<﹣1⇒x>2或x<0,即为x<0.综上得:当a=1时,原不等式的解集为{x|0<x<2或x<0};(2)∵,若x≥a时,∵a>0,由f'(x)=2x﹣a知,在(a,+∞)上,f′(x)≥0,若x<a,由f′(x)=﹣2x+a知,当时,f′(x)>0,当时,f′(x)<0,∴当a>0时,函数f(x)的单调增区间为,(a,+∞),单调减区间为.(3)在区间(0,1]上,函数f(x)的图象总在直线y=m(m∈R,m是常数)的下方,即对∀x∈(0,1]都有f(x)<m,⇔对∀x∈(0,1]都有x|x﹣a|<m+1,显然m>﹣1,即﹣m﹣1<x(x﹣a)<m+1⇒对∀x∈(0,1],恒成立⇒对∀x∈(0,1],,设,,x∈(0,1],则对∀x∈(0,1],恒成立⇔g(x)max<a<p(x)min,x∈(0,1],∵,当x∈(0,1]时g'(x)>0,∴函数g(x)在(0,1]上单调递增,∴g(x)max=﹣m,又∵=,当即m≥0时,对于x∈(0,1],有p′(x)<0,∴函数p(x)在(0,1]上为减函数,∴p(x)min=p(1)=2+m,当,即﹣1<m<0时,当,p′(x)≤0,当,p′(x)>0,∴在(0,1]上,,(或当﹣1<m<0时,在(0,1]上,,当时取等号),又∵当﹣1<m<0时,要g(x)max<a<p(x)min即还需满足⇒m2﹣4m﹣4<0,解得,∴当时,,当m≥0时,﹣m<a<2+m.【点评】本题考查分段函数的运用,考查绝对值不等式的解法和函数的单调性的运用,同时考查不等式恒成立思想的运用,属于中档题.。
广东省各市2015年高考二模数学理试题分类汇编.排列组合

1 广东省各市2015年高考二模数学理试题分类汇编排列组合1.(2015届佛山市)将编号为1, 2, 3, 4, 5的五个球放入编号为1, 2, 3, 4, 5的一个盒子,每个盒内放一个球,若恰好有两个球的编号与盒子编号相同,则不同的投放方法的种数为 .2.(2015届广州市)5名志愿者中安排4人在周六、周日两天参加社区公益活动.若每天安排2人,则不同的安排方案共有_________种(用数字作答).3.(2015届惠州市)将自然数按如图排列,其中处于从左到右第m 列从下到上第n 行的数记为),(n m A ,如4)1,3(=A ,12)2,4(=A ,则=),1(n A __________;=)10,10(A __________.282127152026101419256913182435812172312471116224(2015届深圳市)从1,2,2,3,3,3这六个数字中任取五个,组成五位数,则不同的五位数共有A .50个B .60个C .100个D .120个5(2015届湛江市)已知全集}8,7,6,5,4,3,2,1{=U ,在U 中任取四个元素组成的集合记为},,,{4321a a a a A =,余下的四个元素组成的集合记为},,,{4321b b b b A C U =,43214321b b b b a a a a +++<+++,则集合A 的取法共有____________种.6(2015届肇庆市)某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋 友1本,则不同的赠送方法共有 ▲ 种(用数字作答).答案:20 30 (1),1812n n + B 31 10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
揭阳市2015年高中毕业班第二次高考模拟考试数学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须填写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:棱锥的体积公式:13V Sh =.其中S 表示棱锥的底面积,h 表示棱锥的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知{|31,}A x x k k Z ==-∈,则下列表示正确的是A.1A -∉B.11A -∈C.32k A +∉D.231k A -∈2.已知复数1z i =+,则21z z=- A. 2 B. -2 C. 2i D. -2i 3.命题P :“2,12x Rx x∃∈+<”的否定P ⌝为A. 2,12x R x x ∃∈+> B.2,12x R x x ∃∈+≥ C.2,12x R x x ∀∈+≥ D.2,12x R x x ∀∈+< 4.已知1sin()3πα+=,则cos 2α=B.89C.79-D.795.设向量(12)(23)==,,,a b ,若向量λ-a b 与向量(56)=--,c 共线,则λ的值为 A .43 B .413 C .49- D .4图1侧视图6.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥-≤+-≤-+0101205x y x y x ,则y x 的最小值是A.1B. 4C.23D.0 7.已知点P 在抛物线24x y =上,那么点P 到点(12)M -,的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为A .1(1,)4 B . 1(1,)4- C .(1,2)- D .(1,2)8.连续掷一正方体骰子(各面的点数分别为1,2,3,4,5,6)两次得到的点数分别为m 、n ,作向量(,)a m n =,若(1,1)b =-,则a 与b 的夹角成为直角三角形内角的概率是A.59 B. 712 C.512 D. 710二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9-13题)9.已知幂函数()y f x =的图象过点1(3,)3,则12log (2)f 的值为 .10.6展开式中的常数项为 . 11.图1中的三个直角三角形是一个体积为330cm 则侧视图中的h =_________cm .12.下表记录了某学生进入高三以来各次数学考试的成绩 14. (坐标系与参数方程选做题)在极坐标系(,)ρθ (02)θπ≤<中,曲线x(2cos sin )3ρθθ-=与(cos 2sin )1ρθθ+=-的交点的极坐标为 .15.(几何证明选讲选做题)如图3,点P 在圆O 的直径AB 的 延长线上,且PB=OB=3,PC 切圆O 于C 点,CD ⊥AB 于点D ,则CD 的长为 . 图3三.解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数()sin()6f x A x πω=+(00)A ω>>,的部分图象如图4其中M 1(,0)6-为图象与x 轴的交点,1(,2)3P 为图象的最高点.(1)求A 、ω的值;(2)若2()3f απ=,(,0)3πα∈-,求cos()3πα+的值. 17.(本小题满分12分)某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)甲:132,108,112,121,113,121,118,127,118,129; 乙:133,107,120,113,122,114,125,118,129,127. (1)以百位和十位为茎,个位为叶,在图5中作出甲、乙两班 学生数学成绩的茎叶图,并判断哪个班的平均水平较高;(2)若数学成绩不低于128分,称为“优秀”,求从甲 班这10名学生中随机选取3名,至多有1名“优秀”的概率;(3)以这20人的样本数据来估计整个学校的总体成绩, 若从该校(人数很多)任选3人,记X 表示抽到“优秀”学生 的人数,求X 的数学期望. 18.(本小题满分14分)已知等比数列{}n a 满足:0n a >,15a =,n S 为其前n 项和,且13220S S S ,,7成等差数列.(1)求数列{n a }的通项公式; (2)设525452+2log log log n n b a a a =+++,求数列{1nb }的前n 项和n T . 19.(本小题满分14分)如图6,已知四棱锥P-ABCD 中,侧面PAD ⊥底面ABCD , AB ∥CD ,AD ⊥CD ,PA=PD=CD=2AB=2. (1)求证:AB ⊥PD ;(2)记AD=x ,()V x 表示四棱锥P-ABCD 的体积,当()V x 取得最大值时,求二面角A-PD-B 的余弦值.20.(本小题满分14分)已知椭圆C :22221(0)x y a b a b+=>>的焦点分别为1(F 、2F ,P 为椭圆C 上任一点,12PF PF ⋅uuu r uuu r的最大值为1.(1)求椭圆C 的方程;(2)已知点(1,0)A ,试探究是否存在直线:l y kx m =+与椭圆C 交于D 、E 两点,且使得||||AD AE =?若存在,求出k 的取值范围;若不存在,请说明理由.21.(本小题满分14分)已知函数()1,()f x a R =∈ (1)当1a =时,解不等式()1f x x <-; (2)当0a >时,求函数()f x 的单调区间;(3)若在区间(0,1]上,函数()f x 的图象总在直线(,y m m R m =∈是常数)的下方,求a 的取值范围.揭阳市2015年高中毕业班高考第二次模拟考试数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考 查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数. 一、选择题:DBCD ACBB解析:8.因m 、n 均取自1-6,故向量a 有6636⨯=种取法,由cos ,a b <>=知,0,2a b π<<>≤,则m n ≥,这样的(,)m n 共有12345621+++++=(个),故所求的概率2173612P ==.二、填空题:9. 1;10. 160-;11. 6;12.7;1314. 7)4π;15.2. 三、解答题:16.解:(1)由1(,2)3P 为图象的最高点知2A =,---------------------1分又点M 1(,0)6-知函数()f x 的最小正周期114()236T =+=,-----------------------3分 ∵2T πω=∴ωπ=,-------------------------------------------------5分(2)由(1)知,()2sin()6f x x ππ=+由2()3f απ=得1sin()63πα+=,----------------------------------------6分 ∵(,0)3πα∈-∴666πππα-<+<----------------------------------------7分∴cos()63πα+===-------------------------9分 ∵cos()cos()366πππαα+=++cos()cos sin()sin 6666ππππαα=+-+-------------11分∴cos()3πα+11132326=-⨯=------------12分17.解:(1)甲、乙两班学生数学成绩的茎叶图如右图示:--3分乙班的平均水平较高;----------------------------4分(2)由上数据知:甲班这10人中“优秀”的学生有2名, 则从这10名学生中随机选取3人,至多有1人“优秀”的概率321882310C +14C 15C C P ==.----------------------------8分 (3)因样本20名学生中,“优秀”的有4名,故从这20名学生中任选1名,恰好抽到“优秀”的概率为4=0.220,----------------------------------------------------------------------------------10分 据此可估计从该校中任选1名学生,其为“优秀”的概率为0.2,因(30.2)X B ,,所以30.20.6EX =⨯=.---------------------------------------------------------------------------12分18.解:(1)设数列{}n a 的公比为q ,∵13220,,7S S S 成等差数列,3122207.S S S ∴=+-----------------------------------2分即21111112()207()a a q a q a a a q ++=++,化简得225250q q --=,------4分 解得:5q =或52q =-------------------------------------------------------------------6分 ∵0n a >,∴52q =-不合舍去, ∴111555n n n n a a q --==⨯=.-----------------------------------------7分(2)∵525452+2log log log n n b a a a =+++=24+2+2524225log ()log 5242(+1)n n a a a n +++==+++------------9分(1)(222)(1)(2)2n n n n +++==++,------------------------------------------10分∴1n b =111=(1)(+212n n n n -+++),-----------------------------------------------------12分∴12111n nT b b b =+++111111()()()233412n n =-+-++-++ 11222(2)n n n =-=++.----------------------------------------14分 19.解:(1)证明:∵AB ∥CD ,AD ⊥CD ,∴AB ⊥AD ,-----------------------------1分∵侧面PAD ⊥底面ABCD ,且平面PAD 平面ABCD =AD ,∴AB ⊥平面PAD --------------------------------------------2分 又∵PD ⊂平面PAD ,∴AB ⊥PD------------------------------------------------------3分 (2)取AD 中点E ,连结PE ,∵PA=PD ,∴PE ⊥AD ,----4分又侧面PAD ⊥底面ABCD ,且平面PAD 平面ABCD =AD ,∴PE ⊥底面ABCD ,-------------------------------------------------------------------------5分在Rt ∆PEA 中,PE ==∴1()3ABCD V x S PE =⋅梯形11(12)32=⨯⨯+⨯14=04x <<)------7分∵()V x 124≤=-------------------------------9分当且仅当x =x =“=”成立,即当()V x 取得最大值时AD = -----------------------------------------------------10分解法1:∵AD =222+8PA PD AD ==,∴PD ⊥PA ,--------------------11分 又(1)知AB ⊥PD ,PAAB A =∴PD ⊥平面PAB ,又PB ⊂平面PAB ∴PD ⊥PB ,------------------------------------------13分 ∴APB ∠为二面角A -PD -B 的平面角在Rt PAB ∆中,cosPA APB PB ∠===,即当()V x 取得最大值时,二面角A -PD -B 的余弦值为5.-------------------14分 [解法2:以点E 为坐标原定,EA 所在的直线为x 轴、PE 所在的直线为z 轴建立空间直角坐标系如图示:则E (0,0,0),0,0),D(0,0),P(0,0,B∴(2,1,PB =(PD =,设平面PDB 的法向量为(,,)m a b c =由,m PB m PD ⊥⊥0b +=,0=,令1c =,则1a =-,b = ∴(1m =-------------------------12分 又(0,1,0)AB =是平面PAD 的一个法向量, 设二面角二面角A-PD-B的大小为θ,则25c o s ||||1110m A m A B θ⋅===⋅,即所求二面角A -PD -B --------------------------------------------------14分]20.解:(1)设(,)P x y ,由1(F 、2F 得1(,)PF x y =-uuu r , 2,)PF x y =-uuu r.∴212)PF PF x x y ⋅=-+uuu r uuu r223x y =+-,---------------------2分由22221x y a b +=得2222(1)x y b a=- ∴222122(1)3x PF PF x b a⋅=+--uuu r uuu r 22233x b a =+-,------------------------4分∵220x a ≤≤,∴当22x a =,即x a =±时,12PF PF ⋅uuu r uuu r有最大值,即212max ()331PF PF b ⋅=+-=uuu r uuu r,---------------------------------------6分∴21b =,2224a c b =+=,∴所求双曲线C 的方程为2214x y +=.------------------------------------7分 (其它解法请参照给分)(2)假设存在直线l 满足题设,设1122(,),(,)D x y E x y ,将y kx m =+代入2214x y +=并整理得 222(14)8440k x kmx m +++-=,------------------------------------------------------------8分由222222644(14)(44)16(41)0k m k m m k ∆=-+-=--->,得2241k m +>-----------①又122814kmx x k +=-+--------------------10分由||||AD AE =可得2222112212121212(1)(1)()(2)()()0x y x y x x x x y y y y -+=-+⇒-+-+-+=121212122()0y y x x y y x x -⇒+-++=-212(1)()220k x x km ⇒+++-=228(1)22014kmk km k⇒-++-=+ 化简得2143k m k +=-------------②------------------------------------------12分将②代入①得2221441()3k k k++> 化简得42222010(41)(51)0k k k k +->⇒+->,解得k >k <所以存在直线l ,使得||||AD AE =,此时k 的取值范围为(,)-∞⋃+∞.-------14分21.解:(1)当1a =时,不等式()1f x x <-即|1|x x x -<,显然0x ≠,当0x >时,原不等式可化为:|1|1111x x -<⇒-<-<02x ⇒<<--------------------------2分当0x <时,原不等式可化为:|1|111x x ->⇒->或11x -<-2x ⇒>或0x <,∴0x < 综上得:当1a =时,原不等式的解集为{|020}x x x <<<或---------------3分(2)∵221,()() 1.()x ax x a f x x ax x a ⎧--≥⎪=⎨-+-<⎪⎩--------------------------------------4分若x a ≥时,∵0a >,由'()2f x x a =-知,在(,)a +∞上,'()0f x ≥, 若x a <,由'()2f x x a =-+知,当2ax <时,'()0f x >, 当2ax a <<时,'()0f x <,∴当0a >时,函数()f x 的单调增区间为(,)2a -∞,(,)a +∞,单调减区间为(,)2a a .----6分 (其它解法请参照给分)(3)在区间(0,1]上,函数()f x 的图象总在直线(,y m m R m =∈是常数)的下方,即对(0,1]x ∀∈都有()f x m <,⇔对(0,1]x ∀∈都有||1x x a m -<+,-------7分 显然1m >-,即1()1m x x a m --<-<+⇒对(0,1]x ∀∈,11m m x a x x++-<-<恒成立 ⇒对(0,1]x ∀∈,11m m x a x x x++-<<+------------------------------8分 设1(),(0,1]m g x x x x +=-∈,1()m p x x x +=+,(0,1]x ∈, 则对(0,1]x ∀∈,11m m x a x x x++-<<+恒成立⇔max min ()()g x a p x <<,(0,1]x ∈----9分∵21'()1,m g x x+=+当(0,1]x ∈时'()0g x > ∴函数()g x 在(0,1]上单调递增,∴max ()g x m =-------------------------10分又∵21'()1m p x x +=-1≥即0m ≥时,对于(0,1]x ∈,有'()0p x < ∴函数()p x 在(0,1]上为减函数∴min ()(1)2p x p m ==+----------------------------------------------11分1<,即10m -<<时,当x ∈,'()0p x ≤当x ∈,'()0p x >∴在(0,1]上,min ()p x p ==--------------------------------12分(或当10m -<<时,在(0,1]上,1()m p x x x +=+≥=,当x =时取等号)又∵当10m -<<时,要max min ()()g x a p x <<即m a -<<m >-2440m m ⇒--<,解得22m -<<+- 11 -∴当20m -<<时,m a -<<---------------------------------------------13分 当0m ≥时,2m a m -<<+.-----------------------------------------------------------------14分。
