中考数学题型归类练习及答案mdy
中考数学试题分类及答案

中考数学试题分类及答案一、选择题1. 下列哪个数是无理数?A. 3.14B. √2C. 0.33333…(3循环)D. 22/7答案:B2. 若a < 0,b > 0,且|a| > |b|,则a + b 一定小于:A. 0B. aC. bD. a + b答案:A二、填空题1. 已知一个直角三角形的两条直角边分别为3和4,其斜边的长度是_______ 。
答案:52. 一个数的平方根是4,那么这个数是 _______ 。
答案:16三、计算题1. 计算下列表达式的值:(1) (-3) × √3(2) (-2)² - 3 × √2答案:(1) -3√3(2) 4 - 3√2四、解答题1. 某工厂计划生产一批零件,原计划每天生产100个零件,实际每天生产了120个零件。
若原计划生产周期为10天,实际生产周期缩短了多少天?答案:首先计算原计划总生产量:100 × 10 = 1000个。
然后计算实际生产周期:1000 ÷ 120 ≈ 8.33天。
实际生产周期缩短了10 - 8.33 = 1.67天。
2. 一个长方体的长、宽、高分别为a、b、c,若长方体的体积为V,表面积为S,求证:S = 2(ab + bc + ac)。
答案:长方体的表面积S由六个面组成,分别是两个长宽面、两个长高面、两个宽高面。
长宽面的面积为ab,长高面的面积为ac,宽高面的面积为bc。
因此,S = 2(ab + ac + bc)。
五、证明题1. 证明:直角三角形的斜边的平方等于两直角边的平方和。
答案:设直角三角形的两直角边为a和b,斜边为c。
根据勾股定理,我们有c² = a² + b²。
这证明了直角三角形的斜边的平方等于两直角边的平方和。
六、应用题1. 某公司计划在一个月内完成一项工程,原计划每天完成工程的1/30,但实际每天完成了工程的1/25。
中考数学分类(含答案)综合型问题
第 8 页 共 88 页
∴直线 l 与⊙ A 相切 .
1
3
3
( 3)由题意,把 x=-1 代入 y=- x +1 ,得 y= ,即 D ( -1 , ) .
∴ l= AB +BC +AC = 2 3 + 2 3 DE = 8 3 DE ,解得 DE = 1 , 3
83
∴△ ABC 的周长为
.
3
3 .( 2010 江苏南京 )( 8 分)如图,正方形 ABCD 的边长是 2 ,M 是 AD 的中点,点 E 从 点 A 出发,沿 AB 运动到点 B 停止,连接 EM 并延长交射线 CD 于点 F ,过 M 作 EF 的垂 线交射线 BC 于点 G ,连结 EG 、 FG 。
中考数学分类(含答案)
综合
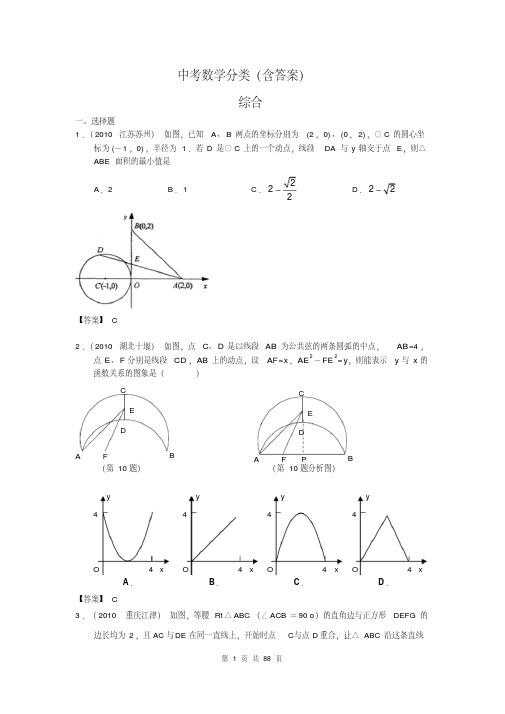
一、选择题 1 .( 2010 江苏苏州) 如图,已知 A、 B 两点的坐标分别为 (2 ,0) 、 (0 , 2) ,⊙ C 的圆心坐
标为 (- 1 ,0) ,半径为 1 .若 D 是⊙ C 上的一个动点,线段 DA 与 y 轴交于点 E,则△ ABE 面积的最小值是
A.2
B 两点, A( 1,0) 。
( 1) 求这条抛物线的解析式;
( 2) 如图,以 AB 为直径作圆,与抛物线交于点 D ,与抛物线的对称轴交于点 F,
依次连接 A、D 、B 、E,点 Q 为线段 AB 上一个动点 (Q 与 A、B 两点不重合) ,
过点 Q 作 QF
AE 于 F , QG
DB 于 G ,请判断 QF
分类汇总中考数学试卷答案

一、选择题答案1. 选择题答案:A2. 选择题答案:B3. 选择题答案:C4. 选择题答案:D5. 选择题答案:A6. 选择题答案:B7. 选择题答案:C8. 选择题答案:D9. 选择题答案:A10. 选择题答案:B二、填空题答案1. 填空题答案:-12. 填空题答案:23. 填空题答案:34. 填空题答案:π5. 填空题答案:46. 填空题答案:√27. 填空题答案:3.148. 填空题答案:89. 填空题答案:1010. 填空题答案:5三、解答题答案1. 解答题答案:(1)设x为所求的数,根据题意列出方程:x + 2 = 4解方程得:x = 2(2)根据题意,画出图形,观察图形可知,三角形ABC为等边三角形,边长为6所以,三角形ABC的周长为:6 + 6 + 6 = 182. 解答题答案:(1)设x为所求的数,根据题意列出方程:x^2 - 5x + 6 = 0解方程得:x1 = 2,x2 = 3(2)根据题意,画出图形,观察图形可知,三角形ABC为等腰三角形,底边AB的长度为4所以,三角形ABC的面积为:1/2 × 4 × 3 = 63. 解答题答案:(1)设x为所求的数,根据题意列出方程:2x - 5 = 3x + 2解方程得:x = -7(2)根据题意,画出图形,观察图形可知,三角形ABC为直角三角形,直角边AC 的长度为3,BC的长度为4所以,三角形ABC的面积为:1/2 × 3 × 4 = 64. 解答题答案:(1)设x为所求的数,根据题意列出方程:2(x - 1) + 3(x + 2) = 4x + 1解方程得:x = -1(2)根据题意,画出图形,观察图形可知,三角形ABC为等腰三角形,底边AB的长度为6所以,三角形ABC的面积为:1/2 × 6 × 4 = 125. 解答题答案:(1)设x为所求的数,根据题意列出方程:x^2 - 4x + 3 = 0解方程得:x1 = 1,x2 = 3(2)根据题意,画出图形,观察图形可知,三角形ABC为直角三角形,直角边AC 的长度为3,BC的长度为4所以,三角形ABC的面积为:1/2 × 3 × 4 = 6四、综合题答案1. 综合题答案:(1)根据题意,画出图形,观察图形可知,三角形ABC为等边三角形,边长为6所以,三角形ABC的周长为:6 + 6 + 6 = 18(2)根据题意,画出图形,观察图形可知,三角形ABC为直角三角形,直角边AC 的长度为3,BC的长度为4所以,三角形ABC的面积为:1/2 × 3 × 4 = 62. 综合题答案:(1)设x为所求的数,根据题意列出方程:2x - 5 = 3x + 2解方程得:x = -7(2)根据题意,画出图形,观察图形可知,三角形ABC为直角三角形,直角边AC 的长度为3,BC的长度为4所以,三角形ABC的面积为:1/2 × 3 × 4 = 63. 综合题答案:(1)设x为所求的数,根据题意列出方程:x^2 - 4x + 3 = 0解方程得:x1 = 1,x2 = 3(2)根据题意,画出图形,观察图形可知,三角形ABC为直角三角形,直角边AC 的长度为3,BC的长度为4所以,三角形ABC的面积为:1/2 × 3 × 4 = 64. 综合题答案:(1)设x为所求的数,根据题意列出方程:2(x - 1) + 3(x + 2) = 4x + 1解方程得:x = -1(2)根据题意,画出图形,观察图形可知,三角形ABC为等腰三角形,底边AB的长度为6所以,三角形ABC的面积为:1/2 × 6 × 4 = 125. 综合题答案:(1)设x为所求的数,根据题意列出方程:x^2 - 5x + 6 = 0解方程得:x1 = 2,x2 = 3(2)根据题意,画出图形,观察图形可知,三角形ABC为等腰三角形,底边AB的长度为6所以,三角形ABC的面积为:1/2 × 6 × 4 = 12以上是中考数学试卷的选择题、填空题、解答题和综合题的答案分类汇总,供同学们参考。
中考数学试题整理及答案

中考数学试题整理及答案一、选择题(每题3分,共30分)1. 若a > 0且b < 0,则a+b的符号是()。
A. 正数B. 负数C. 零D. 无法确定2. 一个数的平方根是3,这个数是()。
A. 9B. -9C. 3D. -33. 以下哪个选项是等腰三角形()。
A. 两边相等的三角形B. 三边相等的三角形C. 两角相等的三角形D. 一边一角相等的三角形4. 函数y=2x+3的图象经过的象限是()。
A. 第一、二、三象限B. 第一、二、四象限C. 第一、三、四象限D. 第二、三、四象限5. 以下哪个选项是正确的比例关系()。
A. 3:4=6:8B. 3:4=6:9C. 3:4=9:12D. 3:4=9:66. 一个圆的半径是5,那么它的周长是()。
A. 10πB. 20πC. 25πD. 30π7. 以下哪个选项是正确的因式分解()。
A. x^2 - 4 = (x+2)(x-2)B. x^2 - 4 = (x+2)(x+2)C. x^2 - 4 = (x-2)(x-2)D. x^2 - 4 = (x-2)(x+2)8. 一个数的绝对值是5,这个数可能是()。
A. 5B. -5C. 5或-5D. 09. 一个数的倒数是1/3,这个数是()。
A. 3B. 1/3C. 3/1D. 1/910. 以下哪个选项是正确的不等式性质()。
A. 如果a > b,那么a+c > b+cB. 如果a > b,那么ac > bcC. 如果a > b,那么a/c > b/cD. 如果a > b,那么a^2 > b^2二、填空题(每题3分,共15分)11. 一个数的立方根是2,这个数是______。
12. 一个数的相反数是-5,这个数是______。
13. 一个数的绝对值是7,这个数可能是______或______。
14. 一个数的平方是16,这个数可能是______或______。
初三数学考试题型及答案

初三数学考试题型及答案一、选择题(每题3分,共30分)1. 下列哪个选项是不等式的基本性质?A. 不等式两边同时乘以一个负数,不等号方向不变B. 不等式两边同时乘以一个正数,不等号方向不变C. 不等式两边同时加上同一个数,不等号方向不变D. 不等式两边同时除以一个正数,不等号方向不变答案:B2. 一个数的平方是9,那么这个数是:A. 3B. -3C. 3或-3D. 以上都不对答案:C3. 函数y=2x+1的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:C4. 一个圆的直径是10cm,那么这个圆的半径是:A. 5cmB. 10cmC. 15cmD. 20cm答案:A5. 一个等腰三角形的两个底角相等,那么这个三角形的顶角是:A. 90度B. 60度C. 30度D. 无法确定答案:D6. 一个数的相反数是-5,那么这个数是:A. 5B. -5C. 10D. -10答案:A7. 一个长方体的长、宽、高分别是2cm、3cm、4cm,那么这个长方体的体积是:A. 24cm³B. 12cm³C. 8cm³D. 6cm³答案:A8. 一个数的绝对值是5,那么这个数是:A. 5B. -5C. 5或-5D. 以上都不对答案:C9. 一个二次函数y=ax²+bx+c的图象开口向上,那么a的值是:A. 正数B. 负数C. 0D. 无法确定答案:A10. 一个等差数列的前三项是2,5,8,那么这个数列的公差是:A. 3B. 2C. 1D. 4答案:A二、填空题(每题3分,共30分)1. 一个数的立方是27,那么这个数是________。
答案:32. 一个直角三角形的两条直角边长分别是3cm和4cm,那么这个三角形的斜边长是________。
答案:5cm3. 一个数的倒数是1/2,那么这个数是________。
答案:24. 一个三角形的内角和是________度。
中考数学题型归类练习 mdy(修正稿)

中考数学题型归类练习湖北竹溪城关中学明道银试题千万万,再累也做不完;题型很有限,掌握一类,攻克一片。
掌握各种题型,就可以摆脱枯燥的重复练习!数学题型分类方式很多。
按知识体系可分为数、式、方程、不等式、函数、统计与概率、几何类题型;按试卷结构可分为选择题、填空题、解答题;按试题条件呈现的方式可分为以文字、符号、图表、图像等为主要信息的题型;按试题结论呈现的方式可分为简答、说理、论证题和计算、作图、归纳探究题;按难易程度可分为基础知识题、基本技能题和综合能力考查题;按新“课标”要求(人人获得必要的、有价值的数学,使得数学在研究领域、研究方式和应用范围等方面得到空前的拓展)可分为代数和几何的基本计算题,应用题(方程、不等式、函数、几何),方案设计、作图题等必要的数学。
探究题(条件探究、结论探究、存在性问题探究,变式探究、开发性问题探究、规律性问题探究和创新型探究),动态性问题、阅读问题等必备观察、分析、比较、判定、归纳、论证、应用的数学研究方式和数学能力,按数学自身特点还有许多热门题型,如几何变换的平移、旋转、对称、位似,最值、比值、取值范围等题型。
这里按考试热点列举一些典型示例供大家练习,有助于你正确、高效的搞好中考数学复习。
一、应用性问题题型【题型1】方程类应用性问题。
1、(2012湖北十堰)一辆汽车开往距离出发地180千米的目的地,按原计划的速度匀速行驶60千米后,再以原来速度的1.5倍匀速行驶,结果比原计划提前40分钟到达目的地,求原计划的行驶速度.2、(湖南长沙市)“5〃12”汶川大地震后,灾区急需大量帐篷.某服装厂原有4条成衣生产线和5条童装生产线,工厂决定转产,计划用3天时间赶制1000顶帐篷支援灾区.若启用1条成衣生产线和2条童装生产线,一天可以生产帐篷105顶;若启用2条成衣生产线和3条童装生产线,一天可生产帐篷178顶. (1)每条成衣生产线和童装生产线每天生产帐篷各多少顶?(2)工厂满负荷全面转产,是否可以如期完成任务?如果你是厂长,你会怎样体现你的社会责任感?3、(2012湖北宜昌10分)[背景资料]低碳生活的理念已逐步被人们接受.据相关资料统计:一个人平均一年节约的用电,相当于减排二氧化碳约18kg;一个人平均一年少买的衣服,相当于减排二氧化碳约6kg.[问题解决] :甲、乙两校分别对本校师生提出“节约用电”、“少买衣服”的倡议.2009年两校响应本校倡议的人数共60人,因此而减排二氧化碳总量为600kg.(1)2009年两校响应本校倡议的人数分别是多少?(2)2009年到2011年,甲校响应本校倡议的人数每年增加相同的数量;乙校响应本校倡议的人数每年按相同的百分率增长.2010年乙校响应本校倡议的人数是甲校响应本校倡议人数的2倍;2011年两校响应本校倡议的总人数比2010年两校响应本校倡议的总人数多100人.求2011年两校响应本校倡议减排二氧化碳的总量.【题型2】不等式类应用性问题。
中考数学应用题分类及参考答案(精编)

中考数学应用题分类及参考答案(精编)一、方程应用1.为加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,第一季度的总营业额是3990万元.求月平均增长率.2.一带一路给沿线地区带来很大的经济效益,某企业的产品对沿线地区实行优惠,决定在原定价基础上每件降价40元,这样按原定价需花费5000元购买的产品,现在只花费了4000元,求每件产品的实际定价是多少元?3.甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前3天完成任务,甲志愿者计划完成此项工作的天数?二、一次函数应用4.低碳生活绿色出行的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.(1)小红从甲地到乙地骑车的速度为_________;(2)当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?三、二次函数应用5.如图,某小区有一块靠墙(墙的长度不限)的矩形空地ABCD,为美化环境,用总长100m的篱笆围成四块矩形花圃(靠墙一侧不用篱笆,篱笆的厚度不计).(1)若四块矩形花圃的面积相等,求证:AE=3BE;(2)在(1)的条件下,设BC的长度为xm,矩形区域ABCD的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.四、解直角三角形应用6.灯塔是港口城市的标志性建筑之一,如图所示,在点B处测得灯塔最高点A的仰角∠ABD=45°,再沿BD方向前进至C处测得最高点A的仰角∠ACD=60°,BC=15.3m,求灯塔的高度AD(结果精确到1m,参考数据:√ 2≈1.41,√ 3≈1.73)7.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:√ 3,且点A,B,C,D,E 在同一平面内,求小明同学测得古塔AB的高度.8.如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B处仰角为30°,求甲楼的高度.五、方程与不等式应用9.某市为创建文明城市,开展美化绿化城市活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.(1)问实际每年绿化面积多少万平方米?(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?六、方程与函数应用10.某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量y(桶)与每桶降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数关系式;(2)在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?七、一次函数与二次函数应用11.某汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数y(辆)有如下关系:(1)观察表格,辆数y(辆)与每辆车的月租金x(元)之间的关系式.(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:请求出公司的最大月收益是多少元.八、解直角三角形与方程应用12.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC 的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.(1)求该滑雪场的高度h;(2)据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3,且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.九、解直角三角形与圆应用13.如图1,Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠C=90°,其外接圆半径为R.根据锐角三角函数的定义:sinA=ac ,sinB=bc,可得asinA=bsinB=csinC=2R,即asinA=bsinB=csinC=2R(规定sin90°=1).(1)探究活动:如图2,在锐角△ABC中,a,b,c分别是∠A,∠B,∠C的对边,其外接圆半径为R,那么:asinA ( )bsinB( )csinC(用>、=或<连接),并说明理由.事实上,以上结论适用于任意三角形.(2)初步应用:在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠A=60°,∠B=45°,a=8,求b.(3)综合应用:如图3,在某次数学活动中,小玲同学测量一古塔CD的高度,在A处用测角仪测得塔顶C的仰角为15°,又沿古塔的方向前行了100m到达B处,此时A,B,D三点在一条直线上,在B处测得塔顶C的仰角为45°,求古塔CD的高度.(结果保留小数点后一位,参考数据:√3≈1.732,sin15°=√6−√24)十、方程、不等式与函数应用14.要制作200个A,B两种规格的顶部无盖木盒,A种规格是长、宽、高都为20cm的正方体无盖木盒,B种规格是长、宽、高各为20cm,20cm,10cm的长方体无盖木盒,如图1.现有200张规格为40cm×40cm的木板材,对该种木板材有甲,乙两种切割方式,如图2.切割,拼接等板材损耗忽略不计.(1)设制作A种木盒x个,则制作B种木盒__________个;若使用甲种方式切割的木板材y 张,则使用乙种方式切割的木板材__________张;(2)该200张木板材恰好能做成200个A和B两种规格的无盖木盒,请分别求出A,B木盒的个数和使用甲,乙两种方式切割的木板材张数;(3)包括材质等成本在内,用甲种切割方式的木板材每张成本5元,用乙种切割方式的木板材每张成本8元.根据市场调研,A种木盒的销售单价定为a元,B种木盒的销售单价定为(20-12a)元,两种木盒的销售单价均不能低于7元,不超过18元.在(2)的条件下,两种木盒的销售单价分别定为多少元时,这批木盒的销售利润最大,并求出最大利润.参考答案1.解:设月平均增长的百分率是x,则该超市二月份的营业额为100(1+x)万元,三月份的营业额为100(1+x)2万元,依题意,得1000+1000(1+x)+1000(1+x)2=3990. 2.解:设每件产品的实际定价是x 元,则原定价为(x+40)元.5000x+40=4000x,解得x =160 ,经检验x =160是原方程的解.3.解:设甲志愿者计划完成此项工作需x 天,故甲的工效都为:1x ,由于甲、乙两人工效相同,则乙的工效为1x ,甲前两个工作日完成了1x ×2,剩余的工作量甲完成了1x (x −2−3),乙在甲工作两个工作日后完成了1x (x −2−3),则2x +2(x−2−3)x=1,解得x=8,经检验,x=8是原方程的解.4.解析:(1)在OA 段,速度=100.5 =20km/h(2)当1.5≤x ≤2.5时,设y=20x+b,把(1.5,10)代入得到,10=20×1.5+b,解得b=﹣20,y=20x ﹣20,当x=2.5时,解得y=30,乙地离小红家30千米.5(1)证明:∵矩形MEFN 与矩形EBCF 面积相等 ∴ME =BE,AM =GH∵四块矩形花圃的面积相等,即S 矩形AMND =2S 矩形MEFN ∴AM =2ME ∴AE =3BE (2)∵篱笆总长为100m∴2AB+GH+3BC =100即2AB+12AB+3BC=100 ∴AB=40-65 BC 设BC 的长度为xm,矩形区域ABCD 的面积为ym 2则y=BC ·AB=x(40- 65x)=−65x 2+40x ∵x>0,40- 65x>0 ∴0<x<1003∴ y=−65x 2+40x(0<x<1003)6.36m7.(20+10√ 3)m 8.(36﹣10√ 3)m9(1)设原计划每年绿化面积为x 万平方米,则实际每年绿化面积为1.6x 万平方米,根据题意,得360x−3601.6x =4解得x=33.75,经检验x=33.75是原分式方程的解,1.6x=1.6×33.75=54(2)设平均每年绿化面积增加a 万平方米,根据题意得54×2+2(54+a)≥360,解得a ≥72,则至少每年平均增加72万平方米. 10(1)y =10x+100(2)由题意得(10x+100)×(55﹣x ﹣35)=1760,整理得x 2﹣10x ﹣24=0,x 1=12,x 2=﹣2(舍去),55﹣x =43,这种消毒液每桶实际售价43元.11(1)设解析式y=kx+b,由题意得{3000k +b =1003200k +b =96,解得{k =−150b =160 ∴y 与x 间的函数关系是y =−150x +160(2)填表如下:(3)W =(−50x +160)(x −150)−(x −3000) =(−150x 2+163x −24000)−(x −3000) =−150x 2+162x −21000=−150(x −4050)2+307050当x=4050时,W 最大=307050,所以,当每辆车的月租金为4050元时,公司获得最大月收益307050元.12(1)过B 作BF ∥AD,过D 过AF ⊥AD,两直线交于F,过B 作BE 垂直地面交地面于E,如图:根据题知∠ABF =∠DAB =30°,AF =12AB =135m,BE:CE =1:2.4 设BE 长t 米,则CE 长2.4t 米. ∵BE 2+CE 2=BC2∴t 2+(2.4t)2=2602,解得t =100m(负值舍去),h =AF+BE =235m(2)设甲种设备每小时的造雪量是xm 3,则乙种设备每小时的造雪量是(x+35)m 3,根据题意得150x=500x+35,解得x =15,经检验,x =15是原方程的解,也符合题意,x+35=50.答:甲种设备每小时的造雪量是15m 3,则乙种设备每小时的造雪量是50m 3. 13(1)探究活动:a sinA = b sinB = csinC理由:如图2,过点C 作直径CD 交⊙O 于点D,连接BD. ∴∠A=∠D,∠DBC=90°∴sinA=sinD,sinD=a 2R ∴asinA = aa 2R=2R同理可证:b sinB =2R,c sinC =2R ∴a sinA = b sinB = csinC =2R (2)初步应用:∵asinA = bsinB =2R ∴8sin60° = bsin45° ∴b=8sin45°sin60°=8√63(3)综合应用:由题意得:∠D =90°,∠A =15°,∠DBC =45°,AB =100 ∴∠ACB =30°设古塔高DC=x,则BC=√2x ,AB sin∠ACB =BCsinA ,100sin30°=√2xsin15°,x=50(√3-1=36.6,古塔CD=36.6m.14(1)要制作200个A,B 两种规格的顶部无盖木盒,制作A 种木盒x 个,故制作B 种木盒(200-x)个;有200张规格为40cm ×40cm 的木板材,使用甲种方式切割的木板材y 张, 故使用乙种方式切割的木板材(200-y)张.(2)使用甲种方式切割的木板材y 张,则可切割出4y 个长、宽均为20cm 的木板,使用乙种方式切割的木板材(200-y)张,则可切割出8(200-y)个长为10cm,宽为20cm 的木板; 设制作A 种木盒x 个,则需要长、宽均为20cm 的木板5x 个,制作B 种木盒(200-x)个,则需要长、宽均为20cm 的木板(200-x)个,需要长为10cm 、宽为20cm 的木板4(200-x)个; 故{4y =5x +(200−x)8(200−y)=4(200−x),解得{x =100y =150 故制作A 种木盒100个,制作B 种木盒100个,使用甲种方式切割的木板150张,使用乙种方式切割的木板材50张.(3)用甲种切割方式的木板材每张成本5元,用乙种切割方式的木板材每张成本8元,且使用甲种方式切割的木板150张,使用乙种方式切割的木板材50张,总成本为150×5+8×50=1150(元)两种木盒的销售单价均不能低于7元,不超过18元,所以{7≤a ≤187≤20−12a ≤18,解得{7≤a ≤184≤a ≤26,a 的取值范围为7≤a ≤18. 设利润为W,则W=100a+100(20-12a)-1150整理得W=850+50a,当a=18时,W 有最大值,最大值为850+50×18=1750,此时B 种木盒的销售单价定为20-12×18=11(元)即A 种木盒的销售单价定为18元,B 种木盒的销售单价定为11元时,这批木盒的销售利润最大,最大利润为1750元.。
初三数学考试题型及答案

初三数学考试题型及答案初三数学考试题型通常包括选择题、填空题、解答题和证明题等。
以下是一份模拟的初三数学考试题型及答案。
1. 选择题(每题3分,共30分)1.1 已知一个等腰三角形的两边长分别为3cm和5cm,那么这个三角形的周长是多少?A. 11cmB. 13cmC. 16cmD. 无法确定答案:B1.2 下列哪个数是无理数?A. 0.33333...B. √2C. 22/7D. 3.14答案:B1.3 一个二次函数的图像开口向上,且经过点(1,0)和(-1,0),那么这个二次函数的对称轴是?A. x=0B. x=1C. x=-1D. x=2答案:A2. 填空题(每题4分,共20分)2.1 如果一个圆的半径为5cm,那么这个圆的面积是_____平方厘米。
答案:78.52.2 一个直角三角形的两条直角边长分别为6cm和8cm,那么这个三角形的斜边长是______cm。
答案:102.3 一个数的相反数是-5,那么这个数是_____。
答案:52.4 一个数的绝对值是7,那么这个数是_____或_____。
答案:7或-73. 解答题(每题10分,共40分)3.1 解方程:2x - 3 = 7。
答案:首先将方程两边同时加3,得到2x = 10,然后将方程两边同时除以2,得到x = 5。
3.2 已知一个长方体的长、宽、高分别为2cm、3cm和4cm,求这个长方体的体积。
答案:体积计算公式为长×宽×高,所以体积为2cm×3cm×4cm = 24立方厘米。
3.3 一个等差数列的首项为3,公差为2,求这个数列的第5项。
答案:等差数列的通项公式为an = a1 + (n-1)d,将首项a1=3,公差d=2,项数n=5代入公式,得到a5 = 3 + (5-1)×2 = 3 + 8 = 11。
3.4 已知一个扇形的圆心角为60°,半径为4cm,求这个扇形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《中考数学题型归类练习》试题千万万,再累也做不完;题型很有限,掌握一类,攻克一片。
掌握各种题型,就可以摆脱枯燥重复的训练!一、应用性问题题型【题型1】方程类应用性问题。
1、(2012湖北宜昌10分)[背景资料]低碳生活的理念已逐步被人们接受.据相关资料统计:一个人平均一年节约的用电,相当于减排二氧化碳约18kg;一个人平均一年少买的衣服,相当于减排二氧化碳约6kg.[问题解决] :甲、乙两校分别对本校师生提出“节约用电”、“少买衣服”的倡议.2009年两校响应本校倡议的人数共60人,因此而减排二氧化碳总量为600kg.(1)2009年两校响应本校倡议的人数分别是多少?(2)2009年到2011年,甲校响应本校倡议的人数每年增加相同的数量;乙校响应本校倡议的人数每年按相同的百分率增长.2010年乙校响应本校倡议的人数是甲校响应本校倡议人数的2倍;2011年两校响应本校倡议的总人数比2010年两校响应本校倡议的总人数多100人.求2011年两校响应本校倡议减排二氧化碳的总量.解:(1)方法一:设2009年甲校响应本校倡议的人数为x人,乙校响应本校倡议的人数为y人,…1分依题意得:解之得x=20,y=40…………………………………4分方法二:设2009年甲校响应本校倡议的人数为x人,乙校响应本校倡议的人数为(60﹣x)人,..1分依题意得:18x+6(60﹣x)=600 ……………………………………………………………………3分解之得:x=20,60﹣x=40 ………………………………………………………………………………4分∴2009年两校响应本校倡议的人数分别是20人和40人.(2)设2009年到2011年,甲校响应本校倡议的人数每年增加m人;乙校响应本校倡议的人数每年增长的百分率为n.依题意得:由①得m=20n,代入②并整理得2n2+3n﹣5=0解之得n=1,n=﹣2.5(负值舍去)………………………………………………………………8分∴m=20…………………………………………………………………………………………………9分∴2011年两校响应本校倡议减排二氧化碳的总量:(20+2×20)×18+40(1+1)2×6=2040(千克) (10)分答:2011年两校响应本校倡议减排二氧化碳的总量为2040千克.【题型2】不等式类应用性问题。
2、(2009湖北十堰)为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.(1)满足条件的方案共有几种?写出解答过程.(2)通过计算判断,哪种建造方案最省钱.解: (1) 设建造A型沼气池x 个,则建造B型沼气池(20-x )个………1分依题意得:()()⎩⎨⎧≥-+≤-+492203018365202015xxxx…………………………………3分解得:7≤x≤9 ………………………………………………………4分∵x为整数∴x = 7,8 ,9 ,∴满足条件的方案有三种.. ………5分(2)设建造A型沼气池x个时,总费用为y万元,则:y = 2x + 3( 20-x) = -x+ 60 ………………………………………6分∵-1< 0,∴y随x 增大而减小,当x=9 时,y的值最小,此时y= 51( 万元) ……………………………7分∴此时方案为:建造A型沼气池9个,建造B型沼气池11个.……8分解法②:由(1)知共有三种方案,其费用分别为:方案一: 建造A型沼气池7个,建造B型沼气池13个,总费用为:7×2 + 13×3 = 53( 万元) ……………………………6分方案二: 建造A型沼气池8个,建造B型沼气池12个,总费用为:8×2 + 12×3 = 52( 万元) ……………………………7分方案三: 建造A型沼气池9个,建造B型沼气池11个,总费用为:9×2 + 11×3 = 51( 万元)∴方案三最省钱. …………………………………………………………8分说明:(1)若只有正确结论,给1分;(2)不带单位不扣分;(3)其它解法请参照上述评分说明给分; 【题型3】二次函数类应用性问题。
3、(2009湖北武汉)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x 元(x 为正整数),每个月的销售利润为y 元.(1)求y 与x 的函数关系式并直接写出自变量x 的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?解:(1)2(21010)(5040)101102100y x x x x =-+-=-++(015x <≤且x 为整数); (2)210( 5.5)2402.5y x =--+.100a =-<Q ,∴当 5.5x =时,y 有最大值2402.5.015x <Q ≤,且x 为整数,当5x =时,5055x +=,2400y =(元),当6x =时,5056x +=,2400y =(元)∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.(3)当2200y =时,21011021002200x x -++=,解得:12110x x ==,.∴当1x =时,5051x +=,当10x =时,5060x +=.∴当售价定为每件51或60元,每个月的利润为2200元.当售价不低于51或60元,每个月的利润为2200元.当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元). 【题型4】方案设计类应用性问题。
4、(2012四川省南充市 )学校6名教师和234名学生集体外出活动,准备租用45座大车或30 座小车.若租用1辆大车2辆小车共需租车费1000元;若租用2辆大车1辆小车共需租车费1100元. (1)求大、小车每辆的租车费各是多少元?(2)若每辆车上至少..要有一名教师,且总组成费用不超过...2300元,求最省钱的租车方案. 解:(1)设大、小车每辆的租车费各是x 、y 元 则 x+2y=1000 x=400 2x+y=1100 解得: y=300 答:大、小车每辆的租车费各是400元、300元(2)240名师生都有座位,租车总辆数≥6;每辆车上至少要有一名教师,租车总辆数≤6.故租车总数事故6辆,设大车辆数是x 辆,则租小车(6-x )辆 45x+30(6-x) ≥240 x ≥4400x+300(6-x)≤2300 解得: x ≤5 ∴ 4≤x ≤5 ∵x 是正整数 ∴ x=4或5于是又两种租车方案,方案1:大车4辆 小车2辆 总租车费用2200元,方案2:大车5辆 小车1辆 总租车费用2300元,可见最省钱的是方案1二、探 究 性 问 题 题 型 【题型5】结论探究性问题。
5、(2011湖北十堰)(本题满分8分)如图,AB 是半圆O 的直径,点C 为半径OB 上一点,过点C 作CD ⊥AB 交半圆O 于点D ,将△ACD 沿A 折叠得到△AED ,AE 交半圆于点F ,连接DF . (1)求证:DE 是半圆的切线;(2)连接OD ,当OC =BC 时,判断四边形ODF A 的形状,并证明你的结论. 证明:(1)如图,连接OD ,则OA=OD , ∴∠OAD=∠ODA , ∵△AED 由△ACD 对折得到, ∴∠CDA=∠EDA , 又∵CD ⊥AB ,∴∠CAD+∠CDA=∠ODA+∠EDA=90°,D 点在半圆O 上, ∴DE 是半圆的切线;【题型6】存在性问题探究。
6. (2012湖北襄阳12分)如图,在矩形OABC 中,AO=10,AB=8,沿直线CD 折叠矩形OABC 的一边BC ,使点B 落在OA 边上的点E 处.分别以OC ,OA 所在的直线为x 轴,y 轴建立平面直角坐标系,抛物线y=ax 2+bx+c 经过O ,D ,C 三点. (1)求AD 的长及抛物线的解析式;(2点N 在抛物线对称轴上,点M 在抛物线上,是否存在这样的点M 与点N ,使以M ,N ,C ,E 为顶点的四边形是平行四边形?若存在,请直接写出点M 与点N 的坐标(不写求解过程);若不存在,请说明理由.解:(1)∵四边形ABCO 为矩形,∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10. 由题意,△BDC ≌△EDC .∴∠B=∠DEC=90°,EC=BC=10,ED=BD .(2)四边形ODF A 是菱形, 如图,连接OF , ∵CD ⊥OB ,∴OC=BC=21OB=21OD , 在Rt △OCD 中,∠ODC=30°, ∴∠DOC=60°,∵∠DOC=∠OAD+∠ODA , ∴∠OAD=∠ODA=∠F AD=30°,∴OD ∥AF ,∠F AO=60°,又∵OF=OA ,∴△F AO 是等边三角形, ∴OA=AF , ∴OD=AF ,∴四边形ODF A 是平行四边形, ∵OA=OD ,∴四边形ODF A 是菱形.由勾股定理易得EO=6.∴AE=10﹣6=4,设AD=x ,则BD=CD=8﹣x ,由勾股定理,得x 2+42=(8﹣x )2,解得,x=3,∴AD=3.∵抛物线y=ax 2+bx+c 过点D (3,10),C (8,0),∴, 解得∴抛物线的解析式为:y=﹣x 2+x .(2)假设存在符合条件的M 、N 点,分两种情况讨论:①EC 为平行四边形的对角线,由于抛物线的对称轴经过EC 中点,若四边形MENC 是平行四边形,那么M 点必为抛物线顶点;则:M (4,);而平行四边形的对角线互相平分,那么线段MN 必被EC 中点(4,3)平分,则N (4,﹣);②EC 为平行四边形的边,则ECMN ,设N (4,m ),则M (4﹣8,m+6)或M (4+8,m ﹣6); 将M (﹣4,m+6)代入抛物线的解析式中,得:m=﹣38,此时 N (4,﹣38)、M (﹣4,﹣32); 将M (12,m ﹣6)代入抛物线的解析式中,得:m=﹣26,此时 N (4,﹣26)、M (12,﹣32); 综上,存在符合条件的M 、N 点,且它们的坐标为:①M 1(﹣4,﹣32),N 1(4,﹣38) ②M 2(12,﹣32),N 2(4,﹣26)③M 3(4,),N 3(4,﹣).【题型7】规律性问题探究。
