高一数学导学案:3.1.1 直线的倾斜角与斜率
3.1.1《直线的倾斜角与斜率》导学案
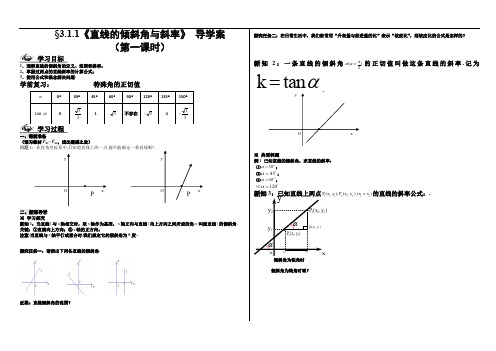
反思:直线倾斜角的范围?鱼知水恩,乃幸福之源也。
鱼离不开水,人离不开亲人和朋友,当你处于逆境和灾难时,帮助你一臂之力,渡过难关的人,都是你的亲人和朋友。
吃水不忘挖井人,度过苦难,不能忘记援助过你的人。
知恩图报,善莫大焉。
一个人要想获得幸福,必须懂得感恩。
生活需要一颗感恩的心来创造,一颗感恩的心需要生活来滋养。
一饭之恩,当永世不忘。
顺境里给你帮助的人,不能全部称作朋友,但是能够在你逆境时依然愿意援助你,走出困境的人,一定是你要用一生去感谢和珍惜的人。
唐代李商隐的《晚晴》里有这样一句诗:天意怜幽草,人间重晚晴。
久遭雨潦之苦的幽草,忽遇晚晴,得以沾沐余辉而平添生意。
当一个人闯过难关的时候,一定要记住那些支撑你,陪你一起走过厄运的朋友和亲人,这个世界谁也不亏欠谁,帮你是情分,不帮你是本分。
如古人所说:淡看世事去如烟,铭记恩情存如血。
学会感恩父母养育之恩,学会感恩朋友的帮助之情,生活里做一个有情有义的人。
你要知道,父母,永远是你最亲近的人,是最爱你的人,不管他们的方法怎么错误?可是爱你的心,都是一样的。
千万不要因为自己一时的私心,而忘记感恩。
我们常常希望别人都对自己有情有义,可是想得到别人你真情,首先你必须先付出真情。
你帮助别人,不要记在心里,别人帮助你,你要懂得感恩和感动,而不是当做理所当然。
你要知道别人帮你是情分,不帮你是本分。
侍父母,要孝顺,对朋友,要真诚。
不管你生活的精彩或者混沌,孝顺父母,颐养天年。
一父养十子,十子养一父。
在这个美好的时代,中华很多的美德都在逐渐消失,做子孝为天,但是总有一些人,自己活在天堂,硬生生的把父母扔进地狱。
鱼知水恩,乃幸福之源也。
鱼离不开水,人离不开亲人和朋友,当你处于逆境和灾难时,帮助你一臂之力,渡过难关的人,都是你的亲人和朋友。
吃水不忘挖井人,度过苦难,不能忘记援助过你的人。
知恩图报,善莫大焉。
一个人要想获得幸福,必须懂得感恩。
生活需要一颗感恩的心来创造,一颗感恩的心需要生活来滋养。
高中数学 第三章 直线与方程 3.1.1 倾斜角与斜率教案数学教案

3.1.1 倾斜角与斜率[提出问题]在平面直角坐标系中,直线l经过点P.问题1:直线l的位置能够确定吗?提示:不能.问题2:过点P可以作与l相交的直线多少条?提示:无数条.问题3:上述问题中的所有直线有什么区别?提示:倾斜程度不同.[导入新知]1.倾斜角的定义:当直线l与x轴相交时,取x轴作为基准,x轴正方向与直线l向上方向之间所成的角叫做直线l的倾斜角.如图所示,直线l的倾斜角是∠APx,直线l′的倾斜角是∠BPx.2.倾斜角的范围:直线的倾斜角α的取值范围是0°≤α<180°,并规定与x轴平行或重合的直线的倾斜角为0°.3.倾斜角与直线形状的关系倾斜角α=0°0°<α<90°α=90°90°<α<180°直线对直线的倾斜角的理解(1)倾斜角定义中含有三个条件:①x轴正向;②直线向上的方向;③小于180°的非负角.(2)从运动变化的观点来看,直线的倾斜角是由x轴按逆时针方向旋转到与直线重合时所成的角.(3)倾斜角是一个几何概念,它直观地描述且表现了直线对x 轴的倾斜程度.(4)平面直角坐标系中的每一条直线都有一个确定的倾斜角,且倾斜程度相同的直线,其倾斜角相等;倾斜程度不同的直线,其倾斜角不相等.[提出问题]日常生活中,常用坡度(坡度=升高量前进量)表示倾斜程度,例如,“进2升3”与“进2升2”比较,前者更陡一些,因为坡度32>22. 问题1:对于直线可利用倾斜角描述倾斜程度,可否借助于坡度来描述直线的倾斜程度?提示:可以.问题2:由上图中坡度为升高量与水平前进量的比值,那么对于平面直角坐标系中直线的倾斜程度能否如此度量?提示:可以.问题3:通过坐标比,你会发现它与倾斜角有何关系?提示:与倾斜角的正切值相等.[导入新知]1.斜率的定义:一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k 表示,即k =tan_α.2.斜率公式:经过两点P 1(x 1,y 1),P 2(x 2,y 2)(x 1≠x 2)的直线的斜率公式为k =y 2-y 1x 2-x 1.当x 1=x 2时,直线P 1P 2没有斜率. 3.斜率作用:用实数反映了平面直角坐标系内的直线的倾斜程度.[化解疑难]1.倾斜角α与斜率k 的关系(1)直线都有倾斜角,但并不是所有的直线都有斜率.当倾斜角是90°时,直线的斜率不存在,此时,直线垂直于x 轴(平行于y 轴或与y 轴重合).(2)直线的斜率也反映了直线相对于x 轴的正方向的倾斜程度.当0°≤α<90°时,斜率越大,直线的倾斜程度越大;当90°<α<180°时,斜率越大,直线的倾斜程度也越大.2.斜率公式(1)直线的斜率与两点的顺序无关,即两点的纵坐标和横坐标在公式中的次序可以同时调换,就是说, 如果分子是y 2-y 1,分母必须是x 2-x 1;反过来,如果分子是y 1-y 2,分母必须是x 1-x 2,即k =y 1-y 2x 1-x 2=y 2-y 1x 2-x 1. (2)用斜率公式时要一看,二用,三求值.一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步;二用,就是将点的坐标代入斜率公式;三求值,就是计算斜率的值,尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.[例1] (1)若直线l 的向上方向与y 轴的正方向成30°角,则直线l 的倾斜角为( )A.30°B.60°C.30°或150° D.60°或120°(2)下列说法中,正确的是( )A.直线的倾斜角为α,则此直线的斜率为tan αB.直线的斜率为tan α,则此直线的倾斜角为αC.若直线的倾斜角为α,则sin α>0D.任意直线都有倾斜角α,且α≠90°时,斜率为tan α[解析] (1)如图,直线l有两种情况,故l的倾斜角为60°或120°.(2)对于A,当α=90°时,直线的斜率不存在,故不正确;对于B,虽然直线的斜率为tan α,但只有0°≤α<180°时,α才是此直线的倾斜角,故不正确;对于C,当直线平行于x轴时,α=0°,sin α=0,故C不正确,故选D.[答案] (1)D (2)D[类题通法]求直线的倾斜角的方法及两点注意(1)方法:结合图形,利用特殊三角形(如直角三角形)求角.(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°.②注意直线倾斜角的取值范围是0°≤α<180°.[活学活用]1.直线l经过第二、四象限,则直线l的倾斜角范围是( ) A.[0°,90°)B.[90°,180°) C.(90°,180°) D.(0°,180°)解析:选C 直线倾斜角的取值范围是[0°,180°),又直线l 经过第二、四象限,所以直线l 的倾斜角范围是(90°,180°).2.设直线l 过原点,其倾斜角为α,将直线l 绕坐标原点沿逆时针方向旋转45°,得到直线l 1,则直线l 1的倾斜角为( )A .α+45°B .α-135°C .135°-αD .当0°≤α<135°时为α+45°,当135°≤α<180°时为α-135°解析:选D 当0°≤α<135°时,l 1的倾斜角是α+45°.当135°≤α<180°时,结合图形和倾斜角的概念,即可得到l 1的倾斜角为α-135°,故应选D.[例2] (1)已知过两点A (4,y ),B (2,-3)的直线的倾斜角为135°,则y =________;(2)过点P (-2,m ),Q (m,4)的直线的斜率为1,则m 的值为________;(3)已知过A (3,1),B (m ,-2)的直线的斜率为1,则m 的值为________.[解析] (1)直线AB 的斜率k =tan 135°=-1,又k =-3-y 2-4,由-3-y 2-4=-1,得y =-5. (2)由斜率公式k =4-m m +2=1,得m =1. (3)当m =3时,直线AB 平行于y 轴,斜率不存在.当m ≠3时,k =-2-1m -3=-3m -3=1,解得m =0.[答案] (1)-5 (2)1 (3)0[类题通法]利用斜率公式求直线的斜率应注意的事项(1)运用公式的前提条件是“x1≠x2”,即直线不与x轴垂直,因为当直线与x轴垂直时,斜率是不存在的;(2)斜率公式与两点P1,P2的先后顺序无关,也就是说公式中的x1与x2,y1与y2可以同时交换位置.[活学活用]3.(2012·河南平顶山高一调研)若直线过点 (1,2),(4,2+3),则此直线的倾斜角是( )A.30° B.45°C.60° D.90°解析:选A 设直线的倾斜角为α,直线斜率k=2+3-24-1=33,∴tan α=3 3 .又∵0°≤α<180°,∴α=30°.[例3] 已知实数x,y满足y=-2x+8,且2≤x≤3,求yx的最大值和最小值.[解] 如图所示,由于点(x,y)满足关系式2x+y=8,且2≤x≤3,可知点P(x,y)在线段AB上移动,并且A,B两点的坐标可分别求得为A(2,4),B(3,2).由于yx 的几何意义是直线OP的斜率,且k OA=2,k OB=23,所以可求得y x 的最大值为2,最小值为23. [类题通法]根据题目中代数式的特征,看是否可以写成y 2-y 1x 2-x 1的形式,若能,则联想其几何意义(即直线的斜率),再利用图形的直观性来分析解决问题.[活学活用]4.点M (x ,y )在函数y =-2x +8的图象上,当x ∈[2,5]时,求y +1x +1的取值范围. 解:y +1x +1=y --1x --1的几何意义是过M (x ,y ),N (-1,-1)两点的直线的斜率.∵点M 在函数y =-2x +8的图象上,且x ∈[2,5],∴设该线段为AB 且A (2,4),B (5,-2).∵k NA =53,k NB =-16, ∴-16≤y +1x +1≤53. ∴y +1x +1的取值范围为[-16,53]. [典例] 已知两点A (-3,4),B (3,2),过点P (1,0)的直线l 与线段AB 有公共点,则l 的倾斜角的取值范围________;直线l 的斜率k 的取值范围________.[解析] 如图,由题意可知k PA =4-0-3-1=-1,k PB=2-03-1=1,则直线l 的倾斜角介于直线PB 与PA 的倾斜角之间,又PB 的倾斜角是45°,PA 的倾斜角是135°,∴直线l 的倾斜角α的取值范围是45°≤α≤135°;要使l 与线段AB 有公共点,则直线l 的斜率k 的取值范围是k ≤-1或k ≥1.[答案] 45°≤α≤135° k ≤-1或k ≥1[易错防范]1.本题易错误地认为-1≤k ≤1,结合图形考虑,l 的倾斜角应介于直线PB 与直线PA 的倾斜角之间,要特别注意,当l 的倾斜角小于90°时,有k ≥k PB ;当l 的倾斜角大于90°时,则有k ≤k PA .2.如图,过点P 的直线l 与直线段AB 相交时,因为过点P 且与x 轴垂直的直线PC 的斜率不存在,而PC 所在的直线与线段AB 不相交,所以满足题意的斜率夹在中间,即k PA ≤k ≤k PB .解决这类问题时,可利用数形结合思想直观地判断直线是夹在中间还是在两边.[成功破障]已知直线l 过点P (3,4),且与以A (-1,0),B (2,1)为端点的线段AB 有公共点,求直线l 的斜率k 的取值范围.解:∵直线PA 的斜率k PA =4-03--1=1,直线PB 的斜率k PB =4-13-2=3,∴要使直线l 与线段AB 有公共点,k 的取值范围为[1,3].[随堂即时演练]1.关于直线的倾斜角和斜率,下列说法正确的是( )A .任一直线都有倾斜角,都存在斜率B .倾斜角为135°的直线的斜率为1C .若一条直线的倾斜角为α,则它的斜率为k =tan αD .直线斜率的取值范围是(-∞,+∞)解析:选D 任一直线都有倾斜角,但当倾斜角为90°时,斜率不存在.所以A 、C 错误;倾斜角为135°的直线的斜率为-1,所以B 错误;只有D 正确.2.已知经过两点(5,m )和(m,8)的直线的斜率等于1,则m 的值是( )A .5B .8C.132 D .7解析:选C 由斜率公式可得8-m m -5=1,解之得m =132. 3.直线l 经过原点和(-1,1),则它的倾斜角为________.解析:k l =1-0-1-0=-1, 因此倾斜角为135°.答案:135°4.已知三点A (a,2),B (3,7),C (-2,-9a )在同一条直线上,实数a 的值为________.解析:∵A 、B 、C 三点共线,∴k AB =k BC ,即53-a =9a +75,∴a =2或29.答案:2或29 5.已知A (m ,-m +3),B (2,m -1),C (-1,4),直线AC 的斜率等于直线BC 的斜率的3倍,求m 的值.解:由题意直线AC 的斜率存在,即m ≠-1.∴k AC =-m +3-4m +1,k BC =m -1-42--1. ∴-m +3-4m +1=3·m -1-42--1. 整理得:-m -1=(m -5)(m +1),即(m +1)(m -4)=0,∴m =4或m =-1(舍去).∴m =4.[课时达标检测]一、选择题1.给出下列说法,正确的个数是( )①若两直线的倾斜角相等,则它们的斜率也一定相等; ②一条直线的倾斜角为-30°;③倾斜角为0°的直线只有一条;④直线的倾斜角α的集合{α|0°≤α<180°}与直线集合建立了一一对应关系.A .0B .1C .2D .3解析:选A 若两直线的倾斜角为90°,则它们的斜率不存在,①错;直线倾斜角的取值范围是[0°,180°),②错;所有垂直于y 轴的直线倾斜角均为0°,③错;不同的直线可以有相同的倾斜角,④错.2.过两点A (4,y ),B (2,-3)的直线的倾斜角为45°,则y =( )A .-32B.32 C .-1D .1 解析:选C tan 45°=k AB =y +34-2,即y +34-2=1,所以y =-1.3.如图,设直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则k 1,k 2,k 3的大小关系为( )A .k 1<k 2<k 3B .k 1<k 3<k 2C .k 2<k 1<k 3D .k 3<k 2<k 1解析:选A 根据“斜率越大,直线的倾斜程度越大”可知选项A 正确.4.经过两点A (2,1),B (1,m 2)的直线l 的倾斜角为锐角,则m 的取值范围是( )A .m <1B .m >-1C .-1<m <1D .m >1或m <-1解析:选C ∵直线l 的倾斜角为锐角,∴斜率k =m 2-11-2>0,∴-1<m <1.5.(2012·广州高一检测)如果直线l 过点(1,2),且不通过第四象限,那么l 的斜率的取值范围是( )A .[0,1]B .[0,2] C.⎣⎢⎡⎦⎥⎤0,12 D .(0,3]解析:选B 过点(1,2)的斜率为非负且最大斜率为此点与原点的连线斜率时,图象不过第四象限.二、填空题6.已知a >0,若平面内三点A (1,-a ),B (2,a 2),C (3,a 3)共线,则a =________.解析:若平面内三点共线,则k AB =k BC ,即a 2+a 2-1=a 3-a 23-2,整理得a 2-2a -1=0,解得a =1+2,或a =1-2(舍去). 答案:1+27.如果直线l 1的倾斜角是150°,l 2⊥l 1,垂足为B .l 1,l 2与x 轴分别相交于点C ,A ,l 3平分∠BAC ,则l 3的倾斜角为________.解析:因为直线l 1的倾斜角为150°,所以∠BCA =30°,所以l 3的倾斜角为12×(90°-30°)=30°. 答案:30°8.已知实数x ,y 满足方程x +2y =6,当1≤x ≤3时,y -1x -2的取值范围为________.解析:y -1x -2的几何意义是过M (x ,y ),N (2,1)两点的直线的斜率,因为点M 在函数x +2y =6的图象上,且1≤x ≤3,所以可设该线段为AB ,且A ⎝ ⎛⎭⎪⎫1,52,B ⎝ ⎛⎭⎪⎫3,32,由于k NA =-32,k NB =12,所以y -1x -2的取值范围是⎝ ⎛⎦⎥⎤-∞,-32∪⎣⎢⎡⎭⎪⎫12,+∞. 答案:⎝ ⎛⎦⎥⎤-∞,-32∪⎣⎢⎡⎭⎪⎫12,+∞ 三、解答题9.已知直线l 过点A (1,2),B (m,3),求直线l 的斜率和倾斜角的取值范围.解:设l 的斜率为k ,倾斜角为α,当m =1时,斜率k 不存在,α=90°,当m ≠1时,k =3-2m -1=1m -1, 当m >1时,k =1m -1>0,此时α为锐角,0°<α<90°, 当m <1时,k =1m -1<0,此时α为钝角, 90°<α<180°.所以α∈(0°,180°),k ∈(-∞,0)∪(0,+∞).10.已知A (3,3),B (-4,2),C (0,-2),(1)求直线AB 和AC 的斜率.(2)若点D 在线段BC (包括端点)上移动时,求直线AD 的斜率的变化范围.解:(1)由斜率公式可得直线AB 的斜率k AB =2-3-4-3=17.直线AC 的斜率k AC =-2-30-3=53.故直线AB 的斜率为17,直线AC 的斜率为53. (2)如图所示,当D 由B 运动到C 时,直线AD 的斜率由k AB 增大到k AC ,所以直线AD 的斜率的变化范围是⎣⎢⎡⎦⎥⎤17,53.。
高中数学人教A版必修2导学案:3.1.1直线的倾斜角和斜率(学生版)

章节
3.1.1 课题直线的倾斜角与斜率教
学目标1、在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素;
2、理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程;
3、掌握过两点的直线的斜率计算公式。
教学重点理解直线的倾斜角与斜率的概念。
教学难点过两点的直线的斜率公式推导【复习回顾】
1.锐角三角函数的定义:如图所示,正弦(sin)等于对边比斜边,sinA=a/c;
余弦(cos)等于邻边比斜边,cosA=b/c;正切(t a n)等于对边比邻边,t a nA=a/b。
2.特殊角的正切值
α0o30o45o60o90o120o135o150o tanα
通过上述表格,你能得出互余的两个角、互补的两个角的正切有怎样的关系?
(1),(2)。
课前预习案
【新知探究】
探究一、确定直线的几何要素
问题1:给出一点P,可以作无数条直线,这些直线组成“直线束”,这些直线的共同点是什么,不同点是什么?由此你能总结出确定直线的几何要素吗?
共同点: ,不同点: 。
确定直线的几何要素:。
探究二、直线的倾斜角与斜率
问题2:平面直角坐标系中,直线l与x轴有几种位置关系?在刻画直线的倾斜程度时,我们取x 轴作为基准线,引入倾斜角的概念,它的定义是什么,取值范围如何?
直线l与x轴的位置关系:。
定义包括两个方面:(1)当直线l与x轴相交时,。
(2)当直线l与x轴平行或重合时,。
取值范围:。
高中数学人教A版必修2导学案:3.1.1直线的倾斜角和斜率(学生版)。
高中数学二 3.1.1 倾斜角与斜率 导学案

3.1.1 直线的倾斜角与斜率学习目标:1。
理解直线的倾斜角和斜率的概念.理解两条直线平行与垂直的条件,能用直线的倾斜角与斜率的关系来判定两条直线平行与垂直。
2.通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合思想学习过程:问题的导入:大家想一下当一高一矮两人抬一根圆木,会出现什么现象?(倾斜)本节课我们就重点研究有关直线的倾斜问题。
A问题1:对平面直角坐标系内的一条直线,它的位置由那些条件确定?(两点)B问题2:一点能确定一条直线吗?经过一点的直线的位置能够确定吗?它的位置会怎样?(观察可以发现过一点有无数条直线并且它们发生了不同程度的倾斜)直线在倾斜时与那个量有关?怎样描述直线的倾斜程度呢?A 问题3:什么是直线的倾斜角?它的范围怎样?写出并背熟,记牢倾斜角及范围!当直线L 与x 轴垂直时, =αA 问题4:除了倾斜角还有其他确定直线倾斜程度的量吗?什么是直线的斜率?只有倾斜角或斜率能确定一直线的位置吗?若不能还需要加什么条件?B 问题5:直线的倾斜角和斜率有什么关系?它们是一一对应的吗?(牢记公式)【温馨提示】(1)时,斜率不存在。
当时,当的增大而减小;随的增大而增大,但随时,,当的增大而增大;也随的增大而增大,随时,当2;0 0,0)2(,0 )2,0 (πααααππαααπα===<∈>∈k k k k k k k (2)平面内任何一条直线都有唯一的倾斜角,但不是每一条直线都有,倾斜角为90°的直线没有斜率,在使用斜率来研究直线时,经常要对直线是否有斜率分情形讨论。
(3)倾斜角和斜率都是反映直线相对于x轴正方向的倾斜程度的,倾斜角是直接反映这种倾斜程度的,斜率等于倾斜角的正切值,在以后的学习中将体会到,研究直线时,使用斜率常常比使用倾斜角更方便.B问题6:阅读教材83-——84页探究如何由直线上的两点求直线的斜率呢?计算公式如何?(牢记公式)典型例题:例1:已知A(3, 2),B(-4,1), C(0, —1),求直线AB、BC、CA的斜率, 并判断它们的倾斜角是钝角还是锐角。
高一数学教案:3.1.1直线的倾斜角和斜率(1)

3.1.1直线的倾斜角和斜率(1)一、教学目标知道一次函数的图象是直线,了解直线方程的概念,掌握直线的倾斜角和斜率的概念以及直线的斜率公式.二、重难点1.重点:通过对一次函数的研究,学生对直线的方程已有所了解,要对进一步研究直线方程的内容进行介绍,以激发学生学习这一部分知识的兴趣;直线的倾斜角和斜率是反映直线相对于x轴正方向的倾斜程度的,是研究两条直线位置关系的重要依据,要正确理解概念;斜率公式要在熟练运用上多下功夫.2.难点:一次函数与其图象的对应关系、直线方程与直线的对应关系是难点.由于以后还要专门研究曲线与方程,对这一点只需一般介绍就可以了.三、教学过程(一)复习一次函数及其图象已知一次函数y=2x+1,试判断点A(1,2)和点B(2,1)是否在函数图象上.初中我们是这样解答的:∵A(1,2)的坐标满足函数式,∴点A在函数图象上.∵B(2,1)的坐标不满足函数式,∴点B不在函数图象上.现在我们问:这样解答的理论依据是什么?(这个问题是本课的难点,要给足够的时间让学生思考、体会.)讨论作答:判断点A在函数图象上的理论依据是:满足函数关系式的点都在函数的图象上;判断点B不在函数图象上的理论依据是:函数图象上的点的坐标应满足函数关系式.简言之,就是函数图象上的点与满足函数式的有序数对具有一一对应关系.(二)直线的倾斜角一条直线l向上的方向与x轴的正方向所成的最小正角,叫做这条直线的倾斜角,如图中的α.特别地,当直线l和x轴平行时,我们规定它的倾斜角为0°,因此,倾斜角的取值范围是0°≤α<180°.点:(1)以x轴正向作为参考方向(始边);(2)直线向上的方向作为终边;(3)最小正角.(三)直线的斜率倾斜角不是90°的直线.它的倾斜角的正切叫做这条直线的斜率.直线的斜率常用k表示,即αk=tan(四)过两点的直线的斜率公式在坐标平面上,已知两点P1(x1,y1)、P2(x2,y2),由于两点可以确定一条直线,直线P1P2就是确定的.当x1≠x2时,直线的倾角不等于90°时,这条直线的斜率也是确定的.怎样用P2和P1的坐标来表示这条直线的斜率?P2分别向x 轴作垂线P1M1、P2M2,再作P1Q ⊥P2M ,垂足分别是M1、M2、Q .那么: α=∠QP1P2(图甲)或α=π-∠P2P1Q(图乙)在图甲中:121212tan x x y y Q P QP --==α在图乙中:xx y y QP QP Q P P --==<-=2121212tan tan α如果P1P2向下时,用前面的结论课得:xx y y x x y y --=--=2122121tan α综上所述,我们得到经过点P1(x1,y1)、P2(x2,y2)两点的直线的斜率公式:对于上面的斜率公式要注意下面四点:(1)当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角为90°;(2)k 与P1、P2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到. (五)例题例1 如图,直线l1的倾斜角α1=30°,直线l2⊥l1,求l1、l2的斜率. 解: ∵l2的倾斜角α2=90°+30°=120°,3120tan 20-==∴k本例题是用来复习巩固直线的倾斜角和斜率以及它们之间的关系的,可由学生课堂练习,学生演板.例2 求经过A(-2,0)、B(-5,3)两点的直线的斜率和倾斜角.∴tgα=-1.∵0°≤α<180°, ∴α=135°.3330tan 10==k因此,这条直线的斜率是-1,倾斜角是135°.讲此例题时,要进一步强调k与P1P2的顺序无关,直线的斜率和倾斜角可通过直线上的两点的坐标求得.(六)课后小结(1)直线的方程的倾斜角的概念.(2)直线的倾斜角和斜率的概念.(3)直线的斜率公式.三、布置作业1.在坐标平面上,画出下列方程的直线:(1)y=x(2)2x+3y=6(3)2x+3y+6=0(4)2x-3y+6=0作图要点:利用两点确定一条直线,找出方程的两个特解,以这两个特解为坐标描点连线即可.2.求经过下列每两个点的直线的斜率,若是特殊角则求出倾斜角:(1)C(10,8),D(4,-4);解:(1)k=2.(3)k=1,α=45°.3.已知:a、b、c是两两不相等的实数,求经过下列每两个点的直线的倾斜角:(1)A(a,c),(b,c);(2)C(a,b),D(a,c);(3)P(b,b+c),Q(a,c+a).解:(1)α=0°;(2)α=90°;(3)α=45°.4.已知三点A(a,2)、B(3,7)、C(-2,-9a)在一条直线上,求实数a的值.∵A、B、C三点在一条直线上,∴kAB=kAC.六、板书设计3.1.1直线的倾斜角和斜率(2)一、教学目标(一)知识教学点复习直线的倾斜角和斜率的概念以及直线的斜率公式.(二)能力训练点通过对知识点的应用(例题1、例题2及课堂练习),巩固学生所学的知识,培养学生分析、解决问题的能力;.(三)学科渗透点分析问题、提出问题的思维品质,事物之间相互联系、互相转化的辩证唯物主义思想. 二、教材分析1.重点:通过上一节课的学习,学生对直线的倾斜角和斜率的求法已有所了解,直线的倾斜角和斜率是反映直线相对于x 轴正方向的倾斜程度的,是研究两条直线位置关系的重要依据,要正确理解概。
人教高一数学教学设计之《3.1.1倾斜角与斜率》

人教高一数学教学设计之《3.1.1倾斜角与斜率》一. 教材分析《3.1.1倾斜角与斜率》是高中数学人教版必修二的第一节,本节课主要介绍直线的倾斜角和斜率的概念,以及它们之间的关系。
通过本节课的学习,学生能够理解直线的倾斜角和斜率的定义,掌握它们的计算方法,并能运用它们解决一些实际问题。
二. 学情分析高一的学生已经具备了一些几何的基础知识,例如直线的倾斜角和斜率的概念,他们对于新的知识有较强的接受能力。
但是,对于如何运用这些知识解决实际问题,他们可能还不够熟练。
因此,在教学过程中,需要注重培养学生的实际应用能力。
三. 教学目标1.知识与技能:理解直线的倾斜角和斜率的定义,掌握它们的计算方法。
2.过程与方法:通过观察和操作,培养学生的空间想象能力。
3.情感态度与价值观:培养学生对数学的兴趣,使他们能够主动探索和发现。
四. 教学重难点1.重点:直线的倾斜角和斜率的定义,它们的计算方法。
2.难点:如何运用直线的倾斜角和斜率解决实际问题。
五. 教学方法1.情境教学法:通过实物和图片,引导学生观察和思考。
2.问题驱动法:通过提问和讨论,激发学生的学习兴趣。
3.实践操作法:通过动手操作,培养学生的实际应用能力。
六. 教学准备1.准备一些直线的倾斜角和斜率的实例,用于讲解和演示。
2.准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过展示一些图片,如直线、斜坡等,引导学生思考:直线的倾斜角和斜率是什么?它们有什么关系?2.呈现(10分钟)讲解直线的倾斜角和斜率的定义,以及它们的计算方法。
通过实物和图片,让学生直观地理解这两个概念。
3.操练(10分钟)让学生动手操作,尝试计算一些直线的倾斜角和斜率。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)出示一些练习题,让学生独立完成。
教师选典型题目进行讲解,巩固所学知识。
5.拓展(10分钟)引导学生思考:如何运用直线的倾斜角和斜率解决实际问题?出示一些实例,让学生分组讨论和解答。
人教版高中数学必修2:3.1.1直线的倾斜角和斜率 导学案设计

§3.1.1直线的倾斜角和斜率两课时【学习目标】: 1.理解直线的倾斜角的定义、范围和斜率;2.掌握过两点的直线斜率的计算公式;3.能用公式和概念解决问题. 重点:倾斜角与斜率的概念。
难点:直线的斜率与倾斜角的关系一、【预习导航】:1.在直角三角形中,当内角α为锐角时,sinα=,cosα=,tanα=,其中x、y分别为角α的邻边、对边,r为斜边.2.α为锐角时:tan(180°-α)= .3.几个特殊角的三角函数值:tan30°=;t an45°=;tan60°=;tan120°=;tan135°=;tan150°= .4.点确定一条直线.5.倾斜角的定义:当直线L与x轴相交时,取作为基准,x轴与直线L之间所成的角α叫做直线L的倾斜角.规定:当直线L与x轴平行或重合时,它的倾斜角为6.倾斜角的范围:直线的倾斜角α的取值范围是.7.斜率的定义:对于倾斜角不是90°的直线,它的倾斜角的叫做直线的斜率,记作K= ;倾斜角为90°的直线的斜率.8. 斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为探究活动:几何图形问题的研究主要通过两种不同的方式:一种方式,直接依据几何图形中的点、线、面的关系研究几何图形的性质。
例如以前学的平面几何、立体几何就是如此。
另一种方式,就是用代数的方法来研究几何图形的性质。
17世纪,法国数学家笛卡尔,有一天躺在床上观察虫子在天花板上爬行位置,激发了灵感,产生了坐标的概念,创立了解析几何。
简单来说,解析几何是通过建立直角坐标系,通过坐标的运算用代数方程来研究几何图形性质问题的一门科学。
直线的倾斜角的概念我们知道, 经过两点有且只有(确定)一条直线. 那么, 经过一点P的直线l的位置能确定吗? 如图, 过一点P可以作无数多条直线a,b,c, …易见,答案是否定的.这些直线有什么联系呢?(1)它们都经过点P. (2)它们的‘倾斜程度’不同.怎样描述这种‘倾斜程度’的不同?引入直线的倾斜角的概念:当直线l与x轴相交时,取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜..角..特别地,当直线l与x轴平行或重合时, 规定α=0°.问: 倾斜角α的取值范围是什么? 0°≤α<180°.当直线l 与x 轴垂直时, α=90°.因为平面直角坐标系内的每一条直线都有确定的倾斜程度, 引入直线的倾斜角之后, 我们就可以用倾斜角α来表示平面直角坐标系内的每一条直线的倾斜程度.若直线a ∥b ∥c, 那么它们的倾斜角α相等吗? 答案是肯定的.所以一个倾斜角α不能确定一条直线.确定平面直角坐标系内的一条直线位置的几何要素: 一个点...P .和一个倾斜角......α. 说明:理解倾斜角的概念时,要注意三个条件:①x 轴正向;②直线向上的方向;③小于180°的非负角. (二)直线的斜率:探究二 直线的斜率问题:生活中你知道有哪些量可以用来表示某一斜坡的倾斜程度(坡度)?斜率的定义:对于倾斜角不是90°的直线,它的倾斜角的 叫做直线的斜率,斜率通常用k 表示,即k= 问题:倾斜角为90°的直线的斜率存在吗?一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k 表示,也就是k=tan α说明:①当倾斜角是90°时,直线的斜率k 不存在,并不是直线不存在,此时,直线垂直于x ;轴;当直线l 与x 轴平行或重合时, α=0°, k=tan0°=0; ②所有的直线都有倾斜角,但不是所有的直线都有斜率;③直线的斜率也反映直线相对于x 轴的正方向的倾斜程度.当0°≤α<90°时,斜率越大,直线的倾斜程度就越大;当90°<α<180°时,斜率越大,倾斜角也越大;当直线绕定点由与x 轴平行(或重合)位置按逆时针方向旋转到与y 轴平行(或重合)时,斜率由0逐渐增大到+∞;按顺时针方向时,斜率由0逐渐减小到-∞,这种方法即可定性分析倾斜角与斜率的关系,也可以定量求解斜率和倾斜角的取值范围.④k >0⇔0°<α<90°;k =0⇔α=0°;k <0⇔90°<α<180°;k 不存在⇔α=90°○5补正切函数图像:○6公式:α为锐角,tan(180°-α)=-tan α 例如, α=45°时, k=tan45°=1;α=135°时, k=tan135°=tan(180°-45°) =-tan45°=-1. 学习了斜率之后, 我们又可以用斜率来表示直线的倾斜程度. 做一做 (熟记下列角的正切值)倾斜角α 00 300 450 600 900 1200 1350 1500αtan 前进量升高量)比(坡度==斜率k给定两点P1(x1,y1),P2(x2,y2),x1≠x2,如何用两点的坐标来表示直线P1P2的斜率?讨论:如图,给定直线L上两点P1(x1,y1),P2(x2,y2)(x1≠x2),如何求直线P1P2的斜率?并判别斜率k的符号.思考1:如图,当P1P2的位置对调,K值如何呢?结论:综上所述,我们得到经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的斜率公式为思考2:当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?思考3:当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?斜率公式: k=2121y yx x--斜率公式要注意下面四点:(1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角α= 90°, 直线与x轴垂直;(2)与两点的顺序无关,也就是说公式中的x1与x2,y1与y2可以同时交换位置;分子是纵坐标之差,分母是对应横坐标之差;(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;(4) 当 y1=y2时, 斜率k=0, 直线的倾斜角α=0°,直线与x轴平行或重合.例1、已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断它们的倾斜角是钝角还是锐角.分析: 已知两点坐标,而且x1≠x2, 由斜率公式代入即可求得k的值;解: 直线AB的斜率k1=1/7>0, 所以它的倾斜角α是锐角;直线BC的斜率k2=-0.5<0, 所以它的倾斜角α是钝角;直线CA的斜率k3=1>0, 所以它的倾斜角α是锐角.例2、在平面直角坐标系中, 画出经过原点且斜率分别为1, -1, 2, 及-3的直线a, b, c, l.分析:要画出经过原点的直线a, 只要再找出a上的另外一点M. 而M的坐标可以根据直线a的斜率确定。
人教版高中数学全套教案导学案3.1.1倾斜角与斜率

3. 1.1 直线的倾斜角与斜率【学习目标 】1.理解直线的倾斜角的定义、范围和斜率;2.掌握过两点的直线斜率的计算公式;3.能用公式和概念解决问题.【教学重难点】重点:倾斜角与斜率的概念难点:直线的斜率与倾斜角的关系【教学过程】一、课前准备(预习教材 82P ~ 86P ,找出疑惑之处)复习 1:在直角坐标系中,只知道直线上的一点,能不 能确定一条直线呢?复习 2:在日常生活中,我们常说这个山坡很陡峭, 有时也说坡度,这里的陡峭和坡度说的是山坡与水平面之间的一个什么关系呢?二、新课导学探究点一:①倾斜角的概念当直线l 与x 轴相交时,取x 轴作为基准, x 轴正向与直线l 向上方向之间所成的角α 叫做直 线l 的倾斜角(angle of inclination ). 发现:①直线向上方向;②x 轴的正方向;③小于平角的正角.注意:当直线与轴x 平行或重合时,我们规定它的倾 斜角为 0 度..思考:在日常生活中,我们经常用“升高量与前进量的比”表示“坡度” ,则坡度的公式是怎样的?②斜率与倾斜角的关系一条直线的倾斜角 α ( ) 的正切值叫做这条直线的斜率(slope).记为k= tan .试试:已知各直线倾斜角,则其斜率的值为(1)α=0°时,则k(2)0°<α< 90°,则k(3)α= 90°,,则k(4)90 °<α< 180°,则k③ 已知直线上两点1p (),11y x ,),(222y x p (21x x ≠)的直线的斜率公式:1212x x y y k --=. 探究任务二: 1.已知直线上两点 ),(),,(2211b a B b a A 运用上述公式计算直线的斜率时,与 A B 两点坐标的顺序有关吗?2.当直线平行于 y 轴时,或与轴y 重合时,上述公式还需要适用吗?为什么?三、典型例题分析例1 已知直线的倾斜角,求直线的斜率:⑴ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:座号:【学习目标】1.理直线的倾斜角的定义、范围和斜率;
2.掌握过两点的直线斜率的计算公式;
3.能用公式和概念解决问题.
【教学重难点】
重点:直线的倾斜角与斜率的概念
难点:直线的斜率与倾斜角的关系
【学习过程】
一、新课导学:
(一)、倾斜角和斜率的概念
探究任务1(阅读课本82--86页,思考并填空)
1.下列叙述中不正确的是()
A.若直线的斜率存在,则必有倾斜角与之对应
B.每一条直线都唯一对应一个倾斜角
C.与坐标轴垂直的直线的倾斜角为 或
D.若直线的倾斜角为 ,则直线的斜率为
2.经过 两点的直线的倾斜角()
A. B. C. D.
3.过点P(-2,m)和Q(m,4)的直线的斜率等于1,则m的值为( )
A.1 B.4 C.1或3 D.1或4
4.直线 经过二、三、四象限, 的倾斜角为 ,斜率为 ,则 为角; 的取值范围.
5.已知直线 的倾斜角为 1,则 关于x轴对称的直线 的倾斜角 为
五、总结提升
1.任何一条直线都有唯一确定的倾斜角,直线斜角的范围是[0,180°).
2.直线斜率的求法:(1)利用倾斜角的正切来求;
(2)已知直线的斜率,求其倾斜角.
⑴ ;⑵ ;⑶ ;⑷ 不存在.
例2:已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
三、交流展示
1.求经过下列两点直线的斜率,并判断其倾斜角是锐角还是钝角.
⑴ ⑵
2.画出斜率为 且经过点 的直线.
3.判断 三点的位置关系,并说明理由.
四、达标检测
(2)利用直线上两点 ( , 的坐标求;
(3)当直线的倾斜角 = 90°时,直线的斜率是不存在的.
3.直线倾斜角、斜率、斜率公式三者之间的关系:
直线的倾斜角
直线的斜率
直线的斜率公式
定义
=tan a
.
取值范围
[0,180°)
( )
【自主反思】优点:
缺点:
在直角坐标系中,只知道直线上的一点,能不能确定一条直线呢?
在直角坐标系中,确定直线位置的几何要素有
1、倾斜角的定义是
注意:(1)定义的关键:①直线向上方向;②x轴的正方向.
(2)当直线与x轴平行或重合时,我们规定它的倾斜角为度.
(3)直线倾斜角的范围为
试试:请描出下列各直线的倾斜角,并用字母 表示
试试:填空:
(二)、斜率的公式:已知直线上两点 ( , ( )的直线的斜率公式:
探究任务3. 1.已知直线上两点 运用上述公式计算直线的斜率时,与A、B两点坐标的顺序有关吗?
2.当直线平行于y轴时,或与y轴重合时,上述公式还需要适用吗?为什么?
二、合作探究
例1:(1)已知直线的倾斜角,求直线的斜率:
① ② ③ ④ ⑤
函数y=x的图象的倾斜角为, y=-x的图象的倾斜角为,
直线x=1倾斜角为,直线y=0倾斜角为
探究任务2:在日常生活中,我们经常用“升高量与前进量的比”表示“坡度”,则坡度的公式是怎样的?
如果我们使用“倾斜角”这个概念,那么这里的“坡度比”就是
2、斜率的定义:一条直线的倾斜角α(α≠900)的叫做这条直线的斜率(slope)记为
