正截面受弯承载力计算 混凝土结构
合集下载
混凝土受弯构件正截面承载力计算
h0—有效高度。 1.最大配筋率及界限相对受压区高度
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度,即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定(本构关系)
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段:裂缝开裂前 • 第二阶段:从开裂到钢筋屈服 • 第三阶段:从钢筋屈服到梁破坏
(1)第I阶段
当荷载比较小时,混凝土基本处 于弹性阶段,截面上应力分布为三 角形,荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大,挠度和截面曲率很小,钢筋 的应力也很小,且都于弯矩近似成 正比。
My
Mu
Failure”,破坏前
可吸收较大的应变
能。
0
f
2.超筋梁(Over reinforced)破坏
钢筋配置过多,将发生这种破坏。 破坏特征:破坏时钢筋没有达到屈服强度,破坏是由 于压区混凝土被压碎引起,没有明显预兆,为脆性破 坏。
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度,即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定(本构关系)
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段:裂缝开裂前 • 第二阶段:从开裂到钢筋屈服 • 第三阶段:从钢筋屈服到梁破坏
(1)第I阶段
当荷载比较小时,混凝土基本处 于弹性阶段,截面上应力分布为三 角形,荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大,挠度和截面曲率很小,钢筋 的应力也很小,且都于弯矩近似成 正比。
My
Mu
Failure”,破坏前
可吸收较大的应变
能。
0
f
2.超筋梁(Over reinforced)破坏
钢筋配置过多,将发生这种破坏。 破坏特征:破坏时钢筋没有达到屈服强度,破坏是由 于压区混凝土被压碎引起,没有明显预兆,为脆性破 坏。
水工砼结构-3.受弯构件正截面承载力计算

应变图
ec max
应力图 M
et max
Mcr
M ft sAs Ia II My
ey
xf M fyAs IIa III Mu fyAs IIIa z T=fyAs D
sAs
I
sAs
各阶段截面应力、应变分布
受弯构件正截面破坏形态
钢筋混凝土受弯构件有两种破坏性质:
塑性破坏(延性破坏):结构或构件在破坏前有明显变形
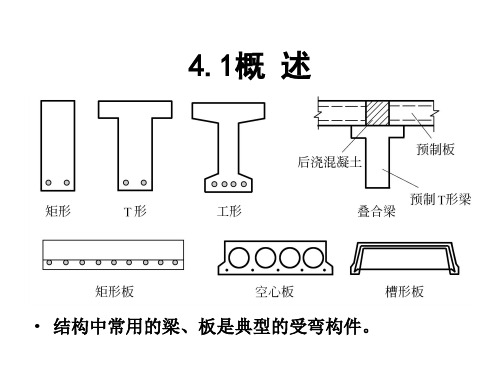
结构中常用的梁、板是典型的受弯构件。
中小跨径,多采用矩形及T形截面 大跨径,多采用工字形或箱形截面
截面尺寸
为统一模板尺寸、便于施工,通常采用梁
宽度b=120、150、180、200、220、250mm, 250mm以上者以50mm为模数递增。 梁高度h=250、300、350、400 、…800mm , 800mm以上者以100mm为模数递增。
As (%) 定义 配筋率 bh0
ρ在一定程度上反映了正
截面上纵向受拉钢筋与混 凝土之间的面积比率,它 是对梁的受力性能有很大 影响的一个重要指标。
受弯构件正截面的受力特性
百分表 应变测点 百分表
位移计
在梁的纯弯段内,沿梁高布置 测点,量测梁截面不同高度处 的纵向应变。
采用预贴电阻应变片或其它方 法量测纵向受拉钢筋应变,从 而得到荷载不断增加时钢筋的 应力变化情况。 在梁跨中的下部设置位移计, 以量测梁跨中的挠度。
受力分为三个阶段
第Ⅰ阶段——未裂阶段
荷载很小,应力与应变之
间基本成线性关系; 荷载↑,砼拉应力达到ft, 拉区呈塑性变形;压区应 力图接近三角形; 砼达到极限拉应变 (et=etu),截面即将开裂 (Ⅰa状态),弯矩为开裂 弯矩Mcr; Ⅰa状态是抗裂计算依据。
正截面受弯承载力计算 混凝土结构

位移计
L/3
L/3
L
受弯构件正截面承载力计算
数据采集系 统
h0
h
As b
2 试验研究 2.2 受弯构件正截面工作的三个阶段
受弯构件正截面承载力计算
2 试验研究 2.2 受弯构件正截面工作的三个阶段
弹性阶段(Ⅰ阶段)
受弯构件正截面承载力计算
2 试验研究 2.2 受弯构件正截面工作的三个阶段
受弯构件正截面承载力计算
• 一裂即断, 由砼的抗拉强度控制, 承载力很低。 • 破坏很突然, 属脆性破坏。 • 砼的抗压承载力未充分利用。 • 设计不允许。
受弯构件正截面承载力计算
3 配筋率对梁正截面破坏形态的影响
由上述分析可知,少筋破坏和超筋破坏都具有脆性 性质,破坏前无明显预兆,破坏时将造成严重后果,材 料的强度得不到充分利用。因此,应避免将受弯构件设 计成少筋构件和超筋构件,只允许设计成适筋构件。
e
受弯构件正截面承载力计算
4 基本假定和基本概念 4.1 基本假定
c
fc
11ee0c
n
fc
c fc
fy
0 e0
砼
ecu
0 fy
e
钢筋
受弯构件正截面承载力计算
4 基本假定和基本概念 4.2 等效矩形应力图形
(1)问题的提出:由于采用混凝土的真实压应力图来计 算极限弯矩Mu,需要进行比较复杂的积分运算,不利于工 程应用。
第 II 阶段 带裂缝工作阶段 有裂缝,挠度还不明显
曲线
第 III 阶段 破坏阶段 钢筋屈服,裂缝宽,挠度大 接近ຫໍສະໝຸດ 平的曲线混受凝
压
土
区
应
力
图
受
混凝土结构受弯构件正截面承载力计算(极限状态法)

fy
(3)
相对受压区高度ξ不仅反映了钢筋与混凝土的面积比(配筋率 ρ),也反映了钢筋与混凝土的材料强度比,是反映构件中两种材 料配比本质的参数。
桥梁工程系-杨 剑
界限相对受压区高度ξb
ecu
x>xb’ Xb ’ x<xb’
ρ<ρmax
ρ=ρmax ρ>ρmax
ey
桥梁工程系-杨 剑
h0
有明显屈服点钢筋:
2
(5) (5a)
桥梁工程系-杨 剑
三. 适用条件
1. b x b h0
或
max b
a fc
f sd
2 0
M M u ,max a s ,max a f cbh
a s a s ,max b (1 - 0.5b )
防止所设计的梁为超筋梁
桥梁工程系-杨 剑
4
受弯构件强度和变形计算 ——混凝土结构规范部分
本章按照混凝土结构设计规范对钢筋砼受弯 构件进行分析
桥梁工程系-杨 剑
本章主要内容
4-1 受弯构件的应力阶段及破坏状态
4-2 受弯构件正截面承载力计算 4-3 单筋矩形截面受弯构件正截面承载力计算 4-4 双筋矩形截面受弯构件正截面承载力计算
4-5 T形截面受弯构件正截面承载力计算
b =(1/3~1/4)h - T形截面,焊接骨架;
简支板可取h = (1/30 ~ 1/35)L
桥梁工程系-杨 剑
给定M时 ● 截面尺寸b、h(h0)越大,所需的As就越少, 越小,但 混凝土用量和模板费用增加,并影响使用净空高度; ● 反之,b、h(h0)越小,所需的As就越大, 增大。
b as
混凝土结构设计原理-受弯构件正截面承载力精选全文

求:截面配筋As
2.已知:矩形截面钢筋混凝土简支梁,计算跨度为6000mm, as=35mm, 作用均布荷载25 kN/m,混凝土强度等级C20,钢筋HRB335级。 ( fc =9.6 N/mm2 , ft =1.1 N/mm2 , fy =300 N/mm2 )
试设计此梁
3.已知:矩形截面梁尺寸b=200mm、h=450mm,as=35mm。混凝土 强度等级C70,钢筋HRB335级,实配4根20mm的钢筋。 ( fc =31.8 N/mm2 , ft =2.14 N/mm2 , fy =300 N/mm2 )
b
max
b
1 fc
fy
受弯构件正截面承载力计算
最小配筋率ρmin
最小配筋率规定了少筋和适筋的界限
m in
As bh
0.45
ft fy
且同时不应小于0.2%
受弯构件正截面承载力计算
造价
总造价
混凝土
钢
经济配筋率
经济配筋率 板:0.4~0.8%
矩形梁:0.6~1.5% T形梁:0.9~1.8%
受弯构件正截面承载力计算
小相等; 2. 等效矩形应力图形与实际抛物线应力图形的形心位置相同,即合
力作用点不变。
受弯构件正截面承载力计算
表 5.1 混凝土受压区等效矩形应力图系数
≤C50 C55
C60
C65
C
0.8
0.99 0.98 0.97 0.96 0.95 0.94 0.79 0.78 0.77 0.76 0.73 0.74
钢筋与混凝土的材料强度比,是反映构件中两种材料配比的本质参数。
基本方程改为:
N 0, M 0,
1 fcb h0 s As M u 1 fcbh02 (1 0.5 )
2.已知:矩形截面钢筋混凝土简支梁,计算跨度为6000mm, as=35mm, 作用均布荷载25 kN/m,混凝土强度等级C20,钢筋HRB335级。 ( fc =9.6 N/mm2 , ft =1.1 N/mm2 , fy =300 N/mm2 )
试设计此梁
3.已知:矩形截面梁尺寸b=200mm、h=450mm,as=35mm。混凝土 强度等级C70,钢筋HRB335级,实配4根20mm的钢筋。 ( fc =31.8 N/mm2 , ft =2.14 N/mm2 , fy =300 N/mm2 )
b
max
b
1 fc
fy
受弯构件正截面承载力计算
最小配筋率ρmin
最小配筋率规定了少筋和适筋的界限
m in
As bh
0.45
ft fy
且同时不应小于0.2%
受弯构件正截面承载力计算
造价
总造价
混凝土
钢
经济配筋率
经济配筋率 板:0.4~0.8%
矩形梁:0.6~1.5% T形梁:0.9~1.8%
受弯构件正截面承载力计算
小相等; 2. 等效矩形应力图形与实际抛物线应力图形的形心位置相同,即合
力作用点不变。
受弯构件正截面承载力计算
表 5.1 混凝土受压区等效矩形应力图系数
≤C50 C55
C60
C65
C
0.8
0.99 0.98 0.97 0.96 0.95 0.94 0.79 0.78 0.77 0.76 0.73 0.74
钢筋与混凝土的材料强度比,是反映构件中两种材料配比的本质参数。
基本方程改为:
N 0, M 0,
1 fcb h0 s As M u 1 fcbh02 (1 0.5 )
混凝土结构受弯构件正截面承载力

(1)
Ms 0
M
1
fcbx(h0
x) 2
(2a)
或
Mc 0
M
f y As (h0
x) 2
(2b)
湖南大学
混凝土结构设计原理.第四章
3.基本公式适用条件 (1)为了防止少筋,要求:
式中
As minbh
(3)
min ——最小配筋率,按腹板全截面
计算,此值取 0.2% 和 45 ft / f y (%)
1 fc (bf b)hf 1 fcbx f y As (37)
M
1 fc (bf b)hf (h0
1
fcbx(h0
x 2
)
hf 2
)
(38)
适用条件:
混凝土结构设计原理.第四章
x bh0
As minbh
(39) (40)
湖南大学
混凝土结构设计原理.第四章
(五)深受弯构件正截面承载力
(三)双筋矩形截面正截面承载力
1.适用情况 ● 结构构件承受应变作用时; ● 弯矩设计值大于单筋截面的最大抵抗弯
矩值而截面尺寸等因素又不宜改变时; ● 受压区由于某种原因已布置受力钢筋时
候。 双筋截面不经济,尽量少用。
湖南大学
2.计算公式及使用条件
混凝土结构设计原理.第四章
X 0 M 0
f y As f y ' A's 1 fcbx
湖南大学
2.梁
(1)截面尺寸:h / l 1 ~ 1
8 16
h/b 2~ 4
混凝土结构设计原理.第四章
;悬臂梁 h / l 1
6
b 120,150,180,200,220,250,300,350,400,
混凝土结构设计原理-04章-受弯构件的正截面受弯承载力

fsd
即:
截面应力图
截面等效应力图
fcdb x k1 fcdb xc
x 2 xc yc 2 1 k2 xc
令:x xc ,可求出 21 k2 ,
k1
21 k2
对 C50 及以下混凝土, 1.0 , 0.8 ;C80时, 0.94
0.74 ,中间内插值。《公路桥规》直接取 1.0。
k2 xc
cu c c d c
0
式中k1、k2与混凝土的 强度等级有关,对C50 及以下混凝土,积分 可得 k1=0.797
k2=0.588
4.3 正截面受弯承载力计算原理
第4章 受弯构件的正截面受弯承载力
3.等效矩形应力图
fcd
等效原则:
合力大小C 相等
合力点位置 yc不变
fsd
4.3 正截面受弯承载力计算原理
第4章 受弯构件的正截面受弯承载力
4.适筋梁与超筋梁的界限及界限配筋率 (1)界限破坏
适筋破坏:受拉钢筋先屈服,
然后混凝土受压区边缘达到极限压
应变。
超筋破坏:受拉钢筋不屈服,
混凝土受压区边缘达到极限压应变。
界限破坏:受拉钢筋屈服的同 时混凝土受压区边缘达到极限压应
适筋、超筋、界限破坏时的截面应变
4.1 梁、板的一般构造
第4章 受弯构件的正截面受弯承载力
常用直径为8mm、10mm、12mm和14mm。 ■ 板内钢筋: 受力钢筋宜采用HPB300、HRB400和HRBF400钢筋。 常用直径为8mm、10mm、12mm和14mm。 分布钢筋宜采用HPB300、HRB335钢筋。 常用直径为6mm、8mm。 ■ 钢筋净距、保护层及有效高度 截面有效高度h0为受拉钢筋合力点至受压区边缘的距离。 h0 h as
混凝土结构基本原理----第三章:正截面受弯承载力计算

载力的设计值,它是由正截面上材料所产生的抗力。
(1) 截面形状
梁、板常用பைடு நூலகம்形、T形、I字形、槽形、空心板和倒 L形梁等对称和不对称截面
(2) 梁、板的截面尺寸
1)矩形截面梁的高宽比h/b一般取2.0~3.5;T形截面梁 的h/b一般取2.5~4.0(此处b为梁肋宽)。矩形截面的宽度 或T形截面的肋宽b一般取为100、120、150、(180)、200、 (220)、250和300mm,300mm以下的级差为50mm;括 号中的数值仅用于木模。
3.1受弯构件的一般构造
与构件的计算轴线相垂直的截面称为正截面。
结构和构件要满足承载能力极限状态和正常使用极
限状态的要求。梁、板正截面受弯承载力计算就是从满
足承载能力极限状态出发的,即要求满足
M≤Mu
(4—1)
式中的M是受弯构件正截面的弯矩设计值,它是由结构上
的作用所产生的内力设计值;Mu是受弯构件正截面受弯承
第三章 正截面受弯承载力计算
其特点是:1)纵向受拉钢筋屈服, 拉力保持为常值;裂缝截面处,受拉区 大部分混凝土已退出工作,受压区混凝 土压应力曲线图形比较丰满,有上升段 曲线,也有下降段曲线;2)弯矩还略有 增加;3)受压区边缘混凝土压应变达到 其极限压应变实验值εcu时,混凝土被 压碎,截面破坏;4)弯矩—曲率关系为 接近水平的曲线。
M0=Mcr0时,在纯弯段抗拉能力最薄弱的某一截 面处,当受拉区边缘纤维的拉应变值到达混凝土极限 拉应变实验值εtu0时,将首先出现第一条裂缝,一旦 开裂,梁即由第I阶段转入为第Ⅱ阶段工作。
随着弯矩继续增大,受压区混凝土压应变与受拉钢 筋的拉应变的实测值都不断增长,当应变的量测标距较 大,跨越几条裂缝时,测得的应变沿截面高度的变化规 律仍能符合平截面假定,
(1) 截面形状
梁、板常用பைடு நூலகம்形、T形、I字形、槽形、空心板和倒 L形梁等对称和不对称截面
(2) 梁、板的截面尺寸
1)矩形截面梁的高宽比h/b一般取2.0~3.5;T形截面梁 的h/b一般取2.5~4.0(此处b为梁肋宽)。矩形截面的宽度 或T形截面的肋宽b一般取为100、120、150、(180)、200、 (220)、250和300mm,300mm以下的级差为50mm;括 号中的数值仅用于木模。
3.1受弯构件的一般构造
与构件的计算轴线相垂直的截面称为正截面。
结构和构件要满足承载能力极限状态和正常使用极
限状态的要求。梁、板正截面受弯承载力计算就是从满
足承载能力极限状态出发的,即要求满足
M≤Mu
(4—1)
式中的M是受弯构件正截面的弯矩设计值,它是由结构上
的作用所产生的内力设计值;Mu是受弯构件正截面受弯承
第三章 正截面受弯承载力计算
其特点是:1)纵向受拉钢筋屈服, 拉力保持为常值;裂缝截面处,受拉区 大部分混凝土已退出工作,受压区混凝 土压应力曲线图形比较丰满,有上升段 曲线,也有下降段曲线;2)弯矩还略有 增加;3)受压区边缘混凝土压应变达到 其极限压应变实验值εcu时,混凝土被 压碎,截面破坏;4)弯矩—曲率关系为 接近水平的曲线。
M0=Mcr0时,在纯弯段抗拉能力最薄弱的某一截 面处,当受拉区边缘纤维的拉应变值到达混凝土极限 拉应变实验值εtu0时,将首先出现第一条裂缝,一旦 开裂,梁即由第I阶段转入为第Ⅱ阶段工作。
随着弯矩继续增大,受压区混凝土压应变与受拉钢 筋的拉应变的实测值都不断增长,当应变的量测标距较 大,跨越几条裂缝时,测得的应变沿截面高度的变化规 律仍能符合平截面假定,
