北京市高考试题立体几何大全
高中数学立体几何(北京题型)精选
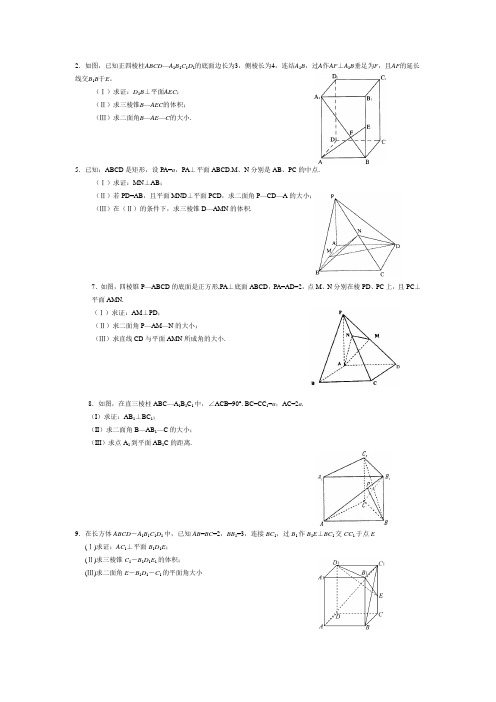
2.如图,已知正四棱柱ABCD —A 1B 1C 1D 1的底面边长为3,侧棱长为4,连结A 1B ,过A 作AF ⊥A 1B 垂足为F ,且AF 的延长线交B 1B 于E 。
(Ⅰ)求证:D 1B ⊥平面AEC ;(Ⅱ)求三棱锥B —AEC 的体积;(Ⅲ)求二面角B —AE —C 的大小.5.已知:ABCD 是矩形,设PA=a ,PA ⊥平面ABCD.M 、N 分别是AB 、PC 的中点.(Ⅰ)求证:MN ⊥AB ;(Ⅱ)若PD=AB ,且平面MND ⊥平面PCD ,求二面角P —CD —A 的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D —AMN 的体积.7.如图,四棱锥P —ABCD 的底面是正方形,PA ⊥底面ABCD ,PA=AD=2,点M 、N 分别在棱PD 、PC 上,且PC ⊥平面AMN.(Ⅰ)求证:AM ⊥PD ;(Ⅱ)求二面角P —AM —N 的大小;(Ⅲ)求直线CD 与平面AMN 所成角的大小.8.如图,在直三棱柱ABC —A 1B 1C 1中,∠ACB=90°. BC=CC 1=a ,AC=2a .(I )求证:AB 1⊥BC 1;(II )求二面角B —AB 1—C 的大小;(III )求点A 1到平面AB 1C 的距离.9.在长方体ABCD -A 1B 1C 1D 1中,已知AB =BC =2,BB 1=3,连接BC 1,过B 1作B 1E ⊥BC 1交CC 1于点E(Ⅰ)求证:AC 1⊥平面B 1D 1E ;(Ⅱ)求三棱锥C 1-B 1D 1E 1的体积;(Ⅲ)求二面角E -B 1D 1-C 1的平面角大小11.直三棱柱ABC -A 1B 1C 1中,AC =CB =AA 1=2,∠ACB =90°,E 是BB 1的中点, D ∈AB ,∠A 1DE =90°.(Ⅰ)求证:CD ⊥平面ABB 1A 1;(Ⅱ)求二面角D -A 1C -A 的大小.16.如图,正三棱柱ABC —A 1B 1C 1,BC=BB 1=1,D 为BC 上一点,且满足AD ⊥C 1D.(I )求证:截面ADC 1⊥侧面BC 1;(II )求二面角C —AC 1—D 的正弦值;(III )求直线A 1B 与截面ADC 1距离.23. 已知,如图四棱锥P —ABCD 中,底面ABCD 是平行四边形,PG ⊥平面ABCD ,垂足为G ,G 在AD 上,且AG=31GD ,BG ⊥GC ,GB=GC=2,E 是BC 的中点,四面体P —BCG 的体积为38.(Ⅰ)求异面直线GE 与PC 所成的角;(Ⅱ)求点D 到平面PBG 的距离;(Ⅲ)若F 点是棱PC 上一点,且DF ⊥GC ,求FCPF 的值.24.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为AA 1、BB 1的中点,求:(I )CM 与D 1N 所成角的余弦值;(II )异面直线CM 与D 1N 的距离.25.如图,四棱锥P —ABCD 的底面是正方形,PA ⊥底面ABCD ,PA=AD=2,点M 、N 分别在棱PD 、PC 上,且PC ⊥平面AMN.(Ⅰ)求证:AM ⊥PD ;(Ⅱ)求二面角P —AM —N 的大小;(Ⅲ)求直线CD 与平面AMN 所成角的大小.28.如图,在斜三棱柱ABC -A 1B 1C 1 中,侧面AA 1B 1B ⊥底面ABC , 侧棱AA 1与底面ABC 成600的角, AA 1= 2.底面ABC 是边长为2的正三角形,其重心为G 点。
北京理科立体几何历年高考题

(16年)6.(5分)(2016•北京)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.1(16年)17.(14分)(2016•北京)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(Ⅰ)求证:PD⊥平面PAB;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值,若不存在,说明理由.(15年)5.某三棱锥的三视图如图所示,则该三棱锥的表面积是().A.2B.4C.2+D.5(15年)17.(本小题满分14分)如图,在四棱锥A EFCB -中,AEF △为等边三角形,平面AEF ⊥平面EFCB ,//EF BC , 4BC =, 2EF a =,060EBC FCB ∠=∠=,O 为EF 的中点.(Ⅰ)求证:AO BE ⊥;(Ⅱ)求二面角F AE B --的余弦值;(Ⅲ)若 BE ⊥平面AOC ,求a 的值.(14年)7.在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(D ,若1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的面积,则( )(A )123S S S ==(B )12S S =且31S S ≠ (C )13S S =且32S S ≠(D )23S S =且13S S ≠(14年)17.(本小题共14分)如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P -中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,。
⑴求证:FG AB //;⑵若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并求线段PH 的长。
(13年)(14)如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上.点P 到直线CC 1的距离的最小值为___________.(13年)(17)(本小题满分14分)如图,在三棱柱111ABC A B C -中,11AA C C 是边长为4的正方形,平面ABC ⊥平面11AA C C ,3AB =,5BC =. (Ⅰ)求证:1AA ⊥平面ABC ;(Ⅱ)求证二面角111A BC B --的余弦值;(Ⅲ)证明:在线段1BC 上存在点D ,使得1AD A B ⊥,并求 1BD BC 的值.(12年)7.某三棱锥的三视图如图所示,该三梭锥的表面积是( )C A 1 C 1B 1A 1CBAA. 28+6B. 30+6C. 56+ 12D. 60+12(12年)16.(本小题共14分)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.(I)求证:A1C⊥平面BCDE;(II)若M是A1D的中点,求CM与平面A1BE所成角的大小;(III)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由5555。
北京高考真题之立体几何

一.1. 已知正三棱锥P ABC−的六条棱长均为6,S是ABC△及其内部的点构成的集合,设集合{5}T Q S PQ=∈,则T表示的区域的面积为(A)34π(B)π(C)2π(D)3π2. 某四面体的三视图如图所示,该四面体的表面积为()A. B. 4 C. 3+ D. 23. 某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为().A. 6+B. 6+C. 12+D. 12+4. 某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.45. 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3B.2C.2D.26. 某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60 B.30 C.20 D.107. 某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.18. (5分)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:.二.1. (2019文)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,底面ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面P AC;(Ⅱ)若∠ABC=60°,求证:平面P AB⊥平面P AE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面P AE?说明理由.2. 如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B﹣PD﹣A的大小;(3)求直线MC与平面BDP所成角的正弦值.3. (2020) 如图,在正方体1111ABCD A B C D −中,E 为1BB 的中点.(Ⅰ)求证:1//BC 平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.5. (2022·)如图,在三棱柱111ABC A B C 中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值. 条件①:AB MN ⊥; 条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.7. (2019理)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,AD⊥CD,AD∥BC,P A=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.(Ⅰ)求证:CD⊥平面P AD;(Ⅱ)求二面角F﹣AE﹣P的余弦值;(Ⅲ)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.8. (14分)如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2.(Ⅰ)求证:AC⊥平面BEF;(Ⅱ)求二面角B﹣CD﹣C1的余弦值;(Ⅲ)证明:直线FG与平面BCD相交.9. 如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(Ⅰ)求证:PD⊥平面PAB;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值,若不存在,说明理由.答案2. 二面角B﹣PD﹣A的大小为60°;直线MC与平面BDP所成角的正弦值为|cos<>|=||=||=3. (Ⅰ)证明见解析;(Ⅱ)2 3.所以PAB为直角三角形,又因为PB=2PB BC+,则PBC为直角三角形,故又因为BC PA⊥PA PB P=,平面PAB,又x轴,过A所以(0,0,1),(1,1,0),(0,1,0),(1,1,AP AC BC PC ====−设平面PAC 的法向量为()111,,m x y z =,则00m AP m AC ⎧⋅=⎪⎨⋅=⎪⎩,即1=,则11y =−,所以(1,1,0)m =−,的法向量为(22,,x n y =00BC PC ⎧⋅=⋅=,即,所以(1,0,1)n =,11,222m n m n m n⋅===⨯,又因为二面角A PC B −−为锐二面角,所以二面角A PC B −−的大小为π系,利用空间向量可求线面角的正弦值. 【详解】(1)取AB 的中点为K ,连接,MK NK , 由三棱柱111ABC A B C 可得四边形11ABB A 为平行四边形, 而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B , 而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B , 而,,NK MK K NK MK =⊂平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B , (2)因为侧面11BCC B 为正方形,故1CB BB ⊥, 而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A , 平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A , 因为//NK BC ,故NK ⊥平面11ABB A , 因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N =, 故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥, 所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===, 设平面BNM 的法向量为(),,n x y z =, 则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−,设直线AB 与平面BNM 所成的角为θ,则4,2n AB =⨯,故1BB M MKN ≅, 111A B BB ⊥, 1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()0,0,0,B 故()()(0,2,0,1,1,0,0,1,2BA BN BM ===设平面BNM 的法向量为(),,n x y z =,00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取,则(2,2,n =−−设直线AB 与平面所成的角为42cos ,233n AB ==⨯6.7. 证明:(Ⅰ)∵P A ⊥平面ABCD ,∴P A ⊥CD , ∵AD ⊥CD ,P A ∩AD =A , ∴CD ⊥平面P AD .解:(Ⅱ)以A 为原点,在平面ABCD 内过A 作CD 的平行线为x 轴, AD 为y 轴,AP 为z 轴,建立空间直角坐标系, A (0,0,0),E (0,1,1),F (,,),P(0,0,2),B(2,﹣1,0),=(0,1,1),=(),平面AEP的法向量=(1,0,0),设平面AEF的法向量=(x,y,z),则,取x=1,得=(1,1,﹣1),设二面角F﹣AE﹣P的平面角为θ,则cosθ===.∴二面角F﹣AE﹣P的余弦值为.(Ⅲ)直线AG在平面AEF内,理由如下:∵点G在PB上,且=.∴G(,﹣,),∴=(,﹣,),∵平面AEF的法向量=(1,1,﹣1),=﹣=0,故直线AG在平面AEF内.8.二面角B﹣CD﹣C1的余弦值为﹣.(III)证明:F(0,0,2),(2,0,1),∴=(2,0,﹣1),∴•=2+0﹣4=﹣2≠0, ∴与不垂直,∴FG 与平面BCD 不平行,又FG ⊄平面BCD , ∴FG 与平面BCD 相交.9. ;.。
北京市高考试题立体几何汇编
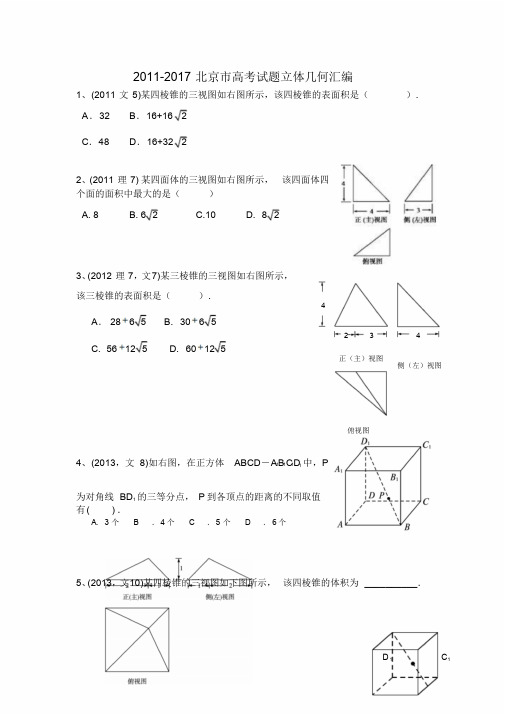
2011-2017 北京市高考试题立体几何汇编1、(2011 文5)某四棱锥的三视图如右图所示,该四棱锥的表面积是(). A.32 B.16+16 2C.48 D.16+32 22、(2011 理7) 某四面体的三视图如右图所示,该四面体四个面的面积中最大的是()A. 8B. 6 2C.10D. 8 23、(2012 理7,文7)某三棱锥的三视图如右图所示,该三棱锥的表面积是().4A.28 6 5 B. 30 6 52 3 4C. 56 12 5D. 60 12 5正(主)视图侧(左)视图俯视图中,P4、(2013,文8)如右图,在正方体ABCD-A1B1C1D1的三等分点,P 到各顶点的距离的不同取值为对角线BD1有( ) .A.3 个 B .4 个 C .5 个 D .6 个5、(2013,文10)某四棱锥的三视图如下图所示,该四棱锥的体积为__________.D1C1A1B11PD CE A B6、(2013,理14)如右图,在棱长为 2 的正方体ABCD A1B1C1D1 中,E 为BC 的中点,点P在线段D1E 上,点P 到直线CC1 的距离的最小值为.7、(2014,理7)在空间直角坐标系Oxyz中,已知A(2,0,0) ,B (2,2,0) ,C (0,2,0) ,D(1,1, ) ,若2 S ,S2 ,S3 分别表示三棱锥 D ABC 在xOy,yOz,zOx 坐标平面上的正1投影图形的面积,则(A)S1 S2 S3 (B)S1 S2 且S1 S3(C)S1 S3 且S2 S3 (D)S2 S3 且S1 S3 2 8、(2014,文11)某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为.9、(2015 理5)某三棱锥的三视图如下图所示,则该三棱锥的表面积是2正(主)视图1 11侧(左)视图A.2 5 B.4 5C.2 2 5 D.5俯视图12正(主)视图1 1 侧(左)视图俯视图10、(2015文7)某四棱锥的三视图如右图所示,该四棱锥最长棱的棱长为(A)1 (B)(B)(D)211、(2016 理6)某三棱锥的三视图如右图所示,则该三棱锥的体积为()A.B.C.D.112、(2016文11)某四棱柱的三视图1如右图所示,则该四棱柱的体积为正(主)视图左(侧)视图________.112俯视图13、(2017 理7)如右图,某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()(A)3 2 (B)2 3(C)2 2 (D) 214、(2017文6)某三棱锥的三视图如图所示,则该三棱锥的体积为()(A)60 (B)30(C)20 (D)1015、(2017 理16)如下图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M 在线段PB上,PD//平面MAC,PA=PD= 6 ,AB=4.(I)求证:M 为PB的中点;(II)求二面角B-P D-A 的大小;(III)求直线MC 与平面BDP所成角的正弦值.316(、2017文18)如图,在三棱锥P–ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D 为线段AC的中点,E为线段PC上一点.(Ⅰ)求证:PA⊥BD;(Ⅱ)求证:平面BDE⊥平面PAC;(Ⅲ)当PA∥平面BDE时,求三棱锥E–BCD的体积.17、(2016 理17)如右图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD= .(Ⅰ)求证:PD⊥平面PAB;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值,若不存在,说明理由.18、(2016文18)如图,在四棱锥P-ABCD 中,PC ⊥平面ABCD ,DC ⊥AC .( Ⅰ) 求证:DC ⊥平面PAC ;( Ⅱ) 求证:平面P A B⊥平面PAC ;(Ⅲ)设点E 为AB 的中点,在棱PB 上是否存在点 F ,使得PA ⊥平面CEF ,说明理由.19、(2015文18)如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC, 且AC=BC= ,O,M 分别为AB,EA的中点。
高考数学的立体几何多选题及答案
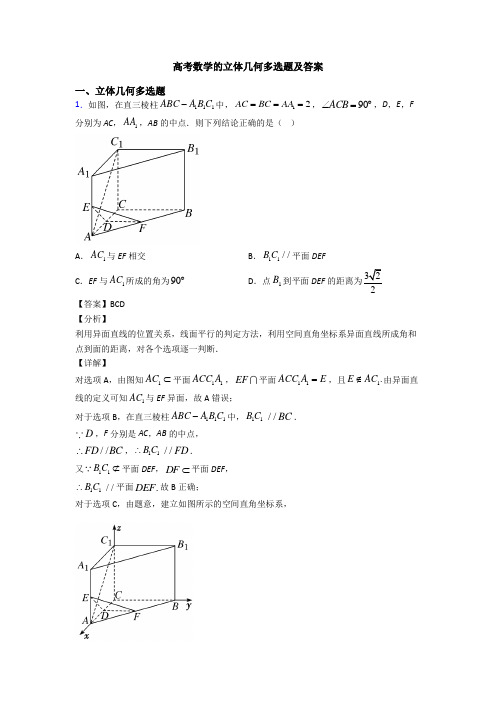
高考数学的立体几何多选题及答案一、立体几何多选题1.如图,在直三棱柱111ABC A B C -中,12AC BC AA ===,90ACB ∠=︒,D ,E ,F分别为AC ,1AA ,AB 的中点.则下列结论正确的是( )A .1AC 与EF 相交B .11//BC 平面DEF C .EF 与1AC 所成的角为90︒D .点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系,线面平行的判定方法,利用空间直角坐标系异面直线所成角和点到面的距离,对各个选项逐一判断. 【详解】对选项A ,由图知1AC ⊂平面11ACC A ,EF 平面11ACC A E =,且1.E AC ∉由异面直线的定义可知1AC 与EF 异面,故A 错误;对于选项B ,在直三棱柱111ABC A B C -中,11B C //BC .D ,F 分别是AC ,AB 的中点, //∴FD BC ,11B C ∴ //FD .又11B C ⊄平面DEF ,DF ⊂平面DEF ,11B C ∴ //平面.DEF 故B 正确;对于选项C ,由题意,建立如图所示的空间直角坐标系,则(0C ,0,0),(2A ,0,0),(0B ,2,0),1(2A ,0,2),1(0B ,2,2),1(0C ,0,2),(1D ,0,0),(2E ,0,1),(1F ,1,0).(1EF ∴=-,1,1)-,1(2AC =-,0,2). 1·2020EF AC =+-=,1EF AC ∴⊥,1EF AC ∴⊥. EF 与1AC 所成的角为90︒,故C 正确;对于选项D ,设向量(n x =,y ,)z 是平面DEF 的一个法向量. (1DE =,0,1),(0DF =,1,0), ∴由n DE n DF ⎧⊥⎨⊥⎩,,,即·0·0n DE n DF ⎧=⎨=⎩,,,得00.x z y +=⎧⎨=⎩,取1x =,则1z =-,(1n ∴=,0,1)-, 设点1B 到平面DEF 的距离为d . 又1(1DB =-,2,2),1·102DB n d n-+∴===, ∴点1B 到平面DEF 的距离为2,故D 正确.故选:BCD 【点睛】本题主要考查异面直线的位置关系,线面平行的判定,异面直线所成角以及点到面的距离,还考查思维能力及综合分析能力,属难题.2.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -所得截面面积为3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.3.已知正方体1111ABCD A B C D -的棱长为2,点E ,F 在平面1111D C B A 内,若||5AE =,AC DF ⊥,则( )A .点E 的轨迹是一个圆B .点F 的轨迹是一个圆C .EF 21-D .AE 与平面1A BD 21530+【答案】ACD 【分析】对于A 、B 、C 、D 四个选项,需要对各个选项一一验证. 选项A :由2211||5AE AA A E =+=1||1A E =,分析得E 的轨迹为圆;选项B :由AC DBF ⊥,而点F 在11B D 上,即F 的轨迹为线段11B D ,; 选项C :由E 的轨迹为圆,F 的轨迹为线段11B D ,可分析得min ||EF d r =-; 选项D :建立空间直角坐标系,用向量法求最值. 【详解】 对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =,即点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上;故A 正确;对于B: 正方体1111ABCD A B C D -中,AC ⊥BD ,又AC DF ⊥,且BD ∩DF=D ,所以AC DBF ⊥,所以点F 在11B D 上,即F 的轨迹为线段11B D ,故B 错误;对于C:在平面1111D C B A 内,1A 到直线11B D 的距离为2,d =当点E ,F 落在11A C 上时,min ||21EF =-;故C 正确; 对于D:建立如图示的坐标系,则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上,可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =,则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1,则()1,1,1n =, 设AE 与平面1A BD 所成角为α,则:22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时,sin α有最大值222153015++=, 故D 正确 故选:CD 【点睛】多项选择题是2020年高考新题型,需要要对选项一一验证.4.在棱长为1的正方体1111ABCD A B C D -中,P 为底面ABCD 内(含边界)一点.( ) A .若13A P =,则满足条件的P 点有且只有一个 B .若12A P =,则点P 的轨迹是一段圆弧 C .若1//A P 平面11B D C ,则1A P 长的最小值为2D .若12A P =且1//A P 平面11B DC ,则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ,B 可利用球的截面小圆的半径来判断;由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD 上,1A P 长的最大值为2;结合以上条件点P 与B 或D 重合,利用12sin 60A P r =︒,求出63r =,进而求出面积. 【详解】对A 选项,如下图:由13A P =,知点P 在以1A 为球心,半径为3的球上,又因为P 在底面ABCD 内(含边界),底面截球可得一个小圆,由1A A ⊥底面ABCD ,知点P 的轨迹是在底面上以A 为圆心的小圆圆弧,半径为22112r A P A A =-=,则只有唯一一点C满足,故A 正确;对B 选项,同理可得点P 在以A 为圆心,半径为22111r A P A A =-=的小圆圆弧上,在底面ABCD 内(含边界)中,可得点P 轨迹为四分之一圆弧BD .故B 正确;对C 选项,移动点P 可得两相交的动直线与平面11B D C 平行,则点P 必在过1A 且与平面11B D C 平行的平面内,由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD上,则1A P 长的最大值为12A B =,则C 不正确; 对选项D ,由以上推理可知,点P 既在以A 为圆心,半径为1的小圆圆弧上,又在线段BD 上,即与B 或D 重合,不妨取点B ,则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆,利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选:ABD 【点睛】(1)平面截球所得截面为圆面,且满足222=R r d +(其中R 为球半径,r 为小圆半径,d 为球心到小圆距离);(2)过定点A 的动直线平行一平面α,则这些动直线都在过A 且与α平行的平面内.5.在三棱锥M ABC -中,下列命题正确的是( ) A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++ C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得.【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.6.在长方体1111ABCD A B C D -中,AB =12AD AA ==,P 、Q 、R 分别是AB 、1BB 、1A C 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系,再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示,建立空间直角坐标系,设(2,,0)P a,0a ⎡∈⎣,(2,)Q b ,[]0,2b ∈,设11A R AC λ=,得到(22,,22)R λλ--,[]0,1λ∈. 1(2,,2)D P a =-,(2,0,)CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;1(22,2)D R λλ=--,12(22)2D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=,解得:15λ=,此时12282()()05555AR D R ---⋅=⋅=,1AR D R ⊥,C 正确;113AC A R =,则44()33R,142()33D R =-,设平面1BDC 的法向量为(,,)n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,n =-,故10n D R ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABCD.【点睛】本题考查了空间向量在立体几何中的应用,是偏难题.7.已知直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==,D 是AC 的中点,O 为1A C 的中点.点P 是1BC 上的动点,则下列说法正确的是( )A .当点P 运动到1BC 中点时,直线1A P 与平面111ABC 5 B .无论点P 在1BC 上怎么运动,都有11A P OB ⊥C .当点P 运动到1BC 中点时,才有1A P 与1OB 相交于一点,记为Q ,且113PQ QA = D .无论点P 在1BC 上怎么运动,直线1A P 与AB 所成角都不可能是30° 【答案】ABD 【分析】构造线面角1PA E ∠,由已知线段的等量关系求1tan EPPA E AE∠=的值即可判断A 的正误;利用线面垂直的性质,可证明11A P OB ⊥即可知B 的正误;由中位线的性质有112PQ QA =可知C 的正误;由直线的平行关系构造线线角为11B A P ∠,结合动点P 分析角度范围即可知D 的正误 【详解】直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==选项A 中,当点P 运动到1BC 中点时,有E 为11B C 的中点,连接1A E 、EP ,如下图示即有EP ⊥面111A B C∴直线1A P 与平面111A B C 所成的角的正切值:1tan EPPA E AE∠= ∵112EP BB =,22111152AE A B B E BB =+= ∴15tan PA E ∠=,故A 正确选项B 中,连接1B C ,与1BC 交于E ,并连接1A B ,如下图示由题意知,11B BCC 为正方形,即有11B C BC ⊥而AB BC ⊥且111ABC A B C -为直三棱柱,有11A B ⊥面11B BCC ,1BC ⊂面11B BCC ∴111A B BC ⊥,又1111A B B C B =∴1BC ⊥面11A B C ,1OB ⊂面11A B C ,故11BC OB ⊥ 同理可证:11A B OB ⊥,又11A B BC B ⋂=∴1OB ⊥面11A BC ,又1A P ⊂面11A BC ,即有11A P OB ⊥,故B 正确选项C 中,点P 运动到1BC 中点时,即在△11A B C 中1A P 、1OB 均为中位线∴Q为中位线的交点∴根据中位线的性质有:112PQQA=,故C错误选项D中,由于11//A B AB,直线1A P与AB所成角即为11A B与1A P所成角:11B A P∠结合下图分析知:点P在1BC上运动时当P在B或1C上时,11B A P∠最大为45°当P在1BC中点上时,11B A P∠最小为23arctan30>=︒∴11B A P∠不可能是30°,故D正确故选:ABD【点睛】本题考查了利用射影定理构造线面角,并计算其正弦值;利用线面垂直证明线线垂直;中位线的性质:中位线交点分中位线为1:2的数量关系;由动点分析线线角的大小8.如图,正方体1111ABCD A B C D-的棱长为1,线段11B D上有两个动点E,F,且2EF=则下列结论正确的是()A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =112213312A BEF BEF V S AO -∆∴=⨯==A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 452FT EF =⨯=⨯=12HG FT ∴== 选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=2AR =由余弦定理得13cos AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.9.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +170【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos AA AC AAC ''==∠=, 所以217042222()105AC '=+-⨯⨯⨯-=.故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.10.半正多面体(semiregularsolid)亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为2,则()A.BF⊥平面EABB.该二十四等边体的体积为20 3C.该二十四等边体外接球的表面积为8πD.PN与平面EBFN所成角的正弦值为2 2【答案】BCD【分析】A用反证法判断;B先补齐八个角成正方体,再计算体积判断;C先找到球心与半径,再计算表面积判断;D先找到直线与平面所成角,再求正弦值判断.【详解】解:对于A,假设A对,即BF⊥平面EAB,于是BF AB⊥,90ABF∠=︒,但六边形ABFPQH为正六边形,120ABF∠=︒,矛盾,所以A错;对于B,补齐八个角构成棱长为2的正方体,则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=,所以B对;对于C,取正方形ACPM对角线交点O,即为该二十四等边体外接球的球心, 其半径为2R =,其表面积为248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS , 所以PN 与平面EBFN 所成角即为PNS ∠, 其正弦值为22PS PN ==,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
北京市部分区高三上学期考试数学分类汇编:立体几何
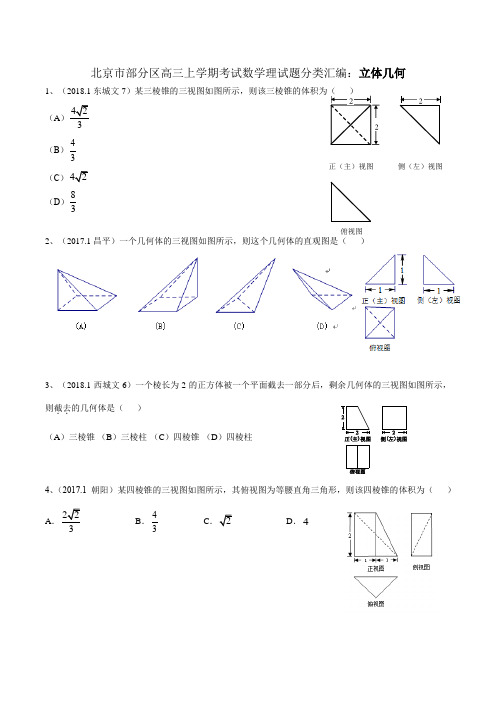
正(主)视图侧(左)视图俯视图北京市部分区高三上学期考试数学理试题分类汇编:立体几何1、(2018.1东城文7(A(B )(C ) (D )2、(2017.1昌平)一个几何体的三视图如图所示,则这个几何体的直观图是( )3、(2018.1西城文6)一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则截去..的几何体是( ) (A)三棱锥 (B )三棱柱 (C )四棱锥 (D)四棱柱4、(2017.1朝阳)某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )AB .43CD .45、(2017.1东城理)某三棱锥的三视图如图所示,则该三棱锥的体积为( )4383(A )23 (B )43 (C )2 (D )836、(2017.1海淀理)若一个几何体由正方体挖去一部分得到,其三视图如图所示,则该几何体的体积为________.7、(2018.1朝阳理5)某四棱锥的三视图如图所示,网格纸上小正方形的边长为1,则该四棱锥的体积为( ) A. 4B.43C.3D.8、(2018.1朝阳理8) 如图1,矩形ABCD 中,AD .点E 在AB 边上, CE DE ⊥且1AE =. 如图2,ADE △沿直线DE 向上折起成1A DE △.记二面角1A DE A --的平面角为θ,当θ()00180∈,时,① 存在某个位置,使1CE DA ⊥; ② 存在某个位置,使1DE AC ⊥;③ 任意两个位置,直线DE 和直线1AC 所成的角都不相等. 以上三个结论中正确的序号是( )A. ①B. ①②C. ①③D. ②③9、(2017.1海淀理)如图,已知正方体1111ABCD A B C D -的棱长为1,,E F 分别是棱AD ,B 1C 1上的动点,设1,AE x B F y ==.若棱.1DD 与平面BEF 有公共点,则x y +的取值范围是( ) A .[0,1]B .13[,]22C .[1,2]D .3[,2]210、(2018.1海淀文8)已知正方体1111-ABCD A BC D 的棱长为2,,M N 分别是棱11、BC C D 的中点,点P 在平面1111A B C D 内,点Q 在线段1A N 上.若=PM PQ 长度的最小值为 ( )(A)1 (B(C)15- (D)511、(2018.1海淀理)已知正方体1111ABCD A B C D -的棱长为M 是棱BC 的中点,点P 在底面ABCD 内,点Q 在线段11AC 上.若1PM =,则PQ 长度的最小值为 .A。
2011-2020北京10年高考解答题立体几何分类汇编

立体几何1.(2011文)如图,在四面体PABC 中,PC AB ⊥,PA BC ⊥,点,,,D E F G 分别为,,,AP AC BC PB 的中点.(Ⅰ)求证:DE ∥平面BCP ; (Ⅱ)求证:四边形DEFG 为矩形;(Ⅲ)是否存在点Q ,到四面体PABC 六条棱的中点的距离相等?说明理由.2.(2012文)如图1,在Rt ABC ∆中,90C ∠=,,D E 分别为,AC AB 的中点,点F 为线段CD 上的一点,将ADE ∆沿DE 折起到1A DE ∆的位置,使1A F CD ⊥,如图2. (Ⅰ)求证:DE ∥平面1ACB ; (Ⅱ)求证:1A F BE ⊥;(Ⅲ)线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ ?说明理由.FGDECA PBACB FD EE DF A 'BC图1图23.(2013文)如图,在四棱锥P ABCD -中,AB CD ∥,AB AD ⊥,2CD AB =,平面PAD ⊥底面ABCD ,PA AD ⊥,E 和F 分别是CD 和PC 的中点,求证: (Ⅰ)PA ⊥底面ABCD ; (Ⅱ)BE ∥平面PAD ;(Ⅲ)平面BEF ⊥平面PCD .4.(2014文)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面,AB BC ⊥,12AA AC ==,1BC =,,E F分别是11,AC BC 的中点.(Ⅰ)求证:平面ABE ⊥平面11B BCC ; (Ⅱ)求证:1C F ∥平面ABE ; (Ⅲ)求三棱锥E ABC -的体积.A DC BEPF ABCFA 1B 1C 1E5.(2015文)如图,在三棱锥V ABC -中,平面VAB ⊥平面ABC ,三角形VAB 为等边三角形,AC BC ⊥,且AC BC ==,O M 分别为,AB VA 的中点. (Ⅰ)求证:VB ∥平面MOC ;(Ⅱ)求证:平面MOC ⊥平面VAB ; (Ⅲ)求三棱锥V ABC -的体积.6.(2016文)如图,在四棱锥P ABCD -中,PC ⊥平面ABCD ,AB DC ∥,DC AC ⊥. (Ⅰ)求证:DC ⊥平面PAC ;(Ⅱ)求证:平面PAB ⊥平面PAC ;(Ⅲ)设点E 为AB 的中点,在棱PB 上是否存在点F ,使得PA ∥平面CEF ?说明理由.7.(2017文)如图,在三棱锥P ABC -中,PA AB ⊥,PA BC ⊥,AB BC ⊥,2PA AB BC ===,D 为线段AC 的中点,E 为线段PC 上一点. (Ⅰ)求证:PA BD ⊥;(Ⅱ)求证:平面BDE ⊥平面PAC ;(Ⅲ)当PA ∥平面BDE 时,求三棱锥E BCD -的体积.VACBOMDE PABCD8.(2018文)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,,E F 分别为,AD PB 的中点. (Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ; (Ⅲ)求证:EF ∥平面PCD .9.(2019文)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为菱形,E 为CD 的中点. (Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若60ABC ∠=︒,求证;平面PAB ⊥平面PAE ;(Ⅲ)棱PB 上是否存在点F ,使得CF ∥平面PAE ?说明理由.10.(2010理)如图,正方形ABCD 和四边形ACEF 所在的平面互相垂直,CE AC ⊥,EF AC ∥,AB =1CE EF ==.(Ⅰ)求证:AF ∥平面BDE ; (Ⅱ)求证:CF ⊥平面BDE ; (Ⅲ)求二面角A BE D --的大小.PABCEFDPABDCE EFDCB11.(2011理)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2AB =,60BAD ∠=︒. (Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若PA AB =,求PB 与AC 所成角的余弦值; (Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.12.(2012理)如图1,在Rt ABC ∆中,90C ∠=︒,3BC =,6AC =,D 、E 分别为AC 、AB 上的点,且DE BC ∥,2DE =,将ADE ∆沿DE 折起到1A DE ∆的位置,使1AC CD ⊥,如图2. (Ⅰ)求证:1A C ⊥平面BCDE ;(Ⅱ)若M 是1A D 的中点,求CM 与平面1A BE 所成角的大小;(Ⅲ)线段BC 上是否存在点P ,使平面1A DP 与平面1A BE 垂直?说明理由.PABCD图2图1CBA 'DE E DB CAM13.(2013理)如图,在三棱柱111ABC A B C -中,11AA C C 是边长为4的正方形.平面ABC ⊥平面11AA C C ,3AB =,5BC =.(Ⅰ)求证:1AA ⊥平面ABC ; (Ⅱ)求二面角111A BC B --的余弦值;(Ⅲ)证明:在线段1BC 存在点D ,使得1AD A B ⊥,并求1BDBC 的值.14.(2014理)如图,正方形AMDE 的边长为2,,B C 分别为,AM MD 的中点,在五棱锥P ABCDE -中,F 为棱PE 的中点,平面ABF 与棱,PD PC 分别交于点,GH . (Ⅰ)求证:AB FG ; (Ⅱ)若PA ⊥底面ABCDE ,且PA AE =,求直线BC 与平面ABF 所成角的大小,并求线段PH 的长.ABCA 1B 1C 1BACMDEPG HF15.(2015理)如图,在四棱锥A EFCB -中,AEF ∆为等边三角形,平面AEF ⊥平面EFCB ,EF BC ∥,4BC =,2EF a =,60EBC FCB ∠==︒,O 为EF 的中点. (Ⅰ)求证:AO BE ⊥;(Ⅱ)求二面角F AE B --的余弦值; (Ⅲ)若BE ⊥平面AOC ,求a 的值.16.(2016理)如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,AB AD ⊥,1AB =,2AD =,AC CD =(Ⅰ)求证:PD ⊥平面PAB ;(Ⅱ)求直线PB 与平面PCD 所成角的正弦值;(Ⅲ)在棱PA 上是否存在点M ,使得BM ∥平面PCD ?若存在,求AMAP的值,若不存在,说明理由.AEBCF O PADBC17.(2017理)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,PD ∥平面MAC,PA PD ==4AB =. (Ⅰ)求证:M 为PB 的中点; (Ⅱ)求二面角B PD A --的大小;(Ⅲ)求直线MC 与平面BDP 所成角的正弦值.18.(2018理)如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,,,,D E F G 分别为1111,,,AA AC AC BB 的中点,AB BC ==,12AC AA ==. (Ⅰ)求证:AC ⊥平面BEF ; (Ⅱ)求二面角1B CD C --的余弦值; (Ⅲ)证明:直线FG 与平面BCD 相交.PABCDMAB C DFGEB 1A 1C 119.(2019理)如图,在四棱锥P ABCD -中,PA ABCD ⊥平面,AD CD ⊥,BC AD ∥,2PA AD CD ===,3BC =.E 为PD 的中点,点F 在PC 上,且13PF PC =. (Ⅰ)求证:CD PAD ⊥平面;(Ⅱ)求二面角F AE P --的余弦值; (Ⅲ)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由.20.(2020)如图,在正方体1111ABCD A B C D -中,E 为1BB 的中点.(Ⅰ)求证:1BC ∥平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.P ADCBEFGD 1AC 1A 1B 1BCDE。
(北京卷)十年真题(2010_2019)高考数学真题分类汇编专题09立体几何文(含解析)
专题09立体几何历年考题细目表历年高考真题汇编【2018年北京文科06】某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()1.A.1 B.2 C.3 D.4【解答】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,AC,CD,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△PAB,△PBC,△PAD.故选:C.2.【2017年北京文科06】某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60 B.30 C.20 D.10【解答】解:由三视图可知:该几何体为三棱锥,该三棱锥的体积10.故选:D.3.【2015年北京文科07】某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1 B.C.D.2【解答】解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,底面为正方形如图:其中PB⊥平面ABCD,底面ABCD为正方形∴PB=1,AB=1,AD=1,∴BD,PD.PC═该几何体最长棱的棱长为:故选:C.4.【2013年北京文科08】如图,在正方体ABCD﹣A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有()A.3个B.4个C.5个D.6个【解答】解:建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=3,则A(3,0,0),B(3,3,0),C(0,3,0),D(0,0,0),A1(3,0,3),B1(3,3,3),C1(0,3,3),D1(0,0,3),∴(﹣3,﹣3,3),设P(x,y,z),∵(﹣1,﹣1,1),∴(2,2,1).∴|PA|=|PC|=|PB1|,|PD|=|PA1|=|PC1|,|PB|,|PD1|.故P到各顶点的距离的不同取值有,3,,共4个.故选:B.5.【2012年北京文科07】某三棱锥的三视图如图所示,该三棱锥的表面积是()A.28+6B.30+6C.56+12D.60+12【解答】解:三视图复原的几何体是底面为直角边长为4和5的三角形,一个侧面垂直底面的等腰三角形,高为4,底边长为5,如图,所以S底10,S后,S右10,S左6.几何体的表面积为:S=S底+S后+S右+S左=30+6.故选:B.6.【2011年北京文科05】某四棱锥的三视图如图所示,该四棱锥的表面积是()A.16B.16+16C.32D.16+32【解答】解:由已知中的三视力可得该几何体是一个四棱锥,棱锥的底面边长为4,故底面面积为16,棱锥的高为2,故侧面的高为:2,则每个侧面的面积为: 4,故棱锥的表面积为:16+16,故选:B.7.【2010年北京文科05】一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所,则该几何体的俯视图为()A.B.C.D.【解答】解:由正视图可知去掉的长方体在正视线的方向,从侧视图可以看出去掉的长方体在原长方体的左侧,由以上各视图的描述可知其俯视图符合C选项.故选:C.8.【2010年北京文科08】如图,正方体ABCD﹣A1B1C1D1的棱长为2,动点E、F在棱A1B1上.点Q是CD的中点,动点P在棱AD上,若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P﹣EFQ的体积()A.与x,y都有关B.与x,y都无关C.与x有关,与y无关D.与y有关,与x无关【解答】解:三棱锥P﹣EFQ的体积与点P到平面EFQ的距离和三角形EFQ的面积有关,由图形可知,平面EFQ与平面CDA1B1是同一平面,故点P到平面EFQ的距离是P到平面CDA1B1的距离,且该距离就是P到线段A1D的距离,此距离只与x有关,因为EF=1,点Q到EF的距离为线段B1C的长度,为定值,综上可知所求三棱锥的体积只与x有关,与y无关.故选:C.9.【2019年北京文科12】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为l,那么该几何体的体积为.【解答】解:由三视图还原原几何体如图,该几何体是把棱长为4的正方体去掉一个四棱柱,则该几何体的体积V.故答案为:40.10.【2019年北京文科13】已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:.【解答】解:由l,m是平面α外的两条不同直线,知:由线面平行的判定定理得:若l⊥α,l⊥m,则m∥α.故答案为:若l⊥α,l⊥m,则m∥α.11.【2016年北京文科11】某四棱柱的三视图如图所示,则该四棱柱的体积为.【解答】解:由已知中的三视图可得:该几何体上部是一个以俯视图为底面四棱柱,棱柱的底面面积S(1+2)×1,棱柱的高为1,故棱柱的体积V,故答案为:12.【2014年北京文科11】某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为.【解答】解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=1;由主视图知CD=2,由左视图知BE=1,在Rt△BCE中,BC,在Rt△BCD中,BD,在Rt△ACD中,AD=2.则三棱锥中最长棱的长为2.故答案为:2.13.【2013年北京文科10】某四棱锥的三视图如图所示,该四棱锥的体积为.【解答】解:几何体为底面边长为3的正方形,高为1的四棱锥,所以体积.故答案为:3.14.【2019年北京文科18】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.【解答】证明:(Ⅰ)∵四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∴BD⊥PA,BD⊥AC,∵PA∩AC=A,∴BD⊥平面PAC.(Ⅱ)∵在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点,∠ABC=60°,∴AB⊥AE,PA⊥AE,∵PA∩AB=A,∴AE⊥平面PAB,∵AE⊂平面PAE,∴平面PAB⊥平面PAE.解:(Ⅲ)棱PB上是存在中点F,使得CF∥平面PAE.理由如下:取AB中点G,连结GF,CG,∵在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点,∴CG∥AE,FG∥PA,∵CG∩FG=G,AE∩PA=A,∴平面CFG∥平面PAE,∵CF⊂平面CFG,∴CF∥平面PAE.15.【2018年北京文科18】如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.(Ⅰ)求证:PE⊥BC;(Ⅱ)求证:平面PAB⊥平面PCD;(Ⅲ)求证:EF∥平面PCD.【解答】证明:(Ⅰ)PA=PD,E为AD的中点,可得PE⊥AD,底面ABCD为矩形,可得BC∥AD,则PE⊥BC;(Ⅱ)由于平面PAB和平面PCD有一个公共点P,且AB∥CD,在平面PAB内过P作直线PG∥AB,可得PG∥CD,即有平面PAB∩平面PCD=PG,由平面PAD⊥平面ABCD,又AB⊥AD,可得AB⊥平面PAD,即有AB⊥PA,PA⊥PG;同理可得CD⊥PD,即有PD⊥PG,可得∠APD为平面PAB和平面PCD的平面角,由PA⊥PD,可得平面PAB⊥平面PCD;(Ⅲ)取PC的中点H,连接DH,FH,在三角形PCD中,FH为中位线,可得FH∥BC,FH BC,由DE∥BC,DE BC,可得DE=FH,DE∥FH,四边形EFHD为平行四边形,可得EF∥DH,EF⊄平面PCD,DH⊂平面PCD,即有EF∥平面PCD.16.【2017年北京文科18】如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA∥平面BDE时,求三棱锥E﹣BCD的体积.【解答】解:(1)证明:由PA⊥AB,PA⊥BC,AB⊂平面ABC,BC⊂平面ABC,且AB∩BC=B,可得PA⊥平面ABC,由BD⊂平面ABC,可得PA⊥BD;(2)证明:由AB=BC,D为线段AC的中点,可得BD⊥AC,由PA⊥平面ABC,PA⊂平面PAC,可得平面PAC⊥平面ABC,又平面PAC∩平面ABC=AC,BD⊂平面ABC,且BD⊥AC,即有BD⊥平面PAC,BD⊂平面BDE,可得平面BDE⊥平面PAC;(3)PA∥平面BDE,PA⊂平面PAC,且平面PAC∩平面BDE=DE,可得PA∥DE,又D为AC的中点,可得E为PC的中点,且DE PA=1,由PA⊥平面ABC,可得DE⊥平面ABC,可得S△BDC S△ABC2×2=1,则三棱锥E﹣BCD的体积为DE•S△BDC1×1.17.【2016年北京文科18】如图,在四棱锥P﹣ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.(1)求证:DC⊥平面PAC;(2)求证:平面PAB⊥平面PAC;(3)设点E为AB的中点,在棱PB上是否存在点F,使得PA∥平面CEF?说明理由.【解答】(1)证明:∵PC⊥平面ABCD,DC⊂平面ABCD,∴PC⊥DC,∵DC⊥AC,PC∩AC=C,∴DC⊥平面PAC;(2)证明:∵AB∥DC,DC⊥AC,∴AB⊥AC,∵PC⊥平面ABCD,AB⊂平面ABCD,∴PC⊥AB,∵PC∩AC=C,∴AB⊥平面PAC,∵AB⊂平面PAB,∴平面PAB⊥平面PAC;(3)解:在棱PB上存在中点F,使得PA∥平面CEF.∵点E为AB的中点,∴EF∥PA,∵PA⊄平面CEF,EF⊂平面CEF,∴PA∥平面CEF.18.【2015年北京文科18】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC 且AC=BC,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB(3)求三棱锥V﹣ABC的体积.【解答】(1)证明:∵O,M分别为AB,VA的中点,∴OM∥VB,∵VB⊄平面MOC,OM⊂平面MOC,∴VB∥平面MOC;(2)∵AC=BC,O为AB的中点,∴OC⊥AB,∵平面VAB⊥平面ABC,OC⊂平面ABC,∴OC⊥平面VAB,∵OC⊂平面MOC,∴平面MOC⊥平面VAB(3)在等腰直角三角形ACB中,AC=BC,∴AB=2,OC=1,∴S△VAB,∵OC⊥平面VAB,∴V C﹣VAB•S△VAB,∴V V﹣ABC=V C﹣VAB.19.【2014年北京文科17】如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点.(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥E﹣ABC的体积.【解答】解:(1)证明:∵三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,∴BB1⊥AB,∵AB⊥BC,BB1∩BC=B,BB1,BC⊂平面B1BCC1,∴AB⊥平面B1BCC1,∵AB⊂平面ABE,∴平面ABE⊥平面B1BCC1;(Ⅱ)证明:取AB中点G,连接EG,FG,则∵F是BC的中点,∴FG∥AC,FG AC,∵E是A1C1的中点,∴FG∥EC1,FG=EC1,∴四边形FGEC1为平行四边形,∴C1F∥EG,∵C1F⊄平面ABE,EG⊂平面ABE,∴C1F∥平面ABE;(3)解:∵AA1=AC=2,BC=1,AB⊥BC,∴AB,∴V E﹣ABC S△ABC•AA1(1)×2.20.【2013年北京文科17】如图,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点,求证:(Ⅰ)PA⊥底面ABCD;(Ⅱ)BE∥平面PAD;(Ⅲ)平面BEF⊥平面PCD.【解答】解:(Ⅰ)∵PA⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,由平面和平面垂直的性质定理可得PA⊥平面ABCD.(Ⅱ)∵AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点,故四边形ABED为平行四边形,故有BE∥AD.又AD⊂平面PAD,BE不在平面PAD内,故有BE∥平面PAD.(Ⅲ)平行四边形ABED中,由AB⊥AD可得,ABED为矩形,故有BE⊥CD①.由PA⊥平面ABCD,可得PA⊥AB,再由AB⊥AD可得AB⊥平面PAD,∴CD⊥平面PAD,故有CD⊥PD.再由E、F分别为CD和PC的中点,可得EF∥PD,∴CD⊥EF②.而EF和BE是平面BEF内的两条相交直线,故有CD⊥平面BEF.由于CD⊂平面PCD,∴平面BEF⊥平面PCD.21.【2012年北京文科16】如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【解答】解:(1)∵D,E分别为AC,AB的中点,∴DE∥BC,又DE⊄平面A1CB,∴DE∥平面A1CB.(2)由已知得AC⊥BC且DE∥BC,∴DE⊥AC,∴DE⊥A1D,又DE⊥CD,∴DE⊥平面A1DC,而A1F⊂平面A1DC,∴DE⊥A1F,又A1F⊥CD,∴A1F⊥平面BCDE,∴A1F⊥BE.(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.∵DE∥BC,∴DE∥PQ.∴平面DEQ即为平面DEP.由(Ⅱ)知DE⊥平面A1DC,∴DE⊥A1C,又∵P是等腰三角形DA1C底边A1C的中点,∴A1C⊥DP,∴A1C⊥平面DEP,从而A1C⊥平面DEQ,故线段A1B上存在点Q,使A1C⊥平面DEQ.22.【2011年北京文科17】如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.(Ⅰ)求证:DE∥平面BCP;(Ⅱ)求证:四边形DEFG为矩形;(Ⅲ)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.【解答】证明:(Ⅰ)∵D,E分别为AP,AC的中点,∴DE∥PC,∵DE⊄平面BCP,∴DE∥平面BCP.(Ⅱ)∵D,E,F,G分别为AP,AC,BC,PB的中点,∴DE∥PC∥FG,DG∥AB∥EF∴四边形DEFG为平行四边形,∵PC⊥AB,∴DE⊥DG,∴四边形DEFG为矩形.(Ⅲ)存在点Q满足条件,理由如下:连接DF,EG,设Q为EG的中点,由(Ⅱ)知DF∩EG=Q,且QD=QE=QF=QG EG,分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN,与(Ⅱ)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM=QN EG,∴Q为满足条件的点.23.【2010年北京文科17】如图,正方形ABCD和四边形ACEF所在的平面互相垂直.EF∥AC,AB,CE =EF=1.(Ⅰ)求证:AF∥平面BDE;(Ⅱ)求证:CF⊥平面BDE.【解答】证明:(Ⅰ)设AC于BD交于点G.因为EF∥AG,且EF=1,AG AC=1,所以四边形AGEF为平行四边形,所以AF∥EG,因为EG⊂平面BDE,AF⊄平面BDE,所以AF∥平面BDE.(Ⅱ)连接FG.因为EF∥CG,EF=CG=1,且CE=1,所以平行四边形CEFG为菱形.所以CF⊥EG.因为四边形ABCD为正方形,所以BD⊥AC.又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG=G,所以CF⊥平面BDE.考题分析与复习建议本专题考查的知识点为:空间几何体的结构、三视图和直观图,空间几何体的表面积与体积,空间点、直线、平面之间的位置关系,直线、平面平行、垂直的判定与性质,空间向量及其运算,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等.历年考题主要以选择填空或解答题题型出现,重点考查的知识点为:三视图和直观图,空间几何体的表面积与体积,直线、平面平行、垂直的判定与性质,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等.预测明年本考点题目会比较稳定,备考方向以知识点三视图和直观图,空间几何体的表面积与体积,直线、平面平行、垂直的判定与性质,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等为重点较佳.最新高考模拟试题AD与BD所成的角为()1.在正方体中, 1A.45?B.90C.60D.120【答案】C【解析】如图,连结BC1、BD和DC1,在正方体ABCD-A1B1C1D1中,由AB=D 1C 1,AB ∥D 1C 1,可知AD 1∥BC 1,所以∠DBC 1就是异面直线AD 1与BD 所成角,在正方体ABCD-A 1B 1C 1D 1中,BC 1、BD 和DC 1是其三个面上的对角线,它们相等.所以△DBC 1是正三角形,∠DBC 1=60°故异面直线AD 1与BD 所成角的大小为60°.故选:C .2.在正方体中,用空间中与该正方体所有棱成角都相等的平面α去截正方体,在截面边数最多时的所有多边形中,多边形截面的面积为S ,周长为l ,则( )A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值【答案】C【解析】正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:与面1A BD 平行的面且截面是六边形时满足条件,不失一般性设正方体边长为1,即六边形EFGHMN ,其中分别为其所在棱的中点,由正方体的性质可得EF =∴六边形的周长l 为定值∴六边形的面积为,由正方体的对称性可得其余位置时也为正六边形,周长与面积不变,故S 与l 均为定值,故选C.3.在四面体P ABC -中,ABC ∆为等边三角形,边长为3,3PA =,4PB =,5PC =,则四面体P ABC -的体积为( )A .3B .C D【答案】C【解析】如图,延长CA 至D ,使得3AD =,连接,DB PD ,因为,故ADB ∆为等腰三角形,又,故,所以即,故CB DB ⊥,因为,所以,所以CB PB ⊥,因,DB ⊂平面PBD ,PB ⊂平面PBD ,所以CB ⊥平面PBD ,所以,因A 为DC 的中点,所以,因为,故PDC ∆为直角三角形,所以,又,而4PB =,故即PBD ∆为直角三角形,所以,所以,故选C.4.若,a b 是不同的直线,,αβ是不同的平面,则下列命题中正确的是( )A .若,则αβ⊥B .若,则αβ‖C .若,则αβ‖D .若,则αβ‖【答案】C【解析】A 中,若,平面,αβ可能垂直也可能平行或斜交,不正确;B 中,若,平面,αβ可能平行也可能相交,不正确;C 中,若,a b αβ⊥⊥,则,a b 分别是平面,αβ的法线,a b ‖必有αβ‖,正确;D 中,若,平面,αβ可能平行也可能相交,不正确.故选C.5.某几何体的三视图如图所示,则该几何体的外接球的体积是( )A .3B .2C .3πD .【答案】B【解析】解:根据几何体的三视图,该几何体是由一个正方体切去一个正方体的一角得到的.故:该几何体的外接球为正方体的外接球,所以:球的半径,则:. 故选:B .6.如图,正方体中,E 为棱1BB 的中点,用过点A 、E 、1C 的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )A .B .C .D .【答案】A【解析】解:正方体中,过点1,,A E C 的平面截去该正方体的上半部分后,剩余部分的直观图如图:则该几何体的正视图为图中粗线部分.故选:A.7.下列说法错误的是()A.垂直于同一个平面的两条直线平行B.若两个平面垂直,则其中一个平面内垂直于这两个平面交线的直线与另一个平面垂直C.一个平面内的两条相交直线均与另一个平面平行,则这两个平面平行D.一条直线与一个平面内的无数条直线垂直,则这条直线和这个平面垂直【答案】D【解析】由线面垂直的性质定理知,垂直于同一个平面的两条直线平行,A正确;由面面垂直的性质定理知,若两个平面垂直,则其中一个平面内垂直于这两个平面交线的直线与另一个平面垂直,B正确;由面面平行的判定定理知,一个平面内的两条相交直线均与另一个平面平行,则这两个平面平行,C正确;当一条直线与平面内无数条相互平行的直线垂直时,该直线与平面不一定垂直,D错误,故选D.-中,8.《九章算术》中,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的四棱锥P ABCD=,点E,F分别为PC,PD的中点,则图中的PD⊥平面ABCD,底面ABCD是正方形,且PD CD鳖臑有()A.2个B.3个C.4个D.5个【答案】C【解析】由题意,因为PD ⊥底面ABCD ,所以PD DC ^,PD BC ⊥,又四边形ABCD 为正方形,所以BC CD ⊥,所以BC ⊥平面PCD ,BC PC ⊥,所以四面体PDBC 是一个鳖臑,因为DE ⊂平面PCD ,所以BC DE ⊥,因为PD CD =,点E 是PC 的中点,所以DE PC ⊥,因为,所以DE ⊥平面PBC ,可知四面体EBCD 的四个面都是直角三角形,即四面体EBCD 是一个鳖臑,同理可得,四面体PABD 和FABD 都是鳖臑,故选C.9.在三棱锥P ABC -中,平面PAB ⊥平面ABC ,ABC △是边长为6的等边三角形,PAB △是以AB 为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______.【答案】48π【解析】如图,在等边三角形ABC 中,取AB 的中点F ,设其中心为O ,由6AB =,得,PAB ∆是以AB 为斜边的等腰角三角形,PF AB ∴⊥,又因为平面PAB ⊥平面ABC ,PF ∴⊥平面 ABC ,PF OF ∴⊥,,则O 为棱锥P ABC -的外接球球心,外接球半径,∴该三棱锥外接球的表面积为,故答案为48π. 10.若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为3,圆心角为23π的扇形,则该圆锥的体积为_______.【答案】3【解析】因为展开图是半径为3,圆心角为23π的扇形,所以圆锥的母线3l =,圆锥的底面的周长为,因此底面的半径1r =,根据勾股定理,可知圆锥的高, 所以圆锥的体积为.11.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列正确命题序号是_____.(1)若m α,n α∥,则m n ∥(2)若m α⊥,m n ⊥则n α∥(3)若m α⊥,n β⊥且m n ⊥,则αβ⊥;(4)若m β⊂,αβ,则m α【答案】(3)(4)【解析】若,则m 与n 可能平行,相交或异面,故(1)错误; 若则n α∥或n α⊂,故(2)错误; 若且m n ⊥,则αβ⊥,故(3)正确; 若,由面面平行的性质可得m α,故(4)正确; 故答案为:(3)(4)12.长方体的底面ABCD 是边长为1的正方形,若在侧棱1AA 上存在点E ,使得,则侧棱1AA 的长的最小值为_______.【答案】2【解析】设侧棱AA 1的长为x ,A 1E =t ,则AE =x ﹣t ,∵长方体ABCD ﹣A 1B 1C 1D 1的底面是边长为1的正方形,∠C 1EB =90°,∴, ∴2+t 2+1+(x ﹣t )2=1+x 2,整理,得:t 2﹣xt+1=0,∵在侧棱AA 1上至少存在一点E ,使得∠C 1EB =90°,∴△=(﹣x )2﹣4≥0,解得x≥2.∴侧棱AA 1的长的最小值为2.故答案为2.13.如图,在Rt ABC ∆中,1AB BC ==,D 和E 分别是边BC 和AC 上一点,DE BC ⊥,将C D E ∆沿DE 折起到点P 位置,则该四棱锥P ABDE -体积的最大值为_______.【解析】在Rt ABC ∆中,由已知,1AB BC ==,DE BC ⊥,所以设, 四边形ABDE 的面积为,当CDE ∆⊥平面ABDE 时,四棱锥P ABDE -体积最大,此时,且,故四棱锥P ABDE -体积为,,0,3x ⎛∈ ⎝⎭时,0V '> ;时,0V '<,所以,当3x =时,max 27V =.14.三棱锥P ABC -的4的球面上,PA ⊥平面ABC ,V ABC 的正三角形,则点A 到平面PBC 的距离为______. 【答案】65【解析】△ABC 的正三角形,可得外接圆的半径2r a sin60==︒2,即r =1. ∵PA ⊥平面ABC ,PA =h ,球心到底面的距离d 等于三棱锥的高PA 的一半即h 2,那么球的半径R ,解得h=2,又由知,得'65d = 故点A 到平面PBC 的距离为65故答案为65. 15.如图,该几何体由底面半径相同的圆柱与圆锥两部分组成,且圆柱的高与底面半径相等.若圆柱与圆锥的侧面积相等,则圆锥与圆柱的高之比为_______.【解析】设圆柱和圆锥的底面半径为R ,则圆柱的高1h =R ,圆锥的母线长为L ,因为圆柱与圆锥的侧面积相等,所以,,解得:L =2R ,得圆锥的高为2h ,所以,圆锥与圆柱的高之比为R=16.直三棱柱中,,设其外接球的球心为O ,已知三棱锥O ABC -的体积为1,则球O 表面积的最小值为__________.【答案】16π.【解析】如图,在Rt ABC ∆中,设,则.分别取11,AC A C 的中点12,O O ,则12,O O 分别为111Rt A B C ∆和Rt ABC ∆外接圆的圆心,连12,O O ,取12O O 的中点O ,则O 为三棱柱外接球的球心.连OA ,则OA 为外接球的半径,设半径为R .∵三棱锥O ABC -的体积为1,即,∴6ac =.在2Rt OO C ∆中,可得,∴,当且仅当a c =时等号成立,∴O 球表面积的最小值为16π.故答案为:16π.17.在三棱锥P ABC -中,ABC ∆是边长为4的等边三角形,,PC =(1)求证:平面PAB ⊥平面ABC ;(2)若点M ,N 分别为棱BC ,PC 的中点,求三棱锥N AMC -的体积V .【答案】(1)见证明;(2) V【解析】(1)取AB 中点H ,连结PH ,HC .∵,4AB =,∴PH AB ⊥,PH =∵等边ABC ∆的边长为4∴HC =PC =∴∴90PHC ∠=,即PH HC ⊥又∵,AB Ì平面ABC ,CH ⊂平面ABC∴PH ⊥平面ABC ,又PH ⊂平面PAB∴平面PAB ⊥平面ABC(2)∵点M ,N 分别为棱BC ,PC 的中点∴点N 到平面ABC 的距离为12PH 且∴三棱锥N AMC -的体积18.如图所示,三棱柱中,90BCA ∠=°,1AC ⊥平面1A BC .(1)证明:平面ABC ⊥平面11ACC A ;(2)若,11A A A C =,求点1B 到平面1A BC 的距离.【答案】(1)见解析;(2【解析】(1)证明:1AC ⊥平面1A BC ,.,,BC ∴⊥平面11ACC A .又BC ⊂平面ABC ,∴平面ABC ⊥平面11ACC A .(2)解:取AC 的中点D ,连接1A D .,.又平面ABC ⊥平面11ACC A ,且交线为AC ,则1A D ⊥平面ABC .1AC ⊥平面1A BC ,,∴四边形11ACC A 为菱形,.又11A A A C =,1A AC ∴是边长为2正三角形,1A D ∴=.面11BB C C ,1BB ⊂面11BB C C1AA ∴面11BB C C设点1B 到平面1A BC 的距离为h .则.,,h ∴=所以点1B 到平面1A BC19.在边长为3的正方形ABCD 中,点E ,F 分别在边AB ,BC 上(如左图),且=BE BF ,将AED ,DCF 分别沿DE ,DF 折起,使A ,C 两点重合于点A ¢(如右图).(1)求证:A D EF '⊥;(2)当13BF BC =时,求点A ¢到平面DEF 的距离.【答案】(1)见解析;(2)5 【解析】(1)由ABCD 是正方形及折叠方式,得:A E A D '⊥',A F A D '⊥',,A D ∴'⊥平面A EF ',平面A EF ',.(2),,,52DEF S ∴= 设点A ¢到平面DEF 的距离为d ,,,解得5d =.∴点A ¢到平面DEF . 20.如图,四棱锥S ABCD -中,SD ⊥平面ABCD ,//AB CD ,AD CD ⊥,SD CD =,AB AD =,2CD AD =,M 是BC 中点,N 是SA 上的点.(1)求证://MN 平面SDC ;(2)求A 点到平面MDN 的距离.【答案】(1)见证明;(2)127d =【解析】(1)取AD 中点为E ,连结ME ,NE ,则//ME DC ,因为ME ⊄平面SDC ,所以//ME 平面SDC ,同理//NE 平面SDC .所以平面//MNE 平面SDC ,从而因此//MN 平面SDC .(2)因为CD AD ⊥,所以ME AD ⊥.因为SD ⊥平面ABCD ,所以SD CD ⊥,ME SD ⊥.所以ME ⊥平面SAD .设2DA =,则3ME =,2NE =,,MD =,ND =在MDN ∆中,由余弦定理,从而,所以MDN ∆面积为72. 又ADM ∆面积为12332⨯⨯=. 设A 点到平面MDN 的距离为d ,由得732d NE =, 因为2NE =,所以A 点到平面MDN 的距离127d =.21.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,PA =//AB CD ,AB AD ⊥,,2AB =,E 为侧棱PA 上一点. (Ⅰ)若13PE PA =,求证:PC //平面EBD ; (Ⅱ)求证:平面EBC ⊥平面PAC ;(Ⅲ)在侧棱PD 上是否存在点F ,使得AF ⊥平面PCD ?若存在,求出线段PF 的长;若不存在,请说明理由.【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)存在,线段PF 长32. 【解析】(Ⅰ)设,连结EG ,由已知AB//CD ,DC 1=,AB 2=,得. 由1PE PA 3=,得AE2EP =.在ΔPAC 中,由AEAGEP GC =,得EG //PC .因为EG ⊂平面EBD ,PC ⊄平面EBD ,所以PC //平面EBD .(Ⅱ)因为PA ⊥平面ABCD ,BC ⊂平面ABCD ,所以BC PA ⊥.由已知得AC =BC =AB 2=,所以.所以BC AC ⊥.又,所以BC ⊥平面PAC .因为BC ⊂平面EBC ,所以平面EBC ⊥平面PAC .(Ⅲ)在平面PAD 内作AF PD ⊥于点F ,由DC PA ⊥,DC AD ⊥,,得DC ⊥平面PAD .因为AF ⊂平面PAD ,所以CD AF ⊥.又,所以AF ⊥平面PCD .由PA =AD 1=,PA AD ⊥, 得3PF 2=. 22.已知三棱柱的底面ABC 是等边三角形,侧面AA C C ''⊥底面ABC ,D 是棱BB '的中点.(1)求证:平面DA C '⊥平面ACC A '';(2)求平面DA C '将该三棱柱分成上下两部分的体积比.【答案】(1)见证明;(2)1:1【解析】(1)取,AC A C ''的中点,O F ,连接OF 与C A '交于点E , 连接DE ,,OB B F ',则E 为OF 的中点,, 且,所以BB FO '是平行四边形. 又D 是棱BB '的中点,所以DE OB P .41 侧面AA C C ''⊥底面ABC ,且OB AC ⊥ ,所以OB ⊥平面ACC A '' . 所以DE ⊥平面ACC A '',又DE Ì平面DA C ',所以平面DA C '⊥平面ACC A ''.(2)连接A B ', 设三棱柱的体积为V .故四棱锥的体积又D 是棱BB '的中点,BCD ∆的面积是BCC B ''面积的14 ,故四棱锥的体积 故平面DA C '将该三棱柱分成上下两部分的体积比为1:1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011 -2017北京市高考试题立体几何汇编1、(2011文5)某四棱锥的三视图如右图所示,该四棱锥的表面积是( )A. 32 B . 16+16,2C. 48 D . 16+32 22、(2011理7)某四面体的三视图如右图所示, 个面的面积中最大的是()A. 8B. 6,2 D.8 23、(2012理7,文7)某三棱锥的三视图如右图所示, 该三棱锥的表面积是()•A . 28 6.5 B. 30 6.5C. 56 12.5D. 60 12,54、(2013,文8)如右图,在正方体 ABCD- ABCD 中,P 为对角线BD 的三等分点,P 到各顶点的距离的不同取值 有().该四面体四— 4—1侧(左)视图正(主)视图A. 3个B . 4个C . 5个D . 6个5、(2013,文10)某四棱锥的三视图如下图所示,该四棱锥的体积为________ .& (2013 ,理14)如右图,在棱长为2的正方体ABCD A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CG的距离的最小值为_______ .7、(2014,理7)在空间直角坐标系Oxyz 中,已知A(2,0,0),B(2,2,0),h—2—L-H M- I ----- 2---- H黜左拠图C(0,2,0),D(1,1^2),若S,S2,S3分别表示三棱锥ABC 在xOy,yOz,zOx 坐标平面上的正投影图形的面积,则(A) S1 S2 S3 (B) S1 S2 且S S3(C)S, S3 且S2 S3 (D)S2 S3 且S S38、(2014,文11)某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为9、(2015理5)某三棱锥的三视图如下图所示,则该三棱锥的表面积是2 \V \\2侧(左)视图A. 2 5C1D1A BCC. 2 2.5 D 510、(2015文7)某四棱锥的三视图如右图所示,该四棱锥最长棱的棱长为(A)1 ( B)诂勺(B) ' (D)211、(2016理6)某三棱锥的三视图如右图所示, 则该三棱锥的体积为()A.丄B.丄C.丄D. 16 3 2<A>am .正(壬[视侧(左)视俯视图C. 2 2.5 D 512、(2016文11)某四棱柱的三视图如右图所示,则该四棱柱的体积为________________________________________________ .?13、(2017理7)如右图,某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()侧(在:•槐国(A) 3 2 (B) 2 _3(C)2 2 (D) 2 ArrayDC 丄PAC PAB丄PAC E AB PB F PA 丄CEF(2)求证:平面MO丄平面EAB.(3)求三棱锥E-ABC的体积。
20、(2015理17)如图,在四棱锥A EFCB中,△ AEF 为等边三角形,平面AEF 平面EFCB , EF II BC , BC 4 , EF 2a , EBC FCB 60 ,0 为EF 的中点.(I )求证:AO BE ;(II)求二面角F AE B的余弦值;C (川)若BE 平面AOC,求a的值.21、(2014文17)如图,在三棱柱 ABC ABQ,中,侧棱垂直于底面,AB BC,AA1 AC 2,E、F分别为AG、BC的中点.(1)求证:平面 ABE 平面B1BCC1 ;(2)求证:GF〃平面ABE ;(3)求三棱锥E ABC的体积.22、(2014理17)如图,正方形AMDE的边长为2 , B、C分别为AM、MD的中点, 在五棱锥P ABCDE中,F为棱PE的中点,平面 ABF与棱PD、PC分别交于点G、H .(I)求证:AB // FG ;(U)若PA 平面ABCDE,且PA AE,求直线BC与平面ABF所成角的大小,23、(2013理17)如图,在三棱柱ABC ABC中,AAGC是边长为4的正方形.平面ABC 平面AAGC,AB 3,BC 5 .(I)求证:AA1 平面ABC ;(U)求证二面角A BG B!的余弦值;(川)证明:在线段BG上存在点D,使得AD AB,并求黑的值.24、(2013 文17)如图,在四棱锥P- ABCD中, AB// CD AB 丄AC,CD= 2AB,平面PADL平面ABCD PA丄和F分别是CD 和PC的中点.求证:并求线段PH的长.AL,B1 B⑴PA丄底面ABCD⑵BE//平面PAR⑶平面BE巳平面PCD25、(2012,文16)如图1,在Rt△ ABC中,/ C=90 , D, E分别为AC AB的中点,点F为线段CD上的一点,将厶AD0ft DE折起到△ ADE 的位置,使AF丄CD如图2。
(I)求证:DE//平面ACB(II)求证:AF丄BE;(III)线段AB上是否存在点Q 使AC丄平面DEQ说明理由。
26、(2012 理16)如图 1,在Rt ABC 中,C AC 6,D、E分别为AC、AB上的点,且ADE DE ADE A,C CD 2 AC BCDEM A1D CM A1BE BC P A,DP ABEP ABCD PA ABCD ABCDAB 2, BAD 60 BD PAC PA AB PBAC PBC PDC PA(I)求证:DE//平面BCR (U)求证:四边形DEF助矩形;(川)是否存在点Q,到四面体PABC六条棱的中点的距离相等说明理由.图1 图2图1 图答案:1、B2C 3、B 4、B 5、3 6、2 一T7、D58 2 2 9、C 10、 C 11 、A12 、3 13 、B 14 、D215、(I )设AC,BD交点为 E ,连接ME •因为PD //平面MAC ,平面MAC^平面PDB ME,所以PD/ME因为ABCD是正方形,所以E为BD的中点,所以M为PB的中点•令工=1,则F 二i,TSM=cu=^)平面PAD 的法向量为& 0),所以=-l«l|Pl 2由题知二面角 B PD A 为锐角,所以它的大小为(III )由题意知 M( 1,2,-^) , C(2,4,0)2设直线MC 与平面BDP 所成角为 ,sin |cos<n,MC>| "| n || MC| 9(II )取 AD 的中点0,连接OP , OE . 因为PA PD ,所以OP AD .又因为平面PAD 平面ABCD ,且OP 因为OE 平面ABCD ,所以OP OE . 因为ABCD 是正方形,所以 OE AD . 平面PAD ,所以OP 平面ABCD .如图建立空间直角坐标系O xyz ,则 P(0,0, . 2),D(2,0,0),B( 2,4,0),BD (4, 4,0), PD (2,0, - 2).谟平面BDP 的法向量为M =(兀,则n m = 0 [n-PD= 0MC (3,2,所以直线MC与平面BDP所成角的正弦值为2-6.916、解:(I)因为PA AB , PA BC,所以PA 平面ABC, 又因为BD 平面ABC,所以PA BD . (II)因为AB BC,D为AC中点,所以BD AC,由(I)知,PA BD,所以BD 平面PAC .所以平面BDE 平面PAC.(Ill )因为PA//平面BDE,平面PACp]平面BDE DE , 所以PA // DE .因为D为AC的中点,所以DE - PA 1 , BD DC .2. 2由(I)知,PA 平面ABC,所以DE 平面PAC .1 1所以三棱锥E BCD的体积V 1BD DC DE -.6 317、(I)证明:•••平面PADL平面ABCD且平面PAD?平面ABCD=AD 且AB丄AD AB?平面ABCD••• AB丄平面PAD••• PD?平面PAD••• AB丄PD,又PDL PA 且PA? AB=A••• PDL平面PAB(U)解:取AD中点为0,连接CO PO-CD=AC=匚,••• CO AD,又••• PA=PD••• POL AD.以0为坐标原点,建立空间直角坐标系如图:则 P (0, 0, 1), B (1,1, 0), D (0,— 1, 0), C (2, 0, 0),由(U)知,A (0, 1 , 0), P (0, 0, 1),區© -1,1), B (1,1, 0),汕:-I,则有…占:可得M (0, 1-入,入),• •閒=(■ 1, ■ k , k), ••• BM/平面PCD ;二(寺 -1, 1)为平面PCD 的法向量,则 PB=(h 1, -1),面-K -1)设;. y . |为平面PCD 的法向量,n 廿D 二0■y 0_口 2s 0-1=°设PB 与平面PCD 的夹角为B ,则…―「二=八-^(川)解:假设存在 M 点使得BM/平面PCD则由则M (0, y 1, Z 1),•••顾■:二0,即一务入十k二0,解得入誌.综上,存在点M,即当时,M点即为所求.AP 418、证明:(I )因为PC丄平面ABCD,所以PC丄DC ,又因为DC丄AC,所以,DC丄平面PAC .(n )因为AB//DC,DC 丄AC,所以AB 丄AC,又因为PC丄平面ABCD,所以AB丄PC,所以AB丄平面PAC .由AB ?平面PAB,所以平面PAB丄平面PAC .(川)棱PB上存在点F,使得PA丄平面CEF,理由如下:取PB的中点F,连结EF, CE, CF .因为点E为AB的中点,所以EF//PA .又因为PA不在平面CEF内,所以PA//平面CEF .19、解:(I )因为O,M分别为AB,VA的中点,所以OM 又因为VE 平面MOC所以VB (II )因为AC = BC,O为AB的中点,所以OC AB.又因为平面VAB 平面ABC,且OC 平面ABC,所以OC 平面VAB .所以平面MOC 平面VAB .(III )在等腰直角三角形ACB中,AC BC 2,所以AB 2 , OC 1.所以等边三角形VAB的面积S VAB 3 .又因为OC 平面VAB ,所以三棱锥C VAB的体积等于-OC S VAB . 3.3 \3又因为三棱锥V ABC的体积与三棱锥C VAB的体积相等,所以三棱锥V ABC■■ 320、解:(I )因为△ AEF是等边三角形,O为EF的中点,所以ACL EF.又因为平面AEF丄平面EFCB AO 平面AEF,所以AO丄平面EFCB.所以AO丄BE.(H)取BC中点G,连接OG.由题设知EFCB是等腰梯形,所以OG! EF.由(I )知AOL平面EFCB又OG平面EFCB所以OA! OG.如图建立空间直角坐标系O-xyz ,则E (a,0,0 ), A (0, 0, . 3a ),B ( 2, 亦(2-a ) , 0) , E A = (-a , 0, ),=(a-2 , ■:;3(a-2 ) ,0 )ax 、3az 0?(a 2)x . 3(a 2)y 0令 z=1 ,贝U x= 3 , y=-1.于是 n= ( 3 , -1,1 ) 平面AEF 是法向量为p= ( 0,1,0 )由题知二维角F-AE-B 为钝角,所以它的余弦值为4 a= .321、( 1)证明:•••三棱柱 ABC- A 1B1G 中,侧棱垂直于底面, ••• BBi 丄 AB•/ AB 丄 BC BB A BC=B• AB 丄B 1BCG,•/ AB?平面 ABE •平面 ABELB 1BCC ;(H)证明:取 AB 中点G,连接EQ FQ 则 •••F 是BC 的中点,设平面ABE 的法向量为 n=(x,y,z )则:n E A?即 BE 0?(川)因为 BEX 平面AOC 所以BE! OC 即乍E OC0), OC = (-2 ,0.因为 BE = ( a-2 , 3 (a-2 ), 所以 B E O C =-2 (a-2 ) -3 (a J3 (2-a ),0),2)2.所以 cos (n , p )=n p _亦 n |p 5由0及0<a<2,解得••• FG// AC FG=L A C,2•••E 是AG 的中点, • FG// EG , FG=EC,•四边形FGEC 为平行四边形,• C i F// EG •C i F?平面 ABE EG?平面 ABE• C i F //平面 ABE(川)解:• AA i =AC=2 BC=1, AB 丄 BCE - AB=22、解: (I )在正方形 AMDE 中,因为B 是AM 的中 点,所以AB//DE .又因为AB 平面PDE ,所以AB//平 面PDE .因为AB ABF ,且平面 ABF 平面PDE FG ,所以 AB//FG .(II )因为 PA 底面 ABCDE ,所以 PA AB ,PA AE .是平面ABF 的法向量,所以n A H0,即 0, 1,1 2 , ,2 20.解得C 2,1,0,P 0,0,2 ,F 0,1,11,1,0 .设平面ABF的法向量为n x, y, z ,则nn 0,,即0,:,0. 令z.所以n0,1,1 .设直线BC 与平面ABF 所成角为 ,则sincos n,n BCn| |B C 1.因此直线BC 与2平面ABF 所成角的大小为n.设点 6 的坐标为 u,v,w .因为点H 在棱PC 上,所以可设PH P C 0 1 ,即 u,v,w 2,1,2 .所以 u 2 , v , w 2 2 .因为n如图建立空间直角坐标系A CYZ ,则 A 0,0,0,B 1,0,0,D一 4 2 2点H的坐标为3,?3 .所以PH24 2.323、解:⑴ 因为AAC i C 为正方形,所以AA 丄AC因为平面ABCL 平面AACC,且AA 垂直于这两个平面的交线 AC,所以AA丄平面ABC (2)由(1)知 AAL AC AAL AB 由题知A 吐3, BC= 5, AC = 4,所以AB 丄AC 如图,以A 为原点建立空间直角坐标系 A - xyz ,则B(0,3,0) , A i (0,0,4), B i (0,3,4) , C(4,0,4). 设平面ABC 的法向量为n = (x , y , z),0,即 3y 4zo,0, 4x 0.令 z = 3,则 x = 0, y = 4,所以 n = (0,4,3). 同理可得,平面BBC 的法向量为(3,4,0).所以 cos 〈n , m 〉=n m 16|n| |m| 25由题知—面角A i — BC — B i 为锐角,所以二面角A — BG — B i 的余弦值为16.25⑶设qx , y , z)是直线BC 上一点,且 所以(x , y — 3, z)=入(4 , — 3,4).解得x = 4入,y = 3 — 3入,z = 4入.由AD •-A 1B = 0,即卩 9 —25 X=0,解得_925因为— € [0,1] ,所以在线段 BC 上存在点 D,使得 25此时, BD9BC 125所以=(4 入,3 — 3 入,4 入).ADL A i B.24、证明:(1)因为平面PADL底面ABCD且PA垂直于这两个平面的交线AD,所以PAL底面ABCD(2)因为AB// CD CD= 2AB, E 为CD的中点,所以AB// DE且A吐DE所以ABED为平行四边形.所以BE// AD又因为BE 平面PAD AD 平面PAD所以BE//平面PAD⑶ 因为AB丄AD而且ABED为平行四边形,所以BEL CD ADL CD由⑴知PA丄底面ABCD所以PAL CD所以CD!平面PAD所以CDL PD因为E和F分别是CD和PC的中点,所以PD// EF所以CDL EF.所以CD!平面BEF平面BEFL平面PCD25、“曲已鬧心扩壮皿〃斫以DE丄』所UM丄W "E W(DD约段"上存在恵0 —平面。
