浙江省金华十校2019届高三4月高考模拟考试数学理试题
2019年金华十校高考模拟考试.doc

2019年金华十校高考模拟考试数学试题卷本试卷分第Ⅰ卷和第Ⅱ卷两部分.考试时间120分钟. 试卷总分为150分。
请考生按规定用笔将所用试题的答案涂、写在答题纸上.参考公式:如果事件A、B互斥,那么柱体的体积公式P(A+B)= P(A)+ P(B)V=Sh如果事件A、B相互独立,那么其中S表示柱体的底面积,h表示柱体的高P(A•B)= P(A)•P(B) 锥体的体积公式如果事件A在一次试验中发生的概率为p,那么n V=13Sh次独立重复试验中事件A恰好发生k次的概率其中S表示锥体的底面积,h表示锥体的高.P n(k)=(1)(0,1,2,,)k k n knC p p k n--=球的表面积公式台体的体积公式S=4πR2V=13(S1S2) h 球的体积公式其中S1、S2表示台体的上、下底面积,h表示棱V=43πR3台的高. 其中R表示球的半径选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合M=1122x x⎧⎫-<<⎨⎬⎩⎭,N={x | x2≤x},则M∩N =A.12⎡⎫⎪⎢⎣⎭,B.112⎛⎤- ⎥⎝⎦,C.112⎡⎫-⎪⎢⎣⎭,D.12⎛⎤- ⎥⎝⎦,2.过点(1,0)且与直线x-2y-2=0垂直的直线方程是A.x-2y+1=0 B.x-2y-1=0 C.2x+y-2=0 D.x+2y-1=03.已知a,b∈R,下列四个条件中,使a>b成立的充分不必要的条件是A.a>b-1 B.a>b+1 C.|a|>|b| D.2a>2b4.若x,y满足约束条件,2,y xx yy⎧⎪+4,⎨⎪-⎩≤≤≥则z=x+2y的最大值是A.8 B.4 C.2 D.65. 在下面四个x∈[-π,π]的函数图象中,函数y=|x|sin2x的图象可能是A .B .C .D . 6. 等差数列{a n },等比数列{b n },满足a 1=b 1=1,a 5=b 3,则a 9能取到的最小整数A .-1B .0C .2D .37.设0<p <1,随机变量ξ的分布列是则当p 在(0,1)内增大时 A .E (ξ)减小,D (ξ)减小 B .E (ξ)减小,D (ξ)增大 C .E (ξ)增大,D (ξ)减小 D .E (ξ)增大,D (ξ)增大8. 如图,AB 是平面α的斜线段,A 为斜足,点C 满足sin ∠CAB =λsin ∠CBA (λ>0),且在平面α内运动,则A .当λ=1时,点C 的轨迹是抛物线B .当λ=1时,点C 的轨迹是一条直线 C .当λ=2时,点C 的轨迹是椭圆D .当λ=2时,点C 的轨迹是双曲线 9. 已知椭圆C :2214x y +=上的三点A ,B ,C ,斜率为负数的直线BC 与y 轴交于M ,若原点O 的重心,且△BMA 与△CMO 的面积 BC 的斜率为A.10. 已知函数f (x )=x e 2x ,下列说法正确的是A .任意12em >-,函数y = f (x )-m 均有两个不同的零点 B .存在实数k ,使得方程f (x )=k (x +2)有两个负数根 C .若f (a )=f (b )(a ≠b ),则-1<a +b <0D .若实数a ,b 满足e 2a +e 2b <2e -1(a ≠b ),则f (a )≠f (b ) 非选择题部分(共110分)第9题图α AB C第8题图二、填空题:本大题共7小题,多空题每小题6分,单空题每小题4分,共36分. 11. 已知复数z 满足(1+2i)z =3-4i ,i 为虚数单位,则z 的虚部是 ▲ ,|z |= ▲ .12. 双曲线2214y x -=的渐近线方程是 ▲ ,离心率为▲ .13.某几何体的三视图如图所示,正视图为腰长为1的等腰直角三角形,侧视图、俯视图均为边长为1的正方形,则该几何体的表面积是 ▲ ,体积是 ▲ .14.已知(2+x )(1-2x )7=a 0+a 1x +a 2x 2+…+a 8x 8,则a 1+a 2+…+a 8= ▲ .a 3= ▲ .15.5位同学分成3组,参加3个不同的志愿者活动,每组 至少1人,其中甲乙2人不能分在同一组,不同的分配方案有 ▲ 种.(用数字作答)16. 在△ABC 中,A ,B ,C 内角所对的边分别为a ,b ,c .已知b =2且c cos B +b cos C =4a sin B sin C ,则c 的最小值为 ▲ . 17. 平面向量a ,m ,n ,满足|a |=4,2210,10,⎧-⋅+=⎨-⋅+=⎩m a m n a n ,当|m -n |=________时,m 与n 的夹角最大.三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤。
浙江省金华十校2019届第二学期高考模拟考试数学试题

○…………○…………绝密★启用前浙江省金华十校2019届第二学期高考模拟考试数学试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.设集合1{|}22M x x =-<<, 2{|}N x x x =≤,则M N ⋂=( ) A .10,2⎡⎫⎪⎢⎣⎭ B .1,12⎛⎤- ⎥⎝⎦ C .11,2⎡⎫-⎪⎢⎣⎭ D .1,02⎛⎤- ⎥⎝⎦2.过点(1,0)且与直线220x y --=垂直的直线方程为( ) A .210x y --= B .210x y -+= C .220x y +-=D .210x y +-=3.已知,a b R ∈,下列四个条件中,使a b >成立的充分不必要的条件是( ) A .1a b >-B .1a b >+C .a b >D .22a b >4.若x ,y 满足约束条件42y xx y y ≤⎧⎪+≤⎨⎪≥-⎩,则2z x y =+的最大值是( )A .8B .4C .2D .65.在下面四个[,]x ππ∈-的函数图象中,函数sin 2y x x =的图象可能是( )A .B .………装…………………………○……※请※※不※※要※※在※※答※※题※※………装…………………………○……C . D .6.等差数列{}n a ,等比数列{}n b ,满足111a b ==,53a b =,则9a 能取到的最小整数是( ) A .1-B .0C .2D .37.设01p <<,随机变量ξ的分布列是则当p 在(0,1)内增大时( ) A .()E ξ减小,()D ξ减小 B .()E ξ减小,()D ξ增大 C .()E ξ增大,()D ξ减小D .()E ξ增大,()D ξ增大8.如图,AB 是平面α的斜线段,A 为斜足,点C 满足sin sin (0)CAB CBA λλ∠=∠>,且在平面α内运动,则( )A .当1λ=时,点C 的轨迹是抛物线B .当1λ=时,点C 的轨迹是一条直线 C .当2λ=时,点C 的轨迹是椭圆D .当2λ=时,点C 的轨迹是双曲线抛物线9.已知椭圆C :2214x y +=上的三点A ,B ,C ,斜率为负数的直线BC 与y 轴交于M ,若原点O 是ABC ∆的重心,且BMA ∆与CMO ∆的面积之比为32,则直线BC 的斜率为( )线…………○……线…………○……A .4-B .14-C .6-D .10.已知函数2()x f x xe =,下列说法正确的是( ) A .任意12m e>-,函数()y f x m =-均有两个不同的零点; B .存在实数k ,使得方程()(2)f x k x =+有两个负数根; C .若()()()f a f b a b =≠,则10a b -<+<;D .若实数a ,b 满足2212()a b e e e a b -+<≠,则()()f a f b ≠.………订…………※※线※※内※※答※※题※※………订…………第II卷(非选择题)请点击修改第II卷的文字说明二、填空题11.已知复数z满足(12)34i z i+=-,i为虚数单位,则z的虚部是_____,z=_____.12.双曲线2214yx-=的渐近线方程是_____,离心率为_____.13.某几何体的三视图如图所示,正视图为腰长为1的等腰直角三角形,侧视图、俯视图均为边长为1的正方形,则该几何体的表面积是_____,体积是_____.14.已知7280128(2)(12)x x a a x a x a x+-=+++,则128.a a a+++=_____,3a=_____.15.5位同学分成3组,参加3个不同的志愿者活动,每组至少1人,其中甲乙2人不能分在同一组,则不同的分配方案有_____种.(用数字作答)16.在ABC∆中,A,B,C内角所对的边分别为a,b,c,已知2b=且cos cos4sin sinc B b C a B C+=,则c的最小值为_____.17.已知平面向量a,m,n,满足4a=r,221010m a mn a n⎧-⋅+=⎨-⋅+=⎩,则当m n-=_____,则m与n的夹角最大.三、解答题18.已知函数()sin()0,02f x xπωϕωϕ⎛⎫=+><<⎪⎝⎭的最小正周期为π,且cos2cos0ϕϕ+=.(1)求ω和(2fπ的值;○…………装…………○…………○…学校:___________姓名:___________班号:___________○…………装…………○…………○…(2)若3((0)25f ααπ=<<,求sin α. 19.设函数2()ln ()f x ax x a R =-∈. (1)讨论函数()f x 的单调性;(2)若()0f x ≥恒成立,求实数a 的取值范围.20.在四棱锥S ABCD -中,底面ABCD 为直角梯形,BC CD ⊥,1SC SD CD DA ====,2CB =,//AD BC ,23SCB π∠=,E 为线段SB 上的中点.(1)证明://AE 平面SCD ;(2)求直线AE 与平面SBC 所成角的余弦值.21.已知抛物线C :22(0)y px p =>的焦点是(1,0)F ,直线1l :1y k x =,2l :2y k x =分别与抛物线C 相交于点A 和点B ,过A ,B 的直线与圆O :224x y +=相切.(1)求直线AB 的方程(含1k 、2k );(2)若线段OA 与圆O 交于点M ,线段OB 与圆O 交于点N ,求MON S ∆的取值范围.22.已知数列{}n a 中,14a =,n a >1314n n n n a a a a +=-+,记22212111...n n T a a a =+++. (1)证明:2n a >;(2)证明:115116n na a +≤<;(3)证明:8454nn nT-<<.参考答案1.A【解析】试题分析:由已知有2{|}N x x x =≤, M N ⋂=,故选A.考点:集合的运算. 2.C 【解析】 【分析】由两直线垂直的性质求出所求直线的斜率,再用点斜式求直线的方程,化为一般式即可. 【详解】由于直线220x y --=的斜率为12,故所求直线的斜率等于2-, 所求直线的方程为02(1)y x -=--,即220x y +-=, 故选:C . 【点睛】本题主要考查两直线垂直的性质,用点斜式求直线的方程,属于基础题. 3.B 【解析】 【分析】根据充分不必要条件的定义,逐一分析给定四个选项与a >b 的关系,可得答案. 【详解】B 选项1a b >+是a b >的充分不必要的条件; A 选项1a b >-是a b >的必要不充分条件;C 选项a b >是a b >的即不充分也不必要条件; B 选项22a b >是a b >的充要条件; 故选:B . 【点睛】本题考查的知识点是充分不必要条件的定义,属于基础题. 4.D【分析】先根据约束条件画出可行域,再转化目标函数,把求目标函数的最值问题转化成求截距的最值问题. 【详解】作出不等式组对应的平面区域如图所示:由4y x x y =⎧⎨+=⎩,解得(2,2)A ,由2z x y =+,得122z y x =-+,平移直线122zy x =-+,由图象可知当直线经过点A , 直线的截距最大,此时z 最大,此时6z =, 故选:D .【点睛】本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法,属于基础题. 5.C 【解析】 【分析】根据函数奇偶性和对称性,以及当x=π时的函数值的对应性进行排除即可. 【详解】因为()sin(2)sin 2()f x x x x x f x -=--=-=-,即()f x 是奇函数,图象关于原点对称,排除,B D ,当x π=时,()sin 20f πππ==,排除A .【点睛】本题主要考查函数图象的识别和判断,结合函数奇偶性,函数值的对应性利用排除法是解决本题的关键,属于基础题. 6.B 【解析】 【分析】等差数列{a n }的公差设为d ,等比数列{b n }的公比设为q ,q ≠0,运用等差数列和等比数列的通项公式,以及二次函数的值域,可得所求最小整数. 【详解】等差数列{}n a 的公差设为d ,等比数列{}n b 的公比设为q ,0q ≠,由111a b ==,53a b =,可得214d q +=, 则2291812(1)211a d q q =+=+-=->-,可得9a 能取到的最小整数是0. 故选:B . 【点睛】本题考查等差数列和等比数列的通项公式,考查化简运算能力和推理能力,属于基础题. 7.A 【解析】 【分析】根据随机变量的期望,方差公式计算出()E ξ,()D ξ后根据函数的单调性可得. 【详解】由题意得11()01212222p p pE ξ-=⨯+⨯+⨯=-,所以当p 在(0,1)内增大时,()E ξ减少; 221()[0(1)][1(1)]2222p p p D ξ=--⨯+--⨯22132[2(1)]222p p p p --++--⨯=231()242p --=,所以当p 在(0,1)内增大时,()D ξ减少. 故选:A . 【点睛】本题考查了离散型随机变量的期望与方差的计算问题,也考查了运算求解能力,属中档题. 8.B 【解析】 【分析】当1λ=时,BC AC =,故C 的轨迹为线段AB 的中垂面与α的交线,当2λ=时,2BC AC =,在平面α内建立坐标系,设(,)C x y ,求出C 的轨迹方程得出结论.【详解】在ABC ∆中,∵sin sin (0)CAB CBA λλ∠=∠>,由正弦定理可得:BCACλ=, 当1λ=时,BC AC =,过AB 的中点作线段AB 的垂面β, 则点C 在α与β的交线上,即点C 的轨迹是一条直线, 当2λ=时,2BC AC =,设B 在平面α内的射影为D ,连接BD ,CD ,设B D h =,2AD a =,则BC = 在平面α内,以AD 所在直线为x 轴,以AD 的中点为y 轴建立平面直角坐标系,设(,)C x y ,则CA =CD =,CB ==2222516393a h x a y ⎛⎫++=+ ⎪⎝⎭.∴C 的轨迹是圆. 故选:B .【点睛】本题考查轨迹方程的求解与判断,分类讨论思想,属于中档题.9.C 【解析】 【分析】设11(,)B x y ,22(,)C x y ,(0,)M m ,33(,)A x y 直线BC 的方程为y kx m =+.可得2BM MC =,1220x x ⇒+=;联立2244y kx mx y =+⎧⇒⎨+=⎩22223614m k m k =-+,利用原点O 是△ABC 的重心,得()3122814km x x x k =-+=+,32214m y k=-+.由223344x y +=,22144k m ⇒+=.由此可得2112k =,∵k 0<.∴k =. 【详解】设11(,)B x y ,22(,)C x y .(0,)M m .33(,)A x y ,直线BC 的方程为y kx m =+. ∵原点O 是ABC ∆的重心,∴BMA ∆与CMO ∆的高之比为3, 又BMA ∆与CMO ∆的面积之比为32,则2BM MC =.即2BM MC =,1220x x ⇒+=…①联立2244y kx mx y =+⎧⇒⎨+=⎩()222418440k x mkx m +++-=. 122814km x x k -+=+,21224414m x x k-=+…②,由①②整理可得:22223614m k m k =-+…③ ∵原点O 是ABC ∆的重心,∴()3122814kmx x x k=-+=+,3211222()[()2]14my y y k x x m k =-+=-++=-+.∵223344x y +=,∴22222282()4()41441414km m k m k k -+=⇒+=++…④.由③④可得2112k =,∵k 0<.∴k =. 故选:C .【点睛】本题考查了椭圆的性质,直线与椭圆的位置关系,韦达定理的应用,考查了计算能力、转化思想,属于中档题. 10.D 【解析】 【分析】函数2()x f x xe =,'2()(12)xf x x e =+,可知:12x =-时,函数()f x 取得极小值即最小值.11()22f e-=-,利用图象及其单调性即可判断出正误. 【详解】∵函数2()x f x xe =,'2()(12)xf x x e =+,可知:12x =-时,函数()f x 取得极小值即最小值.11()22f e -=-,如图所示.由图象可得:A .当102m e-<<时,函数()y f x m =-有两个不同的零点,因此不正确; B .存在实数k ,使得方程()(2)f x k x =+有两个一正一负数根,不可能为两个负数根; C .若()()()f a f b a b =≠,则1a b +<-,因此不正确;D .若()()f a f b =(不妨设102a b ≤-≤<),则222221(12)2a b a a a a e e e e e a e b-+=+>-≥,因此其逆否命题正确. 故选:D .【点睛】本题考查了利用导数研究函数的单调性极值与最值、数形结合方法、方程与不等式的解法,考查了推理能力与计算能力,属于中档题.11.2-【解析】 【分析】把已知等式变形,利用复数代数形式的乘除运算化简求得z 的虚部,再由复数模的公式求|z|. 【详解】由(12)34i z i +=-,得34(34)(12)1212(12)(12)i i iz i i i i ---===--++-,∴z 的虚部是2-,z故答案为:2- 【点睛】本题考查复数代数形式的乘除运算,考查复数的基本概念及复数模的求法,属于基础题.12.2y x =± 【解析】 【分析】由2204y x -=,能求出其渐近线方程,再由2a =,c =【详解】由2204y x -=得其渐近线方程为2y x =±,且2a =,c =,∴2e =故答案为:2y x =±,2.【点睛】本题考查双曲线的性质和应用,解题时要注意公式的合理运用,属于基础题.1332+13 【解析】 【分析】由三视图还原原几何体,该几何体为四棱锥P ABCD -,再由三角形及四边形面积公式求表面积,由棱锥体积公式求体积. 【详解】由三视图还原原几何体如图所示,该几何体为四棱锥P ABCD -, 该几何体的表面积PAB PAD PCD PBC ABCD S S S S S S ∆∆∆∆=++++四边形11331122222=⨯⨯⨯+=+;体积111323V =⨯=.32,13.【点睛】本题考查由三视图求原几何体的表面积、体积,关键是由三视图还原原几何体,属于中档题. 14.5- 476- 【解析】 【分析】由二项式定理及其通项得:令1x =得0128...(21)(121)3a a a a ++++=+-⨯=-,令0x =得02a =,所以128...5a a a +++=-,由7(12)x -展开式的通项为17(2)r r rr T C x +=-,则3a 得解. 【详解】因为7280128(2)(12)x x a a x a x a x +-=+++,令1x =得0128...(21)(121)3a a a a ++++=+-⨯=-, 令0x =得02a =,所以128...5a a a +++=-,由7(12)x -展开式的通项为17(2)r r rr T C x +=-, 则33223772(2)(2)476a C C =⨯-+-=-,故答案为:5- ,476-. 【点睛】本题考查了二项式定理及其二项式展开式的通项,赋值法,属于中档题 15.114 【解析】 【分析】根据题意,分2步进行:①将5位同学分成3组,要求甲乙2人不能分在同一组,需要分2种情况讨论;②将分好的3组全排列,对应3个不同的志愿者活动,由分步计数原理计算可得答案. 【详解】根据题意,分2步进行分析:①,将5位同学分成3组,要求甲乙2人不能分在同一组,若分成1、2、2的三组,有1225422215C C C A =种,其中甲乙分在同一组的情况有23C 3=种,此时有15312-=种分组方法;若分成3、1、1的三组,有3115212210C C C A =种,其中甲乙分在同一组的情况有133C =种,此时有1037-=种分组方法; 则符合题意的分法有12719+=种;②,将分好的3组全排列,对应3个不同的志愿者活动,有336A =种情况, 则有196114⨯=种不同的分配方案; 故答案为:114. 【点睛】本题考查排列、组合的应用,涉及分步、分类计数原理的应用,可以用间接法分析,避免分类讨论,属于中档题. 16.12【解析】 【分析】由正弦定理和三角函数的化简可得1sin sin 4B C =,再根据正弦定理即可求出. 【详解】∵ccos cos 4sin sin B b C a B C +=,∴sin cos sin cos 4sin sin sin C B B C A B C +=, ∴sin()sin 4sin sin sin B C A A B C +==,∵sin 0A ≠,∴1sin sin 4B C =,∴1sin 4sin C B =,由正弦定理可得sin sin b c B C=,即2sin 28sin sin Cc C B =⨯=, 当sin 1B =时,min sin C =14.当1sin 4C =时,则c 的最小值为12.故答案为:12.【点睛】本题考查了三角函数的化简与性质和正弦定理的应用,属于中档题.17【解析】 【分析】设三向量的起点均为O ,求出m ,n 的终点轨迹,利用几何图形知识得出答案. 【详解】设a ,m ,n 的起点均为O ,以O 为原点建立平面坐标系,不妨设(4,0)a =,(,)m x y =,则222m x y =+,4a m x ⋅=, 由210m a m -⋅+=可得22410x y x +-+=,即22(2)3x y -+=,∴m 的终点M 在以(2,0)同理n 的终点N 在以(2,0)显然当OM ,ON 为圆的两条切线时,MON ∠最大,即m ,n 的夹角最大.设圆心为A ,则AM =,∴1OM ==,sin MOA ∠=60MOA ∠=︒,设MN 与x 轴交于点B ,由对称性可知MN x ⊥轴,且2MN MB =,∴22sin 212MN MB OM MOA ==⋅∠=⨯⨯=【点睛】本题考查了平面向量的几何运算,数量积运算,属于中档题.18.(1)2ω=,-(2 【解析】 【分析】(1)由()f x 的周期得ω,结合cos 2cos 0ϕϕ+=,且02πϕ<<,得3πϕ=,进而得()sin(2)3f x x π=+,代入代入计算即可. (2)由3()(0)25f ααπ=<<,得4cos()25πα+=-,展开sin sin 33a a ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦化简求值即可. 【详解】(1)∵函数()sin()0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的最小正周期为2ππω=,∴2ω=.再根据2cos 2cos 2cos 1cos 0ϕϕϕϕ+=-+=,∴cos 1ϕ=-(舍去),或1cos 2ϕ=, ∴3πϕ=,故()sin(2)3f x x π=+,故()sin()23f πππ=+=.(2)∵3()sin()235f απα=+=<2πα+为钝角,故4cos()25πα+==-, 故sin sin sin cos cos sin 333333a a ππππππππ⎡⎤⎛⎫⎛⎫⎛⎫=+-=+-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦3143525210+=⋅+⋅=. 【点睛】本题考查了求三角函数的解析式,同角三角函数的关系,两角和与差的正弦公式的应用,属于基础题.19.(1)见解析;(2)1[,)2e+∞ 【解析】 【分析】(1)求出导函数2'21()(0)ax f x x x-=>.可得当0a ≤时,'()0f x <,函数()f x 在(0,)+∞上单调递减;当0a >时,令()0f x '=求得x 值,把定义域分段,由导函数在不同区间段内的符号可得原函数的单调性;(2)()0f x ≥恒成立,由(1)知()f x 在上单调递减,在)+∞上单调递增,求其最小值,由最小值大于等于0求解a 的取值范围. 【详解】(1)由题意,2'21()(0)ax f x x x-=>.当0a ≤时,'()0f x <,函数()f x 在(0,)+∞上单调递减;当0a >时,令()0f x '=,解得x =∴当x ∈时,'()0f x <,当)x ∈+∞时,'()0f x >. ∴()f x 在上单调递减,在)+∞上单调递增; (2)∵()0f x ≥恒成立,∴(e)0f ≥,可得21a e≥. 由(1)可得,()f x 在上单调递减,在)+∞上单调递增, ∴()f x 的最小值为12f =-.∴102-≥,解得12a e≥.因此,实数a 的取值范围为1[,)2e+∞. 【点睛】本题考查利用导数研究函数的单调性,考查利用导数求函数的最值,考查计算能力,属于中档题.20.(1)见解析;(2)13【解析】 【分析】(1)取SC 的中点F ,连接EF ,DF ,证明四边形ADFE 是平行四边形得出//AE DF ,故而//AE 平面SCD ;(2)取CD 的中点O ,以O 为原点建立空间坐标系,根据23SCB π∠=得出二面角S CD A --的大小,得出S 的坐标,求出平面SBC 的法向量n ,计算AE 和n 的夹角得出结论.【详解】(1)取SC 的中点F ,连接EF ,DF .∵E ,F 是SB ,SC 的中点,∴//EF BC ,12EF BC =, 又//AD BC ,12AD BC =,∴//EF AD ,EF AD =, ∴四边形ADFE 是平行四边形,∴//AE DF ,又DF ⊂平面SCD ,AE ⊄平面SCD ,∴//AE 平面SCD . (2)取CD 的中点O ,连接SO ,过O 作BC 的平行线OM ,以O 为原点,以OD ,OM 和平面ABCD 过点O 的垂线为坐标轴建立空间坐标系O xyz -, ∵1SC CD SD ===,∴SO =,设二面角S CD A --的大小为α,则(0,cos ,sin )22S αα,1(,1,0)2A ,1(,2,0)2B -,1(,0,0)2C -,∴1(,1cos ,)444E αα-+,∴(0,2,0)CB =,1()2CS αα=,∵23SCB π∠=, ∴cos ,CB CS CB CS CB CS⋅<>=12α===-,∴cos α=,sin α=1(0,2S -,13(,44E , ∴31(,,)444AE=--,11(,,222CS =-, 设平面SCD 的法向量为(,,)n x y z =,则00n CB n CS ⎧⋅=⎨⋅=⎩,即20110222y x y z =⎧⎪⎨-+=⎪⎩, 令x =(2,0,1)n =-,∴cos ,n AE n AE nAE ⋅<>=3==-,设直线AE 与平面所成角为θ,则sin cos ,3n AE θ=<>=,∴1cos 3θ=.∴直线AE 与平面所成角的余弦值为13.【点睛】本题考查了线面平行的判定,考查空间向量与空间角的计算,用向量法求线面角,属于中档题.21.(1)1212()40k k x k k y -++=;(2)(2]5【解析】 【分析】(1)由抛物线的焦点可得2p =,即有抛物线的方程,分别联立直线5()25f x -≤-≤:1y k x =,2l :2y k x =,求得,A B 的坐标,可得AB 的斜率和方程;(2)由直线和圆相切的条件:d r =,以及向量的夹角公式和三角形的面积公式,化简整理,结合基本不等式和不等式的性质,可得所求范围. 【详解】(1)焦点是(1,0)F ,可得12p=,即2p =,设11(,)A x y ,22(,)B x y , 抛物线方程为24y x =,联立1y k x =,可得21144(,)A k k ,同理可得22244(,)B k k , 若AB 斜率存在,可得12121212AB y y k kk x x k k -==-+,AB 的方程为122112144()k k y x k k k k -=-+,化为1212()40k k x k k y -++=, AB 的斜率不存在时,也满足上面的方程,则直线AB 的方程为1212()40k k x k k y -++=;(2)过A ,B 的直线与圆O :224x y +=相切,可得2d r ===,化简为221212()()4k k k k ++=,即有1220k k -≤<,cos ||||OA OBAOB OA OB x ⋅∠==⋅=,由221212()()4k k k k ++=,可得cos AOB ∠=,22121212()44sin 52k k k k MON k k --+∠=-,设1252(5,9]t k k =-∈,则222121212()444sin 452MONk k k k S MON k k ∆--+=∠=⋅-2(5)2(5)444t t t----+=⋅218494918()184t t t t t-+-==-+≤-=, 当7t =取等号,即121[2,0)k k =-∈-,所以max ()2MON S ∆=, 又2491618(5)55MON S ∆>-+=,即MON S ∆>, 即有MON S ∆的取值范围为2]. 【点睛】本题考查抛物线的方程和圆的方程的运用,考查直线和圆相切的条件,以及三角形的面积公式和基本不等式的运用,考查方程思想和运算能力,属于中档题. 22.(1)见解析;(2)见解析;(2)见解析 【解析】 【分析】(1)3133(2)(2)1422n n n n n n n na a a a a a a a +---=-+-=-,∴31323221212n n n n n n na a a a a a a +---==---,然后构造函数,利用导数判断单调性,利用单调性可得;(2)2124214111514816n n n n n a a a a a +⎛⎫=-+=-+ ⎪⎝⎭,然后配方可得;(3)先证4n n T <,再证845n n T >-. 【详解】(1)∵3133(2)(2)1422n n n n n n n na a a a a a a a +---=-+-=-, ∴31323221212n n n n n n n a a a a a a a +---==---,令1nt a =,则2312()122n n a m t t t a +-==---,∵n a >(0,)3t ∈,∴'2()260m t t t =--<,∴()m t 在(0,)3单调递减,∴1()103m t m >=-=>,即n a >时,1202n na a +->-恒成立, ∴12n a +-与2n a -同号,又1220a -=>.∴2n a >成立.(2)2124214111514816n n n n n a a a a a +⎛⎫=-+=-+ ⎪⎝⎭221115412816⎛⎫<-+= ⎪⎝⎭,又212111515481616n n n a a a +⎛⎫=-+ ⎪⎝⎭…,∴115116n n a a +≤<. (3)先证4n n T <,因为2n a >,所以2114n a <,所以222121111...44n n n T n a a a =+++<⋅=, 再证845n n T >-,∵1314n n n n a a a a +=-+,∴()121144n n n n a a a a +-=+,又21232141115151481616n n n n n a a a a a +⎛⎫=-+=-+> ⎪⎝⎭,∴11615n n a a +>,∴116()31n n n a a a +<+,又10n n a a +-<,∴2211()4()431n n n n n a a a a a ++->-,所以221222121114...()314n n n n n T a a a a a +=+++>-+4488(416)31443145n n n >-+=->-, 故8454n n n T -<<. 【点睛】本题考查数列递推式的化简和应用,利用放缩法、证明不等式等,考查化简、变形能力,分析问题、解决问题的能力,属于中档题.。
浙江省十校联盟2019届高三数学4月适应性考试试题(PDF)

当 t 5 2 时 ,等号成立
3
3
即当点 N 在线段 DC 靠近 C 的三等分点时,直线 MN 与平面 PAB 所成角最大,最大角的
正弦值为 35 7
20.
……………………………………15 分
(1)由题意,得:
Sn
t
t
1
(an
2)
4 月适应性考试 数学 参考答案 第 2 页 共 7 页
AE∥ DC 同理, AE∥ 平面PDC 又 AE ME E …………………………………6 分
平面AME∥ 平面PDC
………………………………………7
分
(2)以 A 为原点,分别以 AD,AB,AP 所在直线为 X,Y,Z 轴建立空间直角坐标系,则
A(0,0,0), B(0,2,0),C(2,2,0), D(1,0,0),P(0,0,2),M (0,1,1)
18.
(1)由正弦定理,得: a c sin A sin C
sin A a sin C 2 c3
sin C sin A ,且 A 为锐角
………………………………………3 分
cos C 6 , cos A 5 ;
3
3
sin B sin( A C) sin Acos C cos Asin C 2 6 15 9
……….…….…….……15 分
(1)已知 b a 2(a 0), f (x) x 2 bx a ln x ,
f '(x) 2x b a (x 1)(2x a) ,
x
x
由 f '(x) 0
可得
x1
1,x2
2019届浙江省十校联盟高三下学期4月高考适应性考试数学试题(解析版)

【答案】D
【解析】先化简函数解析式,再根据函数 的图象变换规律,可得所求函数的解析式为 ,再由正弦函数的对称性得解.
【详解】
,
将函数图象上各点的横坐标伸长到原来的3倍,所得函数的解析式为
,
再向右平移 个单位长度,所得函数的解析式为
,
,
可得函数图象的一个对称中心为 ,故选D.
【点睛】
画出 的图象,
由图象可得:
对于①, 在 上单调递减,所以①正确;
对于②,函数 与 的图象没有交点,即 没有零点,所以②错误;
对于③,由函数图象的对称性可知③错误;
对于④,函数 和 图象关于原点对称,则 中用 代替 ,用 代替 ,可得 ,所以④正确.
故选:C
【点睛】
本题主要考查了双曲线的简单几何性质,函数的图象与性质,函数的零点概念,考查了数形结合的数学思想.
【答案】 52
【解析】设从第2天开始,每天比前一天多织 尺布,由等差数列前 项和公式求出 ,由此利用等差数列通项公式能求出 .
【详解】
设从第2天开始,每天比前一天多织d尺布,
则 ,
解得 ,即每天增加的数量为 ,
,故答案为 ,52.
【点睛】
本题主要考查等差数列的通项公式、等差数列的求和公式,意在考查利用所学知识解决问题的能力,属于中档题.
A. B. C. D.
【答案】B
【解析】由 得 ,即 ,所以得 ,利用基本不等式求出最小值,得到 ,再由递推公式求出 .
【详解】
由 得 ,
即 ,
,当且仅当 时取得最小值,
此时 .
故选:B
【点睛】
本题主要考查了数列中的最值问题,递推公式的应用,基本不等式求最值,考查了学生的运算求解能力.
2019年第二学期浙江省金华十校高考模拟考试数学试题卷(解析版)
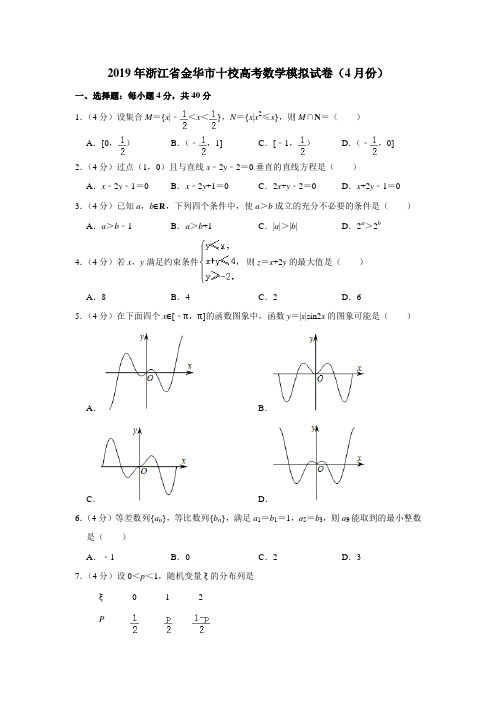
2019年浙江省金华市十校高考数学模拟试卷(4月份)一、选择题:每小题4分,共40分1.(4分)设集合M={x|﹣<x<},N={x|x2≤x},则M∩N=()A.[0,)B.(﹣,1]C.[﹣1,)D.(﹣,0] 2.(4分)过点(1,0)且与直线x﹣2y﹣2=0垂直的直线方程是()A.x﹣2y﹣1=0B.x﹣2y+1=0C.2x+y﹣2=0D.x+2y﹣1=0 3.(4分)已知a,b∈R,下列四个条件中,使a>b成立的充分不必要的条件是()A.a>b﹣1B.a>b+1C.|a|>|b|D.2a>2b4.(4分)若x,y满足约束条件则z=x+2y的最大值是()A.8B.4C.2D.65.(4分)在下面四个x∈[﹣π,π]的函数图象中,函数y=|x|sin2x的图象可能是()A.B.C.D.6.(4分)等差数列{a n},等比数列{b n},满足a1=b1=1,a5=b3,则a9能取到的最小整数是()A.﹣1B.0C.2D.37.(4分)设0<p<1,随机变量ξ的分布列是则当p在(0,1)内增大时()A.E(ξ)减小,D(ξ)减小B.E(ξ)减小,D(ξ)增大C.E(ξ)增大,D(ξ)减小D.E(ξ)增大,D(ξ)增大8.(4分)如图,AB是平面α的斜线段,A为斜足,点C满足sin∠CAB=λsin∠CBA(λ>0),且在平面α内运动,则()A.当λ=1时,点C的轨迹是抛物线B.当λ=1时,点C的轨迹是一条直线C.当λ=2时,点C的轨迹是椭圆D.当λ=2时,点C的轨迹是双曲线抛物线9.(4分)已知椭圆上的三点A,B,C,斜率为负数的直线BC与y轴交于M,若原点O是△ABC的重心,且△BMA与△CMO的面积之比为,则直线BC的斜率为()A.B.C.D.10.(4分)已知函数f(x)=xe2x,下列说法正确的是()A.任意,函数y=f(x)﹣m均有两个不同的零点B.存在实数k,使得方程f(x)=k(x+2)有两个负数根C.若f(a)=f(b)(a≠b),则﹣1<a+b<0D.若实数a,b满足e2a+e2b<2e﹣1(a≠b),则f(a)≠f(b)二、填空题:多空题每小题6分,单空题每小题6分,共36分11.(6分)已知复数z满足(1+2i)z=3﹣4i,i为虚数单位,则z的虚部是,|z|=.12.(6分)双曲线的渐近线方程是,离心率为.13.(6分)某几何体的三视图如图所示,正视图为腰长为1的等腰直角三角形,侧视图、俯视图均为边长为1的正方形,则该几何体的表面积是,体积是.14.(6分)已知,则a1+a2+…a8=a3=.15.(4分)5位同学分成3组,参加3个不同的志愿者活动,每组至少1人,其中甲乙2人不能分在同一组,则不同的分配方案有AB种.(用数字作答)16.(4分)在△ABC中,A,B,C内角所对的边分别为a,b,c,已知b=2且c cos B+b cos C =4a sin B sin C,则c的最小值为.17.(4分)已知平面向量,,,满足,,则当=,则与的夹角最大.三、解答题:5小题,共74分18.(14分)已知函数的最小正周期为π,且cos2φ+cosφ=0.(1)求ω和的值;(2)若,求sinα.19.(15分)设函数f(x)=ax2﹣lnx(a∈R).(1)讨论函数f(x)的单调性;(2)若f(x)≥0恒成立,求实数a的取值范围.20.(15分)在四棱锥S﹣ABCD中,底面ABCD为直角梯形,BC⊥CD,SC=SD=CD=DA=1,CB=2,AD∥BC,,E为线段SB上的中点.(1)证明:AE∥平面SCD;(2)求直线AE与平面SBC所成角的余弦值.21.(15分)已知抛物线C:y2=2px(p>0)的焦点是F(1,0),直线l1:y=k1x,l2:y =k2x分别与抛物线C相交于点A和点B,过A,B的直线与圆O:x2+y2=4相切.(1)求直线AB的方程(含k1、k2);(2)若线段OA与圆O交于点M,线段OB与圆O交于点N,求S△MON的取值范围.22.(15分)已知数列{an}中,a1=4,,,记.(1)证明:a n>2;(2)证明:;(3)证明:.2019年浙江省金华市十校高考数学模拟试卷(4月份)参考答案与试题解析一、选择题:每小题4分,共40分1.【解答】解:集合M={x|﹣<x<},N={x|x2≤x}={x|0≤x≤1},则M∩N={x|0≤x<},故选:A.2.【解答】解:由于直线x﹣2y﹣2=0的斜率为,故所求直线的斜率等于﹣2,故所求直线的方程为y﹣0=﹣2(x﹣1),即2x+y﹣2=0,故选:C.3.【解答】解:a>b+1是a>b的充分不必要的条件;a>b﹣1是a>b的必要不充分条件;|a|>|b|是a>b的即不充分也不必要条件;2a>2b是a>b的充要条件;故选:B.4.【解答】解:作出不等式组对应的平面区域如图:,由,解得A(2,2),由z=x+2y,得y=﹣x+,平移直线y=﹣x+,由图象可知当直线经过点A,直线的截距最大,此时z最大,此时z=6,故选:D.5.【解答】解:f(﹣x)=|﹣x|sin(﹣2x)=﹣|x|sin2x=﹣f(x),即f(x)是奇函数,图象关于原点对称,排除B,D,当x=π时,f(π)=πsin2π=0,排除A,故选:C.6.【解答】解:等差数列{a n}的公差设为d,等比数列{b n}的公比设为q,q≠0,a1=b1=1,a5=b3,可得1+4d=q2,则a9=1+8d=1+2(q2﹣1)=2q2﹣1>﹣1,可得a9能取到的最小整数是0.故选:B.7.【解答】解:Eξ)=0×+1×+2×=1﹣,所以当p在(0,1)内增大时,E(ξ)减少;D(ξ)=[0﹣(1﹣)]2×+[1﹣(1﹣)]2×+(2﹣(1﹣)]2×==,所以当p在(0,1)内增大时,D(ξ)减少.故选:A.8.【解答】解:在△ABC中,∵sin∠CAB=λsin∠CBA(λ>0),由正弦定理可得:=λ,当λ=1时,BC=AC,过AB的中点作线段AB的垂面β,则点C在α与β的交线上,即点C的轨迹是一条直线,当λ=2时,BC=2AC,设B在平面α内的射影为D,连接BD,CD,设BD=h,AD=2a,则BC=,在平面α内,以AD所在直线为x轴,以AD的中点为y轴建立平面直角坐标系,设C(x,y),则CA=,CD=,CB=,∴=2,化简可得(x+)2+y2=+,∴C的轨迹是圆.故选:B.9.【解答】解:设B(x1,y1),C(x2,y2).M(0,m).A(x3,y3),直线BC的方程为y =kx+m.∵原点O是△ABC的重心,∴△BMA与△CMO的高之比为3,又△BMA与△CMO的面积之比为,则2BM=MC..即,⇒2x1+x2=0…①联立⇒整理得(4k2+1)x2+8mkx+4m2﹣4=0.x1+x2=,x1x2=…②由①②整理可得:36k2m2=1﹣m2+4k2…③∵原点O是△ABC的重心,∴,y3=﹣(y2+y1)=﹣[k(x1+x2)+2m]=﹣.∵x+4y=4,∴()2+4()2=4⇒1+4k2=4m2…④.由③④可得k2=,∵k<0.∴.故选:C.10.【解答】解:∵函数f(x)=xe2x,f′(x)=(1+2x)e2x,可知:x=﹣时,函数f(x)取得极小值即最小值.=﹣,如图所示.由图象可得:A.当<m<0时,函数y=f(x)﹣m有两个不同的零点,因此不正确;B.存在实数k,使得方程f(x)=k(x+2)有两个一正一负数根,不可能为两个负数根;C.若f(a)=f(b)(a≠b),则a+b<﹣1,因此不正确;D.若f(a)=f(b)(不妨设a≤﹣≤b<0),则e2a+e2b=e2a+e2a>e2a(1﹣2a)≥2e﹣1,因此其逆否命题正确.故选:D.二、填空题:多空题每小题6分,单空题每小题6分,共36分11.【解答】解:由(1+2i)z=3﹣4i,得z=,∴z的虚部是﹣2,|z|=.故答案为:﹣2,.12.【解答】解:由得其渐近线方程为y=±2x,a=2,c=,∴.故答案为:y=±2x;.13.【解答】解:由三视图还原原几何体如图,该几何体为四棱锥P﹣ABCD,该几何体的表面积S=S△P AB+S△P AD+S△PCD+S△PBC+S四边形ABCD==;体积V=.故答案为:,.14.【解答】解:因为,令x=1得a0+a1+a2+…a8=(2+1)(1﹣2×1)=﹣3,令x=0得a0=2,所以a1+a2+…a8=﹣5,由(1﹣2x)7展开式的通项为T r+1=(﹣2)r x r,则a3=2+=﹣476,故答案为:﹣5,﹣47615.【解答】解:根据题意,分2步进行分析:①,将5位同学分成3组,要求甲乙2人不能分在同一组,若分成1、2、2的三组,有=15种,其中甲乙分在同一组的情况有C32=3种,此时有15﹣3=12种分组方法;若分成3、1、1的三组,有=10种,其中甲乙分在同一组的情况有C31=3种,此时有10﹣3=7种分组方法;则符合题意的分法有12+7=19种;②,将分好的3组全排列,对应3个不同的志愿者活动,有A33=6种情况,则有19×6=114种不同的分配方案;故答案为:114.16.【解答】解:∵c cos B+b cos C=4a sin B sin C,∴sin C cos B+sin B cos C=4sin A sin B sin C,∴sin(B+C)=sin A=4sin A sin B sin C,∵sin A≠0,∴sin B sin C=,∴,当sin B最大值时,sin C最小,且为由正弦定理可得=,即c=2×=8sin2C,当sin C=时,则c的最小值为.故答案为:17.【解答】解:设,,的起点均为O,以O为原点建立平面坐标系,不妨设=(4,0),=(x,y),则=x2+y2,=4x,由﹣+1=0可得x2+y2﹣4x+1=0,即(x﹣2)2+y2=3,∴的终点M在以(2,0)为圆心,以为半径的圆上,同理的终点N在以(2,0)为圆心,以为半径的圆上.显然当OM,ON为圆的两条切线时,∠MON最大,即的夹角最大.设圆心为A,则AM=,∴OM==1,sin∠MOA=,∴∠MOA=60°,设MN与x轴交于点B,由对称性可知MN⊥x轴,且MN=2MB,∴MN=2MB=2•OM sin∠MOA=2×=.故答案为:.三、解答题:5小题,共74分18.【解答】解:(1)∵函数的最小正周期为=π,∴ω=2.再根据cos2φ+cosφ=2cos2φ﹣1+cosφ=0,∴cosφ=﹣1(舍去),或cosφ=,∴φ=,故f(x)=sin(2x+),故f()=sin(π+)=﹣.(2)∵f()=sin(α+)=<,∴α+为钝角,故cos(α+)=﹣=﹣,故sinα=sin[(α+)﹣]=sin(π+)cos﹣cos(π+)sin=•+•=.19.【解答】解:(1)由题意,f′(x)=(x>0).当a≤0时,f′(x)<0,函数f(x)在(0,+∞)上单调递减;当a>0时,令f′(x)=0,解得x=.∴当x∈(0,)时,f′(x)<0,当x∈(,+∞)时,f′(x)>0.∴f(x)在(0,)上单调递减,在(,+∞)上单调递增;(2)∵f(x)≥0恒成立,∴f(e)≥0,可得a≥.由(1)可得,f(x)在(0,)上单调递减,在(,+∞)上单调递增,∴f(x)的最小值为f()=.∴,解得a.因此,实数a的取值范围为[,+∞).20.【解答】(1)证明:取SC的中点F,连接EF,DF.∵E,F是SB,SC的中点,∴EF∥BC,EF=BC,又AD∥BC,AD=BC,∴EF∥AD,EF=AD,∴四边形ADFE是平行四边形,∴AE∥DF,又DF⊂平面SCD,AE⊄平面SCD,∴AE∥平面SCD.(2)解:取CD的中点O,连接SO,过O作BC的平行线OM,以O为原点,以OD,OM和平面ABCD过点O的垂线为坐标轴建立空间坐标系O﹣xyz,∵SC=CD=SD=1,∴SO=,设二面角S﹣CD﹣A的大小为α,则S(0,cosα,sinα),A(,1,0),B(﹣,2,0),C(﹣,0,0),∴E(﹣,1+cosα,sinα),∴=(0,2,0),=(,cosα,sinα),∵∠SCB=120°,∴cos<,>===cosα=﹣,∴cosα=﹣,sinα=.∴S(0,﹣,),E(,,),∴=(﹣,﹣,),=(,﹣,),设平面SCD的法向量为=(x,y,z),则,即,令x=可得=(,0,﹣1),∴cos<>===﹣,设直线AE与平面所成角为θ,则sinθ=|cos<>|=,∴cosθ=.∴直线AE与平面所成角的余弦值为.21.【解答】解:(1)焦点是F(1,0),可得=1,即p=2,设A(x1,y1),B(x2,y2),抛物线方程为y2=4x,联立y=k1x,可得A(,),同理可得B(,),若AB斜率存在,可得k AB==,AB的方程为y﹣=(x﹣),化为k1k2x﹣(k1+k2)y+4=0,AB的斜率不存在时,也满足上面的方程,则直线AB的方程为k1k2x﹣(k1+k2)y+4=0;(2)过A,B的直线与圆O:x2+y2=4相切,可得=2,化为(k1k2)2+(k1+k2)2=4,即有﹣2≤k1k2<0,cos∠AOB===,由(k1k2)2+(k1+k2)2=4,可得cos∠AOB=,sin2∠MON=,设t=5﹣2k1k2∈(5,9],则S△MON2=4sin2∠MON=4•=4•==18﹣(t+)≤18﹣2=4,当t=7,k1k2=﹣1∈[﹣2,0),(S△MON)max=2,又S△MON2>18﹣(5+)=,即S△MON>,即有S△MON的取值范围为(,2].22.【解答】解:(1)∵a n+1﹣2=a n﹣+﹣2=,∴==1﹣﹣,令t=,则m(t)==1﹣t2﹣2t3,∵a n,∴t∈(0,),∴m(t)=﹣2t﹣6t2<0,∴m(t)在(0,)单调递减,∴m(t)>m()=1﹣﹣=>0,即a n>时,>0恒成立,∴a n+1﹣2与a n﹣2同号,又a1﹣2=2>0.∴a>2.(2)=1﹣+=4(﹣)2+<4(﹣)2+=1,又=4(﹣)2+≥,∴≤<1(3)先证T n<,因为a n>2,所以<,所以T n=++…+<•n=,再证T n>﹣,∵a n+1=a n﹣+,∴=+,又=1﹣+=4(﹣)2+>,∴16a n+1>15a n,∴a n<(a n+a n+1),又a n+1﹣a n<0,∴>(a﹣a n2),所以T n=+…+>(a n+12﹣a n2)+>(4﹣16)+=﹣>﹣,故﹣<T n<.。
浙江省金华十校2019届高三4月模拟考试理综试题

浙江省金华十校2019届高三模拟考试理科综合能力测试注意事项:1.本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共32题,满分300分。
2.用黑色钢笔将答案答在答题卷上,答题前将密封线内的项目填写清楚。
3.可能用到的相对原子质量:H-l C-12 N-14 O-16 Al-27第I卷(选择题共120分)一、选择题(本题包括17小题,每小题只有一个选项符合题意,每小题6分)1.下列关于绿色植物叶肉细胞的叙述错误..的是A.叶肉细胞中的RNA主要在细胞核中合成B.黑暗状态下叶肉细胞均有A TP的合成与水解C.离体的叶肉细胞经脱分化丧失光合作用能力D.适宜光照下叶绿体释放的O2量和CO2量相等2.右图为某珊瑚礁群落演替过程中鱼的种数、鱼的个体数及珊瑚礁体积的变化。
下列叙述正确的是A.珊瑚虫和该区域的鱼组成珊瑚礁群落B.珊瑚礁体积变化影响鱼类的多样性C.该珊瑚礁群落的演替过程属于原生演替D.演替至第4年时各种鱼类个体数才达到K值3.将乙肝抗原基因导人到酵母菌中,通过发酵能大量生产乙肝疫苗。
下列叙述正确的是A.目的基因在酵母菌中表达出抗体B.目的基因的表达需要线粒体提供能量C.用限制性核酸内切酶处理目的墓因D.目的基因转录后即可用于翻译4.下图示哺乳动物胚胎工程的有关操作流程。
下列叙述正确的是A.①过程运用超数排卵技术可得到多个胚胎B.③过程可以用胃蛋白酶处理囊胚获得干细胞C.④过程需要在无菌的二氧化碳培养箱中进行D.⑤过程可以直接获得各种效应细胞毒性T细胞5.下图为物质进入骨骼肌细胞方式的示意图。
下列叙述正确的是A.O2以甲方式进入细胞溶胶内参与水的形成B.物质a、b均具有脂溶性和水溶性部分C.胰岛素通过丙方式进入细胞后促进糖元合成D.受刺激后Na+以乙方式进入细胞导致兴奋的产生6.下列有关真核细胞增殖的叙述正确的是A.增殖间期在细胞核内进行蛋白质的合成B.植物细胞增殖只受细胞分裂素的影响C.花药离体组织培养过程涉及减数分裂和有丝分裂D.有丝分裂后期非姐妹染色单体间存在自由组合现象7.化学与科学、技术、社会、环境密切相关。
2019年4月浙江省2019年第二学期金华十校高考模拟考试数学试题卷及解析

2019年4月份浙江省学考选考金华市十校高中数学模拟试卷及解析一、选择题:每小题4分,共40分1.(4分)设集合M={x|﹣<x<},N={x|x2≤x},则M∩N=()A.[0,)B.(﹣,1]C.[﹣1,)D.(﹣,0]2.(4分)过点(1,0)且与直线x﹣2y﹣2=0垂直的直线方程是()A.x﹣2y﹣1=0B.x﹣2y+1=0C.2x+y﹣2=0D.x+2y﹣1=03.(4分)已知a,b∈R,下列四个条件中,使a>b成立的充分不必要的条件是()A.a>b﹣1B.a>b+1C.|a|>|b|D.2a>2b4.(4分)若x,y满足约束条件则z=x+2y的最大值是()A.8B.4C.2D.65.(4分)在下面四个x∈[﹣π,π]的函数图象中,函数y=|x|sin2x的图象可能是()A. B.C. D.6.(4分)等差数列{a n},等比数列{b n},满足a1=b1=1,a5=b3,则a9能取到的最小整数是()A.﹣1B.0C.2D.37.(4分)设0<p<1,随机变量ξ的分布列是则当p在(0,1)内增大时()A.E(ξ)减小,D(ξ)减小B.E(ξ)减小,D(ξ)增大C.E(ξ)增大,D(ξ)减小D.E(ξ)增大,D(ξ)增大8.(4分)如图,AB是平面α的斜线段,A为斜足,点C满足sin∠CAB=λsin∠CBA(λ>0),且在平面α内运动,则()A.当λ=1时,点C的轨迹是抛物线B.当λ=1时,点C的轨迹是一条直线C.当λ=2时,点C的轨迹是椭圆D.当λ=2时,点C的轨迹是双曲线抛物线9.(4分)已知椭圆上的三点A,B,C,斜率为负数的直线BC与y轴交于M,若原点O是△ABC的重心,且△BMA与△CMO的面积之比为,则直线BC的斜率为()A. B. C. D.10.(4分)已知函数f(x)=xe2x,下列说法正确的是()A.任意,函数y=f(x)﹣m均有两个不同的零点B.存在实数k,使得方程f(x)=k(x+2)有两个负数根C.若f(a)=f(b)(a≠b),则﹣1<a+b<0D.若实数a,b满足e2a+e2b<2e﹣1(a≠b),则f(a)≠f(b)二、填空题:多空题每小题6分,单空题每小题6分,共36分11.(6分)已知复数z满足(1+2i)z=3﹣4i,i为虚数单位,则z的虚部是,|z|=.12.(6分)双曲线的渐近线方程是,离心率为.13.(6分)某几何体的三视图如图所示,正视图为腰长为1的等腰直角三角形,侧视图、俯视图均为边长为1的正方形,则该几何体的表面积是,体积是.14.(6分)已知,则a1+a2+…a8=a3=.15.(4分)5位同学分成3组,参加3个不同的志愿者活动,每组至少1人,其中甲乙2人不能分在同一组,则不同的分配方案有AB种.(用数字作答)16.(4分)在△ABC中,A,B,C内角所对的边分别为a,b,c,已知b=2且c cos B+b cos C=4a sin B sin C,则c的最小值为.17.(4分)已知平面向量,,,满足,,则当=,则与的夹角最大.三、解答题:5小题,共74分18.(14分)已知函数的最小正周期为π,且cos2φ+cosφ=0.(1)求ω和的值;(2)若,求sinα.19.(15分)设函数f(x)=ax2﹣lnx(a∈R).(1)讨论函数f(x)的单调性;(2)若f(x)≥0恒成立,求实数a的取值范围.20.(15分)在四棱锥S﹣ABCD中,底面ABCD为直角梯形,BC⊥CD,SC=SD=CD=DA=1,CB=2,AD∥BC,,E为线段SB上的中点.(1)证明:AE∥平面SCD;(2)求直线AE与平面SBC所成角的余弦值.21.(15分)已知抛物线C:y2=2px(p>0)的焦点是F(1,0),直线l1:y=k1x,l2:y=k2x分别与抛物线C相交于点A和点B,过A,B的直线与圆O:x2+y2=4相切.(1)求直线AB的方程(含k1、k2);(2)若线段OA与圆O交于点M,线段OB与圆O交于点N,求S△MON的取值范围.22.(15分)已知数列{an}中,a1=4,,,记.(1)证明:a n>2;(2)证明:;(3)证明:.2019年浙江省金华市十校高中数学模拟试卷(4月份)参考答案与试题解析一、选择题:每小题4分,共40分1.【解答】解:集合M={x|﹣<x<},N={x|x2≤x}={x|0≤x≤1},则M∩N={x|0≤x<},故选:A.2.【解答】解:由于直线x﹣2y﹣2=0的斜率为,故所求直线的斜率等于﹣2,故所求直线的方程为y﹣0=﹣2(x﹣1),即2x+y﹣2=0,故选:C.3.【解答】解:a>b+1是a>b的充分不必要的条件;a>b﹣1是a>b的必要不充分条件;|a|>|b|是a>b的即不充分也不必要条件;2a>2b是a>b的充要条件;故选:B.4.【解答】解:作出不等式组对应的平面区域如图:,由,解得A(2,2),由z=x+2y,得y=﹣x+,平移直线y=﹣x+,由图象可知当直线经过点A,直线的截距最大,此时z最大,此时z=6,故选:D.5.【解答】解:f(﹣x)=|﹣x|sin(﹣2x)=﹣|x|sin2x=﹣f(x),即f(x)是奇函数,图象关于原点对称,排除B,D,当x=π时,f(π)=πsin2π=0,排除A,故选:C.6.【解答】解:等差数列{a n}的公差设为d,等比数列{b n}的公比设为q,q≠0,a1=b1=1,a5=b3,可得1+4d=q2,则a9=1+8d=1+2(q2﹣1)=2q2﹣1>﹣1,可得a9能取到的最小整数是0.故选:B.7.【解答】解:Eξ)=0×+1×+2×=1﹣,所以当p在(0,1)内增大时,E(ξ)减少;D(ξ)=[0﹣(1﹣)]2×+[1﹣(1﹣)]2×+(2﹣(1﹣)]2×==,所以当p在(0,1)内增大时,D(ξ)减少.故选:A.8.【解答】解:在△ABC中,∵sin∠CAB=λsin∠CBA(λ>0),由正弦定理可得:=λ,当λ=1时,BC=AC,过AB的中点作线段AB的垂面β,则点C在α与β的交线上,即点C的轨迹是一条直线,当λ=2时,BC=2AC,设B在平面α内的射影为D,连接BD,CD,设BD=h,AD=2a,则BC=,在平面α内,以AD所在直线为x轴,以AD的中点为y轴建立平面直角坐标系,设C(x,y),则CA=,CD=,CB=,∴=2,化简可得(x+)2+y2=+,∴C的轨迹是圆.故选:B.9.【解答】解:设B(x1,y1),C(x2,y2).M(0,m).A(x3,y3),直线BC的方程为y=kx+m.∵原点O是△ABC的重心,∴△BMA与△CMO的高之比为3,又△BMA与△CMO的面积之比为,则2BM=MC..即,⇒2x1+x2=0…①联立⇒整理得(4k2+1)x2+8mkx+4m2﹣4=0.x1+x2=,x1x2=…②由①②整理可得:36k2m2=1﹣m2+4k2…③∵原点O是△ABC的重心,∴,y3=﹣(y2+y1)=﹣[k(x1+x2)+2m]=﹣.∵x+4y=4,∴()2+4()2=4⇒1+4k2=4m2…④.由③④可得k2=,∵k<0.∴.故选:C.10.【解答】解:∵函数f(x)=xe2x,f′(x)=(1+2x)e2x,可知:x=﹣时,函数f(x)取得极小值即最小值.=﹣,如图所示.由图象可得:A.当<m<0时,函数y=f(x)﹣m有两个不同的零点,因此不正确;B.存在实数k,使得方程f(x)=k(x+2)有两个一正一负数根,不可能为两个负数根;C.若f(a)=f(b)(a≠b),则a+b<﹣1,因此不正确;D.若f(a)=f(b)(不妨设a≤﹣≤b<0),则e2a+e2b=e2a+e2a>e2a(1﹣2a)≥2e﹣1,因此其逆否命题正确.故选:D.二、填空题:多空题每小题6分,单空题每小题6分,共36分11.【解答】解:由(1+2i)z=3﹣4i,得z=,∴z的虚部是﹣2,|z|=.故答案为:﹣2,.12.【解答】解:由得其渐近线方程为y=±2x,a=2,c=,∴.故答案为:y=±2x;.13.【解答】解:由三视图还原原几何体如图,该几何体为四棱锥P﹣ABCD,该几何体的表面积S=S△P AB+S△P AD+S△PCD+S△PBC+S四边形ABCD==;体积V=.故答案为:,.14.【解答】解:因为,令x=1得a0+a1+a2+…a8=(2+1)(1﹣2×1)=﹣3,令x=0得a0=2,所以a1+a2+…a8=﹣5,由(1﹣2x)7展开式的通项为T r+1=(﹣2)r x r,则a3=2+=﹣476,故答案为:﹣5,﹣47615.【解答】解:根据题意,分2步进行分析:①,将5位同学分成3组,要求甲乙2人不能分在同一组,若分成1、2、2的三组,有=15种,其中甲乙分在同一组的情况有C32=3种,此时有15﹣3=12种分组方法;若分成3、1、1的三组,有=10种,其中甲乙分在同一组的情况有C31=3种,此时有10﹣3=7种分组方法;则符合题意的分法有12+7=19种;②,将分好的3组全排列,对应3个不同的志愿者活动,有A33=6种情况,则有19×6=114种不同的分配方案;故答案为:114.16.【解答】解:∵c cos B+b cos C=4a sin B sin C,∴sin C cos B+sin B cos C=4sin A sin B sin C,∴sin(B+C)=sin A=4sin A sin B sin C,∵sin A≠0,∴sin B sin C=,∴,当sin B最大值时,sin C最小,且为由正弦定理可得=,即c=2×=8sin2C,当sin C=时,则c的最小值为.故答案为:17.【解答】解:设,,的起点均为O,以O为原点建立平面坐标系,不妨设=(4,0),=(x,y),则=x2+y2,=4x,由﹣+1=0可得x2+y2﹣4x+1=0,即(x﹣2)2+y2=3,∴的终点M在以(2,0)为圆心,以为半径的圆上,同理的终点N在以(2,0)为圆心,以为半径的圆上.显然当OM,ON为圆的两条切线时,∠MON最大,即的夹角最大.设圆心为A,则AM=,∴OM==1,sin∠MOA=,∴∠MOA=60°,设MN与x轴交于点B,由对称性可知MN⊥x轴,且MN=2MB,∴MN=2MB=2•OM sin∠MOA=2×=.故答案为:.三、解答题:5小题,共74分18.【解答】解:(1)∵函数的最小正周期为=π,∴ω=2.再根据cos2φ+cosφ=2cos2φ﹣1+cosφ=0,∴cosφ=﹣1(舍去),或cosφ=,∴φ=,故f(x)=sin(2x+),故f()=sin(π+)=﹣.(2)∵f()=sin(α+)=<,∴α+为钝角,故cos(α+)=﹣=﹣,故sinα=sin[(α+)﹣]=sin(π+) cos﹣cos(π+) sin=•+•=.19.【解答】解:(1)由题意,f′(x)=(x>0).当a≤0时,f′(x)<0,函数f(x)在(0,+∞)上单调递减;当a>0时,令f′(x)=0,解得x=.∴当x∈(0,)时,f′(x)<0,当x∈(,+∞)时,f′(x)>0.∴f(x)在(0,)上单调递减,在(,+∞)上单调递增;(2)∵f(x)≥0恒成立,∴f(e)≥0,可得a≥.由(1)可得,f(x)在(0,)上单调递减,在(,+∞)上单调递增,∴f(x)的最小值为f()=.∴,解得a.因此,实数a的取值范围为[,+∞).20.【解答】(1)证明:取SC的中点F,连接EF,DF.∵E,F是SB,SC的中点,∴EF∥BC,EF=BC,又AD∥BC,AD=BC,∴EF∥AD,EF=AD,∴四边形ADFE是平行四边形,∴AE∥DF,又DF⊂平面SCD,AE⊄平面SCD,∴AE∥平面SCD.(2)解:取CD的中点O,连接SO,过O作BC的平行线OM,以O为原点,以OD,OM和平面ABCD过点O的垂线为坐标轴建立空间坐标系O﹣xyz,∵SC=CD=SD=1,∴SO=,设二面角S﹣CD﹣A的大小为α,则S(0,cosα,sinα),A(,1,0),B(﹣,2,0),C(﹣,0,0),∴E(﹣,1+cosα,sinα),∴=(0,2,0),=(,cosα,sinα),∵∠SCB=120°,∴cos<,>===cosα=﹣,∴cosα=﹣,sinα=.∴S(0,﹣,),E(,,),∴=(﹣,﹣,),=(,﹣,),设平面SCD的法向量为=(x,y,z),则,即,令x=可得=(,0,﹣1),∴cos<>===﹣,设直线AE与平面所成角为θ,则sinθ=|cos<>|=,∴cosθ=.∴直线AE与平面所成角的余弦值为.21.【解答】解:(1)焦点是F(1,0),可得=1,即p=2,设A(x1,y1),B(x2,y2),抛物线方程为y2=4x,联立y=k1x,可得A(,),同理可得B(,),若AB斜率存在,可得k AB==,AB的方程为y﹣=(x﹣),化为k1k2x﹣(k1+k2)y+4=0,AB的斜率不存在时,也满足上面的方程,则直线AB的方程为k1k2x﹣(k1+k2)y+4=0;(2)过A,B的直线与圆O:x2+y2=4相切,可得=2,化为(k1k2)2+(k1+k2)2=4,即有﹣2≤k1k2<0,cos∠AOB===,由(k1k2)2+(k1+k2)2=4,可得cos∠AOB=,sin2∠MON=,设t=5﹣2k1k2∈(5,9],则S△MON2=4sin2∠MON=4•=4•==18﹣(t+)≤18﹣2=4,当t=7,k1k2=﹣1∈[﹣2,0),(S△MON)max=2,又S△MON2>18﹣(5+)=,即S△MON>,即有S△MON的取值范围为(,2].22.【解答】解:(1)∵a n+1﹣2=a n﹣+﹣2=,∴==1﹣﹣,令t=,则m(t)==1﹣t2﹣2t3,∵a n,∴t∈(0,),∴m(t)=﹣2t﹣6t2<0,∴m(t)在(0,)单调递减,∴m(t)>m()=1﹣﹣=>0,即a n>时,>0恒成立,∴a n+1﹣2与a n﹣2同号,又a1﹣2=2>0.∴a>2.(2)=1﹣+=4(﹣)2+<4(﹣)2+=1,又=4(﹣)2+≥,∴≤<1(3)先证T n<,因为a n>2,所以<,所以T n=++…+<•n=,再证T n>﹣,∵a n+1=a n﹣+,∴=+,又=1﹣+=4(﹣)2+>,∴16a n+1>15a n,∴a n<(a n+a n+1),又a n+1﹣a n<0,∴>(a﹣a n2),所以T n=+…+>(a n+12﹣a n2)+>(4﹣16)+=﹣>﹣,故﹣<T n<.。
浙江省十校联盟 2019 年4月适应性考试数学试题和答案

绝密★考试结束前浙江省十校联盟2019年4月适应性考试数学试题卷考生须知:1.全卷分试卷和答题卷,考试结束后,将答题卷上交。
2.试卷共4页,有3大题,22小题。
满分150分,考试时间120分钟。
3.答题前,请务必将自己的姓名,准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
4.请将答案做在答题卷的相应位置上,写在试卷上无效。
作图时先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}{}2340,13A x x x B x x =-->=-≤≤,则=B A C )(R A .()1,3- B .[]1,3-C .[]1,4-D .()1,4-2.双曲线22:21C x y -=的渐近线方程为 A.0x ±= B .20x y ±= C0y ±=D .20x y ±=3.如图所示,已知某几何体的三视图及其尺寸(单位:cm ),则该几何体的表面积为 A .π152cm B .π212cmC .π242cmD .33π2cm4.若复数12biZ i-=+(i b R,∈为虚数单位)的实部与虚部相等,则b 的值为 A .3B .3±C .3-D.5.将函数2()22cos f x x x =-图像上各点的横坐标伸长到原来的3倍(纵坐标不变),再向右平移8π个单位长度,则所得函数图像的一个对称中心为 A .)0,8π3( B .)1,8π3(-- C .)0,8π3(- D .)1,8π3(-俯视图侧视图正视图5665CBA 6.已知n m ,表示两条不同的直线,βα,表示两个不同的平面,且,βα⊂⊥n m ,则“βα⊥”是“m∥n ”的___________条件.A .充分不必要B .必要不充分C .充要D .既不充分也不必要 7.已知排球发球考试规则:每位考生最多可发球三次,若发球成功,则停止发球,否则一直发到3次结束为止.某考生一次发球成功的概率为(01)p p <<,发球次数为X ,若X 的数学期望() 1.75E X >,则p 的取值范围为 A .10,2⎛⎫ ⎪⎝⎭ B .70,12⎛⎫ ⎪⎝⎭ C .1,12⎛⎫ ⎪⎝⎭ D .7,112⎛⎫ ⎪⎝⎭8.已知方程1x x y y +=-表示的曲线为)(x f y =的图像,对于函数()y f x =有如下结论: ①()f x 在()+-∞∞,上单调递减; ②函数()()F x f x x =+至少存在一个零点;③()y f x =的最大值为1;④若函数()g x 和()f x 图像关于原点对称,则()y g x =由方程1y y x x +=所确定; 则正确命题序号为 A .①③ B .②③ C .①④ D .②④ 9.已知三棱柱111ABC A B C -的所有棱长均相等,侧棱ABC AA 平面⊥1.过1AB 作平面α与1BC 平行,设平面α与平面11A ACC 的交线为l ,记直线l 与直线CA BC AB ,,所成锐角分别为γβα,,,则这三个角的大小关系为 A .βγα>> B .γβα>= C .αβγ>> D .γβα=>10.已知正项数列{}{}n n b a ,满足:⎩⎨⎧+=+=++,,1011n n n n n n b a b b a a 设n n n b ac =,当43c c +最小时, 5c 的值为A .2B .514C .3D .4非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.我国南北朝时期一部数学著作《张丘建算经》卷中,第22题为:“今有女善织,日益功疾,初日织五尺,今一月共织九匹三丈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省金华十校2019届高三4月高考模拟考试数学(理科)试卷 2019.4一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项 是符合题目要求的。
1. 已知集合U={a,b,c,d,e},M={a,d},N={a,c,e},则M ∪ UN 为 A .{c,e} B .{a,b,d} C .{b,d} D .{a,c,d,e} 2. 已知复数z 1=2+i ,z 2=a -i(a ∈R ),z 1·z 2是实数,则a = A .2 B .3 C .4 D .5 3. y =f (x )是定义在R 上的函数,若a ∈R ,则“x ≠a ”是“f (x )≠f (a )”成立的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件4. 关于函数tan 23y x π⎛⎫=- ⎪⎝⎭,下列说法正确的是A .是奇函数B .最小正周期为πC .06π⎛⎫⎪⎝⎭,为图像的一个对称中心 D .其图象由y =tan2x 的图象右移3π单位得到 5. 空间中,若α,β,γ 是三个互不重合的平面,l 是一条直线,则下列命题中正确的是 A .若l ∥α,, l ∥β,则α∥β B .若α⊥β,l ⊥β,则l ∥α C .若l ⊥α,l ∥β,则α⊥β D .若α⊥β,l ∥α,则l ⊥β6. 已知集合A ={1,2,3,4,5,6},在A 中任取三个元素,使它们的和小于余下的三个元素的和,则 取法种数共有 A .4 B .10 C .15 D .20 7. 已知某几何体的三视图(单位:dm )如图所示,则该几何体的体积是A .13dm 3 B .32dm 3 C .1dm 3D .12dm 3 8. “3111a b c++”称为a ,b ,c 三个正实数的“调和平均数”,若正数x , y 满足“x , y , xy的调和平均数为3”,则x +2 y 的最小值是A .3B .5C .7D .89. 如图,已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为F 1,F 2,|F 1F 2|=4,P 是双曲线右支上的一点,F 2P 与y 轴交于点A ,△APF 1的内切圆在边PF 1上的切点为Q ,若|PQ |=1,则双曲线的离心率是A . 3B .2 C.D 10. 已知边长都为1的正方形ABCD 与DCFE 所在的平面互相垂直,点P ,Q 分别是线段BC ,正视图 侧视图 俯视图 11 1(第7题图)DE 上的动点(包括端点),PQPQ 中点的轨迹为ℜ,则ℜ 的长度为A .2 BC .2πD . 4π二、填空题:本大题有7小题,每小题4分,共28分.11. 若两直线x -2y +5=0与2x +my -5=0互相平行,则实数m = ▲ .12.已知函数1,()1,x f x x =<≥ 若f (a )+f (0)=3,则a = ▲ .13. 某程序框图如图所示,则该程序运行后输出的值是 ▲ _. 14. 二项式521+2x x ⎛⎫- ⎪⎝⎭的展开式中x 3项的系数为 ▲ .15. 甲乙两人分别参加某高校自主招生考试,能通过的概率都为23,设考试通过的人数(就甲乙而 言)为X ,则X 的方差D (X )= ▲ .16.对于不等式组2320340210x y x y x y -+⎧⎪--⎨⎪++⎩≥,≤,≥的解(x ,y ),当且仅当=2,=2x y ⎧⎨⎩时,z =x +ay取得最大值,则实数a 的取值范围是 ▲ _.17. 如图,已知:|AC |=|BC |=4,∠ACB =90°,M 为BC 的中点, D 为以AC 为直径的圆上一动点,则AM DC ⋅的最大值是 ▲ _.三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤。
18.(本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2sin tan tan cos CA B A+=.(Ⅰ)求角B 的大小;(Ⅱ)已知3a c c a+=,求11tan tan A C +的值.(第13题图)19. (本小题满分14分) 已知数列{a n }的首项a 1=a ,前n 项和为S n ,且-a 2,S n ,2a n +1成等差. (Ⅰ)试判断{a n }是否成等比数列,并说明理由;(Ⅱ)当a >0时,数列{b n }满足11b a =,且1(2)()()n n n n a b n a a a a +=--≥.记数列{b n }的前n 项和为T n ,求证:1≤aT n <2.20.(本题满分14分)如图,在三棱锥P -ABC 中,AB ⊥AC ,P A =PB =PC ,D ,E 分别是AC ,BC 的中点,AB=,AC =2,PD=Q 为线段PE 上不同于端点的一动点. (Ⅰ)求证:AC ⊥DQ ;(Ⅱ)若二面角B -AQ -E 的大小为60°,求QEPE的值.PQ21.(本小题满分15分)设椭圆2222:1(0)x y C a b a b+=>>的一个顶点与抛物线2:C x =的焦点重合,12,F F 分别是椭圆的左、右焦点,且离心率12e =⋅直线l :y =kx +m (km <0)与椭圆C 交于M N 、两点.(Ⅰ)求椭圆C 的方程;(Ⅱ)若AB 是椭圆C 经过原点O 的弦,AB ∥l ,且2||||AB MN =4.是否存在直线l ,使得2OM ON ⋅=-?若存在,求出直线l 的方程;若不存在,说明理由.22.(本小题满分15分)已知函数32()2ln 3f x x tx t x =-+⋅(t ∈R ). (Ⅰ)若曲线y =f (x )在x =1处的切线与直线y =x 平行,求实数t 的值;(Ⅱ)证明:对任意的x 1,x 2∈(0.1]及t ∈R ,都有|f (x 1)-f (x 2)|≤(|t -1|+1)|ln x 1-ln x 2|成立.金华十校2019年高考模拟考试数学(理科)卷参考答案二. 11 12.4或-3 13.3 14.-1201516.1,3⎛⎫-+∞ ⎪⎝⎭17.8+三.解答题:18.解:(Ⅰ)sin sin sin cos cos sin tan tan cos cos cos cos A B A B A BA B A B A B++=+=sin()sin cos cos cos cos A B C A B A B+==, ……………………………………………………… 3分 ∵2sin tan tan cos C A B A +=,∴sin 2sin cos cos cos C CA B A=, ∴1cos 2B =,∵0B <<π,∴B =3π.……………………………………………… 6分(Ⅱ)2222cos a c a c b ac B c a ac ac+++==, ∵3a cc a +=, ∴22cos 3b ac B ac +=,即22cos 33b ac ac π+=,∴22b ca =,……………………… 9分 而222sin sin 33sin sin sin sin 4sin sin b B ca A C A C A C π===,∴3sin sin 8A C =.…………… 12分∴11cos cos sin()tan tansin sin AC A C A C A C ++=+=sin sin sin B A C ===. ……………………………………………… 14分 19.解:(Ⅰ)∵2122n n S a a +=-+,∴当12222n n n S a a -=-+≥时, 两式相减得()11222,22n n n n n a a a a a n ++=-=故≥ ,…………………………… 3分 又当n =1时,1222122,2a a a a a =-+=得, ……………………………………… 4分当a 1=a =0时,此时a n =0,{a n }不是等比数列,{}1022n n naa a a a +≠=当时,,此时是首项为,公比为的等比数列. …………… 6分(Ⅱ)∵111,2n n b a a a-==⋅,∴2n 当≥时,()()11222n n n na b a a a a --⋅=⋅-⋅⋅- ()()1111211121212121n n n n n a a ---⎛⎫=⋅=⋅- ⎪---⋅-⎝⎭. ………………………………… 8分 ∴12n n T b b b =+++1223111111111212121212121n n a -⎡⎤⎛⎫⎛⎫⎛⎫=+-+-++- ⎪ ⎪ ⎪⎢⎥------⎝⎭⎝⎭⎝⎭⎣⎦11221n a ⎛⎫=- ⎪-⎝⎭, ∴1221n n aT =--,………………………………………………………………… 10分 ∵2n ≥,∴24n ≥,∴513n aT >≥,又1021n >-,∴2n aT <. …………… 12分而当n =1时,aT n =1,故1≤aT n <2.………………………………………………………………………… 14分 20.(Ⅰ)证明:∵P A =PB =PC ,∴P 在底面ABC 的射影是△ABC 的外心E ,∴PE ⊥面ABC ,又AC ⊂面ABC ,从而PE ⊥AC . ……………………………… 3分 又∵P A = PC ,且D 是AC 的中点,∴PD ⊥AC ,∴AC ⊥面PDE .又DQ ⊂面PDE ,∴AC ⊥DQ.………………………………… 6分 (Ⅱ)解法一:过点B 作BF⊥AE 于F ,易证BF ⊥面P AE , 过F 作FG ⊥AQ 于点G,连接BG ,则∠BGF 即为二面角B -AQ -E 的平面角.…………………… 8分 在Rt △ABF中,由30AB BAF =∠=︒得3,AF BF = 在Rt △BGF中,由60BF BGF ∠=︒,所以1GF =. 在△AQF 中,设QE h =,则AQ =由1122AQF S AQ GF AF QE =⋅⋅=⋅⋅△3h ,从而h =,………… 12分又在Rt △PED 中,PD DE =,所以PE =,从而QE PE = 14分 解法二:如图以A 为原点, AB 、AC 分别为x 轴、y 轴,建立空间直角坐标系A -xyz ,则()0,0,0A ,()B ,)E, …………………………………… 8分P ABCEDQF EG Q设点)Q h ,设面AQE 的法向量m =(x 1,y 1,z 1).由1111130,30,AE x y AQ x y hz ⎧⋅=+=⎪⎨⋅=++=⎪⎩m m得1110,0,z y =⎧⎪+= 令11x =,得()1,=m .…………… 10分 设面ABQ 的法向量n =(x 2,y 2,z 2),由2222230,30,AB AQ x y hz ⎧⋅==⎪⎨⋅=++=⎪⎩n n 得2220,0,x y hz =⎧⎨+=⎩令21y =得10,1,h ⎛⎫=- ⎪⎝⎭n .………………… 12分由1cos 602⋅︒===mn m n,得h =,又易求得PE ,所以QE h PE PE == 14分 21.解:(Ⅰ)椭圆的顶点为,即b 12c e a ==,所以2a =,∴椭圆的标准方程为22143x y+=. ……………………………………………… 4分(Ⅱ)设11(,)M x y ,22(,)N x y ,由221,43,x y y kx m ⎧+=⎪⎨⎪=+⎩得222(34)84120k x kmx m +++-=, ∴122834kmx x k +=-+,212241234m x x k -⋅=+, …………………………………… 6分∴△=22226416(43)(3)k m k m-+-=2216(1239)0km -+>,则 |MN |==, ……………………… 8分 令0m =,可得|AB , ……………………………………10分∴22||4||12AB MN k ==,化简得m k =-或m k =(舍去),…………… 12分∴21212121212[()1]OM ON x x yy x x k x x x x ⋅=+=+-++=2222222224124128512(1)234343434k k k k k k k k k ----+-+==-++++解得k = 14分 故直线l 的方程为1)y x =-或1)y x =-.……………………………… 15分22. 解:(Ⅰ) 由题2()22tf x x t x'=-+,且(1)1f '=,解得1t =.………………… 4分(Ⅱ)当12x x =时,结论明显成立, ………………………………………………… 5分 不妨设12x x <,且记|1|1t λ=-+,则1212|()()||ln ln |f x f x x x λ--≤等价于121221(ln ln )()()(ln ln )x x f x fx x x λλ---≤≤ ⇔1122()ln ()ln f x x f x x λλ++≤且1122()ln ()ln f x x f x x λλ--≥,要使得对任意的12,(0,1]x x ∈,1122()ln ()ln f x x f x x λλ++≤恒成立, 只需()f x xλ'-≥对于(0,1]x ∈恒成立,同理可得()f x xλ'≤对于(0,1]x ∈恒成立,即222t x t x x xλλ--+≤≤对于(0,1]x ∈恒成立⇔当t ∈R 时,3(|1|1)22|1|1t x tx t t --+-+-+≤≤对于(0,1]x ∈恒成立.… 9分考虑函数3()22g x x tx t =-+,(0,1]x ∈,则2()62g x x t '=-,(1)当0t ≤时,函数()g x 在(0,1]上单调递增,此时()(1)2g x g t =-≤; (2)当3t ≥时,函数()g x 在(0,1]上单调递减,此时()(0)g x g t <=;(3)当03t <<时,函数()g x 在⎛ ⎝上递减及⎤⎥⎦上递增, 此时()max{(0),(1)}max{,2}g x g g t t <=-综上,当1t <时,()2g x t -≤;当1t ≥时,()g x t ≤,所以322|1|1x tx t t -+-+≤对于(0,1]x ∈成立;………………………………… 13分为证3(|1|1)22t x tx t --+-+≤,可设函数3()|1|221h t t t tx x =-+-++, 即332(1)2,1()2()22,1t x x t h t t x x t ⎧-+=⎨-++<⎩≥,则有3()(1)222h t h x x =-+≥,又由上面3()22g x x tx t =-+的分析可知函数3222y x x =-+((0,1]x ∈)在x =处取到最小,所以3()(1)2220h t h x x =-+>≥,从而3(|1|1)22t x tx t --+-+≤对任意(0,1]x ∈恒成立.……………………… 15分。
