第2章 电阻电路的等效变换总结
合集下载
第二章 电阻电路的等效变换
＋
i
＋
… i
＋ －
u
－
K=1，2 ， i
＋ －
u
Reg
u
G1
in Gn
u
－
Geg
分流公式： 分流公式：ik=Gku=Gk/Geg i n=2时，Reg=R1R2/（R1+R2） 时 （ i1=R2/（R1+R2）， 2=R1/（R1+R2）×i ），i （ （ *混联：有串，又有并 混联：有串， 混联 1 R1 R2 R3 R4
对于△ 对于△形，各电阻中电流为：i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为：
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
＋
1、n个电压源串联：us=∑usk--------等效电压源 、 个电压源串联： 等效电压源 个电压源串联 ＋ － ＋ ○ ○ －○ us1 us2 usn。 。 注：正、负号取 。 。 。 2、n个电流源的并联： 个电流源的并联： 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
＋ uS － i ＋
i
＋
… i
＋ －
u
－
K=1，2 ， i
＋ －
u
Reg
u
G1
in Gn
u
－
Geg
分流公式： 分流公式：ik=Gku=Gk/Geg i n=2时，Reg=R1R2/（R1+R2） 时 （ i1=R2/（R1+R2）， 2=R1/（R1+R2）×i ），i （ （ *混联：有串，又有并 混联：有串， 混联 1 R1 R2 R3 R4
对于△ 对于△形，各电阻中电流为：i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为：
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
＋
1、n个电压源串联：us=∑usk--------等效电压源 、 个电压源串联： 等效电压源 个电压源串联 ＋ － ＋ ○ ○ －○ us1 us2 usn。 。 注：正、负号取 。 。 。 2、n个电流源的并联： 个电流源的并联： 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
＋ uS － i ＋
第二章电阻电路的等效变换
ab
20 100 60
120 60
ab 20 100
100 Rab＝70
ab
20 100 60
40
例2 求: Rab
5
15 6
a 20
b
缩短无
电阻支路
7
6
Rab＝10
4 a b
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7
3
例6
求: Rab c
对称电路 c、d等电位
R
R
R
c R
a R
断路 a
+a
2 +
U
6V –
(a)
b
3 9V +
(b)
解: a
+
+a U b
a +
3A 2 U
3A 3 U
b
(a)
b
(b)
例1: 求下列各电源等效变换
+a
3A 1 U
解:
(c)
b
a
+
1 +
U
3V –
(c)
b
+a
2A 5 U
(d) b
a
+
5 -
U
10V +
(d)
b
例2: 试用电压源与电流源等效变换的方法，计算2
2.1 概述
1 一些概念
1）电阻电路 仅由电源和线性电阻构成的电路。
2）等效的概念：
若结构、元件参数不相同的两部分电路N1、N2，具 有相同的电压、电流关系，则称它们彼此等效。
i
电路第2章电阻等效变换
电路
作业：
2.1、4、5 、
7、8
电路
2.5 电压源、电流源的串联和并联
Series and Parallel Sources
一、电压源的串联
二、电压源的并联
三、电流源的并联
四、电流源的串联
五、电压源、电流源及电阻的串联和并联
电路
一、n个电压源的串联 - +uS21 + uS1 + uSn -2
i + iS u -
u u1
电路
讨论题 + 10V -
I 2
2A
I ?
哪 个 答 案 对
10 I 5A 2 10 I 27A 2 10 4 I 3A 2
?
?
?
电阻的三角形联接:将三个电阻 首尾相连，形成一个三角形， 三角形的三个顶点分别与外电 路的三个结点相连。
电路
2.电阻的Y形连接
.
. .
.
.
.
.
. .
.
. .
.
.
星形连接
Y形连接 T形连接
.
电阻的星形联接:将三个电阻的一 端连在一起，另一端分别与外电 路的三个结点相连。
电路
3.电阻的Y形连接与形连接的等效变换
R31R12 R12+R23+R31 R12R23 R2 =R +R 12 23+R31 R3 = R23R31 R12+R23+R31
Y形连接与形连接的等效变换
R1 R2 R2 R3 R3 R1 R12 R3 Y→Δ R R1 R2 R2 R3 R3 R1 23 T→∏ R1 R1 R2 R2 R3 R3 R1 R31 R2
第2章 电阻电路的等效转换总结.
第二章电阻电路的等效转换◆重点：1、等效变换的概念2、电源的等效变换3、输入电阻、等效电阻的概念与计算◆难点：1、熟练地分析计算纯电阻电路的等效电阻——尤其是含有电桥或者具有对称性的复杂电路2、熟练地计算含受控源的电阻电路的等效输入电阻3、熟练地应用电源的等效变换计算分析电路等效变换：两个电路部分的外部特性相同，则这两个电路可以互称等效电路。
其中所谓“外部特性”是指对于外部电路而言其伏安关系，这样看来，所谓“等效”是只对外部电路而言，对于等效部分内部，并不等效。
比如2-1 电阻的串并联2.1.1 串联1．串联等效电阻的计算2．串联电路的分压关系以两个电阻和串联为例：。
2.1.2 并联1．并联等效电阻的计算或：2．并联电路的分流关系以两个电阻和并联为例：。
熟练地掌握分压关系与分流关系的使用：注意：1）平衡电桥的特点常常用于电阻电路的计算当时，电桥平衡，此时：◆c点电位与f点电位相等◆电阻R上电流为零因此：◆电位相等的点可以短接◆电流为零的支路可以断开2）当电路比较复杂，不容易看出电阻的串并联关系时，可以将电路的节点重新排列，对照原电路的连接关系重画电路，以便计算；3）一般情况下，不能直接使用电阻的串并联计算并不意味着必须应用变换。
通常在使用电阻的串并联计算电阻电路的等效电阻时，要灵活地分析电路的特点，充分应用电路的对称性。
例如求下面的电路的输入电阻，其中所有的电阻均为4。
在计算中就要充分利用电路的对称性。
由于电路的结构对称，电阻值又全部相等，因此兰色的电阻相当于开路。
原电路等效为2-2 电阻的Y形和形连接的等效变换2.2.1 变换公式的推导思路电阻的Y-变换公式的推导的方法是，根据等效的概念，1-2、2-3、1-3间的电压相等，且流入各个节点（1、2、3）的电流相等，根据两种电路形式分别写出其伏安关系式，各项分别相等从而得出Y-变换公式的结论：写成电导式为当然也很容易得出-Y变换公式的结论：2.2.2 主要公式当时，当时，注意：以上结论在三相电路的分析中有广泛的应用。
第02章电阻电路的等效变换(丘关源)
（1-29）
(6)恒压源并联任何元件其两端电压不变；
恒流源串联任何元件其流出电流不变；
a a
+ us
－
+ +
－
对外等效
us
－
b
c
b c
对外等效
is
+
－
d
is
d
（1-30）
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解：
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS＝＋uS1 …－uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件：uS＝uS1＝uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
（1-21）
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS＝＋uS1－uS2
R＝R1 ＋ R2
（1-22）
二、理想电流源的串联和并联
(6)恒压源并联任何元件其两端电压不变；
恒流源串联任何元件其流出电流不变；
a a
+ us
－
+ +
－
对外等效
us
－
b
c
b c
对外等效
is
+
－
d
is
d
（1-30）
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解：
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS＝＋uS1 …－uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件：uS＝uS1＝uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
（1-21）
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS＝＋uS1－uS2
R＝R1 ＋ R2
（1-22）
二、理想电流源的串联和并联
第二章 电阻电路的等效变换
Ib Ic
c
将Y形联接等效变换为∆形联结时 形联接等效变换为∆ 3R 若 Ra=Rb=Rc=RY 时，有Rab=Rbc=Rca= R∆ = 3RY； 将∆形联接等效变换为Y形联结时 形联接等效变换为Y 若 Rab=Rbc=Rca=R∆ 时，有Ra=Rb=Rc=RY =R∆/3
总目录 章目录 返回 上一页 下一页
总目录 章目录 返回 上一页 下一页
+ U –
2.3.2 电阻的并联
I + I1 U – I2 R1 R2 特点: 特点: (1)各电阻联接在两个公共的结点之间； (1)各电阻联接在两个公共的结点之间 各电阻联接在两个公共的结点之间； (2)各电阻两端的电压相同； (2)各电阻两端的电压相同； 各电阻两端的电压相同 (3)等效电阻的倒数等于各电阻倒数之和； (3)等效电阻的倒数等于各电阻倒数之和； 等效电阻的倒数等于各电阻倒数之和 1 1 1 = + Req R1 R2 (4)并联电阻上电流的分配与电阻成反比。 (4)并联电阻上电流的分配与电阻成反比 并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式： 两电阻并联时的分流公式： Req
R R ab ca R = a R +R +R ab bc ca R R bc ab R = b R +R +R ab bc ca R R ca bc R = c R +R +R ab bc ca
总目录 章目录 返回 上一页 下一页
Ia a Ra Ib Ic b Rb Rc c 等效变换
Ia
a Rab RbcRca b
第2章 电阻电路的等效变换 章
2.1 引言 2.2 电路的等效变换 2.3 电阻的串联和并联 2.4 电阻星型联结与三角型联结的等效变换 电阻星型联结与三角型联结的等效变换 2.5 电压源、电流源的串联和并联 电压源、 2.6 实际电源的两种模型及其等效变换 实际电源的两种模型及其等效变换 2.7 输入电阻
第二章--电阻电路的等效变换知识讲解
Y形R两两乘积之和
R△=
Y形不相邻R
若 R1=R2=R3=RY， 则 R12=R23=R31= R△=3 RY
2020/6/22
i1
1
R3 3
i3
R1
R2 2
i2
i'1
1
i31
i12
R31
R12
i'3 3
R23 i23 2 i'2
16
→Y
R12 = +
R1 R2 + R2 R3 + R3 R1 R3
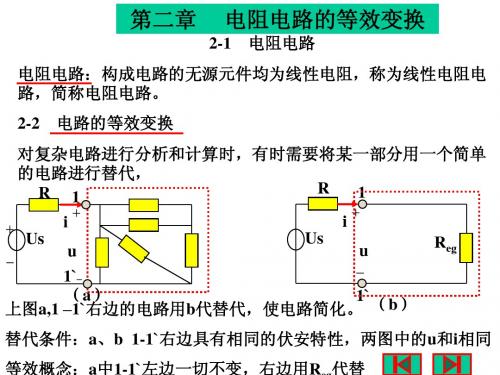
不过，虚线框内的电路，显然是不同的。
1i
R1
1i
R+
i4 R2
+
R
+
+ us
-
u -
R3
R5 u5
R4
-
+ us
-
u -
Req
1'
1'
如果需要计算 i4 和 u5 ， 就必须回到原电路， 用已求得的 i 和 u 计算。
2020/6/22
4
§2－3 电阻的串联与并联
1. 电阻的串联 电阻串联时，每个电 阻流过同一电流。
uk = Rk i
= Rk
u Req
uk =
Rk
n
u
∑ Rk
k=1
k=1，2， ···，n
串联的每个电阻，
其电压值与电阻 值成正比。
i
R1 R2
+ + u1- + u2u
-
Rn
+ un-
对于两个电阻：
i + u -
+ R1 -u1
02第二章电阻电路的等效变换
如果它们彼此等效，那么流入对应端子的电流必须分别相
等。应当有：
i1
i' 1
,
i2
i' 2
,
i3
i' 3
i' 2
2
对，各个电阻的电流分别为：
R31
'
i ' 31
i3 3
1 i'
1
i' 12
u '
12
i 12
R12
R 12
R23
i' 23
i' 2
2
u '
23
i 23
R23
按KCL，端子处 的电流分别为：
§2-1电阻的串联、并联和混联
线性电路：
由时不变线性无源元件、线性受控源和独立电源 组成的电路，称为时不变线性电路，简称线性电 路。
线性电阻电路：
如果构成电路的无源元件均为线性电阻，则称为 线性电阻电路。
直流电路：
当电路中的独立电源都是直流电源时，这类电 路简称直流电路。
等效变换： 对电路进行分析和计算时，有时可以把电路中某一 部分简化，即用一个较简单的电路替代原电路，但端口的电压电 流关系保持不变。
1. 电路特点:
i 1 R1
R2
Rn
u
u1
u2
un
1' (a) 各电阻顺序连接，流过同一电流 (KCL)；
(b) 总电压等于各串联电阻的电压之和 (KVL)。
2. 等效电阻Req
i1
R 1
R2
u
u1
u 2
Rn
i R 1
eq
u n
u
1'
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018年10月15日星期一
Req
def
∑R
k=1
n
k
8
i
+ u1 - + u2 R1
R2
+ un Rn
i 等效 + u -
+ u -
Req
(3)串联电阻的分压 uk = Rk i = Rk u < u Req 表明：电压与电阻成 正比，因此串联电阻 电路可作分压电路。
2018年10月15日星期一
p1 : p2 : : pn = G1 : G2 : : Gn 总功率 p = Gequ2 = Gequ2 = (G1+ G2+ + Gn ) u2
= G1u2 + G2u2 + + Gnu2 = p1 + p2 + + pn 表明
①电阻并联时，各电 阻消耗的功率与电 阻大小成反比；
=
C
B
2018年10月15日星期一
5
例如：
1 i
A R1 R3 1 i R5 R4 + u 1'
B
+ us -
R
+ u 1'
i4
R2
+ u5 -
+ us -
R
Req
• 欲求电流 i、电压 u和 uS 的功率等，可以用 Req 替代端子 1-1' 以右的部分，使问题得到简化。
注意：(1-1' 以右)虚线框内的电路是不同的。 如果需要计算 i4 和 u5 ，就必须回到原电路(A)，
2018年10月15日星期一
利用已求得的 i 和 u 进一步计算。
2018年10月15日星期一
6
+ ①两电路等效变换条件 u 端口具有相同的VCR； ②电路等效变换的对象 为计算外电路C(未变换) 中的电压、电流和功率； C
③电路等效变换的目的 化简电路，方便计算。
明确
i
A
+ u 繁 琐
i B
A
对外 (C电路) 等效， 对内 (A和B内) 不等效!
∑
结论：等效电导等于 并联的各电导之和。
2018年10月15日星期一
Req < Rk 等效电阻小于任
一并联的电阻。
11
i
+ u i1 i2 R1 R2 in Rn
i 等效
+ u Req
(3)并联电阻的分流 电流分配(或分流)公式 i ik = Gk u = Gk Geq Gk ik = i Geq
例 两个电阻的分压：
i
+
u -
R1 R2
+ u = R1 u u1 1 R + R 2 1 + u2 u = R2 u 2 R1 + R2
9
(4)功率
p1=R1i2，p2=R2i2， ，pn=Rni2
p1 : p2 : : pn = R1 : R2 : : Rn 总功率 p = Reqi2 = (R1 + R2 + + Rn ) i2 = R1i2 + R2i2 + + Rni2 = p1+ p2 + + pn 以上分析表明 ①电阻串联时，各电 阻消耗的功率与电 阻大小成正比；
二端 网络 不含电源 无源 一端口
i
若包含电源，则称含源一端口 (网络 )。
2018年10月15日星期一
4
2. 两端电路等效的概念
两个两端电路，若端口具有相同的电压、电 流关系，则称它们是等效(equivalence)的电路。
+ u -
i
A
等效
+ u -
i
B
对C电路中的电流、电压和功率而言，满足： C A
2018年10月15日星期一
② 等效电阻消耗的功率 等于各串联电阻消耗 功率的总和。
10
2. 电阻的并联
i
+ u i1 i2 R1 R2 in Rn
(1)电路特点 ①各电阻两端为同 一电压(KVL)； ②总电流等于流过各并联电阻的电流之和(KCL)。 (2)等效电阻 应用 KCL n def i = i1 + i2 + + in Geq Gk > Gk k=1 =uR1 + uR2 + + uRn 1 = (G1+ G2 + + Gn) u 1 1 1 + + = Geq = + Rn Req R1 R2 i = Geq u
i
+ u i1
R1
i2
R2
R2 1/R1 i1 = i= i 1/R1 + 1/R2 R1+R2 R1 电流分配与电导成正比。 同理 i2 = i + R R1 2 例 两电阻的分流： = i - i1
12
2018年10月15日星期一
(4)功率 p1 = G1u2， p2 = G2u2， ，pn = Gnu2
难点
1. 等效变换的条件和等效变换的目的； 2. 含受控源的一端口电阻网络的输入电阻的求解。 与其他章节的联系：是后续章节的基础。 友情提示：深刻理解 “等效变换”思想，熟练
掌握 “等效变换”方法，在电路分析中很重要。
2018年10月15日星期一
2
§2－1 引言
基本概念
①时不变线性电路 由非时变线性无源元件、线性受控源和 独立电源组成的电路，简称线性电路。 ②线性电阻电路
第二章
电阻电路的等效变换
学习要点
1. 电路的等效变换概念，电阻的串联和并联， Y形连接和△形连接的等效变换；
2. 电源（电压源、电流源）的串联和并联；
3. 实际电源的两种模型及其等效变换；
4. 输入电阻的概念及计算。
2018年10月15日星期一
1
重点
1. 电路等效的概念； 2. 电阻的串、并联、混联； 3. 实际电源的两种模型及其等效变换； 4. 输入电阻的概念及计算。
2018年10月15日星期一C源自简 单等 效 变 换B
7
§2－3 电阻的串联与并联
1. 电阻的串联 (1)电路特点 ①各电阻顺序连接，流 过同一电流 (KCL)；
i
+ u -
+ u1 - + u2 R1 R2
+ un Rn
②总电压等于各串联电阻的电压之和 (KVL)。 u = u1 + u2 + + un 结论：串联电路 (2)等效电阻 由欧姆定律 的总电阻等于各 u = R1i + R2 i + + Rn i 分电阻之和。 = (R1+ R2 + + Rn) i = Req i
仅由电源和线性电阻构成的电路。 分析依据和方法
①依据：欧姆定律和基尔霍夫定律 (两类约束) ； ②方法：等效变换法，也称化简法。
2018年10月15日星期一
3
§2－2 电路的等效变换 1. 两端电路 任何一个复杂的电路，向外引出两个端钮，且从 一个端子流入的电流等于从另一端子流出的电流，
则称这一电路为二端网络 (或称一端口网络)。 i
Req
def
∑R
k=1
n
k
8
i
+ u1 - + u2 R1
R2
+ un Rn
i 等效 + u -
+ u -
Req
(3)串联电阻的分压 uk = Rk i = Rk u < u Req 表明：电压与电阻成 正比，因此串联电阻 电路可作分压电路。
2018年10月15日星期一
p1 : p2 : : pn = G1 : G2 : : Gn 总功率 p = Gequ2 = Gequ2 = (G1+ G2+ + Gn ) u2
= G1u2 + G2u2 + + Gnu2 = p1 + p2 + + pn 表明
①电阻并联时，各电 阻消耗的功率与电 阻大小成反比；
=
C
B
2018年10月15日星期一
5
例如：
1 i
A R1 R3 1 i R5 R4 + u 1'
B
+ us -
R
+ u 1'
i4
R2
+ u5 -
+ us -
R
Req
• 欲求电流 i、电压 u和 uS 的功率等，可以用 Req 替代端子 1-1' 以右的部分，使问题得到简化。
注意：(1-1' 以右)虚线框内的电路是不同的。 如果需要计算 i4 和 u5 ，就必须回到原电路(A)，
2018年10月15日星期一
利用已求得的 i 和 u 进一步计算。
2018年10月15日星期一
6
+ ①两电路等效变换条件 u 端口具有相同的VCR； ②电路等效变换的对象 为计算外电路C(未变换) 中的电压、电流和功率； C
③电路等效变换的目的 化简电路，方便计算。
明确
i
A
+ u 繁 琐
i B
A
对外 (C电路) 等效， 对内 (A和B内) 不等效!
∑
结论：等效电导等于 并联的各电导之和。
2018年10月15日星期一
Req < Rk 等效电阻小于任
一并联的电阻。
11
i
+ u i1 i2 R1 R2 in Rn
i 等效
+ u Req
(3)并联电阻的分流 电流分配(或分流)公式 i ik = Gk u = Gk Geq Gk ik = i Geq
例 两个电阻的分压：
i
+
u -
R1 R2
+ u = R1 u u1 1 R + R 2 1 + u2 u = R2 u 2 R1 + R2
9
(4)功率
p1=R1i2，p2=R2i2， ，pn=Rni2
p1 : p2 : : pn = R1 : R2 : : Rn 总功率 p = Reqi2 = (R1 + R2 + + Rn ) i2 = R1i2 + R2i2 + + Rni2 = p1+ p2 + + pn 以上分析表明 ①电阻串联时，各电 阻消耗的功率与电 阻大小成正比；
二端 网络 不含电源 无源 一端口
i
若包含电源，则称含源一端口 (网络 )。
2018年10月15日星期一
4
2. 两端电路等效的概念
两个两端电路，若端口具有相同的电压、电 流关系，则称它们是等效(equivalence)的电路。
+ u -
i
A
等效
+ u -
i
B
对C电路中的电流、电压和功率而言，满足： C A
2018年10月15日星期一
② 等效电阻消耗的功率 等于各串联电阻消耗 功率的总和。
10
2. 电阻的并联
i
+ u i1 i2 R1 R2 in Rn
(1)电路特点 ①各电阻两端为同 一电压(KVL)； ②总电流等于流过各并联电阻的电流之和(KCL)。 (2)等效电阻 应用 KCL n def i = i1 + i2 + + in Geq Gk > Gk k=1 =uR1 + uR2 + + uRn 1 = (G1+ G2 + + Gn) u 1 1 1 + + = Geq = + Rn Req R1 R2 i = Geq u
i
+ u i1
R1
i2
R2
R2 1/R1 i1 = i= i 1/R1 + 1/R2 R1+R2 R1 电流分配与电导成正比。 同理 i2 = i + R R1 2 例 两电阻的分流： = i - i1
12
2018年10月15日星期一
(4)功率 p1 = G1u2， p2 = G2u2， ，pn = Gnu2
难点
1. 等效变换的条件和等效变换的目的； 2. 含受控源的一端口电阻网络的输入电阻的求解。 与其他章节的联系：是后续章节的基础。 友情提示：深刻理解 “等效变换”思想，熟练
掌握 “等效变换”方法，在电路分析中很重要。
2018年10月15日星期一
2
§2－1 引言
基本概念
①时不变线性电路 由非时变线性无源元件、线性受控源和 独立电源组成的电路，简称线性电路。 ②线性电阻电路
第二章
电阻电路的等效变换
学习要点
1. 电路的等效变换概念，电阻的串联和并联， Y形连接和△形连接的等效变换；
2. 电源（电压源、电流源）的串联和并联；
3. 实际电源的两种模型及其等效变换；
4. 输入电阻的概念及计算。
2018年10月15日星期一
1
重点
1. 电路等效的概念； 2. 电阻的串、并联、混联； 3. 实际电源的两种模型及其等效变换； 4. 输入电阻的概念及计算。
2018年10月15日星期一C源自简 单等 效 变 换B
7
§2－3 电阻的串联与并联
1. 电阻的串联 (1)电路特点 ①各电阻顺序连接，流 过同一电流 (KCL)；
i
+ u -
+ u1 - + u2 R1 R2
+ un Rn
②总电压等于各串联电阻的电压之和 (KVL)。 u = u1 + u2 + + un 结论：串联电路 (2)等效电阻 由欧姆定律 的总电阻等于各 u = R1i + R2 i + + Rn i 分电阻之和。 = (R1+ R2 + + Rn) i = Req i
仅由电源和线性电阻构成的电路。 分析依据和方法
①依据：欧姆定律和基尔霍夫定律 (两类约束) ； ②方法：等效变换法，也称化简法。
2018年10月15日星期一
3
§2－2 电路的等效变换 1. 两端电路 任何一个复杂的电路，向外引出两个端钮，且从 一个端子流入的电流等于从另一端子流出的电流，
则称这一电路为二端网络 (或称一端口网络)。 i