[精编]初一上期末数学试卷含解析
精品解析七年级上学期期末考试数学试题(含答案) (共5套) (3)

七年级数学上学期期末质量检测试题七年级数学参考答案2017.111、 ②③④ 12、 ⎪⎭⎫⎝⎛+y x 23 13、 1 14、 a+2b 15、 3 16、 71017、 1 18、 41-19、 16120、 -27或-1 。
三、解答题(满分60分) 21、解:5366112119722÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛+--- ()5633284÷-+--==-5÷5=-1................................................................................6分 22、解(1)()()⎥⎦⎤⎢⎣⎡+-+--ab a a ab a 2214322ab a a ab a --++-=214322a ab a 21322-+-=...................................................................4分 当a=-2,b=1时,原式=()()22112342-⨯-⨯-⨯+⨯-=-13..............................6分 (2)()()15326222-+--+-+y x bx y ax x15326222+-+-+-+=y x bx y ax x()()663222+-++-=y x a x b .....................................................................9分因为多项式的值与x 无关,所以可得,2-2b=0且a+3=0 所以a=-3,b=1...................................................................................................12分 23、解:(1)8,15.........................................................................................4分(2)y=3n-1....................................................................................8分(3)把n=2016代入y=3n-1,得y=6047所以第2016行白球和黑球的总数为6047个。
第一学期期末考试七年级数学试卷(解析版)

精品基础教育教学资料,请参考使用,祝你取得好成绩!第一学期期末素质测试 七年级数学试题一、选择题(每小题4分,计40分)1. 3的相反数的倒数是( ) A. 3- B. 13-C. 3D. 132.某市实现生产总值达280亿的目标,用科学记数法表示“280亿”为( ) A. 92810⨯ B. 82.810⨯ C. 92.810⨯ D. 102.810⨯3.下列说法中正确的是( ) A. 0不是单项式; B. 316x π的系数为16; C.27ah的次数为2; D. 365x y +-不是多项式; 4.下列说法中,其中正确的的个数是( ) (1)有理数中,有绝对值最小的数;(2)有理数不是整数就是分数;(3)当a 表示正有理数,则a -一定是负数;(4)a 是大于1-的负数,则2a 小于3aA. 1B. 2C. 3D.45.甲、乙两个超市为了促销一种定价相同的商品,甲超市连续两次降价10%,乙超市一次性降价20%,购买此商品更合算的超市是( )A. 甲超市B. 乙超市C. 两超市一样D.与商品价格有关6.下列四个图形中,经过折叠能围成如图一所示的几何图形的是( )(图一)DCA7.在有理数范围内定义运算“*”,其规则为2*3a bA B +=-,则方程(2*3)(4*x)49=的解为( )A. 3- B. 55- C. 56- D.558.方程213x -=与方程3103a x--=的解相同,则的值为( ) A. 3 B. 2 C. 1 D. 539.如图二,在下面的四个几何体中,从它们各自的正面和左面看,不相同的是( )10.下列说法中,不正确的有( ) (1)正方体有8个顶点和6个面;(2)两个锐角的和一定大于90°;(3)若2AOB BOC ∠=∠,则OC 是AOB ∠的平分线;(4)两点之间,线段最短; (5)钝角的补角一定大于这个角的本身;(6)射线OA 也可以表示为射线AO A. 2个 B. 3个 C. 4个 D.5个 二、填空题(每小题5分,计20分)11.若多项式22232(5y 3x mx )x -+-+的值与x 无关,则m 的等于________; 12.写出一个满足下列条件的一元一次方程:(1)未知数的系数为23-;(2)方程的解是6,则这样的方程可写为_____________________________;13.如果线段10AB =,点C 、D 在直线AB 上,6BC =,D 是AC 的中点,则A 、D 两点间的距离是____________;14.有理数a 和b 在数轴的位置如图三所示,则下列结论中:(1) 0a b -> (2) 0ab > (3) 0a b -<< (4) a b a -<-< (5) |a ||b ||a b |+=-其中正确的是________________________(把正确的结论的序号都选上) 三、解答题(共8小题,计90分) 15.(8分)计算:23213|3|(3)()24348-------⨯16.(10分)先化简,再求值:22228102(2a 10ab 8b )a ab b -+--+,其中12a =,13b =-17.(10分)解方程:113(x 1)45225x x x --+=-图三18.(12分)李明家买了一辆轿车,他连续记录了一周中每天行驶的路程(如下表),以为标。
精品解析七年级上学期期末考试数学试题(含答案) (共4套)

七年级数学(上)期末考试试题一、选择题(每小题2,共12分)1. 下列方程中,是一元一次方程的是()A. =3B. x2+1=5C. x=0D. x+2y=3【答案】C故选C.2. 若a>1,则a,﹣a,从大到小排列正确的是()A. a>﹣a>B. a>>﹣aC. >﹣a>aD. >﹣a>a>【答案】B【解析】∵a>1,∴﹣a<0,0<<1,∴a>>﹣a,故选B.3. 下列各式中,正确的是()A. ﹣(2x+5)=2x+5B. ﹣(4x﹣2)=﹣2x+2C. ﹣a+b=﹣(a﹣b)D. 2﹣3x=(3x+2)【答案】C【解析】A、原式=﹣2x﹣5,故A选项错误;B、原式=﹣2x+1,故B选项错误;C、原式=﹣(a﹣b),故C选项正确;D、原式=﹣(3x﹣2),故D选项错误,故选C.4. 由5个大小相同的正方体组成的几何体如图所示,从正面看到的图形是()A. B. C. D.【答案】A【解析】从正面看易得下面一层有3个正方形,上面一层中间有一个正方形,故选A.5. 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为()A. 69°B. 111°C. 159°D. 141°【答案】D【解析】试题分析:如下图,由题意得:∠1=54°,∠2=15°,计算出∠3=90°-54°=36°,再计算∠AOB=36°+90°+15°=141°.故选:D.考点:方位角6. 下列说法中,正确的是()①射线AB和射线BA是同一条射线;②若AB=BC,则点B为线段AC的中点;③同角的补角相等;④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.A. ①②B. ②③C. ②④D. ③④【答案】D【解析】①射线AB和射线BA不是同一条射线,错误;②若AB=BC,点B在线段AC上时,则点B为线段AC的中点,错误;③同角的补角相等,正确;④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10,正确,故选D.【点睛】本题考查了直线、射线、线段;两点间的距离;余角和补角等知识,注意基本概念的掌握是解题的关键.二、填空题(每小题3分,共24分)7. 单项式﹣x2y的次数是_____.【答案】3【解析】单项式的次数是指所有字母指数的和,2+1=3,所以单项式﹣x2y的次数是3,故答案为:3.8. 阅览室某一书架上原有图书20本,规定每天归还图书为正,借出图书为负,经过两天借阅情况如下:(﹣3,+1),(﹣1,+2),则该书架上现有图书_____本.【答案】19【解析】由题意可得20﹣3+1﹣1+2=19本.9. 科学家们发现,太空中距离银河系约2500000光年之遥的仙女星系正在向银河系靠近.其中2500000用科学记数法表示为_____.【答案】2.5×106【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数,2500000用科学记数法表示为2.5×106,故答案为2.5×106.10. 如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为_____.【答案】61°32'【解析】∠β=180°﹣∠α=180°﹣118°28'=61°32',故答案为:61°32'.【点睛】本题考查了平角的定义,熟知平角的定义是解题的关键.11. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是_____.【答案】两点之间线段最短【解析】田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是:两点之间线段最短,故答案为:两点之间线段最短.12. 已知,m,n互为相反数,p、q互为倒数,x的绝对值为2,则代数式+2013pq+的值为_____.【答案】2017【解析】由题意可知,m+n=0,pq=1,x=±2,∴ +2013pq+=0+2013×1+(±2)2=0+2013+4=2017,故答案为:2017.13. 一件商品按成本价提高20%标价,然后打9折出售,此时仍可获利16元,则商品的成本价为_____元.【解析】设成本价为x元,则,解得x=200.14. 如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),把剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则拼得的长方形的周长为_____cm.(用含a的代数式表示)【答案】(4a+16)【解析】根据题意得,长方形的宽为(a+4)﹣(a+1)=3,则拼成得长方形的周长为:2(a+4+a+1+3)=2(2a+8)=(4a+16)cm,故答案为:(4a+16).【点睛】本题主要考查了整式加减的应用,关键是根据题意列出式子.三、解答题(一)(每小题5分,共20分)15. 计算:(2a2b﹣5ab)﹣2(﹣ab+a2b)【答案】﹣3ab【解析】试题分析:去括号后合并同类项即可得.试题解析:原式=2a2b﹣5ab+2ab﹣2a2b=﹣3ab.16. 解方程:﹣=2.【答案】﹣12【解析】试题分析:按去分母、去括号、移项、合并同类项、系数化为1的步骤进行求解即可.试题解析:去分母得,3(x+2)﹣2(2x﹣3)=24,去括号得,3x+6﹣4x+6=24,移项得,3x+6﹣4x+6=24,合并同类项得,﹣x=12,系数化为1得,x=﹣12.17. 计算:﹣14﹣(﹣2)3×﹣16×(﹣+)学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...试题解析:原式=﹣14﹣(﹣8)×﹣8+4﹣6=﹣14+2﹣10=﹣22.18. 已知如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,求∠AOD的度数.【答案】110°【解析】试题分析:首先根据角平分线定义可得∠BOD=2∠BOC=70°,再根据邻补角的性质可得∠AOD的度数.试题解析:∵OC平分∠DOB,∴∠BOD=2∠BOC =2×35°=70°,又∵∠AOB=180°,∴∠AOD=∠AOB﹣∠DOB=180°﹣70°=110°.【点睛】本题主要考查了角平分线定义,关键是掌握角平分线把角分成相等的两部分.四、解答题(二)(每小题7分,共28分)19. 如图,C、D是线段AB上的两点,若CB=4cm,DB=7cm,且D是AC的中点,求AB的长.【答案】10cm【解析】试题分析:根据CB=4cm,DB=7cm可求出DC的长,再根据D是AC的中点可得出AD的长,再根据AB=AD+DB即可求出答案.试题解析:∵CB=4cm,DB=7cm,∴DC=DB﹣CB=3cm,又∵D是AC的中点,∴AD=DC=3cm,∴AB=AD+DB=10cm.20. 列方程解应用题:在某中学矩形的“我的中国梦”征文活动中,七年级和八年级共收到118篇,且七年级收到的征文篇数比八年级收到的征文篇数的一半还少2篇,求七年级收到的征文有多少篇?【答案】38篇【解析】试题分析:根据“七年级收到的征文篇数是八年级收到的征文篇数的一半还少2篇” 设八年级收到的征文有x篇,则七年级收到的征文有(x-2)篇;根据“七年级和八年级共收到征文118篇”列方程,解出方程即可.试题解析:设八年级收到的征文有x篇,则七年级收到的征文有(x﹣2)篇,根据题意得:(x﹣2)+x=118,解得:x=80,∴x﹣2=38,答:七年级收到的征文有38篇.21. 已知m、x、y满足:(1)﹣2ab m与4ab3是同类项;(2)(x﹣5)2+|y﹣|=0.求代数式:2(x2﹣3y2)﹣3()的值.【答案】【解析】试题分析:由同类项的定义可得m的值,由非负数之和为0,非负数分别为0可得出x、y的值,代入所求式子中计算即可得到结果.试题解析:∵﹣2ab m与4ab3是同类项,(x﹣5)2+|y﹣|=0,∴m=3,x=5,y=,则原式=2x2﹣6y2﹣2x2+3y2+3m=﹣3y2+3m=﹣+9=.22. 如图所示是一个长方形.(1)根据图中尺寸大小,用含x的代数式表示阴影部分的面积S;(2)若x=3,求S的值.【答案】(1) 8+2x (2) 14【解析】试题分析:根据图形可知:阴影部分的面积可用长方形的面积减去两个直角三角形的面积.试题解析:(1)由图形可知:S=4×8-×4×8-×4(4-x)=16-8+2x=8+2x(2)将x=3代入上式,S=8+2×3=14五、解答题(三)(每小题8分,共16分)23. 某水果销售店用1000元购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如表所示:进价(元/千克)售价(元/千克)甲种 5 8乙种9 13(1)这两种水果各购进多少千克?(2)若该水果店按售价销售完这批水果,获得的利润是多少元?【答案】(1) 75千克(2) 495元【解析】试题分析:(1)首先设甲种水果x千克,则乙种水果(140-x)千克,根据进价总数列出方程,求出x的值;(2)根据每种水果的利润得出总利润.试题解析:(1)设购进甲种水果x千克,则购进乙种水果(140﹣x)千克,根据题意得:5x+9(140﹣x)=1000,解得:x=65,∴140﹣x=75(千克),答:购进甲种水果65千克,乙种水果75千克。
七年级上册数学 期末试卷测试卷(解析版)

七年级上册数学期末试卷测试卷(解析版)一、初一数学上学期期末试卷解答题压轴题精选(难)1.已知,,点E是直线AC上一个动点(不与A,C重合),点F是BC边上一个定点,过点E作,交直线AB于点D,连接BE,过点F作,交直线AC于点G.(1)如图①,当点E在线段AC上时,求证:.(2)在(1)的条件下,判断这三个角的度数和是否为一个定值?如果是,求出这个值,如果不是,说明理由.(3)如图②,当点E在线段AC的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出之间的关系.(4)当点E在线段CA的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出之间的关系.【答案】(1)解:∵∴∵∴∴(2)解:这三个角的度数和为一个定值,是过点G作交BE于点H∴∵∴∴∴即(3)解:过点G作交BE于点H∴∵∴∴∴即故的关系仍成立(4)不成立| ∠EGF-∠DEC+∠BFG=180°【解析】【解答】解:(4)过点G作交BE于点H∴∠DEC=∠EGH∵∴∴∠HGF+∠BFG=180°∵∠HGF=∠EGF-∠EGH∴∠HGF=∠EGF-∠DEC∴∠EGF-∠DEC+∠BFG=180°∴(2)中的关系不成立,∠EGF、∠DEC、∠BFG之间关系为:∠EGF-∠DEC+∠BFG=180°故答案为:不成立,∠EGF-∠DEC+∠BFG=180°【分析】(1)根据两条直线平行,内错角相等,得出;两条直线平行,同位角相等,得出,即可证明.(2)过点G作交BE于点H,根据平行线性质定理,,,即可得到答案.(3)过点G作交BE于点H,得到,因为,所以,得到,即可求解.(4)过点G作交BE于点H,得∠DEC=∠EGH,因为,所以,推得∠HGF+∠BFG=180°,即可求解.2.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为________;(2)当△PMN所放位置如图②所示时,求证:∠PFD−∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.【答案】(1)∠PFD+∠AEM=90°(2)过点P作PG∥AB∵AB∥CD,∴PG∥AB∥CD,∴∠AEM=∠MPG,∠PFD=∠NPG∵∠MPN=90°∴∠NPG-∠MPG=90°∴∠PFD-∠AEM=90°;(3)设AB与PN交于点H∵∠P=90°,∠PEB=15°∴∠PHE=180°-∠P-∠PEB=75°∵AB∥CD,∴∠PFO=∠PHE=75°∴∠N=∠PFO-∠DON=45°.【解析】【解答】(1)过点P作PH∥AB∵AB∥CD,∴PH∥AB∥CD,∴∠AEM=∠MPH,∠PFD=∠NPH∵∠MPN=90°∴∠MPH+∠NPH=90°∴∠PFD+∠AEM=90°故答案为:∠PFD+∠AEM=90°;【分析】(1)过点P作PH∥AB,然后根据平行于同一条直线的两直线平行可得PH∥AB∥CD,根据平行线的性质可得∠AEM=∠MPH,∠PFD=∠NPH,然后根据∠MPH+∠NPH=90°和等量代换即可得出结论;(2)过点P作PG∥AB,然后根据平行于同一条直线的两直线平行可得PG∥AB∥CD,根据平行线的性质可得∠AEM=∠MPG,∠PFD=∠NPG,然后根据∠NPG-∠MPG=90°和等量代换即可证出结论;(3)设AB与PN 交于点H,根据三角形的内角和定理即可求出∠PHE,然后根据平行线的性质可得∠PFO=∠PHE,然后根据三角形外角的性质即可求出结论.3.已知:O是直线AB上的一点,是直角,OE平分.(1)如图1.若.求的度数;(2)在图1中,,直接写出的度数(用含a的代数式表示);(3)将图1中的绕顶点O顺时针旋转至图2的位置,探究和的度数之间的关系.写出你的结论,并说明理由.【答案】(1)解:∵是直角,,,,∵OE平分,,.(2)解:是直角,,,,∵OE平分,,(3)解:,理由是:,OE平分,,,,,即【解析】【分析】(1)根据平角的定义得出∠BOD,∠COB的度数,根据角平分线的定义得出∠BOE=∠BOC=75°,根据角的和差,由∠DOE=∠BOE−∠BOD即可算出答案;(2)根据平角的定义得出∠BOD90°−a ,∠COB180°−a ,根据角平分线的定义得出∠BOE=∠BOC=90°−a,根据角的和差,由∠DOE=∠BOE−∠BOD即可算出答案;(3)∠AOC=2∠DOE ,根据平角的定义得出∠BOC=180°−∠AOC,根据角平分线的定义得出∠BOE=∠BOC=90°−∠AOC ,根据角的和差得出∠BOD=90°−∠BOC=90°−(180°−∠AOC)=∠AOC−90° ,∠DOE=∠BOD+∠BOE,再整体替换即可得出答案。
七年级数学上册期末试卷测试卷(解析版)
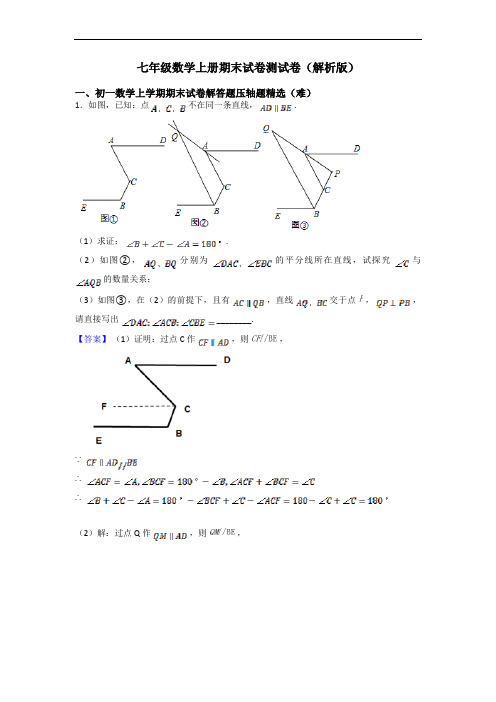
七年级数学上册期末试卷测试卷(解析版)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图,已知:点不在同一条直线, .(1)求证: .(2)如图②,分别为的平分线所在直线,试探究与的数量关系;(3)如图③,在(2)的前提下,且有,直线交于点,,请直接写出 ________.【答案】(1)证明:过点C作,则,∵∴∴(2)解:过点Q作,则,∵,∴∵分别为的平分线所在直线∴∴∵∴(3):1:2:2【解析】【解答】解:(3)∵∴∴∵∴∵∴∴∴∴ .故答案为: .【分析】(1)过点C作,则,再利用平行线的性质求解即可;(2)过点Q作,则,再利用平行线的性质以及角平分线的性质得出,再结合(1)的结论即可得出答案;(3)由(2)的结论可得出,又因为,因此,联立即可求出两角的度数,再结合(1)的结论可得出的度数,再求答案即可.2.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=________;(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=∠AOM,求∠NOB的度数.【答案】(1)25°(2)解:∠BOC=65°,OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°(3)解:∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解:(1)∠MON=90,∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】(1)根据∠MON和∠BOC的度数可以得到∠MON的度数;(2)根据角平分线的性质,由∠BOC=65°,可以求得∠BOM的度数,然后由∠NOM-90°,可得∠BON的度数,从而得解;(3)由∠BOC=65°,∠NOM=90°,∠NOC= ∠AOM,从而可求得∠NOC的度数,然后由∠BOC=65°,从而得解.3.如图,两个形状、大小完全相同的含有30。
七年级上册数学 期末试卷测试卷(解析版)

七年级上册数学 期末试卷测试卷(解析版)一、选择题1.下列说法中不正确的是( ) A .两点之间线段最短B .过直线外一点有且只有一条直线与这条直线平行C .直线外一点与直线上各点连接的所有线段中,垂线段最短D .若 AC=BC ,则点 C 是线段 AB 的中点 2.下列运算正确的是( ) A .332(2)-=- B .22(3)3-=- C .323233-⨯=-⨯ D .2332-=- 3.已知关于x 的方程34x a -=的解是x a =-,则a 的值是( )A .1B .2C .1-D .2-4.在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点。
该几何体模型可能是( ) A .球 B .三棱锥 C .圆锥 D .圆柱 5.己知x=2是关于x 的一元一次方程ax-6+a=0 的解,则a 的值为( ) A .2B .2-C .1D .06.2020的相反数是( )A .2020B .﹣2020C .12020D .﹣120207.有理数a 、b 在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果为( )A .2aB .-2bC .-2aD .2b8.下列图形经过折叠不能围成棱柱的是( ).A .B .C .D .9.小红在计算23202011114444⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭时,拿出 1 张等边三角形纸片按如图所示方式进行操作.①如图1,把 1 个等边三角形等分成 4 个完全相同的等边三角形,完成第 1 次操作;②如图 2,再把①中最上面的三角形等分成 4 个完全相同的等边三角形,完成第 2 次操作;③如图 3,再把②中最上面的三角形等分成 4 个完全相同的等边三角形,······依次重复上述操作.可得23202011114444⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值最接近的数是( )A .13B .12C .23D .110.计算233235x y y x -的正确结果是( ) A .232x y B .322x yC .322x y -D .232x y -11.下列运算正确的是( )A .332(2)-=-B .22(3)3-=-C .323233-⨯=-⨯D .2332-=-12.一个几何体的侧面展开图如图所示,则该几何体的底面是( )A .B .C .D .13.如图,OA 方向是北偏西40°方向,OB 平分∠AOC ,则∠BOC 的度数为( )A .50°B .55°C .60°D .65°14.-5的相反数是( ) A .15B .±5C .5D .-1515.如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的主视图为( )A .B .C .D .二、填空题16.如图,AOB ∠的度数是___________︒17.如图,已知,,AB DE BAC m CDE n ∠=︒∠=︒∕∕,则ACD ∠=___________°.18.单项式-4x 2y 的次数是__.19.若3a b -=,则代数式221b a -+的值等于________.20.点A 在数轴上距离原点2个单位长度,将点沿着数轴向右移动3个单位长度得到点B ,则点B 表示的数是_____.21.用两钉子就能将一根细木条固定在墙上,其数学原理是______.22.科学家们测得光在水中的速度约为225000000米/秒,数字225000000用科学计数法表示为___________.23.在 -2 、-3 、4、5 中选取2个数相除,则商的最小值是________.24.如图,从A 到B 有多条道路,人们通常会走中间的直路,而不走其他的路,这其中的道理是 .25.若线段AB =8cm ,BC =3cm ,且A 、B 、C 三点在同一条直线上,则AC =______cm .三、解答题26.计算:(1)()375244128⎛⎫-+-⨯- ⎪⎝⎭(2)()24123-+⨯-27.如图,直线AB 、CD 相交于点O ,BOD ∠与∠BOE 互为余角,18BOE ∠=︒.求AOC ∠的度数.28.运动场环形跑道周长400米,小红跑步的速度是爷爷的53倍,小红在爷爷前面20米,他们沿跑道的同一方向同时出发,5min 后小红第一次与爷爷相遇.小红和爷爷跑步的速度各是多少? 29.计算 (1)157()362612+-⨯ (2)()421723-+÷-30.同学们,我们知道图形是由点、线、面组成,结合具体实例,已经感受到“点动成线,线动成面”的现象,下面我们一起来进一步探究: (概念认识)已知点 P 和图形 M ,点 B 是图形M 上任意一点,我们把线段 PB 长度的最小值叫做点P 与图形 M 之 间的距离.例如,以点M 为圆心,1cm 为半径画圆如图1,那么点 M 到该圆的距离等于1cm ;若点N 是圆上一点,那么点 N 到该圆的距离等于 0cm ;连接 M N ,若点 Q 为线段 M N 中点,那么点 Q 到该圆的距离等于0.5cm ,反过来,若点 P 到已知点 M 的距离等于1cm ,那么满足条件的所有点 P 就构成了以点 M 为圆心,1cm 为半径的圆.(初步运用)(1)如图 2,若点 P 到已知直线 m 的距离等于1cm ,请画出满足条件的所有点 P .(深入探究)(2)如图3,若点 P 到已知线段的距离等于1cm ,请画出满足条件的所有点 P .(3)如图 4,若点 P 到已知正方形的距离等于1cm ,请画出满足条件的所有点 P .31.如图1,已知数轴上A ,B 两点表示的数分别为-9和7.(1)AB =(2)点P 、点Q 分别从点A 、点B 出发同时向右运动,点P 的速度为每秒4个单位,点Q 的速度为每秒2个单位,经过多少秒,点P 与点Q 相遇?(3)如图2,线段AC 的长度为3个单位,线段BD 的长度为6个单位,线段AC 以每秒4个单位的速度向右运动,同时线段BD 以每秒2个单位的速度向左运动,设运动时间为t 秒①t 为何值时,点B 恰好在线段AC 的中点M 处.②t 为何值时,AC 的中点M 与BD 的中点N 距离2个单位.32.先化简,再求值:()()22225343a b abab a b ---+,其中a=-2,b=12; 33.P 是线段AB 上任一点,12AB cm =,C D 、两点分别从P B 、同时向A 点运动,且C 点的运动速度为2/cm s ,D 点的运动速度为3/cm s ,运动的时间为t s .(1)若8AP cm =, ①运动1s 后,求CD 的长;②当D 在线段PB 上运动时,试说明2AC CD =; (2)如果2t s =时,1CD cm =,试探索AP 的值.四、压轴题34.如图:在数轴上点A 表示数a ,点B 表示数b ,点C 表示数c ,a 是多项式2241x x --+的一次项系数,b 是最小的正整数,单项式2412x y -的次数为.c()1a =________,b =________,c =________;()2若将数轴在点B 处折叠,则点A 与点C ________重合(填“能”或“不能”);()3点A ,B ,C 开始在数轴上运动,若点C 以每秒1个单位长度的速度向右运动,同时,点A 和点B 分别以每秒3个单位长度和2个单位长度的速度向左运动,t 秒钟过后,若点A 与点B 之间的距离表示为AB ,点B 与点C 之间的距离表示为BC ,则AB =________,BC =________(用含t 的代数式表示);()4请问:3AB BC -的值是否随着时间t 的变化而改变?若变化,请说明理由;若不变,请求其值.35.点A 、B 在数轴上分别表示数,a b ,A 、B 两点之间的距离记为AB .我们可以得到AB a b =-:(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5两点之间的距离是 ;数轴上表示1和a 的两点之间的距离是 .(2)若点A 、B 在数轴上分别表示数-1和5,有一只电子蚂蚁在数轴上从左向右运动,设电子蚂蚁在数轴上的点C 对应的数为c .①求电子蚂蚁在点A 的左侧运动时AC BC +的值,请用含c 的代数式表示; ②求电子蚂蚁在运动的过程中恰好使得1511c c ,c 表示的数是多少? ③在电子蚂蚁在运动的过程中,探索15c c 的最小值是 .36.如图,数轴上点A 、B 表示的点分别为-6和3(1)若数轴上有一点P ,它到A 和点B 的距离相等,则点P 对应的数字是________(直接写出答案)(2)在上问的情况下,动点Q 从点P 出发,以3个单位长度/秒的速度在数轴上向左移动,是否存在某一个时刻,Q 点与B 点的距离等于 Q 点与A 点的距离的2倍?若存在,求出点Q 运动的时间,若不存在,说明理由.37.如图,相距10千米的A B 、两地间有一条笔直的马路,C 地位于A B 、两地之间且距A 地4千米,小明同学骑自行车从A 地出发沿马路以每小时5千米的速度向B 地匀速运动,当到达B 地后立即以原来的速度返回,到达A 地停止运动,设运动时间为(时),小明的位置为点P .(1)当0.5=t 时,求点P C 、间的距离(2)当小明距离C 地1千米时,直接写出所有满足条件的t 值(3)在整个运动过程中,求点P 与点A 的距离(用含的代数式表示) 38.某市两超市在元旦节期间分别推出如下促销方式: 甲超市:全场均按八八折优惠;乙超市:购物不超过200元,不给于优惠;超过了200元而不超过500元一律打九折;超过500元时,其中的500元优惠10%,超过500元的部分打八折; 已知两家超市相同商品的标价都一样.(1)当一次性购物总额是400元时,甲、乙两家超市实付款分别是多少? (2)当购物总额是多少时,甲、乙两家超市实付款相同?(3)某顾客在乙超市购物实际付款482元,试问该顾客的选择划算吗?试说明理由. 39.(理解新知)如图①,已知AOB ∠,在AOB ∠内部画射线OC ,得到三个角,分别为AOC ∠,BOC ∠,AOB ∠,若这三个角中有一个角是另外一个角的两倍,则称射线OC 为AOB ∠的“二倍角线”.(1)一个角的角平分线______这个角的“二倍角线”(填“是”或“不是”) (2)若60AOB ∠=︒,射线OC 为AOB ∠的“二倍角线”,则AOC ∠的大小是______;(解决问题)如图②,己知60AOB ∠=︒,射线OP 从OA 出发,以20︒/秒的速度绕O 点逆时针旋转;射线OQ 从OB 出发,以10︒/秒的速度绕O 点顺时针旋转,射线OP ,OQ 同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为t 秒.(3)当射线OP ,OQ 旋转到同一条直线上时,求t 的值;(4)若OA ,OP ,OQ 三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出t 所有可能的值______.40.数轴上有两点A ,B , 点C ,D 分别从原点O 与点B 出发,沿BA 方向同时向左运动. (1)如图,若点N 为线段OB 上一点,AB=16,ON=2,当点C ,D 分别运动到AO ,BN 的中点时,求CD 的长;(2)若点C 在线段OA 上运动,点D 在线段OB 上运动,速度分别为每秒1cm, 4cm ,在点C ,D 运动的过程中,满足OD=4AC ,若点M 为直线AB 上一点,且AM-BM=OM ,求AB OM的值.41.小明在一条直线上选了若干个点,通过数线段的条数,发现其中蕴含了一定的规律,下边是他的探究过程及联想到的一些相关实际问题.(1)一条直线上有2个点,线段共有1条;一条直线上有3个点,线段共有1+2=3条;一条直线上有4个点,线段共有1+2+3=6条…一条直线上有10个点,线段共有 条. (2)总结规律:一条直线上有n 个点,线段共有 条.(3)拓展探究:具有公共端点的两条射线OA 、OB 形成1个角∠AOB (∠AOB <180°);在∠AOB 内部再加一条射线OC ,此时具有公共端点的三条射线OA 、OB 、OC 共形成3个角;以此类推,具有公共端点的n 条射线OA 、OB 、OC…共形成 个角(4)解决问题:曲沃县某学校九年级1班有45名学生毕业留影时,全体同学拍1张集体照,每2名学生拍1张两人照,共拍了多少张照片?如果照片上的每位同学都需要1张照片留作纪念,又应该冲印多少张纸质照片?42.已知∠AOB 和∠AOC 是同一个平面内的两个角,OD 是∠BOC 的平分线. (1)若∠AOB=50°,∠AOC=70°,如图(1),图(2),求∠AOD 的度数;(2)若∠AOB=m 度,∠AOC=n 度,其中090090180m n m n <<,<<,<+且m n <,求∠AOD 的度数(结果用含m n 、的代数式表示),请画出图形,直接写出答案.43.从特殊到一般,类比等数学思想方法,在数学探究性学习中经常用到,如下是一个具体案例,请完善整个探究过程。
七年级上册数学 期末试卷测试卷(解析版)

七年级上册数学期末试卷测试卷(解析版)一、初一数学上学期期末试卷解答题压轴题精选(难)1.结合数轴与绝对值的知识回答下列问题:(1)探究:①数轴上表示5和2的两点之间的距离是多少.②数轴上表示﹣2和﹣6的两点之间的距离是多少.③数轴上表示﹣4和3的两点之间的距离是多少.(2)归纳:一般的,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.应用:①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,求a的值.②若数轴上表示数a的点位于﹣4与3之间,求|a+4|+|a﹣3|的值.③当a取何值时,|a+4|+|a﹣1|+|a﹣3|的值最小,最小值是多少?请说明理由.(3)拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1, A2, A3,A4, A5,…A2014,某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.【答案】(1)解:①数轴上表示5和2的两点之间的距离是3.②数轴上表示﹣2和﹣6的两点之间的距离是4.③数轴上表示﹣4和3的两点之间的距离是7.(2)解:①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,a=10或﹣4.②若数轴上表示数a的点位于﹣4与3之间,|a+4|+|a﹣3|=a+4+3﹣a=7;③当a=1时,|a+4|+|a﹣1|+|a﹣3|取最小值,|a+4|+|a﹣1|+|a﹣3|最小=5+0+2=7,理由是:a=1时,正好是3与﹣4两点间的距离.(3)解:点P选在A1007A1008这条线段上【解析】【分析】(1)根据两点间的距离公式:数轴上表示数m和数n的两点之间的距离等于|m﹣n|,分别计算可得出答案。
(2)① 利用绝对值等于7的数是±7,就可得出a-3=±7,解方程即可;② 由已知数轴上表示数a的点位于﹣4与3之间,可得出a+4>0,a-3<0,先去掉绝对值,再合并同类项即可;③ 根据线段上的点到线段两端的距离的和最短,可得出答案。
初一上学期数学期末考核试卷与解析

初一上学期数学期末考核试卷与解析一、选择题(每题4分,共计40分)1. 下列数中是无理数的是:A. √2B. 3/2C. πD. 0二、填空题(每题4分,共计40分)1. 若平行四边形ABCD的对角线交于点E,则点E是平行四边形ABCD的______。
三、解答题(每题10分,共计60分)1. 解方程:2x - 5 = 32. 已知直角三角形ABC,∠C为直角,AB为斜边,若AC = 3, BC = 4,求斜边AB的长度。
四、应用题(每题15分,共计30分)1. 小明的身高为1.6米,小华的身高为1.5米,请问小明比小华高多少百分比?2. 甲、乙两地相距100公里,小明从甲地骑自行车前往乙地,速度为每小时15公里。
请问小明到达乙地需要多少时间?---答案与解析一、选择题(每题4分,共计40分)1. C. π(解析:π是一个无理数,不能表示为两个整数的比例。
)二、填空题(每题4分,共计40分)1. 对角线的交点(解析:根据平行四边形的性质,对角线交于一点,这一点称为对角线的交点。
)三、解答题(每题10分,共计60分)1. x = 4(解析:将方程2x - 5 = 3移项得2x = 8,再除以2得x = 4。
)2. AB = 5(解析:根据勾股定理,AB² = AC² + BC²,代入AC= 3, BC = 4得AB² = 9 + 16 = 25,所以AB = 5。
)四、应用题(每题15分,共计30分)1. 小明比小华高13.3%(解析:小明比小华高的身高为1.6 -1.5 = 0.1米,所以比例为0.1 / 1.5 ≈ 0.0667,即6.67%,约为13.3%)2. 小明到达乙地需要6.67小时(解析:小明每小时行驶15公里,总共需要行驶100公里,所以时间为100 / 15 ≈ 6.67小时。
)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年贵阳市七年级(上)期末数学试卷一、选择题(以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,请在括号内填上正确选项的字母,每小题3分,共30分)1.(3分)2018的相反数是()A.8102 B.﹣2018 C.D.20182.(3分)若()﹣(﹣5)=﹣3,则括号内的数是()A.﹣2 B.﹣8 C.2 D.83.(3分)一个无盖的正方体盒子的平面展开图可以是下列图形中的()A.图2 B.图1或图2 C.图2或图3 D.图1或图34.(3分)下列各式运算结果正确的是()A.3x+3y=6xy B.﹣x+x=﹣2x C.9y2﹣6y2=3 D.9ab2﹣9ab2=05.(3分)一个正常人的心跳平均每分钟70次,一天大约跳的次数用科学记数法表示这个结果是()A.1.008×105B.100.8×103C.5.04×104D.504×1026.(3分)解方程=x﹣时,去分母正确的是()A.3(x+1)=x﹣(5x﹣1)B.3(x+1)=12x﹣5x﹣1C.3(x+1)=12x﹣(5x﹣1)D.3x+1=12x﹣5x+17.(3分)学校需要了解学生眼睛患上近视的情况,下面抽取样本方式比较合适的是()A.从全校的每个班级中随机抽取几个学生作调查B.在低年级学生中随机抽取一个班级作调查C.在学校门口通过观察统计佩戴眼镜的人数D.从学校的男同学中随机抽取50名学生作调查8.(3分)如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是()A.85°B.160°C.125°D.105°9.(3分)当使用计算器的键,将的结果切换成小数格式19.16666667,则对应这个结果19.16666667,以下说法错误的是()A.它不是准确值B.它是一个估算结果C.它是四舍五入得到的D.它是一个近似数10.(3分)如图,数轴上每两个相邻的点之间距离均为1个单位长度,数轴上的点Q,R所表示数的绝对值相等,则点P表示的数为()A.0 B.3 C.5 D.7二、填空题(本大题共5小题,每小题4分,共20分)11.(4分)将一个半圆绕它的直径所在的直线旋转一周得到的几何体是.12.(4分)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是.13.(4分)国家规定初中每班的标准人数为a人,某中学七年级共有六个班,各班人数情况如下表的代数式表示该中学七年级学生总人数为人.14.(4分)已知x=2是关于x的一元一次方程1﹣2ax=x+a的解,则a的值为.15.(4分)如图是用围棋摆成的按一定规律组成的图案,其中第1行有黑白棋子各一枚,第二行有三枚黑棋两枚白棋,第三行有五枚黑棋三枚白棋,第四行有七枚黑棋四枚白棋,一次类推第n行所用的围棋颗数是枚.(用含n的代数式表示)三、解答题16.(8分)计算:(1)1﹣43×(﹣)(2)7×2.6+7×1.5﹣4.1×8.17.(6分)如图,已知线段AB,请用尺规按下列要求作图.(保留作图痕迹,不写作法)(1)延长线段AB到C,使BC=AB;(2)延长BA到D,使DA=2AB.18.(8分)一个整式A与x2﹣x﹣1的和是﹣3x2﹣6x+2(1)求整式A;(2)当x=2时,求整式A的值.19.(6分)如图,桌面上放置了一些几何体,请按每个图下面的要求画出这些物体的形状图.20.(8分)“天元数学”网络平台是学生自主学习的平台,某中学共有2400名学生,每人每周学习“天元数学”微课视频的数量都在5~17个(这里的5~17表示大于等于5同时小于17),为进一步了解该校学生每周学习“天元数学”微课的情况,学校将收集的全校学生数据整理后绘制成如下的统计图.(1)根据图①中信息求出四个部分在总体中所占的比值;(2)在图②中制作相应的扇形统计图.21.(8分)某城市实施阶梯燃气费的收费方式,当用户使用的燃气量不超过60立方米时,按每立方米3元收费;如果超过60立方米,超过部分按每立方米3.5元收费,已知某单位6月份燃气费平均每立方米费用为3.125元,求该单位6月份燃气的使用量.22.(6分)在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.2017-2018学年贵州省贵阳市七年级(上)期末数学试卷参考答案与试题解析一、选择题(以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,请在括号内填上正确选项的字母,每小题3分,共30分)1.(3分)2018的相反数是()A.8102 B.﹣2018 C.D.2018【解答】解:2018的相反数﹣2018,故选:B.2.(3分)若()﹣(﹣5)=﹣3,则括号内的数是()A.﹣2 B.﹣8 C.2 D.8【解答】解:括号内的数=(﹣3)+(﹣5),=﹣(3+5),=﹣8.故选:B.3.(3分)一个无盖的正方体盒子的平面展开图可以是下列图形中的()A.图2 B.图1或图2 C.图2或图3 D.图1或图3【解答】解:由四棱柱四个侧面和底面的特征可知,①③可以拼成无盖的正方体,而②拼成的是上下都无底,且有一面重合的立体图形.故一个无盖的正方体盒子的平面展开图可以是下列图形中的是①、③.故选:D.4.(3分)下列各式运算结果正确的是()A.3x+3y=6xy B.﹣x+x=﹣2x C.9y2﹣6y2=3 D.9ab2﹣9ab2=0【解答】解:A、3x+3y不能合并,故A错误;B、﹣x+x=0,故B错误;C、9y2﹣6y2=3y2,故C错误;D、9ab2﹣9ab2=0,故D正确;故选:D.5.(3分)一个正常人的心跳平均每分钟70次,一天大约跳的次数用科学记数法表示这个结果是()A.1.008×105B.100.8×103C.5.04×104D.504×102【解答】解:∵一个正常人的平均心跳速率约为每分钟70次,∴一天24小时大约跳:24×60×70=10080=1.008×105(次).故选:A.6.(3分)解方程=x﹣时,去分母正确的是()A.3(x+1)=x﹣(5x﹣1)B.3(x+1)=12x﹣5x﹣1C.3(x+1)=12x﹣(5x﹣1)D.3x+1=12x﹣5x+1【解答】解:方程两边都乘以12,去分母得,3(x+1)=12x﹣(5x﹣1).故选:C.7.(3分)学校需要了解学生眼睛患上近视的情况,下面抽取样本方式比较合适的是()A.从全校的每个班级中随机抽取几个学生作调查B.在低年级学生中随机抽取一个班级作调查C.在学校门口通过观察统计佩戴眼镜的人数D.从学校的男同学中随机抽取50名学生作调查【解答】解:A、从全校的每个班级中随机抽取几个学生作调查适合抽样调查,故A符合题意;故选:A.8.(3分)如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是()A.85°B.160°C.125°D.105°【解答】解:AB于正东方向的夹角的度数是:90°﹣70°=20°,则∠BAC=20°+90°+15°=125°.故选:C.9.(3分)当使用计算器的键,将的结果切换成小数格式19.16666667,则对应这个结果19.16666667,以下说法错误的是()A.它不是准确值B.它是一个估算结果C.它是四舍五入得到的D.它是一个近似数【解答】解:19.16666667是四舍五入得到的近似数,它不是准确值,它不是一个估算结果.故选:B.10.(3分)如图,数轴上每两个相邻的点之间距离均为1个单位长度,数轴上的点Q,R所表示数的绝对值相等,则点P表示的数为()A.0 B.3 C.5 D.7【解答】解:设数轴的原点为O,依图可知,RQ=4又∵数轴上的点Q,R所表示数的绝对值相等∴OR=OQ=RQ=2,∴OP=OQ+OR=2+3=5故选:C二、填空题(本大题共5小题,每小题4分,共20分)11.(4分)将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球.【解答】解:将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球,故答案为:球12.(4分)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是两点确定一条直线.【解答】解:能解释这一实际应用的数学知识是:两点确定一条直线,故答案为:两点确定一条直线.13.(4分)国家规定初中每班的标准人数为a 人,某中学七年级共有六个班,各班人数情况如下表的代数式表示该中学七年级学生总人数为 6a+5 人.【解答】解:该中学七年级学生总人数为6a+(5+3﹣5+4+0﹣2)=6a+5(人),故答案为:6a+5.14.(4分)已知x=2是关于x 的一元一次方程1﹣2ax=x+a 的解,则a 的值为 ﹣ .【解答】解:把x=2代入方程得1﹣4a=2+a ,解得a=﹣.故答案是:﹣.15.(4分)如图是用围棋摆成的按一定规律组成的图案,其中第1行有黑白棋子各一枚,第二行有三枚黑棋两枚白棋,第三行有五枚黑棋三枚白棋,第四行有七枚黑棋四枚白棋,一次类推第n 行所用的围棋颗数是 3n ﹣1 枚.(用含n 的代数式表示)【解答】解:第1行有黑白棋子各一枚,第二行有三枚黑棋两枚白棋,第三行有五枚黑棋三枚白棋,第四行有七枚黑棋四枚白棋,第n行有2n﹣1个黑棋和n个白棋,共3n﹣1个围棋;故答案为:3n﹣1三、解答题16.(8分)计算:(1)1﹣43×(﹣)(2)7×2.6+7×1.5﹣4.1×8.【解答】解:原式=1﹣64×(﹣),=1﹣64×(﹣),=1+8,=9;(2)原式=7×(2.6+1.5)﹣4.1×8,=7×4.1﹣8×4.1,=(7﹣8)×4.1,=﹣4.1.17.(6分)如图,已知线段AB,请用尺规按下列要求作图.(保留作图痕迹,不写作法)(1)延长线段AB到C,使BC=AB;(2)延长BA到D,使DA=2AB.【解答】解:(1)点C如图所示;(2)点D如图所示;18.(8分)一个整式A与x2﹣x﹣1的和是﹣3x2﹣6x+2(1)求整式A;(2)当x=2时,求整式A的值.【解答】解:(1)由题意可知:A+(x2﹣x﹣1)=﹣3x2﹣6x+2,∴A=(﹣3x2﹣6x+2)﹣(x2﹣x﹣1)=﹣3x2﹣6x+2﹣x2+x+1=﹣4x2﹣5x+3;(2)把x=2代入得:A=﹣4x2﹣5x+3═﹣4×22﹣5×2+3=﹣16﹣10+3=﹣23.19.(6分)如图,桌面上放置了一些几何体,请按每个图下面的要求画出这些物体的形状图.【解答】解:如图所示20.(8分)“天元数学”网络平台是学生自主学习的平台,某中学共有2400名学生,每人每周学习“天元数学”微课视频的数量都在5~17个(这里的5~17表示大于等于5同时小于17),为进一步了解该校学生每周学习“天元数学”微课的情况,学校将收集的全校学生数据整理后绘制成如下的统计图.(1)根据图①中信息求出四个部分在总体中所占的比值;(2)在图②中制作相应的扇形统计图.【解答】解:(1)5~8个视频组:900÷2400=;8~11个视频组:800÷2400=;11~14个视频组:400÷2400=;14~17个视频组:300÷3400=;(2)扇形统计图如图所示:21.(8分)某城市实施阶梯燃气费的收费方式,当用户使用的燃气量不超过60立方米时,按每立方米3元收费;如果超过60立方米,超过部分按每立方米3.5元收费,已知某单位6月份燃气费平均每立方米费用为3.125元,求该单位6月份燃气的使用量.【解答】解:设6月份这位用户使用煤气xm3,根据题意得:60×3+3.5(x﹣60)=3.125x,解得:x=80.答:该单位6月份燃气的使用量是80m3.22.(6分)在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.【解答】解:(1)2+3+4=9,9﹣6﹣4=﹣1,9﹣6﹣2=1,9﹣2﹣7=0,9﹣4﹣0=5,如图所示:(2)﹣3+1﹣4=﹣6,﹣6+1﹣(﹣3)=﹣2,﹣2+1+4=3,如图所示:x=3﹣4﹣(﹣6)=5,y=3﹣1﹣(﹣6)=8,x+y=5+8=13.。
