二次函数典型例题解析汇报与习题训练
二次函数详细总结及典型练习例题

二次函数复习导学案教学目标教法:引导式教学、讲练结合1、二次函数的定义:一般地,形如)b a 0(2为常数、、,c a c bx ax y ≠++=的函数,叫做二次函数。
其中x 是自变量,a 是二次项系数,b 是一次项系数,c 常数项。
2.二次函数解析式的三种形式: 一般式: y=ax 2 +bx+c(a ≠0) 顶点式: 2()y a x h k =-+224()24b ac b y a x a a-=-+ 交点式: 12()()y a x x x x =--(轴交点的横坐标)为图像与、x 21x x 3.二次函数图像:(最值问题) 二次函数的图像是一条抛物线,对称轴: 顶点坐标: 与y 轴交点坐标4.增减性:当a 0时,对称轴左边,y 随x 增大而减小;对称轴右边,y 随x 增大而增大; 当a 0时,对称轴左边,y 随x 增大而增大;对称轴右边,y 随x 增大而减小. 5.二次函数图像画法:勾画草图关键点:○1开口方向 ○2对称轴 ○3顶点 ○4与x 轴交点 ○5与y 轴交点 6.图像平移步骤(1)配方 2()y a x h k =-+,确定顶点( )(2)对x 轴 左加右减;对y 轴 上加下减 7.二次函数的对称性:知识与能力:1、二次函数的解析式 对称轴 顶点坐标 最大(最小)值2、懂得利用二次函数解决生活中的实际问题过程与方法:通过复习使学生掌握二次函数知识与其它知识综合形成较为复杂的综合题目的思考方法。
情感、态度和价值观:注重培养学生数形结合的思想和独立思考的能力。
重点:二次函数的图象与性质。
运用函数、方程、几何等知识解决与函数有关的综合题以及函数应用问题。
难点:二次函数知识与其它知识综合形成较为复杂的综合题目的思考方法。
教学过程一、知识点学习y xO二次函数是轴对称图形,有这样一个结论:当横坐标为x 1, x 2 其对应的纵坐标相等那么对称轴122x x x += 8. a 、b 、c 以及△=b 2-4ac 对图象的影响.(1)a 决定:开口方向、开口大小(2)c 决定与y 轴的交点为(0,c ) (3)b 与-b2a 共同决定b 的正负性(b ——对称轴与a 左同右异)9.抛物线与坐标轴的交点(1)求二次函数y =ax 2+bx +c 与x 轴交点当函数值y =0时,求得的x 的值就是抛物线与x 轴交点的 ).如:求y =x 2-2x -3与x 轴交点坐标.(2)求二次函数y =ax 2+bx +c 与y 轴交点当x =0时,则y 的值是抛物线与y 轴交点的 . 如:求抛物线y =x 2-2x -3与y 轴交点坐标. 10.二次函数与一元二次方程的关系抛物线y=ax 2 +bx+c 与x 轴交点的横坐标x 1, x 2 是一元二次方程ax 2 +bx+c=0(a ≠0)的根。
二次函数综合题经典习题(含答案及基本讲解)解析

二次函数综合题训练题型集合1、如图1,已知二次函数图象的顶点坐标为C(1,0),直线m x y +=与该二次函数的图象交于A 、B 两点,其中A 点的坐标为(3,4),B 点在轴y 上. (1)求m 的值及这个二次函数的关系式;(2)P 为线段AB 上的一个动点(点P 与A 、B 不重合),过P 作x 轴的垂线与这个二次函数的图象交于点E 点,设线段PE 的长为h ,点P 的横坐标为x ,求h 与x 之间的函数关系式,并写出自变量x 的取值范围;(3)D 为直线AB 与这个二次函数图象对称轴的交点,在线段AB 上是否存在一点P ,使得四边形DCEP 是平行四边形?若存在,请求出此时明理由.2、如图2,已知二次函数24y axx c =-+的图像经过点A 和点B . (1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P (m ,m )与点Q 均在该函数图像上(其中m >0),且这两点关于抛物线的对称轴对称,求m 的值及点Q 到x 轴的距离图1 图23、如图3,已知抛物线cxbxay++=2经过O(0,0),A(4,0),B(3,3)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.(1)求这条抛物线的函数关系式.(2)两个动点P、Q分别从O、A两点同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着折线A→B→C的路线向C点运动. 设这两个动点运动的时间为t(秒) (0<t<4),△PQA的面积记为S.①求S与t的函数关系式;②当t为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;③是否存在这样的t值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.7、(07海南中考)如图7,直线434+-=xy与x轴交于点A函数的图象经过点A、C和点()0,1-B.(1)求该二次函数的关系式;(2)设该二次函数的图象的顶点为M,求四边形AOCM的面积;(3)有两动点D、E同时从点O出发,其中点D以每秒23个单位长度的速度沿折线OAC 按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,ODE∆的面积为S .①请问D、E两点在运动过程中,是否存在DE∥OC,若存在,请求出此时t的值;若不存在,请说明理由;②请求出S关于t的函数关系式,并写出自变量t的取值范围;4、某公司推出了一种高效环保型除草剂,年初上市后,公司经历了从亏损到盈利的过程. 图4的二次函数图象(部分)反映了该公司年初以来累积利润S (万元)与时间t (月)之间的关系(即前t 个月的利润总和S 与t 之间的关系).根据图象提供信息,解答下列问题: (1)公司从第几个月末开始扭亏为盈;(2)累积利润S 与时间t 之间的函数关系式; (3)求截止到几月末公司累积利润可达30万元; (4)求第8个月公司所获利是多少元?5、(07年海口模拟二)如图5,已知抛物线c x b x a y ++=2的顶点坐标为E (1,0),与y 轴的交点坐标为(0,1). (1)求该抛物线的函数关系式.(2)A 、B 是x 轴上两个动点,且A 、B 间的距离为AB=4,A 在B 的左边,过A 作AD ⊥x 轴交抛物线于D ,过B 作BC ⊥x 轴交抛物线于C. 设A 点的坐标为(t ,0),四边形ABCD 的面积为S.① 求S 与t 之间的函数关系式.② 求四边形ABCD 的最小面积,此时四边形ABCD 是什么四边形?③ 当四边形ABCD 面积最小时,在对角线BD 上是否存在这样的点P ,使得△PAE 的周长最小,若存在,请求出点P 的坐标及这时△PAE 的周长;若不存在,说明理由.x y D图5 E B A C O 1 xyE O 1 备用图-3 0 -1-21 234 S(万元) 图41 2 3 4 5 6 t(月)6、(07浙江中考)如图6,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2。
二次函数经典例题及解答

二次函数经典例题及解答二次函数一、中考导航图1.二次函数的意义2.二次函数的图像3.二次函数的性质顶点对称轴开口方向增减性4.待定系数法确定二次函数解析式5.二次函数与一元二次方程的关系三、中考知识梳理1.二次函数的图像二次函数y=ax2+bx+c(a≠0)的图像可以通过配方法化简为y=a(x+(b/2a))2+(4ac-b2)/4a2的形式。
确定顶点坐标后,可以对称求点列表并画图,或者使用顶点公式来求得顶点坐标。
2.理解二次函数的性质抛物线的开口方向由a的符号来确定。
当a>0时,抛物线开口向上,对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大。
当a0)或左增右减(a<0)。
此时,当x=-b/2a时,y取最值,最小值或最大值的大小为|(4ac-b2)/4a|。
3.待定系数法是确定二次函数解析式的常用方法待定系数法是通过给定的条件来确定二次函数的解析式。
可以任意给定三个点或三组x,y的值来确定解析式,组成三元一次方程组来求解。
也可以在给定条件中已知顶点坐标、对称轴或最值时,设解析式为y=a(x-h)2+k。
在给定条件中已知抛物线与x轴两交点坐标或已知抛物线与x轴一交点坐标和对称轴时,设解析式为y=a(x-x1)(x-x2)来求解。
4.二次函数与一元二次方程的关系抛物线y=ax2+bx+c与x轴的交点可以转化为一元二次方程ax2+bx+c=0的解。
当抛物线与x轴有两个交点时,方程有两个不相等实根;当抛物线与x轴有一个交点时,方程有两个相等实根;当抛物线与x轴无交点时,方程无实根。
5.抛物线y=ax2+bx+c中a、b、c符号的确定抛物线y=ax2+bx+c的开口方向由a的符号来确定。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
b的符号可以表示抛物线与y轴的交点在y轴的上方或下方。
c的符号可以表示抛物线与x轴的交点在x轴的上方或下方。
四、中考题型例析1.确定二次函数解析式例1:求满足以下条件的二次函数的解析式:1)图像经过点A(-1,3)、B(1,3)、C(2,6);2)图像经过点A(-1,0)、B(3,0),函数有最小值-8;3)图像顶点坐标是(-1,9),与x轴两交点间的距离是6.分析:此题主要考查用待定系数法来确定二次函数解析式。
二次函数最值知识点总结典型例题及习题

二次函数最值知识点总结典型例题及习题必修一二次函数在闭区间上的最值一、知识要点:对于一元二次函数在闭区间上的最值问题,关键在于讨论函数的对称轴与区间的相对位置关系。
一般分为对称轴在区间左侧、中间和右侧三种情况。
例如,对于函数f(x) = ax^2 + bx + c (a ≠ 0),求其在闭区间[x1.x2]上的最大值和最小值。
分析:将函数f(x)配方,得到其顶点为(-b/2a。
c - b^2/4a)。
因此,对称轴为x = -b/2a。
当a。
0时,函数f(x)的图像为开口向上的抛物线。
结合数形结合可得在闭区间[x1.x2]上f(x)的最值:1)当对称轴在[x1.x2]之外时,f(x)的最小值为f(-b/2a),最大值为f(x1)和f(x2)中的较大者。
2)当对称轴在[x1.x2]之间时,若x1 ≤ -b/2a ≤ x2,则f(x)的最小值为f(-b/2a),最大值为f(x1)和f(x2)中的较大者;若x1.-b/2a或x2 < -b/2a,则f(x)在闭区间[x1.x2]上单调递增或单调递减,最小值为f(x1),最大值为f(x2)。
当a < 0时,情况类似。
二、例题分析归类:一)正向型此类问题是指已知二次函数和定义域区间,求其最值。
对称轴与定义域区间的相互位置关系往往成为解决这类问题的关键。
此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。
1.轴定区间定二次函数和定义域区间都是给定的,我们称这种情况是“定二次函数在定区间上的最值”。
例如,对于函数y = -x^2 + 4x - 2在区间[0.3]上的最大值为2,最小值为-2.2.轴定区间变二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。
例如,对于函数f(x) = (x-1)^2 + 1,在区间[t。
t+1]上的最值为f(t)和f(t+1)中的较大者。
二次函数经典分类讲解以及练习题_

一、二次函数的定义定义: y=ax ² + bx + c ( a 、 b 、 c 是常数, a ≠ 0 ) 定义要点:①a ≠ 0 ②最高次数为2 ③代数式一定是整式练习:1、y=-x ²,y=2x ²-2/x ,y=100-5 x ²,y=3 x ²-2x ³+5,其中是二次函数的有____个。
2.当m_______时,函数y=(m+1) χ - 2χ+1 是二次函数? 二、二次函数的图像及性质1、二次函数y=kx 2+bx+c(a ≠0)的同象是一条 ,其顶点坐标为 对称轴式 2、增减性练习: 1、y=2x 2对称轴 顶点坐标2、y=x 2-1对称轴 顶点坐标3、y=-3(x+2)2对称轴 顶点坐标4、y=4(x-3)2+1对称轴 顶点坐标5、y=-2x 2+6x-1对称轴 顶点坐标 三、求抛物线解析式的三种方法1、一般式:已知抛物线上的三点,通常设解析式为________________ y=ax2+bx+c(a ≠0)2,顶点式:已知抛物线顶点坐标(h, k ),通常设抛物线解析式为_______________求出表达式后化为一般形式. y=a(x-h)2+k(a ≠0)3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________求出表达式后化为一般形式.y=a(x-x1)(x-x2) (a ≠0) 练习:根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0), (1,-2) , (2,3) 三点; (2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(0,0), (12,0) ,且最高点的纵坐标是3 。
例1已知二次函数y=ax2+bx+c 的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。
求a 、b 、c 。
四、a ,b ,c 符号的确定 练习7.已知二次函数的图像如图所示,下列结论。
二次函数最值知识点总结典型例题及习题

二次函数在闭区间上的最值一、 知识要点:一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。
一般分为:对称轴在区间的左边,中间,右边三种情况.设f x ax bx c a ()()=++≠20,求f x ()在x m n ∈[],上的最大值与最小值。
分析:将f x ()配方,得顶点为--⎛⎝ ⎫⎭⎪b aac b a 2442,、对称轴为x b a =-2 当a >0时,它的图象是开口向上的抛物线,数形结合可得在[m ,n]上f x ()的最值:(1)当[]-∈b a m n 2,时,f x ()的最小值是f b a ac b af x -⎛⎝ ⎫⎭⎪=-2442,()的最大值是f m f n ()()、中的较大者。
(2)当[]-∉b am n 2,时 若-<b am 2,由f x ()在[]m n ,上是增函数则f x ()的最小值是f m (),最大值是f n () 若n b a<-2,由f x ()在[]m n ,上是减函数则f x ()的最大值是f m (),最小值是f n () 当a <0时,可类比得结论。
二、例题分析归类:(一)、正向型是指已知二次函数和定义域区间,求其最值。
对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。
此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。
1. 轴定区间定二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1. 函数y x x =-+-242在区间[0,3]上的最大值是_________,最小值是_______。
练习. 已知232x x ≤,求函数f x x x ()=++21的最值。
2、轴定区间变二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。
二次函数的典型例题的解析
注意:1.用圆规 2等腰三角形:分类讨论
二.难点突破1——函数的面积问题
已知一次函数y 1 x 5 与y 2 交于点A(-1,2),B(- 4,0.5)
22
x
求AOB的面积。
解题思路:1.确定“割”或“补” 2.直线与坐标轴交点
C
S∆AOB=S∆AOC-S∆BOC
解题思路:1.关注“点” AB C MDN
MN ? MN=ND-MD MN=N的纵坐标-M的纵坐标
N(m,-m2+2m+3)
二.难点突破1——函数的面积问题 小结:
E
二.难点突破2——函数的线段最短问题
已知一次函数y 1 x 5 与y 2 交于点A(-1,2),B(- 4,0.5)
22
x
• 已知y= -0.5x2+2x+6与x轴交于点A(-2,0), B,与y轴交于点C,在抛物线的对称轴上存 在一点M,使得MA+MC的值最小,求点M的坐 标。
三.课堂小结
• 1.函数易错题 • 2.面积(最大面积)问题 • 3.线段最短问题
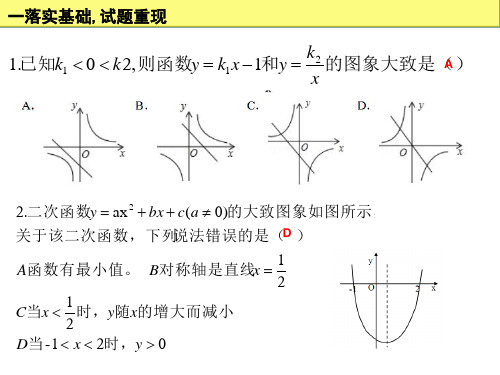
一落实基础,试题重现
• 3.如图,点P是菱形ABCD边上的一动点,它从 点A出发沿在A→B→C→D路径匀速运动到点D, 设△PAD的面积为y,P点的运动时间为x,则y 关于x的函数图象大致为( B )
A
B
C
D
一落实基础,试题重现
4.二次函数y -x2 2x 3如图所示,当函数值y为正数时, 自变量x的取值范围是___1___x___3____ .
注意:巧求交点
5.如图,函数y
k1x
b与y
k2 x
(x
0)交于点A(-1,2),B(-
二次函数十大解题模型汇总(模型+例题+练习题)

角线 a 的关系.
2、已知:一等腰直角三角形的面积为 S,请写出 S 与其斜边长 a 的关系表达式,并分别求出 a=1,a= 2 ,
a=2 时三角形的面积.
1 3、在物理学内容中,如果某一物体质量为 m,它运动时的能量 E 与它的运动速度 v 之间的关系是 E= 2 mv2
(m 为定值).(1)若物体质量为 1,填表表示物体在 v 取下列值时,E 的取值:
例 2、如果人民币一年定期储蓄的年利率是 x,一年到期后,银行将本金和利息自动按一年定期储蓄转存, 到期支取时,银行将扣除利息的 20%作为利息税.请你写出两年后支付时的本息和 y(元)与年利率 x 的 函数表达式.
例 3、某商场将进价为 40 元的某种服装按 50 元售出时,每天可以售出 300 套.据市场调查发现,这种服 装每提高 1 元售价,销量就减少 5 套,如果商场将售价定为 x,请你得出每天销售利润 y 与售价的函数表 达式.
二次函数十大解题模型汇总(模型+例题+练习题)
模型 1:根据二次函数的定义求字母的值
例 1:函数 y=(m+2)x m2−2 +2x-1 是二次函数,则 m=
.
对象:y=(m+2)x m2−2 +2x-1 角度:二次函数的稀疏,次数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
又∵y=x 2-x+m=[x 2-x+(12)2]- 14+m=(x -12
)2+414m -
∴对称轴是直线x=12,顶点坐标为(12
,41
4m -).
(2)∵顶点在x 轴上方, ∴顶点的纵坐标大于0,即41
4
m ->0 ∴m>
14 ∴m>1
4
时,顶点在x 轴上方.
(3)令x=0,则y=m .
即抛物线y=x 2-x+m 与y 轴交点的坐标是A (0,m ). ∵AB ∥x 轴
∴B 点的纵坐标为m .
当x 2-x+m=m 时,解得x 1=0,x 2=1. ∴A (0,m ),B (1,m )
在Rt △BAO 中,AB=1,OA=│m │. ∵S △AOB =1
2
OA ·AB=4. ∴
1
2
│m │·1=4,∴m=±8 故所求二次函数的解析式为y=x 2-x+8或y=x 2-x -8.
【点评】正确理解并掌握二次函数中常数a ,b ,c 的符号与函数性质及位置的关系是解答本题的关键之处.
例2 已知:m ,n 是方程x 2-6x+5=0的两个实数根,且m<n ,抛物线y=-x 2+bx+c 的图像经过点A (m ,0),B (0,n ),如图所示. (1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x 轴的另一交点为C ,抛物线的顶点
为D,试求出点C,D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH 分成面积之比为2:3的两部分,请求出P点的坐标.
【分析】(1)解方程求出m,n的值.用待定系数法求出b,c的值.
(2)过D作x轴的垂线交x轴于点M,可求出△DMC,梯形BDBO,△BOC的面积,用割补法可求出△BCD的面积.
(3)PH与BC的交点设为E点,则点E有两种可能:①EH=3
2EP,②EH=2
3
EP.
【解答】(1)解方程x2-6x+5=0,
得x1=5,x2=1.
由m<n,有m=1,n=5.
所以点A,B的坐标分别为A(1,0),B(0,5).将A(1,0),B(0,5)的坐标分别代入y=-x2+bx+c,
得
10,
5
b c
c
-++=
⎧
⎨
=
⎩
解这个方程组,得
4,
5
b
c
=-
⎧
⎨
=
⎩
所以抛物线的解析式为y=-x2-4x+5.
(2)由y=-x2-4x+5,令y=0,得-x2-4x+5=0.
解这个方程,得x1=-5,x2=1.
所以点C的坐标为(-5,0),由顶点坐标公式计算,得点D(-2,9).过D作x轴的垂线交x轴于M,如图所示.
则S△DMC=1
2×9×(5-2)=27
2
.
S梯形MDBO=1
2
×2×(9+5)=14,
S△BDC =1
2×5×5=25
2
.
并不难解决.
课堂习题
一、填空题
1.右图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图
像,观察图像写出y2≥y1时,x的取值围_______.
2.已知抛物线y=a2+bx+c经过点A(-2,7),B(6,7),
C(3,-8),则该抛物线上纵坐标为-8的另一点的坐标是_______.
3.已知二次函数y=-x2+2x+c2的对称轴和x轴相交于点(m,0),则m的值为______.4.若二次函数y=x2-4x+c的图像与x轴只有1个交点,则c=_______
5.已知抛物线y=ax2+bx+c经过点(1,2)与(-1,4),则a+c的值是______.6.甲,乙两人进行羽毛球比赛,甲发出一十分关键的球,出手点为P,羽毛球飞行的水平
距离s(m)与其距地面高度h(m)之间的关系式为h=-1
12s2+2
3
s+3
2
.如下左图
所示,已知球网AB距原点5m,乙(用线段CD表示)扣球的最大高度为9
4
m,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值围是______.
7.二次函数y=x2-2x-3与x轴两交点之间的距离为______.
8.市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/m2)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8),已知点(x,y)都在一个二次函数的
图像上(如上右图),则6楼房子的价格为_____元/m2.
二、选择题
9.二次函数y=ax2+bx+c的图像如图所示,•则下列关系式不正确的是()A.a<0 B.abc>0 C.a+b+c<0 D.b2-4ac>0
(第9题) (第12题) (第15题)
10.已知二次函数y=ax2+bx+c的图像过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图像上,则下列结论中正确的是()
A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y2
11.抛物线y=ax2+bx+c(a≠0)的对称轴是x=2,且经过点P(3,0),则a+b+c的值为()
A.-1 B.0 C.1 D.2
12.如图所示,抛物线的函数表达式是()
A.y=x2-x+2 B.y=-x2-x+2 C.y=x2+x+2 D.y=-x2+x+2 13.抛物线y=-2x2-4x-5经过平移得到y=-2x2,平移方法是()A.向左平移1个单位,再向下平移3个单位
B.向左平移1个单位,再向上平移3个单位
C.向右平移1个单位,再向下平移3个单位
D.向右平移1个单位,再向上平移3个单位
14.已知二次函数y=x2+bx+3,当x=-1时,y取得最小值,则这个二次函数图像的顶点在()
A.第一象限B.第二象限C.第三象限D.第四象限
15.抛物线y=ax2+2ax+a2+2的一部分图像如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是()
,0)B.(1,0)C.(2,0)D.(3,0)A.(1
2
16.在同一直角坐标系中,函数y=mx+m和y=-mx2+2x+2(m是常数,且m≠0)的图像可能是()
三、解答题
17.如图所示,已知抛物线y=ax2+4ax+t(a>0)交x轴A,B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0)
(1)求抛物线的对称轴及点A的坐标;
(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能
判断四边形ABCP是什么四边形?并证明你的结论;
18.如图所示,m,n是方程x2-6x+5=0的两个实数根,且m<n,•抛物线y=-x2+bx+c 的图像经过点A(m,0),B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线
的顶点为D,试求出点C,D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于点H,若直线BC把△PCH分成面积之比为2:3的两部分,请求出点P的坐标.
19.某地计划开凿一条单向行驶(从正过)的隧道,•其截面是抛物线拱形ACB,而且能通过最宽3m,最高3.5m的厢式货车.按规定,•机动车通过隧道时车身距隧道壁的水平距离和铅直距离最小都是0.5m.为设计这条能使上述厢式货车恰好完全通过的隧道,在图纸上以直线AB为x轴,线段AB的垂直平分线为y轴,建立如图所示的直角坐标系,求抛物线拱形的表达式,隧道的跨度AB和拱高OC.
20.已知一个二次函数的图像过如图所示三点.
(1)求抛物线的对称轴;
,抛物线与(2)平行于x轴的直线L的解析式为y=25
4
(3)x轴交于A,B两点.在抛物线的对称轴上找点P,(4)使BP的长等于直线L与x轴间的距离.求点P的坐标.
21.如图所示,二次函数y=ax2+bx+c(a≠0)的图像与x•轴交于A,B两点,其中A点坐标为(-1,0),点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.(1)求抛物线的解析式;(2)求△MCB的面积.。
