初一上册几何练习的题目50道
几何题初一数学上册

几何题初一数学上册
给出一个适合初一学生的几何题目。
题目:
1.在一张纸上,用直尺和圆规画一个角,标记为∠AOB。
2.以点O为圆心,任意长度r为半径,画一个圆,交OA于点C,交OB于点D。
3.用直尺分别连接点C和点D。
问题:
•请说明为什么线段CD是∠AOB的平分线。
这个问题主要是帮助学生理解角平分线和圆的性质,让他们在实践中加深对这些概念的理解。
同时,这也能够训练他们的动手能力和观察能力。
提示:
•考虑线段CD与∠AOC和∠DOB的关系。
•考虑线段OC和OD的长度(它们都等于r)。
•考虑三角形OCD的性质。
(最新整理)初一上册几何练习题50道

一。选择题
初一上册几何练习题 50 道
1。如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是( )
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)等腰三角形
2。下列给出的各组线段中,能构成三角形的是( ) (A)5,12,13 (B)5,12,7 (C)8,18,7 (D)3,4,8
初一上册几何练习题 50 道
初一上册几何练习题 50 道
编辑整理:
尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对 文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初一上册几何练习题 50 道) 的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈,这将是我们进步 的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步,以 下为初一上册几何练习题 50 道的全部内容。
13。 如图,已知:∠1=∠2,∠D=50°,求∠B 的度数。
14. 已知:如图,AB//CD,∠B=40°,∠E=30°,求∠D 的度数。
3.一个三角形的三边长分别是 15,20 和 25,则它的最大边上的高为( ) (A)12 (B)10 (C) 8 (D) 5
4.两条边长分别为 2 和 8,第三边长是整数的三角形一共有( ) (A)3 个 (B)4 个 (C)5 个 (D)无数个
5.下列图形中,不是轴对称图形的是( ) (A)线段 MN (B)等边三角形 (C) 直角三角形 (D) 钝角∠AOB
BC=
。
9。 如图,∠AOC=2∠COB,OD 是∠AOB 的平分线,已知∠COB=20°,则∠COD=_________。
七年级经典几何难题20道题

七年级经典几何难题20道题以下是七年级经典几何难题20道题:1. 已知等边三角形的一边长为a,求面积。
答案:面积为√3/4 * a²。
2. 如果一个矩形的长比宽大2cm,它的面积是24cm²,求矩形的长和宽。
答案:长为6cm,宽为4cm。
3. 已知一个正方形的边长为4cm,求周长和面积。
答案:周长为4*4=16cm,面积为4*4=16cm²。
4. 求一个直径为10cm的圆的面积。
答案:面积为π*(10/2)²=25πcm²。
5. 求一个等腰三角形底为6cm,高为8cm的面积。
答案:面积为1/2 * 6 * 8 = 24cm²。
6. 已知一个长方形的长为10cm,宽为5cm,求面积。
答案:面积为10*5=50cm²。
7. 求一个正方形的对角线长度为13cm的面积。
答案:面积为(13/2)²=169/4=42.25cm²。
8. 已知一个等边三角形的边长为8cm,求面积。
答案:面积为√3/4 * 8²=16√3 cm²。
9. 求一个半径为5cm的圆的周长。
答案:周长为2π*5=10πcm。
10. 已知一个矩形的长为12cm,宽为3cm,求面积。
答案:面积为12*3=36cm²。
11. 求一个边长为6cm的正方形的对角线长度。
答案:对角线长度为6√2 cm。
12. 已知一个等腰三角形底为10cm,高为12cm,求面积。
答案:面积为1/2 * 10 * 12 = 60cm²。
13. 求一个半径为7cm的圆的面积。
答案:面积为π*7²=49πcm²。
14. 已知一个长方形的长为15cm,宽为2cm,求面积。
答案:面积为15*2=30cm²。
15. 求一个正方形的边长为9cm的面积。
答案:面积为9*9=81cm²。
16. 求一个等边三角形的一边长为6cm的面积。
几何应用题初一上

以下是一些适合初一学生的几何应用题:
角度问题:
一个三角形ABC中,已知∠A = 40°, ∠B = 60°, 求∠C的度数。
边长与周长:
一个矩形ABCD的长是12cm,宽是8cm,求它的周长。
面积问题:
一个正方形的边长是6cm,求它的面积。
相似三角形:
在△ABC和△DEF中,AB = DE, ∠A = ∠D, 如果BC = 5cm且EF = 8cm,求AC与DF的比例。
三角形的中位线:
在△ABC中,D和E分别是AB和AC的中点,BC = 10cm,求DE的长度。
圆的性质:
一个圆的半径是5cm,求它的面积和周长。
体积问题:
一个长方体的长是8cm,宽是6cm,高是4cm,求它的体积。
角度与边长关系:
在一个直角三角形中,已知一条直角边长为3cm,另一条直角边与斜边的夹角为30°,求斜边的长度。
多边形内角和:
求一个五边形的内角和。
坐标与距离:
在二维坐标系中,点A(1,2)和点B(4,6),求A和B之间的距离。
这些题目旨在让学生应用所学的几何知识来解决实际问题,从而加深对几何概念和方法的理解。
在解决这些题目时,学生应使用适当的几何公式和定理,并锻炼他们的逻辑思维和空间想象能力。
完整版)初一几何练习题及答案

完整版)初一几何练习题及答案初一几何:三角形一、选择题(本大题共24分)1.以下列各组数为三角形的三条边,其中能构成直角三角形的是()A。
17,15,8B。
1/3,1/4,1/5C。
4,5,6D。
3,7,112.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()A。
锐角三角形B。
直角三角形C。
钝角三角形D。
等腰三角形3.下列给出的各组线段中,能构成三角形的是()A。
5,12,13B。
5,12,7C。
8,18,7D。
3,4,84.如图已知:Rt△ABC中,∠C=90°,AD平分∠BAC,AE=AC,连接DE,则下列结论中,不正确的是()A。
DC=DEB。
∠___∠ADEC。
∠DEB=90°D。
∠___∠DAE5.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()A。
12B。
10C。
8D。
56.下列说法不正确的是()A。
全等三角形的对应角相等B。
全等三角形的对应角的平分线相等C。
角平分线相等的三角形一定全等D。
角平分线是到角的两边距离相等的所有点的集合7.两条边长分别为2和8,第三边长是整数的三角形一共有()A。
3个B。
4个C。
5个D。
无数个8.下列图形中,不是轴对称图形的是()A。
线段MNB。
等边三角形C。
直角三角形D。
钝角∠AOB9.如图已知:△ABC中,AB=AC,BE=CF,AD⊥BC于D,此图中全等的三角形共有()A。
2对B。
3对C。
4对D。
5对10.直角三角形两锐角的平分线相交所夹的钝角为()A。
125°B。
135°C。
145°D。
150°11.直角三角形两锐角的平分线相交所夹的钝角为()A。
125°B。
135°C。
145°D。
150°12.___已知:∠A=∠D,∠C=∠F,如果△ABC≌△DEF,那么还应给出的条件是()A。
AC=DEB。
AB=DFC。
数学几何题精选50道及答案

数学几何题精选50道及答案**几何数学题1**:题目:在直角三角形ABC中,角A=90°,AB=5cm,BC=12cm。
求AC的长度。
**几何数学题2**:题目:在平行四边形WXYZ中,角W=80°,角X=100°。
求角Y和角Z的度数。
**几何数学题3**:题目:在正五边形PQRST中,每个内角的度数是多少?**几何数学题4**:题目:已知三角形DEF中,角D=60°,角E=45°。
求角F的度数。
**几何数学题5**:题目:在直角三角形LMN中,角L=90°,角M=60°。
若LN=8cm,求MN的长度。
**几何数学题6**:题目:已知平行四边形UVWX中,UV=7cm,WX=5cm,且角U=120°。
求VX的长度。
**几何数学题7**:题目:在等腰三角形PQR中,角P=80°。
求角Q和角R的度数。
**几何数学题8**:题目:在梯形STUV中,ST和UV是平行边,ST=9cm,UV=12cm,SV=5cm。
求TU的长度。
**几何数学题9**:题目:在正方形ABCD中,边长为15cm。
求对角线AC的长度。
**几何数学题10**:题目:在菱形EFGH中,角E=50°。
求角F、角G和角H的度数。
**几何数学题11**:题目:在直角三角形XYZ中,角X=90°,YZ=15cm,XZ=9cm。
求角Y和角Z的度数。
**几何数学题12**:题目:在平行四边形IJKL中,角I=130°,角K=70°。
求角J和角L的度数。
**几何数学题13**:题目:在正七边形ABCDEFGH中,每个内角的度数是多少?**几何数学题14**:题目:已知三角形PQS中,角P=40°,角Q=60°。
求角S的度数。
**几何数学题15**:题目:在直角三角形RST中,角R=90°,角S=45°。
七年级上册数学几何图形初步好题附答案

七年级上册数学几何图形初步好题附答案评卷人得分一.选择题(共17小题)1.如图是一个长方体包装盒,则它的平面展开图是()A.B.C.D.2.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是()A.遇B.见C.未D.来3.一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱4.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是()A.中B.考C.顺D.利5.点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于()A.3 B.2 C.3或5 D.2或66.如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB 的长度为()A.4 B.6 C.8 D.107.如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm8.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是()A.7cm B.3cm C.7cm或3cm D.5cm9.如图,在直线l上有A、B、C三点,则图中线段共有()A.1条 B.2条 C.3条 D.4条10.如图,共有线段()A.3条 B.4条 C.5条 D.6条11.下列说法中,正确的有()个①过两点有且只有一条直线②连接两点的线段叫做两点间的距离③两点之间,线段最短④若AB=BC,则点B是线段AC的中点⑤射线AB和射线BA是同一条射线⑥直线有无数个端点.A.2个 B.3个 C.4个 D.5个12.下列说法正确的是()A.射线比直线短B.两点确定一条直线C.经过三点只能作一条直线D.两点间的长度叫两点间的距离13.下列说法中错误的是()A.A、B两点之间的距离为3cmB.A、B两点之间的距离为线段AB的长度C.线段AB的中点C到A、B两点的距离相等D.A、B两点之间的距离是线段AB14.下列说法中正确的个数为()(1)过两点有且只有一条直线;(2)连接两点的线段叫两点间的距离;(3)两点之间所有连线中,线段最短;(4)射线比直线小一半.A.1个 B.2个 C.3个 D.4个15.2012年12月26日京广高铁全线通车.一列往返于北京和广州的火车,沿途要经过石家庄、郑州、武汉、长沙四站,铁路部门要为这趟列车准备印制()种车票.A.6 B.12 C.15 D.3016.如图所示,下列表示角的方法错误的是()A.∠1与∠AOB表示同一个角B.∠β表示的是∠BOCC.图中共有三个角:∠AOB,∠AOC,∠BOCD.∠AOC也可用∠O来表示17.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB 的方向角是()A.北偏西30°B.北偏西60°C.东偏北30°D.东偏北60°评卷人得分二.填空题(共2小题)18.平面内不同的两点确定一条直线,不同的三点最多确定三条直线.若平面内的不同n个点最多可确定15条直线,则n的值为.19.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为.评卷人得分三.解答题(共21小题)20.如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.21.如图,已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC、AB 的中点,求DE的长.22.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.23.如图,点C、D在线段AB上,D是线段AB的中点,AC=AD,CD=4,求线段AB的长.24.如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.(1)求线段BC、MN的长;(2)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别是线段AC、BC的中点,求MN的长度.25.如图已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC、AB的中点,求DE的长.26.已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD 的中点,CD=6cm,求线段MC的长.27.如图,已知线段AD=10cm,线段AC=BD=6cm.E、F分别是线段AB、CD的中点,求EF的长.28.观察图①,由点A和点B可确定条直线;观察图②,由不在同一直线上的三点A、B和C最多能确定条直线;(1)动手画一画图③中经过A、B、C、D四点的所有直线,最多共可作条直线;(2)在同一平面内任三点不在同一直线的五个点最多能确定条直线、n 个点(n≥2)最多能确定条直线.29.如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.解:∵AB=2cm,BC=2AB,∴BC=4cm.∴AC=AB+ =cm.∵D是AC的中点,∴AD==cm.∴BD=AD﹣=cm.30.如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.(1)若AC=8,CB=6,求线段MN的长;(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;(3)若点C为线段AB延长线上任意一点,且满足AC﹣CB=b,求线段MN的长.31.已知如图(1)如图(1),两条直线相交,最多有个交点.如图(2),三条直线相交,最多有个交点.如图(3),四条直线相交,最多有个交点.如图(4),五条直线相交,最多有个交点;(2)归纳,猜想,30条直线相交,最多有个交点.32.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.33.如图,C是线段AB外一点,按要求画图:(1)画射线CB;(2)反向延长线段AB;(3)连接AC,并延长AC至点D,使CD=AC.34.如图,已知数轴上A、B两点所表示的数分别为﹣2和8.(1)求线段AB的长;(2)若P为射线BA上的一点(点P不与A、B两点重合,M为PA的中点,N 为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.35.如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….(1)“17”在射线上;(2)请任意写出三条射线上数字的排列规律;(3)“2007”在哪条射线上?36.已知线段AB上顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,且AB=56cm.(1)求线段AE的长;(2)若M、N分别是DE、EB的中点,求线段MN的长度.37.你会数线段吗?如图①线段AB,即图中共有1条线段,1=如图②线段AB上有1个点C,则图中共有3条线段,3=1+2=如图③线段AB上有2个点C、D,则图中共有6条线段,6=1+2+3=思考问题:(1)如果线段AB上有3个点,则图中共有条线段;(2)如果线段AB上有9个点,则图中共有条线段;(3)如果线段AB上有n个点,则图中共有条线段(用含n的代数式来表示).38.如图,在平面内有A、B、C三点.(1)画直线AC,线段BC,射线AB;(2)在线段BC上任取一点D(不同于B、C),连接线段AD;(3)数数看,此时图中线段共有条.39.如图,A,B,C,依次为直线L上三点,M为AB的中点,N为MC的中点,且AB=6cm,NC=8cm,求BC的长.40.已知数轴上点A、B、C所表示的数分别是﹣3,+7,x.(1)求线段AB的长;(2)若AC=4,①求x的值;②若点M、N分别是AB、AC的中点,求线段MN 的长度.七年级上册数学几何图形初步好题附答案参考答案与试题解析一.选择题(共17小题)1.如图是一个长方体包装盒,则它的平面展开图是()A.B.C.D.【解答】解:由四棱柱四个侧面和上下两个底面的特征可知,A、可以拼成一个长方体;B、C、D、不符合长方体的展开图的特征,故不是长方体的展开图.故选A.2.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是()A.遇B.见C.未D.来【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“遇”与“的”是相对面,“见”与“未”是相对面,“你”与“来”是相对面.故选D.3.一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱【解答】解:如图所示:这个几何体是四棱锥.故选:A.4.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是()A.中B.考C.顺D.利【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“祝”与“考”是相对面,“你”与“顺”是相对面,“中”与“利”是相对面.故选C.5.点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于()A.3 B.2 C.3或5 D.2或6【解答】解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB 外,所以要分两种情况计算.点A、B表示的数分别为﹣3、1,AB=4.第一种情况:在AB外,AC=4+2=6;第二种情况:在AB内,AC=4﹣2=2.故选:D.6.如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB 的长度为()A.4 B.6 C.8 D.10【解答】解:∵C为AB的中点,∴AC=BC=AB=×12=6,∵AD:CB=1:3,∴AD=2,∴DB=AB﹣AD=12﹣2=10(cm).故选D.7.如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm【解答】解:∵AB=10cm,BC=4cm,∴AC=AB﹣BC=6cm,又点D是AC的中点,∴AD=AC=3cm,答:AD的长为3cm.故选:B.8.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是()A.7cm B.3cm C.7cm或3cm D.5cm【解答】解:(1)当点C在线段AB上时,则MN=AC+BC=AB=5;(2)当点C在线段AB的延长线上时,则MN=AC﹣BC=7﹣2=5.综合上述情况,线段MN的长度是5cm.故选D.9.如图,在直线l上有A、B、C三点,则图中线段共有()A.1条 B.2条 C.3条 D.4条【解答】解:图中线段有AB、AC、BC这3条,故选:C.10.如图,共有线段()A.3条 B.4条 C.5条 D.6条【解答】解:线段AB、AC、AD、BC、BD、CD共六条,也可以根据公式计算,=6,故选D.11.下列说法中,正确的有()个①过两点有且只有一条直线②连接两点的线段叫做两点间的距离③两点之间,线段最短④若AB=BC,则点B是线段AC的中点⑤射线AB和射线BA是同一条射线⑥直线有无数个端点.A.2个 B.3个 C.4个 D.5个【解答】解:①过两点有且只有一条直线,正确,②连接两点的线段叫做两点间的距离,不正确,应为连接两点的线段的长度叫做两点间的距离,③两点之间,线段最短,正确,④若AB=BC,则点B是线段AC的中点,不正确,只有点B在AC上时才成立,⑤射线AB和射线BA是同一条射线,不正确,端点不同,⑥直线有无数个端点.不正确,直线无端点.共2个正确,故选:A.12.下列说法正确的是()A.射线比直线短B.两点确定一条直线C.经过三点只能作一条直线D.两点间的长度叫两点间的距离【解答】解:A、射线,直线都是可以无限延长的,无法测量长度,错误;B、两点确定一条直线,是公理,正确;C、经过不在一条直线的三点能作三条直线,错误;D、两点间线段的长度叫两点间的距离,错误;故选B.13.下列说法中错误的是()A.A、B两点之间的距离为3cmB.A、B两点之间的距离为线段AB的长度C.线段AB的中点C到A、B两点的距离相等D.A、B两点之间的距离是线段AB【解答】解:A、A、B两点之间的距离为3cm,故A选项说法正确;B、A、B两点之间的距离为线段AB的长度,故B选项正确;C、线段AB的中点C到A、B两点的距离相等,故C选项正确;D、A、B两点之间的距离是线段AB,应为AB的长度,故D选项错误.故选:D.14.下列说法中正确的个数为()(1)过两点有且只有一条直线;(2)连接两点的线段叫两点间的距离;(3)两点之间所有连线中,线段最短;(4)射线比直线小一半.A.1个 B.2个 C.3个 D.4个【解答】解:(1)过两点有且只有一条直线,此选项正确;(2)连接两点的线段的长度叫两点间的距离,此选项错误;(3)两点之间所有连线中,线段最短,此选项正确;(4)射线比直线小一半,根据射线与直线都无限长,故此选项错误;故正确的有2个.故选:B.15.2012年12月26日京广高铁全线通车.一列往返于北京和广州的火车,沿途要经过石家庄、郑州、武汉、长沙四站,铁路部门要为这趟列车准备印制()种车票.A.6 B.12 C.15 D.30【解答】解:∵从北京出发的有5种车票,从石家庄出发的有4种车票,从郑州出发的有3种车票,从武汉出发的有2种车票,从长沙出发的有1种车票,∴一列往返于北京和广州的火车,沿途要经过石家庄、郑州、武汉、长沙四站,铁路部门要为这趟列车准备印制2×(5+4+3+2+1)=30种车票,故选D.16.如图所示,下列表示角的方法错误的是()A.∠1与∠AOB表示同一个角B.∠β表示的是∠BOCC.图中共有三个角:∠AOB,∠AOC,∠BOCD.∠AOC也可用∠O来表示【解答】解:A、∠1与∠AOB表示同一个角,正确,故本选项错误;B、∠β表示的是∠BOC,正确,故本选项错误;C、图中共有三个角:∠AOB,∠AOC,∠BOC,正确,故本选项错误;D、∠AOC不能用∠O表示,错误,故本选项正确;故选D.17.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB 的方向角是()A.北偏西30°B.北偏西60°C.东偏北30°D.东偏北60°【解答】解:∵射线OB与射线OA垂直,∴∠AOB=90°,∴∠1=90°﹣30°=60°,故射线OB的方向角是北偏西60°,故选:B.二.填空题(共2小题)18.平面内不同的两点确定一条直线,不同的三点最多确定三条直线.若平面内的不同n个点最多可确定15条直线,则n的值为6.【解答】解:∵平面内不同的两点确定1条直线,;平面内不同的三点最多确定3条直线,即=3;平面内不同的四点确定6条直线,即=6,∴平面内不同的n点确定(n≥2)条直线,∴平面内的不同n个点最多可确定15条直线时,=15,解得n=﹣5(舍去)或n=6.故答案为:6.19.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为8cm.【解答】解:∵线段AB的中点为M,∴AM=BM=6cm设MC=x,则CB=2x,∴x+2x=6,解得x=2即MC=2cm.∴AC=AM+MC=6+2=8cm.三.解答题(共21小题)20.如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.【解答】解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.∵点E、点F分别为AB、CD的中点,∴AE=AB=1.5xcm,CF=CD=2xcm.∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5xcm.∵EF=10cm,∴2.5x=10,解得:x=4.∴AB=12cm,CD=16cm.21.如图,已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC、AB 的中点,求DE的长.【解答】解:∵AC=12cm,CB=AC,∴CB=6cm,∴AB=AC+BC=12+6=18cm,∵E为AB的中点,∴AE=BE=9cm,∵D为AC的中点,∴DC=AD=6cm,所以DE=AE﹣AD=3cm.22.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.【解答】解:设AB=2xcm,BC=5xcm,CD=3xcm所以AD=AB+BC+CD=10xcm因为M是AD的中点所以AM=MD=AD=5xcm所以BM=AM﹣AB=5x﹣2x=3xcm因为BM=6 cm,所以3x=6,x=2故CM=MD﹣CD=5x﹣3x=2x=2×2=4cm,AD=10x=10×2=20 cm.23.如图,点C、D在线段AB上,D是线段AB的中点,AC=AD,CD=4,求线段AB的长.【解答】解:∵AC=AD,CD=4,∴CD=AD﹣AC=AD﹣AD=AD,∴AD=CD=6,∵D是线段AB的中点,∴AB=2AD=12;24.如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.(1)求线段BC、MN的长;(2)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别是线段AC、BC的中点,求MN的长度.【解答】解:(1)∵AC=6cm,M是AC的中点,∴AM=MC=AC=3cm,∵MB=10cm,∴BC=MB﹣MC=7cm,∵N为BC的中点,∴CN=BC=3.5cm,∴MN=MC+CN=6.5cm;(2)如图,∵M是AC中点,N是BC中点,∴MC=AC,NC=BC,∵AC﹣BC=bcm,∴MN=MC﹣NC=AC﹣BC=(AC﹣BC)=b(cm).25.如图已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC、AB的中点,求DE的长.【解答】解:根据题意,AC=12cm,CB=AC,所以CB=8cm,所以AB=AC+CB=20cm,又D、E分别为AC、AB的中点,所以DE=AE﹣AD=(AB﹣AC)=4cm.即DE=4cm.故答案为4cm.26.已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD 的中点,CD=6cm,求线段MC的长.【解答】解:由AB:BC:CD=2:4:3,设AB=2xcm,BC=4xcm,CD=3xcm, (1)分则CD=3x=6,解得x=2.…2分因此,AD=AB+BC+CD=2x+4x+3x=18(cm).…4分因为点M是AD的中点,所以DM=AD=×18=9(cm).…6分MC=DM﹣CD=9﹣6=3(cm).…7分27.如图,已知线段AD=10cm,线段AC=BD=6cm.E、F分别是线段AB、CD的中点,求EF的长.【解答】解:∵AD=10,AC=BD=6,∴AB=AD﹣BD=10﹣6=4,∵E是线段AB的中点,∴EB=AB=×4=2,∴BC=AC﹣AB=6﹣4=2,CD=BD﹣BC=6﹣2=4,∵F是线段CD的中点,∴CF=CD=×4=2,∴EF=EB+BC+CF=2+2+2=6cm.答:EF的长是6cm.28.观察图①,由点A和点B可确定1条直线;观察图②,由不在同一直线上的三点A、B和C最多能确定3条直线;(1)动手画一画图③中经过A、B、C、D四点的所有直线,最多共可作6条直线;(2)在同一平面内任三点不在同一直线的五个点最多能确定10条直线、n 个点(n≥2)最多能确定n(n﹣1)条直线.【解答】解:①由点A和点B可确定1条直线;②由不在同一直线上的三点A、B和C最多能确定3条直线;经过A、B、C、D四点最多能确定6条直线;直在同一平面内任三点不在同一直线的五个点最多能确定10条线、根据1个点、两个点、三个点、四个点、五个点的情况可总结出n个点(n≥2)时最多能确定:条直线.故答案为:1;3,6,10,.29.如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.解:∵AB=2cm,BC=2AB,∴BC=4cm.∴AC=AB+ BC=6cm.∵D是AC的中点,∴AD=AC=3cm.∴BD=AD﹣AB=1cm.【解答】解:∵AB=2cm,BC=2AB,∴BC=4cm,∴AC=AB+BC=6cm,∵D为AC中点,∴AD=AC=3cm,∴BD=AD﹣AB=3cm﹣2cm=1cm,故答案为:BC,6,AC,3,AB,1.30.如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.(1)若AC=8,CB=6,求线段MN的长;(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;(3)若点C为线段AB延长线上任意一点,且满足AC﹣CB=b,求线段MN的长.【解答】解:(1)∵M、N分别是AC、BC的中点,∴MC=AC,CN=CB,∴MN=MC+CN,=(AC+CB)=(8+6)=7;(2)∵若M、N分别是线段AC、BC的中点,∴AM=MC,CN=BN,AM+CM+CN+NB=a,2(CM+CN)=a,CM+CN=,∴MN=a;(3)∵M、N分别是AC、BC的中点,∴MC=AC,NC=BC,∴MN=MC﹣NC=(AC﹣BC)=b.31.已知如图(1)如图(1),两条直线相交,最多有1个交点.如图(2),三条直线相交,最多有3个交点.如图(3),四条直线相交,最多有6个交点.如图(4),五条直线相交,最多有10个交点;(2)归纳,猜想,30条直线相交,最多有435个交点.【解答】解:(1)如图(1),两条直线相交,最多有1个交点.如图(2),三条直线相交,最多有3个交点.如图(3),四条直线相交,最多有6个交点.如图(4),五条直线相交,最多有10个交点.…n条直线相交,最多有个交点;(2)∴30条直线相交,∴最多有=435个交点.32.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.【解答】解:点P的位置如下图所示:作法是:连接AB交L于点P,则P点为汽车站位置,理由是:两点之间,线段最短.33.如图,C是线段AB外一点,按要求画图:(1)画射线CB;(2)反向延长线段AB;(3)连接AC,并延长AC至点D,使CD=AC.【解答】解:34.如图,已知数轴上A、B两点所表示的数分别为﹣2和8.(1)求线段AB的长;(2)若P为射线BA上的一点(点P不与A、B两点重合,M为PA的中点,N 为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.【解答】解:(1)∵A,B两点所表示的数分别为﹣2和8,∴0A=2,OB=8∴AB=OA+OB=l0.(5分)(2)线段MN的长度不发生变化,其值为5.分下面两种情况:①当点P在A、B两点之间运动时(如图甲).MN=MP+NP=AP+BP=AB=5(3分)②当点P在点A的左侧运动时(如图乙).MN=NP﹣MP=BP﹣AP=AB=5(3分)综上所述,线段MN的长度不发生变化,其值为5.(1分)35.如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….(1)“17”在射线OE上;(2)请任意写出三条射线上数字的排列规律;(3)“2007”在哪条射线上?【解答】解:(1)18正好转3圈,3×6;17则3×6﹣1;“17”在射线OE上;(2)射线OA上数字的排列规律:6n﹣5射线OB上数字的排列规律:6n﹣4射线OC上数字的排列规律:6n﹣3射线OD上数字的排列规律:6n﹣2射线OE上数字的排列规律:6n﹣1射线OF上数字的排列规律:6n(3)2007÷6=334…3.故“2007”在射线OC上.36.已知线段AB上顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,且AB=56cm.(1)求线段AE的长;(2)若M、N分别是DE、EB的中点,求线段MN的长度.【解答】解:(1)设AC=2x,则CD、DE、EB分别为3x、4x、5x,由题意得,2x+3x+4x+5x=56,解得,x=4,则AC、CD、DE、EB分别为8cm、12cm、16cm、20cm,则AE=AC+CD+DE=36cm;(2)∵M是DE的中点,∴ME=DE=8cm,N是EB的中点,∴EN=EB=10cm,∴MN=ME+EN=18cm.37.你会数线段吗?如图①线段AB,即图中共有1条线段,1=如图②线段AB上有1个点C,则图中共有3条线段,3=1+2=如图③线段AB上有2个点C、D,则图中共有6条线段,6=1+2+3=思考问题:(1)如果线段AB上有3个点,则图中共有10条线段;(2)如果线段AB上有9个点,则图中共有55条线段;(3)如果线段AB上有n个点,则图中共有条线段(用含n的代数式来表示).【解答】解:(1)1+2+3+4==10,故答案为:10.(2)1+2+3+4+5+6+7+8+9+10==55,故答案为:55.(3)1+2+3+4+…+n+1=,故答案为:.38.如图,在平面内有A、B、C三点.(1)画直线AC,线段BC,射线AB;(2)在线段BC上任取一点D(不同于B、C),连接线段AD;(3)数数看,此时图中线段共有6条.【解答】解:(1)(2)(3)图中有线段6条.39.如图,A,B,C,依次为直线L上三点,M为AB的中点,N为MC的中点,且AB=6cm,NC=8cm,求BC的长.【解答】解:∵M为AB的中点,∴AM=BM=AB=3cm,∵N为MC的中点,∴MN=NC=8cm.∴BN=MN﹣BM=5cm,∴BC=BN+NC=5+8=13(cm).答:BC长为13cm.40.已知数轴上点A、B、C所表示的数分别是﹣3,+7,x.(1)求线段AB的长;(2)若AC=4,①求x的值;②若点M、N分别是AB、AC的中点,求线段MN 的长度.【解答】解:(1)AB=7﹣(﹣3)=10;(2)①∵AC=4,∴|x﹣(﹣3)|=4,∴x﹣(﹣3)=4或(﹣3)﹣x=4,∴x=1或﹣7;②当点A、B、C所表示的数分别是﹣3,+7,1时,∵点M、N分别是AB、AC的中点,∴点M表示的数为2,点N的坐标是﹣1,∴MN=2﹣(﹣1)=3;当点A、B、C所表示的数分别是﹣3,+7,﹣7时,∵点M、N分别是AB、AC的中点,∴点M表示的数为2,点N的坐标是﹣5,∴MN=2﹣(﹣5)=7;∴MN=7或3.。
初一上册几何练习题50道(2)
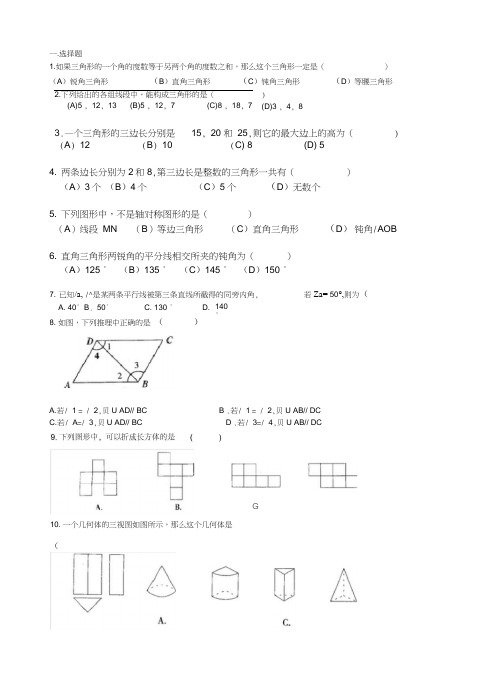
一.选择题1.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形2.下列给出的各组线段中,能构成三角形的是()(D)3 , 4, 8(A)5 , 12, 13 (B)5 , 12, 7 (C)8 , 18, 73.—个三角形的三边长分别是15, 20 和25,则它的最大边上的高为()(A) 12 (B) 10 (C) 8 (D) 54. 两条边长分别为2和8,第三边长是整数的三角形一共有()(A)3个(B)4个(C)5个(D)无数个5. 下列图形中,不是轴对称图形的是()(A)线段MN (B)等边三角形(C)直角三角形(D)钝角/AOB 6. 直角三角形两锐角的平分线相交所夹的钝角为()(A)125 °(B)135 °(C)145 °(D)150 °7. 已知/a, /^是某两条平行线被第三条直线所截得的同旁内角,A. 40°B. 50°C. 130 °8. 如图,下列推理中正确的是()D. 140°若Za= 50°,则为(A.若/ 1 = / 2,贝U AD// BCC.若/ A=/ 3,贝U AD// BC10. 一个几何体的三视图如图所示,那么这个几何体是(B .若/ 1 = / 2,贝U AB// DCD .若/ 3=/ 4,贝U AB// DC)G11. 如图1,在厶ABC 中,AB= AC,点D 在AC 边上,且 BD= BC = AD 则/ A 的度数为()A. 30 °B. 36°C. 45°D. 70°12. 、如图2, AB// CD AC 丄BC 于C,则图中与/ CAB 互余的角有()A. 1个B . 2个C. 3个D. 4个图1 图2图313. 如图3,直线AB CD EF 相交于0,图中对顶角共有()A.3对B. 4对C. 5对D. 6对14. 下列说法错误的是( ) A. 平面内的直线不相交就平行B. 平面内三条直线的交点个数有1个或3个C. 若 a / b , b / c ,贝U a // cD. 平面内过一点有且只有一条直线与已知直线垂直二. 填空题 1. 有一个三角形的两边长为3和5 ,要使这个三角形是直角三角形,它的第三边等 于 ______________________2. 如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是_________ 三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择题
1.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()
(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形
2.下列给出的各组线段中,能构成三角形的是()
(A)5,12,13 (B)5,12,7 (C)8,18,7 (D)3,4,8
3.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()
(A)12 (B)10 (C) 8 (D) 5
4.两条边长分别为2和8,第三边长是整数的三角形一共有()
(A)3个(B)4个(C)5个(D)无数个
5.下列图形中,不是轴对称图形的是()
(A)线段MN (B)等边三角形(C) 直角三角形(D) 钝角∠AOB
6.直角三角形两锐角的平分线相交所夹的钝角为()
(A)125°(B)135°(C)145°(D)150°
7.已知∠α,∠β是某两条平行线被第三条直线所截得的同旁内角,若∠α=50°,则∠β为( )
A.40° B.50°C.130°D.140°
8.如图,下列推理中正确的是( )
A.若∠1=∠2,则AD∥BC B.若∠1=∠2,则AB∥DC
C.若∠A=∠3,则AD∥BC D.若∠3=∠4,则AB∥DC
9.下列图形中,可以折成长方体的是( )
10.一个几何体的三视图如图所示,那么这个几何体是( )
11.如图1,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( ) A.30°B.36°C.45°D.70°
12.、如图2,AB∥CD,AC⊥BC于C,则图中与∠CAB互余的角有( )
A.1个B.2个C.3个D.4个
图1 图2 图3
13. 如图3,直线AB、CD、EF相交于O,图中对顶角共有()
A.3对B.4对C.5对D.6对
14.下列说法错误的是()
A.平面内的直线不相交就平行
B.平面内三条直线的交点个数有1个或3个
C.若a∥b,b∥c,则a∥c
D.平面内过一点有且只有一条直线与已知直线垂直
15. 2. 设α是等腰三角形的一个底角,则α的取值范围是( )
(A)0<α<90°(B)α<90°(C) 0<α≤90°(D) 0≤α<90°
二.填空题
1. 有一个三角形的两边长为3和5,要使这个三角形是直角三角形,它的第三边等于
2. 如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是三角形。
3. 如图,BO、CO分别是∠ABC和∠ACB的平分线,∠BOC=136°,则∠A= 。
第3题第7题
6. 如果等腰三角形的一个外角为80°,那么它的底角为度
7. 如图,已知:△ABC中,AB=AC,AB的垂直平分线DE交AC于E,垂足为D,如果∠A=40˚,那么∠BEC= ;如果△ABC的周长为35cm,△BEC的周长为20cm,那么底边BC= 。
9. 如图,∠AOC=2∠COB,OD是∠AOB的平分线,已知∠COB=20°,则∠COD=_________。
10.如图,直线AB、CD相交于点O,OE平分∠AOD,FO OD于点O,∠1=40°,则∠2=,∠4=。
三.计算题
1. 如图,已知,BE平分∠ABC,∠CBF=∠CFB=650,∠EDF=500,,求证:BC∥AE
2. 如图,点O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,若∠AOD=14°,求∠DOE、∠BOE的度数.
3. 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)指出图中∠AOD的补角,∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
4. 如图4,AB、CD相交于点O,∠DOE=90,∠AOC=37,求∠BOC,∠BOE的度数。
5. 如图,AO⊥CO,BO⊥DO,且∠AOB=160,求∠COD的度数。
6. 如图6所示,已知CD是∠ACB的平分线,∠ACB=50,∠B=70 DE∥BC,求∠EDC和∠BDC的度数。
7. 如图所示,已知∠ABC=50°,∠ACB=60°,BF、CF为∠ABC、∠ACB的平分线且交于点F,过点F作DE∥BC 交AB、AC于点D、E,求∠BFC的度数.
8. 已知:如图,∠ADE=∠B,∠DEC=115°.求∠C的度数.
9. 如图,AD∥BC,∠D=100°,AC平分∠BCD,求∠DAC的度数.
10. 如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
11. 如图,
12. 如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数.
13. 如图,已知:∠1=∠2,∠D=50°,求∠B的度数。
14. 已知:如图,AB//CD,∠B=40°,∠E=30°,求∠D的度数。
15. 如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
四.证明题
1. 如图,已知OM平分∠AOB,ON平分∠BOC,且OM⊥ON,求证:A、O、C在一直线上
2. 已知:如图所示,AB∥CD试说明:∠B+∠BED+∠D=360°
3.已知:如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED,求证:DE//FB
4.已知:如图,∠1=∠2,∠3=∠B,AC//DE,且B、C、D在一条直线上,求证:AE//BD。
5. 如图,AB//CD,AF⊥CD于F,DE⊥AB于E。
连BC,BC交AF于H,交DE于G。
求证:∠BGE=∠CHF.
6. 如图,在ΔABC中,AD平分∠BAC,DE||AC,EF⊥AD交BC延长线于F。
求证:∠FAC=∠B
7. 如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由
8. 如图,AD⊥BC于D,EG⊥BC于G,∠E =∠1,求证AD平分∠BAC。
9. 已知:如图,AD∥BE,∠1=∠2.求证:∠A=∠E.
10. 已知:如图,AB//CD,∠ABE=∠DCF,请说明∠E=∠F的理由。
