f2因子计算
采用f2因子法评价溶出曲线的相似性需注意的问题

发布日20070806期栏目化药药物评价标题采用f2因子法评价溶出曲线的相似性需注意的问题正文审评四部审评八室马玉楠在制剂的开发研究中,通过对比不同处方之间的溶出曲线,可以较准确地反映药物处方、工艺、生产场地及规模等因素变化对药物体外释放行为的影响。
近年来,国外针对溶出曲线的相似性评价方法报道很多,其中f2因子方法因为计算简单、判定结果可靠,作为评价体外溶出曲线相似性的方法,已经被美国FDA的CDER和欧盟EMEA收载并推荐使用。
F2因子的计算公式为:Rt与Tt分别代表参比和受试制剂第t时间点的平均累积释放度,n为测试点数。
其中如果两条溶出曲线完全一致,则:f2=50×lg(100)=100;如果一批样品释药完全,而另一批尚未开始释药,则有:。
因此,f2的值的范围在0~100,而且f2越大,两条曲线的相似性越高。
事实上即使是相同处方的产品,其批次不同,在溶出曲线上也会有一定的差异。
如果受试与参比制剂溶出曲线的差异不大于参比制剂间溶出曲线的差异,那么就可以认为受试与参比制剂溶出曲线具有相似性。
通常认为,同一处方不同批次的样品,在任一取样点释放度的平均差异不超过10%,是可以接受的。
将10%代入式中计算:。
因此,FDA与EMEA规定:若受试与参比制剂的溶出曲线间的f2值不小于50,则认为两者相似。
在某些情况下,如果对于任一取样点释放度的平均差异的限定不是10%,则可通过计算得出相应的f2值(临界值)。
表1提供了一些释放度平均差异与相应的f2临界值。
表1 释放度平均差异与f2临界值表Table 1 Average difference of drug release percent and f2Limit平均偏差(Average difference) 2% 5% 10% 15% 20%F2临界值(f2 Limit) 83 65 50 41 36f2因子的应用条件及注意事项:1.在进行参比与受试制剂的溶出曲线比较的过程中,时间点间隔无需相等,但两者所取各时间点必须一致,一般除0时外,选择3点以上,即n≥3。
f2因子法评价头孢克肟颗粒溶出曲线相似性

’ 通讯作者 ,E malvpce g i z tm.d . - i i. n y@g hc euc : h n
60 9
f因子 法 评 价 头 孢 克 肟 颗 粒 溶 出 曲线 相 似 性 1
陈 伟 鸿 等
8 .% , 中检 所 提 供 ,批 号 :3 5 32 0 0 ) 52 1 0 0 —0 8 3 ;头 孢
克 肟 颗 粒 ( 试 制 剂 ,A) 试 产 品 三批 ,批 号分 别 受 -中
为 l 0 2 、 1 0 2 、 1 0 2 ,批 规 模 : 1 万 袋 ) 0 15 0 16 0 17 0 ;
p .磷 酸 盐 缓 冲 液 ( BS 72 :A= .5 9 . H72 P .) 00 6 C
Ch n W e — o g S n — a g Ch n , i io L u Gu — o g a d Zh n - i g e i n , u Ya g y n , e g Yi Hu Ru - a , i o h n n a g Ke q n h b
( olg f hn s t i dc , u n z o nv ri f hn s eiieGun z o 10 6 C l e iee e a e oC Ma r Me i G ag h uU iesyo iee dc , a gh u5 0 ) a t C M n 0
抗 生 素 ,特 别 是 对 革 兰 阳 性 菌 中 的链 球 菌 属 、肺 炎
可 以有效避 免难 溶性 药物 沉淀 杯底 而漏服 药物 。头 孢 克肟 在体 内溶 出度是 影 响生物 吸 收性能 的重要 参数 ,
球菌、革兰阴性菌中的淋 球菌 等显示 比其它 口头孢
服 更 强 的 抗 菌 作 用 ,其 作 用 为 杀菌 。该 药 是 迄 今 为
溶出曲线F2的使用
药物溶出曲线一致性评价的气息让不少公司不少战友憋足了气,接下来会怎样发展我不想做任何预测或评论。
但对于固体仿制药,如需做体外溶出曲线考察评价,则首推采用F2因子,这点已经无疑。
近来与同事讨论F2相关方法,各有秉持,虽不是什么大分歧,终归还是不利于工作的开展。
因此笔者有意翻阅谢沐风老师撰写的溶出系列,读后虽觉已多方考虑,但难免无法涵盖工作中遇到的所有情况,故又查找相关的国外文献进行解疑。
自己稍稍总结之后又将谢老师几十页的溶出贴从头学习一遍,且做为“实战”丰富经验。
在此将我的一点心得贴出,希望能为大家的工作稍作一些补充(不仅限于一致性评价,对于3类6类药的开发也适用)。
同时也恳请大家分享一些相关的心得经验。
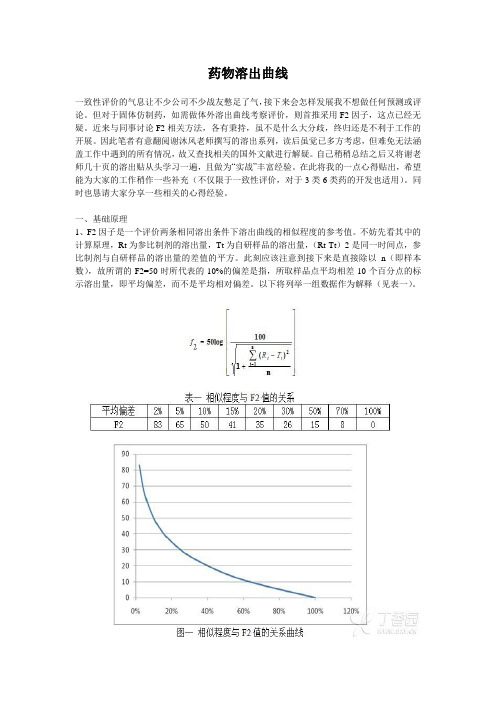
一、基础原理1、F2因子是一个评价两条相同溶出条件下溶出曲线的相似程度的参考值。
不妨先看其中的计算原理,Rt为参比制剂的溶出量,Tt为自研样品的溶出量,(Rt-Tt)2是同一时间点,参比制剂与自研样品的溶出量的差值的平方。
此刻应该注意到接下来是直接除以n(即样本数),故所谓的F2=50时所代表的10%的偏差是指,所取样品点平均相差10个百分点的标示溶出量,即平均偏差,而不是平均相对偏差。
以下将列举一组数据作为解释(见表一)。
常见的问题是如何取点。
谢沐风老师的溶出系列里面已经分列多种情况,但我思考的是究竟不同选点意味着什么?请见表二。
表二4个自研样品与参比制剂的F2值此处不用在意选点是否符合要求,列举这些并计算旨在揭示选点的奥妙。
参比制剂在第四个时间点溶出85%,计算时随着超过85%的点的增加,F2值有增加的趋势。
样品2的F2之所以减少,是因为74与72两者之间代表的偏差极小,而且样品2的曲线与参比制剂的曲线近似平行,可视为正常波动。
而48到52、32与36那却是个质的不一样。
也因此才有超过85%只取一个点。
表三中,样品1与参比制剂各点差值均不超过8%,F2计得60.03;样品2在第1个点有15%的差异,其他点均少于8%,F2计得51.09;样品3在第3个点有超过12%的差异,其他点均少于10%,F2计得51.20;样品4在第1个点有超过19%的差异,其他点完全一致,F2计得50.06;样品5在第2个点有超过17%的差异,其他点均少于10%,F2计得48.05。
(完整版)溶出相似性F2因子评价法计算程序20161012

使用说明:pH4.0时间点个数n6n 参比制剂溶出度%Rt自制制剂溶出度%Tt114.2020.50241.4040.00354.7054.30470.6071.20576.0077.10686.9088.30f2因子水时间点个数n6n 参比制剂溶出度%Rt自制制剂溶出度%Tt116.0014.00257.0052.00378.0077.00492.0090.00f2因子pH1.2时间点个数n3n 参比制剂溶出度%Rt自制制剂溶出度%Tt116.0011.00283.0036.00394.0065.00f2因子计算公式只允许修改黄色部分数据若时间点数超过5个,请在黄色部分3、4行之间插入行若时间点数少于5个,请在黄色部分3、4行之间删除行f2因子时间点个数n6 n参比制剂溶出度%Rt自制制剂溶出度%Tt 116.0014.00581.0052.00691.0077.00f2因子(Rt-Tt)*(Rt-39.691.960.160.361.211.9645.348.55666666734.1859531476.69238465(Rt-Tt)*(Rt-Tt)42514346.66666666738.7298334679.40228148(Rt-Tt)*(Rt-Tt)2522098413075#DIV/0!插入行删除行0.0020.0040.0060.0080.00100.00释放度%#DIV/0! #DIV/0!(Rt-Tt)*(Rt-Tt)48411961041174.57.570111641 43.955114220.00%20.00%40.00%60.00%80.00%00.00%012345时间min原研与自制样品溶出曲线拟合(水)原研自制。
春节学法规普通口服固体制剂溶出度试验技术指导原则

春节学法规普通口服固体制剂溶出度试验技术指导原则普通口服固体制剂溶出度试验技术指导原则一、前言本指导原则适用于普通口服固体制剂,包括以下内容:(1)溶出度试验的一般要求;(2)根据生物药剂学特性建立溶出度标准的方法;(3)溶出曲线比较的统计学方法;(4)体内生物等效性试验豁免(即采用体外溶出度试验代替体内生物等效性试验)的一般考虑。
本指导原则还针对药品的处方工艺在批准后发生变更时,如何通过溶出度试验确认药品质量和疗效的一致性提出了建议。
附录对溶出度试验的方法学、仪器和操作条件进行了概述。
二、背景固体制剂口服给药后,药物的吸收取决于药物从制剂中的溶出或释放、药物在生理条件下的溶解以及在胃肠道的渗透。
由于药物的溶出和溶解对吸收具有重要影响,因此,体外溶出度试验有可能预测其体内行为。
基于上述考虑,建立普通口服固体制剂(如片剂和胶囊)体外溶出度试验方法,有下列作用:1.评价药品批间质量的一致性;2.指导新制剂的研发;3.在药品发生某些变更后(如处方、生产工艺、生产场所变更和生产工艺放大),确认药品质量和疗效的一致性。
在药品批准过程中确定溶出度标准时,应考虑到药物的溶解性、渗透性、溶出行为及药代动力学特性等因素,以保证药品批间质量的一致性、变更以及工艺放大前后药品质量的一致性。
对于新药申请,应提供关键临床试验和/或生物利用度试验用样品以及其他人体试验用样品的体外溶出度数据。
对于仿制药申请,应在溶出曲线研究的基础上制定溶出度标准。
无论是新药还是仿制药申请,均应根据可接受的临床试验用样品、生物利用度和/或生物等效性试验用样品的溶出度结果,制定溶出度标准。
三、生物药剂学分类系统根据药物的溶解性和渗透性,推荐以下生物药剂学分类系统(BCS)(Amidon 1995):1类:高溶解性–高渗透性药物2类:低溶解性–高渗透性药物3类:高溶解性–低渗透性药物4类:低溶解性–低渗透性药物上述分类原则可作为制定体外溶出度质量标准的依据,也可用于预测能否建立良好的体内-体外相关性(IVIVC)。
f2因子法计算电子表格
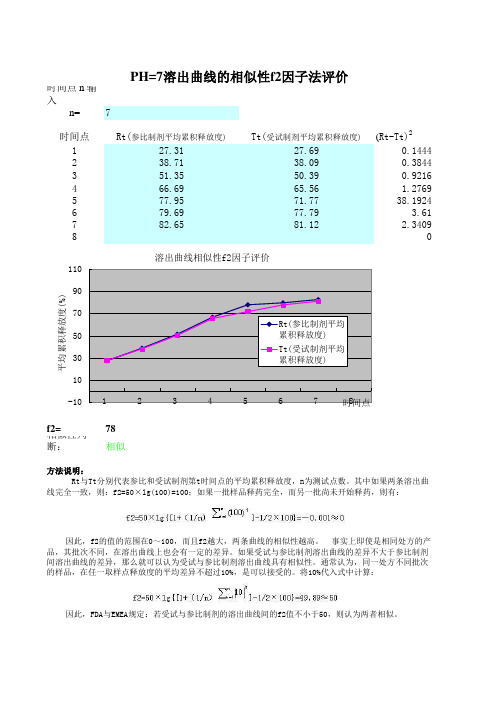
时间点 n 输入n=7时间点Rt(参比制剂平均累积释放度)Tt(受试制剂平均累积释放度)(Rt-Tt)2127.3127.690.1444238.7138.090.3844351.3550.390.9216466.6965.56 1.2769577.9571.7738.1924679.6977.79 3.61782.6581.122.34098f2=78相似性判断:相似方法说明:PH=7溶出曲线的相似性f2因子法评价Rt与Tt分别代表参比和受试制剂第t时间点的平均累积释放度,n为测试点数。
其中如果两条溶出曲线完全一致,则:f2=50×lg(100)=100;如果一批样品释药完全,而另一批尚未开始释药,则有:因此,f2的值的范围在0~100,而且f2越大,两条曲线的相似性越高。
事实上即使是相同处方的产品,其批次不同,在溶出曲线上也会有一定的差异。
如果受试与参比制剂溶出曲线的差异不大于参比制剂间溶出曲线的差异,那么就可以认为受试与参比制剂溶出曲线具有相似性。
通常认为,同一处方不同批次的样品,在任一取样点释放度的平均差异不超过10%,是可以接受的。
将10%代入式中计算:因此,FDA与EMEA规定:若受试与参比制剂的溶出曲线间的f2值不小于50,则认为两者相似。
-101030507090110 123456 78平均累积释放度(%)时间点溶出曲线相似性f2因子评价Rt(参比制剂平均累积释放度)Tt(受试制剂平均累积释放度)f2因子的应用条件及注意事项:1.在进行参比与受试制剂的溶出曲线比较的过程中,时间点间隔无需相等,但两者所取各时间点必须一致,一般除0时外,选择3点以上,即n≥3。
2.f2计算公式只适用于受试与参比制剂的平均累积释放度差值<100时的溶出曲线比较(如果二者的差值>100,就会得到一个负值),普通口服制剂要保证药物溶出90%以上,缓释制剂、肠溶制剂药物释放需达到80%以上,或达到释放平台。
影响因子的定义和计算方法

影响因子的定义和计算方法影响因子(Impact Factor,简称IF)是用来评估学术期刊影响力的指标,它反映了一篇学术论文在一些特定领域内被引用的频率。
影响因子通常由学术出版社或机构每年发布一次,用来衡量期刊的影响力。
计算影响因子的方法主要是通过统计特定期刊上发表的文章在前两年内被引用的次数来得出,然后将这个数字除以这两年内该期刊上发表的论文总数,得到一个表示期刊影响力的数值。
计算影响因子有两种常用的方法,分别是JCR(Journal Citation Reports)方法和Google学术方法。
JCR方法是最常用的计算影响因子的方法,它由ClarivateAnalytics公司(旧名为汤姆森路透)开发。
JCR方法的计算流程如下:1. 首先,选取需要计算影响因子的期刊,一般是在Web of Science (WoS)数据库中收录的期刊。
这个数据库收录了大量学术期刊的论文引用情况。
2.统计选定期刊在前两年内发表的论文数(记为A)。
3.统计选定期刊在前两年内发表的所有论文被引次数的总和(记为B)。
4.计算影响因子,即B/A。
这个数值表示平均每篇论文被引用的次数,可以看作是期刊的影响力。
Google学术方法是一种相对较新的计算影响因子的方法,它是通过Google学术(Google Scholar)平台来进行计算的。
计算流程如下:1. 在Google学术中需要计算影响因子的期刊名称。
2.点击结果中的期刊名称,进入该期刊的页面。
3.在期刊页面中,点击左侧的“自引用”链接,可以看到该期刊自引用的次数(记为C)。
4.统计选定期刊在前两年内发表的论文被引次数的总和(记为D)。
5.计算影响因子,即(D-C)/2、这个数值表示平均每篇论文被其它期刊引用的次数,不包括自引用。
因子分析操作

因子分析作业:全国30个省市的8项经济指标如下:要求:先对数据做标准化处理,然后基于标准化数据进行以下操作1、给出原始变量的相关系数矩阵;2、用主成分法求公因子,公因子的提取按照默认提取(即特征值大于1),给出公因子的方差贡献度表;3、给出共同度表,并进行解释;4、给出因子载荷矩阵,据之分析提取的公因子的实际意义。
如果不好解释,请用因子旋转(采用正交旋转中最大方差法)给出旋转后的因子载荷矩阵,然后分析旋转之后的公因子,要求给各个公因子赋予实际含义;5、先利用提取的每个公因子分别对各省市进行排名并作简单分析。
最后构造一个综合因子,计算各省市的综合因子的分值,并进行排序并作简单分析。
1、输入数据,依次点选分析✍描述统计✍描述,将变量x1到x8选入右边变量下面,点选“将标准化得分另存为变量”,点确定即可的标准化的数据。
依次点选分析✍降维✍因子分析,打开因子分析窗口,将标准化的8个变量选入右边变量下面,点选描述✍相关矩阵下选中系数及KMO和Bartlett的检验,点继续,确定,就可得出8个变量的相关系数矩阵如下图。
由表中数据可以看出大部分数据的绝对值都在0.3以上,说明变量间有较强的相关性。
KMO 和 Bartlett 的检验取样足够度的 Kaiser-Meyer-Olkin 度量。
.621Bartlett 的球形度检验近似卡方231.420df 28Sig. .000由上图看出,sig.值为0,所以拒绝相关系数为0(变量相互独立)的原假设,即说明变量间存在相关性。
2、依次点选在因子分析窗口点选抽取✍方法:主成分;分析:相关性矩阵;输出:未旋转的因3个图。
表看出前3个主成分的累计贡献率就达到了89.599%>85%,所以选取主成分个数为3。
选y1为第一主成分,y2为第二主成分,y3为第三主成分。
且这三个主成分的方差和占全部方差的89.599%,即基本上保留了原来指标的信息。
这样由原来的8个指标变为了3个指标。
