立方根[上学期] 苏科版
【最新】苏科版八年级数学上册《4.2立方根》公开课课件

3
82
思考:
1.一个正方体的体积变为原来的8倍,其边长变为原来 的多少倍?
2.一个正方体的体积变为原来的27倍,其边长变为 原来的多少倍? 3.一个正方体的体积变为原来的n(n>0)倍,其边长 变为原来的多少倍?
归纳:1. 正数的立方根是一个正数
2. 负数的立方根是一个负数
3. 0的立方根是0
填空,你能发现其中的规律吗? 因为
3
3 3 = , 8=_____, -2 -2 8
所以
因为 所以
= 3 8; 8 __
3
-3 -3 3 27 ________, 27 _______,
27. 27 _______ =
1、立方根的定义:如果 一个数的立方等于a,那
a的立方根用 3 2、立方根的性质
a表示
么这个数叫做a的立方根。
a
表示
(1)正数的立方根还是正数 (2)0的平方根还是0 (3)负数的立方根还是负数 3、立方根的求法: 如求8的立方根: ∵ 23 = 8
∴4的平方根是±2
即 4 2
∴8的立方根是2
3
3
3 归纳:
a a
3
例2 求下列各式的值 :
() 1 64 ;() 2 3
3
1 27 ;() 3 3 . 8 64
求下列各式的值:
(1 ) 3
64
3
(2)3
10 125 (3) 3 2 27
( 4) 3
27 64
(5)3 - 64 16
解: (1)
(2) 3
64 4
解: (1) x 3 343
∴x=7 (3)x=23 ∴x=8
八年级数学上册4.2《立方根》教法建议与教材分析素材苏科版

《立方根》教法建议与教材分析教法建议1.从实际问题引入立方根的概念,说明学习数的立方根的意义.立方根的计算有着广泛应用,空间形体都是三维的,有关空间形体的计算经常涉及开立方.2.注意运用类比的方法,使学生清楚新旧知识的区别和联系.通过平方根与立方根的对比,弄清两者的区别和联系.比如不为0的数的立方根与平方根的情况很不同,但0的平方根和立方根都是0本身,在这-点上它们是一致的.通过具体数的计算,让学生体会一个数的立方根的惟一性.教学目标1.了解立方根的概念,会用根号表示一个数的立方根.2.能用立方运算求某些数的立方根,了解开立方与立方互为逆运算.教学重点难点本节的重点是立方根的概念,能用立方运算求某些数的立方根.难点是通过平方根与立方根的对比,弄清两者的区别和联系.尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be someunsatisfactory points. If there are omissions, please correct them. Ihope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
苏科版八年级上册数学 4.2立方根 教案
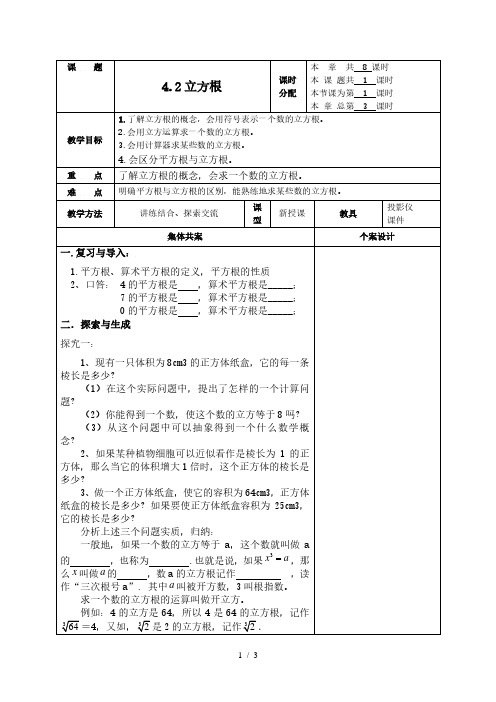
− 125 216
, 0.
正数的立方根是正数 ;
负数的立方根是负数;
0 的立方是 0.
任何数都有唯一立方根
三.透析与应用
例 1:求下列各数的立方根:
(1)64
(2) − 8 125
例 2、计算:
(3)9 (4) 0 (5) 2 10 27
−3 − 1
⑴ 27
(2)
3 −2+ 3 64
例 3:求下列各式中的 x 的值:
棱长是多少?
(1)在这个实际问题中,提出了怎样的一个计算问
题?
(2)你能得到一个数,使这个数的立方等于 8 吗?
(3)从这个问题中可以抽象得到一个什么数学概
念?
2、如果某种植物细胞可以近似看作是棱长为 1 的正
方体,那么当它的体积增大 1 倍时,这个正方体的棱长是
多少?
3、做一个正方体纸盒,使它的容积为 64cm3,正方体
纸盒的棱长是多少?如果要使正方体纸盒容积为 25cm3,
它的棱长是多少?
分析上述三个问题实质,归纳:
一般地,如果一个数的ቤተ መጻሕፍቲ ባይዱ方等于 a,这个数就叫做 a
的
,也称为
.也就是说,如果 x3 = a ,那
么 x 叫做 a 的
,数 a 的立方根记作
,读
作“三次根号 a”. 其中 a 叫被开方数,3 叫根指数。
一个正方体铁块后,其表面积有何变化?试通过计算说明
(假设加工过程中无任何损耗)
六、归纳与总结 1.立方根定义 2.立方根和平方根有何异同? 3.立方根的性质及一个数的立方根的求法.
作业 另附一日一练
板
书
设
计
四维一体机演示区
立方根初中数学八级上册苏科版

4.2 立方根教学目标:1.知识目标.了解立方根的概念,会用根号表示一个数的立方根, 会求一个数的立方根. 2.能力目标.运用数学符号描述开方运算的过程,建立开方的概念,发展抽象思维.教学重、难点:1. 教学重点.掌握立方根的概念,会求一个数的立方根.2. 教学难点.明确平方根与立方根的区别,能熟练地求一个数的立方根.教学方法与教学手段:1.采取“创设情境——类比探究——总结归纳”的教学模式.2.独立思考、合作探究、自主创新.3.多媒体辅助教学.教学过程:一、复习引入1.求下列各数的平方根和算术平方根:625 (-1)20 17981平方根算术平方根2.(1)某种植物细胞可以近似看作是棱长为1的正方体,当它的体积增大1倍时,这个正方体的棱长是多少?棱长为1时,正方体的体积是13=1.设体积为2的正方体的棱长为x,那么x3=2.(2)一般地,如果一个数的立方等于a,这个数就叫做a的立方根,也称三次方根.也就是说,如果x3=a,那么x叫做a的立方根.数a的立方根记作“3a”,读作“三次根号a”.例如,3的立方是27,所以3是27的立方根,记作327 =3.5的立方是______,所以5是______的立方根,记作_________.-2的立方是______,所以-2是______的立方根,记作_________.0的立方是______,所以0是______的立方根,记作_________.(3)1的立方等于多少?还有其他数的立方等于1吗?-3的立方等于多少?还有其他数的立方也等于-27吗?(4)你觉得立方根与平方根有哪些不同?(5)(327 )3=,(3-8 )3=,(3a)3=.你发现了什么?(6)3273=,3(-8)3=,3a3=.你发现了什么?(7)3-8 =,-38 =,二者有何关系?3.-的立方根是,125的立方根是. 4.你还有什么问题?二、数学概念(或模型)三、例题讲解例1 判断正误,若不对,请说明理由,并加以改正.(1)-27的立方根是±3;(2)118的立方根是112;(3)(-8)3的立方根是-8.例2求下列各数的立方根:(1)64;(2)-8125;(3)9.例3 求下列各式中的x:(1)x3=729;(2)x3-1=9;(3)(x-1) 3=827.四、总结反思1.说说你的收获;2.你还有什么问题?五、反馈练习1.求下列各数的立方根:,-(-216),7,10-3.2.求下列各式中的x:(1)x3=-;(2)8x3=27;(3)(x-1) 3=8.3.如果一个正方形的体积增大为原来的64倍,那么它的棱长增大为原来的多少倍?六、作业1.课本第100页习题.2.《评价手册》.。
苏科版数学八年级上册课件:4.2 立方根

-(- 2)2)3 =3 =--2 2 ((66))((33 -22 ))33==--22
5、求下列各数的立方根
)( -1()2 72- ( )2 3732) ( 473 2- )( 2132 264)7 3( 3 324 )73 -(( 21436 ) ) (- 263742 )16(- 42) 16 2674( 4 )(26744)
27 64
交流:下列各数有立方根吗?如果有,请写出 来,如果没有,请说明理由.
282787 00.0.00011 00 --33 --6644 -- 1212126512 65 0.0
121212126565 00.3. 3 π2
π 2
合作交流
归纳:立方根的性质 (1)正数的立方根是一个正数; (2)负数的立方根是一个负数(这与平方根不同) (3)0的立方根是0
=m(||7m)|(47=)±24 =± 2 ( 8()8) m2m=2 =||mm||
A、2个 B、3个 C、4个 D、5个
பைடு நூலகம்
=- _38(_) a33_=32_=a) __3_ =__ __ __ _( __3 _a)_3= 3 a33 23 =______ =_____(3_a)_3=a 3 a3 =a (3
由此你能发现什么规律?
总结反思
1、掌握立方根的定义和性质; 2、会求一个数的立方根; 3、理解并掌握公式: (由立方与开立方的定义可得)
2024秋八年级数学上册第4章实数4.2立方根教学设计(新版)苏科版

组织学生进行讨论,互相交流解题思路和方法,提高问题解决能力。
4.课堂提问(5分钟)
针对本节课的重点内容,进行课堂提问,了解学生对立方根概念、性质和计算方法的掌握程度。
提问方式:随机抽取学生回答,鼓励其他学生补充或纠正。
5.互动环节(5分钟)
创新教学方法,组织学生进行“立方根接龙”游戏。游戏规则:一位学生说出一个数值,下一位学生需要说出这个数值的立方根,依次类推。游戏过程中,教师引导学生关注数值与立方根之间的关系,提高学生的数学思维。
核心素养目标
本节课旨在培养学生以下数学核心素养:逻辑推理、数学抽象和问题解决能力。通过立方根的学习,学生能够逻辑清晰地理解立方根的定义和性质,形成数学抽象思维;能够运用立方根的概念和计算方法,解决实际问题,提高问题解决能力;同时,在探索立方根的过程中,发展学生的数学运算和数学建模素养,为后续数学学习打下坚实基础。
教学资源准备
1.教材:确保每位学生都有苏科版数学八年级上册教材,以便于学生预习和复习本节课内容。
2.辅助材料:准备立方根相关的图片、图表以及立方根计算与应用的视频资料,帮助学生形象理解和记忆立方根的概念。
3.实验器材:无特殊实验需求,只需保证学生有足够的练习本和文具进行计算练习。
4.教室布置:将教室划分为讲解区、讨论区和学生操作区,便于进行课堂讲解、小组讨论和学生练习。设置多媒体设备,以便展示辅助教学材料。
b.关注学生在解决应用题时的思路和方法,指导他们如何将理论知识应用于实际情境。
c.对于拓展题目,鼓励学生尝试不同的解题方法,培养他们的创新思维和问题解决能力。
d.及时给予反馈,对学生的错误进行纠正,并提供具体的改进建议。
e.对于作业完成出色的学生,给予表扬和肯定,增强他们的学习动力和自信心。
苏科版八年级数学上册《立方根》课件

(注意:要理解各式的读法、意义、然后计算)
巩固练习:
1、下列说法正确的是( ) A.任意数 a 的平方根有2个,它们互为相反数; B.任意数 a 的立方根有1个 C.-3是27的负的立方根;
D.(-1) 2 的立方根是-1
(3)表示方法不同; a
3a
(4)被开方数的取值范围不同。
a 中被开方数a是非负数;
3 a 中被开方数a是任何数
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方 法?对你今后的学习有什么帮助?
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月13日星期三2022/4/132022/4/132022/4/13 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/132022/4/132022/4/134/13/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/132022/4/13April 13, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
谢谢观赏
You mad判断正确的是( )
A.64的立方根是 4 B.(-1) 1 的立方根是1
C. 64 的立方根是2 D.如果 3 a =a,则 a=0
3、求下列各式中的X
x 3 +729=0
(x-3) 3 =64
【议一议】 (1)正数有几个立方根? (2)0有几个立方根? (3)负数呢?
小结:
根据立方根的定义, 请你你举出某个数的立 方根?并用符号表示?
苏科版初二数学上册立方根教案

[定义]求一个数的立方根的运算叫做开立方。开立方和立方互为逆运算,因此求一个数的立方根能够通过立方运算来求。
例1:求下列各数的立方根:
⑴ ,⑵ ,⑶0,⑷ .
答案:⑴ ,⑵ ,⑶0,⑷
[总结]立方根的性质:正数的立方根是正数,负数的立方根是负数,0的立方根是0。
苏科版初二数学上册4
4.2立方根
课型
新授
教学目标
1、了解立方根的概念,会用根号表示一个数的立方根
2、会求一个数的立方根
3、运用数学符号描述开方运算的过程,建立开方的概念,进展抽象思维
教学重点
把握立方根的概念,会求一个数的立方根
教学难点
明确平方根与立方根的区别,能熟练地求一个数的立方根
教具预备
投影,小黑板
摸索讨论,尝试解决问题
依惯例如让学生自己举例叙述
尝试解决及时巩固
区分与平方根的不同之处
例2:求下列各式的值:
⑴ ,⑵ ,
⑶ ,⑷ 。
答案:⑴ ,⑵ ,⑶0.7,⑷
例3:求下列各式中的 :
⑴ ,⑵ ,
⑶ 。
答案:略
例4:已知一个正方体的棱长是5cm,再做一个正方体,使它的体积等于原正方体的体积的8倍,求要做的正方体的棱长。
2、若一个数的算术平方根等于那个数的立方根,则那个数是( )
A、±1 B、±1,0 C、0 D、0,1
3、下列说法中,错误的是( )
A、64的立方根是4 B、 立方根
C、 的立方根是2 D、125的立方根是±5
讨论解决问题的方法
把 换成具体的数去检验,加深明白得
独立完成
