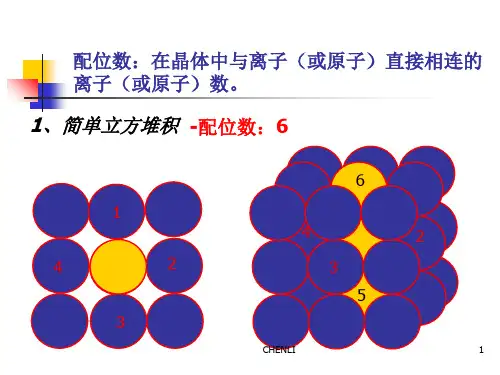
(完整版)晶体的配位数,密度,距离空间利用率计算
合集下载
金属及各类晶体配位数计算图总结
密堆积特点：结合能低，晶体结构稳定；配位数最大为12。
CHENLI
19
(1)六角密积 （Be,Mg,Cd,Zn）
AB
第一层：每个球与6个球相切，有6个空隙， 如编号1,2,3,4,5,6。
第二层：占据1,3,5空位中心。
第三层：在第一层球的正上方形成ABABAB······
排列方式。
CHENLI
20
配位数的确定
高考备考
CHENLI
16
Cl-按面心立方堆积的配位数是12。怎么都 是配位数一会儿是6，一会儿又是12，这怎 么理解？
氯离子按面心立方堆积是没错，但那不是真
正的配位数，因为氯离子是同号离子，是相互斥
的；
同理，钠离子也是按面心立方堆积的，这两
种离子形成的面心立方堆积都产生八面体空穴，
彼此进入对方八面体空穴中就对了，此时异号离
层的垂直方向为三次象转轴。
既是立方体的空间对角线。
原胞当中包含一个粒子，是
布拉菲格子。
CHENLI
7
CHENLI
8
3.典型结构的配位数
(1)六角密积和立方密积的配位数都是十二。即晶体中最
大配位数为十二。
(2)当晶体不是由全同的粒子组成时，相应的配位数要发
生变化—减小。由于晶体的对称性和周期性的特点，以
当0.73r 0.41时，两种球的化排钠列型为 R
o
R Cl - 1 .81 A
rNa 0.52
o
rNa 0 .95 A
RCl CHENLI
13
配位数和半径之比的关系
配位数
r/R
12
1
8
1～0.73
6
0.73～0.41
有关晶体的计算
-
Ca2+：4 F-： 8
碱土金属卤化 物、碱金属氧 化物。
3、边长（晶胞参数）和半径关系
（1）简单立方晶胞参数：边长a
球半径r 与晶胞边长 a 的关系：
a
a
a
a
a=2r
-
3、边长（晶胞参数）和半径关系
（2）体心立方晶胞参数：边长a 球半径r 与晶胞边长 a 的关系：
a
a
a
a
b 3a b 4r
看底面
a 2r
a
2
-
2rsin60
3、边长（晶胞参数）和半径关系 （6）金刚石型
在面心立方基础上，再插入4个球，分别占据8个小立 方体中4个互不相
邻的体心，若1号小体心有球， 则3、6、8号小体心 也有球
8
7
5
6
每个新插入的球，与它所在 小立方 体的顶点4个球相切
4
3
1
2
-
3、边长（晶胞参数）和半径关系 （7）氯化钠型晶胞参数a与离子半径的关系：
2 A3六方晶胞 Zn Cd 内部
6
a=2r
8
12
12
-
各类型离子晶体晶胞的比较
晶体 晶胞 类型 类型
晶胞结构 示意图
距离最近 每个晶 配位数 且相等的 胞含有
相反离子 离子数
实例
NaCl 型
AB CsCl 型
Na+：6 Na+：6 Cl-： 6 Cl-： 6
Cs+：8 Cs+：8 Cl-： 8 Cl-： 8
体积，NA，知道3个可求另一个，因此可能围绕密度出现4种题型。 在晶胞体积中，还可以考察晶胞边长与微粒半径的关系。
-
Ca2+：4 F-： 8
碱土金属卤化 物、碱金属氧 化物。
3、边长（晶胞参数）和半径关系
（1）简单立方晶胞参数：边长a
球半径r 与晶胞边长 a 的关系：
a
a
a
a
a=2r
-
3、边长（晶胞参数）和半径关系
（2）体心立方晶胞参数：边长a 球半径r 与晶胞边长 a 的关系：
a
a
a
a
b 3a b 4r
看底面
a 2r
a
2
-
2rsin60
3、边长（晶胞参数）和半径关系 （6）金刚石型
在面心立方基础上，再插入4个球，分别占据8个小立 方体中4个互不相
邻的体心，若1号小体心有球， 则3、6、8号小体心 也有球
8
7
5
6
每个新插入的球，与它所在 小立方 体的顶点4个球相切
4
3
1
2
-
3、边长（晶胞参数）和半径关系 （7）氯化钠型晶胞参数a与离子半径的关系：
2 A3六方晶胞 Zn Cd 内部
6
a=2r
8
12
12
-
各类型离子晶体晶胞的比较
晶体 晶胞 类型 类型
晶胞结构 示意图
距离最近 每个晶 配位数 且相等的 胞含有
相反离子 离子数
实例
NaCl 型
AB CsCl 型
Na+：6 Na+：6 Cl-： 6 Cl-： 6
Cs+：8 Cs+：8 Cl-： 8 Cl-： 8
体积，NA，知道3个可求另一个，因此可能围绕密度出现4种题型。 在晶胞体积中，还可以考察晶胞边长与微粒半径的关系。
-
金属及各类晶体配位数计算图总结
1.六角密堆积(六角密积)
(1)堆积形式
如图所示，为ABAB…组合
(2)堆积特点
层的垂直方向为6度象转轴。
六角晶系中的 c 轴。它是
一种复式格子。原胞当中
含有两个粒子。
2.立方密堆积(立方密积)
(1)堆积形式
如图所示：ABCABC…组合
(2)堆积特点
层的垂直方向为三次象转轴。
既是立方体的空间对角线。 原胞当中包含一个粒子，是 布拉菲格子。
3(层状结构)、2(链状结构)。
4.氯化铯型结构的配位数
如图所示，大球 ( 半径为 R) 中心为立方体顶角，小 球(半径为r)位于立方体的中心。 如果大球相切，则
立方体的边长为：
空间对角线的长度为： ak
a 2R
Cs
3a 2 3 R
RCl - 1.81 A rC s 1.69 A
3.典型结构的配位数 (1)六角密积和立方密积的配位数都是十二。即晶体中最
大配位数为十二。
(2)当晶体不是由全同的粒子组成时，相应的配位数要发
生变化 —减小。由于晶体的对称性和周期性的特点，以
及粒子在结合成晶体时，是朝着结合能最小、最稳固的
方向发展。因此，相应的配位数只能取:
8(CsCl 型结构 ) 、 6(NaCl 型结构 ) 、 4( 金刚石型结构 ) 、
我们在提到配位数时应当分 析其所处环境。
1、在晶体学中配位数与晶胞类型有关； 2、离子晶体中指一个离子周围最近的异 电性离子的数目； 3、配位化学中，化合物中性原子周围的 配位原子的数目。
一、晶胞密堆积、配位数
1.配位数 一个粒子周围最近邻的粒子数称为配位数。 它可以描述晶体中粒子排列的紧密程度，粒子排列越紧密，
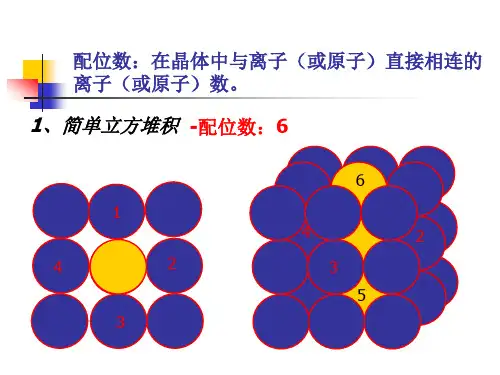
(1)堆积形式
如图所示，为ABAB…组合
(2)堆积特点
层的垂直方向为6度象转轴。
六角晶系中的 c 轴。它是
一种复式格子。原胞当中
含有两个粒子。
2.立方密堆积(立方密积)
(1)堆积形式
如图所示：ABCABC…组合
(2)堆积特点
层的垂直方向为三次象转轴。
既是立方体的空间对角线。 原胞当中包含一个粒子，是 布拉菲格子。
3(层状结构)、2(链状结构)。
4.氯化铯型结构的配位数
如图所示，大球 ( 半径为 R) 中心为立方体顶角，小 球(半径为r)位于立方体的中心。 如果大球相切，则
立方体的边长为：
空间对角线的长度为： ak
a 2R
Cs
3a 2 3 R
RCl - 1.81 A rC s 1.69 A
3.典型结构的配位数 (1)六角密积和立方密积的配位数都是十二。即晶体中最
大配位数为十二。
(2)当晶体不是由全同的粒子组成时，相应的配位数要发
生变化 —减小。由于晶体的对称性和周期性的特点，以
及粒子在结合成晶体时，是朝着结合能最小、最稳固的
方向发展。因此，相应的配位数只能取:
8(CsCl 型结构 ) 、 6(NaCl 型结构 ) 、 4( 金刚石型结构 ) 、
我们在提到配位数时应当分 析其所处环境。
1、在晶体学中配位数与晶胞类型有关； 2、离子晶体中指一个离子周围最近的异 电性离子的数目； 3、配位化学中，化合物中性原子周围的 配位原子的数目。
一、晶胞密堆积、配位数
1.配位数 一个粒子周围最近邻的粒子数称为配位数。 它可以描述晶体中粒子排列的紧密程度，粒子排列越紧密，
晶体空间利用率计算
2r
V球 空间利用率= 100% V晶胞 4 3 r 3 3 100% =52% 8r
1个晶胞中平均含有1个原子 4 3 V =（2r）3=8r3 V球= r 晶胞 3
2、体心立方堆积 a b a
b a a 2 2 2 2 (4r ) a b 3a
2 2 2
4 a r 3
【堆积方式及性质小结】
堆积方式 晶胞类型 空间利 配位数 用率 简单立方 简单立方 体心立方 体心立方 六方堆积 六方 52％ 68% 74% 74% 6 8 12 实例
Po Na、K、Fe
Cu、Ag、Au Mg、Zn、Ti
面心立方 面心立方
12
空间利用率= 4 3 2 r 3 100% 3 a
4 3 2 r 3 100% 4 3 （ r） 3
3 100% 68% 8
3、六方最密堆积 hs
s 2r 3r 2 3r
2
s
V球 100% 空间利用率= V晶胞
4 3 V球 2 r 2r 3 2 6 2 V晶胞 s 2h 2 3r 2 r 8 2r 3 3
【例题1】现有甲、乙、丙、丁四种晶胞，可推 1:1 知甲晶体中与的粒子个数比为——————；乙 DC2 或C2D 晶体 的化学式为—————— ————；丙晶体的 化学式为EF或FE ；丁晶体的化学式为XY Z —————— ———。
2
B
A
Z D C F E X
甲乙丙Fra bibliotek丁Y
甲
乙
丙
【例题2】上图甲、乙、丙三种结构单元中，金属 1:2:3 原子个数比为—————————。 乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
V球 空间利用率= 100% V晶胞 4 3 r 3 3 100% =52% 8r
1个晶胞中平均含有1个原子 4 3 V =（2r）3=8r3 V球= r 晶胞 3
2、体心立方堆积 a b a
b a a 2 2 2 2 (4r ) a b 3a
2 2 2
4 a r 3
【堆积方式及性质小结】
堆积方式 晶胞类型 空间利 配位数 用率 简单立方 简单立方 体心立方 体心立方 六方堆积 六方 52％ 68% 74% 74% 6 8 12 实例
Po Na、K、Fe
Cu、Ag、Au Mg、Zn、Ti
面心立方 面心立方
12
空间利用率= 4 3 2 r 3 100% 3 a
4 3 2 r 3 100% 4 3 （ r） 3
3 100% 68% 8
3、六方最密堆积 hs
s 2r 3r 2 3r
2
s
V球 100% 空间利用率= V晶胞
4 3 V球 2 r 2r 3 2 6 2 V晶胞 s 2h 2 3r 2 r 8 2r 3 3
【例题1】现有甲、乙、丙、丁四种晶胞，可推 1:1 知甲晶体中与的粒子个数比为——————；乙 DC2 或C2D 晶体 的化学式为—————— ————；丙晶体的 化学式为EF或FE ；丁晶体的化学式为XY Z —————— ———。
2
B
A
Z D C F E X
甲乙丙Fra bibliotek丁Y
甲
乙
丙
【例题2】上图甲、乙、丙三种结构单元中，金属 1:2:3 原子个数比为—————————。 乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
晶胞的有关计算
M Z NA V
注意：单位的换算
V-晶胞体积 M-相对分子质量 Z-晶胞中粒子数 NA-阿伏伽德罗常数
例3、金晶体的晶胞是面心立方晶胞，金原子的 直径为d，用NA表示阿伏加德罗常数，M表示金 的摩尔质量。
(1)一个晶胞的体积是多少?
2d
(2)金晶体的密度是多少?
各面对角线上的三个球两两相切
a
（1）设晶胞边长为a，则有a2+a2=(2d)2，即a= 2d
___ pm(列出计算式即可)。(已知D是S，E是Zn） 2 3 4 97 1010
2 NA
（5）空间利用率的计算
空间利用率：指构成晶体的微粒在整个晶体空间中所
占有的体积百分比。
空间利用率
=
球体积 晶胞体积 100%
例5：计算体心立方晶胞中金属原子的空间利用率。
2 4 r3 2 4 ( 3 a)3
祝同学们： 祝学同习学进们步：！金榜题金名榜！题名！
再 见 再见
÷(565.76×10-10cm)3=
g•cm-3。
（6）晶胞有两个基本要素：①原子坐标参数，表示
晶胞内部各原子的相对位置，下图为Ge单晶的晶胞，
其中原子坐标参数A为（0,0,0）；B为（ ，0， ）；
C为 （ ， ，0 ）。则D原子的坐标参数为
（4）原子坐标参数的确定
。 （ 1 ，1，1） 44 4
练习1：
原子D与E所形成化合物晶体的 晶胞如图所示。
① 在该晶胞中，E的配位数为__4____。
② 原子坐标参数可表示晶胞内部各原子的相对位置。 右图晶胞中，原子坐标参数a为(0，0，0)；b为( ,0, )
C为( , ,0 )。则d原子的坐标参数为（__0__,___,__）。
有关晶体的计算
Na +：4 Cl -： 4 Cs +：1 Cl -：1
KBr AgCl、 MgO、CaS、 BaSe
CsCl、CsBr、 CsI、TlCl
ZnS型
Zn 2+ ：4 Zn 2+ ：4 Zn 2+ ：4 ZnS、AgI、 S2- ： 4 S2- ： 4 S2- ：4 BeO
AB 2 CaF2 型
Ca 2+ ：8 Ca 2+ ：8 Ca 2+ ：4 F-： 4 F-： 4 F-： 8
相切
A
14
3、边长（晶胞参数）和半径关系 （8）氟化钙型晶胞参数a与离子半径的关
系： 实际上与金刚石型相同
3a ? 4(r? ? r? )
A
15
3、边长（晶胞参数）和半径关系
（9）CsCl的晶体结构及晶胞构示意图
---Cs+ ---Cl-
Cs+的配位数为：8
Cl-的配位数为：8
A
16
练习：2017全国三卷（5）MgO具有NaCl型结构（如图），其 中阴离子采用面心立方最密堆积方式，X射线衍射实验测得MgO
A
2
1、晶体中的微粒数、化学式 B
A
3
1、晶体中的微粒数、化学式 B
A
4
2、配位数
原子的 完全占有
边长的半 空间占有
晶胞类型 代表
配位数
位置 的原子数
径的关系 率
Po 顶点
1
简单立方
6
a=2r
Li Na 顶 点 、
2
8
A2体心立方 K Fe 体心
Cu Ag 顶 点 、
4
12
A1面心立方 Au Pt 面心
常见晶体模型及晶胞计算
找铜型的晶胞
面心立方最密堆积的空间占有率 =74%
金属晶体的四种堆积模型对比
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
小结：高考常见题型 （一） 晶胞中微粒个数的计算， 求化学式
（二） 确定配位数
（三） 晶体的密度及微粒间距离 的计算
（1）长方体（立方体）：
N=N顶角×1/8 + N棱上×1/4 + N面上×1/2 + N体内
（2）非长方体（非立方体）：
视具体情况分析。
分子晶体 干冰晶体结构 ——晶胞为面心立方体
8个CO2分子位于立方体顶点 6个CO2分子位于立方体面心 在每个CO2周围等距离且相距最近 的CO2共有 12 个。 在每个小立方体中平均分摊到的CO2 分子数为：(8×1/8 + 6×1/2) = 4 个
(2)晶胞的边长为acm，求NaCl晶 体的密度。
ρ=
M / NA×晶胞所含粒子数 晶胞的体积
=
58.5 / NA×4 a3
(3)若NaCl晶体的密度为ρg/cm3，则 NaCl晶体中Na＋与 Na+间的最短距离是多少？
CsCl的晶体结构——晶胞为体心立方体
（1）每个Cs+( Cl-)周围等距
且紧邻的Cl- (Cs+)有 8 个， Cs+( Cl-)的配位数为 8 。
常见晶体模型及晶胞计算
晶胞 描述晶体结构的基本单元
晶胞一般是平行六面体，整块晶体可看作是数量巨大的 晶胞“无隙并置”而成。
三种典型立方晶体结构
简单立方
体心立方
面心立方
晶胞中微粒的计算方法——均摊法
常见晶体模型及晶胞计算
(4)能否 把“NaCl”称为分子式？
练习
－的距离为 a cm，该晶体密度为
（1）设NaCl晶胞的边长为acm，则
示晶为胞中Na+和Cl-的最近距离（( 即小)立
方体的边长）为 a/2 cm，则晶胞中 同种离子的最近距离为 a/2 cm。
(2)晶胞的边长为acm，求NaCl晶 体的密度。
ρ=
M / NA×晶胞所含粒子数 晶胞的体积
镁型[六方密堆积] （Be Mg ⅢB ⅣB ⅦB ）
12
6
3
54
12
6
3
54
12
6
3
54
A B A B A
找镁型的晶胞
1200
每个晶胞含原子数： 2 配位数： 12
空间占有率：
六方密堆积（镁型）的空间利用率计算：
四点间的夹角均为60°
先求S
在镁型堆积中取出六方晶胞，平行六面体的底是
平行四边形，各边长a=2r，则平行四边形的面积：
找铜型的晶胞
面心立方最密堆积的空间占有率 =74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积 的典型代表
空间利用率
配位数
简单立方
Po（钋）
52%
6
体心立方 （钾型）
K、Na、Fe
68%
8
六方最密 （镁型）
Mg、Zn、Ti
74%
12
面心立方最密 （铜型）
Cu, Ag, Au
74%
12
晶胞
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
小结：高考常见题型 （一） 晶胞中微粒个数的计算， 求化学式
练习
－的距离为 a cm，该晶体密度为
（1）设NaCl晶胞的边长为acm，则
示晶为胞中Na+和Cl-的最近距离（( 即小)立
方体的边长）为 a/2 cm，则晶胞中 同种离子的最近距离为 a/2 cm。
(2)晶胞的边长为acm，求NaCl晶 体的密度。
ρ=
M / NA×晶胞所含粒子数 晶胞的体积
镁型[六方密堆积] （Be Mg ⅢB ⅣB ⅦB ）
12
6
3
54
12
6
3
54
12
6
3
54
A B A B A
找镁型的晶胞
1200
每个晶胞含原子数： 2 配位数： 12
空间占有率：
六方密堆积（镁型）的空间利用率计算：
四点间的夹角均为60°
先求S
在镁型堆积中取出六方晶胞，平行六面体的底是
平行四边形，各边长a=2r，则平行四边形的面积：
找铜型的晶胞
面心立方最密堆积的空间占有率 =74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积 的典型代表
空间利用率
配位数
简单立方
Po（钋）
52%
6
体心立方 （钾型）
K、Na、Fe
68%
8
六方最密 （镁型）
Mg、Zn、Ti
74%
12
面心立方最密 （铜型）
Cu, Ag, Au
74%
12
晶胞
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
小结：高考常见题型 （一） 晶胞中微粒个数的计算， 求化学式
2020届高考化学复习《常见晶体模型及晶胞计算》
③六方最密堆积（镁型） Mg、Zn、Ti
六方最密堆积的配位数 =12 每个晶胞含 2 个原子
镁型[六方密堆积] （Be Mg ⅢB ⅣB ⅦB ）
12
6
3
54
12
6
3
54
12
6
3
54ቤተ መጻሕፍቲ ባይዱ
A B A B A
找镁型的晶胞
1200
每个晶胞含原子数： 2 配位数： 12
空间占有率：
六方密堆积（镁型）的空间利用率计算：
思考：NaCl、CsCl同属AB型离子晶体， NaCl晶体中N a+的配位数与CsCl晶体中Cs+的配位数是否相等？
CaF2的晶体结构
（1）每个Ca2+周围等距且 紧邻的F-有 8 个， Ca2+配 位数为 8 。
（2）每个F-周围等距且紧 邻的Ca2+有 4 个， F-配位 数为 4 。
FCa2+
采纳这种堆积 的典型代表
空间利用率
配位数
简单立方
Po（钋）
52%
6
体心立方 （钾型）
K、Na、Fe
68%
8
六方最密 （镁型）
Mg、Zn、Ti
74%
12
面心立方最密 （铜型）
Cu, Ag, Au
74%
12
晶胞
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
（1）设NaCl晶胞的边长为acm，则
示晶为胞中Na+和Cl-的最近距离（( 即小)立
方体的边长）为 a/2 cm，则晶胞中 同种离子的最近距离为 a/2 cm。
有关晶体的计算
②若合金的密度为d g/cm3，晶胞参数 a=________nm。
4、晶胞密度的计算
4、晶胞密度的计算
石墨的密度：设碳原子半径为r，底面边长为a pm，高为h，层 间距为d，则h=2d。 均摊法算出石墨晶胞中有4个C原子（8顶点， 2面，4棱，1内）。
看底面
a 2r
a 2 2rsin60
5、微粒的空间坐标
Na+：4 Cl-： 4 Cs+：1 Cl-：1
KBr AgCl、 MgO、CaS、 BaSe
CsCl、CsBr、 CsI、TlCl
ZnS型
Zn2+：4 Zn2+：4 Zn2+：4 ZnS、AgI、 S2-： 4 S2-： 4 S2-：4 BeO
AB2 CaF2 型
Ca2+：8 Ca2+：8 Ca2+：4 F-： 4 F-： 4 F-： 8
8 4 πr 3 8 4 πr 3
3
3 100% 34%
a3
8
3 r
3
8、夹角求算
9、综合考察
例： 在一定温度下，NiO晶体可以自发地分散并形成 “单分子层”（如下图），可以认为氧离子作密致单 层排列，镍 离子填充其中，列式计算每平方米面积上 分散的该晶体的质量。 （已知NiO的摩尔质量约为74.7 g/mol，氧离子半径为140 pm）
碱土金属卤化 物、碱金属氧 化物。
3、边长（晶胞参数）和半径关系
（1）简单立方晶胞参数：边长a
球半径r 与晶胞边长 a 的关系：
a
a
a
a
a = 2r
3、边长（晶胞参数）和半径关系
（2）体心立方晶胞参数：边长a 球半径r 与晶胞边长 a 的关系：
4、晶胞密度的计算
4、晶胞密度的计算
石墨的密度：设碳原子半径为r，底面边长为a pm，高为h，层 间距为d，则h=2d。 均摊法算出石墨晶胞中有4个C原子（8顶点， 2面，4棱，1内）。
看底面
a 2r
a 2 2rsin60
5、微粒的空间坐标
Na+：4 Cl-： 4 Cs+：1 Cl-：1
KBr AgCl、 MgO、CaS、 BaSe
CsCl、CsBr、 CsI、TlCl
ZnS型
Zn2+：4 Zn2+：4 Zn2+：4 ZnS、AgI、 S2-： 4 S2-： 4 S2-：4 BeO
AB2 CaF2 型
Ca2+：8 Ca2+：8 Ca2+：4 F-： 4 F-： 4 F-： 8
8 4 πr 3 8 4 πr 3
3
3 100% 34%
a3
8
3 r
3
8、夹角求算
9、综合考察
例： 在一定温度下，NiO晶体可以自发地分散并形成 “单分子层”（如下图），可以认为氧离子作密致单 层排列，镍 离子填充其中，列式计算每平方米面积上 分散的该晶体的质量。 （已知NiO的摩尔质量约为74.7 g/mol，氧离子半径为140 pm）
碱土金属卤化 物、碱金属氧 化物。
3、边长（晶胞参数）和半径关系
（1）简单立方晶胞参数：边长a
球半径r 与晶胞边长 a 的关系：
a
a
a
a
a = 2r
3、边长（晶胞参数）和半径关系
（2）体心立方晶胞参数：边长a 球半径r 与晶胞边长 a 的关系：
晶体密度、空间利用率的通用计算方法
晶体密度、空间利⽤率的通⽤计算⽅法晶体密度、空间利⽤率的通⽤计算⽅法以⾦属晶体为例进⾏分析，计算⽅法如下：第⼀步，确定晶胞含有的微粒数。
若1个晶胞中含有x 个微粒，则： (1)1个晶胞中原⼦利⽤的体积 = x ·4 π r 3 / 3 ，其中r 表⽰⾦属原⼦半径。
(2)1个晶胞质量 = x ·M / N A ，其中M 表⽰⾦属的摩尔质量，N A 表⽰阿伏加德罗常数。
若计算对象是离⼦晶体，该式亦然成⽴，M 则表⽰离⼦化合物的摩尔质量。
第⼆步，计算晶胞体积。
不同类型晶胞的体积有不同计算⽅法，⽤a 表⽰晶胞棱长，a 3表⽰晶胞的体积，r 表⽰⾦属原⼦半径，归纳总结如下：(1)简单⽴⽅结构，晶胞体积a 3 ＝(2r ) 3 ＝8r 3 ；侧⾯形状及数据为：,(2)体⼼⽴⽅结构，晶胞体积a 3 ＝64√3r 3 / 9 ；(3)六⽅堆积结构，晶胞体积a 3 ＝ 8√2 r 3 ；晶胞相关数据为为：(4)⾯⼼⽴⽅结构，晶胞体积a 3 ＝16√2 r 3 ；a√2a√3a4r= 2r(1)有关晶体密度的计算通⽤关系式：x·M /N A＝ρ·a3，依据是晶体密度等于晶胞密度，具体计算时把各类型晶胞的体积，代⼊关系式即可，下式亦同。
(2)有关空间利⽤率的计算通⽤关系式：x·4 πr3 / 3＝w%·a3，其中w% 表⽰晶胞空间利⽤率。
注意事项：(1)在实际计算时要注意长度单位换算，晶胞棱长及原⼦半径单位常⽤pm，⽽密度中的体体积单位常⽤(cm)3，存在换算关系1pm=10-10cm。
(2)若计算离⼦晶体密度，⽅法⼤同⼩异，需要综合考虑阴、阳离⼦半径来求晶胞体积。
常见⾦属晶胞结构与性质归纳⼀览表：。
晶体空间利用率计算
混合物晶体空间利用率计算
总结词
混合物晶体空间利用率是指混合物晶体中不同组分原子的堆积密度之和，即单位 体积内所包含的不同组分原子的数目之和。
详细描述
混合物晶体空间利用率计算需要考虑不同组分原子的半径、配位数以及不同组分 之间的相互作用等因素。例如，在铜锌合金中，铜和锌的半径不同，导致它们在 晶体中的排列方式不同，从而影响空间利用率。
引入掺杂元素或分子
有机掺杂
通过引入有机分子或小分子掺杂剂，可以改变晶体的生长过程和 结构，从而提高空间利用率。
无机掺杂
引入无机离子或分子掺杂剂可以调整晶体的能带结构和物理性能， 同时也有助于提高空间利用率。
金属原子掺杂
金属原子掺杂可以改变晶体的导电性和磁性等性质，同时也有助于 优化晶体的空间利用率。
06
未来展望与研究方向
深入研究晶体结构与空间利用率的关系
总结词
深入理解晶体结构与空间利用率的关系是关键，需要进一步研究晶体结构的特点和规律，以及它们对空间利用率 的影响。
详细描述
晶体结构是影响空间利用率的重要因素之一。为了更好地理解空间利用率，需要深入研究晶体结构的组成、排列 方式和相互关系，以及它们对晶体空间利用率的影响。这有助于揭示晶体结构的本质特征，为提高空间利用率提 供理论支持。
意义
空间利用率的高低直接影响到晶体的 物理和化学性质，如熔点、硬度、热 导率等。空间利用率高的晶体具有更 好的机械性能和化学稳定性。
计算方法简介
几何法
通过计算晶体中原子或分子的几 何排列来计算空间利用率。具体 方法包括最近邻法、次近邻法等 。
统计法
通过统计晶体中原子或分子的分 布概率来计算空间利用率。这种 方法考虑了晶体中的涨落效应， 计算结果更为准确。
晶体配位数,空间利用率计算
得：2a 2 + a 2 = (4r) 2
3a 2 16r 2
r 3a 4
空间利用率
= 晶胞含有原子的体积 / 晶胞体积 100%
2 4 r3 2 4 ( 3 a)3
=
3 a3
34 a3
100% 68%
空间利用率计算
例2：求面心立方晶胞的空间利用率.
解：晶胞边长为a，原子半径为r. 由勾股定理： a 2 + a 2 = (4r)2
a = 2.83 r
每个面心立方晶胞含原子数目： 8 1/8 + 6 ½ = 4
= (4 4/3 r 3) / a 3 = (4 4/3 r 3) / (2.83 r ) 3 100 %
= 74 %
配位数：12
7 1 9
6
5
8 2
3 4
10
11
12
空间利用率计算
例1：计算体心立方晶胞中金属原子的空间利用率。
解：体心立方晶胞：中心有1个原子， 8个顶点各1个原子，每个 原子被8个 晶胞共享。每个晶胞含有几个原子:1 + 8 × 1/8 = 2
空间利用率计算
设原子半径为r 、晶胞边长为a ，根据勾股定理，
配位数配位数怎么算面心立方的配位数设备利用率如何计算资产利用率怎么计算配位数和配位多面体资产利用率计算公式晶体计算介电常数计算晶体晶体空间群
配位数：在晶体中与离子直接相连的离子数。
1、简单立方堆积 -配位数：6
1
4
2
3
6
1
4
2
3
5
6
8
7
1
2
4
3
3. 镁型（六方紧密堆积）
3a 2 16r 2
r 3a 4
空间利用率
= 晶胞含有原子的体积 / 晶胞体积 100%
2 4 r3 2 4 ( 3 a)3
=
3 a3
34 a3
100% 68%
空间利用率计算
例2：求面心立方晶胞的空间利用率.
解：晶胞边长为a，原子半径为r. 由勾股定理： a 2 + a 2 = (4r)2
a = 2.83 r
每个面心立方晶胞含原子数目： 8 1/8 + 6 ½ = 4
= (4 4/3 r 3) / a 3 = (4 4/3 r 3) / (2.83 r ) 3 100 %
= 74 %
配位数：12
7 1 9
6
5
8 2
3 4
10
11
12
空间利用率计算
例1：计算体心立方晶胞中金属原子的空间利用率。
解：体心立方晶胞：中心有1个原子， 8个顶点各1个原子，每个 原子被8个 晶胞共享。每个晶胞含有几个原子:1 + 8 × 1/8 = 2
空间利用率计算
设原子半径为r 、晶胞边长为a ，根据勾股定理，
配位数配位数怎么算面心立方的配位数设备利用率如何计算资产利用率怎么计算配位数和配位多面体资产利用率计算公式晶体计算介电常数计算晶体晶体空间群
配位数：在晶体中与离子直接相连的离子数。
1、简单立方堆积 -配位数：6
1
4
2
3
6
1
4
2
3
5
6
8
7
1
2
4
3
3. 镁型（六方紧密堆积）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二. 晶体的配位数，密度，距离，空间利用率计算
1.课本模型图
一个CO2分子周围阳离子的配位数是阳离子的配位数是
有个分子紧邻阴离子的配位数是阴离子的配位数是
阳离子周围的阳离子阳离子周围最近的阳离子数
阴离子周围的阴离子阴离子周围最近的阴离子数CaF2
CaF2
F-的配位数是简单立方堆积体心立方堆积
Ca2+的配位数是配位数是配位数是
Ca2+周围的最近Ca2+数是
F-周围最近的F-数是
面心立方最密堆积六方最密堆积金刚石
配位数是配位数是配位数是
标出A,B,C各层的原子
2、在自然界中TiO2有金红石、板钛矿、锐钛矿三种晶型，其中金红石
的晶胞如右图所示，则其中Ti4+的配位数为化学式为
3.晶体中距每个X原子周围距离最近的Q原子有个．
每个Q原子周围距离最近的X原子有个,
Z原子周围距离最近的X有个,
每个X原子周围距离最近的Z原子有个,
每个Z原子周围距离最近的Q原子有个
4.若en若若若若若若 若
若若若若[Pt(en)2]Cl4若若若若若若若若若 若σ若若若若 若
配离子[PtEn）2]4+的配位数为，该配离子含有的微粒间的作用力类型有
5.立方氮化硼，其结构和硬度都与金刚石相似。
（1）晶胞边长为361.5pm，立方氮化硼的密度是 g/cm3．（只要求列算式）．（2）如图是立方氮化硼晶胞沿z轴的投影图，请在图中圆球上涂“●”和画“×”分别标
明B与N的相对位置．
6.列式表示(NA表示阿伏伽德罗常数的值)
（1）钋原子半径为 r pm，相对原子质量为M,晶体钋的密度空间利用率（2）钠原子半径为 a pm,晶体钠的密度空间利用率
（3）银原子半径为 d cm，银晶体的密度空间利用率
（4）锌原子半径为 b nm 锌晶体的密度空间利用率
7.列式并计算
（1）铁原子半径为 r pm铁晶体有2种分别是钾型铜型，铁晶体的钾型铜型密度之比为（2）金刚石原子半径为 r pm列式并计算表示空间利用率
8.（1）已知CaF2晶体密度为dg/cm3则F﹣与F﹣的最短距离为nm,F﹣与Ca2+最短距离
为pm. （2）CaF2的Ca2+,F-半径分别为 r1,r2pm，把晶胞看成阳离子刚性球堆积，阴离子填充其中列式表示CaF2晶胞空间利用率 Ca2+间最近距离，F-间最近距离
9.已知氧化镍的密度为ρg/cm3；其纳米粒子的直径为Dnm，列式表示其比表面积
m2/g。
答案
12, 6，6,12,12，8，8，6，6 8,4,12,6 6 8 12, 12, 4（1）；
（2）．
6000
D。