最新人教版高中数学选修4-1《圆的切线的性质及判定定理》课堂导学
最新人教版高中数学选修4-1《圆的切线的性质及判定定理》预习导航
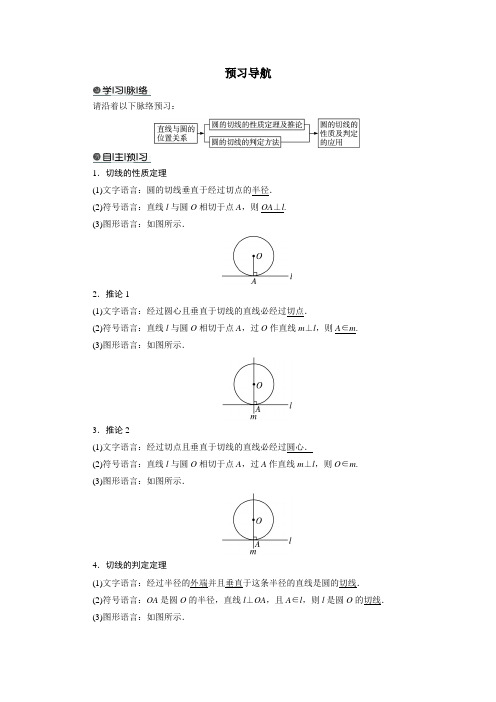
预习导航请沿着以下脉络预习:1.切线的性质定理(1)文字语言:圆的切线垂直于经过切点的半径.(2)符号语言:直线l与圆O相切于点A,则OA⊥l.(3)图形语言:如图所示.2.推论1(1)文字语言:经过圆心且垂直于切线的直线必经过切点.(2)符号语言:直线l与圆O相切于点A,过O作直线m⊥l,则A∈m.(3)图形语言:如图所示.3.推论2(1)文字语言:经过切点且垂直于切线的直线必经过圆心.(2)符号语言:直线l与圆O相切于点A,过A作直线m⊥l,则O∈m.(3)图形语言:如图所示.4.切线的判定定理(1)文字语言:经过半径的外端并且垂直于这条半径的直线是圆的切线.(2)符号语言:OA是圆O的半径,直线l⊥OA,且A∈l,则l是圆O的切线.(3)图形语言:如图所示.1.下列说法:①与圆有公共点的直线是圆的切线;②垂直于圆的半径的直线是圆的切线;③与圆心的距离等于半径的直线是圆的切线;④过直径的端点,且垂直于此直径的直线是圆的切线.其中正确的是().A.①②B.②③C.③④D.①④答案:C解析:与圆有公共点的直线,可能是切线,也可能与圆相交,则①不正确;②不符合切线判定定理的条件,缺少过半径外端的条件,则②不正确;很明显③④正确.2.已知AB是⊙O的切线,在下列给出的条件中,能判定AB⊥CD的是().A.AB与⊙O相切于直线CD上的点CB.CD经过圆心OC.CD是直线D.AB与⊙O相切于C,CD过圆心O答案:D解析:由图①②③可知,根据选项A,B,C中的条件都不能判定AB⊥CD;因为圆的切线垂直于经过切点的半径,所以选项D正确(如图④).3.如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD延长线交于点C,且AD=DC,则∠ABD=__________.答案:45°解析:∵BC为⊙O的切线,∴AB⊥BC.∵AB为⊙O的直径,∴∠ADB=90°,即BD⊥AC.又∵AD=DC,∴∠ABD=∠CBD.∴∠ABD +∠CBD =2∠ABD =∠ABC =90°,即∠ABD =45°.4.如图,AB ,AC 是⊙O 的两条切线,切点分别为B ,C ,D 是优弧 BC上一点,已知∠BAC =80°,那么∠BDC =________.答案:50°解析:∵AB 、AC 是⊙O 的切线,∴OB ⊥AB ,OC ⊥AC .∴∠ABO +∠ACO =180°.∴∠BAC +∠BOC =180°.又∠BAC =80°,∴∠BOC =100°.∴∠BDC =12∠BOC =50°. 5.如图,已知AC 是⊙O 的直径,OE ⊥AD ,OF ⊥AB ,E ,F 为垂足,OE =OF ,AC 是AD 和AB 的比例中项.求证:BC 是⊙O 的切线.证明:∵OE ⊥AD ,OF ⊥AB ,且OE =OF ,∴AC 平分∠BAD .∴∠CAD =∠BAC .∵AC 是AD 和AB 的比例中项,即AC 2=AD ·AB ,∴AC AB =AD AC.∴△ACD ∽△ABC . ∴∠ACB =∠ADC .∵AC 是⊙O 的直径,∴∠ADC =90°.∴∠ACB =90°,即OC ⊥BC .∴BC 是⊙O 的切线.。
2.3 圆的切线的性质及判定定理 教学课件(人教A版选修4-1)

课前探究学习
课堂讲练互动知ຫໍສະໝຸດ 达标演练课后习题解答【变式 3】 如图所示,PB 与⊙O 相切于点 B,PO 交⊙O 于点 A, BC⊥OP 于 C, 若已知 OA=3 cm, OP=4 cm, 则 AC=____cm. 解析 如图所示,连接 OB.
∵PB 是切线,∴OB⊥PB. ∵BC⊥OP,∴OB2=OC· OP. OB2 9 ∴OC= = . OP 4 9 3 ∴AC=OA-OC=3-4=4(cm). 答案 3 4
如果圆的一条直线满足以下三个
条件中的任意两条,那么就一定 满足第三条.它们是:①垂直于切线;②过切点;③过圆心. (2)本定理题设为:一条直线既过圆心又过切点,结论为:这条直 线与圆的切线垂直.如图所示,若直线l切⊙O于A,直线l′经过点
O、A,则直线l′⊥l.
课前探究学习
课堂讲练互动
知能达标演练
课后习题解答
∠PQR=90°-∠OQP.
所以∠RPQ=∠PQR. 所以RP=RQ. 反思感悟 题目中若有圆的切线,首先可以连接圆心和切点,出
现垂直关系.
课前探究学习
课堂讲练互动
知能达标演练
课后习题解答
【变式2】 如图所示,在⊙O中,AB是⊙O的直径,AD是弦,过 点B的切线与AD的延长线交于点 C,且AD=DC,求∠ABD的
割线, ∴PA2=PB· PC.又 PA=10,PB=5, ∴PC=20,BC=15. ∵PA 切⊙O 于 A, ∴∠PAB=∠ACP.
课前探究学习 课堂讲练互动 知能达标演练 课后习题解答
又∠P 为公共角,∴△PAB∽△PCA. AB PA 10 1 ∴CA=PC=20=2. ∵BC 为⊙O 的直径,∴∠CAB=90° . ∴AC2+AB2=BC2=225.∴AC=6 5,AB=3 5. 又∠ABC=∠E,∠CAE=∠EAB, AB AD ∴△ACE∽△ADB,∴AE=AC . ∴AD· AE=AB· AC=3 5×6 5=90.
最新人教版高中数学选修4-1《圆的切线的性质及判定定理》教材梳理

庖丁巧解牛知识·巧学一、圆的切线的性质定理及推论1.圆的切线的性质定理:圆的切线垂直于过切点的半径.此定理强调半径必须经过切点,否则结论不成立.由于过已知点有且只有一条直线与已知直线垂直,所以经过圆心且垂直于切线的直线一定过切点;反过来,过切点且垂直于切线的直线一定经过圆心,由此可以得到两个推论.2.推论1:经过圆心且垂直于切线的直线必经过切点;推论2:经过切点且垂直于切线的直线必经过圆心.知识拓展分析性质定理及两个推论的条件和结论间的关系,可得出如下结论:如果一条直线具备下列三个条件中的任意两个,就可推出第三个:(1)垂直于切线;(2)过切点;(3)过圆心.于是在利用切线性质时,过切点的半径是常作的辅助线.误区警示圆的切线还有两条性质应当注意,一是切线和圆只有一个公共点;二是切线和圆心的距离等于圆的半径.在许多实际问题中,我们也利用它们来解决.二、切线的判定定理1.切线的判定定理是经过半径外端并且垂直于这条半径的直线是圆的切线.在定理中要分清定理的题设和结论,强调“经过半径外端”和“垂直于这条半径”这两个条件缺一不可,否则就不是圆的切线,如图2-3-1的例子就不同时满足两个条件,所以都不是圆的切线.图2-3-12.用判定定理证明一直线与圆相切时,必须满足两个条件:①过半径的外端;②垂直于这条半径.方法归纳在解决相关问题时,若已知要证的切线经过圆上一点,则需把这点与圆心相连,证这直线与这半径垂直;否则需先向这直线作垂线,再证这垂线段是圆的半径.问题·探究问题判断一条直线是否是圆的切线,通常有哪些方法?一般如何选取合适的方法?思路:从圆与直线公共点的个数、直线到圆心的距离、直线与半径的位置思考.探究:判定切线通常有三种方法:(1)和圆有唯一一个公共点的直线是圆的切线;(2)和圆心距离等于半径的直线是圆的切线;(3)过半径外端且和半径垂直的直线是圆的切线. “过半径外端,垂直于这条半径的直线是圆的切线”只是把“到圆心的距离等于半径的直线是圆的切线”的定理具体化,在使用时要根据题目的具体要求选取合适的方法,如果涉及到数值计算或距离问题,通常利用(2),如果涉及到线段的位置关系等,通常选取(3).典题·热题例1如图2-3-2所示,梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为⊙O的直径,图2-3-2求证:⊙O 与CD 相切.思路分析:欲证⊙O 与CD 相切,只需证明圆心O 到直线CD 的距离等于⊙O 的半径即可.证明:过O 点作OE ⊥CD ,垂足为E ,∴AD ∥OE ∥BC.∵O 为AB 的中点,∴E 为CD 的中点.∴OE=21(AD+BC). 又∵AD+BC=AB , ∴OE=21AB=OA,即OE 是⊙O 的半径. ∴⊙O 与CD 相切.方法归纳 在不知道圆与直线是否有公共点的情况下,通常过圆心作直线的垂线段,然后证垂线段的长等于半径,即“作垂直,证半径”,这是证直线与圆相切的常用方法之一.例2如图2-3-3所示,已知AB 为半圆O 的直径,直线MN 切半圆于点C ,AD ⊥MN 于点D ,BE ⊥MN 于点E ,BE 交半圆于点F ,AD=3 cm ,BE=7 cm.图2-3-3(1)求⊙O 的半径;(2)求线段DE 的长.思路分析:(1)连结OC ,证C 为DE 的中点.在解有关圆的切线问题时,常常需要作出过切点的半径.对于(2)则连结AF ,证四边形ADEF 为矩形,从而得到AD=EF ,DE=AF ,然后在Rt △ABF 中运用勾股定理,求AF 的长.解:(1)连结OC.∵MN 切半圆于点C ,∴OC ⊥MN.∵AD ⊥MN ,BE ⊥MN ,∴AD ∥OC ∥BE.∵OA=OB ,∴CD=CE.∴OC=21(AD+BE )=5 cm. ∴⊙O 的半径为5 cm.(2)连结AF.∵AB 为半圆O 的直径,∴∠AFB=90°.∴∠AFE=90°.又∠ADE=∠DEF=90°,∴四边形ADEF 为矩形.∴DE=AF ,AD=EF=3 cm.在Rt △ABF 中,BF=BE-EF=4 cm ,AB=2OC=10 cm.由勾股定理,得AF=2124102222=-=-BF AB ,∴DE=212 cm.深化升华 在梯形当中,最常见的辅助线是高,通过作高,可以构造出直角三角形,然后在直角三角形中进行相关计算;当题目中涉及圆的切线问题时,常常需要作出过切点的半径,通过它可以构建有用的垂直关系.例3如图2-3-4所示,AB 为⊙O 的直径,BC 、CD 为⊙O 的切线,B 、D 为切点,图2-3-4(1)求证:AD ∥OC ;(2)若⊙O 的半径为1,求AD·OC 的值.思路分析:对于(1),连结OD 、BD ,证AD ⊥BD ,OC ⊥BD ;对于(2),连结BD ,证△ABD ∽△OCB 即可.(1)证明:连结OD 、BD.∵BC 、CD 是⊙O 的切线,∴OB ⊥BC ,OD ⊥CD.∴∠OBC=∠ODC=90°.又∵OB=OD ,OC=OC ,∴Rt △OBC ≌Rt △ODC.∴BC=CD.∵OB=OD ,∴OC ⊥BD.又∵AB 为⊙O 的直径,∴∠ADB=90°,即AD ⊥BD.∴AD ∥OC.(2)解:∵AD ∥OC ,∴∠A=∠BOC.又∠ADB=∠OBC=90°,∴△ABD ∽△OCB. ∴OBAD OC AB =. ∴AD·OC=AB·OB=2×1=2.例4如图2-3-5,已知两个同心圆O,大圆的直径AB 交小圆于C 、D ,大圆的弦EF 切小圆于C ,ED 交小圆于G ,若小圆的半径为2,EF=34,试求EG 的长.图2-3-5思路分析:由EF 和小圆切于点C ,易知EF ⊥CD.因为CD 为小圆的直径,联想“直径上的圆周角为90°”,考虑连结GC ,则GC ⊥ED.由已知条件容易求出CD 、EC 的长.在Rt △ECD 中利用勾股定理和射影定理不难求出EG 的长.解:连结GC ,则GC ⊥ED.∵EF 和小圆切于C ,∴EF ⊥CD ,EC=21EF=32. 又CD=4,∴在Rt △ECD 中,有ED=724)32(2222=+=+CD EC .∵EC 2=EG·ED , ∴EG=77672)32(22==ED EC。
高中数学人教A版选修4-1学案第2讲 3 圆的切线的性质及判定定理 Word版含解析

三圆的切线的性质及判定定理
.掌握切线的性质定理及其推论,并能解决有关问题.(重点、难点) .掌握切线的判定定理,会判定直线与圆相切.(易错、易混点)
[基础·初探]
教材整理切线的性质定理及推论
阅读教材倒数第行以上部分,完成下列问题.
.性质定理:圆的切线垂直于经过切点的半径.
如图--,已知切⊙于点,则⊥.
图--
.推论:经过圆心且垂直于切线的直线必经过切点.
.推论:经过切点且垂直于切线的直线必经过圆心.
是⊙的切线,能确定⊥的条件是( )
.∈.过切点
.∈,且过切点.是⊙的直径
【解析】由切线的性质定理知,选项正确.
【答案】
教材整理切线的判定定理
阅读教材~,完成下列问题.
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
下列说法:
①与圆有公共点的直线是圆的切线;
②垂直于圆的半径的直线是圆的切线;
③与圆心的距离等于半径的直线是圆的切线;
④过直径的端点,垂直于此直径的直线是圆的切线.
其中正确的有( ) 【导学号:】
.①②.②③
.③④.①④
【解析】根据切线的定义及判定定理知③④正确.
【答案】
[质疑·手记]
预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:
疑问:
解惑:
疑问:
解惑:
疑问:
解惑:
[小组合作型]
.。
人教A版高中数学选修4-1 第3节圆的切线的性质及判定定理 名师公开课市级获奖课件(57张)

在Rt△AED中,∠AED=90°,∠EAD=30°,
∴AD=2DE. 在Rt△ABD中,∠BAD=90°,∠ABD=30°, ∴BD=2AD=4DE. ∵DE的长是1 cm,∴BD的长是4 cm.
No.2 课堂学案
利用切线的性质求角度
如图所示,点 P 是⊙ O 外的一点, PA、PB 分别与 ⊙O相切于点A和点B,∠APB=40°,C是弧AB上任意一点, 过点C作⊙O的切线分别交PA、PB于点D和点E,求∠DOE的度 数.
第三节
圆的切线的性质及判定定理
课标定位
1.归纳总结圆的切线的有关知识.
2.深入理解圆的切线的性质、判定定理及推论. 3.灵活运用圆的切线的性质、判定定理及推论进行有关 计算与证明.
1.切线的判定与性质的应用.(重点) 2.对切线性质与判定的相关考查常与相似三角形结合在 一起,带有一定的综合性.(难点)
答案: C
3.如图,在半径分别为5 cm和3 cm的两个同心圆中,大 圆的弦AB与小圆相切于点C,则弦AB的长为________cm.
解析:
连接 OA、OC.
∵AB 是小圆的切线, 1 ∴OC⊥AB,∴AC=2AB. ∵在 Rt△AOC 中, AC= 52-32=4(cm). ∴AB=8 cm.
∵AB是直径,∴AD⊥BD. ∴△ABD是等腰直角三角形.
∴∠ABD=45°.
利用切线的性质解决线段的长度问题
如图所示,在△ABC 中,a、b、 c 分别为∠A、∠B、∠C 的对边,且 a、b 是关于 x 的一元二次方程 x2+4(c+2)=(c+ 4)x 的两个根,点 D 在 AB 上,以 BD 为直 径的⊙O 切 AC 于点 E. (1)求证:△ABC 是直角三角形; 3 (2)若 tan A=4,求 AE 的长度.
高中数学人教A版选修4-1课件:2-3圆的切线的性质及判定定理

课堂篇 合作学习 探究一 探究二 探究三 当堂检测
(1)证明:如图,连接OD,BD. ∵BC,CD是☉O的切线, ∴OB⊥BC,OD⊥CD. ∴∠OBC=∠ODC=90°. 又∵OB=OD,OC=OC, ∴Rt△OBC≌Rt△ODC. ∴BC=CD.又∵OB=OD,∴OC⊥BD. ∵AB为☉O的直径,∴∠ADB=90°, 即AD⊥BD.∴AD∥OC. (2)解:∵AD∥OC,∴∠A=∠BOC. 又∠ADB=∠OBC=90°, ������������ ������������ ∴△ABD∽△OCB.∴ = .
课前篇 自主预习
1.切线的性质定理及其推论 (1)性质定理:圆的切线垂直于经过切点的半径. (2)推论1:经过圆心且垂直于切线的直线必经过切点. (3)推论2:经过切点且垂直于切线的直线必经过圆心. 名师点拨1.圆的切线的性质定理及其两个推论可以用一个定理 叙述出来,即如果一条直线满足以下三个条件中的任意两个,那么 就一定满足第三个.它们是:①垂直于切线;②过切点;③过圆心. 2.利用圆的切线的性质定理及其两个推论,可以解决两条直线的 垂直、直线经过点、点在直线上等证明问题.
思考辨析 判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画 “×”. (1)垂直于半径的直线是圆的切线. ( ) (2)切线和圆心的距离等于圆的半径. ( ) (3)圆的切线与圆只有一个公共点. ( ) (4)经过直径的一端且垂直于这条直径的直线是圆的切线. ( ) 答案:(1)× (2)√ (3)√ (4)√
课堂篇 合作学习 探究一 探究二 探究三 当堂检测
变式训练1如图,△ABC为等腰三角形,O是底边BC的中点,☉O与腰 AB相切于点D.求证:AC与☉O相切. 证明:连接OD,过点O作OE⊥AC,垂足为E. ∵☉O与AB相切于点D, ∴OD⊥AB,且OD等于圆的半径. ∵△ABC为等腰三角形,O是底边BC的中点, ∴∠B=∠C,OB=OC. 又∠ODB=∠OEC=90°,∴△ODB≌△OEC. ∴OE=OD,即OE是☉O的半径, 即圆心O到直线AC的距离等于半径. 故AC与☉O相切.
最新人教版高中数学选修4-1《圆的切线的性质及判定定理》课堂探究

课堂探究知能点一:圆的切线的性质题目中若有圆的切线,首先可以连接圆心和切点,出现垂直关系.【例1】如图,已知P AB 是⊙O 的割线,AB 为⊙O 的直径.PC 为⊙O 的切线,C 为切点,BD ⊥PC 交PC 的延长线于点D ,交⊙O 于点E ,P A =AO =OB =1.(1)求∠P 的度数; (2)求DE 的长.(1)要求∠P ,连接OC ,在△POC 中,易证OC ⊥PC ,则sin ∠P =OC OP =12.从而得出∠P =30°.(2)要求DE ,则易转化为求BD -BE ,而BD =12PB =32,易证AE ∥PD ,∠EAB =30°,故BE =12AB =1,得出结论DE =12.解:(1)连接OC .∵C 为切点,∴OC ⊥PC ,△POC 为直角三角形. ∵OC =OA =1,PO =P A +AO =2, ∴sin ∠P =OC PO =12.∴∠P =30°.(2)∵BD ⊥PD ,∴在Rt △PBD 中,由∠P =30°,PB =P A +AO +OB =3,得BD =32.连接AE .则∠AEB =90°,∴AE ∥PD .∴∠EAB =∠P =30°, ∴BE =AB sin 30°=1,∴DE =BD -BE =12.1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O 的切线交AC于E.求证:DE⊥AC.证明:连接OD、AD,如图.∵AB为⊙O直径,∴AD⊥BC.∵AB=AC,即△ABC为等腰三角形,∴AD为BC边上的中线,即BD=DC.又OA=OB,∴OD为△ABC的中位线.∴OD∥AC.∵DE切⊙O于D,∴OD⊥DE.∴DE⊥AC.2.如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN 于点E,BE交半圆于点F,AD=3 cm,BE=7 cm.求⊙O的半径.解:连接OC.因为MN切半圆于点C,所以OC⊥MN.因为AD⊥MN,BE⊥MN,所以AD∥OC∥BE.因为OA=OB,所以CD=CE.所以OC =12(AD +BE )=5 (cm).所以⊙O 的半径为5 cm. 知能点二:圆的切线的判定在不知道圆与直线是否有公共点的情况下通常过圆心作直线的垂线段,然后证垂线段的长等于半径,即“作垂直,证半径”,这是证直线与圆相切的常用方法之一.【例2】如图,△ABC 为等腰直角三角形,O 是底边BC 的中点,⊙O 与腰AB 相切于点D .求证:AC 与⊙O 相切.要证AC 与⊙O 相切,只需证明圆心O 到直线AC 的距离等于⊙O 的半径即可.证明:连接OD ,过点O 作OE ⊥AC ,垂足为E . 因为⊙O 与AB 相切于点D ,所以OD ⊥AB ,且OD 等于圆的半径.因为△ABC 为等腰三角形,O 是底边BC 的中点, 所以∠B =∠C ,OB =OC . 又因为∠ODB =∠OEC =90°, 所以△ODB ≌△OEC .所以OE =OD , 即OE 是⊙O 的半径,即圆心O 到直线AC 的距离等于半径. 所以AC 与⊙O 相切.如图,△ABO 中,OA =OB ,以O 为圆心的圆经过AB 的中点C ,且分别交OA 、OB 于点E 、F .(1)求证:AB 是⊙O 的切线;(2)若△ABO 腰上的高等于底边的一半,且AB =43,求 ECF的长. (1)证明:连接OC ,∵△ABO 为等腰三角形,C 为底边AB 的中点,∴OC ⊥AB . ∴AB 为⊙O 的切线.(2)解:∵△ABO 腰上的高等于底边的一半, ∴∠OAB =∠OBA =π6.∴∠AOB =2π3.又AB =43,∴AC =2 3. ∴OC =AC ·tan30°=23×33=2. ∴=2×2π3=4π3.。
人教新课标版数学高二-高中数学选修4-1 圆的切线的性质及判定定理 学案

[重点校]河南师大附中高中数学选修4-1:圆的切线的性质及判定定理学案【学习目标】1、理解圆和直线的位置关系,直线与圆相切的概念;2、会证明切线的性质定理和两个推论及切线的判定定理;并能利用其解决相关的几何问题.【自主学习】1、直线与圆的位置关系、、 .2、切线的性质定理:圆的切线垂直于经过切点的 .推论1:经过圆心且垂直于切线的直线必经过 .推论2:经过切点且垂直于切线的直线必经过 .3、切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的 .【自主检测】下列命题中正确的是(1)圆的切线垂直于半径(2)垂直于圆的半径的直线是圆的切线(3)过一个圆的直径两端点的两条切线互相平行(4)直线AB与⊙O相切于点A,过O作AB的垂线,垂足必是A(5)若同一个圆的两条切线互相平行,则连结切点所得的线段是该圆的直径(6) 过直径的端点,垂直于直径的直线是圆的切线【典例分析】例1、如图一,AB是⊙O的直径,⊙O过BC的中点D,DE AC⊥. 求证:DE 是⊙O的切线.⊥,例2、如图二,AB是⊙O的直径,P是⊙O外一点,PA AB•弦//BC OP,请判断PC是否为⊙O的切线,说明理由.例3、如图三,AB 是⊙O 的直径,C 为⊙O 上一点,AD 和过C 点的切线互相垂直,垂足为D . 求证:AC 平分DAB ∠.【目标检测】1、AP 为⊙O 切线,P 为切点,OA 交⊙O 于点B ,40A ∠=,则APB ∠=( )A 、25°B 、20°C 、40°D 、35°2、已知P 为⊙O 外一点,以PO 为直径作⊙M ,⊙M 与⊙O 交于点A 、B ,求证:PA 、PB 是⊙O 的切线.3、如右图所示,在梯形ABCD 中,//AD BC ,90C ∠=,且AD BC AB +=,AB 为圆O 的直径,求证:圆O 与CD 相切.4、如图,在RT ABC ∆中,90C ∠=,BE 平分ABC ∠交AC 于点E ,点D 在AB 上,DE EB ⊥求证:AC 是BDE ∆的外接圆的切线.【总结提升】圆的切线的性质定理和和它的两个推论,涉及一条直线的三条性质:经过圆心;经过切点;垂直于切线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂导学
三点剖析
一、切线的性质
【例1】 如图2-3-1,两圆为以O 为圆心的同心圆,大圆的弦AB 是小圆的切线,C 为切点.求证:C 是AB 的中点.
图2-3-1
证明:连结OA 、OC 、OB,
∵OA=OB,
∴△OAB 是等腰三角形.
又∵AC 是小圆切线,C 是切点,
∴OC ⊥AB,即OC 是等腰三角形底边上的高.
∴OC 是AB 边上的中线.
∴C 是AB 的中点.
温馨提示
连结圆心、切点是解决切线问题时常用的作辅助线的方法之一.
二、切线的判定
【例2】 如图2-3-4,AB 是⊙O 的直径,点D 在AB 的延长线上,BD=OB,点C 在圆上,∠CAB =30°.
求证:DC 是⊙O 的切线.
图2-3-4
证明:连结OC 、BC,
∵OA=OC,
∴∠CAB=∠ACO.
∴∠BOC=∠CAB+∠ACO=60°.
∵OB=OC,∴△OBC 是等边三角形.
∵BD=OB,∴BD=BC.
∴∠D=∠BCD.
∵∠OBC=∠D+∠BCD,
∴∠BCD =2
1∠OBC=30°. ∴∠OCD=∠OCB+∠BCD=60°+30°=90°.
∴DC 是⊙O 的切线.
三、切线的性质与判定的综合运用
【例3】 如图2-3-6,直角梯形ABCD 中,以CD 为直径的圆恰好与腰AB 相切.
求证:以AB 为直径的圆也与腰CD 相切.
图2-3-6
思路分析:取CD 、AB 中点O 1、O 2,则O 1、O 2分别是两圆圆心,只需证O 2到CD 距离等于O 2A 或O 2B 即可.
证明:连结O 1O 2,作O 2E ⊥O 1D 于E,DF ⊥O 1O 2于F.
∵O 1C=O 1D,O 2B=O 2A,
∴O 1O 2∥AD ∥BC.
∴AB ⊥O 1O 2.∴DF=AO 2.
∵AB 与⊙O 1相切,∴O 1O 2=O 1D.
∴△O 1O 2E ≌△O 1DF.∴O 2E=DF.∴O 2E=O 2A.
∴⊙O 2与CD 相切于E 点.
各个击破
类题演练1
如图2-3-2,两个同心圆⊙O,大圆的弦AB 和AC 分别和小圆相切于点D 和E.
求证:DE 2
1BC.
图2-3-2
证明:连结OD 、OE,
∵AB 切小圆于D,∴OD ⊥AB.∴AD=BD.同理,AE=EC.
∴DE 是△ABC 的中位线.∴DE 2
1BC. 变式提升1
求证:一圆的两条平行切线的切点连线经过圆心.
图2-3-3
答案:已知:如图l 1、l 2分别切⊙O 于A 、B,l 1∥l 2,求证:O 在AB 上.
证明:连结OA,并延长交l 2于B′,
∵l 1切⊙O 于点A,∴OA ⊥l 1.又∵l 1∥l 2,
∴OA ⊥l 2,即OB′⊥l 2.
∴B 为l 2与⊙O 的切点.∴OB ⊥l 2.
但过O 只有一条直线与l 2垂直.∴B′与B 重合.
即A、O、B在一条直线上,或AB经过点O.
类题演练2
如图2-3-5,已知以Rt△ABC的直角边AB为直径,作⊙O与斜边AC交于点D,E为BC边上的中点,连结DE.
求证:DE是⊙O的切线.
图2-3-5
证明:连结OD、BD.
∵AB是⊙O直径,
∴∠ADB=90°.
∴∠CDB=90°.
∵E是BC中点,
∴CE=EB=DE.
∴∠1=∠2.∵OB=OD,
∴∠3=∠4.
∴∠1+∠4=∠2+∠3.
∵在Rt△ABC中,∠ABC=∠2+∠3=90°,
∴∠EDO=∠1+∠4=90°.
∵D为⊙O上的点,
∴DE是⊙O的切线.
类题演练3
如图2-3-7,已知OC平分∠AOB,D是OC上任意一点,⊙D与OA相切于点E.
求证:OB与⊙D相切.
图2-3-7
证明:连结DE,过D作DF⊥OB,垂足为F.
OB与⊙D相切于点F.。
