博弈论课堂实验
博弈实训报告

随着社会经济的发展,博弈论在各个领域中的应用越来越广泛。
为了更好地理解和掌握博弈论的基本原理和应用,我们学校特组织了本次博弈实训。
本次实训旨在通过模拟实际场景,让学生在实践操作中深化对博弈论的认识,提高分析问题和解决问题的能力。
二、实训目的1. 理解博弈论的基本概念和原理;2. 掌握博弈论在现实生活中的应用;3. 培养团队合作精神,提高沟通协调能力;4. 提升分析问题和解决问题的能力。
三、实训内容1. 博弈论基本概念及原理讲解;2. 案例分析:博弈论在实际生活中的应用;3. 模拟博弈:设计并参与实际场景的博弈游戏;4. 团队合作与沟通协调能力的提升;5. 分析与总结:撰写实训报告。
四、实训过程1. 理论学习:通过课堂讲解、自主学习等方式,让学生掌握博弈论的基本概念、原理和方法。
2. 案例分析:选取具有代表性的博弈论案例,分析其应用场景、策略选择及结果。
3. 模拟博弈:设计实际场景的博弈游戏,如囚徒困境、寡头垄断等,让学生在游戏中体验博弈策略的选择和结果。
4. 团队合作与沟通协调:将学生分为若干小组,每组进行模拟博弈,要求成员之间相互沟通、协作,共同制定策略。
5. 撰写实训报告:在实训结束后,要求学生结合所学知识,撰写一篇关于博弈实训的报告。
1. 学生对博弈论的基本概念、原理和方法有了更深入的理解;2. 学生掌握了博弈论在实际生活中的应用,提高了分析问题和解决问题的能力;3. 学生在团队合作与沟通协调方面取得了显著进步;4. 学生通过撰写实训报告,提高了自己的写作能力。
六、实训总结本次博弈实训取得了圆满成功,达到了预期目的。
以下是实训过程中的一些总结:1. 博弈论在现实生活中的应用非常广泛,如经济、政治、军事、社会等领域;2. 在博弈过程中,策略的选择至关重要,需要充分考虑自身利益和竞争对手的动态;3. 团队合作与沟通协调是博弈成功的关键,成员之间要相互信任、支持,共同制定策略;4. 撰写实训报告有助于学生巩固所学知识,提高自己的写作能力。
博弈论游戏课程设计

博弈论游戏课程设计一、课程目标知识目标:1. 让学生掌握博弈论的基本概念,理解博弈的要素和分类。
2. 使学生了解典型的博弈论模型及其在实际问题中的应用。
3. 引导学生运用博弈论分析解决生活中的竞争与合作问题。
技能目标:1. 培养学生运用博弈论分析问题的能力,提高逻辑思维和判断力。
2. 培养学生团队合作精神,提高沟通协调能力。
3. 培养学生运用数学模型解决实际问题的能力。
情感态度价值观目标:1. 培养学生积极向上的竞争意识,树立正确的合作观念。
2. 引导学生认识博弈论在现实生活中的重要性,激发学习兴趣。
3. 培养学生面对问题时,能从多角度思考,形成开放性思维。
本课程针对高中年级学生,结合博弈论的基本知识,注重培养学生的逻辑思维能力和解决实际问题的能力。
在教学过程中,关注学生的个体差异,鼓励学生主动参与,充分调动学生的积极性。
通过本课程的学习,使学生能够运用博弈论分析生活中的竞争与合作问题,提高自身综合素质。
课程目标具体、可衡量,便于后续教学设计和评估。
二、教学内容1. 博弈论基本概念:博弈、博弈参与者、策略、支付、结果。
2. 博弈论分类:静态博弈、动态博弈、完全信息博弈、不完全信息博弈。
3. 典型博弈论模型:- 鹰鸽博弈:探讨竞争与合作的平衡。
- 猎鹿博弈:分析合作的重要性。
- 零和博弈:了解竞争双方的相互制约。
- 重复博弈:探讨长期合作关系。
4. 博弈论在实际问题中的应用:- 价格竞争、市场份额等经济领域。
- 资源分配、环境保护等社会问题。
- 政治竞选、国际关系等政治领域。
5. 教学内容安排与进度:- 第一周:博弈论基本概念及分类。
- 第二周:典型博弈论模型及案例分析。
- 第三周:博弈论在实际问题中的应用。
- 第四周:总结与拓展,学生分享学习心得。
本教学内容根据课程目标,结合教材《博弈论基础》相关章节,注重科学性和系统性。
在教学过程中,教师需引导学生掌握博弈论的基本概念和模型,通过实际案例分析,使学生更好地理解博弈论在现实生活中的应用。
多样化实验教学之博弈游戏

教学经验总结
提升学生参与度
博弈游戏实验教学通过引入竞争 和合作元素,有效提升了学生的
参与度和学习兴趣。
培养策略思维
学生在博弈游戏中需要制定策略并 预测对手行为,从而锻炼了策略思 维和决策能力。
促进跨学科学习
博弈游戏涉及数学、经济学、心理 学等多学科知识,有助于促进学生 跨学科学习和知识整合。
存在问题与改进方向
实验分组
将学生分成不同的小组,每组 选择一个代表参与博弈。
实验过程
按照游戏规则进行博弈,记录 每轮的决策和结果。
数据收集
实时收集实验数据,包括每轮 的决策、结果和相关信息。
实验数据与结果分析
01
02
03
04
数据整理
对收集到的实验数据进行整理 ,提取有用的信息。
结果展示
通过图表、数据可视化等方式 展示实验结果。
模拟现实场景的博弈游戏
通过模拟现实生活中的场景,让学生在游戏中体 验和实践现实生活中的决策和问题解决过程。
竞技性博弈游戏
组织竞技性博弈游戏,激发学生的竞争意识和团 队合作精神,同时培养学生的抗压能力和心理素 质。
自主研发博弈游戏
鼓励学生自主研发博弈游戏,提高学生的创新能 力和实践能力,同时培养学生的创业意识。
教学反馈
鼓励学生提出问题和建议,及时收集 和处理学生的反馈意见,不断完善和 改进实验教学设计,提高教学质量和 效果。
03
博弈游戏实验教学内容
博弈论基础知识
博弈论定义
介绍博弈论的基本概念、发展 历程和研究领域。
博弈类型
阐述不同类型的博弈,如零和 博弈、非零和博弈、合作博弈 和非合作博弈等。
博弈论中的基本概念
博弈游戏策略分析
博弈论课程设计 (2)

博弈论课程设计1、引言博弈论是现代数学中的一个重要分支,是由经济学家和数学家共同合作发展起来的。
博弈论主要研究人类社会中的决策行为和相互关系,以及在涉及决策行为和相互关系的情景中个体或组织如何做出理性的决策。
博弈论在生物学、心理学、社会学、管理学、工程学等领域也有广泛的应用。
在博弈论的学习过程中,理论与实践相结合是必不可少的。
本文将介绍一些博弈论的课程设计,旨在帮助学生更好地理解和应用博弈论的知识。
2、课程设计2.1 美国拍卖模拟实验美国拍卖是一种竞价拍卖。
在竞拍过程中,买家通过不断提高他们的出价来争夺商品,最后出价最高者获得商品所有权。
美国拍卖的特点是出价者可以随时根据拍卖过程中的信息改变他们的出价。
该模拟实验的目的是通过竞卖过程的模拟来让学生学习博弈论中的核心概念,如策略、博弈纳什均衡等。
该实验还可以帮助学生分析竞价策略与结果的关系,提高学生思考和策略制定的能力。
2.2 博弈纳什均衡实验博弈纳什均衡是博弈论中的一个重要概念。
在一个博弈中,如果所有参与者都选择了他们各自的最优策略,那么这个博弈就到达了一个均衡状态,称为纳什均衡。
该实验可以让学生自己尝试找到博弈的纳什均衡,提高学生的逻辑推理和自主思考能力。
同时,这个实验中涉及到的博弈模型也可以用来分析和解决现实生活中的问题。
2.3 连续混合策略实验连续混合策略是博弈论中的一个重要概念,它在实际应用中有广泛的应用。
在连续混合策略中,玩家有一个概率分布,他们可以随机选择他们的行动。
在竞争和合作的情况下,连续混合策略被用来描述下注、选择行为模型等。
在本实验中,学生将学习如何制定连续混合策略并评估它们的效果。
通过该实验,学生将加深对复杂博弈策略的理解和应用,提高学生的计算能力和分析能力。
3、结语博弈论不仅仅是一种专业的数学知识,它已经成为了理解和解决社会问题的一种重要的工具。
实践是理论的检验,课程设计可以帮助学生更好地理解和应用博弈论的知识。
希望本文介绍的三个课程设计能够为读者提供一些启示,帮助读者更好地理解博弈论的知识和应用。
博弈论课堂实验
博弈论课堂实验。
第一个实验是二级价格拍卖,拍卖品被强制地规定为对每个同学价值10元。
让他们出价。
结果有1人出8元,有2人出9元,有9人出10元,有5人出11元,有2人出12元,有1人出13元,还有7人出到15元或以上。
第二个实验是苏比克拍卖。
我以10元人民币向同学拍卖。
依次有同学出价5元,6元,7元,10元,11元,最后叫10元的同学放弃。
我10元钱拍卖得到21元(净赚11元)。
第三个实验是选美博弈,结果如下:学生编号第一轮第二轮第三轮第四轮15039722252533331318644023335252020762817727236223208303010292512761013121001152161250507113909014141425561001551000163212176860148181111192626422035153221444411220022232520752440000251010032625120527555002825481552930291573030327431388443225138633157523415258235250.9 2.5336303073372510010=====================补充:二级价格拍卖规则是,每个人写下他们的出价交给拍卖者,出价最高的人得到拍卖物品,但他只需要付出次高价格的价钱。
其余人未得到物品,也不付钱。
课堂的实验结果表明约有1半的人出价超过了其对于物品的评价,这并不是理性的选择。
理性的结果应该是出价为其对物品的评价。
但是,这也可能是因为事前强制了物品对他们价值10元有关(每个人都清楚此物对其他人价值十元)。
不过,出价高于、低于十元仍是不理性的。
苏比克拍卖规则:直接叫价拍卖,喊价最高者得到拍卖品(10元钱),但是喊价最高和次高的都需要付出其喊价给拍卖者。
理性的做法是不参加拍卖,或者一旦有人参加则自己放弃参加。
博弈论经典案例

博弈论经典案例1. 恶魔的游戏 (Devil's game)这是一种博弈论的思想实验,假设有两个玩家 A 和 B 同时选择一个数字,如果两个数字相等,则 A 赢;如果两个数字不相等,则 B 赢。
问题在于,无论 A 和B 怎样选择,是否存在一种策略,使得 A 有必胜的把握?答案是不存在这样的必胜策略。
因为无论 A 和 B 怎样选择,都有 50% 的概率两个数字相等,这个概率不受选择策略的影响。
所以,这个游戏是一个“随机游戏”,任何一方都没有必胜策略。
2. 囚徒困境 (Prisoner's dilemma)囚徒困境是最著名的博弈论案例之一。
在这个游戏里,有两个人被抓住了,被判处各自坐牢20 年。
检察官给他们一个选择:如果两个人都认罪,那么各坐8 年;如果其中一个人认罪,而另一个人不认罪,那么认罪的人不用坐牢,而不认罪的人要坐 30 年;如果两个人都不认罪,那么各坐 20 年。
问题在于,两个人应该做什么选择才能最大化自己的利益?这个游戏的特殊之处在于,两个人之间的合作可以带来更大的利益,但是他们又互相不信任。
如果两个人都认罪,那么他们的利益是最小的,但是这么做可以避免另一个人的背叛,因此是一种安全策略。
如果两个人都不认罪,那么他们的利益也不是最大的,因为他们错失了合作的机会。
最终,由于信任问题,两个人可能会都选择认罪,而得到不太理想的结果。
3. 鸽子和猫 (Pigeon and Cat)这是一个有趣的案例。
假设有一个狭长的走廊,有一只鸽子和一只猫在两端等待。
如果鸽子朝左走,那么猫就会朝右走;如果鸽子朝右走,那么猫就会朝左走。
如果两只动物在同一个地方相遇,那么鸽子就会被吃掉。
问题在于,这个走廊有多长时,鸽子才有足够的概率逃脱?答案是 2/3。
如果走廊长度小于等于 2/3,那么猫可以直接守在鸽子的对面,而鸽子无法逃脱。
如果走廊长度大于 2/3,那么猫不得不冒着追错方向的风险前进,这就给了鸽子逃脱的机会。
博弈论实验报告

实验名称:最后通牒博弈实验目的:通过参与博弈实验进一步认识经济学关于“理性人”假设和竞争的关系,发现经济学中理性人假设、效用函数理论等存在的缺陷和不足之处,加深对竞争及经济人假设等经济思想的认知,检验社会偏好对博弈均衡的影响。
实验准备:在本实验中需要实验者收益记录表、实验者数据汇总表、实验数据统计总表等实验表格若干份。
实验内容:从参加实验的人当中,随机地选出两个人,配对进行博弈。
随机地指定A组一个人先行动,即A有权先选择行动策略,然后B再回应。
这个博弈中,A和B两人共同分配100元,这个100元是无条件地送给两人,但条件是他们必须对分配方案达成一致。
由A提出分配方案,比如说A占百分之60,B占百分之40。
这样的一个方案,B可以接受,也可以不接受,当B 接受了以后,实验者就把这100元按A的方案分配给他们两个人(模拟,最后据得益计算实验成绩,得益高者成绩也高):如果B不接受A提出的方案,AB两个就都什么也得不到。
所以,这里面有一个博弈的过程,因为B可以否决,如果觉得自己分得的太少了,不公平,可以否决A的方案,但否决的结果是自己也什么也得不到。
就是说B惩罚了A,自己也付出了成本,失去了本来可以得到的部分,最后双方都是0了。
实验过程:1.实验人员的选择和分组(1)实验人员的选择。
采用随机数或抽奖软件随机抽取若干名同学作为实验参与者,选取2名同学作为实验工作人员,负责发放相关表格和统计数据。
(2)分组。
将选定的实验参与者分成A、B两组,A组实验者为提议者,其编号为A1,A2,A3,...;B组实验者为响应者,其编号为B1,B2,B3,...(3)座位调整。
为了避免个人关系等因素的干扰,在实验过程中不能让两组实验参与者坐在一起,应让他们隔离相向坐于教室的左右两端。
2.发放实验材料向A组实验者发放写好编号的实验卡片,向所有实验参与者发放实验收益记录表。
向A组每位实验者发放100元虚拟货币。
3.宣读展示实验说明(1)每一位实验参与者都应收益的最大化为目标。
博弈论实验课教案模板范文

课程名称:博弈论实验课程目标:1. 让学生了解博弈论的基本概念和原理。
2. 通过实验,使学生能够将博弈论应用于实际问题分析。
3. 培养学生的逻辑思维能力和团队协作精神。
课程内容:一、导入1. 介绍博弈论的定义和基本类型。
2. 通过生活中的例子引入博弈论的概念。
二、理论讲解1. 博弈论的基本要素:参与者、策略、支付矩阵。
2. 非合作博弈与合作博弈的区别。
3. 常见的博弈模型:囚徒困境、智猪博弈、最后通牒博弈等。
三、实验准备1. 实验规则讲解。
2. 实验道具准备:卡片、纸、笔等。
3. 学生分组,每组5-6人。
四、实验实施1. 最后通牒博弈实验:- 每位学生随机扮演“提议者”或“接收者”角色。
- 提议者从10元中提出给接收者的金额,接收者决定是否接受。
- 如果接收者接受,双方按照提议分配金额;如果拒绝,双方都得不到任何金额。
- 每位学生进行3轮博弈,记录每轮的提议和接受情况。
2. 囚徒困境实验:- 学生分为两组,每组进行多轮博弈。
- 每轮博弈中,组内成员可以选择“合作”或“背叛”。
- 根据选择,计算每轮博弈的收益,并记录下来。
五、数据分析和讨论1. 对实验数据进行整理和分析。
2. 讨论不同博弈模型下的策略选择。
3. 分析实验结果与理论预测的差异。
六、总结与反思1. 总结博弈论的基本原理和应用。
2. 学生分享实验心得,反思实验过程中的策略选择。
3. 教师点评,总结课程内容。
教学资源:1. 教材:《博弈论》2. 网络资源:博弈论相关视频、文章等。
3. 实验道具:卡片、纸、笔等。
教学评估:1. 学生对博弈论基本概念和原理的掌握程度。
2. 学生在实验中的策略选择和分析能力。
3. 学生对实验结果的讨论和反思。
备注:1. 教师可根据实际情况调整实验内容和时间。
2. 鼓励学生在实验过程中积极思考和交流。
3. 实验结束后,教师应组织学生进行总结和讨论,提高学生的综合能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
博弈论课堂实验。
第一个实验是二级价格拍卖,拍卖品被强制地规定为对每个同学价值10元。
让他们出价。
结果有1人出8元,有2人出9元,有9人出10元,有5人出11元,有2人出12元,有1人出13元,还有7人出到15元或以上。
第二个实验是苏比克拍卖。
我以10元人民币向同学拍卖。
依次有同学出价5元,6元,7元,10元,11元,最后叫10元的同学放弃。
我10元钱拍卖得到21元(净赚11元)。
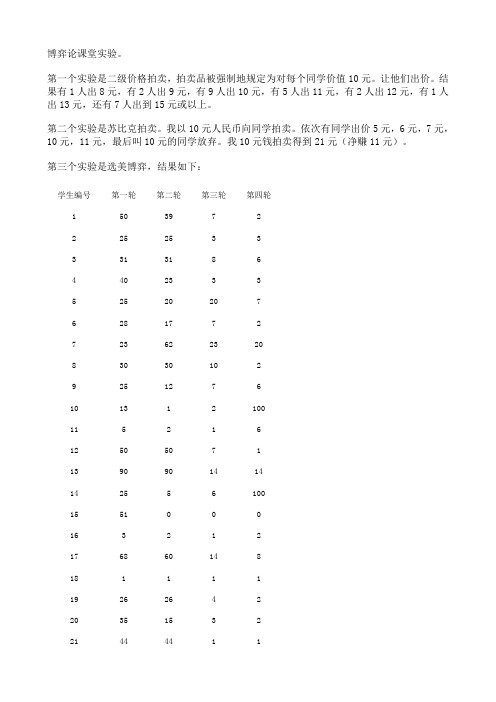
第三个实验是选美博弈,结果如下:
学生编号第一轮第二轮第三轮第四轮
1503972
2252533
3313186
4402333
52520207
6281772
723622320
83030102
9251276
101312100
115216
12505071
1390901414
142556100
1551000
163212
176860148
181111
19262642
20351532
21444411
220022
23252075
2440000
25101003
26251205
2755500
282548155
293029157
30303274
3138844
32251386
3315752
34152582
35250.9 2.53
36303073
372510010
=====================
补充:二级价格拍卖规则是,每个人写下他们的出价交给拍卖者,出价最高的人得到拍卖物品,但他只需要付出次高价格的价钱。
其余人未得到物品,也不付钱。
课堂的实验结果表明约有1半的人出价超过了其对于物品的评价,这并不是理性的选择。
理性的结果应该是出价为其对物品的评价。
但是,这也可能是因为事前强制了物品对他们价值10元有关(每个人都清楚此物对其他人价值十元)。
不过,出价高于、低于十元仍是不理性的。
苏比克拍卖规则:直接叫价拍卖,喊价最高者得到拍卖品(10元钱),但是喊价最高和次高的都需要付出其喊价给拍卖者。
理性的做法是不参加拍卖,或者一旦有人参加则自己放弃参加。
因为会出现轮番加价的陷阱。
选美博弈规则:每人任选[0,100]区间的一个整数,然后以众人的选择求平均,再在平均值基础上乘0.5,得到一个数,与这个数越接近的选择就得到越高的回报(成绩分数,譬如确定分数计算的公式为100-|xi-0.5∑xi/n|,以此记载学生平时成绩一次)。
标准的博弈论解最后是大家都会选择0。
但是很多实验表明结果并不如此,因为很多时候人们不一定有这么深的推理能力,即使自己有这样的推理能力也不能确保其他人有同样深的推理能力。
课堂实验结果与其他许多同样的实验结果是差不多的。
最初人们多选择20-40的数字,但是重复数次后就出现向零方向的收敛,尤其是在获悉前次博弈的结果的时候。
选美博弈的思想最早可
追溯到凯恩斯:“……专业投资者的情况可以和报纸上的选美竞赛相比拟。
在竞赛中,参与者要从100张照片中选出最漂亮的6张。
选出的6张照片最接近于全部参与者一起所选出的6张照片的人就是得奖者。
由此可见,每一个参与者所要挑选的并不是他自己认为是最漂亮的人,而是他设想的其他参与者所要挑选的人。
全部参与者都以与此相同办法看待这个问题。
这里的挑选并不是根据个人判断力来选出最漂亮的人,甚至也不是根据真正的平均的判断力来选出的最漂亮的人,而是运用智力来推测一般人所推测的一般人的意见为何。
在这里,我们已经达到了第三个推测的层次;我相信,有人还会进行第四、第五和更多的层次。
”(摘自《就业、利息和货币通论》,P.159-160,约翰·梅纳德·凯恩斯,高鸿业重译本)聚点
选美博弈中略有例外的情况是,第10和14号同学,他们的前三次的选择符合收敛的性质,但是第四次选择都选择了100(不可思议!),其他同学的选择也基本上都符合收敛的性质。
实验完毕让10、14号两同学描述一下他的决策过程,为什么这样选择。
一个同学的解释是,他知道最后大家都会选向0,但是他不想让大家都得到0——其实可能有误解,因为大家都选0并不意味着大家都得到零,都选0的结果是大家的成绩都会是100,另外也有恶搞的成分,另一位同学承认他第4轮就是故意恶作剧的。
其实,有人恶作剧可能是大家不会都选0的原因,因为在选择者的推理中,大概也需要把恶作剧纳入考虑。
不过时间有限,未能继续做实验检验。
