必修一 1.2函数及其表示 习题课
人教版教材必修一1.2函数及其表示课后练习word版

A 组1、 求下列函数定义域:(1)3()4x f x x =- (2)()f x =(3)26()32f x x x =-+ (4)()1f x x =-2、下列那一组中的函数()f x 与()g x 相等?(1)()1f x x =-,2()1x g x x=- (2)2()f x x =,4()g x =(3)2()f x x =,()g x =3、画出下列函数的图像,并说出函数的定义域、值域(1)3y x = (2)8y x=(3)45y x =-+ (4)267y x x =-+4、已知函数2()352f x x x =-+,求((),(3),()(3)f f a f a f a f -++的值5、已知函数2()6x f x x +=-, (1)点)(3,14在()f x 的图像上吗?(2)当4x =时,求()f x 的值;(3)当()2f x =,求x 的值。
6、若2()f x x bx c =++,且(1)0,(3)0f f ==,求(1)f -的值。
7、画出下列函数的图像:(1)0,0,()1,0;x F x x ≤⎧=⎨>⎩ (2)()31,{1,2,3}G n n n =+∈8、如图,矩形的面积为10,如果矩形的长为x ,宽为y ,对角线为d ,周长为l ,那么你能获得关于这些量的哪些函数?9、一个圆柱容器的底部直径为d cm ,高是h cm 。
现在以3/vcm s 的速度向容器内注入某种溶液,求容器液体的高度x cm 关于注入溶液的时间t s 的函数解析式,并写出函数的定义域和值域。
10、设集合{,,},{0,1}A a b c B ==。
试问:从A 到B 的映射共有几个?并将它们分别表示出来。
B 组1、 函数()r f p =的图像如图所示。
(1) 函数()r f p =的定义域是什么?(2) 函数()r f p =的值域是什么?(3) r 取何值时,只有唯一的p 值与之对应?2、 画出定义域为{38,5}x x x -≤≤≠且,值域为{12,0}y y y -≤≤≠的一个函数的图像。
高中数学第一章集合与函数概念1.2函数及其表示1.2.2第1课时函数的表示法练习新人教A版必修1

第1课时 函数的表示法A 级 基础巩固一、选择题1.以下形式中,不能表示“y 是x 的函数”的是( ) A.B.C .y =x 2D .x 2+y 2=1解析:根据函数的定义可知,x 2+y 2=1不能表示“y 是x 的函数”. 答案:D2.已知x ≠0,函数f (x )满足f ⎝⎛⎭⎪⎫x -1x =x 2+1x2,则f (x )的表达式为( )A .f (x )=x +1xB .f (x )=x 2+2C .f (x )=x 2D .f (x )=⎝ ⎛⎭⎪⎫x -1x 2解析:因为f ⎝ ⎛⎭⎪⎫x -1x =x 2+1x 2=⎝ ⎛⎭⎪⎫x -1x 2+2,所以f (x )=x 2+2. 答案:B3.已知f (x )的图象恒过点(1,1),则f (x -4)的图象恒过点( ) A .(-3,1) B .(5,1) C .(1,-3)D .(1,5)解析:由f (x )的图象恒过点(1,1)知,f (1)=1,即f (5-4)=1.故f (x -4)的图象恒过点(5,1).答案:B4.已知函数f (2x +1)=6x +5,则f (x )的解析式是( ) A .3x +2B .3x +1C .3x -1D .3x +4解析:方法一:令2x +1=t ,则x =t -12.所以f (t )=6×t -12+5=3t +2,所以f (x )=3x +2.方法二:因为f (2x +1)=3(2x +1)+2, 所以f (x )=3x +2. 答案:A5.在函数y =|x |(x ∈[-1,1])的图象上有一点P (t ,|t |),此函数与x 轴、直线x =-1及x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图可表示为( )解析:由题意知,当t >0时,S 的增长会越来越快,故函数S 图象在y 轴的右侧的切线斜率会逐渐增大.答案:B 二、填空题6.已知函数f (x ),g (x )分别由下表给出:则f [g (1)]的值为x =____________. 解析:f [g (1)]=f (3)=1.因为g [f (x )]=2, 所以f (x )=2, 所以x =1. 答案:1 17.已知f (x )是一次函数,且其图象过点A (-2,0),B (1,5)两点,则f (x )=__________. 解析:据题意设f (x )=ax +b (a ≠0), 又图象过点A (-2,0),B (1,5).所以⎩⎪⎨⎪⎧-2a +b =0,a +b =5,解得a =53,b =103.所以f (x )=53x +103.答案:53x +1038.如图,函数f (x )的图象是折线段ABC ,其中点A ,B ,C 的坐标分别为(0,4),(2,0),(4,2),则f (f (f (2)))=________.解析:f (f (f (2)))=f (f (0))=f (4)=2. 答案:2 三、解答题9.若x ∈R,y =f (x )是y =2-x 2,y =x 这两个函数中的较小者,画出y =f (x )的图象,并求y =f (x )的值域.解:在同一坐标系中画出函数y =2-x 2,y =x 的图象,如图所示,根据题意知图中实线部分即为函数y =f (x )的图象,由2-x 2=x 得x =-2或1,由图象可知,函数y =f (x )的值域为(-∞,1].10.画出二次函数f (x )=-x 2+2x +3的图象,并根据图象解答下列问题: (1)比较f (0)、f (1)、f (3)的大小;(2)若x 1<x 2<1,比较f (x 1)与f (x 2)的大小; (3)求函数f (x )的值域.解:f (x )=-(x -1)2+4的图象,如图所示: (1)f (0)=3,f (1)=4,f (3)=0, 所以f (1)>f (0)>f (3).(2)由图象可以看出, 当x 1<x 2<1时,函数f (x )的函数值随着x 的增大而增大, 所以f (x 1)<f (x 2).(3)由图象可知二次函数f (x )的最大值为f (1)=4,则函数f (x )的值域为(-∞,4].B 级 能力提升1.若f (1-2x )=1-x 2x 2(x ≠0),那么f ⎝ ⎛⎭⎪⎫12=( ) A .1 B .3 C .15 D .30 解析:方法一:令1-2x =t ,则x =1-t2(t ≠1),所以f (t )=1-⎝ ⎛⎭⎪⎫1-t 22⎝ ⎛⎭⎪⎫1-t 22=-t 2+2t +3(t -1)2.所以f (x )=-x 2+2x +3(x -1)2,所以f ⎝ ⎛⎭⎪⎫12=15.方法二:令1-2x =12,得x =14,所以f (12)=1-⎝ ⎛⎭⎪⎫142⎝ ⎛⎭⎪⎫142=15.答案:C2.函数y =x 2-4x +6,x ∈[1,5)的值域是________.解析:画出函数的图象,如图所示,观察图象可得图象上所有点的纵坐标的取值范围是[f (2),f (5)),即函数的值域是[2,11).答案:[2,11)3.用长为l 的铁丝弯成下部为矩形、上部为半圆形的框架(如图所示),若矩形底边AB 长为2x ,求此框架围成的面积y 与x 的函数关系式,并写出其定义域.解:因为AB =2x , 所以CD ︵的长为πx ,AD =l -2x -πx 2,所以y =2x ·l -2x -πx 2+πx 22=-⎝ ⎛⎭⎪⎫π2+2x 2+lx . 由⎩⎪⎨⎪⎧2x >0,l -2x -πx 2>0,解得0<x <lπ+2,故函数的定义域为⎝ ⎛⎭⎪⎫0,l π+2.。
人教A版高中数学必修1(教学课件+练习)1.2函数及其表示1.2.2第2课时

第一章 1.2 1.2.2第2课时
1.如下图给出的四个对应关系,其中构成映射的是()
A.(1)(2)B.(1)(4)
C.(1)(2)(4) D.(3)(4)
解析:在(2)中,元素1和4没有对应元素;(3)中元素1和2都有两个元素与它们对应,不满足映射的定义;(1)、(4)符合映射定义.故选 B.
答案:B
2.下列图形是函数y=-|x|(x∈[-2,2])的图象的是()
解析:y=-|x|=
x,-2≤x<0
-x,0≤x≤2
,其图象是x轴下方的两条线段,包括x=±2时的两个端点.
答案:B
3.已知函数f(x)=2x,x≥0,
x x+1,x<0,
则f(-2)等于()
A.1B.2 C.3 D.4 解析:∵-2<0,∴f(-2)=-2(-2+1)=2.
答案:B
4.函数y=2x x>0,
-4x<0
的定义域为________.
解析:{x|x>0}∪{x|x<0}={x|x≠0}.答案:{x|x≠0}
5.集合A={a,b},集合B={c,d,e}.则由A到B的映射共有________个.
解析:由于映射的对应形式只有“一对一”、“多对一”两种情况,故由A到B的映射有以下9种情况,如图所示.
答案:9
6.已知f(x)=x+1x>0,
πx=0,
0x<0.
求f(f(f(-3)))的值.
解:∵-3<0,∴f(-3)=0.
∴f(f(-3))=f(0)=π.
又π>0,∴f(f(f(-3)))=f(π)
=π+1.。
人教A版高中数学必修1《1.2 函数及其表示 习题1.2》_0
学生1配凑法
学生2换元法
学生独立思考并完成例2,
教师提问,查看学生掌握情况,对于例2(2)可采用试错法让学生提出问题,解决问题
师生共同总结换元的解题步骤及注意事项
教师板书解题过程及小结
学生学生独立思考并完成.
学生总结该题的方法
学生思考受阻
教师提示问题3
学生:独立完成思考例4与问题3的关系,得出方法.
函数的表示法习题课(一)教学设计
【教学目标】:
1.会用代入法,换元法,及待定系数法求解析式.
2.通过解析式的求法的教学,培养学生抽象概括能力及严谨的思维品质.
【教学重点】:代入法,换元法,及待定系数法求解析式
【教学难点】:换元法求解析式
【教学策略与方法】:
1.教学方法:启发讲授式,问题探究式
2.教具准备:多媒体
变式1:已知f(3x﹣5)=2(3x﹣5)+3求f(x)
变式2:已知f(3x﹣5)=6x﹣7,求f(x)
例2:(1)已知f(2x+1)=4x2+8x+3,求f;
例3:(1)已知二次函数的图象的顶点坐标是(1,﹣3),且经过点P(2,0),求这个函数的解析式.
教师提问学生能用几种方法解决
例4已知 ,求f(x)
问题3:f(1),f(2)怎么求?
变式3:函数f(x)满足2f(x)﹣f(﹣x)=x+1,求f(x)
学生独立思考并完成例1:对于定义域中的任意x,在“对应法则f”的作用下,即可得到y.因此,f是使“对应”得以实现的方法和途径.是联系x与y的纽带,例1中f(x)的对应关系是乘2加3
学生总结
让学生养成解后反思总结的学习习惯,培养学生总结概括能力.
高一数学必修1《1.2函数及其表示》单元测试题(含答案)
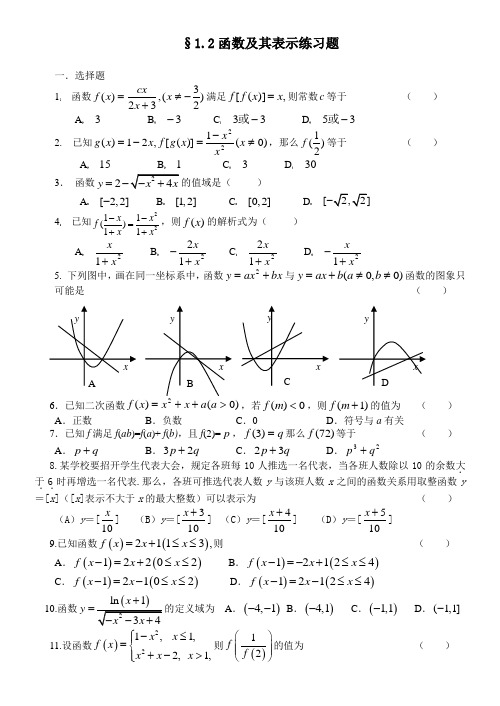
§1.2函数及其表示练习题一.选择题1 函数)23(,32)(-≠+=x x cx x f 满足,)]([x x f f =则常数c 等于 ( ) A 3 B 3- C 33-或 D 35-或2. 已知)0(1)]([,21)(22≠-=-=x x x x g f x x g ,那么)21(f 等于 ( ) A 15 B 1 C 3 D 303.函数2y =的值域是( )A [2,2]-B [1,2]C [0,2] D[]4 已知2211()11x x f x x--=++,则()f x 的解析式为( ) A21x x + B 212x x +- C 212x x + D 21x x+-5. 下列图中,画在同一坐标系中,函数bx ax y +=2与)0,0(≠≠+=b a b ax y 函数的图象只可能是( )6.已知二次函数)0()(>++=a ax x x f ,若0)(<m f ,则)1(+m f 的值为 ( ) A .正数 B .负数 C .0 D .符号与a 有关 7.已知f 满足f (ab )=f (a )+ f (b),且f (2)=p ,q f =)3(那么)72(f 等于 ( )A .q p +B .q p 23+C .q p 32+D .23q p +8.某学校要招开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大.于.6.时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( )(A )y =[10x ] (B )y =[310x +] (C )y =[410x +] (D )y =[510x +] 9.已知函数()()2113,f x x x =+≤≤则 ( )A .()()12202f x x x -=+≤≤B .()()12124f x x x -=-+≤≤C .()()12102f x x x -=-≤≤D .()()12124f x x x -=-≤≤ 10.函数ln 1x y +=的定义域为 A .()4,1-- B .()4,1- C .()1,1- D .(1,1]-11.设函数()221, 1,2, 1,x x f x x x x ⎧-≤⎪=⎨+->⎪⎩则()12f f ⎛⎫⎪ ⎪⎝⎭的值为 ( )A .1516 B .2716- C .89D.18 12.已知A 、B 两地相距150千米,某人开汽车以60千米/小时的速度从A 地到达B 地,在B 地停留1小时后再以50千米/小时的速度返回A 地,把汽车离开A 地的距离S 表示为时间t (小时) 的函数表达式是 ( ) A .S=60t B .S=60t +50tC .S=⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD .S=⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t13.下列函数中与函数y =有相同定义域的是 ( ) A .()ln f x x = B. ()1f x x= C. ()f x x = D. ()x f x e =14.下列各组函数表示同一函数的是 ( ) A.2(),()f x g x == B .0()1,()f x g x x ==C .())()()t t g x x x x x f =⎩⎨⎧<-≥=,00D .21()1,()1x f x x g x x -=+=- 15 设⎩⎨⎧<+≥-=)10()],6([)10(,2)(x x f f x x x f 则)5(f 的值为 ( )A 10B 11C 12D 13 二.填空题1. 函数1(0)y x x x=+>的值域为 2. 设()x x x f -+=22lg ,则⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛x f x f 22的定义域为3.已知()234log 3233,x f x =+则()()()()82482f f f f ++++ 的值等于4.已知2211f x x x x ⎛⎫-=+ ⎪⎝⎭,则函数值()3f = 5. 设函数.)().0(1),0(121)(a a f x x x x x f >⎪⎪⎩⎪⎪⎨⎧<≥-=若则实数a 的取值范围是 6. 函数xx f -=11)(的定义域为M ,x x g +=1)(的定义域为N ,则=⋂N M ________7. 已知一次函数)(x f 满足关系式52)2(+=+x x f ,则=)(x f_____________ 8. 全集U ={1,2,3,4,5},A ={1,2},若{3}⊆B UA ,则集合B 可能是_____________§1.2函数及其表示练习题答题卡班级:______ 姓名:______ 成绩:________一、选择题1-5_____________ 6-10_____________ 11-15_____________二、填空题1、_________ 2、_________ 3、_________ 4、_________5、_________6、_________7、_________8、_________三、解答题1 设,αβ是方程24420,()x mx m x R -++=∈的两实根,当m 为何值时,22αβ+有最小值?求出这个最小值2 求下列函数的值域(1)x x y -+=43 (2)152222++++=x x x x y (3) 13y x x =-+-3. (1) 设,)1(2)()(x xf x f x f =-满足求)(x f(2) 已知:1)0(=f ,对于任意实数x 、y ,等式)12()()(+--=-y x y x f y x f 恒成立,求)(x f .4.动点P 从边长为1的正方形ABCD 的顶点A 出发顺次经过B 、C 、D 再回到A ;设x 表示P 点的行程,y 表示PA 的长,求y 关于x 的函数解析式.5 已知函数2()23(0)f x ax ax b a =-+->在[0,3]有最大值5和最小值2,求a 、b 的值6.动物园要建造一面靠墙的2间面积相同的矩形熊猫居室(如图),如果可供建造围墙的材料总长是30m ,那么宽x (单位:m )为多少才能使建造的熊猫居室面积最大?最大面积是多少?§1.2函数及其表示练习题答案BACCB ABBDC ADACB 1.()3,(),32()3223cf x x cxx f x c f x c x x ====-+-+得2. 令[]2211111(),12,,()()152242x g x x x f f g x x -=-===== 3224(2)44,02,20x x x -+=--+≤≤-≤≤022,02y ≤≤≤≤4. 令22211()1121,,()11111()1t x t t t t x f t t x t t t----+====-+++++则11. 解析:法一:特殊取值法,若x=56,y=5,排除C 、D ,若x=57,y=6,排除A ,所以选B 法二:设)90(10≤≤+=ααm x ,,时⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤≤10103103,60x m m x αα19. [][](5)(11)(9)(15)(13)11f f f f f f f =====二.填空题答案1. 因为0>x ,于是2121=⋅≥+=xx x x y ,当且仅当x =1时取等号 所以1(0)y x x x=+>的值域为),2[+∞ 2. 由202x x +>-得,()f x 的定义域为22x -<<。
人教A版高中数学必修1《1.2 函数及其表示 习题1.2》_21

②本节主要是讲分段函数,同时以分段函数为载体,渗透了函数的三种表示方法,让学生深刻体会到三种方法的强大功效。图象法体现了数形结合思想,把抽象问题形象化,从而值域迎刃而解,列表法把繁琐的数量关系马上理清,解决了学生的拦路虎;
教学设计表
章节名称
人教A版《必修1》1.2.2函数的表示方法习题课
计划学时
1
学习内容分析
①我们学校是面上中学,学生基础比较薄弱;
②学生刚从初中过渡到高中,逻辑思维和抽象思维都比较缺乏;
学习者分析
函数是比较抽象的概念,而分段函数就更抽象了,因此必须在过渡连接上设计得顺畅自然,以及力求形象具体上阐述本课.
问题设计意图
师生活写.
师:统一个 了,那么 等于多少?这样 行吗?为什么?
生:不行,因为不知什么时候等于 或 ,还要加上条件.
(7)
函数有什么特点?
通过分析和对比函数 ,得出分段函数的定义.
师:此函数有什么特点?与函数 有什么区别?
生: 分成了两段.
师:所以顾名思义叫做分段函数.
师:那接着用什么方法写出来?
生:分类讨论.
(5)①
②
把刚才埋下的伏笔拿出来( 是一个函数),让学生认识到函数始终只能有唯一 对应,所以上面的两个 要统一为一个 .
师:刚才我们说 是个函数吗?
生:是.
师:那么函数有什么要求?
生:任何一个 有唯一 对应.
师:那上面的两个 是否要统一为一个 ?
生:要.
问题
教师及时板书小结:分段函数始终是一个函数.
(8)思考判断:分段函数的定义域是各段上“定义域”的并集,其值域是各段上“值域”的并集.
人教A版高中数学必修1《1.2 函数及其表示 习题1.2》_11

函数及其表示习题课课 型:习题课教学目标:(1)知识与技能:懂得求一些简单函数的定义域和值域相关知识;(2)过程与方法:掌握分段函数、区间、函数的三种表示法以及判断方法;(3)情感态度与价值观:培养学生独立自主的抽象数学思维和价值观.教学重点:理解函数的模型化思想,求定义域与值域,解决函数简单应用问题。
教学难点:理解函数的模型化思想,并对函数记号的理解。
教学过程:一、基础习题练习:1.说出下列函数的定义域与值域: 432+=x y ;242++=x y x ; 3422+-=x y x ; 2.已知22-=x y ,求)1(f , ((3))f f , (())f f x ; 3.已知0(0)()(0)1(0)x f x x x x π<⎧⎪==⎨⎪+>⎩,(1)作出()f x 的图象;(2)求(1),(1),(0),{[(1)]}f f f f f f -- 的值二、讲授典型例题:例1.已知函数)(x f =5x+3,g(x)=x 2+1, 求f[f(x)],f[g(x)],g[f(x)],g[g(x)].例2.求下列函数的定义域:(1)0y =(2)12622-+-=x x x y ;例3.若函数y =a 的取值范围. ([]1,9a ∈)三.巩固练习:1.已知)(x f =x 2-2x+1 ,求:f(x+3),f(x-3) ,f(x 2)的值; 2.已知函数2()3f x ax ax =+-的定义域为R,求实数a 的取值范围; 3.设二次函数)(x f 满足)2()2(x f x f -=+且)(x f =0的两实根平方和为10,图象过点(0,3),求)(x f 的解析式. 4.若x x x f 2)1(-=-,求函数(x f )的解析式.四、归纳小结:本节课是函数及其表示的习题课,带领学生进一步掌握数学语言的学习和转换能力,系统地归纳了函数的有关概念,表示方法,进一步巩固知识.五、作业布置:1. 习题1.2 B 组题1,3;2. 课后复习相关内容并预习函数的基本性质。
人教A版高中数学必修1《1.2 函数及其表示 习题1.2》_16

必修一1.2 函数及其表示(习题课)【教学目标】1.知识与技能:根据要求求函数的解析式、了解分段函数及其简单应用.2.过程与方法:通过学习函数的表示形式,其目的不仅是研究函数的性质和应用的需要,而且是为加深理解函数概念的形成过程。
3.情感态度价值观:让学生感受到学习函数表示的必要性,渗透数形结合的思想方法。
【重点难点】1.教学重点:函数解析式的求法和映射概念的理解.2.教学难点:函数解析式的求法和映射概念的理解.【教学策略与方法】1.教学方法:启发讲授式与问题探究式.2.教具准备:多媒体【教学过程】【答案】D【解析】函数的定义域为{x|x≠0},可排除C,当x=1时,y=2,可排除=-1时,y=-2,可排除A.D.作出函数y=x2-2x-2(0≤x≤3)的图像并求其值域.=x2-2x-2是一元二次函数,定义域为{x|0≤x≤3},所以,该函数由图可知,函数的最小值在顶点此时x=1,最大值在x=x=1时,y=-3;当x所以函数的值域为-3,作出下列函数的图像:1(x∈Z);2x(x∈(-1,2]).这个函数的图像由一些点组成,这些点都在直线y=x+1上,如图因为x∈(-1,2],所以这个函数的图像是抛物线y=x2-2x介于-1<x≤2之间的一部分,如图(2)所示.考点二、函数解析式的求法] (1)对于一次函数和二次函数,在一定条件下,如何求函数的解析求函数的解析式一般有哪些方法?利用待定系数法求一次函数和二次函数的解析式.待定系数法,代入法,换元法,构造方程组法.(1)已知f(x)是一次函数,且ff(x)]+3,则f(x)的解析式为()x)=-2x-3 B.f(x)=2x)=2x+3 D.f(x)=-2x-3=2x+1] D] (1)将x =2代入对应关系得(2,3).由⎩⎪⎨⎪⎧x +1=32,x 2+1=54,解得x =12.故对应集合B 中的元素为(2+1,3),对应集合A 中的元素为12.只有③④满足映射和函数的条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修一 1.2函数及其表示 习题课 A.∅ B.[a,1-a] 2、 A.[1,+∞) B.(1,+∞) 3、 A.(-∞,43)∪(43,+∞) D.(-∞,23)∪(43,+∞) 4、 A.y=(x)2 B.y=x2 C. D.y=3x3 5、 6、 A.[-2,2] B.[0,2] 7、 A.f(x) B.-f(x) 9、 10、 则B中点(3,2)对应的A中点的坐标为____________. 三、解答题 (1)求f(-3),f[f(-3)]; (3)若f(a)=12,求a的值. 12、 13、 以下是答案 1、 ∴A∩B=[2,+∞).] 3、 y=2x-3+7x-3=2+7x-3. ∵7x-3≠0,∴y≠2.] 4、 的函数与y=|x|的对应关系不同,B正确.] 5、 6、 ∴f(x)的定义域为[-1,2].] 7、 二、填空题 解析 ∵-2<0,∴f(-2)=(-2)2=4, 9、 解析 ∵f(x+1)=x+2x 10、 解析 由题意 x-y=3x+y=2,∴ x=52y=-12. ∴f(-3)=-3+5=2, 当-1 12、 ∵f(1)+f(a+1)=5,∴f(a+1)=0. 13、 原式变为3f(t)+2f(-t)=2(t+1),① 由①②消去f(-t),得f(t)=2t+25. 即f(x)=2x+25.
一、选择题
1、
已知函数f(x)的定义域为[0,1],则函数f(x-a)+f(x+a)(0
C.[-a,1+a] D.[0,1]
若集合A={x|y=x-1},B={y|y=x2+2},则A∩B等于( )
C.[2,+∞) D.(0,+∞)
函数y=2x+1x-3的值域为( )
B.(-∞,2)∪(2,+∞)
C.R
与y=|x|为相等函数的是( )
已知集合A={a,b},B={0,1},则下列对应不是从A到B的映射的是( )
已知f(x2-1)的定义域为[-3,3],则f(x)的定义域为( )
C.[-1,2] D.[-3,3]
函数f(x)=xx2+1,则f(1x)等于( )
C.1fx D.1f-x
二、填空题
8、
已知函数,则f(f(-2))=______________________________.
已知f(x+1)=x+2x,则f(x)的解析式为___________________________________.
设集合A=B={(x,y)|x∈R,y∈R},点(x,y)在映射f:A→B的作用下对应的点是(x-y,x+y),
11、
已知函数
(2)画出y=f(x)的图象;
已知,若f(1)+f(a+1)=5,求a的值
若3f(x-1)+2f(1-x)=2x,求f(x).
一、选择题
B [由已知,得 0≤x+a≤1,0≤x-a≤1⇒ -a≤x≤1-a,a≤x≤1+a.
又∵0
C [化简集合A,B,则得A=[1,+∞),B=[2,+∞).
B [用分离常数法.
B [A中的函数定义域与y=|x|不同;C中的函数定义域不含有x=0,而y=|x|中含有x=0,D中
C [C选项中,和a相对应的有两个元素0和1,不符合映射的定义.故答案为C.]
C [∵x∈[-3,3],∴0≤x2≤3,∴-1≤x2-1≤2,
A [f(1x)=1x1x2+1=x1+x2=f(x).]
8、
4
又∵4≥0,∴f(4)=4,∴f(f(-2))=4.
f(x)=x2-1(x≥1)
=(x)2+2x+1-1=(x+1)2-1,
∴f(x)=x2-1.
由于x+1≥1,所以f(x)=x2-1(x≥1).
(52,-12)
三、解答题
11、
解 (1)∵x≤-1时,f(x)=x+5,
∴f[f(-3)]=f(2)=2×2=4.
(2)函数图象如右图所示.
(3)当a≤-1时,f(a)=a+5=12,a=-92≤-1;
故a的值为-92或±22.
解 f(1)=1×(1+4)=5,
当a+1≥0,即a≥-1时,
有(a+1)(a+5)=0,
∴a=-1或a=-5(舍去).
当a+1<0,即a<-1时,
有(a+1)(a-3)=0,无解.
综上可知a=-1.
解 令t=x-1,则1-x=-t,
以-t代t,原式变为3f(-t)+2f(t)=2(1-t),②
