Lingo层次分析法
层次分析法(详解)
第六章层次分析法决策是人们选择或进行判断的一种思维活动,在人们的实践活动中,常常要对某些系统的重要性作出恰当的评价,以便列出它们的轻重缓急,从而集中解决重要的问题。
有些决策是简单易断的,而有些决策则是复杂困难的,因此常常先把复杂问题分解成因素,然后把这些因素按支配关系分组形成有序的递阶层次结构,并衡量各方面的影响,最后综合人的判断,以决定决策诸因素相对重要性的先后优劣次序,这就是层次分析法的基本思路。
层次分析法的(Analytic Hierarchy Process 简记为AHP)是美国著名的运筹学家T.L.Saaty 教授于70年代初首先提出的一种定性与定量分析相结合的多准则决策方法。
该方法是社会、经济系统决策的有效工具,目前在工程计划、资源分配、方案排序、政策制定、冲突问题、性能评价等方面都有广泛的应用。
6.1 层次分析法的基本原理层次分析法的核心问题是排序,包括递阶层次结构原理、测度原理和排序原理。
下面分别予以介绍。
1.递阶层次结构原理。
一个复杂的结构问题可分解为它的组成部分或因素,即目标、准则、方案等。
每一个因素称为元素。
按照属性的不同把这些元素分组形成互不相交的层次,上一层次的元素对相邻的下一层次的全部或部分元素起支配作用,形成按层次自上而下的逐层支配关系。
具有这种性质的层次称为递阶层次。
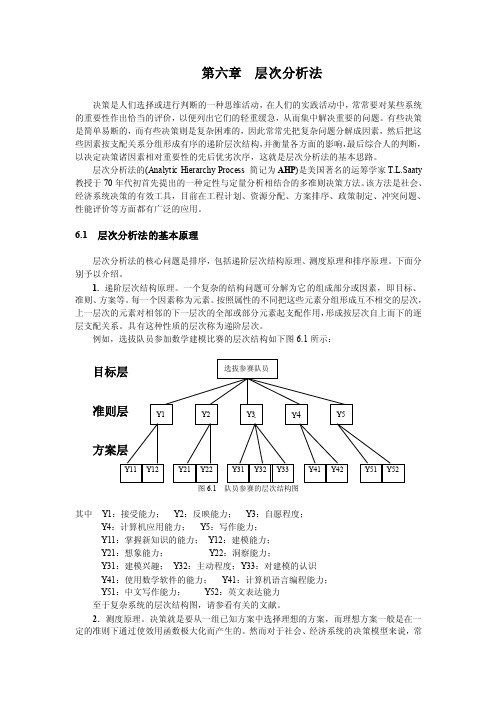
例如,选拔队员参加数学建模比赛的层次结构如下图6.1所示:图6.1 队员参赛的层次结构图其中Y1:接受能力;Y2:反映能力;Y3:自愿程度;Y4:计算机应用能力;Y5:写作能力;Y11:掌握新知识的能力;Y12:建模能力;Y21:想象能力;Y22:洞察能力;Y31:建模兴趣;Y32:主动程度;Y33:对建模的认识Y41:使用数学软件的能力;Y41:计算机语言编程能力;Y51:中文写作能力;Y52:英文表达能力至于复杂系统的层次结构图,请参看有关的文献。
2.测度原理。
决策就是要从一组已知方案中选择理想的方案,而理想方案一般是在一定的准则下通过使效用函数极大化而产生的。
层次分析法2

C5 单排序 权值
C6 单排序 权值
D1 0.1667 D2 0.8333
D1 0.2500 D2 0.7500
CR 0.0000
CR 0.0000
可以看出,所有单排序的C.R.<0.1,认为每个判断矩阵的一致性是可以 接受的 4. 层次总排序与检验 层次总排序及检验结果见下: 表3-15 C层次总排序(CR = 0.0000)表
D2
1
C4 D1 D2
D1 1 7
D2
1
C5 D1 D2
D1 1 1/5
D2
1
C6 D1 D2
D1 1 1/3
D2
1
3. 层次单排序与检验
对于专家填写后的判断矩阵,利用一定数学方法进行层次排序。
需要注意的是,在层层排序中,要对判断矩阵进行一致性检验。
前面提到,在特殊情况下,判断矩阵可以具有传递性和一致性。一般情
表3-12 判断矩阵表
A B1 B2 B3 B1 C1 C2 B2 C3 C4 B3 C5 C6
B1 1 1/3 1/3 C1 1 1 C3 1 3 C5 1 3
B2
1 1 C2
1 C4
1 C6
1
B3
1
C1 D1 D2 D1 1 5
D2
1
C2 D1 D2
D1 1 3
D2
1
C3 D1 D2
D1 1 1/5
A 单(总) 排序权 值
B1 单排序 权值
B2 单排序 权值
B3 单排序 权值
B1 0.1429
C1 0.500
B2 0.4286 B3 0.4286 CR 0.0000
C2 0.5000 CR 0.0000
数学建模——层次分析法

数学建模——层次分析法层次分析法(Analytic Hierarchy Process,AHP)是一种用于复杂决策和评估问题的定量方法,旨在帮助决策者在多个准则和选项之间进行权衡和选择。
该方法由美国学者Thomas L. Saaty于1970年代初提出,已经广泛应用于管理、工程、经济学、环境科学等领域。
方法步骤:1.建立层次结构:将复杂的决策问题分解为不同层次的因素和准则,形成层次结构。
层次结构包括目标层、准则层和选择层。
2.创建比较矩阵:对每个层次内的准则和选择进行两两比较,确定它们之间的相对重要性。
使用尺度来表示两者之间的相对优先级,通常是1到9之间的数值。
3.计算权重:通过计算比较矩阵的特征向量,得出每个准则和选择的权重。
特征向量反映了每个准则和选择对目标的贡献程度。
4.一致性检验:检查比较矩阵的一致性,确保所做的两两比较是合理的。
如果比较矩阵不够一致,需要进行调整。
5.计算综合得分:将每个选择的权重与其所属准则的权重相乘,得出每个选择的综合得分。
综合得分反映了每个选择在整体目标中的重要性。
6.做出决策:根据综合得分,确定最佳选择。
较高的综合得分通常意味着更优选。
示例:选择旅游目的地假设你想选择一个旅游目的地,考虑了三个因素:景色美丽度、文化体验和交通便利性。
你将这三个因素作为准则,然后列出了三个潜在的旅游目的地:A、B 和C。
步骤:1.建立层次结构:2.目标层:选择最佳旅游目的地3.准则层:景色美丽度、文化体验、交通便利性4.选择层:A、B、C5.创建比较矩阵:比较准则之间的相对重要性,如景色美丽度相对于文化体验的比较,以及文化体验相对于交通便利性的比较。
使用1到9的尺度,表明一个因素比另一个因素重要多少。
6.计算权重:计算每个准则和每个选择的权重,使用特征向量法。
7.一致性检验:检查比较矩阵的一致性。
如果一致性不够,可能需要重新考虑比较。
8.计算综合得分:将每个选择的权重与其所属准则的权重相乘,得出每个选择的综合得分。
层次分析法数学建模

在某些情况下,层次分析法可能无法合理地分配权重,导致决策结果 与实际情况存在较大偏差。
无法处理动态变化
层次分析法主要用于静态决策问题,对于动态变化的决策问题处理能 力较弱。
05 结论与展望
结论
层次分析法是一种有效的决策分析方法,能够将复杂问题 分解为多个层次和因素,通过比较和判断各因素之间的相 对重要性,为决策提供依据。
实例三:风险评估问题
总结词
层次分析法在风险评估问题中,能够综合考虑风险的多种来源和影响因素,确定各因素之间的权重关 系,为风险的有效控制提供科学的依据。
详细描述
风险评估问题涉及到如何识别、评估和控制各种潜在的风险。层次分析法可以将风险的多种来源和影 响因素进行比较和判断,确定各因素之间的权重关系,为风险的有效控制提供科学的依据。同时,层 次分析法还可以用于制定风险应对策略和预案,提高组织的抗风险能力。
层次单排序与一致性检验
层次单排序
根据判断矩阵的性质和计算方法,计 算出各组成元素的权重值,并按照权 重值的大小进行排序。
一致性检验
对判断矩阵的一致性进行检验,以确 保各组成元素之间的相对重要性关系 符合逻辑和实际情况。
层次总排序与一致性检验
层次总排序
根据各层次的权重值和组成元素的权重值,计算出整个层次结构模型的权重值, 并进行总排序。
确定层次
根据问题的复杂程度和组 成元素的性质,将层次结 构划分为不同的层次,以 便于分析和计算。
判断矩阵的建立
确定判断标准
根据问题的特点和要求,确定判 断各组成元素之间相对重要性的 标准和方法。
构造判断矩阵
根据判断标准,构造出一个判断 矩阵,用于表示各组成元素之间 的相对重要性关系。
层次分析法详解

构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标,即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of country risk为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为iA ,准则层为B i ,子准则层为C i ,方案层为D i 。
5.2.2 重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
进行定性的成对比较时,我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1~9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表Table 5.2 Described table of AHP important degree 定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、绝对强于前者1/3、1/5、1/7、1/9例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1:B2=3:1也就是3。
层次分析法概述

层次分析法一、层次分析法概述层次分析法(Analytic Hierarchy Process )是美国运筹学家T. L. Saaty教授于20世纪70年代初期提出的一种简便、灵活而又实用的多方案或多目标的决策方法,它是一种定性和定量相结合的、系统化的、层次化的分析方法,是一种具有定性分析与定量分析相结合的决策方法,可将决策者对复杂对象的决策思维过程系统化、模型化、数量化。
其基本思想是通过分析复杂问题包含的各种因素及其相互关系,将问题所研究的全部元素按不同的层次进行分类,标出上一层与下层元素之间的联系,形成一个多层次结构。
在每一层次,均按某一准则对该层元素进行相对重要性判断,构造判断矩阵,并通过解矩阵特征值问题,确定元素的排序权重,最后再进一步计算出各层次元素对总目标的组合权重,为决策问题提供数量化的决策依据。
层次分析法特别适用于无结构问题的建模。
自1982年被介绍到我国以来,由于它在处理复杂的决策问题上的实用性和有效性,以及其系统灵活简洁的优点,迅速地在我国社会经济各个领域内,如能源系统分析、城市规划、经济管理、科研评价行为科学、军事指挥、运输、农业、教育、人才、医疗、环境保护、冲突求解及决策预报等领域得到了广泛的重视和应用。
二、层次分析法的基本思想基本思想层次分析法的采用先分解后综合的系统思想,整理、综合人们的主观判断,将所要分析的问题层次化,根据问题的性质和要达到的总目标,将问题分解成不同的组成因素,按照因素间的相互关系及隶属关系,将因素按不同层次聚集组合,形成一个多层分析结构模型,最终归结为最低层(方案、措施、指标等)、中间层(准则层)、最高层(总目标)。
把实际问题转化为分析同层因素间相对重要程度的权重值或相对优劣次序的问题,使定性分析与定量分析有机结合,实现定量化决策。
三、确定权重值的基本原理人们在进行社会、经济以及科学管理领域问题的系统分析中,面临的常常是一个相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
层次分析法简单介绍

层次分析法层次分析法(AHP)又称多层次权重分析法,是一种用于定性分析的多目标分析方法。
它能有效地分析指标体系各层次之间排序关系,有效地综合衡量和判断评价者的意图。
适用于多目标、多准则、多因素、难以量化的大型复杂系统,已广泛应用于资源系统分析、建设管理、交通、评标、经济评价等各个社会领域。
层次分析法解决复杂问题的基本思想是:首先,将总目标进行分层,并根据各个指标之间隶属关系和相关影响,将各个指标按不同层次进行分类。
形成指标层、准则层和目标层,然后利用层次分析法,求本各层次的指标对上一层次指标的权重,然后利用最大特征值方法依次归并,最终求出总目标权重系数。
指标越重要,其指标权重系数越大。
因此,层次分析方法的计算需要以下步骤:(1)建立层次结构模型首先,将问题分解为不同的组成部分,并根据各个指标之间的相互影响和隶属关系,对各指标进行分组和组合,形成多层次结构,相对于确定最高层的综合相对重要性系数,即相对优序,系统分析被简化到最底层。
(2)调查问卷设计,对同一层次的指标将进行重要性等级进行两两访问对比,确定其重要性,然后利用比例标度法,。
构成比较判断矩阵。
表1-1 比例标度法Table4-1 Proportional scaling method两指标影响比较相等稍微重要明显重要非常重要极其重要δ1113579(3)调查对象的构成在选择范围上,主要选择具有绿色施工、绿色建筑、节能环保等研究领域的高校专家和学者、建设单位项目管理人员、工程项目施工单位工作人员和涉及环保监督政府人员。
(4)整理分析问卷并构建判断矩阵整理出问卷中的信息,并将问卷中信息进行汇总分析,计算出各因素的要性程度,建立判断矩阵。
见表1-2。
表1-2 各因素相对重要性判断矩阵Table4-2 Relative importance judgment matrixB k B 1 B 2 B n B 1 δ11 δ12 ... δ1n B 2 δ21 δ22 ... δ2n ... ... ... ... ... B nδn1δn2...δnn其中,δij 是对于A k 而言,B i 对B j 的相对重要性的数值表示,δij 是δi 与δj 的比值。
层次分析法步骤

层次分析法步骤层次分析法(Analytic Hierarchy Process,简称AHP)是一种用于多准则决策的定量分析工具,可以帮助决策者以一种系统化的方法比较和评估不同准则和选择之间的重要性。
它由美国数学家托马斯·L·塞蒂(Thomas L. Saaty)于20世纪70年代初提出,并逐渐得到广泛应用。
层次分析法的基本思想是将复杂的决策问题分解为多个层次,并在每个层次上进行比较和评估,最后得出一个综合的决策方案。
整个分析过程包括以下几个步骤:1.确定目标和准则:首先需要明确决策的目标以及与之相关的准则。
目标是决策问题的总体要求,而准则则是用来评估和比较不同选择的标准。
2.建立层次结构:将决策问题分解为层次结构,利用层次结构可以清晰地表示不同层次之间的关系。
层次结构由目标层、准则层和选择层组成。
目标层位于最高层,准则层位于中间层,选择层位于最底层。
3.构建判断矩阵:通过对不同层次的元素两两进行比较,构建判断矩阵。
判断矩阵中的每个元素表示一些准则或选择相对于其他准则或选择的重要性。
判断矩阵需要满足一致性要求,即矩阵的特征向量要满足一致性指标。
4.计算权重向量:通过对判断矩阵进行特征值分解,可以得到特征向量。
特征向量表示各个准则或选择的重要性权重,可以用于比较和评估不同准则和选择之间的优先级关系。
5.一致性检验:对于判断矩阵的一致性要求需要进行检验,通常使用一致性指标和一致性比率来评估判断矩阵的一致性程度。
如果判断矩阵的一致性指标超过了一些阈值,就需要重新调整判断矩阵,直到满足一致性要求为止。
6.综合评估和决策:根据权重向量可以对不同准则和选择进行综合评估,计算出每个选择的得分。
最终选择具有最高得分的方案作为决策方案。
7.灵敏度分析:对比不同决策方案的得分,可以进行灵敏度分析,评估权重向量的变动对决策结果的影响程度。
层次分析法兼容主观和客观因素,能够定量评估和比较不同准则和选择之间的重要性,提高决策的科学性和准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用层次分析法解决策问题 一、问题背景 随着电子商务的兴起,网络购物已经成为一种趋势,伴随而来的就是人们对物流运输服的要求也越来越高。物流运输服务质量一般包括物流运输技术质量和物流运输功能质量。物流运输技术质量是物流服务的结果,一般可以用某种形式度量。物流运输功能质量是物流服务的过程,是客户对过程的主观感觉和认识。客户对物流运输质量的评价,是根据所获得的物流运输服务效果和所经历的服务感受,两者综合在一起所形成的完整感受。
二、实例研究 通过市场调查,我们了解到顾客对物流运输的需求主要集中在以下四个方面:保证性(运输设施设备水平、顾客跟踪查询信息的便利性、运输作业流程标准化程度)服务性(运输服务价格合理性、运输方式灵活、运输服务人员的专业素质水平)可靠性(运输货物准确率、运输事故率、订单满足率)时间性(信息反馈水平、订单处理周期、货物准时到达率)。在众多物流运输服务质量影响因素中,我们采用层次分析法来确定顾客需求信息的重要度。方 便物流企业提高运输服务质量以满足顾客需求。用 AHP 分析问题要经过五个步骤:(1)建立层次结构模型(2)构造判断矩阵(3)层次单排序(4)层次总排序(5)一致性检验。 (1)、建立层次结构模型 基于对物流运输服务关键质量需求的分析,其层次结构模型如图1所示。
( 物流运输服务关键质量需求 A
顾客跟踪查询信息便利性 保证性 B1 服务性 B2 可靠性 B3 时间性 B4 作业流程标准化的程度 运输设施水平
运输服务价格合理性 运输方式灵活性
服务人员的专业素质水平
货物准确率 订单满足率
运输事故率 信息反馈时间 货物准时到达率 订单处理时间 (2)、构造判断矩阵 标度及描述:构造同层成对比较矩阵,即把n个因素对上层某一目标的影响程度排序。这种 比较是两两因素之间进行的比较,比较时取 1- 9 尺度,记为 aij,见表 1
表1 1—9尺度的含义 标度 定义(比较因素i与j) 1 因素i与j同样重要 3 因素i与j稍微重要 5 因素i与j较强重要 7 因素i与j强烈重要 9 因素i与j绝对重要 2、4、6、8 两个相邻判断因素的中间值 倒数 因素i与j比较得判断矩阵a ij,则因素j与i相比的判断为aji=1/aij 注:aij表示要素i与要素j相对重要度之比,且有下述关系: aij=1/aji ;aii=1; i,j=1,2,…,n 显然,比值越大,则要素i的重要度就越高。
判断矩阵是层次分析法的基本信息,也是进行权重计算的重要依据。 表2至表6为专家对物流运输质量的二级指标相对于最高层目标、三级指标相对于二级目标两两比较得出的 判断矩阵。
表2 判断矩阵A-B A B1 B2 B3 B4 B1 1 1/3 1/4 1/5 B2 3 1 1/2 1/4 B3 4 2 1 1/2 B4 5 4 2 1
表3 判断矩阵B1-B1i B1 B11 B12 B13 B11 1 3 5 B12 1/3 1 3 B13 1/5 1/3 1
表4 判断矩阵B2-B2i B2 B21 B22 B23 B21 1 2 3 B22 1/2 1 3 B23 1/3 1/3 1 表5 判断矩阵B3-B3i B3 B31 B32 B33 B31 1 6 2 B32 1/6 1 1/4 B33 1/2 4 1
表6 判断矩阵B4-B4i B4 B41 B42 B43 B41 B42 B43
(3)、计算各判断矩阵的特征值、特征向量及一致性检验指标 根据层次分析法来计算权重W,如下表所示。再计算判断矩阵最大特征根λmax,进行一致性检验。n 阶判断矩阵 A 最大特征根 λmax等于n时,矩阵 A 具有完全一致性,λmax比 n 大的越多,A的不一致性越严重。用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。为此引入能够衡量矩阵 A不一致性程度的指标 CI:CI=(λmax- n)/(n- 1)CI 越大,矩阵 A的不一致程度越大。再引入一致性比率指标 CR:CR=CI/RI。RI 是随机一致性指标,其值可通过查表获得(见表 7)。
表7 平均随机一致性指标 阶数 3 4 5 6 7 8 9 10 11 12 13 14 RI 0.58 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58
一般,当一致性比率 CR=CI/RI<0.1 时,认为 A 的不一致程度在容许的范围内,即通过一致性检验,可用其归一化特征向量作为权向量,否则要重新构造成对比较矩阵,对矩阵A 加以调整,直至通过一致性检验为止。对构成物流运输服务关键质量需求总目标评价的准则层B1、B2、B3、B4的判断矩阵 A 按列归一,按行相加并且正规化得表8 。
表 8 准则层判断矩阵、权重和一致性检验结果 A B1 B2 B3 B4 开方 权重W AW 最大特征根 4.0725
B1 1 0.33333 0.25 0.2 0.359 0.0709 0.291 CI 0.0242 B2 3 1 0.5 0.25 0.783 0.1543 0.63 RI 0.9 B3 4 2 1 0.5 1.414 0.2789 1.119 CR 0.0269 <0.1 B4 5 4 2 1 2.515 0.4959 2.025 转置 0.0709 0.15432 0.279 0.496 由于CR<0.1,断矩阵 A 通过一致性检验。 最后依次计算最底层指标要素相对于准则层的权重系数,见表9至表12 。 表9 保证性 B1 对应的指标层判断矩阵、权重和一致性检验结果 B1 B11 B12 B13 开方 权重W AW 最大特征根 3.03851
B11 1 3 5 2.466 0.637 1.9355 CI 0.01926 B12 0.3333 1 3 1 0.258 0.7848 RI 0.58 B13 0.2 0.33333 1 0.405 0.105 0.3182 CR 0.0332 <0.1 转置 0.637 0.25828 0.105
表10 服务柔性B2对应的指标层判断矩阵、权重和一致性检验结果 B2 B21 B22 B23 开方 权重W AW 最大特征根 3.05362
B21 1 2 3 1.817 0.528 1.6118 CI 0.02681 B22 0.5 1 3 1.145 0.333 1.0154 RI 0.58 B23 0.3333 0.33333 1 0.481 0.14 0.4264 CR 0.04623 <0.1 转置 0.5278 0.33252 0.14
表11 可靠性B3对应的指标层判断矩阵、权重和一致性检验结果 B3 B31 B32 B33 开方 权重W AW 最大特征根 3.0092
B31 1 6 2 2.289 0.588 1.7683 CI 0.0046 B32 0.1667 1 0.25 0.347 0.089 0.2678 RI 0.58 B33 0.5 4 1 1.26 0.323 0.9731 CR 0.00793 <0.1 转置 0.5876 0.08898 0.323
表12 时间性B4对应的指标层判断矩阵、权重和一致性检验结果 B4 B41 B42 B43 开方 权重W AW 最大特征根 3.02906
B41 1 5 3 2.466 0.659 1.9951 CI 0.01453 B42 0.2 1 1 0.585 0.156 0.4731 RI 0.58 B43 0.3333 1 1 0.693 0.185 0.5609 CR 0.02505 <0.1 转置 0.6586 0.15618 0.185 准则层 B1到 B4的一致性比率 CR<0.1,都具有满意的一致性,因此其特征向量 Wij都可作 为相应指标对应的权重。
(4)、层次总排序 获得同一层次各要素之间的相对重要度后,就可以自上而下地计算各级要素对总体的综合重要度。依据各方案综合重要度的大小,可对方案进行排序、决策。 层次总排序如表13 所示。
表13 层次总排序表 层数 B1 0.079 B2 0.15432 B3 0.279 B4 0.496 C1 0.637 C4 0.52783 C7 0.587 C10 0.6586 C2 0.2583 C5 0.33251 C8 0.088 C11 0.1561 C3 0.1047 C6 0.13965 C9 0.323 C12 0.1851
表14 顾客需求信息的重要度 层数 C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
比重 0.045 0.018 0.007 0.081 0051 0.021 0.164 0.025 0.09 0.327 0.077 0.092
通过层次分析法逐次排序,在表14中我们可以看出,在影响顾客物流运输服务众多的质量需求信息中,最受顾客关注的因素比重最大的是:信息反馈水平、运输货物准确率、货 物准时到达率以及运输服务价格合理性。
三、学习小结 通过本问题我们得出结论,在物流运输与人们息息相关的今天,顾客不仅仅是对货物位移这样的物流运输实体关注,同时对物流信息越来越关注。最为普遍的利用软件随时查询跟踪货物运输进程,近些年也广为关注。本题目来自文献《基于QFD的物流运输服务质量进》。 通过层次分析法量化了众多影响顾客物流运输服务因素的权重,对于实践与理论研究都具有重要意义。一方面对于物流企业,不光要加强运输的准时安全性,在物流信息的及时准确反馈以及综合服务方面也应该加强。另一方面对于学术研究,通过对影响因素的量化,促使我们发现现在物流体系存在的问题,寻找到物流运输影响顾客满意度的规律,提出更好的 解决方案。
