分质工具中注入聚合物表观黏度变化数学模型的建立及应用
聚合物的粘性流动-聚合物流变学基础课件
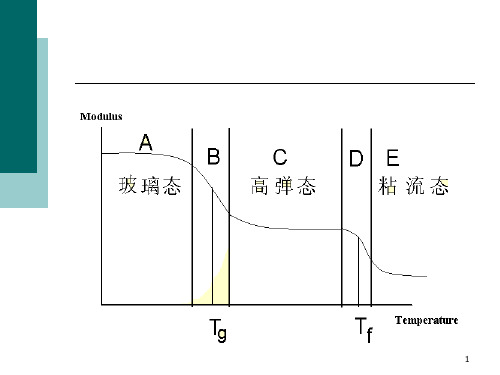
9.1.2 聚合物熔体流动特点
(1)粘度大,流动性差: 这是因为高分子链的流动 是通过链段的相继位移来实现分子链的整体迁移, 类似蚯蚓的蠕动。 (2)不符合牛顿流动规律:在流动过程中粘度随 切变速率的增加而下降(剪切变稀)。
(3)熔体流动时伴随高弹形变:因为在外力作用 下,高分子链沿外力方向发生伸展,当外力消失后, 分子链又由伸展变为卷曲,使形变部分恢复,表现 出弹性行为。
M > Mc 0 =KMw3~3.4
logMc logM
23
不同用途对分子量有不同的要求: 合成橡胶一般控制在20万; 塑料居橡胶和与纤维之间, 合成纤维一般控制在1.5万~10万;
不同加工方法对分子量有不同要求: 挤出成型要求分子量较高; 注射成型要求分子量较低; 吹塑成型在挤出和注射两者之间。
When T >Tg+100
a AeE/RT
E - 粘流活化能 viscous flow energy
高分子流动时的运动单元: 链段(的协同运动)
E 由链段的运动能力决定, 与分子链的
柔顺性有关, 而与分子量无关!!
29
a AeE/RT
刚性链 E大 粘度对温度敏感
柔性链
E小
粘度对温度不敏感 对剪切速率敏感
工业上常用MI值作为衡量聚合物分子量大小的一种相对指标,分 子量越大,MI值越小。
15
锥板式旋转粘度计
锥板粘度计是用于测定聚合物熔体粘度的常用仪器。
门尼粘度计
在一定温度下(通常 100C)和一定的转子速 度下,测定未硫化的橡 胶对转子转动的阻力
Mooney Index
100C
M
I100 34
预热3min
熔融指数(Melt index ——简MI ):指在一定的温度下和规定
高分子物理--聚合物的粘弹性ppt课件

粘弹体的应力与应变的相位关系
一、 粘弹性现象 (二) 动态粘弹性
力学损耗:由于滞后,周期性应力应变变化过程将伴随能量消耗, 称之为力学损耗。 损耗的大小同滞后角有关,常以tanδ 表示
橡胶拉伸与回缩的应力-应变关系示意图
一、 粘弹性现象 (二) 动态粘弹性
聚合物的内耗与频率的关系
表示在复平面上的复模量 E* D* ﹦1
一、 粘弹性现象 (三) 粘弹性参数
G*﹦G1+iG2
J* ﹦ J1 - iJ2
tan δ ﹦ E2 / E 1
﹦ D2 / D 1 ﹦ G2 / G 1 ﹦ J2 / J 1
链段运动的松弛时间同 作用频率(速率)相匹 配时(ω ~ 1/τ ),粘 弹性现象最显著。
二、 粘弹性的数学描述
(一) Boltzmann叠加原
在Δ σ31 、、
u2 、 ……
u3 、 Δ σn
……
un时刻,对试样加应力Δ σ1 、 Δ σ2 、
ε(t)﹦ ∑Δσi D(t-ui)
i: 1→ n
连续对试样加应力,变化率为? σ (u)/? u
t﹥ un
ε(t)﹦ ∫ D(t-u)(? σ (u)/? u) du u:- ∞ → t
ηs*﹦ηs1-ηs2 ηs1 ﹦(σ0/γ0 ω)sinδ ηs2 ﹦(σ0/γ0 ω)cosδ
ηs1 ﹦G2/ω
ηs2 ﹦G 1/ω
二、 粘弹性的数学描述
(一) Boltzmann叠加原
1. 数理学表达式
在零时刻,对试样加应力σ0 ε0 (t)﹦σ0 D(t)
在u1时刻,对试样加应力σ1 ε1 (t)﹦σ1 D(t-u1)
粘性响应 理想液体
基于分数阶导数的静态黏弹性本构模型与应用

参考内容
引言
蠕变是指材料在长时间内发生的缓慢变形现象,是材料内部结构发生改变的 结果。非定常蠕变是指材料在蠕变过程中,应变和应力不再满足线性关系。分数 阶导数非定常蠕变本构模型能够描述材料在蠕变过程中应力和应变的关系,是研 究材料蠕变行为的重要工具。本次演示将介绍基于分数阶导数的非定常蠕变本构 模型的研究,包括研究现状、研究方法、实验结果及分析、结论与展望等方面。
4、实验技术与测量精度:提高实验技术与测量精度对于验证和完善静态黏 弹性本构模型至关重要。未来将需要发展更精确、非破坏性的实验技术,以捕捉 材料的微妙变化。
结论
基于分数阶导数的静态黏弹性本构模型在描述材料的黏弹性质方面具有重要 应用价值。本次演示介绍了分数阶导数的基本概念、静态黏弹性本构模型的建立 及其应用和未来研究趋势。通过提高测量精度、发展新理论和跨尺度研究等途径, 静态黏弹性本构模型将在未来取得更多突破性成果,为材料科学和工程领域的发 展做出更大贡献。
分数阶导数非定常蠕变本构模型 研究现状
近年来,分数阶导数非定常蠕变本构模型得到了广泛和研究。现有的分数阶 导数非定常蠕变本构模型主要分为两大类:基于唯象学理论的和基于微观结构的。
基于唯象学理论的分数阶导数非定常蠕变本构模型主要从实验现象出发,通 过引入分数阶导数来描述材料蠕变过程中的非线性行为。代表性的模型有分数阶 牛顿模型、分数阶unified模型等。这些模型的优点是能够描述材料的非线性蠕 变行为,缺点是模型参数难以确定,且对材料内部结构的描述不够准确。
一、引言
岩石是一种复杂的材料,其力学行为受多种因素影响,如加载速率、温度、 湿度等。在长时间尺度下,岩石的应力松弛现象成为描述其力学性质的重要参数。 传统的线性弹性模型无法准确描述岩石在复杂应力状态下的这种非线性行为。近 年来,分数阶微积分被广泛应用于描述材料的黏弹性行为,特别是在岩石力学领 域。本次演示旨在探讨基于分数阶微积分的岩石非线性黏弹性应力松弛模型。
高聚物粘弹性力学模型的几个问题课件

建立有效的模型来描述高聚物微观结构(如分子链的排列、交联密度等)与宏观性能(如弹性模量、粘度等)之间的关系是当前研究的热点。
非线性粘弹性
传统的高聚物粘弹性模型主要基于线性假设,但实际高聚物在复杂应力状态下表现出显著的的非线性粘弹性行为。因此,发展非线性粘弹性模型是未来的重要方向。
VS
宏观模型是从高聚物宏观结构和宏观尺度行为出发,通过建立宏观尺度模型来描述高聚物的粘弹性行为。这种模型通常包括本构方程、状态方程和传递方程等。
宏观模型的优点是能够方便地描述高聚物的宏观粘弹行为,如应力松弛、蠕变和滞后等。然而,宏观模型通常缺乏对高聚物内部结构和分子动力学的考虑,难以揭示粘弹行为的微观机制。
高聚物粘弹性在许多领域都有广泛应用,如塑料、橡胶、涂料、胶粘剂等。
高聚物粘弹性在材料设计、加工、性能优化等方面具有重要价值,能够提高材料的性能和稳定性。
BIG DATA EMPOWERS TO CREATE A NEWERA
高聚物粘弹性力学模型
唯象模型是从实验现象出发,通过建立数学模型来描述高聚物的粘弹性行为。这种模型通常包括粘壶模型、弹簧模型和阻尼器模型等。
模型在不同应力状态下的适用性也不同,如拉伸、压缩、剪切等。
适用应力状态
03
参数优化
通过优化算法对模型参数进行优化,以使预测结果与实验结果尽可能一致。
01
实验数据
确定模型参数通常需要实验数据支持,如时间-温度-应力等依赖性实验数据。
02
参数敏感性分析
对于模型参数的微小变化可能会对预测结果产生显著影响的情况,需要进行参数敏感性分析。
高聚物粘弹性力学模型的几个问题课件
BIG DATA EMPOWERS TO CREATE A NEWERA
聚合物分子量的测定——粘度法

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载聚合物分子量的测定——粘度法地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容聚合物分子量的测定—黏度法一.实验目的学会一种测定分子量的方法二.实验原理由于聚合物具有多分散性,所以聚合物的分子量是一个平均值。
有许多测定分子量的方法(如光散射法、渗透压法、超速离心法、端基分析法等),但简单、而使用范围又广的是粘度法。
由粘度法测得的聚合物的分子量叫粘均分子量,以“”表示。
粘度法又分多点法和一点法:1、多点法多点法测定聚合物粘均分子量的计算依据是:(7-1)式中: [η]-特性粘数;k,α--与温度和溶剂有关的常数;--聚合物的粘均分子质量;若设溶剂的粘度为η0,聚合物溶液浓度为 c(100mL 所含聚合物的克数表示)时的粘度为η,则聚合物溶液粘度与浓度间有如下关系:(7-2)(7-3)以ηSP /c, Inηr/c 对 c 作图,外推直线至 c 为 0(参考图 7-1)求[ η],即、(7-4)图7-1 特性粘数的求法由于 k、α是与温度、溶剂有关的常数,所以对一定温度和特定的溶剂,k、α有确定的数值。
例如,30℃时,以 1mol/L 硝酸钠溶液作溶剂,用粘度法测定聚丙烯酰胺粘均分子量的经验式可表示如下:(7-5)即:=1.40*105[η]3/2 (7-6)因此,只要测定不同浓度下聚合物溶液的粘度,即可通过上述的数据处理,求出聚合物的粘均分子量。
2、单点法对低浓度的聚合物溶液,其特性粘数可由下式计算:(7-7)实验时,只要测定一个低浓度的聚合物溶液的相对粘度,即可由式 7-7 求得所测试样的特性粘数。
本实验采用如图 7-2 所示的乌氏粘度计测定聚合物溶液在不同浓度下的粘度。
模料的粘度模型及本构方程的建立

模料的粘度模型及本构方程的建立1.引言模料的粘度是指在给定温度下,模料的流动性能,它是塑料加工过程中一个重要的物性参数。
粘度的大小直接影响着挤出成型的均匀性、填充性能以及表面质量等。
因此,建立准确的粘度模型及本构方程对于工程应用非常重要。
2.粘度模型的分类粘度模型一般可以分为两类:经验模型和物理模型。
经验模型是基于实验数据的统计分析而建立的。
这类模型用数学公式描述物料粘度与应力和变形率之间的关系。
例如,在Newton粘度模型中,粘度与变形率成正比。
经验模型的优点是简单易用,但是缺点是精度较低,通用性差。
物理模型是通过理论推导建立的,它基于对物料分子结构和运动状态的理解,从而描述粘度与其它参数的关系。
这类模型的优点在于可以更准确地预测物料的流变性能,但是缺点在于建立过程较复杂。
3.粘度模型的本构方程建立粘度模型的本构方程是描述粘度与应力、变形率等参数之间关系的方程。
通常可以采用以下一些常用的本构方程:3.1非牛顿流体本构方程非牛顿流体本构方程是用来描述粘度与应力和变形率之间非线性关系的方程。
常见的非牛顿流体本构方程有:(1)Bingham模型:粘度与应力成线性关系,当应力超过一定阈值时开始流动。
(2)Casson模型:粘度与应力的平方根成线性关系,且考虑初始流动。
3.2线性粘弹性模型线性粘弹性模型是用来描述粘度与应力和变形率之间线性关系的方程。
(1)Maxwell模型:粘度与应力和变形率之和成比例。
(2)Kelvin-Voigt模型:粘度与应力和变形率之差成比例。
3.3流变学模型流变学模型是用来描述粘度与应力、变形率以及其它参数之间关系的方程。
常见的流变学模型有:(1)Jeffreys模型:粘度与应力和变形率的幂函数成比例。
(2)Power-law模型:粘度与应力和变形率的幂函数成正比。
4.结论粘度模型及本构方程的建立对于塑料加工的优化设计和预测有着重要的意义。
根据具体的应用需求,可以选择适合的粘度模型和本构方程进行建立,以提高生产过程的可控性和效率。
大学本科高分子物理第七章《聚合物的粘弹性》课件

学习各种描述高分子材料粘弹性的模型。
7.2 粘弹性的数学描述 (唯象描述)——直观
亦称为复 数模量
损耗角正切
E' 0 cos 0
E'' 0 sin 0
tg E''
E'
——也可以用 来表示内耗
讨 =0, tg =0, 没有热耗散 论 =90°, tg = , 全耗散掉
本讲小结
第十九讲 粘弹性的数学描述
主要内容:
•力学模型
重点及要求:
聚合物材料在力学模型及数学描述;
/ cost /
/ d sintdt
1.5
1
/() cost 0.5
最大值
Strain
0 -0.5 0
-1
/()sin(t / 2) -1.5
滞后/2
90
180
270
360
t degree
Comparing
stress or strain
1.5 1
0.5 0
-0.5 0 -1
第十八讲 聚合物的粘弹性现象
主要内容:
聚合物的粘弹性现象 •蠕变现象 •应力松弛现象
本讲重点及要求:
聚合物材料在受力情况下所产生的蠕变和应力 松弛的粘弹现象及分子运动机理。
7.1粘弹性现象
普通粘、弹概念
粘 – 同黏:象糨糊或胶水等所具有的、能
使一个物质附着在另一个物体上的性质。
弹 – 由于物体的弹性作用使之射出去。
弹簧 – 利用材料的弹性作用制得的零件,在外力 作用下能发生形变(伸长、缩短、弯曲、扭转
等),除去外力后又恢复原状。
Viscous – thick and sticky, semi-fluid, that does not flow easily
粘弹性流体力学模型与应用研究

粘弹性流体力学模型与应用研究粘弹性流体力学是研究粘弹性流体的运动行为和力学性质的学科领域。
粘弹性流体是指具有同时表现出粘性和弹性特性的流体,其运动行为不仅受到流体的黏度和密度等因素的影响,还受到流体的弹性特性的影响。
在实际应用中,粘弹性流体力学模型可以用于解释和预测各种流体的行为,包括聚合物溶液、胶体悬浮液、生物体液等。
粘弹性流体力学的研究对象通常是非牛顿流体,即流体的黏度随着应力的变化而变化。
与牛顿流体不同,非牛顿流体的流动行为无法用简单的线性关系来描述,而是需要引入更复杂的模型来描述其流动行为。
其中,最常用的模型包括Maxwell模型、Kelvin模型和Oldroyd模型等。
Maxwell模型是最简单的粘弹性流体模型之一,它将粘弹性流体的应力应变关系分为两个部分:弹性部分和粘性部分。
弹性部分描述了流体在受到应力时的弹性回复,而粘性部分则描述了流体在受到应力时的黏滞阻力。
Kelvin模型在Maxwell模型的基础上增加了一个弹性元件,用于描述流体的弹性特性。
而Oldroyd模型则是将Maxwell模型和Kelvin模型相结合,用于描述更复杂的粘弹性流体。
粘弹性流体力学模型的应用非常广泛。
在化工工艺中,粘弹性流体力学模型可以用于设计和优化各种流体的混合、输送和分离等过程。
在生物医学领域,粘弹性流体力学模型可以用于研究血液的流动行为、细胞的变形特性等。
在地质学和地球物理学领域,粘弹性流体力学模型可以用于模拟地下岩石和土壤的变形和流动行为。
此外,粘弹性流体力学模型还可以应用于材料科学、食品工程、环境工程等领域。
例如,在材料科学中,粘弹性流体力学模型可以用于研究聚合物材料的加工和成型过程,以及纳米颗粒的悬浮和固液分离等。
在食品工程中,粘弹性流体力学模型可以用于研究食品的流变性质和质感特性等。
在环境工程中,粘弹性流体力学模型可以用于研究水体和土壤的流动行为,以及废水处理和土壤污染修复等。
总之,粘弹性流体力学模型在科学研究和工程应用中具有重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要:针对聚合物驱油过程中油层渗透率低、层间矛盾大而导致油层动用程度较低的问题,油田现场一般采用分注工具。
分注工具包括分质工具和分压工具。为系统地反映分质工具剪切作用对聚合物溶液黏度的影响,建立了分质工具中注入
聚合物表观黏度变化数学黏度的影响。结果表明:聚合
中国分类号:TE357.6
文献标识码:A
A mathematical model for the effect of shearing action on the apparent viscosity of polymer injected by a different medium injection tool
Engineering, Daqing Oilfield, PetroChina, Daqing, Heilongjiang 163453, China)
Abstract: Aiming at the low production level of the oil layer caused by the reservoirs with low permeability and the large contradic⁃ tion between oil layers, we commonly use different medium injection tools in the oil fields to realize the match of polymer injection and polymer molecular weight to the oil layer. In order to reflect the effect of shearing on viscosity of polymer solution when it across the interstitial injection tools, a mathematical model about the impact on polymer apparent viscosity affected by shearing was established, and the influence of the structural parameters of interstitial injection tools and injection volume on the apparent viscosi⁃ ty of polymer was analyzed. The results showed that the apparent viscosity of the polymer solution went up when the length of con⁃ tractile section, radius of cylindrical section, maximum diameter of dilated section and length of dilated section increased, while the apparent viscosity of polymer solution went down when the radius of the contractile section increased. And the length of cylindrical section had no effect on the apparent viscosity of polymer solution. The apparent viscosity of polymer solution decreased when the injection volume of the polymer solution increased. The calculation results can provide a theoretical reference for optimizing the structural parameters of the different medium injection tool. Key words: polymer flooding, different medium injection tool, polymer molecular weight, apparent viscosity, shearing action
物溶液的表观黏度随着分质工具收缩段长度、圆柱段半径、扩张段最大直径、扩张段长度的增大而增大;随着收缩段半径
的增大而减小;分质工具圆管段长度对聚合物溶液的表观黏度大小无明显影响。聚合物溶液的表观黏度随着聚合物溶液
注入量的增大而减小。计算结果可为工程实际需要进行优选分质工具结构参数提供理论参考依据。
关键词:聚合物驱;分质工具;聚合物分子量;表观黏度;剪切作用
第8卷 第5期
油气藏评价与开发
RESERVOIR EVALUATION AND DEVELOPMENT
2018 年 10 月
分质工具中注入聚合物表观黏度变化 数学模型的建立及应用
黄 斌 1,李晓慧 1,傅 程 1,2,王 鑫 3
(1. 东北石油大学石油工程学院,黑龙江 大庆 163318;2. 中国石油大庆油田博士后科研工作站,黑龙江 大庆 163458; 3. 中国石油大庆油田采油工程研究院,黑龙江 大庆 163453)
Huang Bin1, Li Xiaohui1, Fu Cheng1,2 and Wang Xin3
(1.School of Petroleum Engineering, Northeast Petroleum University, Daqing, Heilongjiang 163318, China; 2.Post-doctoral Research Station, Daqing Oilfield, PetroChina, Daqing, Heilongjiang 163458, China; 3.Research Institute of Oil Production
