九年级四边形知识点归纳总结
四边形知识点归纳
四边形知识点归纳四边形是一个具有四个边和四个角的多边形。
四边形的性质和特点因其形状和边长的不同而不同。
在以下内容中，我将对四边形的几个主要性质和特点进行详细归纳。
一、四边形的基本性质：1.四边形的内角和为360度：四边形的四个内角之和始终等于360度。
换句话说，四边形的任意两个相邻内角的和始终等于180度。
2.对角线交点：四边形的对角线是相邻顶点之间的连线。
对角线的交点称为对角线交点（或称为对角线的交叉点）。
对角线交点将四边形分为两个三角形。
3.对称关系：四边形中有两种对称关系，即对边对称和对角线对称。
对边对称是指围绕四边形的中心点将对边进行折叠，使得两条对边重合。
对角线对称是指围绕四边形的对角线交点将对边进行折叠，使得两条对边重合。
二、四边形的分类：1.平行四边形：有两组对边平行的四边形被称为平行四边形。
它的对角线相等且对角线互相平分。
2.矩形：具有四个直角（内角为90度）的四边形被称为矩形。
它的对边相等且平行。
3.正方形：具有四个直角（内角为90度）和相等对边的矩形被称为正方形。
它的对角线相等且互相平分。
4.梯形：具有两边平行的四边形被称为梯形。
它的对角线不相等，且其中一条对角线是另一条对角线的中线。
5.平行四边形的性质：（1）对边平行：平行四边形的对边互相平行。
（2）对边相等：平行四边形的对边相等。
（3）对角线互相平分：平行四边形的对角线互相平分。
6.矩形的性质：（1）四个直角：矩形的四个内角均为90度。
（2）对边相等：矩形的对边相等且平行。
（3）对角线相等：矩形的对角线相等。
（4）对角线互相平分：矩形的对角线互相平分。
7.正方形的性质：（1）四个直角：正方形的四个内角均为90度。
（2）对边相等：正方形的对边相等且平行。
（3）对角线相等：正方形的对角线相等且互相平分。
8.梯形的性质：（1）两边平行：梯形的两边平行，且不平行的两边称为梯形的斜边。
（2）底角相等：梯形的相邻底角（底边上的内角）相等。
初中四边形基础知识点总结
初中四边形基础知识点总结一、四边形的定义四边形是由四条线段组成的封闭几何图形。
这四条线段的顶点依次相连，形成一个内部没有异于角的多边形。
四边形主要包括矩形、正方形、平行四边形、梯形和菱形等。
二、四边形的分类1. 矩形：矩形是一种特殊的平行四边形，它的对边相等且相互平行，对角线相等且相交垂直。
2. 正方形：正方形是一种特殊的矩形，它的对边相等且相互平行，对角线相等且相交垂直，且具有四条相等的边。
3. 平行四边形：平行四边形是一种具有对边平行的四边形，它的对边相等且相互平行。
4. 梯形：梯形是一种至少有两条平行边的四边形，它的两条对边都不平行。
5. 菱形：菱形是一种具有对边相等的四边形，它的对角线互相垂直且相等。
三、四边形的性质1. 内角和：四边形的内角和等于360度，即∠A+∠B+∠C+∠D=360°。
2. 对角线：四边形有两条对角线，它们的交点被称为对角点。
对角点将四边形分成两个三角形，这两个三角形的面积之和等于四边形的面积。
3. 直角矩形的性质：直角矩形的对边相等且相互平行，对角线相等且相交垂直，它的面积等于矩形的宽乘以高。
4. 正方形的性质：正方形的对边相等且相互平行，对角线相等且相交垂直，它的面积等于边长的平方。
5. 平行四边形的性质：平行四边形的对边相等且相互平行，它的相邻角互补，且对角线互相垂直且相等。
6. 梯形的性质：梯形至少有两条平行边，它的上底和下底的平均值等于高乘以底长。
7. 菱形的性质：菱形的对边相等，它的对角线互相垂直且相等，且每个角都是直角。
四、四边形的计算1. 面积：四边形的面积可以根据其形状和性质进行计算。
例如，矩形的面积等于宽乘以高，正方形的面积等于边长的平方，平行四边形的面积等于底边乘以高度，梯形的面积等于上底和下底的平均值乘以高，菱形的面积等于对角线的乘积的一半。
2. 周长：四边形的周长等于其四条边的长度之和。
五、四边形的应用1. 基础几何图形：四边形是平面几何中的基础图形，它在数学中具有重要的地位，是其他图形和几何知识的基础。
中考数学总复习知识点总结四边形
中考数学总复习知识点总结四边形四边形是指具有四条边的几何图形，在数学中有着重要的地位。
下面是中考数学总复习知识点总结四边形的内容。
一、基本定义和性质1.四边形的定义：具有四个顶点、四条边和四个内角的几何图形称为四边形。
2.四边形的分类：a.顶点关系分类：凸四边形和凹四边形；b.边长关系分类：等边四边形、等腰四边形和普通四边形；c.内角关系分类：矩形、正方形、平行四边形、菱形、梯形等。
3.四边形的性质：a.任意一条对角线将四边形分成两个三角形；b.对角线互相平分；c.相对边平行；d.相对角和为180度。
二、特殊四边形1.平行四边形：a.定义：对边平行的四边形；b.性质：i.对边相等；ii. 相邻内角互补；iii. 对角相等。
c.定理：1）如果一条对角线把平行四边形分成两个等腰三角形，则这条对角线是平行四边形的对称轴；2）如果一个四边形的对角线互相平分，则这个四边形是平行四边形。
2.矩形：a.定义：对边平行且四个内角都是直角的四边形；b.性质：i.两对对边相等；ii. 对角线相等；iii. 相邻内角互补；iv. 对角线互相平分。
3.菱形：a.定义：四个边都相等的平行四边形；b.性质：i.相邻内角互补；ii. 对角线互相垂直；iii. 对角线平分相应的内角。
4.正方形：a.定义：对边相等且四个内角都是直角的矩形；b.性质：i.两对对边相等；ii. 对角线相等；iii. 对角线互相垂直；iv. 对角线平分相应的内角。
5.等腰梯形：a.定义：有两对对边平行且有两条边相等的梯形；b.性质：i.上底和下底平分相应的内、外角；ii. 对角线等分梯形的积。
三、四边形的面积和周长1.面积：a.矩形的面积等于长度乘以宽度；b.平行四边形的面积等于底边长乘以高；c.三角形的面积等于底边长乘以高的一半；d.梯形的面积等于上底和下底的平均值乘以高；e.菱形的面积等于对角线的乘积的一半；f.正方形的面积等于一条边长的平方。
2.周长：a.四边形的周长等于四条边的长度之和；b.正方形的周长等于边长的四倍。
中考四边形综合知识点总结
中考四边形综合知识点总结一、四边形的性质1. 任意四边形的内角和为360度2. 对角线互相垂直的四边形是矩形3. 对边平行且相等的四边形是平行四边形4. 有一对对边平行的四边形是梯形5. 有一对对边相等的四边形是菱形6. 对角线相等的四边形是菱形7. 有一对对边互相垂直且相等的四边形是正方形8. 矩形和菱形都是平行四边形二、矩形1. 定义：有四个顶点和四条边的四边形2. 性质：内角和为360度，对角线长度相等，对角线互相垂直，相邻边互相垂直且相等3. 公式：周长=2*(长+宽)，面积=长*宽三、平行四边形1. 定义：有四个顶点和四条边的四边形，对边平行且相等2. 性质：内角和为360度，对角线互相平分，对边互相相等3. 公式：周长=2*(a+b)，面积=底*高四、梯形1. 定义：有四个顶点和四条边的四边形，有一对对边平行2. 性质：内角和为360度，底边平行，上底和下底长度相等，两个底边平行线段的中线互相平行3. 公式：周长=上底+下底+两腰，面积=(上底+下底)*高/2五、菱形1. 定义：有四个顶点和四条边的四边形，对边互相平行且相等2. 性质：内角和为360度，对角线相等，对角线互相平分，对角线互相垂直3. 公式：周长=4*边长，面积=对角线1*对角线2/2六、正方形1. 定义：有四个顶点和四条边的四边形，对角线相等，对边互相平行且相等2. 性质：内角和为360度，对角线相等，对角线互相垂直，边互相平行且相等3. 公式：周长=4*边长，面积=边长^2七、计算题1. 计算四边形的周长和面积2. 计算梯形的高3. 根据题目条件运用四边形的性质进行计算4. 判断四边形的类型和性质八、应用题1. 根据实际场景运用四边形的性质进行解决问题2. 通过综合应用四边形的知识解决问题3. 运用数学推理和逻辑思维解答四边形的实际问题以上就是中考四边形综合知识点总结，希望对大家有所帮助。
2020届九年级中考数学知识点《四边形》
2020届九年级中考数学知识点《四边形》摘要：一、四边形概念与性质1.四边形的定义2.四边形的分类3.四边形的性质二、四边形常见类型1.矩形2.平行四边形3.菱形4.正方形5.梯形三、四边形与坐标系1.坐标系与四边形的关系2.四边形在坐标系中的表示方法四、四边形的应用1.四边形在实际生活中的应用2.四边形在数学问题中的应用正文：一、四边形概念与性质四边形是由四条线段依次首尾相接围成的平面图形。
根据四边形的边长和角度关系，四边形可以分为矩形、平行四边形、菱形、正方形和梯形等多种类型。
各种类型的四边形具有不同的性质，如矩形具有对角线相等且互相平分的性质，平行四边形具有对边平行且相等的性质，菱形具有所有边相等的性质，正方形具有所有边相等且四个角为直角的性质，梯形具有两对边分别平行且不相等的性质。
二、四边形常见类型1.矩形：矩形是一种四边形，它的对边相等且内角为直角。
矩形可以细分为正矩形和长方形。
正矩形的四个角为直角，四条边相等；长方形的对边相等，但四个角不一定是直角。
2.平行四边形：平行四边形是一种四边形，它的对边平行且相等。
根据对角线的关系，平行四边形可以分为矩形、菱形和梯形。
3.菱形：菱形是一种四边形，它的所有边相等，且对角线互相垂直平分。
根据对角线长度关系，菱形可以分为正菱形和斜菱形。
4.正方形：正方形是一种矩形，它的所有边相等且四个角为直角。
正方形是特殊的矩形和菱形，具有矩形和菱形的所有性质。
5.梯形：梯形是一种四边形，它有一对边平行，另一对边不平行。
根据平行边的位置关系，梯形可以分为直角梯形、锐角梯形和钝角梯形。
三、四边形与坐标系在平面直角坐标系中，四边形的顶点可以用坐标表示。
横坐标表示四边形在x 轴上的位置，纵坐标表示四边形在y 轴上的位置。
根据四边形的顶点坐标，可以计算出四边形的面积、周长和内角和等性质。
四、四边形的应用四边形在实际生活中有着广泛的应用，如建筑、地理、物理和数学等领域。
在建筑中，四边形可以用来设计矩形、菱形和梯形的建筑结构；在地理中，四边形可以用来绘制地图和地球仪；在物理中，四边形可以用来描述物体的运动轨迹；在数学中，四边形可以用来解决几何和代数问题。
九年级四边形知识点总结大全
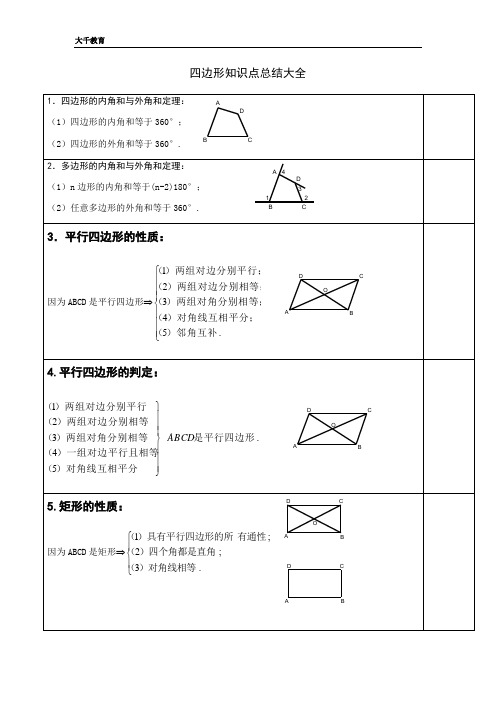
四边形知识点总结大全1．四边形的内角和与外角和定理： （1）四边形的内角和等于360°； （2）四边形的外角和等于360°.2．多边形的内角和与外角和定理： （1）n 边形的内角和等于(n-2)180°； （2）任意多边形的外角和等于360°.3．平行四边形的性质：因为ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321）邻角互补（）对角线互相平分；（）两组对角分别相等；（）两组对边分别相等；（）两组对边分别平行；（4.平行四边形的判定：是平行四边形）对角线互相平分（）一组对边平行且相等（）两组对角分别相等（）两组对边分别相等（）两组对边分别平行（ABCD ⎪⎪⎪⎭⎪⎪⎪⎬⎫54321.5.矩形的性质：因为ABCD 是矩形⇒⎪⎩⎪⎨⎧.3;2;1）对角线相等（）四个角都是直角（有通性）具有平行四边形的所（A BCD 1234AB CDABDOCABDOCA D BCAD BCO6. 矩形的判定：⎪⎭⎪⎬⎫+边形）对角线相等的平行四（）三个角都是直角（一个直角）平行四边形（321⇒四边形ABCD 是矩形.7．菱形的性质：因为ABCD 是菱形⇒⎪⎪⎩⎪⎪⎨⎧.(4)321角线乘积的一半菱形的面积等于两条对角）对角线垂直且平分对（）四条边都相等；（有通性；）具有平行四边形的所（8．菱形的判定：⎪⎭⎪⎬⎫+边形）对角线垂直的平行四（）四个边都相等（一组邻边等）平行四边形（321⇒四边形ABCD 是菱形.9．正方形的性质：因为ABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角）对角线相等垂直且平（角都是直角；）四个边都相等，四个（有通性；）具有平行四边形的所（ CDAB（1）A BCD O（2）（3）CDBAOCDBAOADBCADB CO10．正方形的判定：⎪⎭⎪⎬⎫++++一组邻边等矩形）（一个直角）菱形（一个直角一组邻边等）平行四边形（321⇒四边形ABCD 是正方形.(3)∵ABCD 是矩形 又∵AD=AB∴四边形ABCD 是正方形11．等腰梯形的性质：因为ABCD 是等腰梯形⇒⎪⎩⎪⎨⎧.321）对角线相等（；）同一底上的底角相等（两底平行，两腰相等；）（12．等腰梯形的判定：⎪⎭⎪⎬⎫+++对角线相等）梯形（底角相等）梯形（两腰相等）梯形（321⇒四边形ABCD 是等腰梯形 (3)∵ABCD 是梯形且AD ∥BC∵AC=BD∴ABCD 四边形是等腰梯形14．三角形中位线定理：三角形的中位线平行第三边，并且等于它的一半.15．梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半.E FD ABCE DCBAA BCD OABC DOCD AB。
初中数学四边形知识点归纳
初中数学四边形知识点归纳四边形(四边形具有不稳定性)1定理四边形的内角和等于360°2四边形的外角和等于360°3多边形内角和定理 n边形的内角的和等于(n-2)×180°4推论任意多边的外角和等于360°5平行四边形性质定理1 平行四边形的对角相等6平行四边形性质定理2 平行四边形的对边相等7推论夹在两条平行线间的平行线段相等8平行四边形性质定理3 平行四边形的对角线相互平分9平行四边形判定定理1 两组对角分别相等的四边形是平行四边形10平行四边形判定定理2 两组对边分别相等的四边形是平行四边形11平行四边形判定定理3 对角线相互平分的四边形是平行四边形12平行四边形判定定理4 一组对边平行相等的四边形是平行四边形13矩形性质定理1 矩形的四个角都是直角14矩形性质定理2 矩形的对角线相等15矩形判定定理1 有三个角是直角的四边形是矩形16矩形判定定理2 对角线相等的平行四边形是矩形17菱形性质定理1 菱形的四条边都相等18菱形性质定理2 菱形的对角线相互垂直，并且每一条对角线平分一组对角19菱形面积=对角线乘积的一半，即s=(a×b)÷220菱形判定定理1 四边都相等的四边形是菱形216菱形判定定理2 对角线相互垂直的平行四边形是菱形22正方形性质定理1 正方形的四个角都是直角，四条边都相等23正方形性质定理2正方形的两条对角线相等，并且相互垂直平分，每条对角线平分一组对角24定理1 关于中心对称的两个图形是全等的25定理2 关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分26逆定理假如两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称27等腰梯形性质定理等腰梯形在同一底上的两个角相等28等腰梯形的两条对角线相等29等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形30对角线相等的梯形是等腰梯形31平行线等分线段定理假如一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等32 推论1 经过梯形一腰的中点与底平行的直线，必平分另一腰33推论2 经过三角形一边的中点与另一边平行的直线，必平分第三边34 三角形中位线定理三角形的中位线平行于第三边，并且等于它的一半36 梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半 l=(a+b)÷2 s=l×h37 (1)比例的基本性质假如a:b=c:d,那么ad=bc 假如ad=bc,那么a:b=c:d38 (2)合比性质假如a/b=c/d,那么(a±b)/b=(c±d)/d39 (3)等比性质假如a/b=c/d=…=m/n(b+d+…+n≠0),那么 (a+c+…+m)/(b+d+…+n)=a/b40平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例41 推论平行于三角形一边的直线截其他两边(或两边的延长线)，所得的对应线段成比例42 定理假如一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形的第三边43平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例44 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相像45 相像三角形判定定理1 两角对应相等，两三角形相像(asa)46 直角三角形被斜边上的高分成的两个直角三角形和原三角形相像47 判定定理2 两边对应成比例且夹角相等，两三角形相像(sas)48 判定定理3 三边对应成比例，两三角形相像(sss)49 定理假如一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相像50 性质定理1 相像三角形对应高的比，对应中线的比与对应角平分线的比都等于相像比51 性质定理2 相像三角形周长的比等于相像比52 性质定理3 相像三角形面积的比等于相像比的平方53任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值54任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值大家看过中学数学知识点归纳之四边形，大家要熟记多边形内角和定理为n边形的内角的和等于(n-2)×180°。
九年级四边形知识点归纳总结
九年级四边形知识点归纳总结四边形是几何学中常见的一个概念，它是指由四个边和四个顶点组成的图形。
在九年级的几何学中，我们学习了关于四边形的各种性质、分类以及相关定理。
本文将对九年级四边形的知识点进行归纳总结。
一、四边形的基本概念四边形是一个有四条边和四个顶点的几何图形。
四边形的两两边不共线，并且任意三条边不在一条直线上。
二、四边形的分类1. 平行四边形：有两组对边互相平行的四边形。
2. 矩形：四个内角均为直角的四边形。
3. 菱形：四个边长度相等的四边形。
4. 正方形：具备菱形和矩形两种性质的四边形。
5. 梯形：有一对对边平行的四边形。
6. 平行四边形的特殊形式：长方形、正方形、菱形都是平行四边形的特殊形式。
三、四边形的性质和定理1. 平行四边形的性质：a. 对边相等性质：平行四边形的对边相等。
b. 对角线性质：平行四边形的对角线互相平分。
2. 矩形的性质：a. 内角性质：矩形的内角均为直角。
b. 对边性质：矩形的对边相等。
c. 对角线性质：矩形的对角线相等。
3. 菱形的性质：a. 对边性质：菱形的对边相等。
b. 内角性质：菱形的内角均为直角。
c. 对角线性质：菱形的对角线互相垂直、平分。
4. 正方形的性质：a. 对边性质：正方形的对边相等。
b. 内角性质：正方形的内角均为直角。
c. 对角线性质：正方形的对角线相等、互相垂直、平分。
5. 梯形的性质：a. 底边性质：梯形的两条底边平行。
b. 顶角性质：梯形的两个顶角之和为180度。
四、四边形的相关定理1. 平行四边形的定理：a. 对边定理：平行四边形的对边相等。
b. 对角线定理：平行四边形的对角线互相平分。
2. 矩形的定理：a. 内角定理：矩形的内角均为直角。
b. 对边定理：矩形的对边相等。
c. 对角线定理：矩形的对角线相等。
3. 菱形的定理：a. 对边定理：菱形的对边相等。
b. 内角定理：菱形的内角均为直角。
c. 对角线定理：菱形的对角线互相垂直、平分。
四边形基本图形知识点总结
四边形基本图形知识点总结四边形是几何学中常见的图形，它有许多重要的性质和知识点。
本文将带您深入了解四边形的基本概念、分类和特性。
一、四边形的基本概念四边形是指具有四条边的图形。
它是多边形的一种特殊情况，由四个顶点和四条边构成。
尽管四边形是一个广义的概念，但在几何学中我们通常讨论的是平面四边形。
二、四边形的分类根据四边形的性质，我们可以将其分类为以下几种常见类型：1.矩形：四个角都是直角的四边形。
矩形的对边相等且平行。
2.正方形：具有四个相等边长和四个直角的矩形。
3.平行四边形：有两组对边分别平行的四边形。
4.梯形：有一对对边平行的四边形。
5.菱形：四个边长相等的梯形。
6.不规则四边形：没有对边平行或边长相等的四边形。
三、四边形的性质和特性1.内角和：四边形的内角和等于360度。
2.外角和：四边形的外角和等于360度。
3.对角线：四边形的对角线是相邻顶点之间的直线段。
对角线有以下重要性质：–矩形的对角线相等；–平行四边形的对角线互相平分；–菱形的对角线互相垂直且平分；–梯形的对角线不相交。
4.邻边和对边：在平行四边形中，邻边是指两个相邻的边，对边是指不相邻但平行的边。
在矩形和正方形中，邻边和对边是相同的。
5.矩形和正方形的特性：–矩形的对边相等且平行；–矩形的对角线相等；–正方形是一种特殊的矩形，具有四个相等的边长和四个直角。
四、四边形的计算在解决与四边形相关的问题时，我们经常需要计算其面积和周长。
下面是一些常见四边形的计算公式：1.矩形的面积为长度乘以宽度，周长为两倍长度加两倍宽度。
2.正方形的面积为边长的平方，周长为四倍边长。
3.平行四边形的面积为底边乘以高，周长为两倍底边加两倍高。
4.梯形的面积为上底加下底乘以高的一半，周长为所有边长之和。
五、应用实例四边形的概念和性质在日常生活和工作中都有广泛的应用。
例如：1.建筑设计：在建筑设计中，矩形和正方形的特性被广泛应用于房屋的布局和结构设计。
2.地理测量：平行四边形的特性可用于测量地块面积或河流的宽度。
九年级四边形知识点总结
九年级四边形知识点总结在初中数学的学习过程中，四边形是一个非常重要的概念，它涵盖了多种形状和性质。
在九年级的学习中，我们深入研究了四边形的各种特点和性质，下面就让我们一起来总结一下九年级四边形的知识点。
四边形是由四条线段所围成的图形，根据边的性质可以分为平行四边形、矩形、正方形、菱形和梯形等五种类型。
首先，让我们来看平行四边形。
平行四边形是指四边形的对边是平行的。
在平行四边形中，有以下几个重要的性质。
首先，平行四边形的对边长度相等，即对边 AB = CD，BC = AD。
其次，平行四边形的对角线相互平分，即对角线 AC 和 BD 互相平分。
还有，平行四边形的任意一条对角线分割平行四边形面积成两个相等的三角形。
接着，我们来看矩形。
矩形是特殊的平行四边形，它的四个内角都是直角。
矩形具有以下性质。
首先，矩形的对边相等且平行，也就是说 AB = CD，BC = AD，并且 AB ∥ CD，BC ∥ AD。
其次，矩形的对角线相等，即 AC = BD。
另外，矩形的面积可以通过长度和宽度相乘来计算，即面积等于长乘以宽。
正方形是矩形的特殊情况，它的四个边长和四个角都相等，同时也是一个菱形。
正方形的性质非常特殊，首先，正方形的对角线相等且互相垂直，即 AC = BD，AC ⊥ BD。
其次，正方形的内角都是直角。
最后，正方形的面积可以通过边长的平方来计算，即面积等于边长的平方。
另外一个重要的四边形是菱形。
菱形的特点是四个边长相等，且对角线互相垂直。
菱形具有以下性质。
首先，菱形的对角线相等，即 AC = BD。
其次，菱形的对角线互相垂直，即 AC ⊥ BD。
最后，菱形的面积可以通过对角线的乘积除以2来计算，即面积等于对角线的乘积除以2。
最后，我们来看梯形。
梯形是由两个平行的底边和两个不平行的腰边所组成的四边形。
梯形具有以下性质。
首先，梯形的底边平行，即 AB ∥ DC。
其次，梯形的腰边不平行。
然后，梯形的两个腰边长度相等，即 AD = BC。
数学四边形知识点大全总结
数学四边形知识点大全总结一、四边形的定义四边形是指一个平面图形，其中有四条边和四个顶点。
四边形是平面图形中最简单的多边形之一，同时也是很多其他几何图形的基础和组成部分。
二、四边形的分类根据四边形的性质和特点，可以将其分为以下几种主要类型：1. 矩形：拥有四个直角的四边形，对角线相等，且对角线互相垂直；2. 正方形：拥有四条相等边和四个直角的四边形；3. 平行四边形：拥有对边平行且长度相等的四边形；4. 菱形：拥有四条相等边但非直角的四边形；5. 梯形：至少有一对对边平行的四边形；6. 不规则四边形：没有特定性质和特点的四边形。
在这些基本类型的基础上，还可以根据四边形的角度、边长、对角线等特点对其进行更详细的分类和讨论。
三、四边形的性质1. 任意四边形的内角和等于360度；2. 对角线互相垂直的矩形和正方形；3. 平行四边形的对边相等且平行；4. 菱形的对角线互相垂直，且互相垂直；5. 梯形的一对对边平行；6. 不规则四边形没有特定的性质和特点。
四、四边形的相关定理1. 四边形内角和定理：任意四边形的内角和等于360度；2. 平行四边形定理：如果一对对边平行且长度相等，则该四边形是平行四边形；3. 矩形的性质定理：对角线平分，互相垂直；4. 正方形的性质定理：拥有四条相等边和四个直角；5. 平行四边形的性质定理：对边相等且平行；6. 菱形的性质定理：对角线互相垂直；7. 梯形的性质定理：一对对边平行。
五、四边形的应用和延伸1. 利用四边形的性质和定理进行几何证明和计算；2. 将四边形的性质应用到实际问题中，如建筑设计、工程测量等；3. 通过四边形的性质和特点，进行图形的合理分类和摆放，以满足设计和美学的要求；4. 采用四边形的相关知识进行几何推理和问题解决，培养逻辑思维和问题解决能力。
总结：四边形作为平面几何中最基本的图形之一，其性质和特点对于理解和运用其他更复杂的几何图形具有重要意义。
通过系统地学习和掌握四边形的定义、分类、性质和定理等知识点，可以提高学生的几何思维和解决问题的能力，在实际生活和工作中有着广泛的应用价值。
四边形知识点总结[1]
![四边形知识点总结[1]](https://img.taocdn.com/s3/m/2c1024737375a417866f8f80.png)
四边形一 基本概念：四边形，四边形的内角，四边形的外角，多边形，平行线间的距离，平行四边形，矩形，菱形，正方形，中心对称，中心对称图形，梯形，等腰梯形，直角梯形，三角形中位线，梯形中位线. 二 定理：中心对称的相关定理※1．关于中心对称的两个图形是全等形.※2．关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分.※3．如果两个图形的对应点连线都经过某一点，并且被这个点平分，那么这两个图形关于这个点对称. 三 公式：1．S 菱形 =21ab=ch.（a 、b 为菱形的对角线 ,c 为菱形的边长 ，h 为c 边上的高） 2．S 平行四边形 =ah. a 为平行四边形的边，h 为a 上的高） 3．S 梯形 =21（a+b ）h=Lh.（a 、b 为梯形的底，h 为梯形的高,L 为梯形的中位线） 四 常识：※1．若n 是多边形的边数，则对角线条数公式是：2)3n (n -. 2．规则图形折叠一般“出一对全等，一对相似”. 3．如图：平行四边形、矩形、菱形、正方形的从属关系.4．常见图形中，仅是轴对称图形的有：角、等腰三角形、等边三角形、正奇边形、等腰梯形 …… ；仅是中心对称图形的有：平行四边形 …… ；是双对称图形的有：线段、矩形、菱形、正方形、正偶边形、圆 …… .注意：线段有两条对称轴.平行四边形矩形菱形正方形四边形知识点归纳平行四边形平行四边形定义：两组对边分别平行的四边形叫做平行四边形。
平行四边形是中心对称图形，对称中心是两条对角线的交点。
平行四边形性质1：平行四边形的两组对边分别相等。
平行四边形性质2：平行四边形的两组对角分别相等。
平行四边形性质3：平行四边形的两条对角线互相平分。
平行四边形判定1：两组对边分别平行的四边形是平行四边形。
平行四边形判定2：两组对边分别相等的四边形是平行四边形。
平行四边形判定3：两组对角分别相等的四边形是平行四边形。
平行四边形判定4：两条对角线互相平分的四边形是平行四边形。
初中四边形模型总结知识点
初中四边形模型总结知识点一、四边形的定义四边形是几何学中的基本图形之一，它是一个由四条线段组成的封闭图形。
四边形有四条边和四个顶点，并且四边形的内部是闭合的，没有空隙。
四边形是平面图形，由于它由四条线段组成，所以它也是一个多边形。
在几何学中，四边形是一个非常重要的概念，它是许多几何学知识的基础。
二、四边形的性质1. 内角和为360度四边形的最基本的性质就是它的内角和为360度。
也就是说，四边形的四个内角的度数相加等于360度。
这一性质是四边形的基本特征，能够帮助我们计算四边形内部角度的度数。
2. 对角线的关系四边形的对角线是连接四边形的两个不相邻顶点的线段。
对角线有很多重要的性质，例如：- 对角线相等：某些特殊的四边形，如平行四边形、矩形、菱形等，它们的对角线相等。
- 对角线互相平分：某些特殊的四边形，如菱形、矩形等，它们的对角线会互相平分，即将四边形分成两个全等的三角形。
3. 邻边角的关系邻边角是指四边形中相邻的两个内角。
有些四边形的邻边角有特殊的关系，例如：- 相邻角的和为180度：在某些特殊的四边形中，相邻角的和总是等于180度，这一性质可以帮助我们求解四边形内角的度数。
4. 边的关系四边形的边也有一些重要的性质，例如：- 对边相等：在某些特殊的四边形中，对边相等。
比如在矩形中，对边相等。
- 邻边的和大于对角边：在任何一个四边形中，相邻两边的长度和大于对角线的长度。
以上就是四边形的一些基本性质，这些性质是我们研究四边形的基础，同时也是解题的关键。
三、四边形的分类根据四边形的性质和形状，我们可以将四边形分为多种不同的类型。
常见的四边形包括：平行四边形、矩形、菱形、正方形、梯形、梯形等。
下面我们分别介绍一下这些四边形的性质。
1. 平行四边形平行四边形是一种特殊的四边形，它具有以下性质：- 对边相等- 对角线相等- 相对角相等- 对角线互相平分平行四边形具有以上特殊的性质，这些性质都可以通过几何推理进行证明。
四边形知识点归纳
四边形知识点归纳在初中数学的学习中，四边形是一个重要的章节，它包含了丰富的知识和多样的性质。
接下来，让我们系统地归纳一下四边形的相关知识点。
一、四边形的定义由不在同一直线上的四条线段依次首尾相接围成的封闭的平面图形或立体图形叫四边形。
二、常见的四边形1、平行四边形两组对边分别平行的四边形叫做平行四边形。
它具有以下性质：对边平行且相等。
对角相等，邻角互补。
对角线互相平分。
平行四边形的判定方法有：两组对边分别平行的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
一组对边平行且相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
2、矩形有一个角是直角的平行四边形叫做矩形。
矩形除了具有平行四边形的所有性质外，还具有以下特殊性质：四个角都是直角。
对角线相等。
矩形的判定方法有：有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形。
有三个角是直角的四边形是矩形。
3、菱形有一组邻边相等的平行四边形叫做菱形。
菱形具有以下性质：四条边都相等。
对角线互相垂直，并且每一条对角线平分一组对角。
菱形的判定方法有：一组邻边相等的平行四边形是菱形。
对角线互相垂直的平行四边形是菱形。
四条边都相等的四边形是菱形。
4、正方形四条边都相等，四个角都是直角的四边形叫做正方形。
正方形具有平行四边形、矩形和菱形的所有性质。
正方形的判定方法有：有一个角是直角的菱形是正方形。
有一组邻边相等的矩形是正方形。
5、梯形一组对边平行，另一组对边不平行的四边形叫做梯形。
其中，平行的两边叫做梯形的底，不平行的两边叫做梯形的腰。
等腰梯形：两腰相等的梯形叫做等腰梯形。
等腰梯形具有以下性质：同一底上的两个角相等。
对角线相等。
直角梯形：有一个角是直角的梯形叫做直角梯形。
等腰梯形的判定方法有：同一底上的两个角相等的梯形是等腰梯形。
对角线相等的梯形是等腰梯形。
三、四边形的内角和与外角和四边形的内角和为 360 度。
四边形的外角和为 360 度，这是所有多边形外角和的通用性质。
初中四边形知识点总结归纳
初中四边形知识点总结归纳一、四边形的基本概念。
1. 四边形的定义。
- 由不在同一直线上的四条线段依次首尾相接围成的封闭的平面图形或立体图形叫四边形。
在初中阶段，我们主要研究平面四边形。
2. 四边形的内角和与外角和。
- 内角和：四边形的内角和为360°。
可以通过三角形内角和为180°，将四边形分割成两个三角形来证明。
- 外角和：四边形的外角和为360°。
任何多边形的外角和都是360°，对于四边形，在每个顶点处取一个外角，它们的和是360°。
3. 四边形的对角线。
- 连接四边形不相邻的两个顶点的线段叫做四边形的对角线。
四边形有两条对角线。
二、平行四边形。
1. 平行四边形的定义。
- 两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“▱”表示，如平行四边形ABCD记作“▱ABCD”。
2. 平行四边形的性质。
- 边：平行四边形的两组对边分别平行且相等。
即AB = CD，AD = BC；AB∥CD，AD∥BC。
- 角：平行四边形的两组对角分别相等，邻角互补。
即∠A = ∠C，∠B = ∠D；∠A+∠B = 180°，∠B + ∠C=180°等。
- 对角线：平行四边形的对角线互相平分。
即OA = OC，OB = OD（设AC、BD相交于点O）。
3. 平行四边形的判定。
- 边：- 两组对边分别平行的四边形是平行四边形（定义）。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
- 角：两组对角分别相等的四边形是平行四边形。
- 对角线：对角线互相平分的四边形是平行四边形。
4. 平行四边形的面积。
- 平行四边形的面积 = 底×高，即S = ah（a为底边长，h为这条底边对应的高）。
三、矩形。
1. 矩形的定义。
- 有一个角是直角的平行四边形叫做矩形。
2. 矩形的性质。
- 具有平行四边形的所有性质。
初三四边形所有知识点总结
初三四边形所有知识点总结四边形是初中数学中重要的几何图形，在初三阶段，学生需要掌握四边形的定义、性质、分类、面积计算等知识点。
本文将对初三四边形的所有知识点进行总结，希望对学生的学习有所帮助。
一、四边形的定义和性质1. 四边形的定义四边形是一个有四条边的几何图形，它是由四个顶点和四条边组成的。
2. 四边形的性质（1）四边形的内角和四边形的内角和是360°。
即：A+B+C+D = 360°（2）四边形的对角线四边形有两条对角线，分别连接相对的顶点。
对角线的交点称为对角线的交点。
对角线的长度可以通过勾股定理求得。
（3）四边形的对边四边形的相对边称为对边。
二、四边形的分类根据四边形的特征和性质，可以将四边形分为以下几类：1. 平行四边形2. 矩形3. 菱形4. 正方形5. 梯形6. 平行四边形7. 不规则四边形三、平行四边形的性质1. 平行四边形的定义平行四边形是有两对边平行的四边形，即两对对边是平行的四边形。
2. 平行四边形的性质（1）对角线平行四边形的对角线相交于90°的角，并且两条对角线相等。
（2）对边及角平行四边形的对边相等，对角相等。
（3）周长和面积平行四边形的周长可以通过对边和对角线求得。
平行四边形的面积可以通过底和高求得。
四、矩形的性质1. 矩形的定义矩形是有四条边且所有内角都是直角的四边形。
2. 矩形的性质（1）四边相等矩形的四条边相等。
（2）对角线相等矩形的两条对角线相等。
（3）对边平行矩形的对边是平行的。
（4）周长和面积矩形的周长可以通过长和宽求得。
矩形的面积可以通过长和宽求得。
五、菱形的性质1. 菱形的定义菱形是有四条边且两两相等的四边形。
2. 菱形的性质（1）对角线相等菱形的两条对角线相等。
（2）相邻角相等菱形的两个相邻角是相等的。
（3）周长和面积菱形的周长可以通过边长求得。
菱形的面积可以通过对角线求得。
六、正方形的性质1. 正方形的定义正方形是有四条边，相等且所有内角都是直角的四边形。
九年级数学四边形知识点
九年级数学四边形知识点数学是一门既有挑战性又充满乐趣的学科，在九年级阶段，我们将学习四边形的相关知识。
四边形作为平面几何的基础，关乎到我们日常生活中的方方面面。
本文将深入探讨九年级数学中的四边形知识点，帮助同学们更好地理解和应用这些概念。
1. 四边形的定义和分类四边形是由四条边组成的平面图形。
根据边的长短和角的大小，我们可以将四边形分为不同的类型。
正方形是四边形的一种特殊情况，具有相等的边和相等的角。
长方形则拥有相等的边和对角线相等的特点。
2. 角和边的关系四边形中的角和边之间存在着一定的关系。
例如，对角线会将四边形分为两个三角形，我们可以利用它们之间的关系来求解未知数。
并且，我们可以通过计算四边形的边长和角度来判断它是否是一个等边四边形或等腰四边形。
3. 四边形的性质四边形有着独特的性质，我们可以通过这些性质来研究和推导其他未知信息。
首先，四边形的内角和为360度。
此外，正方形和长方形的对边平行且相等，而平行四边形的对边相等。
利用这些性质，我们可以解决很多与四边形相关的问题。
4. 三角形和四边形的关联在九年级数学中，我们还会涉及到将三角形和四边形联系起来的知识。
例如，我们可以通过将一个四边形切割成两个三角形来计算其面积。
同时，通过计算四边形和三角形的面积比例，我们可以推导出它们的特殊关系。
5. 应用领域四边形是数学在实际生活中的重要应用之一。
例如，在建筑设计中，我们需要合理地利用四边形的性质和运算来确定建筑结构的稳定性。
类似地，在地图测量和地理学中，我们也需要应用四边形的知识来测量区域的面积和形状。
6. 解决问题的方法在解决与四边形有关的问题时，我们可以采用不同的方法。
常见的方法有几何证明、比例关系和三角函数等。
根据问题的不同，我们可以选择合适的方法来解答。
7. 进一步学习的建议对于九年级的同学来说，掌握四边形的相关知识是非常重要的。
在课堂上，我们应该认真听讲、积极思考，并与同学们一起讨论解题方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
九年级四边形知识点归纳总结在九年级的几何学中，四边形是一个十分重要的概念。
它是由四条直线段组成的平面图形，具有一些独特的性质和特点。
在本文中，我们将对九年级四边形的知识点进行归纳总结，以帮助同学们更好地理解和掌握这一内容。
四边形的定义是由四条线段组成的平面图形，它有四个顶点和四条边。
我们可以从定义中看出，四边形是一个具有几何形状的图形，同时它也是一个闭合的图形，因为它的所有边都相连接，形成一个封闭的形状。
在四边形的分类中，我们首先需要了解梯形和平行四边形这两种形状。
梯形有两条并行边，其它两边不一定平行。
平行四边形则是四边形的一种特殊情况，它具有四条边都是平行的特点。
除此之外，还有矩形、正方形和菱形这几种特殊的四边形形状。
矩形是一种具有四个直角的四边形。
它的特点是对角线相等且相交于中点，同时它的所有边都平行。
矩形经常出现在我们日常生活中的物体上，比如书桌、窗户等等。
正方形是一种特殊的矩形，它的所有边都相等，对角线相等且相交于90度角。
菱形也是一种特殊的四边形。
它的特点是所有边都相等，且对
角线相交于90度角。
菱形可以看作是两个相交的直角三角形组成的，因此它具有一些与直角三角形相似的性质。
菱形也经常出现
在我们的生活中，比如扑克牌、断桥残雪图案等等。
在四边形的性质中，我们还需要了解它的角度和边长之间的关系。
首先是梯形的角度性质。
梯形的两个底角（与底边相对的两
个内角）之和等于180度，而顶角（与顶边相对的内角）之和等
于180度。
这是因为梯形的两个底边是平行的，顶角与底角之和
等于180度。
平行四边形的角度性质较为简单。
它内部的对边对应角相等，
而对角则互补。
这是因为平行四边形具有一对对边是平行的特点，因此对边对应角相等。
同时平行四边形的对角形成的角度之和也
等于180度。
矩形和正方形的角度性质与梯形和平行四边形有些类似。
它们
的两个对角线上的角都是90度，对角线相等且相交于中点。
因为
矩形和正方形都是特殊的平行四边形，所以它们具有平行四边形
的一些性质。
菱形的角度性质与梯形和平行四边形略有不同。
菱形的每个角都是60度，因为菱形可以看作是两个相交的等边三角形组成的。
同时它的对角线相互垂直，对角线相交于中点。
这些性质使得菱形具有一些特殊的特点。
总结起来，九年级四边形的知识点包括四边形的定义及分类，矩形、正方形、菱形和梯形的性质等。
通过理解和掌握这些知识点，同学们可以更好地解决与四边形相关的问题，进一步提高自己的几何学应用能力。
希望本文对大家的学习有所帮助！。