理论力学试题及答案计算题专练
理论力学复习题及答案(计算题部分)
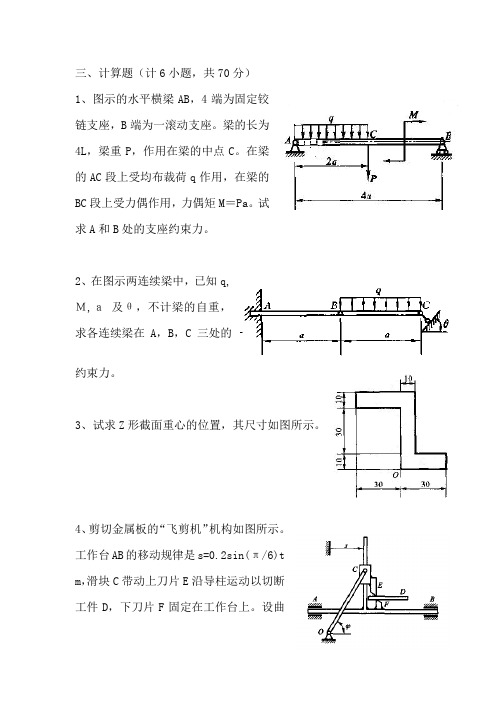
三、计算题(计6小题,共70分)1、图示的水平横梁AB,4端为固定铰链支座,B端为一滚动支座。
梁的长为4L,梁重P,作用在梁的中点C。
在梁的AC段上受均布裁荷q作用,在梁的BC段上受力偶作用,力偶矩M=Pa。
试求A和B处的支座约束力。
2、在图示两连续梁中,已知q,M,a及θ,不计梁的自重,求各连续梁在A,B,C三处的约束力。
3、试求Z形截面重心的位置,其尺寸如图所示。
4、剪切金属板的“飞剪机”机构如图所示。
工作台AB的移动规律是s=0.2sin(π/6)tm,滑块C带动上刀片E沿导柱运动以切断工件D,下刀片F固定在工作台上。
设曲柄OC=0.6m,t=1 s时,φ=60 º。
求该瞬时刀片E相对于工作台运动的速度和加速度,并求曲柄OC转动的角速度及角加速度。
5、如图所示,在筛动机构中,筛子的摆动是由曲柄连杆机构所带动。
已知曲柄OA的转速n OA=40 r/min,OA=0.3 m。
当筛子BC运动到与点O在同一水平线上时,∠BAO=90 º。
求此瞬时筛子BC的速度。
6、在图示曲柄滑杆机构中,曲柄以等角速度ω绕 O 轴转动。
开始时,曲柄OA水平向右。
已知:曲柄的质量为m1,沿块4的质量为m2,滑杆的质量为m3,曲柄的质心在OA的中点,OA=l;滑杆的质心在点C。
求:(1)机构质量中心的运动方程;(2)作用在轴O的最大水平约束力。
7、无重水平粱的支承和载荷如题图所示。
已知力F、力偶矩为M的力偶和强度为q的均布载荷。
求支座A和B处的约束力。
8、在图所示两连续梁中,已知M 及a,不计梁的自重,求各连续梁在A ,B ,C 三处的约束力。
9、工宇钢截面尺寸如图所示。
求此截面的几何中心。
10、如图所示,半径为R 的半圆形凸轮D 以等速v 0沿水平线向右运动,带动从动杆AB 沿铅直方向上升,求φ=30º时杆AB 相对于凸轮的速度和加速度。
11、图示机构中,已知: ,OA=BD=DE=0.1m ,曲柄OA 的角速度ω=4rad/s 。
理论力学考试题及答案详解

理论力学考试题及答案详解一、选择题(每题2分,共10分)1. 牛顿第一定律又称为惯性定律,它指出:A. 物体在受力时,会改变运动状态B. 物体在不受力时,会保持静止或匀速直线运动C. 物体在受力时,会做圆周运动D. 物体在受力时,会保持原运动状态答案:B2. 根据胡克定律,弹簧的弹力与弹簧的形变量成正比,比例系数称为:A. 弹性系数B. 刚度系数C. 硬度系数D. 柔度系数答案:A3. 在理论力学中,一个系统动量守恒的条件是:A. 系统外力为零B. 系统外力和内力都为零C. 系统外力和内力之和为零D. 系统外力和内力之差为零答案:C4. 一个物体做自由落体运动,其加速度为:A. 0B. g(重力加速度)C. -gD. 取决于物体的质量答案:B5. 刚体的转动惯量与以下哪个因素无关?A. 质量B. 质量分布C. 旋转轴的位置D. 物体的形状答案:A二、填空题(每空2分,共10分)6. 一个物体受到三个共点力平衡,如果撤去其中两个力,而保持第三个力不变,物体的加速度将________。
答案:等于撤去的两个力的合力除以物体质量7. 根据动能定理,一个物体的动能等于工作力与物体位移的________。
答案:标量乘积8. 在光滑水平面上,两个冰球相互碰撞后,它们的总动能将________。
答案:守恒9. 一个物体在水平面上做匀速圆周运动,其向心力的方向始终________。
答案:指向圆心10. 刚体的角速度与角动量的关系是________。
答案:成正比三、简答题(共20分)11. 什么是达朗贝尔原理?请简述其在解决动力学问题中的应用。
答案:达朗贝尔原理是分析动力学问题的一种方法,它基于牛顿第二定律,用于处理作用在静止或匀速直线运动的物体上的力系。
在应用达朗贝尔原理时,可以将物体视为受力平衡的状态,即使物体实际上是在加速运动。
通过引入惯性力的概念,可以将动力学问题转化为静力学问题来求解。
12. 描述一下什么是科里奥利力,并解释它在地球上的表现。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学考试题及答案

理论力学考试题及答案**理论力学考试题及答案**一、单项选择题(每题2分,共20分)1. 质点系中,内力的矢量和为零,这是基于()。
A. 牛顿第三定律B. 牛顿第二定律C. 牛顿第一定律D. 动量守恒定律答案:D2. 质心的位置由()决定。
A. 质点的质量B. 质点的位置C. 质点的加速度D. 质点的速度答案:B3. 刚体的转动惯量是关于()的量。
A. 质量B. 距离C. 力D. 速度答案:B4. 角动量守恒的条件是()。
A. 外力矩为零B. 外力为零C. 内力矩为零D. 内力为零答案:A5. 两质点组成的系统,若两质点质量相等,它们之间的万有引力为F,则系统的质心位置位于()。
A. 两质点连线的中点B. 质量较大的质点处C. 质量较小的质点处D. 无法确定答案:A6. 刚体绕固定轴的转动惯量I与()有关。
A. 质量分布B. 轴的位置C. 轴的方向D. 以上都是答案:D7. 刚体的平行轴定理表明,刚体绕任意轴的转动惯量等于绕通过质心的平行轴的转动惯量加上()。
A. 刚体的质量B. 刚体的转动惯量C. 刚体质量与两轴间距离的平方的乘积D. 刚体质量与两轴间距离的乘积答案:C8. 刚体的平面运动可以分解为()。
A. 任意两个不同的平面运动的叠加B. 平移和旋转的叠加C. 两个垂直平面内的旋转D. 任意两个不同的旋转的叠加答案:B9. 刚体的瞬时转轴是()。
A. 刚体上所有点速度相同的直线B. 刚体上所有点加速度相同的直线C. 刚体上所有点角速度相同的直线D. 刚体上所有点线速度为零的直线答案:D10. 刚体的定轴转动中,角速度的大小和方向()。
A. 与参考系的选择有关B. 与参考系的选择无关C. 与参考系的选择有关,但大小无关D. 与参考系的选择无关,但方向有关答案:B二、填空题(每题2分,共20分)1. 牛顿第二定律的数学表达式为:\( F = ma \),其中F表示力,m表示质量,a表示________。
理论力学试题和答案
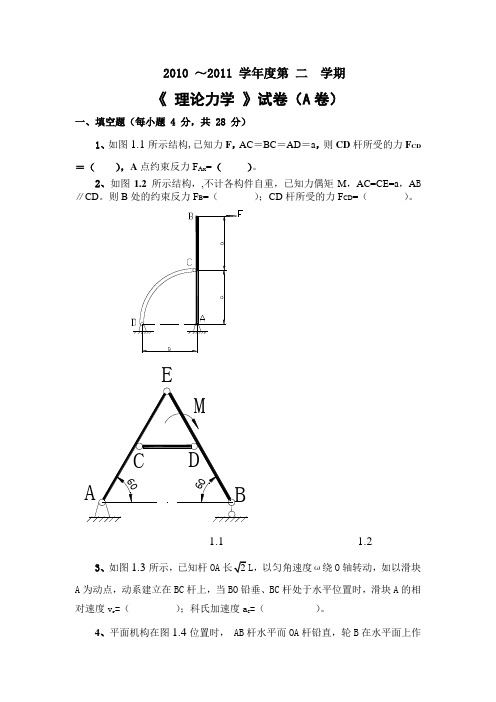
2010 ~2011 学年度第 二 学期《 理论力学 》试卷(A 卷)一、填空题(每小题 4 分,共 28 分)1、如图1.1所示结构,已知力F ,AC =BC =AD =a ,则CD 杆所受的力F CD =( ),A 点约束反力F Ax =( )。
2、如图1.2 所示结构,,不计各构件自重,已知力偶矩M ,AC=CE=a ,A B ∥CD 。
则B 处的约束反力F B =( );CD 杆所受的力F CD =( )。
E 1.1 1.23、如图1.3所示,已知杆OA L ,以匀角速度ω绕O 轴转动,如以滑块A 为动点,动系建立在BC 杆上,当BO 铅垂、BC 杆处于水平位置时,滑块A 的相对速度v r =( );科氏加速度a C =( )。
4、平面机构在图1.4位置时, AB 杆水平而OA 杆铅直,轮B 在水平面上作纯滚动,已知速度v B ,OA 杆、AB 杆、轮B 的质量均为m 。
则杆AB 的动能T AB =( ),轮B 的动能T B =( )。
1.3 1.45、如图1.5所示均质杆AB 长为L ,质量为m,其A 端用铰链支承,B 端用细绳悬挂。
当B 端细绳突然剪断瞬时, 杆AB 的角加速度 =( ),当杆AB 转到与水平线成300角时,AB 杆的角速度的平方ω2=( )。
6、图1.6所示机构中,当曲柄OA 铅直向上时,BC 杆也铅直向上,且点B 和点O 在同一水平线上;已知OA=0.3m,BC=1m ,AB=1.2m,当曲柄OA具有角速度ω=10rad/s 时,则AB 杆的角速度ωAB =( )rad/s,BC 杆的角速度ωBC =( )rad/s 。
AB1.57、图1.7所示结构由平板1、平板2及CD 杆、EF 杆在C 、D 、E 、F 处铰接而成,在力偶M 的作用下,在图上画出固定铰支座A 、B 的约束反力F A 、F B 的作用线方位和箭头指向为( )(要求保留作图过程)。
1.7二、单项选择题(每小题 4 分,共28 分)1、如图2.1所示,四本相同的书,每本重均为P ,设书与书间的摩擦因数为0.1,书与手间的摩擦因数为0.25,欲将四本书一起抱起,则两侧手应加的压力至少大于( )。
(完整版)理论力学计算题及答案

1. 图示圆盘受一平面力系作用,已知圆盘半径R =0.1m ,F 1=100N ,F 2=200N ,M 0=400Nm 。
求该平面任意力系的合力及其作用线与AC 或其延长线的交点位置。
平面任意力系简化191.42,54.82,199.12391.347.16R xyF N F N F NM NmOE m==-==-=∑∑∑2. 求图示桁架中各杆的内力。
桁架内力计算,截面法与节点法:13F F =3. 已知图示结构中2m a =,在外力5kN F =和力偶矩=10kN m M ⋅作用下,求A 、B 和D处的约束反力。
力系的平衡条件的应用,隔离体与整体分析:()()()1010D Ax Ay Bx By A F F F F F kN M kNm↑=→=↓====4. 已知图示结构中1m =60,a οθ=,在外力10kN F =和力偶矩0=20kN m M ⋅作用下,求A 、C 处的约束反力。
同上()20,0,20,17.32Ax Ay A c F kN F M kNm F kN =→===5. 图示构件截面均一,图中小方形边长为b ,圆形半径均为R ,若右图中大方形和半圆形材料密度分别为12,ρρ,试计算确定两种情况下平面图形的质心位置。
以圆心为原点:()()3222c b x =-R b π→-左以方形下缘中点为原点:()()()12212123238c 2x =ρπρρρπρ++↑+右6. 斜坡上放置一矩形匀质物体,质量m=10kg ,其角点A 上作用一水平力F ,已知斜坡角度θ=30°,物体的宽高比b/h=0.3,物体与斜坡间的静摩擦系数s f =0.4。
试确定不致破坏平衡时F 的取值范围。
计算滑动和翻倒两种情况得到(1)滑动平衡范围14.12124.54N F N -≤≤,(2)翻倒平衡范围:8.6962.27N F N ≤≤7. 如图机构,折杆OBC 绕着O 轴作顺时针的匀速定轴转动,角速度为ω,试求此时扣环M 的速度和加速度。
理论力学考试试卷(附答案)
理论力学考试试卷(附答案)一、 名词解释(每个4分,共20分)1、刚化原理2、加减平衡力系公理3、相对运动、牵连运动4、质点系动量守恒定理5、质点系动能定理二、 单项选择题(每个4分,共20分)1、已知F1、F2、F3、F4为作用于刚体上A 、B 、C 、D 四点的平面一般力系,其力矢关系如下图所示为平行四边形,由此可知 ( )。
2(A )力系可以合成为一个力偶 (B )力系可以合成为一个力(C )力系可以合成为一个力和一个力偶 (D )力系的合力为零,力系平衡2、物块重P ,与水面的摩擦角o20m ϕ=,其上作用一力Q ,且已知P=Q ,方向如图,则物块的状态为( )。
(A )静止(非临界平衡状态) (B )临界平衡状态(C )滑动状态 (D )不能确定 3、图(a )、(b)为两种结构,那么( )。
(A )图(a )为静不定,图(b )为静定 (B )图(a )、(b )均为静不定 (C )图(a )、(b )均为静定 (D )图(a )为静定,图(b )为静不定4、点作匀变速曲线运动是指( )。
(A )点的加速度大小a =常量 (B )点的加速度a =常矢量(C )点的切向加速度大小τa =常量 (D )点的法向加速度大小na =常量5、边长为a 2的正方形匀质薄板,截去四分之一后悬挂在A 点,今若使BC 边保持水平,则点A 距右端的距离x= ( )。
(A) a (B) 3a /2 (C) 6a /7 (D)5a /6三、计算题(15分)结构的尺寸及荷载如下图所示,已知q=1.5kN/m ,试求支座A 的反力。
(a)(b)a aaaxBAC四、计算题(15分)已知P=5kN ,试求图示桁架中1、2、3杆的内力。
五、计算题(15分)在图示机构中,已知m r B O A O 4.021===,AB O O =21,A O 1杆的角速度4rad s ω=,角加速度22rad s α=,求三角板C 点的加速度,并画出其方向。
理论力学习题及答案
一.选择填空和填空题(每题5分,共30分)1.某任意力系向O 点简化,得到cm 10N N,10'R ⋅==O M F ,方向如图所示;若将该力系向A 点简化,则得到: A 。
A. 0N,10R ==A M F ;B. cm 10N N,10'R ⋅==A M F ;C. cm 0N 2N,10'R ⋅==A M F 。
2.已知杆AB =40cm ,以rad/s 31=ω绕A 轴转动,而杆CD 又绕B 轴以rad/s 12=ω转动,BC =BD =30cm ,图示瞬时AB ⊥CD ,若取AB 为动坐标,则此时C 点的牵连速度大小为 C 。
A. 30cm/s ;B. 120cm/s ;C. 150cm/s ;D. 160cm/s 。
第1题图 第2题图 3.一直角曲杆(重量不计)上各受力偶M 的作用,如图所示,A 1和A 2处的约束反力分别为F A 1和F A 2,则它们的大小应满足条件 C 。
A. 21A A F F >;B. 21A A F F =;C. 21A A F F <。
第3题图 4.若作用于质点系的外力在某段时间内在固定坐标Ox 轴上投影的代数和等于零,则在这段时间内B 。
A. 质点系质心的速度必保持不变;B. 质点系动量在x 轴上的投影保持不变;C. 质点系质心必保持不动。
5.物块重量为10N ,放在粗糙水平面上,已知物块与水平面间的静滑动摩擦系数为21.0=f ,动滑动摩擦系数为2.0=′f ,当物块受一与铅垂线成°=30θ夹角的力N 20=F 作用时(如图),作用在该物块上的摩擦力大小为 5.464N 。
6.匀质细圆环的半径为r ,质量为m 1=m ,与一根质量同为m 2=m ,长为2r 的匀质细直杆OA 刚性连接,可在水平面内以匀角速度ω绕O 轴定轴转动,如图所示。
则系统对O 轴的动量矩为 ω2334mr ;系统的动能为 22317ωmr 。
理论力学试题及答案
理论力学试题及答案一、选择题(每题2分,共20分)1. 牛顿第一定律描述的是:A. 物体在受力时的运动状态B. 物体在不受力时的运动状态C. 物体在受力时的加速度D. 物体在受力时的位移答案:B2. 根据牛顿第二定律,物体的加速度与作用力和物体质量的关系是:A. 加速度与作用力成正比,与质量成反比B. 加速度与作用力成反比,与质量成正比C. 加速度与作用力成正比,与质量成正比D. 加速度与作用力成反比,与质量成反比答案:A3. 以下哪个不是刚体的运动特性?A. 刚体的质心保持静止或匀速直线运动B. 刚体的各部分相对位置不变C. 刚体的各部分速度相同D. 刚体的各部分加速度相同答案:C4. 角动量守恒定律适用于:A. 只有重力作用的系统B. 只有内力作用的系统C. 外力矩为零的系统D. 外力为零的系统答案:C5. 以下哪个是能量守恒定律的表述?A. 一个封闭系统的总动能是恒定的B. 一个封闭系统的总势能是恒定的C. 一个封闭系统的总能量是恒定的D. 一个封闭系统的总动量是恒定的答案:C二、简答题(每题10分,共20分)6. 简述牛顿第三定律的内容及其在实际中的应用。
答案:牛顿第三定律,又称作用与反作用定律,表述为:对于两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
在实际应用中,例如在推门时,门对人的作用力和人对门的作用力大小相等,方向相反。
7. 描述什么是简谐振动,并给出一个生活中的例子。
答案:简谐振动是一种周期性振动,其回复力与位移成正比,且总是指向平衡位置。
生活中的例子包括弹簧振子,当弹簧被拉伸或压缩后释放,它会在原始平衡位置附近做周期性的往复运动。
三、计算题(每题15分,共30分)8. 一个质量为m的物体,从静止开始,沿着一个斜面下滑,斜面的倾角为θ。
如果斜面的摩擦系数为μ,求物体下滑的加速度。
答案:首先,物体受到重力mg的作用,分解为沿斜面方向的分力mg sinθ和垂直斜面方向的分力mg cosθ。
理论力学测试题及答案
理论力学测试题及答案一、单项选择题(每题2分,共10分)1. 牛顿第一定律描述的是:A. 物体在没有外力作用下的运动状态B. 物体在受到平衡力作用下的运动状态C. 物体在受到非平衡力作用下的运动状态D. 物体在任何力作用下的运动状态答案:A2. 以下哪个不是惯性参考系的特点?A. 牛顿第一定律在其中成立B. 牛顿第二定律在其中成立C. 牛顿第三定律在其中成立D. 物体在其中不受任何力的作用答案:D3. 动量守恒定律适用于:A. 只有重力作用的系统B. 只有弹力作用的系统C. 只有摩擦力作用的系统D. 只有保守力作用的系统答案:D4. 以下哪个是矢量?A. 质量B. 速度C. 时间D. 温度答案:B5. 以下哪个是标量?A. 力B. 位移C. 功D. 速度答案:C二、填空题(每空1分,共10分)1. 牛顿第二定律的数学表达式为:\[ F = ma \],其中\( F \)代表______,\( m \)代表______,\( a \)代表______。
答案:力;质量;加速度2. 根据牛顿第三定律,作用力和反作用力大小相等,方向______,作用在______。
答案:相反;不同物体上3. 动量的定义是质量与______的乘积。
答案:速度4. 功的定义是力与力的方向上的______的乘积。
答案:位移5. 动能的定义是\( \frac{1}{2}mv^2 \),其中\( m \)代表______,\( v \)代表______。
答案:质量;速度三、简答题(每题10分,共20分)1. 简述牛顿第二定律的物理意义。
答案:牛顿第二定律表明,物体的加速度与作用在物体上的合外力成正比,与物体的质量成反比,即力是改变物体运动状态的原因。
2. 描述动量守恒定律在碰撞过程中的应用。
答案:在没有外力作用的系统中,两个或多个物体发生碰撞时,碰撞前后系统的总动量保持不变。
这意味着碰撞前后各物体动量的矢量和相等。
四、计算题(每题15分,共30分)1. 一辆质量为1500kg的汽车以20m/s的速度行驶,突然刹车,经过5秒后停止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(每题3分,共15分)。
请将答案的序号填入划线内)
1. 三力平衡定理是( )
A 共面不平行的三个力互相平衡必汇交于一点;
B 共面三力若平衡,必汇交于一点;
C 三力汇交于一点,则这三个力必互相平衡。
2. 空间任意力系向某一定点O 简化,若主矢0≠'R ,主矩00≠M ,
则此力系简化的最后结果--------------------。
A 可能是一个力偶,也可能是一个力;
B 一定是一个力;
C 可能是一个力,也可能是力螺旋;
D 一定是力螺旋。
3. 如图所示,=P 60kM ,T F =20kN ,A , B 间
的静摩擦因数s f =0.5,动摩擦因数f =0.4,则物块A 所受的摩擦力F 的大小为-----------------------。
① 25 kN ;② 20 kN ;③ 310kN ;④ 0
4. 点作匀变速曲线运动是指------------------。
① 点的加速度大小a =常量; ② 点的加速度a =常矢量;
③ 点的切向加速度大小τa =常量; ④ 点的法向加速度大小n a =常量。
二、填空题(共24分。
请将简要答案填入划线内。
)
1. 双直角曲杆可绕O 轴转动,图
示瞬时A 点的加速度2s /cm 30=A a ,方向如图。
则B 点加速度的大小为
------------2s /cm ,方向与直线------------成----------角。
(6分)
T
F P
A
B
30m
3m 3m
4
3A B A
a O
2. 平面机构如图所示。
已知AB 平行于21O O ,且AB =21O O =L ,r BO AO ==21,ABCD 是矩形板,AD=BC=b ,1AO 杆以匀角速度ω绕1O 轴转动,则矩形板重心1C 点的速度和加速度的大小分别为v = -----------------, a = --------------。
(4分)
(应在图上标出它们的方向)
3. 在图示平面机构中,杆AB =40cm ,以1ω=3rad/s 的匀角速度绕A 轴转动,而CD 以2ω=1rand/s 绕B 轴转动,BD =BC =30cm ,图示瞬时AB 垂直于CD 。
若取AB 为动坐标系,则此时D 点的牵连速度的大小为 -------------,牵连加速度的大小为 -------------------。
(4分)
(应在图上标出它们的方向)
4. 质量为m 半径为r 的均质圆盘,
可绕O 轴转动,其偏心距OC =e 。
图示瞬时其角速度为ω,角加速度为ε。
则该圆盘的动量
p
=--------------,动量矩=o L ------------------------------------,动能T =
-----------------------,惯性力系向O 点的简化结果为----------------------------------------------------------。
(10分)
(若为矢量,则应在图上标出它们的方向)
三、计算题(15分)。
刚架由AC 和BC 两部分组成,所受荷载如图所示。
已知F =40 kN, M = 20kN ·m, q =10kN/m, a =4m, 试求A , B 和C 处约束力。
O
B
A ωD C 1O 2
O 1
C A B
C D
1
ω2
ωe C
ε
F
四、计算题 图示系统中,曲柄OA 以匀角速度ω绕O 轴转动,通过滑块A 带动半圆形滑道BC 作铅垂平动。
已知:OA = r = 10 cm ,ω = 1 rad/s ,R = 20 cm 。
试求ϕ = 60°时杆BC 的加速度。
M A B
C
a
2
/a 2
/a q
a
五、计算题(14分)。
两重物1M 和2M 的质量分别为1m 和2m ,系在两条质量不计的绳索上,两条绳索分别缠绕在半径为1r 和2r 的塔轮上,如图所示。
塔轮对轴O 的转动惯量为23ρm (3m 为塔轮的质量),系统在重力下运动,试求塔轮的角加速度和轴承O 对塔轮的竖直约束力。
六、计算题(16分)。
均质圆盘和均质薄圆环的质量均为m,外径相同,用细杆AB绞接于二者的中心,如图所示。
设系统沿倾角为θ的斜面作无滑动地滚动,不计细杆的质量,试求杆AB的加速度、杆的内力及斜面对圆盘和圆环的约束力。
答案
一、选择题
1.①
2. ③
3. ③
4. ③
5. ④
二、填空题
1. 2s /cm 50 OB 成 30角。
2. r ω r 2ω。
3. s /cm 150 2s /cm 450。
4. e m ω ω)2(2122e r m + 222)2(41ωe r m + 24αω+me α)2(2
1
22e r m +。
三、计算题
)
(↑=-⨯+⨯=
kN 35)2
2(1M a
qa a F a F B ; )(kN 40←==qa F Cx ,)
(↑=-=-=kN 53540B Cy F F F ; )(kN 80←=Ax F ,)(kN
5↑=Ay F ,m kN 240⋅=A M (逆时针)。
四、计算题
杆瞬时平动,所以)(0↓==r v v A B ω,0=AB ω。
以A 为基点,由基点法有BA A B a a a +=,其中)(20→=r a A ω,a a AB BA α=。
① )(45tan 20↓===r a a a A A B ω ;
② ,2220
r a a A BA ω==a
r
AB 202ωα=
(逆时针); 由瞬心法或基点法有
βθωβωωt a n
s i n c o s 001
a r
b r BC v
B BO ===,βωβωωtan sin 011
1
1
r b C O v BO BO O =⋅=⋅=; ③ βωωtan 01
1
R
r
R v O O ==(逆时针)
; ④ βθ
ωβ
ωωtan sin cos 001
a r
b r
BO =
=
(顺时针)。
五、计算题
由质点系动量矩定理有
221122221123)(gr m gr m r m r m m -=++αρ 故塔轮的角加速度为
2
22211232
211r m r m m gr m gr m ++-=
ρα。
由达朗培尔原理(或质点系动量定理)有
)()(1122321r m r m g m m m F Oy -+++=(此即轴承O 对塔轮的竖直约束力)。
六、计算题
设A 点沿斜面下滑s 时,其速度为v 。
采用动能定理:∑-=-)(2112e W T T ,其中:
2222
22474321
21mv mv mv r v mr T =++⎪⎭⎫ ⎝⎛=,01=T ,s mg W e ⋅=-θsin 2)(21,
即:s mg mv ⋅=θsin 24
7
2。
对上式求一次导数,并注意到t
s
v d d =,t v a d d =,有
θsin 7
4
g a =(此即杆AB 的加速度)。
取圆环进行受力分析,由刚体平面运动微分方程(或达朗培尔原理),有
r F r
a
mr RC ⋅=⋅
2,0cos =-θmg F C ,ma F F mg RC AB =-+θsin 由此求出斜面对圆环的切向约束力(摩擦力)和法向约束力分别为
θsin 7
4
mg ma F RC ==,θcos mg F C =,杆AB 的内力为 θsin 7
1
mg F AB =。
取圆轮,同理有
r F r
a
mr RD ⋅=⋅221,得圆轮的切向约束力(摩擦力) θsin 7
2
21mg ma F RD ==
及圆轮的法向约束力 θcos mg F D =。
