第五章 激光振荡特性1
ch5-激光振荡特性解读

F s
h p V
F 21 l s
-泵浦光子能量 V-工作物质总体积
2019/2/25
6
2、三能级系统 n1 n2 n3 n1 n2 n (1)特点 n 0 2 f2 忽略能级简并(如红宝石): n n2 f n1 n2 n1
2、振荡条件: n nth 21 ,0 l
2019/2/25 3
特例: 0 4、讨论
21 ,0 21
n nth
0
21 l
不同模式(频率)具有不同的阈值反转粒子数密度。 中心频率处阈值反转粒子数最低。 损耗越大,发射截面越小,腔长越短,阈值反 转粒子数密度越大。
2019/2/25 1
有: dn dt 0; dNl dt 0
速率方程 代数方程 (2) 脉冲激光器 ( t0 <<τ2 )——非稳定工作状态 (非稳态) 泵浦持续时间短, 各能级粒子数及腔内光子数密 度处于剧烈的变化之中。未达到平衡,泵浦作用 终止。
属于非稳态; 需要数值求解或用小信号微扰或其 他近似方法处理速率方程。
理由:对三能级系统,要将(n+ Δnt )/2粒子激励到 E2 ,而n/2>> Δnt ,可忽略Δnt 。而对四能级系统, 只需将Δnt个粒子激发到E2,而Δnt ∝δ 。但当δ很 大,使得Δnt也很大,达到可以与n/2相比拟时,才 要考虑损耗对三能级系统阈值的影响。 3、 Ppt, Ept 与工作物质特性有关 F , 21, s , F
F , 21 , s Ppt , E pt
2 v 2 A21 ln 2 v 均匀加宽 21 2 2 非均匀加宽 21 3 2 2 A21 4 0 H 4 0 D
激光原理知识点汇总201905

激光原理知识点汇总第一章电磁场和物质的共振相互作用1.相干光的光子描述,光的受激辐射基本概念1)1960年7月Maiman报道第一台红宝石固体激光器,波长694.3nm。
2)光的基本性质:能量ε=hνh: Planck常数,ν :光波频率运动质量m=ε/c2=hv/c2静止质量0动量knhnchnmcp=•===22λππν3)光子的相干性:在不同的空间点、不同时刻的光波场某些特性的相关性相干体积相干面积,相干长度,相干时间光源单色性越好,相干时间越长:相格空间体积以及一个光波摸或光子态占有的空间体积度等于相干体积属于同一状态的光子或同一模式的光波是相干的4)黑体辐射的planck公式在温度T的热平衡下,黑体辐射分配到腔内每个模式上的平均能量1-=kThehEνν腔内单位体积、单位频率间隔内的光波摸式数338chnνπν=Planck公式:11833-==kThechνννπρ单色能量密度,k:Boltzmann常数Bohr定则:νhEE=-125)光的受激放大a.普通光源在红外和可见光波段是非相干光,黑体是相干光黑体辐射的简并度KTnmnmKTnmKTncmKTkThhEn50000,1,110,6.0,3001,60,30010,30,3001)exp(1353=≈=≈==≈==≈==→-==-μλμλμλλννb.让特定、少数模式震荡,获得高的光子简并度21212121338AWABchn===ννρνπρ6)光的自激振荡a.自激振荡概念分数单位距离光强衰减的百自损耗系数)(1)(zIdzzdI-=αdzzIIgzdI)(])([)(..α-=考虑增益和损耗])ex p[()(0zgIzIα-=αααsmsmIgIIIgIg)(1)(0-=→=+=光腔作用: (1)模式选择; (2)提供轴向光波摸的反馈;b.震荡条件等于号是阈值振荡ααα≥→≥-=000)(gIgI sm是工作物质长度llgL...........0δδα≥→=lg0单程小信号增益因子7)激光的特性:单色性、相干性、方向性、高亮性。
第五章 激光振荡特性

P=
η 0 =T / 2δ表征腔内激光功率转化为输出激光功率的转换效率,S 为工作物质截面积 表征腔内激光功率转化为输出激光功率的转换效率, Pp 、Ppt 分别为工作物质吸收的泵浦功率和阈值吸收泵浦功率, 分别为工作物质吸收的泵浦功率和阈值吸收泵浦功率,
输出功率和光泵电功率的关系
P ν0A η0η1η pt P − 1 ν pS PPt
(ν) g 0 (ν) g 01 (ν) t (ν)
g 00 (ν) t (ν)
g 0 ≥ gt =
δ
l
不同的纵模具有相同的损耗δ 不同的纵模具有相同的损耗δ ,因而有相同的阈值 不同的横模具有不同的衍射损耗, 不同的横模具有不同的衍射损耗,因而有不同的阈值
ν
ν
00 q - 1
ν
00 q
ν
00 q + 1
2 2 ν −ν − (4ln 2) 1 0 g ml ∆ν D 单模输出功率为 P = AI +T = AI sT − 1 e δ
2.非均匀加宽单模激光器 2.非均匀加宽单模激光器
当单模激光频率等于增益曲线中心频率时, 当单模激光频率等于增益曲线中心频率时,正反两束激光在增益曲线中心烧出 一个孔,烧孔深度取决于腔内平均光强: 一个孔,烧孔深度取决于腔内平均光强:
n2 (t ) =
η1W13 n
η2
A21
+ η1W13
5.1 激光器的振荡阈值
一、阈值反转粒子数密度
假设谐振腔的长度L为模体积为V 假设谐振腔的长度L为模体积为VR ,工作物质的长度为 l 模体积为Va , 模体积为V 第l个模的光子数随时间变化速率
激光原理与技术完整ppt课件

够存在于腔内的驻波(以某一波矢k为标志)称为电磁被的模式或光波模。一种模式是电
磁波运动的一种类型,不同模式以不同的k区分。同时,考虑到电磁波的两种独立的偏振,
同一波矢k对应着两个具有不同偏振方向的模。
精选ppt
9
下面求解空腔v内的模式数目。设空腔为V=ΔxΔyΔz的立方体,则沿三个
坐标轴方向传播的波分别应满足的驻波条件为
第八章 激光器特性的控制和改善
8.1 模式选择 8.2 频率稳定 8.3 Q调制 8.4 注入锁定 8.5 锁模
精选ppt
5
第九章 激光器件
9.1 固体激光器 9.2 气体激光器 9.3 半导体激光器 9.4 染料激光器
精选ppt
6
第一章 激光的基本原理
本章概激光器基本原理。讨论的重点是光的相干性和光波模式的联系、光的受激辐
(1.1.4)
式中E0为光波电场的振幅矢量,ν为单色平面波的频率,r为空间位置坐标矢量,k为波
矢。而麦克斯韦方程的通解可表为一系列单色平面波的线性叠加。
在自由空间,具有任意波矢k的单色平面波都可以存在。但在一个有边界条件限制的
空间V(例如谐振腔)内,只能存在一系列独立的具有特定波矢k的平面单色驻波。这种能
第六章 激光器的放大特性
6.1 激光放大器的分类 6.2 均匀激励连续激光放大器的增益特性 6.3 纵向光均匀激励连续激光放大器
的增益特性 6.4 脉冲激光放大器的增益特性 6.5 放大的自发辐射(ASE) 6.6 光放大的噪声
精选ppt
4
第七章 激光振荡的半经典理论
7.1 激光振荡的自洽方程组 7.2 原子系统的电偶级距 7.3 密度距阵
二、光波模式和光子状态相格 从上面的叙述已经可以看出,按照量子电动力学概念,光波的模式和光子的状态是等
激光振荡特性 - 成都信息工程学院光电技术学院

第五章激光振荡特性一、激光振荡特性振荡条件、激光形成、模竞争、输出功率或能量、弛豫振荡、激光线宽、频率牵引等。
讨论方法:速率方程和工作物质增益饱和。
二、激光器的分类1、分类标准:工作方式-按泵浦方式分类2、分类(1) 连续或长脉冲激光器( t0>>τ2 )——稳定工作状态(稳态)在泵浦时间内,各能级粒子数及腔内光子数密度可以达到稳定状态。
dtdndN=dt;0=有:l速率方程代数方程(2) 脉冲激光器( t0 <<τ2 )——非稳定工作状态(非稳态)泵浦持续时间短, 各能级粒子数及腔内光子数密度处于剧烈的变化之中。
未达到平衡,泵浦作用终止。
属于非稳态; 需要数值求解或用小信号微扰或其他近似方法处理速率方程。
分类根据事例:上一章第8题的分析讨论。
第一节激光器的振荡阈值一、阈值种类①阈值反转集居数密度②阈值增益系数③连续或长脉冲激光器的阈值泵浦功率④短脉冲激光器的阈值泵浦能量二、阈值反转集居数密度从速率方程出发,自激振荡条件:0≥dt dN l1、阈值反转集居数密度)ln th 021,υυσδ=∆l :工作物质的长度2、振荡条件:)ln n th 0210,υυσδ=∆≥∆特例:υυ=)21021,συυσ=ln n th 210σδ=∆≥∆不同模式(频率)具有不同的阈值反转粒子数密度。
中心频率处阈值反转粒子数最低。
4、讨论损耗越大,发射截面越小,腔长越短,阈值反转粒子数密度越大。
三、阈值增益系数1、阈值增益系数:)()0210,υυσδυt t n l g g ∆==≥2、推证:)()0210,υυσυn g ∆=)ll δυυσδ=≥021,3、讨论的不同纵模具有相同的损耗,因而具有相同的。
不向的横模具有不同的损耗,因而有不同的,高次横模的比基模的大。
δt g δt g t g 四、连续或长脉冲激光器的阈值泵浦功率1、四能级系统(1) 特点:S 10大,则1≈n 21122n n f f n n ≈-=∆ln n t t 212σδ=∆=( 的情况)υυ=(2) 阈值泵浦功率sF p sF t p st p Pt l Vh Vn h Vn h P τσηδυτηυτηηυ2121=∆=∆=(3) 推证(自己理解)h υ-泵浦光子能量V -工作物质总体积2、三能级系统(1)特点2≈n n n n n n ≈+=++21321忽略能级简并(如红宝石):121122n n n ff n n -=-=∆()n n n ∆+=212()2212n n n n t t ≈∆+=nn t <<∆ (2) 阈值泵浦功率sF p Pt nV h P τηυ2=(3) 推证(自己理解)五、短脉冲激光器( t 0<<τ2)的阈值泵浦能量1、特点:泵浦时间短,在t 0时间内,可以忽略自发辐射(A 21)及无辐射跃迁(S 21),只考虑泵浦激励作用。
激光原理 周炳琨版课后习题答案

6.某一分子的能级 到三个较低能级 、 和 的自发跃迁几率分别是 , 和 ,试求该分子 能级的自发辐射寿命 。若 , , ,在对 连续激发并达到稳态时,试求相应能级上的粒子数比值 、 和 ,并回答这时在哪两个能级间实现了集居数反转。
解:该分子 能级的自发辐射寿命 为:
在连续激发时,对能级 、 和 分别有:
即该物质的增益系数约为 。
第二章
习题
1.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:
其往返矩阵为:
由于是共焦腔,有
往返矩阵变为
若光线在腔内往返两次,有
可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
当 时, 小
当 时, 小
3. 在 波长时 ,试求在内径为 的 波导管中 模和 模的损耗 和 ,分别以 , 以及 来表示损耗的大小。当通过 长的这种波导时, 模的振幅和强度各衰减了多少(以百分数表示)?
解:由
,
, 。
当 时, ,
4.试计算用于 波长的矩形波导的 值,以 及 表示,波导由 制成, , ,计算由 制成的同样的波导的 值,计算中取 。
得
10m
1m
10cm
0
2.00cm
2.08cm
2.01cm
2.00cm
2.40
22.5
55.3
56.2
从上面的结果可以看出,由于f远大于F,所以此时透镜一定具有一定的聚焦作用,并且不论入射光束的束腰在何处,出射光束的束腰都在透镜的焦平面上。
17. 激光器输出光 , =3mm,用一F=2cm的凸透镜距角,求欲得到 及 时透镜应放在什么位置。
精品课件- 激光振荡特性
当E2能级上集居数密度n2稳定于问时,单位时间内在单位体积中有n2t/η2τs个粒子自E2能级 跃迁到El能级。为使n2稳定于n2t,单位时间内在单位体积中必须有噩n2t/η2τs个粒子自E3能 级跃迁到E2能级,因此在单位时间内单位体积中必须有n2t/ηFτs个粒子自E0能级跃迁E3附级。 为此须吸收的泵浦功率称作激光器的阈值泵浦功率,以Ppt表示。
(5.0.1) t>t0时,W12(t)=0,可得
若t0<τ2时,则在整个激励持续期间,n2(t)处在不断增长的非稳定状态。
若t0<τ2时,则在整个激励持续期间,n2(t)处在不断增长的非稳定状态。由以上分析可 知,脉冲激光器中,由于脉冲泵浦持续时间短,在尚未达到新的平衡之前,过程就结束了,所以 在整个工作过程中,各能级的粒子数及腔内光子数均处于剧烈变化中,系统处于非稳态。而 连续激光器中各能级粒子数及腔内辐射则处于稳定状态。非稳态是系统打破原有热平衡状 态到达新的稳态过程的一个阶段。若脉冲泵浦持续时间t0>>τ2(长脉冲),脉冲激光器也达 到稳定状态,因此长脉冲激光器也可看成一个连续激光器。脉冲激光器和连续激光器的特 性既有差别,又有联系。
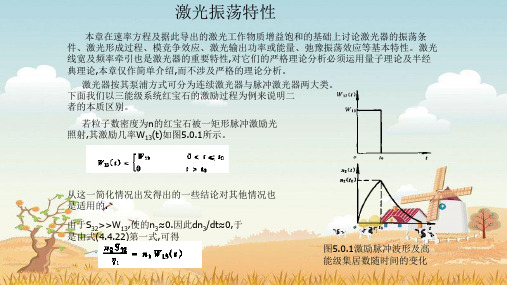
若粒子数密度为n的红宝石被一矩形脉冲激励光 照射,其激励几率W13(t)如图5.0.1所示。
从这一简化情况出发得出的一些结论对其他情况也 是适用的.
由于S32>>W13,使的n3≈0.因此dn3/dt≈0,于 是由式(4.4.22)第一式,可得
图5.0.1激励脉冲波形及高 能级集居数随时间的变化
式中η1=S32/(S32+A31)表示E3能级向E2能级元辐射跃迁的量子效率。将上式代入式(4.4.22) 第二式,并考虑到在未形成自激振荡或在阑值附近时受激辐射很微弱的情形,此式中第一项 可以忽略不计,从而得出 式中η2=A21/(A21+S21)为E2能级向基态跃迁的荧光效率。由上式可解出当0<t≤t0时 的n2(t):
周炳坤激光原理与技术课件第五章-激光的振荡特性精选全文完整版

≈ hν0 σ21(ν1,ν0)τs
(4.5.8)
Ppt
=
hνpΔnt ⋅V ηF ⋅τS
=
hνpδ ⋅V ηFσ21(ν,ν0)τSl
(5.1.6)
将上三式代入(5.3.3)式可得输出功率
P
= ν0 νP
⋅
Aη
S
0η1Ppt
(
Pp Ppt
−1)
(5.3.5)
P
=
1 2
AT
hν0 σ21(ν ,ν0)τ2
η1
hν
=
η1σ 21
pδV (ν ,ν 0
)l
三能级系统光泵能量阈值为
(5.1.8)
E pt
=
hν pnV 2η1
(5.1.9)
关于t0与τ 2 可以比拟时,阈值泵浦功率的情况,待典型激光器讲
述后再回过头来看
§5.2 激光器的振荡模式
§5.2.1 均匀加宽连续激光器中的模式竞争
一、增益曲线均匀饱和引起的自选模式作用
( Pp Ppt
−1)
=
1 2
ATLeabharlann ηFν0L δν pV⋅
Ppt
(
Pp Ppt
−1)
η0
=T
2δ
,工作物质横截面S
=
V L
,ηF
→η1
= ν0 νP
⋅
SAη0η1Ppt
(
Pp Ppt
−1)
结论:1.由(5.3.3)和(5.3.5)式,输出功率正比于饱和
光增强加,Is输(ν出q )功且率随随激光发泵参泵数浦G功ο 率H (ν线q性)l
为
P
=
1 2
ATIS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
gt nt 21 ( , 0 ) 21 ( , 0 ) l
阈值反转集居数密度
特例:频率为 0 的模式
21 21 ( 0 , 0 )
激光器的阈值反转集居数密度:
nt 21l
讨论:影响阈值反转粒子数密度的 因素有哪些 ?
不同模式(频率)具有不同的阈值反转集居数密度。
01q 1 01q 01q 1 01q 2
均匀加宽激光器中的模竞争
小结(横模竞争情况): a.横模间也有竞争; b.横模竞争情况较复杂;
c.可通过选模措施获得单横模输出。
均匀加宽激光器中的模竞争
2.空间烧孔引起多模振荡 增益的空间烧孔效应:波腹处光
I q
n
L
z
强大,用去的反转粒子数多,增 益系数下降的也大; 波节处光强小,用去的反转粒子 数少,增益系数下降的也少
(
A21
2
1W13 ) t
]
n2 ( t ) 按上式规律随t增长 。
激光器的运转方式
二、长脉冲和连续运转
2. s t t0
n2 ( t )
1W13 n
A21
[1 e
(
A21
2
1W13 ) t
]
2
1W13
n2 ( t )
1W13 n
A21
2
1W13
激光器的运转方式
粒子数密度为 n的红宝石(三能级)被矩形脉冲激 励光照射,其激励几率:
W13 (t )
W13 0 t t0 W13 (t ) 0 t t0
W13
0
t0
t
图5.0.1(a)
激光器的运转方式
一、短脉冲运转
1. t t 0 :n3) E(抽运高能级 3
W13 (t ) W13
n2 ( t 0 )
n2 ( t ) 完成增长过程而达到稳定值,保持为常数。
激光器的运转方式
二、长脉冲和连续运转 3.t t0
A21
n2 (t ) n2 (t0 )e
2
( t t0 )
n2 ( t ) 随时间t按上式规律指数下降
激光器的运转方式
二、长脉冲和连续运转 3. 连续激光器 结论:在泵浦时间内,各能级粒子数及腔内光子 数可以达到并处于稳定状态。
阈值泵浦功率(阈值上能级粒子数密度)
Pump power threshold
阈值增益系数
光在无源腔内往返一周后的光强: 光在有源腔内往返一周后 的光强(不考虑损耗):
I1 I0e
2
I1 I 0 e
2 g0l
光在谐振腔内往返一周后 的光强(考虑损耗与增益):
I1 I 0 e
2( g 0 l )
g
I (z)
0
g
Im
0
z
I0 0
图1.4.1
z
阈值反转集居数密度
E2
n1 n2
E1
n n2 n1
nt ?
阈值反转集居数密度
增益系数和反转集居数密度间的关系:
g( ) n 21 ( , 0 )
g ( ) n 21 ( , 0 )
讨论:此时的反转集居数密度 阈值适合作为考量一台激光器 的指标吗?
E S 10 F s 1
n2t /( F s ) 个粒子 E E 0 3
F s 21l
E0 基态
阈值泵浦功率
(一)连续或长脉冲(t0 s )激光器的阈值泵浦功率:
2.三能级系统
E(抽运高能级) 3 S32 (激光上能级) E2亚稳态 A21 S21 W21 W12
n1 n2 n,n2 n1 n
阈值泵浦功率
关于激光器阈值泵浦功率的三点结论:
(1)三能级系统所需的阈值能量比四能级大得多;
(2)三能级系统激光器中 对阈值功率(能量)影响不大, 四能级系统中,阈值功率(能量)正比于 ;
(3)四能级系统的阈值功率(能量)正比于 F 。
思考: 三能级系统所需的阈值能量比四能级大还是小? 为什么? (从激光上能级阈值粒子数密度来考虑)
思考:
dN i dt 0 dN dt 0 ,
为什么激光器会有脉冲和连续运转之分?与泵浦有什么关 联?
激光器的振荡阈值
思考:激光器设计中,“阈值条件”的意义是什么
振荡阈值:
?
能够使激光器产生并维持激光振荡的最低条件。 阈值增益系数
gain threshold
阈值条件
阈值反转集居数密度
Population inversion threshold
均匀加宽激光器中的模竞争
g0 ( )
思考:均匀加宽激光器横模之间如何竞争 竞争结果:
?
gt
01
gt 00
a、阈值增益系数较小的横 模最靠近中心频率的一个纵 模取胜,形成稳定振荡。 b、该横模的其它纵模都被 抑制而熄灭。 c、阈值较大的横模的各纵模 都被抑制而熄灭。
00q 1 00q 00q 1 00q 2
gm gm l gt
反映了激光器外界激 发作用的大小与谐振 腔损耗大小的比值。
g0 ( )
gt
T
q
问题思考: 试说明某个频率的光要成为激光的纵模 并起振,它必须突破几个关口?
参考: ① 满足腔的谐振条件,成为腔的梳状模之一。 ② 频率落入工作物质的谱线线型范围 ΔνT 内,即对应小信 号增益系数大于阈值增益系数。
W13 (t ) W13
W13 0
dn2 (t ) A21n2 (t ) dt 2
0
( t t0 )
t0
t
n2 (t ) n2 (t0 )e
A21
n2 ( t )
n2 (t0 )
2
激光上能级粒子数密度随时间t 按上式规律指数下降
0
t0
t
激光器的运转方式
一、短脉冲运转
4. 若泵浦脉冲以周期T重复施于激光器
g ( q ) g t
增益曲线下降到曲线3: 图5.2.1
q 1 0 q q 1
g( q ) gt
均匀加宽激光器中的模竞争
1.增益曲线均匀饱和引起的自选模作用
竞争结果:最靠近中心频率的一个纵模取胜,形成稳 定振荡,其他纵模都被抑制而熄灭。
小结: 理想情况下,均匀加宽稳态激光器的输出模式是单 纵模,单纵模频率总是位于谱线中心频率附近,且 模增益系数就等于阈值增益系数 gt 。
0
t0
t
激光器的运转方式
一、短脉冲运转 2. t t 0
W13 (t ) W13
A21
n2 ( t )
1W13 n
A21
[1 e
(
2
1W13 ) t0
]
2
1W13
0
n2 ( t )
n2 (t0 )
t0
t
激光上能级粒子数密度达最大值
0
t0
t
激光器的运转方式
一、短脉冲运转 3. t t0
n2t nt 21 ( , 0 )l
频率为 0 的模式: n2 t
E1(激光下能级)
E0 基态 S30, A30 S32 nt 21l S10 较大
S21 A21
阈值泵浦功率
(一)连续或长脉冲(t0 s )激光器的阈值泵浦功率:
1.四能级系统
第五章 激光振荡特性
§5.2 激光器的振荡模式
核心问题: 与饱和效应相关的模式(纵模或横模)之间的竞争!
g0 ( )
起振模式数:
gt
T
q
T 激光器小信号增益系数中大于 阈值增益系数的那部分曲线所 对应的频率范围 激发参数:
—— 单程损耗因子(Loss factor )
g 0 —— 小信号增益系数(Gain coefficient )
阈值增益系数
起振条件:
I1 I 0
阈值增益系数:
2( g l ) 0
0
g
0
l
gt
l
讨论:影响阈值增益系数的因素有哪些
?
不同纵模的 相同,故具有相同的
gt 也较大) 不同横模的 不同,故 gt 不同(横模 较大,
中心频率处阈值反转粒子数最低。
阈值泵浦功率
(一)连续或长脉冲(t0 s )激光器的阈值泵浦功率:
1.四能级系统
E(抽运高能级) 3
n1 0,n n2 n1 n2
E2 能级阈值粒子数密度:
W03 A30 S30
S32 E2(激光上能级)
A21 S21 W21 W12 S10
均匀加宽激光器中的模竞争
1.增益曲线均匀饱和引起的自选模作用
g
g0 ( )
起始:
g( q1 )、g( q )、g( q1 ) gt
1 2
3
gt
增益曲线下降到曲线1: g ( q 1 ) g t
g ( q 1 )、 g ( q ) g t
增益曲线下降到曲线2: g ( q 1 ) g t
I q
z z
若 q 的波腹与 q 的波节重合, 则 q 模式可能得到较高的增益 系数而形成振荡。
连续激光器
输出功率一般都比较低,适合于要求激光连续工作(激光通信、 激光手术等)的场合
以连续光源激励的固体激光器和以连续电激励方式工作的气体激光 器及半导体激光器,均属此类。 长脉冲激光器:泵浦功率有很短时间间隔的关断以减小热影响。
短脉冲激光器
