《数学实验》实验报告——定积分的近似求解
《数学实验》实验报告——定积分的近似求解
3
2 梯形法程序如下: f=input('请输入被积函数 f(x)='); qujian=input('请输入积分区间[a,b]='); n=input('请输入子区间个数 n='); s=0; for i=1:n-1 x=qujian(1)+(qujian(2)-qujian(1))/n*i; y=eval(f); s=s+y; end x=qujian(1); y=eval(f); s=s+y/2; x=qujian(2); y=eval(f); s=s+y/2; disp('定积分的近似值是:'); s=s*(qujian(2)-qujian(1))/n
《数学实验》实验报告
班级 试验 内容 **** 学号 **** 姓名 试验 类别
自选试验
****
成绩 试验 时间 2011 年 5 月 20 日—22 日
定积分的近似求解
试验问题:
用梯形法与抛物法,通过 MATLAB,计算 x 2 dx 的近似值,取 n=10,比较结果的差异,研究
0 1
定积分的两种近似计算方法。
1 1 1 2 ph 3 6rh h(2 ph 2 6r ) h( y 0 4 y1 y 2 ) 3 3 3 。 ba n ,则上面所求的 S 等于区间 [ x0 , x2 ] 上以抛物线为曲边的曲边梯形的面积。同理可
取
以得到区间 [ xi 1 , xi 1 ] 上以抛物线为曲边的曲边梯形的面积:
试验目的:
通过分别用梯形法与抛物线法计算定积分的近似值, 进而熟练掌握运用 MATLAB 来解决 定积分的近似求解,体会 MATLAB 的强大功能。
[整理]定积分的近似计算
![[整理]定积分的近似计算](https://img.taocdn.com/s3/m/d23ddc1703020740be1e650e52ea551810a6c967.png)
[整理]定积分的近似计算实验⼆定积分的近似计算⼀、问题背景与实验⽬的利⽤⽜顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适⽤于被积函数的原函数能⽤初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑近似计算的⽅法.在定积分的很多应⽤问题中,被积函数甚⾄没有解析表达式,可能只是⼀条实验记录曲线,或者是⼀组离散的采样值,这时只能应⽤近似⽅法去计算相应的定积分.本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法.对于定积分的近似数值计算,Matlab有专门函数可⽤.⼆、相关函数(命令)及简介1.sum(a):求数组a的和.2.format long:长格式,即屏幕显⽰15位有效数字.(注:由于本实验要⽐较近似解法和精确求解间的误差,需要更⾼的精度).3.double():若输⼊的是字符则转化为相应的ASCII码;若输⼊的是整型数值则转化为相应的实型数值.4.quad():抛物线法求数值积分.格式:quad(fun,a,b) ,注意此处的fun是函数,并且为数值形式的,所以使⽤*、/、^等运算时要在其前加上⼩数点,即.*、./、.^等.例:Q = quad('1./(x.^3-2*x-5)',0,2);5.trapz():梯形法求数值积分.格式:trapz(x,y)其中x为带有步长的积分区间;y为数值形式的运算(相当于上⾯介绍的函数fun)例:计算0sin()dx xπx=0:pi/100:pi;y=sin(x);trapz(x,y)6.dblquad():抛物线法求⼆重数值积分.格式:dblquad(fun,xmin,xmax,ymin,ymax),fun可以⽤inline定义,也可以通过某个函数⽂件的句柄传递.例1:Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi)顺便计算下⾯的Q2,通过计算,⽐较Q1 与Q2结果(或加上⼿⼯验算),找出积分变量x、y的上下限的函数代⼊⽅法.Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi)例2:Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi)这时必须存在⼀个函数⽂件integrnd.m:function z = integrnd(x, y)z = y*sin(x);7.fprintf (⽂件地址,格式,写⼊的变量):把数据写⼊指定⽂件.例:x = 0:.1:1;y = [x; exp(x)];fid = fopen('exp.txt','w'); %打开⽂件fprintf(fid,'%6.2f %12.8f\n',y); %写⼊fclose(fid) %关闭⽂件8.syms 变量1 变量2 …:定义变量为符号.9.sym('表达式'):将表达式定义为符号.解释:Matlab 中的符号运算事实上是借⽤了Maple 的软件包,所以当在Matlab 中要对符号进⾏运算时,必须先把要⽤到的变量定义为符号.10.int(f,v,a,b):求f 关于v 积分,积分区间由a 到b .11.subs(f ,'x',a):将 a 的值赋给符号表达式 f 中的 x ,并计算出值.若简单地使⽤subs(f),则将f 的所有符号变量⽤可能的数值代⼊,并计算出值.三、实验内容1.矩形法根据定积分的定义,每⼀个积分和都可以看作是定积分的⼀个近似值,即1()d ()nbi i a i f x x f x ?==?∑?在⼏何意义上,这是⽤⼀系列⼩矩形⾯积近似⼩曲边梯形的结果,所以把这个近似计算⽅法称为矩形法.不过,只有当积分区间被分割得很细时,矩形法才有⼀定的精确度.针对不同i ?的取法,计算结果会有不同,我们以 120d 1x x +?为例(取100=n ),(1)左点法:对等分区间b x i na b a x x a x n i =<<-+=<<<= 10,在区间],[1i i x x -上取左端点,即取1-=i i x ?,12 01d ()1n i i i x f x x ?==?≈+∑?0.78789399673078,理论值 12 0d 14x x π=+?,此时计算的相对误差 0.7878939967307840.0031784ππ-=≈(2)右点法:同(1)中划分区间,在区间],[1i i x x -上取右端点,即取i i x =?,12 01d ()1n i i i x f x x ?==?≈+∑0.78289399673078,理论值 12 0d 14x x π=+?,此时计算的相对误差 0.7828939967307840.0031884ππ-=≈(3)中点法:同(1)中划分区间,在区间1[,]i i x x -上取中点,即取12i i i x x ?-+=, 12 01d ()1n i i i x f x x ?==?≈+∑0.78540024673078,理论值 12 0d 14x x π=+?,此时计算的相对误差 60.785400246730784 2.653104ππ--=≈? 如果在分割的每个⼩区间上采⽤⼀次或⼆次多项式来近似代替被积函数,那么可以期望得到⽐矩形法效果好得多的近似计算公式.下⾯介绍的梯形法和抛物线法就是这⼀指导思想的产物.2.梯形法等分区间b x i n a b a x x a x n i =<<-+=<<<= 10,na b x -=? 相应函数值为n y y y ,,,10 (n i x f y i i ,,1,0),( ==).曲线)(x f y =上相应的点为n P P P ,,,10 (n i y x P i i i ,,1,0),,( ==)将曲线的每⼀段弧i i P P 1-⽤过点1-i P ,i P 的弦i i P P 1-(线性函数)来代替,这使得每个],[1i i x x -上的曲边梯形成为真正的梯形,其⾯积为x y y i i ??+-21,n i ,,2,1 =.于是各个⼩梯形⾯积之和就是曲边梯形⾯积的近似值,11 11()d ()22n n b i i i i a i i y y x f x x x y y --==+?≈??=+∑∑?,即 011 ()d ()22bn n a y y b a f x x y y n --≈++++?,称此式为梯形公式.仍⽤ 120d 1x x +?的近似计算为例,取100=n , 10112 0d ()122n n y y x b a y y x n --≈++++=+?0.78539399673078,理论值 12 0d 14x x π=+?,此时计算的相对误差 60.785393996730784 5.305104ππ--=≈? 很显然,这个误差要⽐简单的矩形左点法和右点法的计算误差⼩得多.3.抛物线法由梯形法求近似值,当)(x f y =为凹曲线时,它就偏⼩;当)(x f y =为凸曲线时,它就偏⼤.若每段改⽤与它凸性相接近的抛物线来近似时,就可减少上述缺点,这就是抛物线法.将积分区间],[b a 作n 2等分,分点依次为b x i n a b a x x a x n i =<<-+=<<<=2102 ,na b x 2-=?,对应函数值为n y y y 210,,, (n i x f y i i 2,,1,0),( ==),曲线上相应点为n P P P 210,,, (n i y x P i i i 2,,1,0),,( ==).现把区间],[20x x 上的曲线段)(x f y =⽤通过三点),(000y x P ,),(111y x P ,),(222y x P 的抛物线)(12x p x x y =++=γβα来近似代替,然后求函数)(1x p 从0x 到2x 的定积分:20 1 ()d x x p x x =?20 2 ()d x x x x x αβγ++=?)()(2)(30220223032x x x x x x -+-+-γβα]4)(2)()()[(62022022202002γβαγβαγβα++++++++++-=x x x x x x x x x x 由于2201x x x +=,代⼊上式整理后得 20 1 ()d x x p x x ?)](4)()[(612122202002γβαγβαγβα++++++++-=x x x x x x x x )4(621002y y y x x ++-=)4(6210y y y na b ++-= 同样也有 42 2 ()d x x p x x ?)4(6432y y y na b ++-=……222 ()d n n x n x p x x -?)4(621222n n n y y y na b ++-=-- 将这n 个积分相加即得原来所要计算的定积分的近似值: 222 22212 11()d ()d (4)6i i n n b x i i i i a x i i b a f x x p x x y y y n ---==-≈=++∑∑?,即021******* ()d [4()2()]6b n n n a b a f x x y y y y y y y y n---≈++++++++? 这就是抛物线法公式,也称为⾟⼘⽣(Simpson )公式.仍⽤ 120d 1x x +?的近似计算为例,取100=n , 102132124222 0d [4()2()]16n n n x b a y y y y y y y y x n ---≈+++++++++?=0.78539816339745,理论值 12 0d 14x x π=+?,此时计算的相对误差 160.785398163397454 2.827104ππ--=≈?4. 直接应⽤Matlab 命令计算结果(1)数值计算 120d .1x x +? ⽅法1:int('1/(1+x^2)','x',0,1) (符号求积分)⽅法2:quad('1./(1+x.^2)',0,1) (抛物线法求数值积分)⽅法3:x=0:0.001:1;y=1./(1+x.^2);trapz(x,y) (梯形法求数值积分)(2)数值计算 2 12 0 1d d x x y y -+?? ⽅法1:int(int('x+y^2','y',-1,1),'x',0,2) (符号求积分)⽅法2:dblquad(inline('x+y^2'),0,2,-1,1) (抛物线法⼆重数值积分)四、⾃⼰动⼿1.实现实验内容中的例⼦,即分别采⽤矩形法、梯形法、抛物线法计算 12 0d 1x x +?,取258=n ,并⽐较三种⽅法的精确程度.2.分别⽤梯形法与抛物线法,计算 2 1d x x,取120=n .并尝试直接使⽤函数trapz()、quad()进⾏计算求解,⽐较结果的差异.3.试计算定积分 0sin d x x x+∞?.(注意:可以运⽤trapz()、quad()或附录程序求解吗?为什么?)4.将 120d 1x x +?的近似计算结果与Matlab 中各命令的计算结果相⽐较,试猜测Matlab 中的数值积分命令最可能采⽤了哪⼀种近似计算⽅法?并找出其他例⼦⽀持你的观点.5.通过整个实验内容及练习,你能否作出⼀些理论上的⼩结,即针对什么类型的函数(具有某种单调特性或凹凸特性),⽤某种近似计算⽅法所得结果更接近于实际值?6.学习fulu2sum.m 的程序设计⽅法,尝试⽤函数 sum 改写附录1和附录3的程序,避免for 循环.五、附录附录1:矩形法(左点法、右点法、中点法)(fulu1.m )format longn=100;a=0;b=1;inum1=0;inum2=0;inum3=0;syms x fxfx=1/(1+x^2);for i=1:nxj=a+(i-1)*(b-a)/n; %左点xi=a+i*(b-a)/n; %右点fxj=subs(fx,'x',xj); %左点值fxi=subs(fx,'x',xi); %右点值fxij=subs(fx,'x',(xi+xj)/2); %中点值inum1=inum1+fxj*(b-a)/n;inum2=inum2+fxi*(b-a)/n;inum3=inum3+fxij*(b-a)/n;endinum1inum2inum3integrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum1 and real-value is about: %d\n\n',...abs((inum1-integrate)/integrate))fprintf('The relative error between inum2 and real-value is about: %d\n\n',...abs((inum2-integrate)/integrate))fprintf('The relative error between inum3 and real-value is about: %d\n\n',...abs((inum3-integrate)/integrate))附录2:梯形法(fulu2.m)format longn=100;a=0;b=1;inum=0;syms x fxfx=1/(1+x^2);for i=1:nxj=a+(i-1)*(b-a)/n;xi=a+i*(b-a)/n;fxj=subs(fx,'x',xj);fxi=subs(fx,'x',xi);inum=inum+(fxj+fxi)*(b-a)/(2*n);endinumintegrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum and real-value is about: %d\n\n',... abs((inum-integrate)/integrate))附录2sum:梯形法(fulu2sum.m),利⽤求和函数,避免for 循环format long n=100;a=0;b=1;syms x fxfx=1/(1+x^2);i=1:n;xj=a+(i-1)*(b-a)/n; %所有左点的数组xi=a+i*(b-a)/n; %所有右点的数组fxj=subs(fx,'x',xj); %所有左点值fxi=subs(fx,'x',xi); %所有右点值f=(fxi+fxj)/2*(b-a)/n; %梯形⾯积inum=sum(f) %加和梯形⾯积求解integrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum and real-value is about: %d\n\n',... abs((inum-integrate)/integrate))附录3:抛物线法(fulu3.m)format longn=100;a=0;b=1;inum=0;syms x fxfx=1/(1+x^2);for i=1:nxj=a+(i-1)*(b-a)/n; %左点xi=a+i*(b-a)/n; %右点xk=(xi+xj)/2; %中点fxj=subs(fx,'x',xj);fxi=subs(fx,'x',xi);fxk=subs(fx,'x',xk);inum=inum+(fxj+4*fxk+fxi)*(b-a)/(6*n);endinumintegrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum and real-value is about: %d\n\n',...。
matlab实验报告--定积分的近似计算

abs((inum2-integrate)/integrate))
fprintf('the relative error between inum3 and real-value is about: %g\n\n',...
abs((inum3-integrate)/integrate)) 【调试结果】
○2 使用函数 quad()
quad('sin(x)./x',0,inf) 【调试结果】 ans =
NaN
○3 程序法
%矩阵法
format long
n=inf;a=0;b=inf;
syms x fx
fx=sin(x)./x;
i=1:n;
xj=a+(i-1)*(b-a)/n; xi=a+i*(b-a)/n;
实验目的:
本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法。对于定 积分的近似数值计算,Matlab 有专门函数可用。
实验原理与数学模型:
1. 矩形法 根据定积分的定义,每一个积分和都可以看作是定积分的一个近似值,即
在几何意义上,这是用一系列小矩形面积近似小曲边梯形的结果,所以把这个近似计 算方法称为矩形法.不过,只有当积分区间被分割得很细时,矩形法才有一定的精确度.
【调试结果】
inum =
0.78539816339745
the relative error between inum and real-value is about: 2.82716e-016
【情况记录】
1、梯形法和抛物线法程序设计较为顺利。但要注意使用 for 循环函数和求和函数时
的不同 matlab 命令,避免混淆出错。使用函数 trapz(),quad()时要注意被积函数是数 值形式,应使用数组计算,应用点除即 ./ ,否则将出错,不能调试出结果。
定积分的近似运算

(1)y=x^2
矩形法inum1 =0.328350000000000 inum2 = 0.338350000000000
inum3 =0.333325000000000
integrate =1/3 integrate = 0.333333333333333
the relative error between inum1 and real-value is about: 0.01495
the relative error between inum2 and real-value is about: 0.01505
the relative error between inum3 and real-value is about: 2.5e-05
梯形法inum =0.333350000000000 integrate =1/3
the relative error between inum1 and real-value is about: 0.0199
the relative error between inum2 and real-value is about: 0.0201
the relative error between inum3 and real-value is about: 5e-05
fx1=subs(fx,x,x1);
fx2=subs(fx,x,x2);
si=(fx0+4*fx1+fx2)*(b-a)/(6*n);
inum=inum+si;
end
inum
integrate=int(fx,0,1);
integrate=double(integrate)
综合实验一 定积分的近似计算

a
f ( x )dx ≈ ∑ f ( xi )xi = h ∑ f ( xi )
i =1 i =1
n
中点法:
b
a
f ( x )dx ≈ ∑
i =1
n
n xi 1 + xi xi 1 + xi f( )xi = h ∑ f ( ) 2 2 i =1
矩形法举例
数学实验
例:用不同的矩形法计算下面的定积分 ( 取 n=100 ), 并比较这三种方法的相对误差.
解: a=0, b=1, n=100 ==> h =1/100=0.01, xi = i*h,
dx ≈ h f ( x ) = h 1 左点法:∫0 ∑ i1 ∑ 1 + x 2i1 1 + x2 i =1 i =1
1
1 n
dx ∫0 1 + x 2
1
n
n
(i = 0,1,2,...,100)
dx ≈ h ∑ f ( xi ) ≈ 0.78289399673078 右点法: ∫0 2 1+ x i =1
二重积分的计算
抛物线法计算二重积分: dblquad
数学实验
dblquad(f,a,b,c,d,tol)
∫∫
a
b
ห้องสมุดไป่ตู้
d
c
f ( x, y )dxdy
tol 为计算精度,若不指定,则缺省精度为 10-6 f(x,y) 可以由 inline 定义,或通过一个函数句柄传递 [a,b] 是第一积分变量的积分区间,[c,d] 是第二积分变量 的积分区间 按字母顺序,大写字母排在小写字母的前面
实验二, 实验二,定积分的近似计算
矩形法
定积分的近似计算

fxj=subs(fx,'x',xj);%符号运算,替换
fxi=subs(fx,'x',xi);%符号运算,替换
sum=sum+(fxi+fxj)*(b-a)/(2*n);%求矩形面积
end
sum%如果没有这句话就算不出最后的积分
结果:sum =0.6932
(2)抛物线法:
fzz=subs(fx,'x',zz);
f=(fxx+4*fyy+fzz)*(b-a)/(6*n);
s=sum(f)
结果:s=0.7854
实验结果报告及实验总结:
1.实验结果报告:
(1)梯形法:结果:sum =0.6932
(2)抛物线法:结果:sum = 0.6931
(3)trapz()法:结果:ans =0.6931
n=120;
a=1;
b=2;
sum=0;
syms x fx;
fx=1/x;
for i=1:n
xx=a+(2*i-2)*(b-a)/(2*n);%第一点的自变量取值后面是除2*n,不是n
yy=a+(2*i-1)*(b-a)/(2*n);%第二点的自变量取值后面是2*i-1
zz=a+(2*i-0)*(b-a)/(2*n);%复制后没改自变量的名字
且发现trapz()的调试结果与梯形法结果相同,故可猜测该Matlab中的数值积分命令函数trapz()采用了梯形法近似计算方法。
2.实验结果报告:
(1)使用int:结果:ans =pi/2
(2)使用函数trapz():
结果:Maximum variable size allowed by the program is exceeded.
定积分的近似计算97786

数学实验报告实验序号:4 日期:2012 年12 月13 日实验名称定积分的近似计算问题背景描述:利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的原函数能用初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积分.实验目的:本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法。
对于定积分的近似数值计算,Matlab有专门函数可用。
实验原理与数学模型:1.矩形法根据定积分的定义,每一个积分和都可以看作是定积分的一个近似值,即在几何意义上,这是用一系列小矩形面积近似小曲边梯形的结果,所以把这个近似计算方法称为矩形法.不过,只有当积分区间被分割得很细时,矩形法才有一定的精确度.针对不同的取法,计算结果会有不同。
(1)左点法:对等分区间,在区间上取左端点,即取。
(2)右点法:同(1)中划分区间,在区间上取右端点,即取。
(3)中点法:同(1)中划分区间,在区间上取中点,即取。
2.梯形法等分区间,相应函数值为().曲线上相应的点为()将曲线的每一段弧用过点,的弦(线性函数)来代替,这使得每个上的曲边梯形成为真正的梯形,其面积为,.于是各个小梯形面积之和就是曲边梯形面积的近似值,,即,称此式为梯形公式。
3.抛物线法将积分区间作等分,分点依次为,,对应函数值为(),曲线上相应点为().现把区间上的曲线段用通过三点,,的抛物线来近似代替,然后求函数从到的定积分:由于,代入上式整理后得同样也有……将这个积分相加即得原来所要计算的定积分的近似值:,即这就是抛物线法公式,也称为辛卜生(Simpson)公式.实验所用软件及版本:Matlab 7.0主要内容(要点):1.分别用梯形法与抛物线法,计算,取.并尝试直接使用函数trapz()、quad()进行计算求解,比较结果的差异.2.试计算定积分.(注意:可以运用trapz()、quad()或附录程序求解吗?为什么?)3.学习fulu2sum.m的程序设计方法,尝试用函数sum 改写附录1和附录3的程序,避免for 循环。
定积分的近似计算

定积分的近似计算实验项目: 定积分的三种近似计算算法一、实验目的学习定积分的三种近似计算算法:符号法(矩形法)、梯形法和抛物线法。
二、实验内容及要求1.对于定积分的近似计算matlab 有专门函数可用。
int ()符号法求积分;quad ()抛物线法求数值积分;trapz ()梯形法求数值积分;dblquad ()抛物线法求二重数值积分。
2.注意:matlab 的符号运算事实上是借用了maple 的软件包,所以当在matlab 中进行符号运算时,必须先把要用到的变量定义为符号。
例如求1201d x x +⎰的值,程序如下:sym x; int('1/(1+x^2)','x',0,1)3.实验内容(1)分别用符号法、梯形法和抛物线法求1201d x x +⎰(2)计算0sin x d x x +∞⎰,能用quad ()和trapz ()求解吗?(3)用符号法和抛物线法求21201()d x x y d y -+⎰⎰三、实验结果和程序(1) 程序:符号法:syms x yy=1./(1+x.^2);f=int (y,x,0,1)结果:f = 1/4*pi梯形法:x=0:0.001:1;y=1./(1+x.^2);format long ;trapz(x,y)结果:ans = 0.785398121730782抛物线法:format long ;quad('1./(1+x.^2)',0,1)结果:ans = 0.785398149243260(2)程序:符号法:syms x;f=int('sin(x)/x','x',0,inf)结果:f =1/2*pi梯形法:x=0:0.001:100;y=sin(x)./x;format long;f=trapz(x,y)结果:f = NaN抛物线法:syms x;format long;ff=@(x)(sin(x)./x);f=quad(ff,0,inf)结果:f = NaN(3)程序:符号法:syms x ys=vpa(int(int(x+y.^2,y,-1,1),x,0,2))抛物线法:z=inline('x+y.^2','x','y')s=dblquad(z,0,2,-1,1)结果:s =5.333333333333333。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
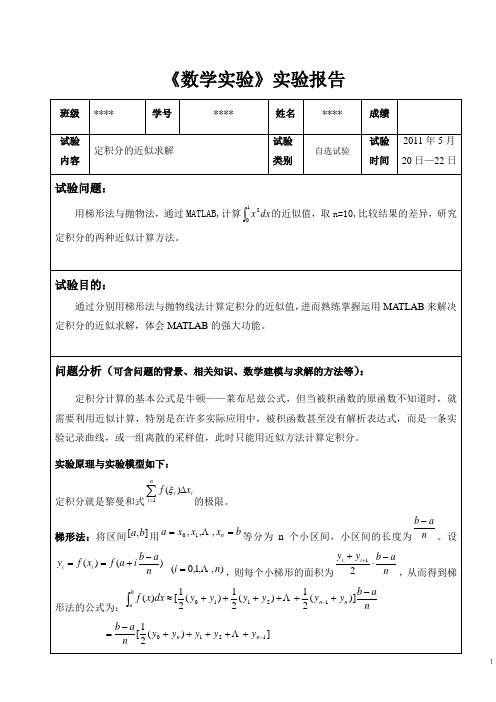
2 梯形法程序如下: f=input('请输入被积函数 f(x)='); qujian=input('请输入积分区间[a,b]='); n=input('请输入子区间个数 n='); s=0; for i=1:n-1 x=qujian(1)+(qujian(2)-qujian(1))/n*i; y=eval(f); s=s+y; end x=qujian(1); y=eval(f); s=s+y/2; x=qujian(2); y=eval(f); s=s+y/2; disp('定积分的近似值是:'); s=s*(qujian(2)-qujian(1))/n
k k 1 ba [ f (a) f (b) 4 f ( x2i 1 ) 2 f ( x2i )] 6k i 1 i 1
试验步骤(根据问题分析及试验目的所计划的试验步骤) :
1、编程用矩形法计算定积分的近似值; 2、编程用梯形法计算定积分的近似值;
2
3、在 MATLAB 中运行,并比较两种方法的结果。
1 1 1 ba f ( x)dx [ ( y 0 y1 ) ( y1 y 2 ) ( y n 1 y n )] 2 2 2 n
形法的公式为:
b
a
ba 1 [ ( y 0 y n ) y1 y 2 y n 1 ] n 2
1
b a f (a) f (b) n ba [ f (a i )] n 2 n i 1
S ( px 2 qx r )dx 2 ( px 2 r )dx
h 0 h h
2 3 ph 2rh 3 ,
2 2 2 由 y0 ph qh r, y1 r, y2 ph qh r 得: ph y0 y2 2 y1
故
S h
定积分就是黎曼和式
f ( )x
i 1 i
n
i
的极限。
ba a x , x , , x b [ a , b ] 0 1 n 梯形法:将区间 用 等分为 n 个小区间,小区间的长度为 n 。设
y i f ( xi ) f ( a i
y i y i 1 b a ba ) (i 0,1,, n) ,则每个小梯形的面积为 n 2 n ,从而得到梯
Si
n ba ( y i 1 4 y i y i 1 ), i 1,2,, n 1 。于是,将这 2 个曲边梯形的面积加起来,得到定 3n
ba Sn [ y 0 y n 4( y1 y 3 y n 1 ) 2( y 2 y 4 y n 2 )] 3n 积分的近似值为 (设 n 2k ) :
抛物线法:用分点 a x0 , x1 , x2 ,, xn b ,将积分区间 n 等分(这里要求 n 为偶数) ,各分点 对应的函数值为 y0 , y1 , y2 ,, yn ,即
y i f ( xi ) f ( a i ba ) n 。平面上三点可以确定一条抛物
2 线 y px qx r ,而相邻的两个小区间上经过曲线上的三个点,则由这三点做抛物线(因
MATLAB 运行结果如下:
4
结果分析:
由两种方法得出的结果来看,用梯形法计算更接近;而且,子区间个数少时精确度不够 高,取子区间个数为 10000 时结果就比较精确。
总结体会:
这一次通过 MATLAB 编程来计算定积分的近似值,感觉方便快捷,很好用。通过这一次 的试验,让我深深感受到数学软件的博大精深。很多无法人工解决的数学问题,用软件来解 决那是小菜一碟。 MATLAB 在矩阵计算、做图方面很强大,借助它更能提高学数学的效率。而一旦掌握了数 学软件的运用,对于以后的数学教学可谓是如虎添翼。以后有时间的话,我还会好好学习各 种数学软件的运用,让它们更好地服务于数学研究以及数学教学!
《数学实验》实验报告
班级 试验 内容 **** 学号 **** 姓名 试验 类别
自选试验
****
成绩 试验 时间 20பைடு நூலகம்1 年 5 月 20 日—22 日
定积分的近似求解
试验问题:
用梯形法与抛物法,通过 MATLAB,计算 x 2 dx 的近似值,取 n=10,比较结果的差异,研究
0 1
定积分的两种近似计算方法。
试验过程(含详细试验步骤、程序清单及异常情况记录等)
1、矩形法程序设计如下: f=input('请输入被积函数 f(x)='); qujian=input('请输入积分区间[a,b]='); n=input('请输入子区间个数 n='); s=0; for i=1:n x=qujian(1)+(qujian(2)-qujian(1))/n*i; y=eval(f); s=s+y; end disp('定积分的近似值是:'); s=s*(qujian(2)-qujian(1))/n MATLAB 运行结果如下:
试验目的:
通过分别用梯形法与抛物线法计算定积分的近似值, 进而熟练掌握运用 MATLAB 来解决 定积分的近似求解,体会 MATLAB 的强大功能。
问题分析(可含问题的背景、相关知识、数学建模与求解的方法等) :
定积分计算的基本公式是牛顿——莱布尼兹公式,但当被积函数的原函数不知道时,就 需要利用近似计算,特别是在许多实际应用中,被积函数甚至没有解析表达式,而是一条实 验记录曲线,或一组离散的采样值,此时只能用近似方法计算定积分。 实验原理与实验模型如下:
此抛物线法必须将区间等分为偶数个小区间) ,把这些抛物线构成的曲边梯形的面积相加,就 得到了所求定积分的近似 值。计算在区间 [ x0 , x2 ] 上以抛物线为曲边的曲边梯形面积。先计算区间 h, h 上,以过
(h, y0 ), (0, y1 ), (h, y2 ) 三 点 的 抛 物 线 y px2 qx r 为 曲 边 的 曲 边 梯 形 面 积 S :
1 1 1 2 ph 3 6rh h(2 ph 2 6r ) h( y 0 4 y1 y 2 ) 3 3 3 。 ba n ,则上面所求的 S 等于区间 [ x0 , x2 ] 上以抛物线为曲边的曲边梯形的面积。同理可
取
以得到区间 [ xi 1 , xi 1 ] 上以抛物线为曲边的曲边梯形的面积:
