山东省青岛市2011届高三教学质量3月统一检测(数学理)

合集下载

数学_2011年山东省某校高考数学三模试卷(理科)_(含答案)

2011年山东省某校高考数学三模试卷（理科）一、选择题（共12小题，每小题5分，满分60分）1. 已知全集U ＝{1, 2, 3, 4, 5, 6, 7, 8}，M ＝{1, 3, 5, 7}，N ＝{5, 6, 7}，则∁U (M ∪N)＝（）A {5, 7}B {2, 4}C {2, 4, 8}D {1, 3, 5, 6, 7}2. 在等差数列{a n }中，已知a 1+a 3+a 11=6，那么S 9=( )A 2B 8；C 18D 363. 已知a ，b ，l 是不同的直线α，β是不重合的平面，有下理命题：①若a ⊥β，α⊥β，则a // α；②若a // α，a ⊥b ，则b ⊥α③若a // b ，l ⊥α，则l ⊥b ；④α⊥γ，β⊥γ则α // β以上命题正确的个数是（）A 1B 2C 3D 44. 设ω>0，函数y =sin(ωx +π3)+2的图象向右平移4π3个单位后与原图象重合，则ω的最小值是（）A 23B 43C 32D 3 5. 设a =log 54，b =(log 53)2，c =log 45，则( )A a <c <bB b <c <aC a <b <cD b <a <c6. 设p:x 2−x −20>0，q:1−x 2|x|−2<0，则p 是q 的（）A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件 7. ∫(π2−π21+cosx)dx 等于（）A πB 2C π−2D π+28. 某校开设A 类选修课3门，B 类选择课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有（）A 30种B 35种C 42种D 48种9. 已知F 1，F 2是双曲线x 2a 2−y 2b 2=1，(a >b >0)的左、右焦点，过F 1且垂直于x 轴的直线与双曲线的左支交于A 、B 两点△ABF 2是正三角形，那么双曲线的离心率为（）A 2B √2C 3D √310. 已知A 、B 、C 是锐角△ABC 的三个内角，向量p →=(−sinA,1)q →=(1,cosB)，则p →与q →的夹角是（）A 锐角B 钝角C 直角D 不确定11. 设x ，y 满足约束条件{2x −y +2≥08x −y −4≤0x ≥0,y ≥0，若目标函数z =abx +y(a >0, b >0)的最大值为8，则a +b 的最小值为（）A 2B 4C 6D 812. 下列关于函数f(x)=(2x −x 2)e x 的判断正确的是( )①f(x)>0的解集是{x|0<x <2}；②f(−√2)是极小值，f(√2)是极大值；③f(x)没有最小值，也没有最大值．A ①③B ①②③C ②D ①②二、填空题（共4小题，每小题4分，满分16分）13. 抛物线y=2x2的准线方程是________．14. 已知(x32+x−13)n的展开式中各项系数的和是128，则展开式中x5的系数是________．（以数字作答）15. 在△ABC中，A=120∘，b=1，面积为√3，则a+b+csinA+sinB+sinC=________．16. 函数y=f(x)定义在R上单调递减且f(0)≠0，对任意实数m、n，恒有f(m+n)=f(m)⋅f(n)，集合A={(x, y)|f(x2)⋅f(y2)>f(1)}，B={(x, y)|f(ax−y+2)=1, a∈R}，若A∩B=φ，则a的取值范围是________．三、解答题（共6小题，满分74分）17. 设函数f(x)=cos(2x+π3)+sin2x．（1）求函数f(x)的最大值和最小正周期．（2）设A，B，C为△ABC的三个内角，若cosB=13，f(C3)=−14，且C为非钝角，求sinA．18. 已知各项均为正数的数列{a n}满足2a n+12+3a n+1⋅a n−2a n2=0，n为正整数，且a3+ 132是a2，a4的等差中项，（1）求数列{a n}通项公式；（2）若C n=−log12a na n⋅T n=C1+C2+⋯+C n求使T n+n⋅2n+1>125成立的正整数n的最小值．19. 甲、乙两个奥运会主办城市之间有7条网线并联，这7条网线能通过的信息量分别为1，1，2，2，2，3，3．现从中任选三条网线，设可通过的信息量为ξ．若可通过的信息量ξ≥6，则可保证信息通畅．（1）求线路信息通畅的概率；（2）求线路可通过的信息量ξ的分布列和数学期望．20. 在如图所示的多面体中，已知正方形ABCD和直角梯形ACEF所在的平面互相垂直，EC⊥AC，EF // AC，AB=√2，EF=EC=1，（1）求证：平面BEF⊥平面DEF；（2）求二面角A−BF−E的大小．21. 已知椭圆的中心在原点，焦点在x轴上，一个顶点为B(0, −1)，且其右焦点到直线x−y+2√2=0的距离为3．（1）求椭圆的方程；（2）是否存在斜率为k(k≠0)，且过定点Q(0,32)的直线l，使l与椭圆交于两个不同的点M、N，且|BM|=|BN|？若存在，求出直线l的方程；若不存在，请说明理由．22. 设f(x)=ax+xlnx，g(x)=x3−x2−3．（1）当a=2时，求曲线y=f(x)在x=1处的切线方程；（2）如果存在x1，x2∈[0, 2]，使得g(x1)−g(x2)≥M成立，求满足上述条件的最大整数M；（3）如果对任意的s,t∈[12，2]，都有f(s)≥g(t)成立，求实数a的取值范围．2011年山东省某校高考数学三模试卷（理科）答案1. C2. C3. A4. C5. D6. A7. D8. A9. D10. B11. B12. D13. y=−1814. 3515. 2√716. −√3≤a≤√317. 解：（1）f(x)=cos(2x+π3)+sin2x=cos2xcosπ3−sin2xsinπ3+1−cos2x2=12−√32sin2x∴ 函数f(x)的最大值为1+√32，最小正周期π．（2）f(C3)=12−√32sin2C3=−14，∴ sin2C3=√32，∵ C为三角形内角，∴ 2C3=π3，∴ C=π2，∴ sinA=cosB=13．18. 解：（1）根据题意可得：2a n+12+3a n+1⋅a n −2a n 2=0，所以(a n+1+2a n )(2a n+1−a n )=0，因为数列{a n }各项均为正数，所以a n+1=12a n ，所以数列{a n }是等比数列，并且公比为12．因为a 3+132是a 2，a 4的等差中项，所以a 2+a 4=2a 3+116，即a 1q +a 1q 3=2a 1q 2+116，解得：a 1=12．所以数列{a n }通项公式为a n =(12)n ．（2）由（1）可得C n =−n ⋅2n ，所以T n =−2−2×22−3×23−...−n ×2n …①，所以2T n =−22−2×23−3×24...−(n −1)2n −n ×2n+1…②所以①-②并且整理可得：T n =(1−n)⋅2n−1−2．所以要使T n +n ⋅2n+1>125成立，只要使2n+1−2>125成立，即2n+1>127，所以n ≥6，所以使T n +n ⋅2n+1>125成立的正整数n 的最小值为6．19. 解：（1）∵ 通过的信息量ξ≥6，则可保证信息通畅．∴ 线路信息通畅包括三种情况，即通过的信息量分别为8，7，6，这三种情况是互斥的，根据互斥事件的概率公式和等可能事件的概率公式得到 P(ξ=8)=C 22C 31C 73=335， P(ξ=7)=C 32C 21+C 22C 21C 73=835， P(ξ=6)=C 21C 31C 21+C 33C 73=1335，∴ 线路信息通畅的概率为P =335+835+1335=2435．（2）线路可通过的信息量ξ，ξ的所有可能取值为4，5，6，7，8．P(ξ=5)=C 22C 21+C 32C 21C 73=835， P(ξ=4)=C 22C 31C 73=335． P(ξ=8)=C 22C 31C 73=335， P(ξ=7)=C 32C 21+C 22C 21C 73=835， P(ξ=6)=C 21C 31C 21+C 33C 73=1335，∴ ξ的分布列为∴ Eξ=4×335+5×835+6×1335+7×835+8×335=6． 20. 解：（1）∵ 平面ACEF ⊥平面ABCD ， EC ⊥AC ，∴ EC ⊥平面ABCD ；建立如图所示的空间直角坐标系C −xyz ，是A(√2,√2,0) B(0,√2，0)，D(√2,0,0)，E(0,0,1)，F(√22,√22,1)， ∴ EF →=(√22,√22,0)，BE →=(0,−√2,1)，DE →=(−√2,0,1)设平面BEF 、平面DEF 的法向量分别为m →=(x 1,y,1)，n →=(x 2,y 2,1)，则m →⋅EF →=√22x 1+√22y 1=0①m →⋅BE →=−√2y 1+1=0②n →⋅EF →=√22x 2+√22y 2=0③n →⋅DE →=−√2x 2+1=0④由①②③④解得x 1=−√22，y 1=√22；x 2=√22，y 2=−√22， ∴ m →=(−√22,√22,1)，n →=(√22,−√22,1) ∴ m →⋅n →=−12−12+1=0，∴ m →⊥n →，故平面BEF ⊥平面DEF（2）设平面ABF 的法向量p →=(x 1,y 1,1)，∵ BF =(√22，−√22，1)，BA →=(√2,0,0) ∴ p →⋅BF →=√22x 3−√22y 3+1=0，p →⋅BA →=√2x 3=0，解得x 3=0，y 3=√2 ∴ p →=(0,√2,1)∴ cos <m →，p →>=|m →|⋅|p →|˙=2√2⋅√3=√63由图知，二面角A −BF −E 的平面角是钝角，故所求二面角的大小为：π−arccos√63． 21. 解：（1）设椭圆的方程为x 2a 2+y 2b 2=1，(a >b >0)，由已知得b =1．设右焦点为(c, 0)，由题意得√2√2=3，∴ c =√2，∴ a 2=b 2+c 2=3．∴ 椭圆的方程为x 23+y 2=1．（2）直线l 的方程y =kx +32，代入椭圆方程，得 (1+3k 2)x 2+9kx +154=0．由△=81k 2−15(1+3k 2)>0得k 2>512，设点M(x 1, y 1)，N(x 2, y 2)，则x 1+x 2=−9k1+3k 2，设M 、N 的中点为P ，则点P 的坐标为(−9k 2+6k 2，32+6k 2)．∵ |BM|=|BN|，∴ 点B 在线段MN 的中垂线上． k BP =−1k =32+6k 2+1−9k2+6k 2，化简，得k 2=23． ∵ 23>512，∴ k =±√63，所以，存在直线l 满足题意，直线l 的方程为√63x −y +32=0或√63x +y −32=0．22. 解：（1）当a =2时，f(x)=2x +xlnx ，f′(x)=−2x 2+lnx +1，f(1)=2，f ′(1)=−1，所以曲线y =f(x)在x =1处的切线方程为y =−x +3；（2）存在x 1，x 2∈[0, 2]，使得g(x 1)−g(x 2)≥M 成立等价于：[g(x 1)−g(x 2)]max ≥M ，考察g(x)=x 3−x 2−3，g′(x)=3x 2−2x =3x(x −23)，由上表可知：g(x)min =g(23)=−8527，g(x)max =g(2)=1，[g(x 1)−g(x 2)]max =g(x)max −g(x)min =11227，所以满足条件的最大整数M =4；（3）当x ∈[12，2]时，f(x)=ax +xlnx ≥1恒成立等价于a ≥x −x 2lnx 恒成立，记ℎ(x)=x −x 2lnx ，ℎ′(x)=1−2xlnx −x ，ℎ′(1)=0．记m(x)=1−2xlnx−x，m′(x)=−3−2lnx，，2]，m′(x)=−3−2lnx<0，由于x∈[12，2]上递减，所以m(x)=ℎ′(x)=1−2xlnx−x在[12，1)时, ℎ′(x)>0, x∈(1, 2]时，ℎ′(x)<0，当x∈[12，1)上递增, 在区间(1, 2]上递减，即函数ℎ(x)=x−x2lnx在区间[12所以ℎ(x)max=ℎ(1)=1，所以a≥1．。

青岛市高三教学质量检测XXXX03试卷(一套)

XX市高三统一质量检测基本能力本试卷分第一部分和第二部分，共15页，满分100分。

考试用时120分钟。

答题前，考生务必用0.5毫米的黑色签字笔将自己的XX、座号、XX号填写在答题卡和试卷规定的位置。

考试结束后，将答题卡交回。

每小题选出答案后，用2B铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

不涂在答题卡上，只答在试卷上不得分。

第一部分（共70分）注意事项：第一部分共70题，全部为单项选择题，每题1分，共70分。

每题给出的四个选项中，只有一个选项最符合题目要求。

一、亲近自然，敬畏自然。

大自然是人类的生命之根、力量之源、艺术之泉。

1．泰山有时会出现云海奇观。

关于泰山云海，以下说法不正确的是A．泰山云海多见于雨雾较多的夏天B．当云海与山风同时出现时，有时会看到漫过山头的“爬山云”和沿山坡奔流直下的“云瀑布”奇观C．中国画技法表现云海，常见手法是“留白”，以虚衬实，虚实相生D．五彩斑斓的云海是太阳光遇到云雾中的水滴经过反射作用产生的2．中国古代的对外交流促进了民族关系的发展，下列说法正确的是A．X和下西洋选择冬季出发，是因为南亚地区冬季盛行西南季风，航向与风向相同B．《土尔扈特全部归顺记》弘扬了热爱祖国、团结统一的中华民族精神C．丝绸之路是促进亚非各国和中国的友好往来、沟通东西方文化的友谊之路D．昭君出塞不仅给汉朝和匈奴带来了和平，而且加强了中原与西域的经济文化交流3．中餐馆的女服务员着中式工作装（右图），①②③是领口和袖口的花边，④⑤⑥是服务员穿的鞋子，其中最与服装相配的分别是A．① ④ B．② ⑤ C．③ ⑥ D．① ⑤粗铁丝4．文学创作基于作家对生活的观察，对下列诗文句子解释正确的是A ．“臣心一片磁针石，不指南方誓不休”说明磁铁具有吸附性B ．“冰，水为之而寒于水”说明冰的温度一定比水低C ．“飞流直下三千尺”中“飞流直下”的水的重力势能在增大D ．“北风卷地百草折”中“百草折”的原因是力使物体发生形变5．《祖孙四代》是现代国画家X 文西的作品，表现的是勤劳的陕北人在劳作之余休息的场景。

山东省青岛市高三统一质量监测数学(理)试题

高三统一质量检测数学（理科）本试题卷共6页，23题(含选考题)。

全卷满分150分。

考试用时120分钟。

一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}2|10,2,1,0,1A x x B =->=--，则()R C A B =A ． {}2,1--B ．{}2-C ．{}1,0,1-D ．{}0,12.设复数1z i =-+（i 是虚数单位），z 的共轭复数为z ，则11z z+=- A ．1255i + B ．1255i -+ C ．1255i - D ．1255i -- 3.若1sin ,0,432ππαα⎛⎫⎛⎫-=∈ ⎪ ⎪⎝⎭⎝⎭，则cos α的值为 A ．426- B ．426+ C ．718D ．23 4.已知双曲线()222210,0y x a b a b-=>>的一个焦点为()0,2F -，一条渐近线的斜率为3，则该双曲线的方程为A ．2213x y -=B ．2213y x -= C.2213y x -= D ．2213x y -= 5.某空间几何体的三视图如图所示，则该几何体的体积为A ．563B ．5683π-C.643D ．6483π-6.中国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n = A ．2 B ．3 C.4 D ．57.已知三棱柱111ABC A B C -的侧棱与底面垂直，12,2,2AA AB AC BC ====，则三棱柱111ABC A B C -外接球的表面积为A ．4πB ．6π C.8π D ．12π 8.函数()1ln1xf x x-=+的大致图像为9.已知151x e dxn e =-⎰，其中 2.71,e e =为自然对数的底数，则在42nx x ⎛⎫-- ⎪⎝⎭的展开式中2x 的系数是A ．240B ．80 C.-80 D ．-240 10.已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的最小周期为4π，且其图像向右平移23π个单位后得到的图像关于y 轴对称，则ϕ= A ．6π- B ．3π- C.6π D ．3π11.已知点A 是抛物线()2:20C x py p =>的对称轴与准线的交点，过点A 作抛物线C 的两条切线，切点分别为,P Q ，若APQ ∆的面积为4，则p 的值为 A ．12 B ．1 C.32D ．2 12.若函数()()2.718,x e f x e e =为自然对数的底数在()f x 的定义域上单调递增，则称函数()f x 具有M 性质.给出下列函数：①()ln f x x =；②()21f x x =+；③()sin f x x =；④()3f x x =.以上函数中具有M 性质的个数为A ．1B ．2 C.3 D ．4二、填空题：本大题共4个小题，每小题5分.13.已知向量()4,2a =，向量()2,1b k k =--，若a b a b +=-，则k 的值为_____．14.已知实数,x y 满足110x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则22x y x ++的最小值为____________．15.已知定义在R 上的偶函数()f x 在[)0,+∞上单调递减，在[]4,4-上随机地取一个数x ，则事件“不等式()()11f x f -≥”发生的概率是______． 16.如图所示，在四边形ABCD 中，22,,36AB BC ABC ADB ππ==∠=∠=，则CD 的取值范围为__．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17题~21题为必考题，每个考题都必须作答.第22、23题为选考题，考生根据要求解答.（一）必考题：共60分17.(12分)已知等差数列{}n a 的公差为2，等比数列{}n b 的公比为2，且2nn n a b n =.（1）求数列{}n a 和{}n b 的通项公式；（2）令231log n n n c a b +=，记数列{}n c 的前n 项和为n T ，试比较n T 与38的大小.18.（12分）如图，圆柱H 横放在底面边长为1的正六棱锥P ABCDEF -的顶点P 上，1O 和2O 分别是圆柱左和右两个底面的圆心，正六棱锥P ABCDEF -底面中心为,1,M N O PO =、分别是圆柱H 的底面1O 的最高点和最低点，G 是圆柱H 的底面2O 的最低点，P 为NG 中点，点1M O N A O D G P 、、、、、、、共面，点1O P D 、、共线，四边形ADGN 为矩形. （1）证明：//MG 平面PCD ；（2）求二面角M CD A --大小. 注：正棱锥就是底面是一个正多边形，顶点在底面上的正投影为底面的中心的棱锥.19.（12分）某校高三年级的500名学生参加了一次数学测试，已知这500名学生的成绩全部介于60分到140分之间（满分150分），为统计学生的这次考试情况，从这500名学生中随机抽取50名学生的考试成绩作为样本进行统计.将这50名学生的测试成绩的统计结果按如下方式分成八组：第一组[)60,70，第二组[)70,80，第三组[)80,90，……，第八组[]130,140.如图是按上述分组方法得到的频率分布直方图的一部分.（1）求第七组的频率，并完成频率分布直方图；（2）估计该校高三年级的这500名学生的这次考试成绩的中位数；（3）若从样本成绩属于第一组和第六组的所有学生中随机抽取2名，记这2名学生中属于第一组的人数为ξ，令21ηξ=+，求ξ的分布列及()E η.20.（12分）已知O 为坐标原点，点A B 、在椭圆22:12x C y +=上，点3030,E ⎛⎫- ⎪ ⎪⎝⎭在圆()222:0D x y rr +=>上，AB 在中点为Q ，满足O E Q 、、三点共线.（1）求直线AB 的斜率；（2）若直线AB 与圆D 相交于M N 、两点，记OAB ∆的面积为1,S OMN ∆的面积为2S ，求12S S S =+的最大值.21（12分）.已知函数()2x x x f x ae ae xe =--()0, 2.718,a e e ≥=为自然对数的底数若()0f x ≥对于x R ∈恒成立. （1）求实数a 的值；（2）证明：()f x 存在唯一极大值点0x ，且()02ln 211244f x e e +≤<. (二)选考题：共10分.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程(10分) 已知曲线12cos :sin 1x t C y t =+⎧⎨=-⎩（t 为参数），24cos :sin x C y αα=⎧⎨=⎩（α为参数），在以原点O 为极点，x 轴非负半轴为极轴的极坐标系中，直线()3:4C R πθρ=∈.（1）求曲线12,C C 的普通方程，并说明它们分别表示什么曲线；（2）若2C 上的点P 对应的参数,2Q πα=为1C 上的点，求PQ 的中点M 到直线3C 距离d的最小值.23.选修4-5：不等式选讲（10分）设函数()121f x x x =-+-. （1）解不等式()34f x x >-；（2）若()2165f x x m m +-≥-对一切实数x 都成立，求m 的取值范围.。

山东省青岛市2014届高三数学3月统一质量检测理(青岛市一模)新人教A版

青岛市高三统一质量检测数学（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试时间120分钟．注意事项：1．答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔（中性笔）将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试题卷上．3．第Ⅱ卷必须用0.5毫米黑色签字笔（中性笔）作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 若集合2{|02},{|1}A x x B x x =≤≤=>，则A B =A ．{|01}x x ≤≤B ．{|0x x >或1}x <-C ．{|12}x x <≤D ．{|02}x x <≤2. 已知向量(1,2)a =-,(3,)b m =,R m ∈,则“6m =-”是“//()a a b +”的 A ．充要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件3. 右图是一容量为100的样本的重量的频率分布直方图，则由图可估计样本重量的中位数为A ．11B ．11.5C ．12D ．12.54. 双曲线22145x y -=的渐近线方程为A．y x = B．y x = C．y x = D．y = 5. 执行右图所示的程序框图，则输出的结果是 A ．5B ．7C ．9D ．116. 函数22cos ()2y x π=+图象的一条对称轴方程可以为A ．4x π=B ．3x π= C ．34x π= D ．x π=7.过点P 作圆221O x y ：＋＝的两条切线，切点分别为A 和B ，则弦长||AB =AB ．2 CD ．48. 已知实数y x ,满足约束条件04340x x y y >⎧⎪+≤⎨⎪≥⎩，则1y w x +=的最小值是A ．2-B ．2C ．1-D ．1 9. 由曲线1xy =，直线,3y x x ==所围成封闭的平面图形的面积为A ．329B ．4ln3-C ．4ln3+D ．2ln3- 10. 在实数集R 中定义一种运算“*”，对任意,R a b ∈，a b *为唯一确定的实数，且具有性质：（1）对任意R a ∈，0a a *=；（2）对任意,R a b ∈，(0)(0)a b ab a b *=+*+*．关于函数1()()xxf x e e =*的性质，有如下说法：①函数)(x f 的最小值为3；②函数)(x f 为偶函数；③函数)(x f 的单调递增区间为(,0]-∞．其中所有正确说法的个数为 A ．0 B ．1C ．2D ．3第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共25分． 11. 已知2a ib i i+=+（R a b ∈，），其中i 为虚数单位，则a b += ；12. 已知随机变量ξ服从正态分布(0,1)N ，若(1)P a ξ>=，a 为常数,则(10)P ξ-≤≤= ；13. 二项式621()x x -展开式中的常数项为； 14. 如图所示是一个四棱锥的三视图，则该几何体的体积为；15. 已知函数213,1()log , 1x x x f x x x ⎧-+≤⎪=⎨>⎪⎩ ，()|||1|g x x k x =-+-，若对任意的12,R x x ∈，都有12()()f x g x ≤成立，则实数k 的取值范围为 .三、解答题：本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤. 16. （本小题满分12分）在ABC ∆中, c b a ,,分别是角C B A ,,的对边，且2cos cos (tan tan 1)1A C A C -=. （Ⅰ）求B 的大小;（Ⅱ）若2a c +=，b =求ABC ∆的面积.17．（本小题满分12分）2013年6月“神舟 ”发射成功．这次发射过程共有四个值得关注的环节，即发射、实验、授课、返回．据统计，由于时间关系，某班每位同学收看这四个环节的直播的概率左视图分别为34、13、12、23，并且各个环节的直播收看互不影响．（Ⅰ）现有该班甲、乙、丙三名同学，求这3名同学至少有2名同学收看发射直播的概率; （Ⅱ）若用X 表示该班某一位同学收看的环节数,求X 的分布列与期望．18．（本小题满分12分）如图几何体中，四边形ABCD 为矩形，24AB BC ==，DE AE CF BF ===，2EF =，//EF AB ，CF AF ⊥.（Ⅰ）若G 为FC 的中点，证明：//AF 面BDG ；（Ⅱ）求二面角A BF C --的余弦值.19．（本小题满分12分）已知{}n a 是等差数列，首项31=a ，前n 项和为n S .令(1)(N )n n n c S n *=-∈,{}n c 的前20项和20330T =.数列}{n b 是公比为q 的等比数列，前n 项和为n W ，且12b =，39q a =.（Ⅰ）求数列{}n a 、{}n b 的通项公式；（Ⅱ）证明：1(31)(N )n n n W nW n *++≥∈.20．（本小题满分13分）CABDE FG已知椭圆1C 的中心为原点O ，离心率e =2，其一个焦点在抛物线2:C 22y px =的准线上，若抛物线2C 与直线: 0l x y -+=相切．（Ⅰ）求该椭圆的标准方程；（Ⅱ）当点(,)Q u v 在椭圆1C 上运动时，设动点(,)P v u u v 2-+的运动轨迹为3C ．若点T 满足：OT MN OM ON =+2+，其中,M N 是3C 上的点，直线OM 与ON 的斜率之积为1-2，试说明：是否存在两个定点,F F 12，使得TF TF 12+为定值？若存在，求,F F 12的坐标；若不存在，说明理由．21．（本小题满分14分）已知函数()ln f x ax x =+，函数()g x 的导函数()xg x e '=，且(0)(1)g g e '=，其中e 为自然对数的底数．（Ⅰ）求()f x 的极值；（Ⅱ）若(0,)x ∃∈+∞，使得不等式()g x<成立，试求实数m 的取值范围；（Ⅲ）当0a =时，对于(0,)x ∀∈+∞，求证：()()2f x g x <-．青岛市高三统一质量检测数学（理科）参考答案及评分标准一、选择题：本大题共10小题．每小题5分，共50分． C A C B C D A D B C二、填空题：本大题共5小题，每小题5分，共25分． 11.1 12.12a - 13.15 14．4 15．34k ≤或54k ≥ 三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16. （本小题满分12分）解：（Ⅰ）由2cos cos (tan tan 1)1A C A C -=得：sin sin 2cos cos (1)1cos cos A CA C A C-= ………………………………………………………2分∴2(sin sin cos cos )1A C A C -=∴1cos()2A C +=-，………………………………………………………………………4分∴1cos 2B =，又0B π<<3B π∴=……………………………………………………………………………………6分（Ⅱ）由余弦定理得：2221cos 22a cb B ac +-== 22()2122a c acb ac +--∴=， ………………………………………………………………8分又2a c +=，b =27234ac ac --=，54ac = ……………………………10分115sin 224216ABC S ac B ∆∴==⨯⨯=………………………………………………12分 17．（本小题满分12分）解: （Ⅰ）设“这3名同学至少有2名同学收看发射直播”为事件A ,则22333333327()()(1)()44432P A C C =⨯-+=. …………………………………………………4分（Ⅱ）由条件可知X 可能取值为0,1,2,3,4.31121(0)(1)(1)(1)(1);432336P X ==-⨯-⨯-⨯-=31123112(1)(1)(1)(1)(1)(1)(1)432343233112311213(1)(1)(1)(1)(1)(1);4323432372P X ==⨯-⨯-⨯-+-⨯⨯-⨯-+-⨯-⨯⨯-+-⨯-⨯-⨯= 311231123112(2)(1)(1)(1)(1)(1)(1)4323432343233112311231127(1)(1)(1)(1)(1)(1);43234323432318P X ==⨯⨯-⨯-+⨯-⨯⨯-+⨯-⨯-⨯+-⨯⨯⨯-+-⨯⨯-⨯+-⨯-⨯⨯= 31123112(3)(1)(1)432343233112311223 (1)(1);4323432372P X ==-⨯⨯⨯+⨯-⨯⨯+⨯⨯-⨯+⨯⨯⨯-=31121(4);432312P X ==⨯⨯⨯=即…………………………………………………………………10分X 的期望11372319()0123436721872124E X =⨯+⨯+⨯+⨯+⨯=.………………………12分18．（本小题满分12分）解：（Ⅰ）连接AC 交BD 于O 点，则O 为AC 的中点，连接OG 因为点G 为FC 中点，所以OG 为AFC ∆的中位线，所以//OG AF………………………………………………………………………2分AF ⊄面BDG ，OG ⊂面BDG ，所以//AF 面BDG ………………4分（Ⅱ）取AD 中点M ，BC 的中点Q ，连接MQ ，则////MQ AB EF ，所以MQFE 共面作FP MQ ⊥于P ，EN MQ ⊥于N ，则//EN FP 且EN FP =AE DE ==BF CF =，AD BC = ADE ∴∆和BCF ∆全等，EM FQ ∴= ENM ∴∆和FPQ ∆全等，1MN PQ ∴==BF CF =，Q 为BC 中点，BC FQ ∴⊥又BC MQ ⊥，FQMQ Q =，BC ∴⊥面MQFEPF BC ∴⊥，PF ∴⊥面ABCD …………………………………………………………6分以P 为原点，PF 为z 轴建立空间直角坐标系如图所示，则(3,1,0)A ，(1,1,0)B -，(1,1,0)C --，设(0,0,)F h ，则(3,1,)AF h =--，(1,1,)CF h =AF CF ⊥，203102AF CF h h ∴⋅=⇒--+=⇒=设面ABF 的法向量1111(,,)n x y z =(3,1,2)AF =--，(1,1,2)BF =-由111111110320200n AF x y z x y z n BF ⎧⋅=--+=⎧⎪⇒⎨⎨-+=⋅=⎩⎪⎩，令11110,2z x y =⇒==1(0,2,1)n ∴= ………………………………………………………………………………8分设面CBF 的法向量2222(,,)n x y z =(1,1,2)BF =-，(0,2,0)BC =-由222222020200n BF x y z y n BC ⎧⋅=-+=⎧⎪⇒⎨⎨-=⋅=⎩⎪⎩，令22210,2z y x =⇒==-2(2,0,1)n ∴=-……………………………………………………………………………10分 1212121cos ,5||||5n n n n n n ⋅∴<>===⋅设二面角A BF C --的平面角为θ，则12121cos cos(,)cos ,5n n n n θπ=-<>=-<>=- …………………………………12分 19．（本小题满分12分）解：(Ⅰ)设等差数列的公差为d ，因为(1)nn n c S =-所以20123420330T S S S S S =-+-+++=则24620330a a a a ++++=则10910(3)23302d d ⨯++⨯= 解得3d =，所以33(1)3n a n n =+-=……………………………………………………4分所以3927q a ==，3q =所以123n n b -=⋅………………………………………………………………………………6分(Ⅱ)由(Ⅰ)知，2(13)3113n n n W -==-- 要证1(31)n n n W nW ++≥，只需证1(31)(31)(31)nn n n ++-≥-即证：321nn ≥+……………………………………………………………………………8分当1n =时，321nn =+下面用数学归纳法证明：当2n ≥时，321nn >+（1）当2n =时，左边9=，右边5=，左>右，不等式成立（2）假设(2)n k k =≥，321kk >+ 则1n k =+时，13333(21)632(k+1)+1k k k k +=⨯>+=+>1n k ∴=+时不等式成立根据（1）（2）可知：当2n ≥时，321nn >+综上可知：321n n ≥+对于N n *∈成立所以1(31)(N )n n n W nW n *++≥∈ ………………………………………………………12分20．（本小题满分13分）解：（I）由22220-0y pxy py x y ⎧=⎪⇒-+=⎨=⎪⎩，抛物线2:C 22y px =与直线: -0l x y +=相切，240p p ∴∆=-=⇒=……………………………………………………2分 ∴抛物线2C的方程为：2y =，其准线方程为：x =c ∴=离心率e =2，∴2c e a ==∴2222, 2a b a c ==-=，故椭圆的标准方程为221.42x y +=…………………………………………………………5分（II ）设1122(,),(,)M x y N x y ，(,)P x y ''，(,)T x y则2x v u y u v '=-⎧⎨'=+⎩1(2)31()3u y x v x y ⎧''=-⎪⎪⇒⎨⎪''=+⎪⎩当点(,)Q u v 在椭圆1C 上运动时，动点(,)P v u u v 2-+的运动轨迹3C2222111[(2)]2[()]44233u v y x x y ''''∴+=⇒-++= 2 2212x y ''⇒+= 3C ∴的轨迹方程为：22212x y += ………………………………………………………7分由OT MN OM ON =+2+得212111221212(,)(,)2(,)(,)(2,2),x y x x y y x y x y x x y y =--++=++12122,2.x x x y y y =+=+设,OM ON k k 分别为直线OM ，ON 的斜率，由题设条件知12121,2OM ON y y k k x x ⋅==-因此121220,x x y y +=…………………………………………9分因为点,M N 在椭圆22212x y +=上，所以22221122212,212x y x y +=+=，故222222*********(44)2(44)x y x x x x y y y y +=+++++2222112212121212(2)4(2)4(2)604(2).x y x y x x y y x x y y =+++++=++所以22260x y +=，从而可知：T 点是椭圆2216030x y +=上的点， ∴存在两个定点,F F 12，且为椭圆2216030x y +=的两个焦点，使得TF TF 12+为定值，其坐标为12(F F ． …………………………………………………13分21．（本小题满分14分）解：(Ⅰ) 函数()f x 的定义域为(0,)+∞，1()f x a x'=+(0)x >．当0a ≥时，()0f x '>，()f x ∴在(0,)+∞上为增函数，()f x 没有极值；……………1分当0a <时，1()()a x a f x x+'=，若1(0,)x a ∈-时，()0f x '>；若1(,)x a∈-+∞时，()0f x '< ()f x ∴存在极大值，且当1x a =-时，11()()ln()1f x f a a=-=--极大综上可知：当0a ≥时，()f x 没有极值；当0a <时，()f x 存在极大值，且当1x a=-时，11()()ln()1f x f a a=-=--极大 …………………………………………………………4分(Ⅱ) 函数()g x 的导函数()x g x e '=，()xg x e c ∴=+ (0)(1)g g e '=，(1)c e e ∴+=0c ⇒=，()x g x e =……………………………………5分(0,)x ∃∈+∞，使得不等式()g x<成立，∴(0,)x ∃∈+∞，使得3m x e <-成立，令()3h x x e =-，则问题可转化为：max ()m h x <对于()3h x x e =-，(0,)x ∈+∞，由于()1x h x e '=-，当(0,)x ∈+∞时，1x e >≥=1x e ∴>，()0h x '∴<，从而()h x 在(0,)+∞上为减函数，()(0)3h x h ∴<=3m ∴<………………………………………………………………………………………9分 (Ⅲ)当0a =时，()ln f x x =，令()()()2x g x f x ϕ=--，则()ln 2xx e x ϕ=--， ∴1()xx e xϕ'=-，且()x ϕ'在(0,)+∞上为增函数设()0x ϕ'=的根为x t =，则1t e t =，即t t e -= 当(0,)x t ∈时，()0x ϕ'<，()x ϕ在(0,)t 上为减函数；当(,)x t ∈+∞时，()0x ϕ'>，()x ϕ在(,)t +∞上为增函数，min ()()ln 2ln 22t t t t x t e t e e e t ϕϕ-∴==--=--=+-(1)10e ϕ'=->，1()202ϕ'=<，1(,1)2t ∴∈由于()2t t e t ϕ=+-在1(,1)2t ∈上为增函数，12min 11()()222022t x t e t e ϕϕ∴==+->+->-= ()()2f x g x ∴<- …………………………………………………………………………14分。

山东省青岛市2011届高三教学质量3月统一检测(文综)

青岛市高三教学质量统一检测文科综合 2011.03本试卷分第Ⅰ卷和第Ⅱ卷两部分，共16页。

满分240分。

考试用时150分钟。

答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、科类等填写在答题卡规定的位置。

考试结束后，将答题卡交回。

第Ⅰ卷（必做，共100分）注意事项：1．第Ⅰ卷共25小题，每小题4分，共100分。

在每小题给出的四个选项中，只有一项是最符合题目要求的。

2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不涂在答题卡上，只答在试卷上不得分。

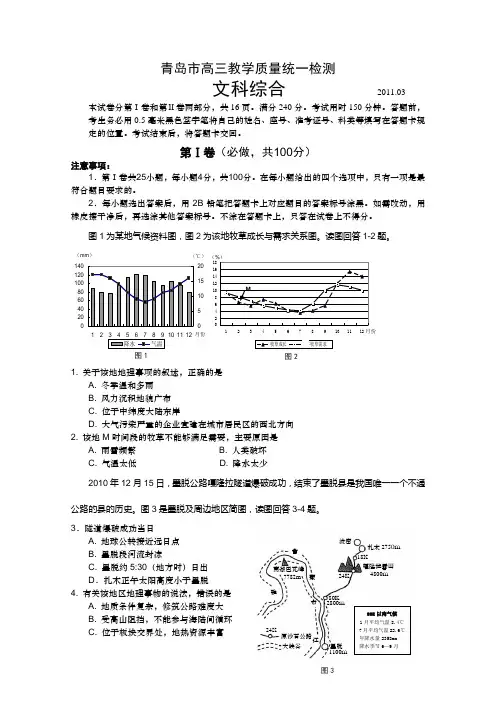
图1为某地气候资料图，图2为该地牧草成长与需求关系图。

读图回答1-2题。

1. 关于该地地理事项的叙述，正确的是A. 冬季温和多雨B. 风力沉积地貌广布C. 位于中纬度大陆东岸D. 大气污染严重的企业宜建在城市居民区的西北方向 2. 该地M 时间段的牧草不能够满足需要，主要原因是A. 雨雪频繁B. 人类破坏C. 气温太低D. 降水太少2010年12月15日，墨脱公路嘎隆拉隧道爆破成功，结束了墨脱县是我国唯一一个不通公路的县的历史。

图3是墨脱及周边地区简图，读图回答3-4题。

3．隧道爆破成功当日A. 地球公转接近远日点B. 墨脱段河流封冻C. 墨脱约5:30（地方时）日出 D ．扎木正午太阳高度小于墨脱4. 有关该地区地理事物的说法，错误的是A. 地质条件复杂，修筑公路难度大B. 受高山阻挡，不能参与海陆间循环C. 位于板块交界处，地热资源丰富图2图3鲁藏雅南迦巴瓦峰7782m 原沙石公路大峡谷24K波密扎木2750m 嘎隆拉雪山 4800m24K80K 2800m墨脱 1100m18K布江80K 以南气候 1月平均气温8.4℃7月平均气温22.6℃ 年降水量2358mm降水季节6—9月D. 墨脱地处喜马拉雅山迎风坡，降水丰沛图4是某城市制造业与服务业空间分布模式图。

读图回答5-6题。

六校2011届高三第三次联考(理数.269K)

六校2011届高三第三次联考数学（理科）（中山纪中、深圳实验、东莞中学、珠海一中、惠州一中、广州二中）本试卷分选择题和非选择题两部分，共4页，满分为150分。

考试用时120分钟。

注意事项：1、答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和学号填写在答题卡和答卷密封线内相应的位置上，用2B 铅笔将自己的学号填涂在答题卡上。

2、选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案；不能答在试卷上。

3、非选择题必须用黑色字迹的钢笔或签字笔在答卷纸上作答，答案必须写在答卷纸各题目指定区域内的相应位置上，超出指定区域的答案无效；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4、考生必须保持答题卡的整洁和平整。

参考公式：（1）锥体的体积公式是Sh V 31=（2）记 f(k)+f(k+1)+f(k+2)++f(n)=∑=nki i f )(,其中k, n 为正整数且k ≤n 一、选择题:(每小题5分，共40分)1．若A=04|{2<-x x x }，B={}|30x x -<，则A B =（）A ． (0,3) B. (0,4) C. (0,3) D. (3，4) 2. 等比数列}{n a 中,已知4,242==a a ,则=6a （） A. 6 B. 8 C. 10 D. 163. 下列函数中，既是偶函数又在()0,+∞上单调递增的是A. 3y x = B. c o s y x = C.x y tan= D . ln y x = 4. 已知空间向量)1,3,(),0,1,3(-==x b a ，且a b ⊥ ，则x =（） A ．3- B.1- C. D. 35、已知椭圆的长轴长是短轴长的3倍，则椭圆的离心率等于（）． A ．31 B ．32 C ．322 D ．3106. 设a 、b 是两条不同的直线，α、β是两个不同的平面，是下列命题中正确的是（）A ．若//a b ，//a α，则//b αB ．若αβ⊥，//a α，则a β⊥C ．若αβ⊥，a β⊥，则//a αD ．若a b ⊥，a α⊥，b β⊥，则αβ⊥7. 方程 03log 3=-+x x 的解所在的区间是（） A ．（0,1） B. (1,2) C.(2,3) D. (3,4)8. 已知过点（1，2）的二次函数c bx ax y ++=2的图象如右图，给出下列论断：①0>abc ，②0<+-c b a ,③1<b ， ④21>a . 其中正确论断是（） A ． ①③ B. ②④C. ②③D. ②③④二、填空题：（每小题5分，共30分，把正确答案填写在答卷相应地方上） 9. 已知}{n a 是首项为1的等差数列，且512,a a a 是的等比中项，且n n a a >+1，则}{n a 的前n 项和n S =______10. 在ABC ∆中，a=15,b=10,A=60°，则cos 2B =_______11. 如图所示，为了计算图中由曲线轴及与直线x x xy 222== 所围成的阴影部分的面积S=_____________。

山东省青岛市2011届高三教学质量3月统一检测(数学文)

青岛市高三教学质量统一检测 2011.03数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)两部分，共150分，考试时间120分钟. 注意事项：1. 答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2. 第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试题卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.参考公式：台体的体积公式为：121(3V S S h =++，其中1S ，2S 分别为台体的上、下底面积，h 为台体的高.第Ⅰ卷 (选择题共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 复数31ii++（i 为虚数单位）的虚部是 A. 2- B. 2 C. i - D. 1-2. 某时段内共有100辆汽车经过某一雷达地区，时速频率分布直方图如右图所示,则时速超过60km/h 的汽车数量为 A.38辆 B.28辆 C.10辆 D.5辆3. 已知全集R U =,集合2{|20}A x x x =->,{|lg(1)}B x y x ==-,则()U B A ð等于A. {|2x x >或0}x <B. {|12}x x <<C. {|12}x x <≤D. {|12}x x ≤≤ 4. 下列四个函数中,在区间(0,1)上为减函数的是 A.2log y x =B.1y x =C.1()2xy =- D.13y x =5. 设,a b 为两条不重合的直线,,αβ为两个不重合的平面,下列命题中为真命题的是 A ．若,a b 与α所成角相等,则//a bB ．若//,//,//a b αβαβ,则//a bC ．若,,//a b a b αβ⊂⊂,则//αβD ．若,,a b αβαβ⊥⊥⊥,则a b ⊥6. 已知4cos 5α=-,且(,)2παπ∈,则tan()4πα-等于 A ．17-B ．7-C ．71D ．77. 已知实数m 是2,8的等比中项,则双曲线221y x m-=的离心率为 ABCD8. 右图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,的等腰梯形,则该几何体的体积是 A.283π B.73π C.28π D. 7π9. “0a =”是“函数ln ||y x a =-为偶函数”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分又不必要条件 10. 定义运算a bc d ,ad bc =-则函数3()1f x =s i n c o s xx图象的一条对称轴方程是 A ．56x π=B ．23x π=C ．3x π=D ．6π=x 11. 若0,0,a b >>且4=+b a ,则下列不等式恒成立的是A ．211>abB ．111≤+ba C ．2≥ab D ．228a b +≥ 12. 若函数)(x f 满足1()1(1)f x f x +=+,当[0,1]x ∈时,()f x x =,若在区间(1,1]-上,()()g x f x mx m =--有两个零点,则实数m 的取值范围是A. )21,0[B. 1[,)2+∞C. )31,0[D. ]21,0(第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分． 13. 已知向量a 、b 的夹角为60,||2,||3a b ==, 则|2|a b -= ;14. 右面程序框图中输出S 的值为 ;侧视图俯视图 8 第题15. 若001x y x y y -≤⎧⎪+≥⎨⎪≤⎩,则2z x y =+的最大值是__________;16．点P 是曲线2y x x =-上任意一点,则点P 到直线3y x =-的距离的最小值是；三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤．17．（本小题满分12分）设集合{1,2}A =,{1,2,3}B =,分别从集合A 和B 中随机取一个数a 和b .(Ⅰ)若向量(,),(1,1)m a b n ==-,求向量m 与n 的夹角为锐角的概率;(Ⅱ) 记点(,)P a b ,则点(,)P a b 落在直线x y n +=上为事件n C (25)n n ≤≤∈N ，, 求使事件n C 的概率最大的n .18. （本小题满分12分）已知向量1(sin ,1),(3cos ,)2a xb x =-=-, 函数()()2f x a b a =+⋅-. (Ⅰ)求函数()f x 的最小正周期T ;(Ⅱ)已知a 、b 、c 分别为ABC ∆内角A 、B 、C 的对边, 其中A 为锐角,4a c ==,且()1f A =,求,A b 和ABC ∆的面积S .19．（本小题满分12分）如图所示,正方形ADEF 与梯形ABCD 所在的平面互相垂直,,//,22AD CD AB CD CD AB AD ⊥==.(Ⅰ)求证：BC BE ⊥；(Ⅱ)在EC 上找一点M ,使得//BM 平面ADEF ,请确定M 点的位置,并给出证明．20．（本小题满分12分）数列}{n a 的前n 项和记为n S ,t a =1,点1(,)n n S a +在直线EBA CDF21y x =+上,N n *∈．(Ⅰ)当实数t 为何值时,数列}{n a 是等比数列？ (Ⅱ)在(Ⅰ)的结论下,设31log n n b a +=,n T 是数列11{}n n b b +⋅的前n 项和,求2011T 的值．21.（本小题满分12分）已知函数32()2f x x ax x =+++．(Ⅰ)若1a =-,令函数()2()g x x f x =-,求函数()g x 在(1,2)-上的极大值、极小值； (Ⅱ)若函数()f x 在1(,)3-+∞上恒为单调递增函数,求实数a 的取值范围.22．（本小题满分14分）已知圆221:(1)8C x y ++=,点2(1,0)C ,点Q 在圆1C 上运动,2QC 的垂直平分线交1QC 于点P . (Ⅰ) 求动点P 的轨迹W 的方程；(Ⅱ) 设,M N 是曲线W 上的两个不同点,且点M 在第一象限,点N 在第三象限,若122OM ON OC +=,O 为坐标原点,求直线MN 的斜率k ；(Ⅲ)过点)31,0(-S 且斜率为k 的动直线．．．l 交曲线W 于,A B 两点,在y 轴上是否存在定点D ,使以AB 为直径的圆恒过这个点？若存在,求出D 的坐标,若不存在,说明理由．青岛市高三教学质量统一检测 2011.03数学 (文科) 参考答案及评分标准一、选择题：本大题共12小题．每小题5分，共60分． D A C B D D A B A A D D二、填空题：本大题共4小题，每小题4分，共16分． 13. 13 14. 94 15. 3 16．三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤． 17．（本小题满分12分）解：(Ⅰ) 设向量m 与n 的夹角为θ因为θ为锐角 ∴cos 0m n m nθ⋅=>，且向量m 与n 不共线,因为0,0a b >>,(1,1)n =-,显然m 与n 不共线,所以,0m n a b ⋅=->,a b >………………………2分分别从集合A 和B 中随机取一个数a 和b 的基本事件有;(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)………………………………………5分所以向量m 与n 的夹角为锐角的概率16P =………………………………………6分 (Ⅱ)由(Ⅰ)知;当2n =时，满足条件的概率216P =………………………7分当3n =时，满足条件的概率313P =………………………………………8分当4n =时，满足条件的概率413P =………………………………………9分当5n =时，满足条件的概率516P =………………………………………10分所以使事件n C 的概率最大的n 值为3或4……………………………………12分 18. （本小题满分12分）解: (Ⅰ) 2()()22f x a b a a a b =+⋅-=+⋅-21sin 1cos 22x x x =+++-…………………………………………2分1cos 21222x x -=-12cos 22x x =-sin(2)6x π=-…………………4分因为2ω=,所以22T ππ==…………………………………………6分 (Ⅱ) ()sin(2)16f A A π=-=因为5(0,),2(,)2666A A ππππ∈-∈-，所以262A ππ-=，3A π=……………8分则2222cos a b c bc A =+-，所以211216242b b =+-⨯⨯，即2440b b -+= 则2b =…………………………………………10分从而11sin 24sin 602322S bc A ==⨯⨯⨯=12分 19．（本小题满分12分）证明： (Ⅰ)因为正方形ADEF 与梯形ABCD 所在的平面互相垂直，DE AD ⊥ 所以DE ⊥平面ABCD DE BC ∴⊥………………………………………1分因为AB AD =，所以,4ADB BDC π∠=∠=BD ==取CD 中点N ，连接BN则由题意知：四边形ABND 为正方形所以BC ====，BD BC =则BDC ∆为等腰直角三角形则BD BC ⊥…………5分则BC ⊥平面BDE则BC BE ⊥………………7分 (Ⅱ)取EC 中点M ，则有//BM 平面ADEF …………8分证明如下：连接MN由(Ⅰ)知//BN AD ，所以 //BN 平面ADEF又因为M 、N 分别为CE 、CD 的中点，所以 //MN DE 则//MN 平面ADEF ………………10分则平面//BMN 平面ADEF ，所以//BM 平面ADEF ……………………12分 20．（本小题满分12分）解： (Ⅰ)由题意得121n n a S +=+，121n n a S -=+(2)n ≥ ……1分两式相减得)2(3,211≥==-++n a a a a a n n n n n 即，……4分所以当2≥n 时，}{n a 是等比数列，要使1≥n 时，}{n a 是等比数列，则只需31212=+=tt a a ，从而1=t ． ……7分 (Ⅱ)由(Ⅰ)得知13n n a -=，31log n n b a n +==，……9分11111(1)1n n b b n n n n +==-⋅++ ……10分201112201120121111111(1)()()22320112012T b b b b =+⋅⋅⋅+=-+-+⋅⋅⋅+-20112012= …12分 21. （本小题满分12分）解：(Ⅰ)3232()2(2)2g x x x x x x x x =--++=-++-，所以2()321g x x x '=-++EBACNDFM由()0g x '=得13x =-或1x =………………………………………2分所以函数()g x 在3x =-处取得极小值27-；在1x =处取得极大值1-………………6分 (Ⅱ) 因为2()321f x x ax '=++的对称轴为3a x =-（1）若133a -≥-即1a ≤时，要使函数()f x 在1(,)3-+∞上恒为单调递增函数，则有24120a ∆=-≤，解得：a ≤≤1a ≤≤；………………………8分（2）若133a -<-即1a >时，要使函数()f x 在1(,)3-+∞上恒为单调递增函数，则有2111()3()2()10333f a -=⋅-+⋅-+≥，解得：2a ≤，所以12a <≤；…………10分综上，实数a 的取值范围为2a ≤≤………………………………………12分 22．（本小题满分14分）解: (Ⅰ) 因为2QC 的垂直平分线交1QC 于点P . 所以2PC PQ =222211112=>==+=+C C QC PQ PC PC PC所以动点P 的轨迹W 是以点21,C C 为焦点的椭圆……………3分设椭圆的标准方程为12222=+by a x则22,222==c a ，1222=-=c a b ，则椭圆的标准方程为2212x y +=……5分 (Ⅱ) 设1122(,),(,)M a b N a b ，则2222112222,22a b a b +=+= ①因为122OM ON OC +=，则121222,20a a b b +=-+= ②由①②解得112215,,2448a b a b ===-=-……………8分所以直线MN 的斜率k 212114b b a a -==-……………10分 (Ⅲ)直线l 方程为13y kx =-，联立直线和椭圆的方程得: 221312y kx x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 得229(12)12160k x kx +--=…………11分由题意知：点)31,0(-S 在椭圆内部，所以直线l 与椭圆必交与两点，设).,(),,(2211y x B y x A 则121222416,3(12)9(12)k x x x x k k +==-++ 假设在y 轴上存在定点),0(m D ，满足题设，则1122(,),(,)DA x y m DB x y m =-=- 因为以AB 为直径的圆恒过点D ,则1122(,)(,)0DA DB x y m x y m ⋅=-⋅-=，即:1212()()0x x y m y m +--= (*)因为112211,33y kx y kx =-=-则(*)变为21212121212()()()x x y m y m x x y y m y y m +--=+-++…………12分21212121111()()()3333x x kx kx m kx kx m =+----+-+221212121(1)()()339k x x k m x x m m =+-+++++222218(1)(9615)9(21)m k m m k -++-=+ 由假设得对于任意的R k ∈,0DA DB ⋅=恒成立，即221096150m m m ⎧-=⎪⎨+-=⎪⎩解得1m =. 因此，在y 轴上存在满足条件的定点D ，点D 的坐标为(0,1).………………14分。

2011届高三数学月考、联考、模拟试题汇编直线和圆

直线和圆题组一一、选择题1．（北京龙门育才学校2011届高三上学期第三次月考）直线x-y+1=0与圆（x+1）2+y 2=1的位置关系是（） A ．相切 B ．直线过圆心 C ．直线不过圆心但与圆相交 D ．相离答案 B.2．（北京五中2011届高三上学期期中考试试题理）若过定点)0,1(-M 且斜率为k 的直线与圆05422=-++y x x 在第一象限内的部分有交点，则k 的取值范围是( ))(A 50<<k )(B 05<<-k )(C 130<<k )(D 50<<k答案 A.3、（福建省三明一中2011届高三上学期第三次月考理）两圆042222=-+++a ax y x 和0414222=+--+b by y x 恰有三条公切线，若R b R a ∈∈,，且0≠ab ，则2211b a +的最小值为（）A ．91B ．94C ．1D ．3答案 C.3．（福建省厦门双十中学2011届高三12月月考题理）已知点P 是曲线C:321y x x =++上的一点，过点P 与此曲线相切的直线l 平行于直线23y x =-，则切线l 的方程是（） A ．12+=x y B ．y=121+-xC ．2y x =D ．21y x =+或2y x =答案 A.4. （福建省厦门双十中学2011届高三12月月考题理）设斜率为1的直线l 与椭圆124:22=+y x C 相交于不同的两点A 、B ，则使||AB 为整数的直线l 共有（） A ．4条 B ．5条 C ．6条 D ．7条答案 C.5.（福建省厦门外国语学校2011届高三11月月考理）已知圆22670x y x +--=与抛物线22(0)y px p =>的准线相切，则p ＝（ ▲ ）A 、1B 、2C 、3D 、4答案 B.6．（甘肃省天水一中2011届高三上学期第三次月考试题理）过点M(1,5)-作圆22(1)(2)4x y -+-=的切线,则切线方程为（） A ．1x =-B ．512550x y +-=C ．1512550x x y =-+-=或D ．15550x x y =-+-=或12答案 C.7．（甘肃省天水一中2011届高三上学期第三次月考试题理）已知圆222410x y x y ++-+=关于直线220ax by -+=41(0,0),a b a b>>+对称则的最小值是（）A ．4B ．6C ．8D ．9答案 D.8．（广东省惠州三中2011届高三上学期第三次考试理）已知直线x y a +=与圆224x y +=交于A 、B 两点，O 是坐标原点，向量OA 、OB满足||||OA OB OA OB +=-，则实数a 的值是（）（A ）2 （B ）2- （C 或（D ）2或2- 答案 D.9. （广东省清远市清城区2011届高三第一次模拟考试理）曲线321y x x x =-=-在处的切线方程为（ A ．20x y -+= B ．20x y +-= C ． 20x y ++= D ．20x y --=答案 C.10.（贵州省遵义四中2011届高三第四次月考理）若直线02=+-c y x 按向量)1,1(-=a 平移后与圆522=+y x 相切，则c 的值为（）A ．8或－2B ．6或－4C ．4或－6D ．2或－8邪恶少女漫画/wuyiniao/ 奀莒哂答案 A.11.（黑龙江大庆实验中学2011届高三上学期期中考试理）若直线y x =是曲线322y x x ax =-+的切线，则a =（）.1A .2B .1C - .1D 或2 答案 D.邪恶少女漫画/wuyiniao/ 奀莒哂12．（黑龙江哈九中2011届高三12月月考理）“3=a ”是“直线012=--y ax ”与“直线046=+-c y x 平行”的（）A ．充分不必要条件 C ．必要不充分条件D ．充要条件D ．既不充分也不必要条件答案 B.13．（湖北省南漳县一中2010年高三第四次月考文）已知α∥β，a ⊂α，B ∈β，则在β内过点B 的所有直线中A ．不一定存在与a 平行的直线B ．只有两条与a 平行的直线C ．存在无数条与a 平行的直线D ．存在唯一一条与a 平行的直线答案 D.14．（重庆市南开中学2011届高三12月月考文）已知圆C 与直线040x y x y -=--=及都相切，圆心在直线0x y +=上，则圆C 的方程为（）A ．22(1)(1)2x y ++-=B ．22(1)(1)2x y -++=C ．22(1)(1)2x y -+-=D ．22(1)(1)2x y +++=答案 B. 二、填空题14．（湖北省南漳县一中2010年高三第四次月考文）已知两点(4,9)(2,3)P Q --,，则直线PQ 与y 轴的交点分有向线段PQ的比为．答案 2.15. （福建省厦门外国语学校2011届高三11月月考理）已知椭圆的中心为坐标原点O ，焦点在x 轴上，斜率为1且过椭圆右焦点的直线交椭圆于A 、B 两点，)1,3(-=+与共线，求椭圆的离心率▲▲.答案 36=e . 16．（甘肃省天水一中2011届高三上学期第三次月考试题理）设直线30ax y -+=与圆22(1)(2)4x y -+-=相交于A 、B 两点，且弦AB 的长为a = 答案 0.17. （广东省中山市桂山中学2011届高三第二次模拟考试文）在极坐标中，圆4cos ρθ=的圆心C 到直线sin()4πρθ+=的距离为 .18．（河南省郑州市四十七中2011届高三第三次月考文）如下图，直线PC 与圆O 相切于点C ，割线PAB 经过圆心O ，弦CD ⊥AB 于点E ， 4PC =，8PB =，则CE = .答案12519.（黑龙江省哈尔滨市第162中学2011届高三第三次模拟理）已知函数()x f 的图象关于直线2=x 和4=x 都对称，且当10≤≤x 时，()x x f =.求()5.19f =_____________。

2.山东省济宁市2011届高三3月模拟考试(数学理)word版

山东省济宁市2011届高三3月高考模拟考试数学试题（理科）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分。

考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上参考公式：V sh =柱，其中s 是柱体的底面积，h 是柱体的高。

13V sh =锥体，其中s 是锥体的底面积，h 是锥体的高。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集U R =，集合{|24}x M x =<和{||1|2}N x x =-<的关系的韦恩（venn ）图如图所示，则阴影部分所表示的集合是（）A ．{|3}x x ≥B ．{|23}x x <<C ．{|2}x x ≥D ．{|12}x x -<< 2．已知复数z 的实部为1，虚部为-1，则i z 表示的点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．等差数列{}n a 的前n 项和为n S ，若27121330,a a a S ++=则的值是（）A ．130B ．65C ．70D ．75 4．过点(2,0)-且倾斜角为4π的直线l 与圆225x y +=相交于M 、N 两点，则线段MN 的长为（）A ．B ．3C ．D ．65．如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h 随时间t 变化的图象可能是（）6．阅读右面程序框图，任意输入一次(01)x x ≤≤与(01)y y ≤≤，则能输出数对(,)x y 的概率为（）A ．13B ．23 C ．14 D ．34 00x a <<，7．已知a 是函数12()2log x f x x =-的零点，若则0()f x 的值满足（）A ．0()0f x =B ．0()0f x <C ．0()0f x >D ．0()f x 的符号不确定8．已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=+>><<为奇函数，该函数的部分图象如图所示，EFG ∆是边长为2的等边三角形，则(1)f 的值为（）A ．B ．C D ．9．已知函数2010()sin x f x x e x =++，令1213()(),()(),(n n f x f x f x f x f x f x f x f x +''''==== ，则2011()f x =（）A ．sin x x e +B ．cos x x e +C ．sin x x e -+D ．cos xx e -+ 10．已知1:0,:420x x x p q m x -≤+-≤，若p q 是的充分条件，则实数m 取值范围是（）A ．2m >+B ．2m ≤+C ．2m ≥D ．6m ≥ 11．已知抛物线22(0)y px p =>上一点(1,)(0)M m m >到其焦点的距离为5，双曲线221x y a-=的左顶点为A ，若双曲线的一条渐近线与直线AM 平行，则实数a 的值是（） A ．125 B ．19 C ．15 D ．1312．给定两个长度为1的平面向量OA OB 和，它们的夹角为90︒，如图所示，点C 在以O 为圆心的圆弧AB 上运动，若CO xOA yOB =+ ，其中,x y R ∈，则x y +的最大值是（）A ．1 BC D ．2 第Ⅱ卷（非选择题，共90分）注意事项：1．第II 卷必须使用0.5毫米的黑色墨水签字笔书写，作图时，可用2B 铅笔。

数学理卷·2011届山东省青岛市高三教学质量3月统一检测(2011.03)

山东省青岛市2011届高三教学质量统一检测 2011.03数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)两部分，共150分，考试时间120分钟. 注意事项：1. 答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2. 第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试题卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.参考公式：台体的体积公式为：121(3V S S h =+，其中1S ，2S 分别为台体的上、下底面积，h 为台体的高.第Ⅰ卷 (选择题共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 已知复数21iz i =-，则复数z 的共轭复数为 A .1i + B .1i -+ C .1i - D .1i --2. 已知全集U R =，集合2{|20}A x x x =->，{|lg(1)}B x y x ==-，则()U A B ð等于A .{|20}x x x ><或B .{|12}x x <<C . {|12}x x <≤D .{|12}≤≤x x3. 下列四个函数中，在区间(0，1)上是减函数的是A .2log y x =B . 1y x =C .1()2xy =- D .13y x =4. 已知直线 l 、m ，平面α、β，且l α⊥，m β⊂，则//αβ是l m ⊥的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件5. 二项式62()x x-的展开式中，2x 项的系数为A .15B .15-C .30D .606. 以坐标轴为对称轴，原点为顶点且过圆222690x y x y +-++=圆心的抛物线方程是A .2233y x y x ==-或B .23y x =C .2293y x y x =-=或D .22-9y x y x ==或7. 右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4A .283π B .73πC .28πD .7π8. 若00x y x y y a -≤⎧⎪+≥⎨⎪≤⎩，若2z x y =+的最大值为3，则a 的值是A .1B .2C .3D .49. 已知等差数列{}n a 的前项和为n S ，若M 、N 、P 三点共线，O 为坐标原点，且156ON a OM a OP=+(直线MP 不过点O )，则20S 等于 A .15 B .10 C .40 D .2010. 定义运算：12142334a a a a a a a a =-，将函数sin ()cos xf x x -=向左平移m 个单位(0)m >，所得图象对应的函数为偶函数，则m 的最小值是 A .6π B .3π C .56π D .23π11. 下列四个命题中，正确的是A .已知函数0()sin af a xdx =⎰，则[()]1cos12f f π=-；B .设回归直线方程为 2 2.5y x =-，当变量x 增加一个单位时，y 平均增加2个单位；C .已知ξ服从正态分布(0N ,2)σ，且(20)0.4P ξ-≤≤=，则(2)0.2P ξ>=D .对于命题p ：x R ∃∈,使得210x x ++<，则p ⌝：x R ∀∈，均有210x x ++>12. 若1()1(1)f x f x +=+，当[0x ∈，1]时，()f x x =，若在区间(1-，1]内()()g x f x mx m =--有两个零点，则实数m 的取值范围是A .[0，1)2B .1[2，)+∞C .[0，1)3D .(0，1]2正视图侧视图俯视图第Ⅱ卷 (选择题共60分)二、填空题：本大题共4小题，每小题4分，共16分.13. 某时段内共有100辆汽车经过某一雷达地区，时速频率分布直方图如右图所示，则时速超过60/km h 的汽车数量为14. 执行如图所示的程序框图，若输出的b 的值为16，图中判断框内?处应填的数为 15. 若不等式1|21|||a xx-?对一切非零实数x 恒成立，则实数a 的取值范围16. 点P 是曲线2ln y x x =-上任意一点，则点P 到直线2y x =-的距离的最小值是三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)已知向量(sin m x =u r，1)-，向量n x =r ，1)2-，函数.()()f x m n m =+u r r u r .(Ⅰ)求()f x 的最小正周期T ；(Ⅱ)已知a ，b ，c 分别为ABC D 内角A ，B ，C 的对边，A为锐角，a =4c =，且()f A 恰是()f x 在[0，]2p上的最大值，求A ，b 和ABC D 的面积S . 18. (本小题满分12分)如图，PDCE 为矩形，ABCD 为梯形，平面PDCE ^平面ABCD ，90BADADC?? ，12AB AD CD a ===，PD (Ⅰ)若M 为PA 中点，求证：//AC 平面MDE ； (Ⅱ)求平面PAD 与PBC 所成锐二面角的余弦值.19. (本小题满分12分)某单位实行休年假制度三年以来，50名职工休年假的次数进行的调根据上表信息解答以下问题：(Ⅰ)从该单位任选两名职工，用h 表示这两人休年假次数之和，记“函数2()1f x x x =--h 在区间(4，6)上有且只有一个零点”为事件A ，求事件A 发生的概率P ；(Ⅱ)从该单位任选两名职工，用x 表示这两人休年假次数之差的绝对值，求随机变量x 的分布列及数学期望E x .20.(本小题满分12分)已知数列{}n b 满足11124n n b b +=+，且172b =，n T 为{}n b 的前n 项和.(Ⅰ)求证：数列1{}2n b -是等比数列，并求{}n b 的通项公式； (Ⅱ)如果对任意*n N Î，不等式1227122nkn n T ?+-恒成立，求实数k 的取值范围.21.(本小题满分12分)已知函数322()233f x x ax x =-++. (Ⅰ)当14a =时，求函数()f x 在[2-，2]上的最大值、最小值； (Ⅱ)令()ln(1)3()g x x f x =++- ，若()g x 在1(2-，)+ 上单调递增，求实数a 的取值范围.22.(本小题满分14分)已知圆1C ：22(1)8x y ++=，点2(1C ，0)，点Q 在圆1C 上运动，2QC 的垂直平分线交1QC 于点P .(Ⅰ)求动点P 的轨迹W 的方程；(Ⅱ)设、M N 分别是曲线W 上的两个不同点，且点M 在第一象限，点N 在第三象限，若1+22OM ON OC =uuu r uuu r uuu r，O 为坐标原点，求直线MN 的斜率k ；(Ⅲ)过点(0S ，1)3-且斜率为k 的动直线l 交曲线W 于，A B 两点，在y 轴上是否存在定点D ，使以AB 为直径的圆恒过这个点？若存在，求出D 的坐标，若不存在，说明理由.青岛市高三教学质量统一检测 2011.03高中数学 (理科)参考答案及评分标准一、选择题：本大题共12小题．每小题5分，共60分． A C B B D D B A B A A D二、填空题：本大题共4小题，每小题4分，共16分．13. 38 14. 3 15.13[,]22- 16．三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤．17. （本小题满分12分）解: (Ⅰ)21()()sin 1cos 2f x m n m x x x =+⋅=+++ …………2分1cos 2112222x x -=+++12cos 2222x x =-+ sin(2)26x π=-+…………5分因为2ω=，所以22T ππ==…………6分(Ⅱ) 由(Ⅰ)知：()sin(2)26f A A π=-+[0,]2x π∈时,52666x πππ-≤-≤由正弦函数图象可知,当262x ππ-=时()f x 取得最大值3所以262A ππ-=,3A π=…………8分由余弦定理，2222cos a b c bc A =+-∴211216242b b =+-⨯⨯∴2b =………10分从而11sin 24sin 6022S bc A ==⨯⨯= 12分 18．（本小题满分12分）(Ⅰ) 证明:连结PC ,交DE 与N ,连结MN ，PAC ∆中，,M N 分别为两腰,PA PC 的中点 ∴//MN AC …………2分因为MN ⊂面MDE ,又AC ⊄面MDE ，所以//AC 平面MDE …………4分(Ⅱ) 设平面PAD 与PBC 所成锐二面角的大小为θ，以D 为空间坐标系的原点，分别以,,DA DC DP 所在直线为,,x y z 轴建立空间直角坐标系，则),(,,0),(0,2,0)P B a a C a(,,),(,,0)PB a a BC a a ==-…………6分设平面PAD 的单位法向量为1n，则可设1(0,1,0)n =…………7分设面PBC 的法向量2(,,1)n x y =，应有22(,,1)(,,)0(,,1)(,,0)0n PB x y a a n BC x y a a ⎧==⎪⎨=-=⎪⎩即：00ax ay ax ay ⎧+=⎪⎨-+=⎪⎩，解得：22x y ⎧=⎪⎪⎨⎪=⎪⎩，所以2n = …………10分∴12121cos 2||||n n n n θ⋅===…………11分x所以平面PAD 与PBC 所成锐二面角的余弦值为12…………12分 19．（本小题满分12分）解:(Ⅰ) 函数()21f x x x η=--过(0,1)-点，在区间(4,6)上有且只有一个零点，则必有(4)0(6)0f f <⎧⎨>⎩即：1641036610ηη--<⎧⎨-->⎩，解得：153546η<< 所以，4η=或5η=…………3分当4η=时，211201015125068245C C C P C +==，当5η=时，11201522501249C C P C ==…………5分 4η=与5η=为互斥事件，由互斥事件有一个发生的概率公式所以12681212824549245P P P =+=+=…………6分 (Ⅱ) 从该单位任选两名职工，用ξ表示这两人休年假次数之差的绝对值，则ξ的可能取值分别是0,1,2,3，…………7分于是()22225102015250207C C C C P C ξ+++===，1111115101020152025022(1)49C C C C C C P C ξ++===，1111520101525010(2)49C C C C P C ξ+===，115152503(3)49C C P C ξ===…………10分从而ξ的分布列：ξ的数学期望：0123749494949E ξ=⨯+⨯+⨯+⨯=． …………12分20．（本小题满分12分）解: (Ⅰ) 对任意*N n ∈,都有11124n n b b +=+，所以1111()222n n b b +-=- 则1{}2n b -成等比数列,首项为1132b -=，公比为12…………2分所以1113()22n n b --=⨯，1113()22n n b -=⨯+…………4分(Ⅱ) 因为1113()22n n b -=⨯+ 所以2113(1)111123(1...)6(1)1222222212n n n n n n n T --=+++++=+=-+-…………6分因为不等式1227(122)n k n n T ≥-+-，化简得272nn k -≥对任意*N n ∈恒成立…………7分设272n n n c -=，则1112(1)72792222n n n nn n n nc c ++++----=-=…………8分当5n ≥,1n n c c +≤,{}n c 为单调递减数列，当15n ≤<,1n n c c +>,{}n c 为单调递增数列45131632c c =<=,所以, 5n =时, n c 取得最大值332…………11分所以, 要使272nn k -≥对任意*N n ∈恒成立，332k ≥…………12分 21．（本小题满分12分）解: (Ⅰ)14a =时, 3221()332f x x x x =-++，2()23(23)(1)f x x x x x '=-++=--+ 令()0f x '=,得1x =-或3x =…………2分可以看出在1x =-取得极小值,在2x =取得极大值…………5分而48(2),(2)33f f -==由此, 在[2,2]-上,()f x 在1x =-处取得最小值116-,在32x = 处取得最小值278…………6分(Ⅱ)()ln(1)3()g x x f x '=++-2ln(1)3(243)x x ax =+---++2ln(1)24x x ax =++-2'144(1)14()4411x a x ag x x a x x +-+-=+-=++…………7分在1(,)2-+∞上恒有10x +>考察2()44(1)14h x x a x a =+-+-的对称轴为44182a a x --=-= (i)当1122a -≥-,即0a ≥时，应有216(1)16(14)0a a ∆=---≤ 解得:20a -<≤，所以0a =时成立…………9分(ii)当1122a -<-,即0a <时，应有1()02h ->即:114(1)1402a a --⨯+-> 解得0a <…………11分综上：实数a 的取值范围是0a ≤…………12分 22. （本小题满分14分）解: (Ⅰ) 因为2QC 的垂直平分线交1QC 于点P . 所以2PC PQ =222211112=>==+=+C C QC PQ PC PC PC所以动点P 的轨迹ω是以点21,C C 为焦点的椭圆……………2分设椭圆的标准方程为12222=+by a x则22,222==c a ，1222=-=c a b ，则椭圆的标准方程为2212x y +=……4分 (Ⅱ) 设1122(,),(,)M a b N a b ，则2222112222,22a b a b +=+= ①因为122OM ON OC +=则121222,20a a b b +=-+= ②由①②解得112215,,2448a b a b ===-=-……………7分所以直线MN 的斜率k 212114b b a a -==-……………8分 (Ⅲ)直线l 方程为13y kx =-，联立直线和椭圆的方程得: 221312y kx x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 得229(12)12160k x kx +--=…………9分由题意知：点)31,0(-S 在椭圆内部，所以直线l 与椭圆必交与两点，设).,(),,(2211y x B y x A 则121222416,3(12)9(12)k x x x x k k +==-++ 假设在y 轴上存在定点),0(m D ，满足题设，则1122(,),(,)DA x y m DB x y m =-=-因为以AB 为直径的圆恒过点D ,则1122(,)(,)0DA DB x y m x y m ⋅=-⋅-=，即:1212()()0x x y m y m +--= (*)因为112211,33y kx y kx =-=-则(*)变为21212121212()()()x x y m y m x x y y m y y m +--=+-++…………11分21212121111()()()3333x x kx kx m kx kx m =+----+-+221212121(1)()()339k x x k m x x m m =+-+++++222216(1)1421()9(21)33(21)39k k k m m m k k +=--++++++ 222218(1)(9615)9(21)m k m m k -++-=+ 由假设得对于任意的R k ∈,0DA DB ⋅=恒成立，即221096150m m m ⎧-=⎪⎨+-=⎪⎩解得1m =……13分因此，在y 轴上存在满足条件的定点D ，点D 的坐标为(0,1).………………14分。

山东省青岛市2011届高三三月质检(二)(理数)

7 8 9 94 5 6 4 7 3第2题图高三自主检测数学（理） 2011.03本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试时间120分钟．注意事项：1．答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔（中性笔）将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试题卷上．3．第Ⅱ卷必须用0.5毫米黑色签字笔（中性笔）作答，答案必须写在答题纸上各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 复数ii 21)1(2+-等于A ．5254i --B ．5254i +-C ．5254i -D ．5254i + 2. 如图是2011年元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为A ．84，85B ．84，84C ．85，84 D. 85，853. 已知幂函数()af x x =（a 为常数）的图象过点1(2,2，则()f x 的一个单调递减区间是 A ． (,0]-∞ B ．(,)-∞+∞ C ．(1,1)- D ．(1,2)4. 已知)0(54)2sin(ππ<<-=+x x ，则sin 2x 的值为 A ．1225B ．2512-C ．2425 D. 2425-5. 如图所示正三角形中阴影部分的面积S 是(0)h h H ≤≤的函数，则该函数的图象是6. 已知 αβ、是平面， m n 、是直线，给出下列命题 ①若 m m αβ⊥⊂，，则αβ⊥；②若α⊂m ，α⊂n ，// //m n ββ，，则//αβ;③如果 m n αα⊂⊄，， m n 、是异面直线，那么n 与α相交;④若m αβ=，//n m ，且 n n αβ⊄⊄，，则//n α且//n β.其中正确命题的个数是A ．3 B ．2 C ．1 D ．07. 把函数sin()(0 ||)y x ωϕωϕπ=+><，的图象向左平移6π个单位，再将图象上所有点的横坐标变为原来的2倍（纵坐标不变），所得的图象解析式为sin y x =，则 A ．26πωϕ==， B ．32πϕω-==， C ．126πωϕ==， D ．1221πϕω==， 8．若偶函数()f x 在,0](-∞上是减函数，则下列关系中成立的是A. 02020(01)(11)(11)f f f (6).<.<. B. 02002(11)(11)(01)f f f ..6..<.<. C. 02020(01)(11)(11)f f f (6).>.>. D. 02020(11)(01)(11)f f f (6).<.<.9．过(2,2)点且与曲线222220x y x y ++--=相交所得弦长为A ．3420x y -+=B ．3420x y -+=或2x =C ．3420x y -+=或2y =D ．2x =或2y =10．设0x 是函数()log xb f x a x =-的一个零点，其中011a b <<>，则有 A.0(1,1)x ∈- B.0(0,)x b ∈ C.0(,1)(1,)x b b ∈-- D.0(,1)(0,1)x b ∈--11. 在ABC ∆中，NC AN 31=，P 是BN 上的一点，若m 112+=，则实数m 的值为A ．911 B ．511 C. 211 D. 31112．定义在R 上的偶函数()f x 对任意的实数x 都有3()()2f x f x =-+，且(1)1f -=，(0)2f =-，则(1)(2)(3)...(2011)f f f f ++++的值为A. 2-B. 1-C. 1D. 0第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分．13．某位高三学生要参加高校自主招生考试，现从6所高校中选择3所报考，由于其中两所学校的考试时间相同，因此该生不能同时选择这两所学校，则该学生不同的选学校方法种数是．14．在ABC Rt ∆中,若90,,C AC b BC a ∠===,则ABC ∆外接圆半径222b a r +=; 运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为c b a ,,，则其外接球的半径R = ．15．已知),(y x 满足⎩⎨⎧≤≤≤≤1010y x ，求点),(y x 落在曲线y =y x =所围成区域内的概率为．16．双曲线22221(0,0)x y a b a b -=>>的离心率为2，则ab 312+的最小值为 .三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤．17. （本小题满分12分）ABC ∆中，角A B C 、、所对应的边分别为a b c 、、，若sin sin sin a c Bb c A C-=-+. (Ⅰ)求角A ；(Ⅱ)若函数22()cos ()sin ()sin ([0,])2f x x A x A x x π=+--+∈，求函数()f x 的取值范围.18．（本小题满分12分）某同学报名参加“星光大道”青年志愿者的选拔．已知在备选的10道试题中，该同学能答对其中的6题，规定每次考试都从备选题中随机抽出3题进行测试（必须3题全部答完），至少答对2题才能入选.(Ⅰ)求该同学答对试题数ξ的概率分布列及数学期望；(Ⅱ)设η为该同学答对试题数与该同学答错试题数之差的平方，记“函数1()||2xf x η=-在定义域内单调递增”为事件C ，求事件C 的概率． 19．（本小题满分12分）一个多面体的直观图及三视图分别如图1和图2所示（其中正视图和侧视图均为矩形，俯视图是直角三角形），M N 、分别是111 AB AC 、的中点，1MN AB ⊥.(Ⅰ)求实数a 的值并证明//MN 平面11BCC B ；(Ⅱ)在上面结论下，求平面11AB C 与平面ABC 所成锐二面角的余弦值. 20．（本小题满分12分）已知数列}{n a 满足2121 (22)n n n a a a a a +++=+（其中*N n ∈）,01≠a ,且01≠+-n n a a . (Ⅰ)求}{n a 的通项公式；(Ⅱ)请比较n a2与n n a a +2的大小，并说明理由. 21．（本小题满分12分）设椭圆 221221(0)x y C a b a b+=>>：的左、右焦点分别是12 F F 、，下顶点为A ，线段OA 的中点为B （O 为坐标原点），若抛物线2:C 21y x =-与y 轴的交点为B ，且经过12 F F 、点．(Ⅰ)求椭圆1C 的方程；(Ⅱ)设4(0,)5M -，N 为抛物线2C 上的一动点，过点N 作抛物线2C 的切线交椭圆1C 于P Q 、两点，求MPQ ∆面积的最大值．正视图侧视图22. （本小题满分14分）已知函数()(R)xf x e kx x =-∈(Ⅰ)若k e =，试确定函数()f x 的单调区间；(Ⅱ)若0k >且对任意R x ∈，(||)0f x >恒成立，试确定实数k 的取值范围; (Ⅲ)设函数()()()F x f x f x =+-，求证：12(1)(2)(3)...()(2)n n F F F F n e +⋅⋅>+，*N n ∈高三自主检测数学 (理) 参考答案及评分标准 2011.03一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1—12 A A D D C B B A C C D C 二、填空题：本大题共4小题，每小题4分，共16分．13． 16 14．15． 6116．2三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤． 17.解：(Ⅰ)由sin sin sin a c B b c A C -=-+，得a c bb c a c-=-+………………1分即222a b c bc =+-，即222bc b c a =+-，所以，222122b c a bc +-=……………3分由余弦定理，1cos 2A =，因为,0A π<<所以3A π= …………………5分 (Ⅱ)22()cos ()sin ()sin f x x A x A x =+--+22cos ()sin ()sin 33x x x ππ=+--+221cos(2)1cos(2)33sin 22x x x ππ++--=-+…………………7分1cos 2sin 2x x =-+…………………9分22113sin sin (sin )224x x x =+-=+-…………………10分因为[0,]2x π∈，所以sin [0,1]x ∈………………11分由二次函数的图象，所以函数()f x 的取值范围13[,]22-…………12分 18．解：(Ⅰ)依题意，答对试题数ξ的可能取值为0,1,2,3………………1分则343101(0)30C P C ξ===，12643103(1)10C C P C ξ⋅=== 21643101(2)2C C P C ξ⋅===，363101(3)6C P C ξ=== …………………………5分其分布列如下：………………………………6分答对试题数ξ的数学期望：1311901233010265E ξ=⨯+⨯+⨯+⨯=……………8分 (Ⅱ)η的可能取值为1,9……………9分当1η=时, 11()||()22x xf x η=-=在定义域内是减函数. 当9η=时, 117()||()22x xf x η=-=在定义域内是增函数………………………10分其中 9η=分别是答对题数为0和3的情形，两事件为互斥事件1161()(0)(3)306305P C P P ξξ==+==+==………………………12分19.解: (Ⅰ)由图可知，111ABC A B C -为直三棱柱，侧棱1CC a =，底面为直角三角形，,3,4AC BC AC BC ⊥==以C 为坐标原点，分别以1,,CA CB CC 为,,x y z 轴建立空间直角坐标系，则13(3,0,0),(0,4,),(,0,)2A B a N a ，所以，3(,2,)22a M ，1(0,2,),(3,4,)2aMN AB a =--=-因为1MN AB ⊥，所以1(0,2,)(3,4,)02aMN AB a =---= 解得：4a =………………………………3分此时，(0,2,2)MN =--，平面11BCC B 的法向量(1,0,0)b =(1,0,0)(0,2,2)0MN b =--=MN 与平面11BCC B 的法向量垂直，且MN ⊄平面11BCC B所以，//MN 平面11BCC B ……………………………6分 (Ⅱ) 平面ABC 的法向量(0,0,1)m =设平面11AB C 的法向量为(,,1)n x y =,平面11AB C 与平面ABC 所成锐二面角的大小等于其法向量所成锐角θ的大小，法向量n 满足:110,0n AC n AB == ………………8分因为11(3,0,0),(0,0,4),(0,4,4)A C B ,11(3,0,4),(3,4,4)AC AB =-=-所以,11(3,0,4)(,,1)340(3,4,4)(,,1)3440n AC x y x n AB x y x y ⎧=-=-+=⎪⎨=-=-++=⎪⎩所以,430x y ⎧=⎪⎨⎪=⎩，4(,0,1)3n =………………10分所以, 3cos 5||||16m n m n θ===平面11AB C 与平面ABC 所成锐二面角的余弦值为35………………12分 20. (Ⅰ)解：因为221212n n n a a a a a +=+++ （1）所以 211121212---+=+++n n n a a a a a （2n ≥）（2）………………1分所以2n ≥时，（1）－（2）得：))((21)(21111---+-+-=n n n n n n n a a a a a a a ………2分变形可得 0))(1(11=+----n n n n a a a a由于01≠+-n n a a ，所以 11=--n n a a ，即}{n a 是公差为1的等差数列…………4分在（1）式中取1n =，可得2112121a a =，而01≠a ，故11=a ……………5分所以1(1)n a a n d n =+-=…………………6分 (Ⅱ)当1n =时, 22222na n n n a a n n ==+=+=；当2,3,4n =时, 22n a n n a a <+；当5n ≥时, 22na n n a a >+…………………8分证明:4n ≤时,计算比较可得结论……………………9分5n ≥时，采用数学归纳法证明上述结论 i)当5n =时,55222325530a==>+=ii)假设:(5)n k k =≥时结论成立，即22kk k >+(5)k ≥……………10分则当1n k =+时，有11222222.22()(21)(1)(2)k a k k k k k k k k k ++==>+=+++++-- 2(21)(1)(2)(1)k k k k k =+++++-+当5k ≥时，(2)(1)0k k -+>所以，222(21)(1)(2)(1)(21)(1)(1)1k k k k k k k k k k +++++-+>++++=+++ 即：只要(5)n k k =≥时结论成立，当1n k =+时，结论22na n n a a >+就成立…11分综合i) ii)可得：当5n ≥时, 2222na n n n a a n n =>+=+即：4n ≤时，22na n n a a ≤+5n ≥时, 22n a n n a a >+…………………12分21．解：由题意可知(0,1)B -，则(0,2)A -，故2b =………………1分令0y =得210x -=即1x =±，则12(1,0),(1,0)F F -，故1c =………………2分所以2225a b c =+=………………3分于是椭圆1C 的方程为：22154x y +=……………4分 (Ⅱ)设2(,1)N t t -，由于'2y x =知直线PQ 的方程为：2(1)2()y t t x t --=-．即221y tx t =--………………5分代入椭圆方程整理得：222224(15)20(1)5(1)200t x t t x t +-+++-=………6分222222400(1)80(15)[(1)4]t t t t ∆=+-++-4280(183)t t =-++,21225(1)15t t x x t++=+ , 221225(1)204(15)t x x t +-=+……………7分故12PQ x =-==…………………8分设点M 到直线PQ 的距离为d，则d ==…………………9分所以，MPQ ∆的面积12S PQ d =⋅2211215t t +=+=10分5=≤= 当3t =±时取到“=”，经检验此时0∆>，满足题意．综上可知，MPQ ∆………………12分 22．(Ⅰ) k e =,()xf x e ex =-()x f x e e '=-………………1分令()0f x '=，解得1x =………………2分当(1,)x ∈+∞时，0()f x >'，所以()f x 在(1,)+∞单调递增当(,1)x ∈-∞时，0()f x '<，()f x 在(,1)-∞单调递减所以, k e =时,函数()f x 的单调增区间为(1,)+∞,减区间为(,1)-∞……………4分 (Ⅱ)因为(||)f x 为偶函数，(||)0f x >恒成立等价于()0f x >对0x ≥恒成立当0x ≥时，()xf x e k '=-，令()0f x '=，解得ln x k =…………5分（i ）当ln 0k >，即1k >时，()f x 在(0,ln )k 减，在(ln ,)k +∞增min ()(ln )ln 0f x f k k k k ==->，解得1k e <<，所以1k e <<……………7分（ii ）当ln 0k ≤，即01k <≤时，()0xf x e k '=-≥，()f x 在[0,)+∞上单调递增，所以min ()(0)10f x f ==>，符合，所以01k <≤………………8分综合（i ）（ii ）,若0k >且对任意R x ∈,(||)0f x >恒成立,实数(0,)k e ∈………9分 (Ⅲ) nnxxee n F e e F e e x F ---+=+=+=)(,)1(,)(111111(1)()2n n n n n F F n e e e e e +-+---+⋅=+++>+………………11分12211(2)(1)2n n n n n F F n e e e e e +-+---+⋅-=+++>+…………………12分…………………………1()(1)2n F n F e +⋅>+……………………13分将上述n 个式子相乘,可得: 所以12(1)(2)()(2)n n F F F n e+>+……………………14分。

山东省青岛市高三数学3月统一质量检测试题理(含解析)

2015年山东省青岛市高考数学一模试卷（理科）一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2015•青岛一模）设i为虚数单位，复数等于（）A．﹣1+i B．﹣1﹣i C． 1﹣i D． 1+i【考点】：复数代数形式的乘除运算．【专题】：数系的扩充和复数．【分析】：直接利用复数代数形式的乘除运算化简求值．【解析】：解：=．故选：D．【点评】：本题考查了复数代数形式的乘除运算，是基础的计算题．2．（5分）（2015•青岛一模）设全集I=R，集合A={y|y=log2x，x＞2}，B={x|y=}，则（）A． A⊆B B． A∪B=A C．A∩B=∅ D．A∩（∁I B）≠∅【考点】：集合的包含关系判断及应用．【专题】：计算题；集合．【分析】：化简集合A，B，即可得出结论．【解析】：解：由题意，A={y|y=log 2x，x＞2}=（1，+∞），B={x|y=}==1.6．故选B．【点评】：本题考查茎叶图、平均数和方差，对于一组数据通常要求的是这组数据的众数，中位数，平均数，方差，它们分别表示一组数据的特征，这样的问题可以出现在选择题或填空题．4．（5分）（2015•青岛一模）“∀n∈N*，2a n+1=a n+a n+2”是“数列{a n}为等差数列”的（） A．充分不必要条件 B．必要不充分条件C．充要条件 D．即不充分也不必要条件【考点】：必要条件、充分条件与充要条件的判断；等差数列的性质．【专题】：等差数列与等比数列．【分析】：由2a n+1=a n+a n+2，可得a n+2﹣a n+1=a n+1﹣a n，可得数列{a n}为等差数列；若数列{a n}为等差数列，易得2a n+1=a n+a n+2，由充要条件的定义可得答案．【解析】：解：由2a n+1=a n+a n+2，可得a n+2﹣a n+1=a n+1﹣a n，由n的任意性可知，数列从第二项起每一项与前一项的差是固定的常数，即数列{a n}为等差数列，反之，若数列{a n}为等差数列，易得2a n+1=a n+a n+2，故“∀n∈N*，2a n+1=a n+a n+2”是“数列{a n}为等差数列”的充要条件，故选C【点评】：本题考查充要条件的判断，涉及等差数列的判断，属基础题．5．（5分）（2015•青岛一模）某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值是（）A． 2 B． C． D． 3【考点】：简单空间图形的三视图．【专题】：计算题；空间位置关系与距离．【分析】：根据三视图判断几何体为四棱锥，再利用体积公式求高x即可．【解析】：解：根据三视图判断几何体为四棱锥，其直观图是：V==3⇒x=3．故选D．【点评】：由三视图正确恢复原几何体是解题的关键．6．（5分）（2015•青岛一模）已知双曲线﹣=1（a＞0，b＞0）的一条渐近线平行于直线l：x+2y+5=0，双曲线的一个焦点在直线l上，则双曲线的方程为（） A．﹣=1 B．﹣=1C．﹣=1 D．﹣=1【考点】：双曲线的标准方程．【专题】：圆锥曲线的定义、性质与方程．【分析】：由已知得，由此能求出双曲线方程．【解析】：解：∵双曲线﹣=1（a＞0，b＞0）的一条渐近线平行于直线l：x+2y+5=0，双曲线的一个焦点在直线l上，∴，解得a=2，b=，∴双曲线方程为﹣=1．故选：A．【点评】：本题考查双曲线方程的求法，是基础题，解题时要认真审题，注意双曲线性质的合理运用．7．（5分）（2015•青岛一模）设m，n是不同的直线，α，β是不同的平面，下列命题中正确的是（）A．若m∥α，n⊥β，m⊥n，则α⊥β B．若m∥α，n⊥β，m⊥n，则α∥βC．若m∥α，n⊥β，m∥n，则α⊥β D．若m∥α，n⊥β，m∥n，则α∥β【考点】：平面与平面之间的位置关系．【专题】：空间位置关系与距离．【分析】：利用线面平行、垂直的判定定理和性质定理及面面垂直的判定定理即可判断出答案．【解析】：解：选择支C正确，下面给出证明．证明：如图所示：∵m∥n，∴m、n确定一个平面γ，交平面α于直线l．∵m∥α，∴m∥l，∴l∥n．∵n⊥β，∴l⊥β，∵l⊂α，∴α⊥β．故C正确．故选C．【点评】：正确理解和掌握线面平行、垂直的判定定理和性质定理及面面垂直的判定定理是解题的关键．8．（5分）（2015•青岛一模）函数y=4cosx﹣e|x|（e为自然对数的底数）的图象可能是（）A． B． C． D．【考点】：函数的图象．【专题】：函数的性质及应用．【分析】：先验证函数y=4cosx﹣e|x|是否具备奇偶性，排除一些选项，在取特殊值x=0时代入函数验证即可得到答案．【解析】：解：∵函数y=4cosx﹣e|x|，∴f（﹣x）=4cos（﹣x）﹣e|﹣x|=4cosx﹣e|x|=f（x），函数y=4cosx﹣e|x|为偶函数，图象关于y轴对称，排除BD，又f（0）=y=4cos0﹣e|0|=4﹣1=3，只有A适合，故选：A．【点评】：本题主要考查函数的图象，关于函数图象的选择题，通常先验证奇偶性，排除一些选项，再代特殊值验证，属于中档题．9．（5分）（2015•青岛一模）对于函数y=sin（2x﹣），下列说法正确的是（） A．函数图象关于点（，0）对称B．函数图象关于直线x=对称C．将它的图象向左平移个单位，得到y=sin2x的图象D．将它的图象上各点的横坐标缩小为原来的倍，得到y=sin（x﹣）的图象【考点】：函数y=Asin（ωx+φ）的图象变换；正弦函数的图象．【专题】：三角函数的图像与性质．【分析】： A，将x=代入可得y≠0，故不正确；B，将x=代入可得：y=﹣1，由正弦函数的图象和性质可知正确；C，求出平移后的函数解析式即可判断．D，求出平移后的函数解析式即可判断．【解析】：解：A，将x=代入可得：y=sin（2×﹣）=1，故不正确；B，将x=代入可得：y=sin（2×﹣）=﹣1，由正弦函数的图象和性质可知正确；C，将它的图象向左平移个单位，得到y=sin=sin（2x+）的图象，故不正确；D，将它的图象上各点的横坐标缩小为原来的倍，得到函数y=sin（4x﹣）的图象，故不正确．故选：B．【点评】：本题考查正弦函数的对称性、周期性，考查综合分析与应用能力，属于中档题．10．（5分）（2015•青岛一模）已知点G是△ABC的外心，是三个单位向量，且2++=，如图所示，△ABC的顶点B，C分别在x轴的非负半轴和y轴的非负半轴上移动，O是坐标原点，则||的最大值为（）A． B． C． 2 D． 3【考点】：向量的加法及其几何意义．【专题】：平面向量及应用．【分析】：根据题意，得出：①G是BC的中点，△ABC是直角三角形，且斜边BC=2；②点G的轨迹是以原点为圆心、1为半径的圆弧；③OA经过BC的中点G时，||取得最大值为2||．【解析】：解：∵点G是△ABC的外心，且2++=，∴点G是BC的中点，△ABC是直角三角形，∠BAC是直角；又∵是三个单位向量，∴BC=2；又∵△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动，∴点G的轨迹是以原点为圆心、1为半径的圆弧；又∵||=1，∴OA经过BC的中点G时，||取得最大值，最大值为2||=2．故选：C．【点评】：本题考查了平面向量的加法与减法的几何意义与应用问题，是基础题目．二、填空题：本大题共5小题，每小题5分，共25分．11．（5分）（2015•青岛一模）已知函数f（x）=tanx+sinx+2015，若f（m）=2，则f（﹣m）= 4028 ．【考点】：函数奇偶性的性质．【专题】：函数的性质及应用．【分析】：根据解析式得出f（﹣x）+f（x）=4030，f（m）+f（﹣m）=4030，即可求解．【解析】：解：∵函数f（x）=tanx+sinx+2015，∴f（﹣x）=﹣tanx﹣sinx+2015，∵f（﹣x）+f（x）=4030，∴f（m）+f（﹣m）=4030，∵f（m）=2，∴f（﹣m）=4028．故答案为：4028．【点评】：本题考查了函数的性质，整体运用的思想，属于容易题，难度不大．12．（5分）（2015•青岛一模）执行如图所示的程序框图，则输出的结果是132 ；【考点】：程序框图．【专题】：图表型；算法和程序框图．【分析】：模拟执行程序框图，依次写出每次循环得到的s，i的值，当i=10时，不满足条件i≥11，退出循环，输出s的值为132．【解析】：解：模拟执行程序框图，可得i=12，s=1满足条件i≥11，s=12，i=11满足条件i≥11，s=132，i=10不满足条件i≥11，退出循环，输出s的值为132．故答案为：132．【点评】：本题主要考查了程序框图和算法，依次正确写出每次循环得到的s，i的值是解题的关键，属于基本知识的考查．13．（5分）（2015•青岛一模）设a=∫12（3x2﹣2x）dx，则二项式（ax2﹣）6展开式中的第6项的系数为﹣24 ．【考点】：定积分；二项式系数的性质．【专题】：导数的概念及应用；二项式定理．【分析】：先根据定积分的计算法则求出a的值，再根据二项式展开式的通项公式求出第6项的系数．【解析】：解：a=∫12（3x2﹣2x）dx=（x3﹣x2）|=4，∴（ax2﹣）6=（4x2﹣）6，∵T k+1=，∴T6=T5+1=﹣•4x﹣3，=﹣24x﹣3，∴展开式中的第6项的系数为﹣24，故答案为：﹣24．【点评】：本题考查了定积分的计算法则和根据二项式展开式的通项公式，属于与基础题．14．（5分）（2015•青岛一模）若目标函数z=kx+2y在约束条件下仅在点（1，1）处取得最小值，则实数k的取值范围是（﹣4，2）．【考点】：简单线性规划．【专题】：不等式的解法及应用．【分析】：作出不等式对应的平面区域，利用线性规划的知识，确定目标取最优解的条件，即可求出k的取值范围．【解析】：解：作出不等式对应的平面区域，由z=kx+2y得y=﹣x+，要使目标函数z=kx+2y仅在点B（1，1）处取得最小值，则阴影部分区域在直线z=kx+2y的右上方，∴目标函数的斜率﹣大于x+y=2的斜率且小于直线2x﹣y=1的斜率即﹣1＜﹣＜2，解得﹣4＜k＜2，即实数k的取值范围为（﹣4，2），故答案为：（﹣4，2）．【点评】：本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．根据条件目标函数仅在点（1，1）处取得最小值，确定直线的位置是解决本题的关键．15．（5分）（2015•青岛一模）若X是一个集合，τ是一个以X的某些子集为元素的集合，且满足：①X属于τ，∅属于τ；②τ中任意多个元素的并集属于τ；③τ中任意多个元素的交集属于τ．则称τ是集合X上的一个拓扑．已知集合X={a，b，c}，对于下面给出的四个集合τ：①τ={∅，{a}，{c}，{a，b，c}}；②τ={∅，{b}，{c}，{b，c}，{a，b，c}}；③τ={∅，{a}，{a，b}，{a，c}}；④τ={∅，{a，c}，{b，c}，{c}，{a，b，c}}．其中是集合X上的拓扑的集合τ的序号是②④．【考点】：集合的包含关系判断及应用．【专题】：压轴题；新定义．【分析】：根据集合X上的拓扑的集合τ的定义，逐个验证即可：①{a}∪{c}={a，c}∉τ，③{a，b}∪{a，c}={a，b，c}∉τ，因此①③都不是；②④满足：①X属于τ，∅属于τ；②τ中任意多个元素的并集属于τ；③τ中任意多个元素的交集属于τ，因此②④是，从而得到答案．【解析】：解：①τ={∅，{a}，{c}，{a，b，c}}；而{a}∪{c}={a，c}∉τ，故①不是集合X上的拓扑的集合τ；②τ={∅，{b}，{c}，{b，c}，{a，b，c}}，满足：①X属于τ，∅属于τ；②τ中任意多个元素的并集属于τ；③τ中任意多个元素的交集属于τ因此②是集合X上的拓扑的集合τ；③τ={∅，{a}，{a，b}，{a，c}}；而{a，b}∪{a，c}={a，b，c}∉τ，故③不是集合X上的拓扑的集合τ；④τ={∅，{a，c}，{b，c}，{c}，{a，b，c}}．满足：①X属于τ，∅属于τ；②τ中任意多个元素的并集属于τ；③τ中任意多个元素的交集属于τ因此④是集合X上的拓扑的集合τ；故答案为②④．【点评】：此题是基础题．这是考查学生理解能力和对知识掌握的灵活程度的问题，重在理解题意．本题是开放型的问题，要认真分析条件，探求结论，对分析问题解决问题的能力要求较高．三、解答题：本大题共6小题，共75分．请写出必要的文字说明、证明过程或演算步骤．16．（12分）（2015•青岛一模）设△ABC的内角A，B，C所对的边分别为a，b，c，已知，b=3．（Ⅰ）求角B；（Ⅱ）若sinA=，求△ABC的面积．【考点】：余弦定理；正弦定理．【专题】：解三角形．【分析】：（I）利用正弦定理与余弦定理即可得出；（II）利用正弦定理、两角和差的正弦公式、三角形的面积计算公式即可得出．【解析】：解：（Ⅰ）∵，∴，∴a2﹣b2=ac﹣c2，∴，∵B∈（0，π），∴．（Ⅱ）由b=3，，，得a=2，由a＜b得A＜B，从而，故，∴△ABC的面积为．【点评】：本题考查了正弦定理与余弦定理、正弦定理、两角和差的正弦公式、三角形的面积计算公式，考查了推理能力与计算能力，属于中档题．17．（12分）（2015•青岛一模）某大学准备在开学时举行一次大学一年级学生座谈会，拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加，各学院邀请的学生数如下表所示：学院机械工程学院海洋学院医学院经济学院人数 4 6 4 6（Ⅰ）从这20名学生中随机选出3名学生发言，求这3名学生中任意两个均不属于同一学院的概率；（Ⅱ）从这20名学生中随机选出3名学生发言，设来自医学院的学生数为ξ，求随机变量ξ的概率分布列和数学期望．【考点】：离散型随机变量及其分布列；列举法计算基本事件数及事件发生的概率；离散型随机变量的期望与方差．【专题】：概率与统计．【分析】：（Ⅰ）从20名学生随机选出3名的方法数为，选出3人中任意两个均不属于同一学院的方法数为，由此利用等可能事件概率计算公式能求出这3名学生中任意两个均不属于同一学院的概率．（Ⅱ）ξ可能的取值为0，1，2，3，分别求出相应的概率，由此能求出随机变量ξ的概率分布列和数学期望．【解析】：（本小题满分12分）解：（Ⅰ）从20名学生随机选出3名的方法数为，选出3人中任意两个均不属于同一学院的方法数为：…（4分）所以…（6分）（Ⅱ）ξ可能的取值为0，1，2，3，，…（10分）所以ξ的分布列为0 1 2 3P所以…（12分）【点评】：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要注意排列组合知识的合理运用．18．（12分）（2015•青岛一模）如图，在四棱柱ABCD﹣A1B1C1D1中，侧棱AA1⊥底面 ABCD，底面ABCD是直角梯形，AD∥BC，∠BAD=90°，AD=AA1=3，BC=1，E1为A1B1中点．（Ⅰ）证明：B1D∥平面AD1E1；（Ⅱ）若AC⊥BD，求平面ACD1和平面CDD1C1所成角（锐角）的余弦值．【考点】：二面角的平面角及求法；直线与平面平行的判定．【专题】：空间位置关系与距离；空间角．【分析】：（Ⅰ）连结A1D交AD1于G，四边形ADD1A1为平行四边形，从而B1D∥E1G，由此能证明B1D∥平面AD1E1．（Ⅱ）以A为坐标原点，AB，AD，AA1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，求出平面ACD1的一个法向量和平面CDD1C1的一个法向量，由此利用向量法能求出平面ACD1和平面CDD1C1所成角（锐角）的余弦值．【解析】：（本小题满分12分）（Ⅰ）证明：连结A1D交AD1于G，因为ABCD﹣A1B1C1D1为四棱柱，所以四边形ADD1A1为平行四边形，所以G为A1D的中点，又E1为A1B1中点，所以E1G为△A1B1D的中位线，从而B1D∥E1G…（4分）又因为B1D⊄平面AD1E1，E1G⊂平面AD1E1，所以B1D∥平面AD1E1．…（5分）（Ⅱ）解：因为AA1⊥底面ABCD，AB⊂面ABCD，AD⊂面ABCD，所以AA1⊥AB，AA1⊥AD，又∠BAD=90°，所以AB，AD，AA1两两垂直．…（6分）如图，以A为坐标原点，AB，AD，AA1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系．设AB=t，则A（0，0，0），B（t，0，0），C（t，1，0），D（0，3，0），C1（t，1，3），D1（0，3，3）．从而，．因为AC⊥BD，所以，解得．…（8分）所以，．设是平面ACD1的一个法向量，则即令x1=1，则．…（9分）又，．设是平面CDD1C1的一个法向量，则即令x2=1，则．…（10分）∴，∴平面ACD1和平面CDD1C1所成角（锐角）的余弦值．…（12分）【点评】：本小题考查空间中直线与平面的位置关系、空间向量的应用等基础知识，考查空间想象能力、推理论证能力及运算求解能力，考查化归与转化思想、函数与方程思想．19．（12分）（2015•青岛一模）已知数列{a n}是等差数列，S n为{a n}的前n项和，且a10=19，S10=100；数列{b n}对任意n∈N*，总有b1•b2•b3…b n﹣1•b n=a n+2成立．（Ⅰ）求数列{a n}和{b n}的通项公式；（Ⅱ）记c n=（﹣1）n，求数列{c n}的前n项和T n．【考点】：数列的求和；等差数列的前n项和．【专题】：等差数列与等比数列．【分析】：（1）由题意和等差数列的前n项和公式求出公差，代入等差数列的通项公式化简求出a n，再化简b1•b2•b3…b n﹣1•b n=a n+2，可得当n≥2时b1•b2•b3…b n﹣1=2n﹣1，将两个式子相除求出b n；（2）由（1）化简c n=（﹣1）n，再对n分奇数和偶数讨论，分别利用裂项相消法求出T n，最后要用分段函数的形式表示出来．【解析】：解：（Ⅰ）设{a n}的公差为d，则a10=a1+9d=19，，解得a1=1，d=2，所以a n=2n﹣1…（3分）所以b1•b2•b3…b n﹣1•b n=2n+1…①当n=1时，b1=3，当n≥2时，b1•b2•b3…b n﹣1=2n﹣1…②①②两式相除得因为当n=1时，b1=3适合上式，所以…（6分）（Ⅱ）由已知，得则T n=c1+c2+c3+…+c n=…（7分）当n为偶数时，==…（9分）当n为奇数时，==…（11分）综上：…（12分）【点评】：本题考查数列的递推公式，等差数列的通项公式、前n项和公式，裂项相消法求数列的和，以及分类讨论思想，考查化简、计算能力，属于中档题．20．（13分）（2015•青岛一模）已知椭圆C：+y2=1与直线l：y=kx+m相交于E、F两不同点，且直线l与圆O：x2+y2=相切于点W（O为坐标原点）．（Ⅰ）证明：OE⊥OF；（Ⅱ）设λ=，求实数λ的取值范围．【考点】：椭圆的简单性质．【专题】：方程思想；直线与圆；圆锥曲线的定义、性质与方程．【分析】：（Ⅰ）由直线l与圆O相切，得圆心到直线l的距离d=r，再由直线l与椭圆C 相交，得出E、F点的坐标关系，从而证明OE⊥OF；（Ⅱ）根据直线l与圆O相切于点W，以及OE⊥OF，得出λ=的坐标表示，求出λ的取值范围．【解析】：解：（Ⅰ）因为直线l与圆O相切，所以圆x2+y2=的圆心到直线l的距离d==，∴；…（2分）由，得：（1+2k2）x2+4kmx+2m2﹣2=0；设E（x1，y1），F（x2，y2），则，；…（4分）所以所以OE⊥OF；…（6分）（Ⅱ）∵直线l与圆O相切于W，，∴；…（8分）由（Ⅰ）知x1x2+y1y2=0，∴x1x2=﹣y1y2，即；从而，即，∴；…（12分）因为﹣≤x1≤，所以λ∈．…（13分）【点评】：本题考查了直线与圆锥曲线的综合应用问题，也考查了直线与圆相切的应用问题，考查了方程思想的应用问题，是综合性题目．21．（14分）（2015•青岛一模）已知函数f（x）=x2+kx+1，g（x）=（x+1）ln（x+1），h（x）=f（x）+g'（x）．（Ⅰ）若函数g（x）的图象在原点处的切线l与函数f（x）的图象相切，求实数k的值；（Ⅱ）若h（x）在上单调递减，求实数k的取值范围；（Ⅲ）若对于∀t∈，总存在x1，x2∈（﹣1，4），且x1≠x2满f（x i）=g（t）（i=1，2），其中e为自然对数的底数，求实数k的取值范围．【考点】：利用导数研究曲线上某点切线方程；利用导数求闭区间上函数的最值．【专题】：函数的性质及应用；导数的概念及应用；导数的综合应用；不等式的解法及应用．【分析】：（Ⅰ）求出g（x）的定义域和导数，求得切线的斜率和切点，写出切线方程，联立f（x），消去y，运用判别式为0，即可得到k；（Ⅱ）求出h（x）的导数，h（x）在上单调递减，则h'（x）≤0对x∈恒成立，运用导数求出h'（x）在的最大值，解不等式即可得到k的范围；（Ⅲ）分别求出g（t）在t∈的值域A和f（x）在x∈（﹣1，4）的值域B，由题意可得A包含于B，得到不等式组，解出即可得到k的范围．【解析】：解：（Ⅰ）函数g（x）的定义域为（﹣1，+∞），g'（x）=ln（x+1）+1，则g（0）=0，g'（0）=1，∴切线l：y=x，由，∵l与函数f（x）的图象相切，∴；（Ⅱ），导数，令，对x∈恒成立，则在递增，即h'（x）在上为增函数，∴，∵h（x）在上单调递减，∴h'（x）≤0对x∈恒成立，即，∴；（Ⅲ）当时，g'（x）=ln（x+1）+1＞0，∴g（x）=（x+1）ln（x+1）在区间上为增函数，∴时，，∵的对称轴为x=﹣k，∴为满足题意，必须﹣1＜﹣k＜4，此时，f（x）的值恒小于f（﹣1）和f（4）中最大的一个，∵对于，总存在x1，x2∈（﹣1，4），且x1≠x2满足f（x i）=g（t）（i=1，2），∴，∴，∴．【点评】：本题考查导数的运用：求切线方程和单调区间及极值、最值，同时考查任意存在问题注意转化为函数的值域的包含关系，考查运算能力，属于中档题和易错题．。

山东省文综

山东省青岛市2011届高三教学质量3月统一检测文科综合 2010.03本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共14页。

满分240分，考试用时150分钟。

考试结束后，将答题纸交回。

答卷前，考生务必将自己的姓名、准考证号、考试科目等填涂在答题纸规定的位置。

K.s.5.u第Ⅰ卷（必做，共100分）注意事项：1．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不涂在答题卡上，只答在试卷上无效。

2．第Ⅰ卷共25小题，每小题4分，共100分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

K.s.5.u图1是“世界局部地区图”，一艘海轮从甲地出发驶往丁地。

此时图中PQ 线为昏线，且与极圈相切。

据此完成1—2题。

1．当日，甲地与丁地相比A ．正午太阳高度小B ．白昼时间长C ．自转线速度小D ．日出方位不同 2．下列叙述正确的是A ．图中山脉位于板块生长边界B ．轮船经过乙处海峡时逆风逆水C ．甲地和丁地气候类型相同D ．丙地很适宜种植水稻图2是“某山地海拔高度与植物生长量、年平均气温、年降水量、年太阳辐射量的关系图”，横坐标表示植物生长量、年平均气温、年降水量和年太阳辐射量。

读图完成3—4题。

3. 与图中①②③④曲线对应正确的是A ．①—年太阳辐射量B ．②—年平均气温C ．③—植物生长量D ．④—年降水量 4. ②曲线在2500米左右有明显弯曲变化，其主要的影响因素是A ．地面状况B ．大气环流C ．地形坡度D ．牧业发展图3中，M 、N 、G 分别为原料地、能源地和市场。

P1点是某企业生产产品的运费最低点和劳动力费用最高点，以P1为圆心的同心圆是该企业的等运费线（单位：元）。

表1是该企业生产单位产品所需劳动力费用（单位：元）。

据此完成5—6题。

5．若仅从运费和劳动力费用成本考虑，企业厂址应选择A ．P1点B ．P2点C ．P3点D ．P4点°图1236．若企业的厂址选择在P4，则该企业可能是A ．印刷厂B ．制糖厂C ．电子元件厂D ．电解铝厂图4为“某河流河床、水位变化及其流域气候资料统计图”。

山东省青岛市高三下学期数学3月模拟考试试卷

山东省青岛市高三下学期数学3月模拟考试试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共14分)1. （1分） (2017高二下·南通期中) 已知全集U={﹣1，2，3，a}，集合M={﹣1，3}．若∁UM={2，5}，则实数a的值为________．2. （1分）已知z=x+yi，x，y∈R，i为虚数单位，且z=（1+i）2 ，则ix+y=________3. （1分） (2018高二上·安庆期中) 一名射箭运动员5次射箭命中环数的“茎叶图”如图，则他5次射箭命中环数的方差为________．4. （1分） (2017高一上·上海期中) 函数的定义域是________．5. （1分）连续抛一枚均匀的硬币3次，恰好2次正面向上的概率为________．6. （1分） (2018高二上·齐齐哈尔月考) 执行如图所示的程序框图，若输入的值为3，则输出的的值为________.7. （1分）若方程表示双曲线，则实数k的取值范围是________8. （1分）(2018·徐州模拟) 已知等差数列满足，，则的值为________.9. （1分）设a＜﹣1，则关于x的不等式a（x﹣a）（x﹣）＜0的解集是________．10. （1分） (2017高三上·蓟县期末) 某空间几何体的三视图如图所示，则该几何体的表面积是________．11. （1分） (2017高二上·湖南月考) 若直线与曲线相切，则 ________．12. （1分）(2019·湖州模拟) 我国古代某数学著作中记载了一个折竹抵地问题：“今有竹高二丈，末折抵地，去本六尺，问折者高几何？”意思是：有一根竹子（与地面垂直），原高二丈（1丈=10尺），现被风折断，尖端落在地上，竹尖与竹根的距离为六尺，则折断处离地面的高为________尺．13. （1分） (2016高一下·溧水期中) 已知△ABC中，，则 =________．14. （1分）已知函数，若H（x）=f2（x）﹣2bf（x）+3有8个不同的零点，则实数b的取值范围为________．二、解答题 (共11题；共95分)15. （10分）(2016·四川文) 如图，在四棱锥P﹣ABCD中，PA⊥CD，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD．（1）在平面PAD内找一点M，使得直线CM∥平面PAB，并说明理由；（2）证明：平面PAB⊥平面PBD．16. （10分）(2017高一下·长春期末) 已知分别为三个内角的对边，.（1）求A；（2）若，求的面积.17. （10分） (2017高三上·常州开学考) △ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．（1）求∠C；（2）若c= ，△ABC的面积为，求△ABC的周长；（3）若c= ，求△ABC的周长的取值范围．18. （10分）(2020·漳州模拟) 已知椭圆与双曲线有相同的焦点坐标，且点在椭圆上.（1）求椭圆的标准方程；（2）设A、B分别是椭圆的左、右顶点，动点M满足，垂足为B，连接AM交椭圆于点P（异于A），则是否存在定点T，使得以线段MP为直径的圆恒过直线BP与MT的交点Q，若存在，求出点T的坐标；若不存在，请说明理由.19. （5分） (2019高三上·衡水月考) 已知函数， .（1）若在区间内单调递增，求的取值范围；（2）若在区间内存在极大值，证明： .20. （15分）(2017·许昌模拟) 已知函数的最小值为m．（1）求m的值；（2）若a，b，c是正实数，且a+b+c=m，求证：2（a3+b3+c3）≥ab+bc+ca﹣3abc．21. （5分）(2014·福建理) 已知矩阵A的逆矩阵A﹣1=（）．（1）求矩阵A；（2）求矩阵A﹣1的特征值以及属于每个特征值的一个特征向量．22. （5分） (2018高二上·嘉兴期中) 已知圆 .（Ⅰ）若圆的切线在轴和轴上的截距相等，求此切线的方程；（Ⅱ）从圆外一点向该圆引一条切线，切点为，为坐标原点，且，求使取得最小值的点的坐标.23. （5分）已知a＞0，b＞0，c＞0，函数f（x）=|x+a|+|x﹣b|+c的最小值为4．（1）求a+b+c的值；（2）求a2+b2+c2的最小值．24. （10分）(2012·湖南理) 如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是CD的中点．（1）证明：CD⊥平面PAE；（2）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P﹣ABCD的体积．25. （10分）某商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖．每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出2个球．在摸出的4个球中，若都是红球，则获一等奖；若只有3个红球，则获二等奖；若只有2个红球，则获三等奖；若只有1个红球，则获四等奖；若没有红球，则不获奖．（1）求顾客抽奖1次能获一等奖的概率；（2）求顾客抽奖1次能获二等奖的概率（3）求顾客抽奖1次能获奖的概率．参考答案一、填空题 (共14题；共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共11题；共95分)15-1、15-2、16-1、16-2、17-1、17-2、17-3、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、23-1、24-1、24-2、25-1、25-2、25-3、。

2011年山东省青岛市高三教学质量统一检测

2011年山东省青岛市高三教学质量统一检测语文2011.03本试卷分第Ⅰ卷和第Ⅱ卷两部分，共8页，满分150分。

考试时间150分钟。

考试结束后，将答题卡交回。

注意事项：1.答卷前，考生务必用0.5毫米黑色签字笔将姓名、准考证号、县区和科类填写在答题卡和试卷规定的位置上。

2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

答案不能写在试题卷上。

3.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡个题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

4.第Ⅱ卷第六题为选做题，考生须从所给的（一）（二）两题中任选一题作答，不能全选。

第Ⅰ卷（共36分）一、（15分，每小题3分）1.下列词语中，字形与加点字的读音全都正确的一组是A．消融漂．白（p iǎo）流言蜚．语（fēi）钩玄．提要（xián）B．惊蜇豆荚．（．jiá）大展鸿．图（hóng）秣．兵利马（mò）C．丰采露．怯（lòu）妙趣横．生（héng）纤．毫毕现（xiàn）D．寥落囤．粮（tún）鸠．占雀巢（jiū）引吭．高歌（háng）2.依次填入下列各句中横线处的词，最恰当的一组是①全国多家银行的负责人和新疆自治区的领导齐聚乌鲁木齐，共同探讨新疆发展大计，银行也表示将_____支持新疆实现跨越式发展。

②久在南国，我以切身感受到江南文化的典雅和细腻，然而_____江南绿油油的稻田多么迷人，我_____不能忘掉西藏的青稞。

③随着“千人诵经典”活动的举行，第四届校园读书节拉开了帷幕。

此次读书节旨在倡导师生广泛阅读，_____我校师生良好的阅读风貌。

A．全力不管/也展示 B.全力尽管/还显示C．鼎力尽管/还展示 D.鼎力不管/也显示3.下列语句中，加点的成语使用最恰当的一句是A．针对我国房地产市场的现状，中央要求各级政府部门要顺应民意，从谏如流．．．．，及时出台有力措施，遏制房价过快上涨的趋势。

山东省青岛市高三数学3月统一质量检测(青岛市一模第2

山东省青岛市高三3月统一质量检测考试（第二套）数学（理科）试卷第Ⅰ卷（共50分）一、选择题：本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 复数21ii+（i 是虚数单位）的虚部为( ) A ．1- B ．i C ．1 D ．22.已知全集R U =，集合{}2|0A x x x =->，{}|ln 0B x x =≤，则()U C A B =I ( )A ．(0,1]B ．(,0)(1,)-∞+∞UC ．∅D ．(0,1)3.某中学高中一年级有400人，高中二年级有320人，高中三年级有280人，现从中抽取一个容量为200人的样本，则高中二年级被抽取的人数为( )A ．28B ．32C ．40D ．64 【答案】D 【解析】试题分析：由已知，样本容量为4003202801000++=，所以，高中二年级被抽取的人数为200320641000⨯=，选D . 考点：分层抽样4.曲线32y x x =-在(1,1)-处的切线方程为( )A ．20x y --=B ．20x y -+=C ．20x y +-=D ．20x y ++=5.设a 、b 是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是( )A ．若//,//,a b a α则//b αB ．若,//,a αβα⊥则a β⊥C ．若,,a αββ⊥⊥则//a αD ．若,,,a b a b αβ⊥⊥⊥则αβ⊥6.设,z x y =+其中实数,x y 满足2000x y x y y k +≥⎧⎪-≤⎨⎪≤≤⎩，若z 的最大值为12，则z 的最小值为( )A ． 3-B ．6-C ．3D ．6【答案】B【解析】试题分析：画出可行域及直线0x y +=，如图所示. 平移直线0x y +=，当其经过点(,)A k k 时，max 212,z k ==当直线经过点(2,)B k k -时，min ,z k =所以，6k =，min 6z =-.考点：简单线性规划7.函数()sin()f x A x ωϕ=+(0,0,)2A πωϕ>><的部分图象如图所示，若12,(,)63x x ππ∈-，且12()()f x f x =，则12()f x x +=( )A ． 1B ．21 C ．22 D ．23考点：正弦型函数8.在实验室进行的一项物理实验中，要先后实施6个程序，其中程序A 只能出现在第一或最后一步，程序B 和C 在实施时必须相邻，则实验顺序的编排方法共有( ) A ．34种 B ．48种C ．96种D ．144种9.函数2()ln(2)f x x =+的图象大致是( )10.如图，从点0(,4)M x 发出的光线，沿平行于抛物线28y x =的对称轴方向射向此抛物线上的点P ，经抛物线反射后，穿过焦点射向抛物线上的点Q ，再经抛物线反射后射向直线:100l x y --=上的点N ，经直线反射后又回到点M ，则0x 等于( )A ．5B ．6C ．7D ．8第Ⅱ卷（共100分）二、填空题（每题5分，满分25分，将答案填在答题纸上）11.已知向量()2,1a =r ，()1,b k =-r，若b a ⊥，则实数k =______;12.圆22:2440C x y x y +--+=的圆心到直线:3440l x y ++=的距离d = ; 【答案】3 【解析】试题分析：由已知圆心为(1,2)，由点到直线的距离公式得，223.34d ==+考点：圆的方程，点到直线的距离公式.13.如图是某算法的程序框图，若任意输入[1,19]中的实数x ，则输出的x 大于49的概率为 ;14.已知,x y 均为正实数，且3xy x y =++，则xy 的最小值为__________；【答案】9 【解析】试题分析：因为,x y 均为正实数，所以2,x y xy +≥3xy x y =++可化为23xy xy ≥，即(3)(1)0,xy xy ≥3,9,xy xy ≥≥故当且仅当x y =时，xy 取得最小值9.考点：基本不等式的应用，一元二次不等式解法.15.如果对定义在R 上的函数()f x ，对任意两个不相等的实数12,x x ，都有11221221()()()()x f x x f x x f x x f x +>+，则称函数()f x 为“H 函数”.给出下列函数①31y x x =-++;②32(sin cos )y x x x =--;③1xy e =+;④ln 0()00x x f x x ⎧≠⎪=⎨=⎪⎩.以上函数是“H 函数”的所有序号为 .三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.） 16.（本小题满分12分）已知向量)sin ,)62(sin(x x π+=，)sin ,1(x =，21)(-⋅=n m x f . （Ⅰ）求函数()f x 的单调递减区间；（Ⅱ）在ABC ∆中,c b a ,,分别是角C B A ,,的对边,3a =1()22A f =, 若C C A cos 2)sin(3=+，求b 的大小.【答案】（Ⅰ）()f x 递减区间是3,,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. （Ⅱ）42【解析】试题分析：（Ⅰ）利用平面向量的坐标运算及三角函数公式，将)(x f 化简为x 2sin 23，确定得到()f x 递减区间.17.（本小题满分12分）袋中装有大小相同的黑球和白球共9个，从中任取2个都是白球的概率为512．现甲、乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取…，每次摸取1个球，取出的球不放回，直到其中有一人取到白球时终止．用X表示取球终止时取球的总次数．（Ⅰ）求袋中原有白球的个数；（Ⅱ）求随机变量X的概率分布及数学期望()E X．（Ⅱ）由题意，X 的可能取值为1,2,3,4. 由古典概型概率的计算公式，计算可得分布列为：进一步应用期望的计算公式，即得所求.试题解析：(Ⅰ)设袋中原有n 个白球，则从9个球中任取2个球都是白球的概率为229nC C …2分由题意知229512n C C =，化简得2300n n --=．解得6n =或5n =-（舍去）……………………5分故袋中原有白球的个数为6……………………6分（Ⅱ）由题意，X 的可能取值为1,2,3,4.2(1)3P X ==； 361(2)984P X ⨯===⨯； 3261(3)98714P X ⨯⨯===⨯⨯；32161(4)987684P X ⨯⨯⨯===⨯⨯⨯.所以取球次数X 的概率分布列为：……………10分X1234P2314114184X1234P2314114184所求数学期望为211110()12343414847E X =⨯+⨯+⨯+⨯=…………………12分考点：简单组合应用问题，古典概型概率的计算，随机变量的分布列及数学期望.18.（本题满分12分）如图，四棱锥P ABCD -中, PA ⊥面ABCD ，E 、F 分别为BD 、PD 的中点，=1EA EB AB ==，2PA =.（Ⅰ）证明：PB ∥面AEF ；（Ⅱ）求面PBD 与面AEF 所成锐角的余弦值.【答案】(Ⅰ)见解析；（Ⅱ）12121211cos ,19n n n n n n ⋅==u r u u r u r u u r u r u u r . 【解析】试题分析：（Ⅰ）(Ⅰ) 利用三角形中位线定理，得出EF ∥PB .（Ⅱ）利用平几何知识，可得一些线段的长度及BA AD ⊥，进一步以,,AB AD AP 为,,x y z 轴建立坐标系，得到133(1,0,2),3,2),(2PB PD AE AF =-=-==u u u r u u u r u u u r u u u r ，确定面PBD 与面AEF 的法向量1111(,,)n x y z =u r 、2222(,,)n x y z =u u r ：由111120320x z y z -=⎧⎪-=，可得令123n =u r ；由又2222301302y z x y ⎧+=⎪⎨⎪=⎪⎩，可得令23(3,1,)n =u u r ，进一步得到12121211cos ,19n n n n n n ⋅==u r u u r u r u u r u r u u r .所以313(1,0,0),3,0),(0,0,2),(2B D P F E 则133(1,0,2),3,2),(,(0,222PB PD AE AF =-=-==u u u r u u u r u u u r u u u r ………8分设1111(,,)n x y z =u r 、2222(,,)n x y z =u u r分别是面PBD 与面AEF 的法向量则111120320x z y z -=⎧⎪-=，令13(2,3n =u r 又22223013022y z x y +=⎨⎪+=⎪⎩，令23(3,1,n =u u r……………11分所以12121211cos ,19n n n n n n ⋅==u r u u ru r u u r u r u u r ……………12分考点：直线与平面、平面与平面垂直，二面角的定义，空间向量的应用.19.（本小题满分12分）在数列{}n a )N (*∈n 中，其前n 项和为n S ，满足22n n S n -=.（Ⅰ）求数列{}n a 的通项公式; （Ⅱ）设⎪⎩⎪⎨⎧=+-=⋅=k n n n k n n b n a n 2,2112,22（k 为正整数）,求数列{}n b 的前n 2项和n T 2.【答案】(Ⅰ) n a n -=1.（Ⅱ）222024209924(1)n n n nT n +=-+⋅+.【解析】试题分析：(Ⅰ)根据22n n S n -=,计算n S S a n n n -=-=-11 )2(≥n验证当1=n 时，011==S a ,明确数列{}n a 是01=a 为首项、公差为1-的等差数列即得所求.（Ⅱ）由(Ⅰ)知: ⎪⎩⎪⎨⎧=+-=⋅=-k n n n k n n b n n 2,)2(112,21利用“裂项相消法”、“错位相减法”求和.试题解析：(Ⅰ)由题设得:22n n S n -=,所以)2()1(1221≥---=-n n n S n所以n S S a n n n -=-=-11 )2(≥n ……………2分当1=n 时，011==S a ,数列{}n a 是01=a 为首项、公差为1-的等差数列故n a n -=1.……………5分20.（本小题满分13分）已知函数()1x f x e x =--．（Ⅰ）求()f x 的最小值；（Ⅱ）当函数自变量的取值区间与对应函数值的取值区间相同时，这样的区间称为函数的保值区间.设2()(()1)(1)g x f x x '=+-，试问函数()g x 在(1,)+∞上是否存在保值区间？若存在，请求出一个保值区间；若不存在，请说明理由.【答案】（Ⅰ）()f x 在0x =处取得最小值(0)0f =．（Ⅱ）函数()g x 在()1,+∞上不存在保值区间,证明见解析.【解析】试题分析：（Ⅰ）求导数，解0()f x '<得函数的减区间()0-∞，；解0()f x '>，得函数的增区间(0,)+∞．确定()f x 在0x =处取得最小值(0)0f =．也可以通过“求导数、求驻点、研究函数的单调区间、确定极值（最值）” .21.（本小题满分14分）设1F ,2F 分别是椭圆D ：)0(12222>>=+b a by a x 的左、右焦点，过2F 作倾斜角为3π的直线交椭圆D 于A ,B 两点, 1F 到直线AB 的距离为3,连接椭圆D 的四个顶点得到的菱形面积为4.（Ⅰ）求椭圆D 的方程；（Ⅱ）已知点），（01-M ，设E 是椭圆D 上的一点，过E 、M 两点的直线l 交y 轴于点C ,若CE EM λ=u u u r u u u u r , 求λ的取值范围；（Ⅲ）作直线1l 与椭圆D 交于不同的两点P ,Q ,其中P 点的坐标为(2,0)-,若点),0(t N 是线段PQ 垂直平分线上一点,且满足4=⋅NQ NP ,求实数t 的值.【答案】（Ⅰ）1422=+y x ；（Ⅱ）23λ≥-或2λ≤-；（Ⅲ）满足条件的实数t 的值为22±=t 或5142±=t . 【解析】试题分析：（Ⅰ）设1F ,2F 的坐标分别为)0,(),0,(c c -,其中0>c由题意得AB 的方程为:)(3c x y -=根据1F 到直线AB 的距离为3,可求得3=c ，将3222==-c b a 与42221=⨯⨯b a 联立即可得到1,2==b a . （Ⅱ）设11(,)E x y ,),0(m C ，由CE EM λ=u u u r u u u u r 可得λλλ+=+-=1,111m y x ，代人椭圆D 的方程得04)2)(23(2≥++=λλm ，即可解得23λ≥-或2λ≤-. （Ⅱ）由(Ⅰ)知椭圆D 的方程为1422=+y x 设11(,)E x y ,),0(m C ，由于CE EM λ=u u u r u u u u r ,所以有),1(),(1111y x m y x ---=-λλλλ+=+-=∴1,111m y x ……………7分又E 是椭圆D 上的一点,则1)1(4)1(22=+++-λλλm所以04)2)(23(2≥++=λλm 解得：23λ≥-或2λ≤- ……………9分（Ⅲ）由)0,2(-P , 设),(11y x Q根据题意可知直线1l 的斜率存在，可设直线斜率为k ,则直线1l 的方程为)2(+=x k y 把它代入椭圆D 的方程,消去y ,整理得: 0)416(16)41(2222=-+++k x k x k 由韦达定理得22141162k k x +-=+-,则2214182k k x +-=,=+=)2(11x k y 2414k k + 所以线段PQ 的中点坐标为,418(22k k +-)4122kk +。

数学理科答案(青岛高三理科数学一模试题答案)

青岛市高三教学质量统一检测 2011.03数学 (理科)参考答案及评分标准一、选择题：本大题共12小题．每小题5分，共60分． A C B B D D B A B A A D二、填空题：本大题共4小题，每小题4分，共16分．13. 38 14. 3 15.13[,]22- 16．三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤．17. （本小题满分12分）解: (Ⅰ)21()()sin 1cos 2f x m n m x x x =+⋅=+++ …………2分1cos 211sin 2222x x -=+++12cos 2222x x =-+ sin(2)26x π=-+…………5分因为2ω=，所以22T ππ==…………6分 (Ⅱ) 由(Ⅰ)知：()sin(2)26f A A π=-+[0,]2x π∈时,52666x πππ-≤-≤由正弦函数图象可知,当262x ππ-=时()f x 取得最大值3所以262A ππ-=,3A π=…………8分由余弦定理，2222cos a b c bc A =+-∴211216242b b =+-⨯⨯∴2b =………10分从而11sin 24sin 6022S bc A ==⨯⨯= 12分 18．（本小题满分12分）(Ⅰ) 证明:连结PC ,交DE 与N ,连结MN ，PAC ∆中，,M N 分别为两腰,PA PC 的中点 ∴//MN AC …………2分因为MN ⊂面MDE ,又AC ⊄面MDE ，所以//AC 平面MDE …………4分(Ⅱ) 设平面PAD 与PBC 所成锐二面角的大小为θ，以D 为空间坐标系的原点，分别以,,DA DC DP 所在直线为,,x y z 轴建立空间直角坐标系，则),(,,0),(0,2,0)P B a a C a(,,),(,,0)PB a a BC a a ==-…………6分设平面PAD 的单位法向量为1n，则可设1(0,1,0)n =…………7分设面PBC 的法向量2(,,1)n x y =，应有22(,,1)(,,)0(,,1)(,,0)0n PB x y a a n BC x y a a ⎧==⎪⎨=-=⎪⎩即：00ax ay ax ay ⎧+=⎪⎨-+=⎪⎩，解得：22x y ⎧=⎪⎪⎨⎪=⎪⎩，所以2(22n = …………10分∴12121cos 2||||n n n n θ⋅===…………11分所以平面PAD 与PBC 所成锐二面角的余弦值为12…………12分 19．（本小题满分12分）解:(Ⅰ) 函数()21f x x x η=--过(0,1)-点，在区间(4,6)上有且只有一个零点，则必有(4)0(6)0f f <⎧⎨>⎩即：1641036610ηη--<⎧⎨-->⎩，解得：153546η<<x所以，4η=或5η=…………3分当4η=时，211201015125068245C C C P C +==，当5η=时，11201522501249C C P C ==…………5分 4η=与5η=为互斥事件，由互斥事件有一个发生的概率公式所以12681212824549245P P P =+=+=…………6分 (Ⅱ) 从该单位任选两名职工，用ξ表示这两人休年假次数之差的绝对值，则ξ的可能取值分别是0,1,2,3，…………7分于是()22225102015250207C C C C P C ξ+++===，1111115101020152025022(1)49C C C C C C P C ξ++===，1111520101525010(2)49C C C C P C ξ+===，115152503(3)49C C P C ξ===…………10分从而ξ的分布列：ξ的数学期望：0123749494949E ξ=⨯+⨯+⨯+⨯=． …………12分 20．（本小题满分12分）解: (Ⅰ) 对任意*N n ∈,都有11124n n b b +=+，所以1111()222n n b b +-=- 则1{}2n b -成等比数列,首项为1132b -=，公比为12…………2分所以1113()22n n b --=⨯，1113()22n n b -=⨯+…………4分 (Ⅱ) 因为1113()22n n b -=⨯+所以2113(1)111123(1...)6(1)1222222212n n n n n n n T --=+++++=+=-+-…………6分因为不等式1227(122)n k n n T ≥-+-，化简得272nn k -≥对任意*N n ∈恒成立…………7分设272n n n c -=，则1112(1)72792222n nn n n n n nc c ++++----=-=…………8分当5n ≥,1n n c c +≤,{}n c 为单调递减数列，当15n ≤<,1n n c c +>,{}n c 为单调递增数列45131632c c =<=,所以, 5n =时, n c 取得最大值332…………11分所以, 要使272n n k -≥对任意*N n ∈恒成立，332k ≥…………12分21．（本小题满分12分）解: (Ⅰ)14a =时, 3221()332f x x x x =-++，2()23(23)(1)f x x x x x '=-++=--+ 令()0f x '=,得1x =-或3x =…………2分可以看出在1x =-取得极小值,在2x =取得极大值…………5分而48(2),(2)33f f -==由此, 在[2,2]-上,()f x 在1x =-处取得最小值116-,在32x = 处取得最小值278…………6分(Ⅱ)()ln(1)3()g x x f x '=++-2ln(1)3(243)x x ax =+---++2ln(1)24x x ax =++-2'144(1)14()4411x a x ag x x a x x +-+-=+-=++…………7分在1(,)2-+∞上恒有10x +> 考察2()44(1)14h x x a x a =+-+-的对称轴为44182a a x --=-= (i)当1122a -≥-,即0a ≥时，应有216(1)16(14)0a a ∆=---≤ 解得:20a -<≤，所以0a =时成立…………9分(ii)当1122a -<-,即0a <时，应有1()02h ->即:114(1)1402a a --⨯+-> 解得0a <…………11分综上：实数a 的取值范围是0a ≤…………12分 22. （本小题满分14分）解: (Ⅰ) 因为2QC 的垂直平分线交1QC 于点P . 所以2PC PQ =222211112=>==+=+C C QC PQ PC PC PC所以动点P 的轨迹ω是以点21,C C 为焦点的椭圆……………2分设椭圆的标准方程为12222=+by a x则22,222==c a ，1222=-=c a b ，则椭圆的标准方程为2212x y +=……4分 (Ⅱ) 设1122(,),(,)M a b N a b ，则2222112222,22a b a b +=+= ①因为122OM ON OC +=则121222,20a a b b +=-+= ②由①②解得112215,,2448a b a b ===-=-……………7分所以直线MN 的斜率k 212114b b a a -==-……………8分 (Ⅲ)直线l 方程为13y kx =-，联立直线和椭圆的方程得:221312y kx x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 得229(12)12160k x kx +--=…………9分由题意知：点)31,0(-S 在椭圆内部，所以直线l 与椭圆必交与两点，设).,(),,(2211y x B y x A 则121222416,3(12)9(12)k x x x x k k +==-++ 假设在y 轴上存在定点),0(m D ，满足题设，则1122(,),(,)DA x y m DB x y m =-=-因为以AB 为直径的圆恒过点D ,则1122(,)(,)0DA DB x y m x y m ⋅=-⋅-=，即:1212()()0x x y m y m +--= (*)因为112211,33y kx y kx =-=-则(*)变为21212121212()()()x x y m y m x x y y m y y m +--=+-++…………11分21212121111()()()3333x x kx kx m kx kx m =+----+-+221212121(1)()()339k x x k m x x m m =+-+++++222216(1)1421()9(21)33(21)39k k k m m m k k +=--++++++222218(1)(9615)9(21)m k m m k -++-=+由假设得对于任意的R k ∈,0DA DB ⋅=恒成立，即221096150m m m ⎧-=⎪⎨+-=⎪⎩解得1m =……13分因此，在y 轴上存在满足条件的定点D ，点D 的坐标为(0,1).………………14分。

山东省青岛市2011届高三教学质量统一检测(理综)

青岛市高三教学质量统一检测理科综合2011.03本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共16页，满分240分，考试时间150分钟。

第Ⅰ卷（必做，共88分）注意事项：1.答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔（中性笔）将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上。

2.第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

答案不能答在试题卷上。

3.第Ⅱ卷必须用0.5毫米黑色签字笔（中性笔）作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

以下数据可供答题时参考：可能用到的相对原子质量H1O16Cu64一、选择题（本题包括15小题。

每小题只有一个选项符合题意）1.关于细胞结构和功能的说法正确的是A.线粒体内膜上只分布着合成ATP 的酶B.核孔是生物大分子可以选择性进出的通道C.神经细胞在静息状态下膜上的载体蛋白不再进行葡萄糖的跨膜运输D.所有细胞中核糖体的形成都与核仁密切相关2.胸腺嘧啶脱氧核苷（简称胸苷）在细胞内可以转化为胸腺嘧啶脱氧核糖核苷酸，后者是合成DNA 的原料。

用含有3H-胸苷的营养液，处理活的菜豆的幼根处，一定时间后洗去游离的3H-胸苷。

连续48小时检测下图a 和b 部位（a 是分生区），则随生长进程，a 和b 部位的放射性含量变化情况为3.人类每条染色体上都有很多基因。

下图表示1号染色体上的几种基因对性状的控制及基因在染色体上的分布位置，若不考虑染色体交叉互换，据此不能得出的结论是A.他们的儿子可能出现椭圆形红细胞概率为1/2B.他们的孩子不可能是Rh 阴性C.母亲正常减数分裂第一极体中的基因组成是aDeD.他们有的孩子可能不产生淀粉酶4.以下关于蛋白质及其对应功能的描述，正确的是A.动物激素都是蛋白质，对生命活动具有重要调节作用B.生长激素由下丘脑分泌，主要促进蛋白质的合成和骨的生长C.胰岛素和胰高血糖素能通过反馈调节维持血糖平衡D.神经递质受体位于突触前膜，能与递质发生特异性结合，从而改变突触后膜对离子的通透性5.有关免疫细胞的说法，正确的是A.记忆细胞再次受到相同抗原的刺激后都能迅速产生抗体B.B细胞、T细胞和浆细胞遇到刺激后都能不断进行分裂C.一个浆细胞内的基因数目与其产生的抗体数量是相同的D.浆细胞的寿命比记忆B细胞短且所含的内质网相对发达6.某草原生态系统一条食物链A→B→C中，各种群对能量的同化、利用、传递等数量关系如下表。

山东省青岛市10—11下学期高三数学(理科)月考考试试卷

山东省青岛市2011届高三教学质量统一检测数学(理科)2011.03本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)两部分，共150分，考试时间120分钟. 注意事项：1．答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试题卷上.3．第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效. 参考公式：台体的体积公式为：121(3V S S h =++，其中1S ，2S 分别为台体的上、下底面积，h 为台体的高.第Ⅰ卷 (选择题共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知复数21iz i =-，则复数z 的共轭复数为 A ．i +1B ．1i -+C ．1i -D ．1i --2．已知全集U R =，集合2{|20}A x x x =->，{|lg(1)}B x y x ==-，则()U A Bð等于A ．{|20}x x x ><或B ．{|12}x x <<C ．{|12}x x <≤D ．{|12}≤≤x x3．下列四个函数中，在区间(0，1)上是减函数的是A ．2log y x =B ．1y x =C ．1()2xy =-D ．13y x =4．已知直线l 、m ，平面α、β，且l α⊥，m β⊂，则//αβ是l m ⊥的A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件5．二项式62()x x-的展开式中，2x 项的系数为A ．15B ．15-C ．30D ．606．以坐标轴为对称轴，原点为顶点且过圆222690x y x y +-++=圆心的抛物线方程是 A ．2233y x y x ==-或 B ．23y x =C ．2293y x y x =-=或D ．22-9y x y x ==或7．右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4积是A ．283πB ．73π C ．28πD ．7π8．若00x y x y y a -≤⎧⎪+≥⎨⎪≤⎩，若2z x y =+的最大值为3，则a 的值是A ．1B ．2C ．3D ．49．已知等差数列{}n a 的前项和为n S ，若M 、N 、P 三点共线，O 为坐标原点，且156ON a OM a OP =+(直线MP 不过点O )，则20S 等于A ．15B ．10C ．40D ．2010．定义运算：12142334a a a a a a a a =-，将函数sin ()cos x f x x -=向左平移m 个单位(0)m >，所得图象对应的函数为偶函数，则m 的最小值是 A ．6πB ．3πC ．56πD ．23π 11．下列四个命题中，正确的是A ．已知函数0()sin af a xdx =⎰，则[()]1cos12f f π=-；B ．设回归直线方程为2 2.5y x =-，当变量x 增加一个单位时，y 平均增加2个单位；C ．已知ξ服从正态分布(0N ，2)σ，且(20)0.4P ξ-≤≤=，则(2)0.2P ξ>=D ．对于命题p ：x R ∃∈，使得210x x ++<，则p ⌝：x R ∀∈，均有210x x ++>12．若1()1(1)f x f x +=+，当[0x ∈，1]时，()f x x =，若在区间(1-，1]内()()g x f x mx m =--有两个零点，则实数m 的取值范围是A ．[0，1)2B ．1[2，)+∞C ．[0，1)3D ．(0，1]2第Ⅱ卷 (选择题共60分)二、填空题：本大题共4小题，每小题4分，共16分.13．某时段内共有100辆汽车经过某一雷达地区，时速频率分布直方图如右图所示，则时速超过60/km h 的汽车数量为____________14．执行如图所示的程序框图，若输出的b 的值为16，图中判断框内?处应填的数为________ 15．若不等式1|21|||a xx-?对一切非零实数x 恒成立，则实数a 的取值范围_______________ 16．点P 是曲线2ln y x x =-上任意一点，则点P 到直线2y x =-的距离的最小值是____________ 三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤. 17．(本小题满分12分)已知向量(sin m x =u r ，1)-，向量n x =r ，1)2-，函数.()()f x m n m =+u r r u r .(Ⅰ)求()f x 的最小正周期T ；(Ⅱ)已知a ，b ，c 分别为ABC D 内角A ，B ，C 的对边，A为锐角，a =4c =，且()f A 恰是()f x 在[0，]2p上的最大值，求A ，b 和ABC D 的面积S .18．(本小题满分12分)如图，PDCE 为矩形，ABCD 为梯形，平面PDCE ^平面A B C ，90BAD ADC ???，12AB AD CD a ===，PD =. (Ⅰ)若M 为PA 中点，求证：//AC 平面MDE ； (Ⅱ)求平面PAD 与PBC 所成锐二面角的余弦值. 19．(本小题满分12分)某单位实行休年假制度三年以来，50名职工休年假的次数进行的调查统计结果如下表所示：(Ⅰ)从该单位任选两名职工，用h 表示这两人休年假次数之和，记“函数2()1f x x x =--h 在区间(4，6)上有且只有一个零点”为事件A ，求事件A发生的概率P ；(Ⅱ)从该单位任选两名职工，用x 表示这两人休年假次数之差的绝对值，求随机变量x 的分布列及数学期望E x .20．(本小题满分12分)已知数列{}n b 满足11124n n b b +=+，且172b =，n T 为{}n b 的前n 项和. (Ⅰ)求证：数列1{}2n b -是等比数列，并求{}n b 的通项公式； (Ⅱ)如果对任意*n N Î，不等式1227122nkn n T ?+-恒成立，求实数k 的取值范围.21．(本小题满分12分)已知函数322()233f x x ax x =-++. (Ⅰ)当14a =时，求函数()f x 在[2-，2]上的最大值、最小值； (Ⅱ)令()ln(1)3()g x x f x =++-?，若()g x 在1(2-，)+?上单调递增，求实数a 的取值范围.22．(本小题满分14分)已知圆1C ：22(1)8x y ++=，点2(1C ，0)，点Q 在圆1C 上运动，2QC 的垂直平分线交1QC 于点P .(Ⅰ)求动点P 的轨迹W 的方程；(Ⅱ)设、M N 分别是曲线W 上的两个不同点，且点M 在第一象限，点N 在第三象限，若1+22OM ON OC =uuu r uuu r uuu r，O 为坐标原点，求直线MN 的斜率k ；(Ⅲ)过点(0S ，1)3-且斜率为k 的动直线l 交曲线W 于，A B 两点，在y 轴上是否存在定点D ，使以AB 为直径的圆恒过这个点？若存在，求出D 的坐标，若不存在，说明理由.青岛市高三教学质量统一检测高中数学(理科)参考答案及评分标准2011.03一、选择题：本大题共12小题．每小题5分，共60分． ACBBD DBABA AD二、填空题：本大题共4小题，每小题4分，共16分．13．38 14．3 15．13[,]22- 16三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤．17．(本小题满分12分)解：(Ⅰ)21()()sin 1cos 2f x m n m x x x =+⋅=+++…………2分1cos 211sin 2222x x -=+++12cos 2222x x =-+sin(2)26x π=-+…………5分因为2ω=，所以22T ππ==…………6分 (Ⅱ)由(Ⅰ)知：()sin(2)26f A A π=-+[0,]2x π∈时，52666x πππ-≤-≤由正弦函数图象可知，当262x ππ-=时()f x 取得最大值3所以262A ππ-=，3A π=…………8分由余弦定理，2222cos a b c bc A =+-∴211216242b b =+-⨯⨯∴2b =………10分从而11sin 24sin 602322S bc A ==⨯⨯=12分 18．(本小题满分12分)(Ⅰ)证明：连结PC ，交DE 与N ，连结MN ，PAC ∆中，,M N 分别为两腰,PA PC 的中点∴//MN AC …………2分因为MN ⊂面MDE ，又AC ⊄面MDE ，所以//AC 平面MDE …………4分(Ⅱ)设平面PAD 与PBC 所成锐二面角的大小为θ，以D 为空间坐标系的原点，分别以,,DA DC DP 所在直线为,,x y z 轴建立空间直角坐标系，则),(,,0),(0,2,0)P B a a C a(,,2),(,,0)PB a a a BC a a =-=-…………6分设平面PAD 的单位法向量为1n ，则可设1(0,1,0)n =…………7分设面PBC 的法向量2(,,1)n x y =，应有22(,,1)(,,2)0(,,1)(,,0)0n PB x y a a a n BC x y a a ⎧=-=⎪⎨=-=⎪⎩即：00ax ay ax ay ⎧+=⎪⎨-+=⎪⎩，解得：22x y ⎧=⎪⎪⎨⎪=⎪⎩，所以22(22n =…10分∴121212cos 2||||1n n n n θ⋅===⨯…………11分所以平面PAD 与PBC 所成锐二面角的余弦值为12…………12分 19．(本小题满分12分)解：(Ⅰ)函数()21f x x x η=--过(0,1)-点，在区间(4,6)上有且只有一个零点，则必有(4)0(6)0f f <⎧⎨>⎩即：1641036610ηη--<⎧⎨-->⎩，解得：153546η<< 所以，4η=或5η=…………3分当4η=时，211201015125068245C C C P C +==，当5η=时，11201522501249C C P C ==…5分 4η=与5η=为互斥事件，由互斥事件有一个发生的概率公式所以12681212824549245P P P =+=+=…………6分 (Ⅱ)从该单位任选两名职工，用ξ表示这两人休年假次数之差的绝对值，则ξ的可能取值分别是0,1,2,3，…………7分于是()22225102015250207C C C C P C ξ+++===， 1111115101020152025022(1)49C C C C C C P C ξ++===，1111520101525010(2)49C C C C P C ξ+===，115152503(3)49C C P C ξ===…………10分从而ξ的分布列：ξ的数学期望：0123749494949E ξ=⨯+⨯+⨯+⨯=． …………12分 20．(本小题满分12分)解：(Ⅰ)对任意*N n ∈，都有11124n n b b +=+，所以1111()222n n b b +-=- 则1{}2n b -成等比数列，首项为1132b -=，公比为12…………2分所以1113()22n n b --=⨯，1113()22n n b -=⨯+…………4分(Ⅱ)因为1113()22n n b -=⨯+所以2113(1)111123(1...)6(1)222222212n n n n n n n T --=+++++=+=-+-…6分因为不等式1227(122)n k n n T ≥-+-，化简得272nn k -≥对任意*N n ∈恒成立…………7分设272n n n c -=，则1112(1)72792222n nn n n n n nc c ++++----=-=…………8分当5n ≥，1n n c c +≤，{}n c 为单调递减数列，当15n ≤<，1n n c c +>，{}n c 为单调递增数列45131632c c =<=，所以，5n =时，n c 取得最大值332…………11分所以，要使272n n k -≥对任意*N n ∈恒成立，332k ≥…………12分21．(本小题满分12分)解：(Ⅰ)14a =时，3221()332f x x x x =-++，2()23(23)(1)f x x x x x '=-++=--+ 令()0f x '=，得1x =-或3x =…………2分可以看出在1x =-取得极小值，在2x =取得极大值…………5分而48(2),(2)33f f -==由此，在[2,2]-上，()f x 在1x =-处取得最小值116-，在32x =处取得最小值278…………6分(Ⅱ)()ln(1)3()g x x f x '=++-2ln(1)3(243)x x ax =+---++2ln(1)24x x ax =++-2'144(1)14()4411x a x ag x x a x x +-+-=+-=++…………7分在1(,)2-+∞上恒有10x +> 考察2()44(1)14h x x a x a =+-+-的对称轴为44182a a x --=-= (i )当1122a -≥-，即0a ≥时，应有216(1)16(14)0a a ∆=---≤ 解得：20a -<≤，所以0a =时成立…………9分 (ii )当1122a -<-，即0a <时，应有1()02h ->即：114(1)1402a a --⨯+-> 解得0a <…………11分综上：实数a 的取值范围是0a ≤…………12分22．(本小题满分14分)解：(Ⅰ)因为2QC 的垂直平分线交1QC 于点P . 所以2PC PQ =222211112=>==+=+C C QC PQ PC PC PC所以动点P 的轨迹ω是以点21,C C 为焦点的椭圆……………2分设椭圆的标准方程为12222=+b y a x则22,222==c a ，1222=-=c a b ，则椭圆的标准方程为2212x y +=……4分 (Ⅱ)设1122(,),(,)M a b N a b ，则2222112222,22a b a b +=+= ①因为122OM ON OC +=则121222,20a a b b +=-+= ②由①②解得112215,,2448a b a b ===-=……………7分所以直线MN 的斜率k 212114b b a a -==-……………8分 (Ⅲ)直线l 方程为13y kx =-，联立直线和椭圆的方程得： 221312y kx x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 得229(12)12160k x kx +--=…………9分由题意知：点)31,0(-S 在椭圆内部，所以直线l 与椭圆必交与两点，设).,(),,(2211y x B y x A 则121222416,3(12)9(12)k x x x x k k +==-++ 假设在y 轴上存在定点),0(m D ，满足题设，则1122(,),(,)DA x y m DB x y m =-=- 因为以AB 为直径的圆恒过点D ，则1122(,)(,)0DA DB x y m x y m ⋅=-⋅-=，即：1212()()0x x y m y m +--= (*) 因为112211,33y kx y kx =-=-则(*)变为21212121212()()()x x y m y m x x y y m y y m +--=+-++…11分21212121111()()()3333x x kx kx m kx kx m =+----+-+221212121(1)()()339k x x k m x x m m =+-+++++222216(1)1421()9(21)33(21)39k k k m m m k k +=--++++++222218(1)(9615)9(21)m k m m k -++-=+ 由假设得对于任意的R k ∈，0DA DB ⋅=恒成立，即221096150m m m ⎧-=⎪⎨+-=⎪⎩解得1m =……13分因此，在y 轴上存在满足条件的定点D ，点D 的坐标为(0,1).………14分。

山东省青岛市2011届高三教学质量3月统一检测(数学理)

数学_2011年山东省某校高考数学三模试卷(理科)_(含答案)

青岛市高三教学质量检测XXXX03试卷(一套)

山东省青岛市高三统一质量监测数学(理)试题

山东省青岛市2014届高三数学3月统一质量检测 理(青岛市一模)新人教A版

山东省青岛市2011届高三教学质量3月统一检测(文综)

六校2011届高三第三次联考(理数.269K)

山东省青岛市2011届高三教学质量3月统一检测(数学文)

2011届高三数学月考、联考、模拟试题汇编 直线和圆

2.山东省济宁市2011届高三3月模拟考试(数学理)word版

数学理卷·2011届山东省青岛市高三教学质量3月统一检测(2011.03)

山东省青岛市2011届高三三月质检(二)(理数)

山东省青岛市高三数学3月统一质量检测试题 理(含解析)

山东省文综

山东省青岛市高三下学期数学3月模拟考试试卷

2011年山东省青岛市高三教学质量统一检测

山东省青岛市高三数学3月统一质量检测(青岛市一模第2

数学理科答案(青岛高三理科数学一模试题答案)

山东省青岛市2011届高三教学质量统一检测(理综)

山东省青岛市10—11下学期高三数学(理科)月考考试试卷

山东省青岛市2014届高三数学3月统一质量检测理(青岛市一模)新人教A版

2011届高三数学月考、联考、模拟试题汇编直线和圆

山东省青岛市高三数学3月统一质量检测试题理(含解析)