第六章数理统计的基本概念
合集下载
概率与统计学课件-第六章-数理统计的基本概念2-1

6.1
�总体与样本
基本概念: 总体:研究的问题所涉及的对象的全体 个体:总体中的每个成员 样本:从总体中抽取部分个体 样本容量:样本所包含的个体数量 样本观测值:
数的属性 样本的二重性 随机变量的属性
设X1,X2, …,Xn为总体X的一个容量为 n的 样本。若它满足 独立性,即X1,X2, …,Xn 相互独立; 同分布性,即每个 Xi都与总体X服从相 同的分布. 则称这样的样本为简单随机样本,简称为 样本。
�统计量
设是总体X的样本,g(X1,X2, …,Xn)是样本 的实值函数,且不包含任何未知参数,则 称g(X1,X2, …,Xn)为统计量。
例2.若X1,X2, X3是来自总体X~N(μ, σ 2)的 其中参数μ未知, σ2已知,则
X 1 X 3 − 3µ , X12 + 4 X 22 + 5µ 都不是统计量
�定理
若X1,X2, …,Xn是来自总体X的样本,设X 的分布函数为 F(x),则样本X1,X2, …,Xn的 联合分布函数为
n
∏ F (x )
i i =1
例1.若X1,X2, …,Xn是来自总体X的样本,设 X的分布函数为 F(x),则样本 X1,X2, …,Xn的联合分布函数为
⎧ n − λ xi (1 − e ), xi > 0(i = 1, 2,⋯ , n) ⎪∏ F ( x1 , x2 ,⋯ , xn ) = ⎨ i =1 ⎪ 0 , 其他 ⎩
1/8, 25 ≤ x<27 2/8, 27 ≤ x<30 3/8, 30 ≤ x<33 Fn(x)= 5/8, 33 ≤ x<35 6/8, 35 ≤ x<45 7/8, 45 ≤ x<65 1, 65 ≤ x
�总体与样本
基本概念: 总体:研究的问题所涉及的对象的全体 个体:总体中的每个成员 样本:从总体中抽取部分个体 样本容量:样本所包含的个体数量 样本观测值:
数的属性 样本的二重性 随机变量的属性
设X1,X2, …,Xn为总体X的一个容量为 n的 样本。若它满足 独立性,即X1,X2, …,Xn 相互独立; 同分布性,即每个 Xi都与总体X服从相 同的分布. 则称这样的样本为简单随机样本,简称为 样本。
�统计量
设是总体X的样本,g(X1,X2, …,Xn)是样本 的实值函数,且不包含任何未知参数,则 称g(X1,X2, …,Xn)为统计量。
例2.若X1,X2, X3是来自总体X~N(μ, σ 2)的 其中参数μ未知, σ2已知,则
X 1 X 3 − 3µ , X12 + 4 X 22 + 5µ 都不是统计量
�定理
若X1,X2, …,Xn是来自总体X的样本,设X 的分布函数为 F(x),则样本X1,X2, …,Xn的 联合分布函数为
n
∏ F (x )
i i =1
例1.若X1,X2, …,Xn是来自总体X的样本,设 X的分布函数为 F(x),则样本 X1,X2, …,Xn的联合分布函数为
⎧ n − λ xi (1 − e ), xi > 0(i = 1, 2,⋯ , n) ⎪∏ F ( x1 , x2 ,⋯ , xn ) = ⎨ i =1 ⎪ 0 , 其他 ⎩
1/8, 25 ≤ x<27 2/8, 27 ≤ x<30 3/8, 30 ≤ x<33 Fn(x)= 5/8, 33 ≤ x<35 6/8, 35 ≤ x<45 7/8, 45 ≤ x<65 1, 65 ≤ x
第六章 数理统计的基本概念pdf_(一)基本要求

分别为总体的样本均值和样本方差分别为总体的样本均值和样本方差独立同服从分布由分布的性质知为来自x的简单随机样本x是样本均值为总体x的样本为总体y的样本的样本均值分别表示总体证明由抽样分布的知识可得11独立又两个总体相互独立
.第六章 数理统计基本概念
一、基本要求、重点与难点
(一)基本要求
1.理解总体、个体、简单随机样本和统计量的概念。掌握样本均值和样本 方差的计算。
(2)设 X ~ χ 2 (n) ,则 E(X)=n,D(X)=2n .
若 X ~ χ 2 (n) ,对于α (0 < α < 1) ,称满足 P( X > χα2 (n)) = α的点χα2 (n) 为 χ 2 (n) 分布的
上侧α 分位点。当 n>45 时,R.A.Fisher 证明了下面的近似公式
( ) χα2
(n)
≈
1 2
uα +
2
2n −1 ,
其中 uα 为标准正态分布的上侧α 分位点。
2、 自由度为 n 的 t 分布:
定义设 X1, X2 独立,X1~N(0,1), X2~ χ 2 (n) ,则称
T (n) = X1 X 2 n
的分布是自由度为 n 的 t 分布,简记为 t(n) ,亦称为学生(student)分布。这种分布是英国人 w.s.Gosset 在 1908 年以笔名”student”发表的,它是数理统计中最重要的分布之一。 命题 设 T(n)是自由度为 n 的 t 分布,则它的概率密度函数为:
2.会列出分组数据统计表。 3.了解X2-分布、t-分布和F-分布的定义及性质。了解分位数的概念并会查
表计算。 4.掌握正态总体的抽样分布规律。
(二)重点
1.样本均值和样本方差的计算。 2.分组数据统计表。 3.正态总体的抽样分布规律。
.第六章 数理统计基本概念
一、基本要求、重点与难点
(一)基本要求
1.理解总体、个体、简单随机样本和统计量的概念。掌握样本均值和样本 方差的计算。
(2)设 X ~ χ 2 (n) ,则 E(X)=n,D(X)=2n .
若 X ~ χ 2 (n) ,对于α (0 < α < 1) ,称满足 P( X > χα2 (n)) = α的点χα2 (n) 为 χ 2 (n) 分布的
上侧α 分位点。当 n>45 时,R.A.Fisher 证明了下面的近似公式
( ) χα2
(n)
≈
1 2
uα +
2
2n −1 ,
其中 uα 为标准正态分布的上侧α 分位点。
2、 自由度为 n 的 t 分布:
定义设 X1, X2 独立,X1~N(0,1), X2~ χ 2 (n) ,则称
T (n) = X1 X 2 n
的分布是自由度为 n 的 t 分布,简记为 t(n) ,亦称为学生(student)分布。这种分布是英国人 w.s.Gosset 在 1908 年以笔名”student”发表的,它是数理统计中最重要的分布之一。 命题 设 T(n)是自由度为 n 的 t 分布,则它的概率密度函数为:
2.会列出分组数据统计表。 3.了解X2-分布、t-分布和F-分布的定义及性质。了解分位数的概念并会查
表计算。 4.掌握正态总体的抽样分布规律。
(二)重点
1.样本均值和样本方差的计算。 2.分组数据统计表。 3.正态总体的抽样分布规律。
概率论与数理统计-6

一、统计量
定义1 设X1, X2, …, Xn是总体X的样本,样本函数g(X1, X2, …, Xn)是样 本的实体函数,且不含有任何未知参数,则称这类样本函数g(X1, X2, …, Xn)为统计量。
由于样本具有二重性,统计量作为样本的函数也具有二重性,即对 一次具体的观测或试验,它们都是具体的数值,但当脱离开具体的某 次观测或试验,样本是随机变量,因此统计量也是随机变量。
n i 1
( xi
x )2
1n (
n 1 i1
xi2
nx 2 )
。
(3)样本标准差
S
S2
1 n 1
n i 1
(Xi
X
)2
它的观测值记为 s
s2
1 n 1
n i 1
( xi
x )2
。
(6-5)
(4)样本k阶原点矩
Ak
1 n
n i 1
X
k i
(k
1,2 ,3,
)
它的观测值记为 ak
解 将样本的观察值由小到大排列为 1 2 3 3 4 4 4 5 6 8
所以样本的频率分布如表所示
X
1
2
3
4
5
6
8
fn
0.1
0.1
0.2
0.3
0.1
0.1
0.1
例1 设总体服从泊松分布,容量为10的样本观察值如下:
214 3 5 6 4 8 4 3 试构造样本的分布函数F10(x)。
例1 设随机变量 X ~ (0 ,1) 分布,求D(X)。
解 因为 X ~ (0 ,1)
所以 又
E(X ) p E( X 2 ) 0 (1 p) 12 p p
数理统计基本概念

n1 Γ( ) 2 n 1 x 2 fT ( x ) (1 ) 2 , n n n Γ ( ) 2
P{6.262 χ 2 24.996}
2 2
P{χ 6.262} P{χ 24.996}
0.975 0.05 0.925
注意 应注意分布表的定义与查法!
#
数理统计基本概念
3.自由度为 n的 t 分布 作笔名发表文章.
T~t(n)
又称学生氏分布--第一个研究者以Student
( X 1 , X 2 , , X n ) ~ ( 2 ) e
n 2 2
i 1
( xi )2 2 2
n
数理统计基本概念
四、统计量 定义6.1.2 设X1 , X2 , ·, Xn是总体X的样本, · · T为n元实值函数,若样本的函数 T=T(X1 , X2 , ·, Xn) · · 是随机变量且不含未知参数,称 T为统计量. 对相应的样本值( x1 , x2 , … , xn ) ,称 t =T( x1 , x2 , … , xn )
理
统
计
的
引
入
数理统计基本概念
某厂生产的一批产品中次品率为 p 。从中 抽取10件产品装箱。 概
1)没有次品的概率 2)平均有几件次品
率
3)为以 0.95的概率保证箱中 有10件正品,箱中至少要装多 少件产品。
数
理
统
计
的
引
入
数理统计基本概念
所有这些问题的关键是 p 是已知的! 如何获取 p ? 这就是数理统计的任务了!
定的α(0<α<1),数uα满足
P{ X u } ,
(C ) u1 ;
P{6.262 χ 2 24.996}
2 2
P{χ 6.262} P{χ 24.996}
0.975 0.05 0.925
注意 应注意分布表的定义与查法!
#
数理统计基本概念
3.自由度为 n的 t 分布 作笔名发表文章.
T~t(n)
又称学生氏分布--第一个研究者以Student
( X 1 , X 2 , , X n ) ~ ( 2 ) e
n 2 2
i 1
( xi )2 2 2
n
数理统计基本概念
四、统计量 定义6.1.2 设X1 , X2 , ·, Xn是总体X的样本, · · T为n元实值函数,若样本的函数 T=T(X1 , X2 , ·, Xn) · · 是随机变量且不含未知参数,称 T为统计量. 对相应的样本值( x1 , x2 , … , xn ) ,称 t =T( x1 , x2 , … , xn )
理
统
计
的
引
入
数理统计基本概念
某厂生产的一批产品中次品率为 p 。从中 抽取10件产品装箱。 概
1)没有次品的概率 2)平均有几件次品
率
3)为以 0.95的概率保证箱中 有10件正品,箱中至少要装多 少件产品。
数
理
统
计
的
引
入
数理统计基本概念
所有这些问题的关键是 p 是已知的! 如何获取 p ? 这就是数理统计的任务了!
定的α(0<α<1),数uα满足
P{ X u } ,
(C ) u1 ;
数理统计的基本概念

(n 2) n n
n 1 2
, x .
t 分布的概率密度图形
图形关于 x 0 对称, lim f ( x; n) 0 , 且 x 当 n 充分大时,f (x; n) 趋近于标准正态 分布的概率密度。
定理 4: X 1, 2, , n 是抽自正态总体 设 X X
若总体 X 是离散型的,其分布律为:
则样本的联合分布为
§6.2 抽样分布
6.2.1 统计量的概念 由样本推断总体的某些情况时,需要对样本进行“ 加工”,构造出若干个样本的已知 (确定)的函数, 其作用是把样本中所含的某一方面的信息集中起来 。 这种不含任何未知参数的样本的函数称为统计量。 它是完全由样本所决定的量。 定义2:设 X 1 , X 2 , , X n 是来自总体X的样本, g( X 1 , X 2 , , X n ) 是样本 X 1 , X 2 , , X n 的函数,如果 g( X 1 , X 2 , , X n ) 中不包含任何未知参数,则称它 是一个统计量。
1 (0.82)
1 0.7939 0.2061
X ~ N (0, 22 ), X1 , X 2 , X3 , X 4 为其样本,求a,b 例2:总体
(2). (n 1)S / ~ (n 1)
2
X (1). X ~ N ( , / n), 或 ~ N (0,) ; 1 / n 2 2 2
2
X (3). X 与 S 相互独立; (4). ~ t(n 1). S/ n
定理5:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自总体 2 两样本独立, X ~ N ( 1 , 12 )和Y ~ N ( 2 , 2 )的样本, 2 S12 / S2 则有 F 2 ~ F ( m 1, n 1). 2 1 / 2 定理6*:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自
n 1 2
, x .
t 分布的概率密度图形
图形关于 x 0 对称, lim f ( x; n) 0 , 且 x 当 n 充分大时,f (x; n) 趋近于标准正态 分布的概率密度。
定理 4: X 1, 2, , n 是抽自正态总体 设 X X
若总体 X 是离散型的,其分布律为:
则样本的联合分布为
§6.2 抽样分布
6.2.1 统计量的概念 由样本推断总体的某些情况时,需要对样本进行“ 加工”,构造出若干个样本的已知 (确定)的函数, 其作用是把样本中所含的某一方面的信息集中起来 。 这种不含任何未知参数的样本的函数称为统计量。 它是完全由样本所决定的量。 定义2:设 X 1 , X 2 , , X n 是来自总体X的样本, g( X 1 , X 2 , , X n ) 是样本 X 1 , X 2 , , X n 的函数,如果 g( X 1 , X 2 , , X n ) 中不包含任何未知参数,则称它 是一个统计量。
1 (0.82)
1 0.7939 0.2061
X ~ N (0, 22 ), X1 , X 2 , X3 , X 4 为其样本,求a,b 例2:总体
(2). (n 1)S / ~ (n 1)
2
X (1). X ~ N ( , / n), 或 ~ N (0,) ; 1 / n 2 2 2
2
X (3). X 与 S 相互独立; (4). ~ t(n 1). S/ n
定理5:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自总体 2 两样本独立, X ~ N ( 1 , 12 )和Y ~ N ( 2 , 2 )的样本, 2 S12 / S2 则有 F 2 ~ F ( m 1, n 1). 2 1 / 2 定理6*:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自
概率论与数理统计 第六章--数理统计的基本概念

F分布性质2 若X ~t(n),则X2~F(1,n)
例4.设X1,X2, …,Xn是来自正态总体N(0,1) 的样本,试问c=( )统计量
c
2 X i 3 i 1 n
X
i 4
2 i
服从F分布?
抽样分布的分位点
设α为给定的常数,且0<α<1.若存在χα2(n)使
P ( n)
分位点的性质
(1) u1 u (2)
t1 (n) t (n)
1 (3) F (m, n) F1 (n, m)
回顾1. 设X1 ,X2 ,X3, X4是来自总体N(0,4)的简单 随机样本,X=a(X1-2 X2)2+b(3X3 -4X4)2,问当 a,b为何值时,统计量X服从 2分布 .
Max=1572, Min=738, 组数=6 组距=(Max-Min)/6=139140 取a0=735, 则分组区间及相关数据如下
组序 1 2 分区区间 (735,875] (875,1015] 频数 6 8 频率 0.2 0.27 累计频率 0.2 0.47
3
4 5 6 合计
(1015,1155]
2
所服从的分布为自由度为 n 的 分布 记为
2
~ (n)
2 2
分布的密度函数为
2
n x 1 1 n2 x2 e 2 f ( x; n ) 2 ( n 2 ) 0
x0 x0
其中伽玛函数 ( x )通过积分
( x ) e t dt, x 0 0 来定义.
(1155,1295] (1295,1435] (1435,1575]
9
4 2 1 30
0.3
概率论第六章 数理统计的基本概念(2)

15 March 2020
概率论与数理统计
理学院数学系
第六章 数理统计的基本概念
6.3.4 正态总体的抽样分布
第10页
一、单个正态总体的抽样分布
定理6.3.1(抽样分布基本定理)设( X1, X2 ,..., Xn )是来自总体X ~ N (0,1)
的一个样本, 则样本均值X
~
N (0,
1 n
),样本方差Sn2
满足:nSn2
~
2 (n 1),
并且X 与Sn2 相互独立.
注:
Sn2
1 n
n i 1
(Xi
X )2
为
X 的函数,
但两者独立.
15 March 2020
概率论与数理统计
理学院数学系
第六章 数理统计的基本概念
第11页
推论6.3.1 设 (X1,X2,…,Xn) 是来自总体X~N(μ,σ2) 的一个样本, 则
概率论与数理统计
理学院数学系
第六章 数理统计的基本概念
第13页
例 2: 设 X1, X 2 , , X10 是来自总体 X ~ N(,4) 的样本,
求修正样本方差 Sn*2 大于 2.622 的概率.
解 :由于
(10 1)Sn*2 ~ 2 (9)
4
P(Sn*2
2.622)
P
9 4
推论6.3.2 设(X1, X2,..., X n )是来自总体X ~ N (, 2 )的
一个样本, X与Sn2分别为其样本均值与样本方差,则
(X )
Sn*
n = X
Sn
n-1 ~ t(n 1)
概率论与数理统计(叶慈南 刘锡平 科学出版社)第6章 数理统计的基本概念教程
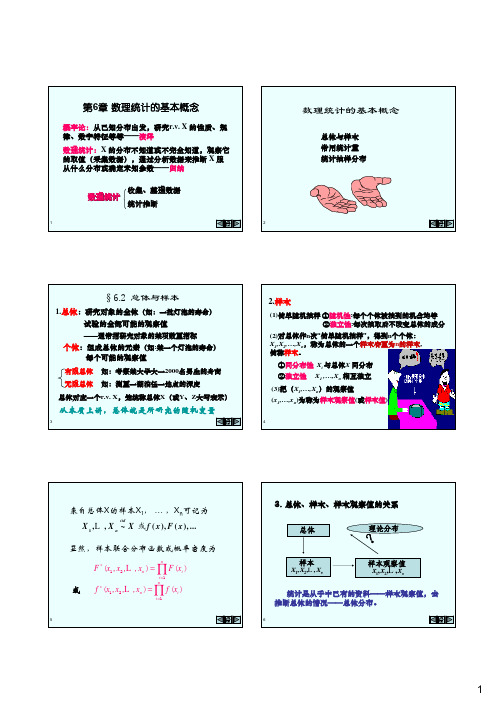
3.样本k阶(原点)矩 Ak = 样本k阶中心矩
Bk =
1 n k ∑ X i 反映总体k阶矩E(Xk)的信息 n i =1 P E ( X k ) = k , k = 1, 2, L →
反映总体k
9
1 n P → ∑ ( X i X )k E {[ X E ( X )]k } = mk n i =1 k=1,2,…
1o
X ~ N ( ,
σ2 ) n
即
X ~ N (0,1) σ/ n
2o 3o
(n 1) S 2 ~ χ 2 ( n 1) σ2 X 与 S 2 相互独立 4o X ~ t ( n 1) S/ n
23
24
4
1o
X ~ N ( , X=
σ2 ) n
即
X ~ N ( 0, 1) σ/ n
4o
正态总体的抽样分布定理
例 设 X1,…,X10 是取自N(0,0.32)的样本,求
P{∑ X i > 1.44}
2 i =1 10
定理一,二,三
2 2 设 X 1 ,..., X n 是来总体 N ( , σ ) 的样本, X , S 分别为样
本均值和样本方差,则
例 设 X 1 , X 2 , L , X 15 是来自总体 N (0,1)的一个简单随 2 2 X 12 + X 2 + L + X 10 机样本, Y= 则 服从 分布. 2 2 2 2( X 11 + X 12 + L + X 15 )
4
个体:组成总体的元素(如:某一个灯泡的寿命)
每个可能的观察值
有限总体 无限总体 如:考察某大学大一2000名男生的身高 如:考察某大学大一2000名男生的身高 如:测量一湖泊任一地点的深度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23
例如,若在例1从5000个产品中随机地抽检一个产品 中用有放回的抽样方法随机地检验n个产品,则得 到的样本X1,X2,…,Xn就是独立的且与总体X有相同 的分布,即 Xi P 0 1-p 1 p
i=1,2,…,n.
因此,这种抽样方法是简单随机抽样,而得到的样 本是简单随机样本.
24
17
显然,对总体X的任何一次容量为n的抽样结果 “x1,x2,…,xn” 是n个完全确定的数值; 但由于抽样是一个随机试验,所以这n个观察值是 随每次抽样而改变的,它具有随机性. 换句话说,对具体某次抽样来说,抽样结果是n个 确定的数值: x1,x2,…,xn; 而离开了特定的某次抽样来说,抽样结果是n个随 机变量: X1,X2,…,Xn.
22
这样得到的样本X1,X2,…,Xn满足下面的两个条件: (1)X1,X2,…,Xn相互独立; (2)每个Xi(i=1,2,…,n )与总体X有相同的分布. 人们把满足这两个条件的抽样方法称为简单随机抽 样(Simple random sampling),而得到的样本称为 简单随机样本.
14
以上所考察的个体的数量指标只有一个,即只需要 用一维随机变量来描述; 如果同时要考察的数量指标不止一个,那么就需要 用多维随机变量来描述. 例如,对上述某城市现有大学生的这个总体,若要 同时考察大学生的身高X、体重Y和肺活量Z,那么 就需要三维随机变量(X,Y,Z). 同样,为了叙述方便,人们把总体与(X,Y,Z)或它 的分布等同起来,并称这样的总体为三维总体. 在本书中我们主要讨论一维总体,多维总体是多元 统计分析主要研究的对象.
15
第六章
数理统计的基本概念
6.1 总体与样本
6.1.3
样本(Sample)
在6.1.1中已经说过,为了对例1和例2中所提出的问 题作出估计或推断,就必须从所研究对象的全部元 素中随机地抽取一小部分进行观察. 所谓随机地是指总体中的每个个体被观察到的机会 是一样的,而所谓抽取一部分个体进行观察,其实 就是对总体X重复进行若干次观察以获得X的若干个 观察数值. 16
若将分布列写成
P( X xi ) p (1 p)
xi
1 xi
, xi 0或1
则由独立性,样本的分布可写成
P( X 1 x1 , X 2 x2 ,, X n xn ) P( X i xi ) p (1 p)
xi i 1 i 1 n n 1 xi
3
例1 从5000个产品中随机地抽检一个产品,结果可 能合格,也可能不合格. 由概率论可知,这个现象可以用两点分布来描述: X 0 1
P
1−p
p
这里,“X= 0”表示产品不合格,“X= 1”表示产品 不合格,p为不合格率. 但是,p等于多少是事先未知的,也就是说0—1分布 中的参数是未知的.
19
样本值 x1,x2,…,xn 可以看作n维空间的一个点 (x1,x2,…,xn), 称之为样本点.
样本点的全体称为样本空间,它是n维空间或n维空 间的一个子集.
20
前面把抽样结果看作n维随机变量,并称之为样本, 这一点是很重要的. 因为只有这样才能运用概率论的理论对总体X进行 各种推断以及研究比较各种推断方法的好坏. 数理统计的主要任务之一,就是研究如何根据样本 来推断总体. 样本能很好地反映总体的特性
(c)样本(X1,X2,…,Xn)的每一个观察值 (x1,x2,…,xn) 称为样本值(或样本的一次实现),样本值的集合称 为总体X的容量为n的样本空间.
28
为了数理统计的需要,人们引入了标准正态分布 N(0,1)的上侧分位数的概念. 设X~ N(0,1),对给定的α (0< α <1),若数uα
因此,对总体的研究实际上就是对某一个随机变量 X的概率分布的研究.
13
为了便于叙述,一旦所考察的数量指标明确以后, 就可以把总体与数量指标及相应的概率分布等同起 来,也就是说,总体是一个概率分布或服从这个概 率分布的随机变量. 如在例1从5000个产品中随机地抽检一个产品检查是 否合格的试验中,总体就是0—1分布或服从这个分 布的随机变量X, 在例2考察齿轮的径向综合误差的试验中,总体就是 描述齿轮的径向综合误差的随机变量X或它所服从 的分布.
概率论与数理统 计
第六章 数理统计的基本概念
1
第六章
数理统计的基本概念
6.1 总体与样本
6.1.1
数理统计的基本问题
在前面的章节中,介绍了概率论的基本内容,从本 章开始将介绍一些数理统计的基本知识和一些常用 的数理统计方法. 概率论中许多问题的讨论,常常是从已给的随机变 量X出发来研究X的种种性质,那里X的概率分布都 是已知的,或者假设是已知的.
18
人们称这n个随机变量 X1,X2,…,Xn 为来自总体X的一个容量为n的样本(或子样). 而 x1,x2,…,xn 称为样本的一个观察值(Observations),简称为样 本值,有时也称为样本的一个实现. 容量为n的一个样本可以看作n维随机变量 (X1,X2,…,Xn), 它的分布就称为样本的分布.
6
试问 (a)如何求出或近似地求出F(x)(或f(x))的值?
(b)如果人们根据以往的生产经验提出假设: “X服从正态分布N(μ ,σ 2)” (μ 和σ 2已知或未知), 那么,是接受这个假设还是否定这个假设呢?
应该用什么方法来判断? (c)如果人们只需要知道X的数学期望和方差,那么, 如何估计它们的数值?
11
如在例1从5000个产品中随机地抽检一个产品检查是 否合格的试验中,每个产品是个体,5000个产品就 是一个总体,它是有限的; 在例2考察齿轮的径向综合误差的试验中,每一件齿 轮是个体,生产出来的全部齿轮是一个总体,它是 无限的, 这是因为我们可以设想,工厂生产这种齿轮可以在 相同的条件下无限地生产下去. 再如,某城市现有大学生组成的集合是个有限总体, 而该城市在一定条件下培养起来的大学生组成的集 合是个无限总体.
12
当用数理统计方法研究总体时,人们主要关心的不 是每个个体本身,而仅仅是与每个个体的某种数量 指标(或特征)的有关问题. 如在例1从5000个产品中随机地抽检一个产品检查是 否合格的试验中,人们关心的是刻画产品合格与否 的数量指标X的概率分布问题;
在例2考察齿轮的径向综合误差的试验中,人们关心 的是齿轮的径向综合误差X的概率分布问题.
21
通常 人们假设对总体X的n次观察是在相同的条件下重复 进行的. 这样得到的样本X1,X2,…,Xn满足下面的两个条件: (1)X1,X2,…,Xn相互独立; (2)每个Xi(i=1,2,…,n )与总体X有相同的分布. 上面的两个条件,实际上就是样本具有代表性的反 映; 另外,有了独立性,就可以方便地应用概率论中有 关独立随机变量的种种结果.
2
概率论中许多问题的讨论,常常是从已给的随机变 量X出发来研究X的种种性质,那里X的概率分布都 是已知的,或者假设是已知的. 但是在实际问题中,一般说来,人们事先并不知道 随机事件的概率、随机变量的概率分布和数字特征, 而需要对它们进行估计或作某种推断,这就产生了 数理统计的问题.
下面看两个例子.
例如,若在例1中随机地抽检5个产品,结果分别是 “合格”、“不合格”、“合格”、“合格”和 “不合格”,那么就得到X的5个观察值:0,1,0, 0,1. 一般说来,从总体X中随机抽检n个个体,则可以得 到的n个观察值:x1,x2,…,xn. 为了叙述方便,人们把从总体X中随机抽检(或观察) n个个体的试验,称为随机抽样(Sampling),简称 抽样,n称为容量(Size).
i 1
n
今后,如果不作特殊的声明,所说的抽样皆为简单 随机抽样,所说的的样本皆为简单随机样本.
26
最后,将前面讲的总体和样本的概念用定义的形式 小结如下: 定义6.1 (a)称随机变量X的概率分布为一个总体,或称随机 变量X为一个总体,而X的分布称为总体的分布; (b)如果X1,X2,…,Xn是相互独立且与总体X有相同 分布的n个随机变量,即如果它们的联合分布函数 为
7
怎样解决这些问题呢? 对例1来说,由于产品总数是有限的,人们可以对所 有产品逐个检验,求出不合格产品所占的比例,就 得到概率p; 同时,假设“p<0.05”是否成立的问题也就得到了解 决. 但是,这种普查的方法是不可取的,有时也是行不 通的. 因为对5000个产品逐个检验,一般来说要耗费很多 的人力、物力和时间; 特别是,当产品质量的检验是属于破坏性检验时, 根本就不可能逐个检验.
4
试问 (a)如何求出或近似地求出p的值?
(b)如果人们根据以往的生产经验提出假设: “p<0.05”,
那么,是同意这个假设还是否定这个假设呢?应该 用什么方法来检验?
5
例2 一个工厂生产某种规格的圆柱齿轮. 由于原料和加工过程中的种种随机因素的影响,各 个齿轮的径向综合误差X的数值一般是不同的,因 此加工出来的齿轮,它的径向综合误差X是一个随 机变量. 但是X的分布函数FX(x)(或概率密度fX(x))是什么, 事前是未知的. 试问 (a)如何求出或近似地求出F(x)(或f(x))的值?
u
满足条件 即
