七年级数学上册鲁教版(五四制):3.3勾股定理的应用举例
鲁教版七年级数学上册《勾股定理的应用举例》教案

《勾股定理的应用举例》教案教学目标教学知识点能运用勾股定理及直角三角形的判别条件(即勾股定理的逆定理)解决简单的实际问题.能力训练要求1、学会观察图形,勇于探索图形间的关系,培养学生的空间观念.2、在将实际问题抽象成几何图形过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.情感与价值观要求:1、通过有趣的问题提高学习数学的兴趣.2、在解决实际问题的过程中,体验数学学习的实用性,体现人人都学有用的数学.教学重点难点重点:探索、发现给定事物中隐含的勾股定理及其逆及理,并用它们解决生活实际问题.难点:利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题. 教学过程1、创设问题情境,引入新课前几节课我们学习了勾股定理,你还记得它有什么作用吗?例如:欲登12米高的建筑物,为安全需要,需使梯子底端离建筑物5米,至少需多长的梯子?根据题意,(如图)AC是建筑物,则AC=12米,BC=5米,AB是梯子的长度.所以在Rt △ABC中,AB2=AC2+B C2=122+52=132;AB=13米.所以至少需13米长的梯子.2、讲授新课:①蚂蚁怎么走最近?A BA B出示问题:有一个圆柱,它的高等于12cm ,底面上圆的周长等于18cm .在圆行柱的下底面点A 点有一只蚂蚁,它想吃到上底面上与A 点相对的B 点处的食物,沿圆柱侧面爬行的的最短路程是多少?(1)自己做一个圆柱,尝试从A 点到B 点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?(小组讨论)(2)如图1-12,将圆柱侧面剪开展开成一个长方形,从A 点到B 点的最短路线是什么?你画对了吗?(3)蚂蚁从A 点出发,想吃到B 点上的食物,它沿圆柱侧面爬行的最短路程是多少?(学生分组讨论,公布结果)我们知道,圆柱的侧面展开图是一长方形,好了,现在咱们就用剪刀沿母线AA ′将圆柱的侧面展开(如下图).我们不难发现,刚才几位同学的走法:(1)A →A ′→B ; (2)A →B ′→B ;(3)A →D →B ; (4)A →B .哪条路线是最短呢?你画对了吗?第(4)条路线最短.因为“两点之间的连线中线段最短”.②做一做李叔叔想要检测雕塑底座正面的边AD 和边BC 是否分别垂直于底边AB ,但他随身只带了卷尺.(1)你能替他想办法完成任务吗?(2)李叔叔量得边AD 长是30cm ,边AB 长是40cm ,边BD 长是50cm ,AD 边垂直于AB 边吗?为什么?(3)小明随身只有一个长度为20cm 的刻度尺,他能有办法检验边AD 是否垂直于边AB 吗?边BC 与边AB 呢?也就是要检测∠DAB =90°,∠CBA =90°.连结BD 或AC ,也就是要检测△DAB 和△C BA 是否为直角三角形.很显然,这是一个需用勾股定理的逆定理来解决的实际问题.解答:(2) ∴AD 和AB 垂直.③随堂练习(1)甲、乙两位探险者,到沙漠进行探险.某日早晨8∶00甲先出发,他以6km /h 的速度向正东行走.1时后乙出发,他以5km /h 的速度向正北行走.上午10∶00,甲、乙两人相距多远?分析:首先我们需要根据题意将实际问题转化成数学模型.解:(如图)根据题意,可知A 是甲、乙的出发点,10∶00时甲到达B 点,则AB =2×6=12(km );乙到达C 点,则AC =1×5=5(km).在Rt △ABC 中,BC 2=AC 2+AB 2=52+122=169=132,所以BC =13km .即甲、乙两人相距13km .例题:1、在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?我们可以将这个实际问题转化成数学模型.解:如图,设水深为x 尺,则芦苇长为(x +1)尺,由勾股定理可求得(x +1)2=x 2+52,x 2+2x +1=x 2+25解得x =12则水池的深度为12尺,芦苇长13尺.2、某隧道的界面是一个半径为4.2m 的半圆形,一辆高3.6m ,宽3m的卡250040302222=+=+AB AD 25002=BD 222BD AB AD =+∴车能通过该隧道吗?课时小结这节课我们利用勾股定理和它的逆定理解决了生活中的几个实际问题.我们从中可以发现用数学知识解决这些实际问题,更为重要的是将它们转化成数学模型.课后作业课本习题3.4、3.5.。
七年级数学上册 3.3 勾股定理的应用举例教学设计3 鲁教版五四制

勾股定理的应用举例教材与学情分析本节课是在探究了勾股定理后运用勾股定理解决生活中的实际问题,本节内容分两课时,第一课时有两部分内容,第一部分立体图形表面上两点间最短距离,构造的直角三角形中已知两边,可以直接运用勾股定理解决实际问题;第二部分已知三角形的三边判断所构造的三角形是否为直角三角形,应用勾股定理的逆定理解决实际问题。
第二课时在第一课时的基础上,进一步研究勾股定理的两方面实际应用,第一是在直角三角形中已知一边和其他两边等量关系时,要运用方程思想求未知边;第二是决策问题:判断车能否过隧道问题,构造已知两边的直角三角形,判断第三边。
学生在学习勾股定理的直接应用后,当已知两边能熟练求直角三角形的第三边。
因此本课时的重点利用勾股定理的等量关系式列方程求未知边,和通过计算判断并作出决策。
其中难点是在决策问题中如何构造直角三角形。
教学目标知识与技能应用勾股定理解决简单的实际问题,当所构造的直角三角形中只有一边已知时,可以根据勾股定理列方程解决问题应用勾股定理解决生活中一类决策问题过程与方法在探究问题解决方法的过程中感受方程思想方法,感受构建方程模型的必要性在探究问题过程中如何构造直角三角形,体会转化的数学思想方法情感态度与价值观在讨论问题过程中,进一步认识勾股定理的悠久历史和广泛应用,了解我国古代人民的聪明才智,从而增强学习数学的兴趣.教学资源PPT 课件、几何画板课件、三角板等教学设计思路复习总结→创设问题引入新课→合作探究解决问题→巩固提升→梳理总结升华收获五、教学实施过程:(一)复习导入师:同学们,前面学习了勾股定理,知道根据勾股定理能求出直角三角形的边长,请看:1、如图,在Rt △ABC 中,∠C=90°,则总结并板书1)已知两直角边能求斜边2)已知一直角边和斜边能求另一直角边【设计意图】让学生明确直角三角形已知两边第三边能直接运用勾股定理求出第三边,为下面例1中只知一条边时求边要借助方程的方法,不能直接运用勾股定理做好铺垫. ===222b a c ,,AC B a cb师:勾股定理是一个非常重要的定理,从古代到现代,人们在生活中广泛应用。
鲁教版五四制七年级数学上册第三章勾股定理1探索勾股定理

勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 b2 c2
直角三角形两直角边的平方和等于斜边的平方.
a
c
b
勾
弦
股
我们用另外一种方法来说明勾股定理是正确的
c
c
c
c
•
13、生气是拿别人做错的事来惩罚自 己。22.3.2322.3.2317:59:0317:59:03March 23, 2022
•
14、抱最大的希望,作最大的努力。2022年3月23日 星期三 下午5时59分3秒17:59:0322.3.23
•
15、一个人炫耀什么,说明他内心缺 少什么 。。2022年3月 下午5时59分22.3.2317:59M arch 23, 2022
9
16
?
怎么求SR的大小? 有几种方案?
P
Q CR
用“补”的方法
SR
49 4 ( 1 4 3) 2
25.
P
Q CR
用“割”的方法
SR
4
1 2
4
3
1
25.
探究勾股定理
(1)在图中,正方形A中含
C A
B
有 9 个小方格,即A的面积 是 9 个单位面积.
正方形B的面积是__9__ 个单位面积.
(图中每个小方格代表1个单位面积)
C A
(2)在图2中,正方形A, B,C中各含有多少个小方 格?它们的面积各是多少?
B
图1
C A
B
图2
(3)你能发现图1中三个 正方形A,B,C的面积之 间有什么关系吗?图2呢?
鲁教版数学七年级上册:3.3《勾股定理的应用举例

A
鲁教版七上
在一棵树的10米高处B有两只猴子,其中一 只猴子爬下树走到离树20米的池塘A,另一只 猴子爬到树顶D后直接跃向池塘的A处,如果 两只猴子所经过距离相等,试问这棵树有多高?
D B.
C
A
鲁教版小七结上
你 能说说运用勾股定理的知识
可以解决实际生活中哪些问题吗?
鲁教版七高上中物理·选修3-3·粤教版
BD长是50厘米AD边垂直于AB边吗?
(3) 小明随身只有一个长度为20厘米的刻度尺,他能有办 法检验AD边是否垂直于AB边吗?BC边与AB边呢?
鲁教版随七堂上 练习
甲、乙两位探险者到沙漠进行探险.某日早晨 8:00甲先出发,他以6千米/小时的速度向东行走,1小 时后乙出发,他以5千米/小时的速度向北行进,上午 10:00,甲、乙二人相距多远?
C.液体分子的热运动没有长期固定的平衡位置 D.液体的扩散比固体的扩散快 答案 A
鲁课教堂版七讲上义
解析 液体具有一定的体积,是液体分子密集 在一起的缘故,但液体分子间的相互作用不像 固体微粒那样强,所以B是正确的、A是错误 的;液体具有流动性的原因是液体分子热运动 的平衡位置不固定,液体分子可以在液体中移 动;也正是因为液体分子在液体里移动比固体 容易,所以其扩散也比固体的扩散快,C、D都 是正确的.
(2)液晶具有液体的流动性.原因是液晶分子
鲁课教堂版七讲上义
3.长丝状液晶 (1)分子排列特点:呈长棒形排列,自然状态 下分子有彼此平行排列的倾向,沿一定方向 的排列比较整齐,但彼此间前后左右的位置 可以变动. (2)特性及应用:对外界的作用很敏感,当外 加电压时,液晶分子不再平行排列,液晶由 透明状态变成混浊状态,去 掉电压又恢复透 明,因此可制作显示元件.
鲁教版五四制七年级数学上册第三章勾股定理2一定是直角三角形吗

•
10、低头要有勇气,抬头要有低气。* **5/3/2021 8:32:52 AM
•
11、人总是珍惜为得到。21.5.3**May- 213-M ay-21
•
12、人乱于心,不宽余请。***Monday, May 03, 2021
•
13、生气是拿别人做错的事来惩罚自 己。21.5.321.5.3**May 3, 2021
2 一定是直角三角形吗
1.经历直角三角形的判别条件(即勾股定理的逆定 理)的探究过程,发展推理论证能力. 2.掌握勾股定理的逆定理及勾股数的定义,并能进 行简单的应用.
古埃及人曾用下面的方法得到直角: 用13个等距的结把一根绳子分成等长的12段,一
个工匠同时握住绳子的第1个结和第13个结,两个助 手分别握住第4个结和第8个结,拉紧绳子就得到一个 直角三角形, 其直角在第4个结处.
•
12、人乱于心,不宽余请。2021/5/32021/5/32021/5/3Monday, May 03, 2021
•
13、生气是拿别人做错的事来惩罚自 己。2021/5/32021/5/32021/5/32021/5/35/3/2021
•
14、抱最大的希望,作最大的努力。2021年5月3日 星期一2021/5/32021/5/32021/5/3
4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成 的三角形是直角三角形吗?为什么? 【解析】是直角三角形,因为a2+b2=c2,满足勾股定 理的逆定理.
1.下列三角形是直角三角形吗?
D
64ຫໍສະໝຸດ EF 7不是
A
12
9
B
15
C
是
2.(眉山·中考)如图,每个小正方形的边长为1,A, B,C是小正方形的顶点,则∠ABC的度数为( ) A.90° B.60° C.45° D.30°
鲁教版七年级上3.3勾股定理的应用举例同步测试含答案解析

知能提升作业(十八)3 勾股定理的应用举例(30分钟 50分)一、选择题(每小题4分,共12分)1.如图,有一个圆锥,高为8cm,底面直径为12cm.在圆锥的底边B点处有一只蚂蚁,它想吃掉圆锥顶部A处的食物,则它需要爬行的最短路程是( )(A)8cm (B)9cm(C)10cm (D)11cm2.如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )(A)45m (B)40m(C)50m (D)56m3.如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.则小明到达的终止点与原出发点的距离是( )(A)90米(B)100米(C)120米(D)150米二、填空题(每小题4分,共12分)4.在一棵树的10米高B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边,另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高________米.5.如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为________cm.6.如图,在Rt△ABC中,∠C=90°,AC=11cm,BC=9cm,点P从点A出发沿AC以1cm/s的速度移动,点Q从点C出发沿CB以2cm/s的速度移动,如果P,Q分别从A,C两点同时出发,当它们相距10cm时所用的时间为________.三、解答题(共26分)7.(8分)一个抽屉内壁的长、宽、高分别是24cm,32cm,9cm,要把一个长42cm 的画轴放入抽屉,能不能放进去(画轴半径忽略不计),为什么?8.(8分)我国古代数学中有这样一道数学题:有一棵枯树直立在地上,树高2丈,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,(如图)则这根藤条有几尺?(注:枯树可以看成圆柱;树粗3尺,指的是:圆柱底面周长为3尺,1丈=10尺)【拓展延伸】9.(10分)如图,小丽荡秋千,秋千架高2.4m,秋千座位离地0.4m,小红荡到最高时,座位离地0.8m.此时小红荡出的水平距离是多少?(荡到秋千架两边的最高点之间的距离)答案解析1.【解析】选C.如图,点A,点B和圆锥底面圆的圆心O构成一个直角三角形,其中OA=8cm,OB=6cm,则AB2=62+82=102,所以AB=10cm.2.【解析】选 B.因为AO=32m,BO=24m,所以AB2=BO2+AO2=242+322=1600,则AB=40m.3.【解析】选B.如图,构造Rt△ABC,根据勾股定理得AC2=(40+40)2+(70-10)2=10000=1002,即AC=100(米).4.【解析】设树的高度为x米,因两只猴子所经过的距离相等都为10+20=30(米).由勾股定理得:x2+202=[30-(x-10)]2,解得x=15(米).故这棵树高15米.答案:155.【解析】如图所示,因为PA=2×(4+2)=12cm,AQ=5cm,所以PQ2=PA2+AQ2=122+52=132,所以PQ=13cm.答案:136.【解析】在Rt△PCQ中,QC2+PC2=102,设P,Q相遇距10cm时所用时间为ts,则(2t)2+(11-t)2=(10)2,解得t=3或1.4.当时间为3s时,PC=8cm,QC=6cm;当时间为1.4s时,PC=9.6cm,QC=2.8cm,均符合题意.答案:3s或1.4 s7.【解析】不能.如图,连接FH,CF,在Rt△FGH中,FH2= FG2+GH2=242+322=402,所以FH=40cm.在Rt△CFH中,CF2= CH2+FH2=92+402=412,所以CF=41cm.因为41cm<42cm,故画轴不能放入抽屉.8.【解析】在Rt△ABC中,由勾股定理得,AB2=BC2+AC2,因为BC=20,AC=3×7=21,所以AB2=202+212=841,所以AB=29,所以这根藤条有29尺.9.【解析】如图为秋千侧面图,座位最低点为A,最高点为B,则OA=OB=2m,过B点作OA的垂线,垂足为C,则AC=0.8-0.4=0.4(m),OC=2-0.4=1.6(m),由勾股定理得:BC2=OB2-OC2= 22-1.62=1.22,所以BC=1.2m,所以2BC=2×1.2=2.4(m),故小红荡出的水平距离是2.4m.。
鲁教版数学七上3.3《勾股定理的应用举例》

问题1:
地面上,一只蚂蚁在爬行到A处想吃在B处 的食物怎样走最近?用数学知识解释?
蛋糕 B
A
问题2
如图,有一个圆柱体,它的高 等于12厘米,底面周长等于18厘米, 在圆柱下底面的A点有一只蚂蚁, 它想吃到上底面与A点相对的B处的 食物,问:
(1)蚂蚁在圆柱体表面爬向食物时,沿怎样的路线 爬行,路程最短?你是怎样想的?能曲面的问题转化 为平面的问题解决吗?试画出最短路线图
蛋糕 B
A
(2)你能用相关的知识求出需要爬行的最短路程是多少?
O
蛋糕 B
C
9cm
B
高 12cm
12
A
A
长18cm
解:蚂蚁沿如图路线走最短 ∵ AB2=AC2+BC2 =92+122=81+144=225= 152 ∴ AB=15(cm)
蚂蚁爬行的最短路程是15厘米.
变式训练
有一个棱柱,它的 高等于12厘米,底面边长 等于2.5厘米,在棱柱下底 面上的A点有一只蚂蚁, 它想从点A爬到点B , 蚂 我怎么走 会最近呢? D A C G H F B
蚁沿着需要爬行的最短
路程是多少?
试一试
( 1 )从 A 点到 B 点沿棱柱侧面画出的几条路 线,你觉得哪条路线最短呢?
H H
G
F
B G
F
B G
H F
B
D A C
D
D A C
A
C
提示:你能把A点和B点所在的侧面变成同 一平面吗?有几种展开方法?那条最短?
G
F
B
H G A
H
A
C
D
C
A
E
(2) 将棱柱沿侧棱剪开,展成一个长方形,从A点到 B点的最短线路是什么?
新鲁教版(五四制)七年级数学上册教案:第三章3.3勾股定理的应用举例教案
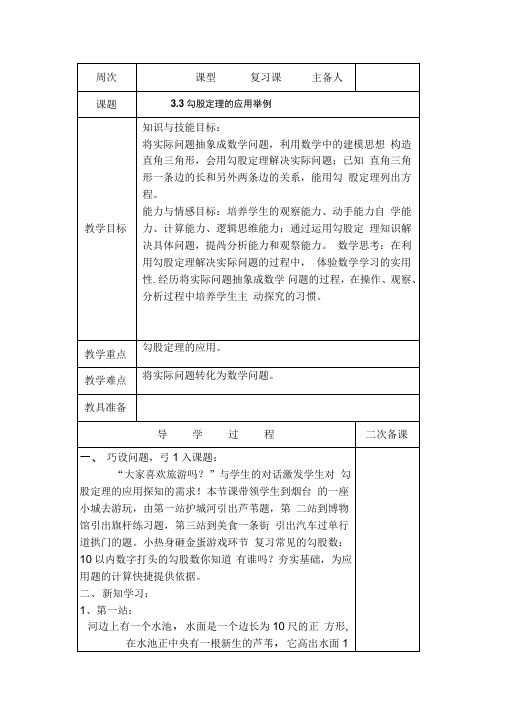
尺.如果把这根芦苇拉向
岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:设水池的水深AC为x尺, 则这
根芦苇长为
AD=AB=(x+1)尺,在直角三角形
ABC中,BC=5尺.
由勾股定理得:BC2+AC2=AB2. 即
52+ x2= (x+1)).
25+x2= x2+2x+1.
2x=24.
x=12, x+1=13.
答:水池的水深12尺,这根芦苇长13尺.
2、第二站:(学生自做,计时5分钟竞赛)
你想知道博物馆旗杆的高度,而又不能把旗杆放倒测量,当地工作人员发现旗杆顶端的绳子垂到地面还多2米,当他们把绳子下端拉开8米后,绳子刚好斜着拉直下端接触地面,你能算算旗杆的高度吗?
~尸十严 ~~尸 k h ~
3、第三站:
美食街是个单行车道,你乘坐的车要通过一个拱门,此拱门的截面是一个半径为3.9m的半圆形,你乘坐的车高3.5m、宽3m你能顺利通过该拱门吗?(本环节是教学重点:1、我通过演示拱门和汽车模型进行分析,通过演示,让学生明白汽车过拱门单行道走中间。
2、学生会根据立体图形画出几何图形,进行合理探究。
)
利用三种方法进行探究,方法一、先引导学生通过已知汽车宽度、半径、求出能通过的汽车的最大高度,与已知高度进行比较进行决策;方法二、利用已知高、宽求能通过
的最小拱门的半径,再与已知半径进行比较进行决策(这是课本的方法);方法三、利用已知高、半径求能通过的汽车的最大宽度,与已知宽度进行比较进行决策(学生自己总结此方法)。
本环节主要探究第一种,其他两种孩子自然就很容易想到。
板书设计教学反思。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思
例1 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题
的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方
向拉向岸边,那么它的顶端恰好到达岸边的水面.这个水池的深度和这根芦苇
的长度各是多少?
OB=OC
1尺
C
D
A
5尺
B
10尺
O
展展议
例1 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题
的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方
关键 构建直角三角形
O
数学 已知直角三角形的一直角边
D
C 问题 和斜边求另一直角边
方法二 比较另一直角边与车高的大小
A
B
检
如图,一座城墙高11.7m,墙外有一条宽为9m的护 城河,那么一个长为15m的云梯能否到达城墙的顶端?
收获平台
这节课我学会了…… 我发现了…… 使我体会最深的是…… 使我感到困难的是…… 我想我将…
义务教育教科书山东教育出版社七年级上册
测
勾股定理
导
学习目标
1、应用勾股定理解决简单的实际问题,当所构 造的直角三角形中只有一边已知时,可以根据勾股 定理列方程解决问题
2、在探究问题解决方法的过程中感受方程思想 方法,感受构建方程模型的必要性;在探究问题过 程中如何构造直角三角形,体会转化的数学思 想方法
数学来源于我们的生活,
又服务于我们的生活, 让我们用心来发现它, 用知识来解决它, 你会体验到数学给你带来的巨大乐趣!
一辆高3.6m、宽3m卡车能通过该隧道吗?
D
C 3.在长方形中,哪个点最有可能被
半圆形卡住?
4.长方形放在半圆形的什么位置表
A
B
思考
示“沿正中间走”?
1. 如果不能通过隧道,最可能是受到卡车的哪个部位的影响?
2. 如果能通过隧道,卡车沿隧道的哪条线走最容易通过?
前进隧道
展
例2 如图,某隧道的截面是一个半径为4.2m的半圆形,
转 化
关键
构建直角三角形
数学问题 已知直角三角形的一边和其他两边的数量关系求边
方法 根据勾股定理列方程
C
D
A
5尺
B
O
检
一架梯子若靠墙直立时比窗户的下沿高1m,若斜靠 在墙上,当梯子的下端离墙4m时,梯子的上端恰好 与窗户的下沿对齐.求梯子的长度.
1m
B
4m
A
C
议思
例2 如图,某隧道的截面是一个半径为4.2m的半圆形,
r2=4.22=17.64 >15.21 OC<r 所以卡车可以沿着隧道中间顺利通过
评
实际问题 判断卡车能否通过隧道
转
化 关键 构建直角三角形 数学问题 已知直角三角形的两直角边求斜边
方法 比较斜边与隧道半径的大小
D
C
拓展提高
AO B
评
例2 如图,某隧道的截面是一个半径为4.2m的半圆形, 一辆高3.6m、宽3m卡车能通过该隧道吗?
一辆高3.6m、宽3m卡车能通过该隧道吗? 解:长方形ABCD是卡车截面的示意图,
AB的中点O是隧道的截面半圆的圆
D
C
心
在ORBt=△1.B5OmC,中B,C=根3.据6m勾,股∠定OB理C=,90有°
AO B
OC2=OB2+BC2
即 OC2=1.52+3.62=15.21 隧道的截面半径r=4.2m,
向拉向岸边,那么它的顶端恰好到达岸边的水面.这个水池的深度和这根芦苇
的长度各是多少?
OB=OC
D
1.线段 OA 的长度表示水池的深度 2.线段 OC或OB 的长度表示芦苇的长度
1尺
C
A
5尺
B
10尺
3. △AOB 是直角三角形.它的三边分别
是 O际问题 求芦苇长度和水池深度
