上海理工大学高等代数试卷11
高代题库试题与答案

高等代数(下)试题(10)一 填空题 (每小题三分共15分)1 A,B 为n 阶可逆矩阵, C=⎪⎭⎫ ⎝⎛O B A O ,则C 1-=________。
2 A 为n 阶矩阵, A =21,则*1)3(A A --=_______ 3 设f 是一个n 元负定的二次型,则二次型f 的秩等于______________.4 设n ααα,...,21线性无关,W=L (n ααα,...,21),则W 的维数为______________ 。
5 数量矩阵A=aE 的 特征根 为 _______________。
二 单项选择题(每小题三分共15分)1 设A 是m n ⨯矩阵, B 是n ⨯m 矩阵,则( ) (A) 当m>n 时,必有行列式AB ≠0 (B )当m>n 时,必有行列式AB =0 (C )当n>m 时,必有行列式AB ≠0 (D )当n>m 时,必有行列式AB =02设A ,B ,C 均为n 阶矩阵,且秩A=秩B ,则 ( )(A) AB 的秩与AC 的秩不一定相等。
(B) AB 的秩与AC 的秩一定相等。
(C) AB 的秩与AC 的秩一定不相等。
(D) AB 的秩一定不超过C 的秩。
3 设向量空间V 中含有r 个向量,则下列结论成立的是 ( ) ( A ) r=1; (B )r=2 ; (C ) r=m (有限数); (D ) r=1或∞4 数域F 上 n 维向量空间V 有( )个基( A ) 1; (B ) n ; (C ) n!; (D )无穷多.5 设向量空间W= {(a,2a,3a) R a ∈},则W 的基为: ( ) (A ) ( 1, 2, 3,) ; (B ) (a, a ,a );(C ) ( a , 2a 3a) ; (D ) (1 ,0, 0), (0, 2 ,0), (0 ,0, 3) 三 (15分)⎪⎪⎭⎫ ⎝⎛--121011322X=⎪⎪⎭⎫ ⎝⎛-417 求X 四 (15分) 把二此型f (,x 2,x 3)= x 1x 2+ x 1,x 3+ x 2x 3通过非退化线性替换化成平方和。
线性代数练习题(含答案)
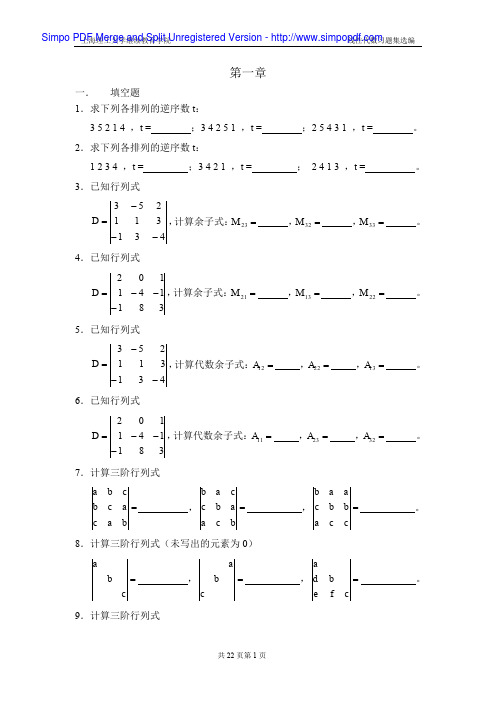
, ( AB ) T
。
1 0 3 0 4 , B 0 1 4.已知矩阵 A 。 1 5 2 1 1
AB
, BA
, ( BA) T
。
2 3 1 1 1 1 5.已知三阶方阵 A 1 1 1 , B 1 2 4 。 5 1 1 1 1 0
2 AT
, 3B T
, (2 A 3B) T
。
共 22 页第 3 页
Simpo PDF Merge and Split Unregistered Version - 上海理工大学继续教育学院 线性代数习题集选编
1 0 3 0 1 , C 2 1 。 ,B 0 2 8.已知矩阵 A 1 3 0 1 3 1 0
Simpo PDF Merge and Split Unregistered Version - 上海理工大学继续教育学院 线性代数习题集选编
第一章
一. 填空题 1.求下列各排列的逆序数 t: 3 5 2 1 4 ,t = ;3 4 2 5 1 ,t = ;2 5 4 3 1 ,t = 。
1)求 A 1 ; 2)解矩阵方程 AX B C 。
1 4 2 0 3 1 8.已知矩阵 A B C 1 2 1 1 0 1
1)求 A 1 , B 1 ;
2)解矩阵方程 AXB C 。
2 2 3 1 3 2 1 9.已知矩阵 A 1 1 0 B 5 3 C 2 0 1 2 1 3 1
A
, A*
, A 1
。
2 7 25.已知二阶方阵 A 。 1 3
2020-2021某大学《高等代数》期末课程考试试卷合集(含答案)

【解】
(1) 方法一:数学归纳法证明 Dn = (n +1)an . k = 1时, D1 = 2a ,
假设 k n −1时, Dk = (n +1)ak .则当 k = n 时,
Dn = 2aDn−1 − a2Dn−2 = 2anan−1 − a2 (n −1)an−2 = (n +1)an.
方法二:递推法.
5、在
中,
是 的维数 则 在基
下的矩阵为_________________。
6. 元实二次型
是正定的充分必要条件是它的正惯
性指数等于___________________.
7.对于线性空间 V 中向量
,若在数域 P 中有 个
不全为零的数
,使
,则向量
称为_________.
8.相似矩阵的特征值__________.
(D) 1 + 22 ,2 + 23,3 + 21 . 3 线性方程组 Ax = b 的系数矩阵式 45 矩阵,且 A 的行向量线性无关,则错误的命题是
( D ).
(A) 齐次方程组 AT x = 0 只有零解;
(B)齐次方程组 AT Ax = 0 必有非零解; (C) 对任意的 b ,方程组 Ax = b 必有无穷多解; (D) 对任意的 b ,方程组 AT x = b 必有唯一解.
考试日期:
考试时间:120 分钟
试卷总分:100 分
一、填空(共 50 分,每小题 5 分)
1、设矩阵
与
相似,则
。
2、已知
是矩阵
的一个特征向量,则
特征向量 对应的特征值
。
3、 满足________时,二次型
2021-2022年部分高校高等代数考研真题

A
=
1 0 2
−1 1 3
−1 0 1
2 0 −1
1 −2 −2 −1
求 A 的包含 ε1 的最小的不变子空间.
3 1 −1 3. 求 A = −1 3 1 的若尔当标准形及有理标准形.
022
二、证明题.
1. 已知向量组 α1, α2, · · · , αr 线性无关, 且可由向量组 β1, β2, · · · , βs 线性表 出, 证明: 存在某个向量 βj (1 ≤ j ≤ s), 使得向量组 βj, α2, · · · , αr 线性无关.
1 2
1 1
c −2 0
112
(1) 若 A 有特征值 4, 1, −2 , 求 a, b, c. (2) 设 α = (1, k, 1)T 是 B−1 的一个特征向量, 求 k .
五、(15 分) 设 A, B 都是 n 阶实对称矩阵, 且 A 正定, 证明: AB 的特征值 都是实数.
六、(15 分) 设 σ 是 n 维线性空间 V 上的一个线性变换, 证明: σ 的秩 +σ 的零度 = n.
1
北京交通大学 2022 年高等代数考研真题
北京交通大学 2022 年高等代数考研真题
一、填空题 (每题 3 分)
1. 2n 级排列 13 · · · (2n − 1)(2n)(2n − 2) · · · 42 的逆序数为
.
2. 设 4 阶方阵 A, B 的伴随矩阵为 A∗, B∗, 且它们的秩为 r(A) = 3, r(B) =
1
2x1 3x1
+ 3x2 + 5x2
+ (a + 2)x3 + 4x4 = b + 3 + x3 + (a + 8)x4 = 5
上海理工大学高数期末复习试题

释 疑 解 难(第七章)(第七章)一、求垂直于平面0=z 且通过点)1,1,1(0-M 到直线îíì==+-001:x z y L 垂线的平垂线的平 面方程。
面方程。
解:解:直线L 的方向向量}1,1,0{--=l,过点0M 与直线L 的平面N 的方程的方程 0)1()1(=--+-z y ,即0=+z y解方程组ïîïíì=+==+-0001z y x z y ,得直线L 与平面N 的交点)21,21,0(1-M 由题意,设所求平面方程为0=++D By Ax ,将0M 、1M 坐标代入,得坐标代入,得ïîïíì=+-=+-02D B D B A ,解得D A =,D B 2=,所求的平面方程为:012=++y x 。
二、证明两直线二、证明两直线231212-=-+=-z y x 与112111-=+=--z y x共面,并求该平面方程。
共面,并求该平面方程。
解:解:记)3,2,2(1-M ,}2,1,1{1-=l ,)1,1,1(2-M ,}1,2,1{2-=l则}2,1,1{21--=M M∵0211121211)(2121=----=×´M M l l ∴两直线共面。
∴两直线共面。
取}1,3,5{21--=´=l l n则所求平面方程为则所求平面方程为0)3()2(3)2(5=-++---z y x ,即0135=--+z y x 。
三、求平面02122=++-z y x 与05247=-+z x 所成二面角的平分面方程。
所成二面角的平分面方程。
解:解:过两平面交线的平面束方程过两平面交线的平面束方程0)5247(2122=-++++-z x z y x l ,即,即0)521()242(2)71(=-+++-+l l l z y x其法向量}242,2,71{l l +-+=n,已知两平面法向量分别是,已知两平面法向量分别是}2,2,1{1-=n 与}24,0,7{2=n由题意知||||||||2211n n n n n n n n ×±=×,解得253±=l 所以所求平面方程为所以所求平面方程为025*******=++-z y x 和027011252=+--z y x 。
上海理工大学专升本入学考试高等数学试题

一、 选择题(每题 3 分,共 15 分)
1.
lim
x 1
x
____C_____。
x 2x 1
A. 0
B.
C. 不存在
1
D. e 2
2
1. 0 | x 1 | dx ___1____
2. f (x) 在 [a,b] 上 连 续 是 f (x) 在 [a,b] 上可积的____充分_____条件。
3. 方 程 xy 2x2 y x3 y 4 y sin x 是_____三_____阶微分方程。
2. 两 个 无 穷 大 的 和 一 定 是
___D____。
A. 无 穷 大 量
B. 常 数
C. 没有极限
D. 上述都不对
4. 平行于向量 m {6,7,6} 的单位向
量
是
_
6 11
,
7 11
连续可导,求 2 z 。 xy
令
x r cos
y
r
s in
原式
y
rdrd 1
2 d
1
1
d
(1
r
2
)
ln(1 r 2 ) 1
ln
D 1 r2 2 0
0 1 r2
4
04
x
0
1
z f 2x x
2 z 2xf (2 y) 4xyf xy
C. 无穷间断点
D. 震荡间断点
二、 填空题(每空 3 分,共 15 分)
三、 计算题(每题 6 分,共 36 分)
2x
1. lim 0 ln(1 t)dt x0 1 cosx
上海理工大学高数试卷_A1_1

五. (6 分)计算 I n 六. (8 分)设
0 x n e x dx .
xeห้องสมุดไป่ตู้ x , f x 1 , 4 x2
2
x0 2 x0
, 计算1 f x 3dx .
4
七. (8 分)求由抛物线 y 2 x , y x 围成的平面图形的面积,以及此图形绕 x 轴旋转而成
2 2
的立体体积. 八. (6 分)若 f x 在 a, b 上连续,在 a, b 内可导,且 f a f b 0 , 求证:存在一点 x0 a, b ,使 f x0 f x0 0 .
2
8. 设
f x x a x , x 在x a 处 连续,求f a .
x0
,
f x x 二. (8 分)设 f x 在 , 有连续的二阶导数, f 0 0, g x f 0
上海理工大学
第一学期《高等数学 A》试卷-1
编号 一 二 三 四 五 六 七 八
姓 名
得分 阅卷人 一. 计算下列各题.(48 分) 1. lim (csc x ).
x0
学 号
班 级
任 课 教 师
装 订 线 外 不 要 答 题 , 装 订 线 内 不 要 写 姓 名 、 学 号 、 班 级 、 任 课 老 师 , 违 者 试 卷 按
0
1 x
2. .
y ln( x 1 x 2 ) ,求 y 和 y .
y 1 xe y ,求
dy . dx
3.
4.
2
1
x
1 3 x dx .
2
11-12(2)高等代数与解析几何试卷(A)参考答案及评分标准

中国计量学院2011 ~ 2012学年第 2 学期《高等代数》(2)课程试卷(A )参考答案及评分标准一、单项选择题(每小题3分,共15分)1.D2.B3.D4.C5.A二、填空题(每小题3分,共15分)1.1111⎛⎫ ⎪-⎝⎭;2. __1,-3__;3.100010011⎛⎫⎪ ⎪⎪⎝⎭; 4. 20x y +-= 5.222x y pz +=.三、计算题1.(12分)设A 是3P 中的线性变换,且A 在基)1,1,1(1-=η,)1,0,1(2-=η,)1,1,0(3=η下的矩阵为101110121A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭求A 在基123(1,0,0),(0,1,0),(0,0,1)εεε===下的矩阵.解 因为(1η,2η,3η)=(1ε,2ε,3ε)⎪⎪⎪⎭⎫⎝⎛--111101011, 所以 (1ε,2ε,3ε)=(1η,2η,3η)⎪⎪⎪⎭⎫ ⎝⎛---101110111=(1η,2η,3η)X ,-------------4分故A 在基1ε,2ε,3ε下的矩阵为B =X 1-AX=⎪⎪⎪⎭⎫ ⎝⎛--111101011⎪⎪⎪⎭⎫ ⎝⎛-121011101⎪⎪⎪⎭⎫ ⎝⎛---101110111=⎪⎪⎪⎭⎫⎝⎛--203022211 -------------12分2.(12分)求λ矩阵222211λλλλλλλλλλ()A ⎛⎫-⎪=- ⎪ ⎪+-⎝⎭的标准形、不变因子、行列式因子、初等因子.解 对-λ矩阵作初等变换,有A =)(λ ⎪⎪⎪⎭⎫⎝⎛-+--222211λλλλλλλλλ→ ⎪⎪⎪⎭⎫⎝⎛--222101λλλλλλ→ ⎪⎪⎪⎭⎫⎝⎛+--)1(00001λλλλ → )()1(0000001λλλλD =⎪⎪⎪⎭⎫⎝⎛+ 标准形为: ⎪⎪⎪⎭⎫⎝⎛+=)1(000001)(λλλλD ;----------------------6分 不变因子为:)1()(,)(,1)(321+===λλλλλλd d d ;----------------------8分 行列式因子为:)1()(,)(,1)(2321+===λλλλλλD D D ;----------------------10分 初等因子为:1,,2+λλλ.----------------------12分3.(12分) 设二次型()222123123121323,,22448f x x x x x x x x x x x x =---++ ,求一正交变换 x Ty =,将二次型化为标准形. 解 二次型对应的矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=242422221A ,----------------------2分且A 的特征多项式为 2)2)(7(-+=-λλλA E ,特征值为2,7321==-=λλλ.---------------------4分 相应的特征向量为 ()()()1,0,2,0,1,2,2,2,1321=-=-=ααα,---------------------6分正交化,可得()()⎪⎭⎫ ⎝⎛=-=-=1,54,52,0,1,2,2,2,1321βββ, 再单位化,有⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=535,534,532,0,51,52,32,32,31321ηηη, ----------------------8分令X=TY ,其中⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=53503253451325325231T ,----------------------10分 则 232221'227y y y AX X ++-=.----------------------12分4.(12分) 求顶点在原点,准线为01,0122=+-=+-z y z x 的锥面方程. 解 设为锥面上任一点),,(z y x M ,过M 与O 的直线为:z Zy Y x X ==----------------------3分 设其与准线交于),,(000Z Y X ,即存在t ,使zt Z yt Y xt X ===000,,, -----------6分 将它们代入准线方程,并消去参数t ,得:0)()(222=-+--y z y z z x即:0222=-+z y x此为所要求的锥面方程. ----------------------12分5. (12分)求过双曲抛物面z y x =-41622上的点(2,1,0)的直母线方程. 解:双曲抛物面z y x =-41622的两族直母线为:⎪⎪⎩⎪⎪⎨⎧=-=+z y x u uy x )24(24 及 ⎪⎪⎩⎪⎪⎨⎧=+=-z yx v v yx 24(24----------------------6分将点(2,1,0)分别代入上面两族直母线的方程,求得,1==v u----------------------10分因此,所求的直母线方程为:⎪⎪⎩⎪⎪⎨⎧=-=+z y x yx 24124 及 ⎪⎩⎪⎨⎧==-024z y x ----------------------12分四、证明题((每小题5分,共10分)1.在2R 中,定义变换(,)(2,2)x y x y x y σ=++. (1)证明:σ是2R 的线性变换.(2)取2R 的一组基:12(1,0),(0,1)εε==,求σ的值域2()σR 及2()σR 的一组基.证明(1)设1221x x A y y σξ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,σ是2R 到R 的映射,且2,,k αβ∀=∈∀∈R R ,有()()k l A k l kA lA σαβαβαβ+=+=+,所以σ是线性变换;-----------------3分(2) 对于2R 的基:12(1,0),(0,1)εε==,有12()(1,2),()(2,1)σεσε==,易知12(),()σεσε线性无关,于是它们构成2()σR 的一组基,且值域为 12()((),())((1,2),(2,1))L L σσεσε==3R .-----------------5分 2.欧氏空间V 中的线性变换A 称为反对称的,如果对任意α,β∈V ,有(A α,β)= —(α,A β). 证明:如果V 1是反对称线性变换A —子空间,则V 1⊥也是A —子空间.证明 任取∈αV 1⊥,可证A ∈αV 1⊥,即A ∈αV 1,事实上,任取β∈V 1,由于V 1是A 子空间,因此A β1V ∈,而∈αV 1⊥,故(α,A β)=0.----------------------3分再由题设,A 是反对称的,知(A α,β)= —(α,A β)=0,----------------------4分由β的任意性,即证A ∈αV 1 .从而V 1⊥也是A —子空间.----------------------5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海理工大学
研究生试题
/学年第 1 学期
课程名称:高等代数
教师签章:年月日教研室主任审查意见:
签章:年月日1.编号栏由研究生部填写。
上海理工大学研究生课程试题*
/ 学年第 1学期 考试课程 高等代数 学 号 姓 名 得 分
一、已知二次型)0(2332),,(322
32221321>+++=a x ax x x x x x x f 通过正交变换化为标准形
2
3222152y y y f ++=,求a 的值及所作的正交变换.(15分)
二、(1)已知5级λ-矩阵A(λ)的各级行列式因子:
3212345()()()1,
()(1),()(1)D D D D D λλλλλλλλλ====-=-
求A(λ)的不变因子和A(λ)的标准形;
(2)设n n
A C
⨯∈,若E A λ-的标准形为:
12()()()n d d d λλλ⎛⎫
⎪
⎪ ⎪ ⎪
⎝⎭
求A 的特征多项式E A λ-和A 的最小多项式.(16分)
三、设n εεε,,,21 是欧氏空间n
R 的一组标准正交基,k ααα,,,21 是n
R 中的任k 个向量,试证k ααα,,,21 为标准正交向量组的充要条件是
⎩
⎨⎧=≠=∑=j i j
i n
s s
j s i ,1,0),)(,(1εαεα (12分)
四、3
P 中,
线性变换σ关于基)1,1,1(1-=α,)1,0,1(2-=α,
)1,1,0(3=α的矩阵为⎪⎪⎪
⎭
⎫
⎝⎛-=121011101A (1)求σ关于标准基321,,εεε的矩阵;
(2)设3216αααα-+=,321εεεβ+-=,求)(),(βσασ关于基},,{321ααα的坐标. (15分)
五、设σ是3
R 的线性变换,)2,,2(),,(32132321321x x x x x x x x x x x -++-+=σ
(1)求)Im(σ的一个基和维数;
(2)求)(σKer 的一个基和维数.(15分)
六、在线性空间P 4中,求由基1234,,,αααα到基1234,,,ββββ的过渡矩阵,并求(1,4,2,3)α=在基1234,,,αααα下的坐标,其中
1234(1,0,0,0),(4,1,0,0),(3,2,1,0),(2,3,2,1)αααα===-=-
*
注:考题全部写在框内,不要超出边界。
内容一律用黑色墨水书写或计算机打印,以便复印。
1234(1,1,8,3),(0,3,7,2),(1,1,6,2),(1,4,1,1).ββββ====---(12分)
七、设)(),(x g x f 是数域F 上的互素的多项式,A 是F 上的n 阶矩阵,
证明:齐次线性方程组0)()(=X A g A f 的解空间是0)(=X A f 的解空间与0)(=X A g 的解空间的直和. (15分)。
