广州市2002年高中阶段学校招生考试
广州历届中考真题数学试卷

广州历届中考真题数学试卷第一卷第一部分:选择题1. 单选题(共15小题,每小题1分,共计15分)请在每小题的括号中填入相应的字母。
1) 设a = 2, b = -3, c = 4,则下列哪个等式成立?()A. a^2 - b^2 = -25B. a^3 + b^3 = -1C. a^2 - b^2 + c^2 = 7D. a^3 + b^3 + c^3 = 22) 下列哪个数是有理数?()A. √2B. πC. 0D. e3) 已知〈ABC〉是一条直线段,点X在〈AB〉上,点Y在〈BC〉上,若AX : XB = 1:2,BY : YC = 2:1,则∠AXY等于()A. 30°B. 45°C. 60°D. 90°4) 若2loga = log(a^2 - 4),则a的值是()A. -2B. 0C. 1D. 35) 已知函数y = 3x^2 + bx + 2的图象过点(1,4),则b的值是()A. -2B. 0C. 2D. 46) 若a + b + c + d = 10,且abcd = 9,则ab + ac + ad + bc + bd + cd 的最大值是()A. 16B. 18C. 19D. 207) (sinα + cosα)(sinα - cosα)的值等于()A. 1B. sin2α - cos2αC. sin2α - 2cos2αD. sin2α + cos2α8) 在函数y = 2^x + ax - 1的图象上,存在两点A和B,已知A(-1, -1)和B(0, 1),则a的值为()A. -3B. -2C. 2D. 39) 已知直线l过点A(6,3)及B(-2,5),P是l上的一点,且AP : PB = 2:3,则线段AB的中点坐标是()A. (2, 4)B. (3, 4)C. (4, 3)D. (4, 2)10) 一根长为10cm的软铁线,弯成一个圆形,再将该圆形展开形成一个圆环,圆环是否比圆形长?()A. 是B. 否11) 在锐角三角形ABC中,已知a/sinA = b/sinB = c/sinC = 2√3,其中a,b,c分别为BC,CA,AB的长度,则△ABC的面积等于()A. 3B. 6C. 9D. 1212) 在平面直角坐标系中,点A(-1,4),点B(5,2),点C(-3,-2)的图象与坐标轴所围成的面积是()A. 14B. 16C. 18D. 2013) 若a,b是正数,且a:(a+b) = 2:5,则a的值是()A. 2/3B. 1/3C. 3D. 514) 在菱形ABCD中,点E是AD边上的一点,且AE : ED = 1:2,则BE与CD的交点是()A. EB. 稍右上方区域C. 稍左下方区域D. 真菱形15) 在平行四边形ABCD中,点E在对角线AC上,若AE : EC = 1:3,则BE : ED的值是()A. 1:3B. 3:1C. 1:4D. 4:1第二部分:非选择题第二卷第三部分:解答题1. 解答题(共5小题,共计50分)解答下列各题。
广州历年中考录取分数线(02年_08年)

独立招生学校录取线院校名称招生区域广州市第二中学(公办公费,校本部)全市广州市第一O九中学(公办公费,校本部)全市广州市美术中学(公办公费,校本部)全市广州市西关外国语学校(原广州市第十二中学)老三区广州市越秀外国语学校老三区学校名称招生区域1广州市培正中学(公办公费,教学点:校本部)老三区2从化市从化中学(公办公费,教学点:校本部)从化市3广州市第四中学(公办公费,教学点:校本部)老三区4增城市郑中钧中学(公办公费,教学点:校本部)增城市5广州市育才中学(公办公费,教学点:校本部)老三区6花都区实验中学(公办公费,教学点:校本部)花都区8广州市番禺区象贤中学(公办公费,教学点:校本部)番禺区9增城市华侨中学(公办公费,教学点:校本部)增城市10广州市第九十七中学(公办公费,教学点:校本部)老三区11从化市第六中学(公办公费,教学点:校本部)从化市12广州市禺山高级中学(公办公费,教学点:校本部)番禺区13广州市第二十一中学(公办公费,教学点:校本部)老三区14广州市南武中学(公办公费,教学点:校本部)老三区15广州市第十七中学(公办公费,教学点:校本部)老三区16中山大学附属中学(民办,教学点:校本部)全市18广州市番禺区东涌中学(公办公费,教学点:校本部)番禺区19广州市真光中学(公办公费,教学点:校本部)老三区20广州市天河中学(公办公费,教学点:校本部)天河区21广州市番禺区石基第三中学(公办公费,教学点:校本部)番禺区22广州市第六十五中学(公办公费,教学点:校本部)白云区23广州市知用中学(公办公费,教学点:校本部)老三区24广州市第八十中学(公办公费,教学点:校本部)白云区25广州市花都区新华中学(公办公费,教学点:校本部)花都区26广州市番禺区洛溪新城中学(公办公费,教学点:校本部)番禺区27广州市番禺区大岗中学(公办公费,教学点:校本部)番禺区28南海中学(原广州市第十一中学)(公办公费,教学点:校本部)老三区29增城市高级中学(公办公费,教学点:校本部)增城市30广州市第一一三中学(公办公费,教学点:校本部)天河区广州市第一一三中学(公办公费,教学点:校本部)跨区31广州市第十三中学(公办公费,教学点:校本部)老三区32广东外语外贸大学附设外语学校(民办,教学点:校本部)全市33广州市第七十五中学(公办公费,教学点:校本部)天河区广州市第七十五中学(公办公费,教学点:校本部)跨区34广州市白云中学(公办公费,教学点:校本部)白云区35广州市花都区第一中学(公办公费,教学点:校本部)花都区36广州市第四十一中学(公办公费,教学点:校本部)老三区37广州市恒福中学(公办公费,教学点:恒福中学东校区(高中部))老三区38广东华侨中学(公办公费,教学点:校本部)老三区39广州石化中学(公办公费,教学点:校本部)黄埔区40广州市培英中学(太和校区)(公办公费,教学点:校本部)白云区41华师附中南海实验高中(民办,教学点:校本部)全市普通高中第一批院校录取录取线42广州市西关外国语学校(原十二中)(公办公费,教学点:校本部)老三区43广州市南沙第二中学(公办公费,教学点:校本部)南沙区45广州市华美英语实验学校(民办,教学点:校本部)全市46南海执信中学(民办,教学点:校本部)全市47增城市新塘中学(公办公费,教学点:校本部)增城市48广州市南沙中学(公办公费,教学点:校本部)南沙区49增城市荔城中学(公办公费,教学点:校本部)增城市50广州市东圃中学(公办公费,教学点:校本部)天河区广州市东圃中学(公办公费,教学点:校本部)跨区51广州市第八十九中学(公办公费,教学点:校本部)天河区广州市第八十九中学(公办公费,教学点:校本部)跨区53花都区圆玄中学(公办公费,教学点:校本部)花都区54广州市南沙区麒麟中学(公办公费,教学点:校本部)南沙区55广州市番禺区市桥第二中学番禺区56广州市华师附中番禺学校全市21广州市番禺区祈福英语实验学校(民办,教学点:校本部)全市24广州市番禺区南村中学(公办公费,教学点:校本部)番禺区31广州市第九十一中学(公办公费,教学点:校本部)萝岗区32广州市第八十三中学(公办公费,教学点:校本部)萝岗区广州市第三中学老三区暨南大学附中全市广东实验中学附属天河学校民办广州市第七十一中学白云区广州市番禺区石基中学番禺区广州市番禺区石楼中学番禺区院校名称招生区域1广州市第十中学(公办公费,教学点:校本部)老三区2广州市白云中学(公办公费,教学点:校本部)白云区3广州市西关培英中学(29中)(公办公费,教学点:校本部)老三区4广州市东环中学(公办公费,教学点:校本部)老三区5从化市第二中学(公办公费,教学点:校本部)从化市8广州市第四十二中学(公办公费,教学点:校本部)老三区9广州市第一O九中学(公办公费,教学点:校本部)老三区11从化市第五中学(公办公费,教学点:校本部)从化市12广州市荔湾区汾水中学(公办公费,教学点:校本部)老三区15广州市第四十四中学(公办公费,教学点:校本部)天河区16广州市番禺区鱼窝头镇中学(公办公费,教学点:校本部)番禺区18广州市流花中学(公办公费,教学点:校本部)老三区20广州大学实验中学(公办公费,教学点:校本部)老三区22广州市第七十一中学(公办公费,教学点:校本部)白云区23广州市花都区第二中学(公办公费,教学点:校本部)花都区26东莞市新世纪英才学校(民办,教学点:校本部)全市27广州英豪学校(民办,教学点:校本部)全市28广州市第八十七中学(公办公费,教学点:校本部)黄埔区普通高中第二批院校录取线29广州市花都区狮岭中学(公办公费,教学点:校本部)花都区30广州市花都区花东中学(公办公费,教学点:校本部)花都区33增城市新塘镇永和中学(公办公费,教学点:校本部)增城市34从化市第三中学(公办公费,教学点:校本部)从化市35增城市仙村中学(公办公费,教学点:校本部)增城市36从化市第四中学(公办公费,教学点:校本部)从化市37增城市中新中学(公办公费,教学点:校本部)增城市38增城市派潭中学(公办公费,教学点:校本部)增城市39广州市第八十四中学(公办公费,教学点:校本部)黄埔区40广州市第七十九中学(公办公费,教学点:校本部)老三区41广州市海珠中学全市42广州市思源学校全市43广州市华美英语实验学校全市45从化市第五中学从化市46广州中大附属雅宝学校全市47广州市番禺区石北中学番禺区48广州市越秀外国语学校老三区2广州市第七十六中学(公办公费,教学点:校本部)老三区3广州市第七十八中学(公办公费,教学点:校本部)老三区广州市美术中学全市广州市第六十三中学白云区广州大学附属实验学校全市普通高中第三批院校录取线院校名称招生区域4广州大学附属实验学校(民办,教学点:校本部)全市5广州市第六十六中学(公办公费,教学点:校本部)白云区6广州市第九十五中学(公办公费,教学点:校本部)老三区7广州市第六十三中学(公办公费,教学点:校本部)白云区8广州市第六十八中学(公办公费,教学点:校本部)白云区9广州市第八十一中学(公办公费,教学点:校本部)白云区12华南师范大学附属康大学校(民办,教学点:校本部)全市13广州市英东中学(民办,教学点:校本部)全市广州市北大附中广州实验学校(民办)全市广州市海珠中学(民办)全市广州市培才高级中学(民办)全市普通高中第四批院校录取录取线学校名称招生区域1暨南大学附中(民办,教学点:校本部)全市3广州市北大附中广州实验学校(民办,教学点:校本部)全市4广州南洋英文学校(民办,教学点:校本部)全市5番禺成人教育中心学校(成人高中普通班)(公办自筹经费)全市8广州同德南方中学(民办,教学点:校本部)全市10中山大学附属雅宝学校(民办,教学点:校本部)全市11广州市思源学校(民办,教学点:校本部)全市12广州市培才高级中学(民办,教学点:校本部)全市广东实验中学附属天河学校(民办)全市广州市英东中学(民办)全市华南师范大学附属康大学校(民办)全市广州英豪学校(民办)全市。
广东省人事厅转发人事部办公厅关于做好2002年全国普通高等学校毕业生接收工作的通知

广东省人事厅转发人事部办公厅关于做好2002年全国普通高等学校毕业生接收工作的通知文章属性•【制定机关】广东省人事厅•【公布日期】2002.07.25•【字号】粤人发[2002]170号•【施行日期】2002.07.25•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】人力资源综合规定正文广东省人事厅转发人事部办公厅关于做好2002年全国普通高等学校毕业生接收工作的通知(粤人发[2002]170号)各市、县人事局,省直和中央驻粤各厅(局)级单位:现将人事部办公厅《关于做好2002年全国普通高等学校毕业生接收工作的通知》(人办发[2002]34号)转发给你们,并结合我省实际,提出以下意见,请一并贯彻执行。
一、加强领导,统一认识,有的放矢地做好大中专毕业生(以下简称毕业生)就业工作。
毕业生就业工作,是人才资源开发利用、配置的一项战略性工作任务,事关经济社会发展和社会稳定的大局。
各市、县人事局和各单位的毕业生就业主管部人要以江泽民“三个代表” 重要思想为指导,坚决贯彻国办发[2002]19号文件精神,充分认识毕业生结构性过剩、部分人就业观念不合时宜、部分用人单位盲目追求高学历问题的严重性,以及学校调整培养专业和层次结构以满足毕业生继续学习、引导毕业生树立正确的择业观、用人单位树立唯才是用和适才适用思想的紧迫性,切实采取各种有效措施,提高毕业生就业率,满足毕业生提高学历学习或继续选修适用专业的需求,尽量减少毕业生待业率。
二、各级政府人事部门要加大人才市场建设力度,强化人才服务中心和人才市场的中介服务功能,为毕业生与用人单位(包括各种所有制单位,下同)提供包括人事代理在内的各种相关的社会化服务;要坚决按照《人才市场管理规定》进一步整顿和规范毕业生就业市场秩序,严格跨地区的毕业生就业专场招聘会的审批和监管;要结合本地实际情况,在本行政区域内开展毕业生供求信息发布工作,为毕业生自主择业和用人单位自主用人提供信息服务,逐步建立起市场导向、政府调控、学校推荐、学生与用人单位双向选择的就业机制。
广州中考考试题目及答案

广州中考考试题目及答案一、选择题(每题2分,共10分)1. 广州的市花是什么?A. 桂花B. 木棉花C. 菊花D. 牡丹花答案:B2. 广州的气候属于什么类型?A. 温带季风气候B. 亚热带季风气候C. 热带雨林气候D. 寒带气候答案:B3. 广州的著名景点之一“白云山”位于哪个区?A. 天河区B. 越秀区C. 海珠区D. 白云区答案:D4. 广州话中的“饮茶”是什么意思?A. 喝茶B. 吃饭C. 喝酒D. 喝咖啡答案:A5. 广州地铁的第一条线路是?A. 1号线B. 2号线C. 3号线D. 4号线答案:A二、填空题(每题2分,共10分)6. 广州的别称是______。
答案:羊城7. 广州的著名地标建筑“小蛮腰”是指______。
答案:广州塔8. 广州的著名美食之一“双皮奶”源自于______。
答案:顺德9. 广州的______是全国最大的服装批发市场之一。
答案:白马服装市场10. 广州的______是广东省内最大的图书馆。
答案:广东省立中山图书馆三、简答题(每题5分,共10分)11. 简述广州的地理位置特点。
答案:广州位于中国南部,珠江三角洲的北缘,东临南海,南濒珠江口,西接佛山,北靠清远,是中国南部重要的中心城市。
12. 描述广州的气候特征。
答案:广州属于亚热带季风气候,夏季炎热潮湿,冬季温暖少雨,四季分明,雨量充沛。
四、论述题(每题15分,共30分)13. 论述广州在历史上的重要地位。
答案:广州是中国历史上著名的对外贸易港口,自秦汉时期起就是海上丝绸之路的重要起点之一。
在唐宋时期,广州成为全国最大的对外贸易港口,明清时期更是“一口通商”的重要港口,对中外文化交流和经济发展起到了重要作用。
14. 分析广州在现代中国经济发展中的作用。
答案:广州作为中国南部的经济中心,拥有强大的制造业和服务业,是全国重要的商贸中心和交通枢纽。
广州的高新技术产业和现代服务业发展迅速,对推动区域经济发展和国家经济转型具有重要意义。
2002年春季高考试数学试卷(北京文、理)及答案

2002年普通高等学校春季招生考试数学试卷(北京文、理)一、选择题(1)不等式组⎩⎨⎧<-<-030122x x x 的解集( )(A ){x|–1<x<1} (B ){x|0<x,3} (C ){x|0<x<1} (D ){x|–1<x<3}(2)已知三条直线m 、n 、l ,三个平面α、β、γ,下列四个命题中,正确的是( )(A )βαγβγα//⇒⎭⎬⎫⊥⊥ (B )ββ⊥⇒⎭⎬⎫⊥l m l m //(C )n m n m //////⇒⎭⎬⎫γγ (D )n m n m //⇒⎭⎬⎫⊥⊥γγ(3)已知椭圆的焦点是F 1、F 2、P 是椭圆上的一个动点.如果延长F 1P 到Q ,使得|PQ|=|PF 2|,那么动点Q 的轨迹是( )(A )圆 (B )椭圆 (C )双曲线的一支 (D )抛物线 (4)如果θ∈(π/2,π)那么复数(1+i)(cos θ+isin θ)的辐角的主值是( )(A )θ+9π/4 (B )θ+π/4 (C )θ–π/4 (D )θ+7π/4 (5)若角α满足条件sin2α<0,cos α–sin α<0,则α在( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限(6)从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作.若其中甲、乙两名支援者都不能从事翻译工作,则选派方案共有( )(A )280种 (B )240种 (C )180种 (D )96种 (7)在∆ABC 中,AB=2,BC=1.5,∠ABC=120︒(如图).若将∆ABC绕直线BC 旋转一周,则所形成的旋转体的体积是()(A )9π/2 (B )7π/2 (C )5π/2 (D )3π/2 (8)(理)圆2x 2+2y 2=1与直线xsin θ+y –1=0 (θ∈R, θ≠π/2+k π, k ∈Z)的位置关系是( ) (A )相交 (B )相切 (C )相离 (D )不能确定 (文)到两坐标轴距离相等的点的轨迹方程是( )(A )x –y=0 (B )x+y=0 (C )|x|–y=0 (D )|x|–|y|=0 (9)(理)在极坐标系中,如果一个圆的方程ρ=4cos θ+6sin θ,那么过圆心且与极轴平行的直线方程是( ) (A )ρsin θ=3 (B )ρsin θ = –3 (C )ρcos θ =2 (D )ρcos θ = –2 (文)函数y=2sinx 的单调增区间是( )(A )[2k π–π/2, 2k π+π/2] (k ∈Z) (B )[2k π+π/2, 2k π+3π/2] (k ∈Z) (C )[2k π–π, 2k π] (k ∈Z) (D )[2k π, 2k π+π] (k ∈Z) (10)(理)对于二项式(1/x+x 3)n ,四位同学作出了四种判断:①存在n ∈N ,展开式中有常数项;②对任意n ∈N ,展开式中没有常数项;③对任意n ∈N ,展开式中没有x 的一次项;④存在n ∈N ,展开式中有x 的一次项.上述判断中正确的是( )(A )①与③ (B )②与③ (C )②与④ (D )④与① (文)在(1/x+x 2)6的展开式中,x 3的系数和常数项依次是( )(A )20,20 (B )15,20 (C )20,15 (D )15,15(11)若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,则这个数列有( ) (A )13项 (B )12项 (C )11项 (D )10项(12)用一张钢板制作一个容积为4m 3的无盖长方体水箱.可用的长方形钢板有四种不同的规格(长×宽的尺寸如各项所示,单位均为m ).若既要够用,又要所剩够用,则应选择钢板的规则是( ) (A )2×5 (B )2×5.5 (C )2×6.1 (D )3×5二、填空题(13)若双曲线x 2/4–y 2/m=1的渐近线方程为y=±√3 x/2,则双曲线的焦点坐标是 (14)如果cos θ= –12/13 θ∈(π, 3π/2),那么cos(θ+π/4)的值等于_____(15)正方形ABCD 的边长是2,E 、F 分别是AB 和CD 的中点,将正方形沿EF 折成直二面角(如图所示).M 为矩形AEFD 内 的一点,如果∠MBE=∠MBC ,MB 和平面BCF 所成角的正切值 为1/2,那么点M 到直线EF 的距离为________(16)对于任意两个复数z 1=x 1+y 1i ,z 2=x 2+y 2i (x 1、y 1、x 2、y 2为实数),定义运算⊙为:z 1⊙z 2=x 1x 2+y 1y 2.设非零复数w 1、w 2在复平面内对应的点分别为P 1、P 2,点为O 为坐标原点.如果w 1⊙w 2=0,那么在∆P 1OP 2中,∠P 1OP 2的大小为_______ 三、解答题(17)在∆ABC 中,已知A 、B 、C 成等差数列,求tg(A/2)+3tg(A/2)tg(C/2)+tg(C/2)的值.(18)已知f(x)是偶函数,而且在(0,+∞)上是减函数.判断f(x)在(–∞,0)上是增函数还是减函数,并加以证明(19)在三棱锥S –ABC 中,∠SAB=∠SAC=∠ACB=90︒,AC=2,BC=√13,SB=√29. (Ⅰ)证明:SC ⊥BC ;(Ⅱ)求侧面SBC 与底面ABC 所成的二面角大小; (Ⅲ)(理)求异面直线SC 与AB 所成的角的大小(用反三角函数表示). (文)求三棱锥的体积V S –ABC .(20)假设A 型进口汽车关税税率在2001年是100﹪,在2006年是25﹪,2001年A 型进口车每辆价格为64万元(其中含32万元关税税款).(Ⅰ)已知与A 型车性能相近的B 型国产车,2001年每辆价格为46万元.若A 型车的价格只受关税降低影响,为了保证2006年B 型车的价格不高于A 型车价格的90﹪,B 型车价格要逐年降低,问平均每年至少下降多少万元?(Ⅱ)某人在2001年将33万元存入银行,假如该银行扣利息税后的年利率为1.8﹪(五年内不变),且每年按复利计算(例如,第一年的利息记入第二年的本金),那么五年到期时这笔钱连本带息是否一定够买一辆按(Ⅰ)中所述降价后的B 型汽车? (21)(理)已知点的序列A n (x n ,0),n ∈N ,其中x 1=0,x 2=a (a>0),A 3是线段A 1A 2的中点,A 4是线段A 2A 3的中点,···,A n 是线段A n –2A n –1的中点,···.(Ⅰ)写出x n 与x n –1、x n –2之间的关系式 (n ≥3);(Ⅱ)设a n =x n+1–x n ,计算a 1,a 2,a 3,由此推测数列{a n }的通项公式,并加以证明;(Ⅲ)求n n x ∞→lim .(文)同理(22)(Ⅰ)(Ⅱ) (22)(理)已知某椭圆的焦点是F 1(–4,0)、F 2(4,0),过点F 2并垂直于x 轴的直线与椭圆的一个交点为B ,且|F 1B|+|F 2B|=10,椭圆上不同的两点A(x 1,y 1)、C(x 2,y 2)满足条件:|F 2A|、|F 2B|、|F 2C|成等差数列. (Ⅰ)求该椭圆方程;(Ⅱ)求弦AC 中点的横坐标;(Ⅲ)设弦AC 的垂直平分线的方程为y=kx+m ,求m 的取值范围. (文)同理(21)参考答案一、选择题:CDABB BDC (D)A(A)D (C) AC 二、填空题;(13)(±√7, 0);(14)-7√2/26;(15)√2/2;(16)π/2. 三、解答题:(17)√3;(18)增函数;(19)(Ⅰ)略;(Ⅱ)60︒;(Ⅲ)(理)arccos √17/17,(文)125√3/6; (20)(Ⅰ)2万元;(Ⅱ)5年后本息和为36 .07692>36,可以. (21)(理)(Ⅰ)x n =(x n –1+x n –2)/2;(Ⅱ)a n =(–1/2)n –1 (n ∈N);(Ⅲ)2a/3; (文)同理(Ⅰ)(Ⅱ). (22)(理)(Ⅰ)x 2/25+y 2/9=1;(Ⅱ)x 0=4;(Ⅲ)–16<m<16/5;(文)同理 (21).2002年普通高等学校招生全国统一考试数学理参考答案(13)2 (14)1 (15)1008 (16)27 三、解答题(17)解:由12cos cos 2sin 2sin 2=-+αααα,得 0cos 2cos sin 2cos sin 42222=-+ααααα0)1sin sin 2(cos 222=-+ααα 0)1)(sin 1sin 2(cos 22=+-ααα∵)2,0(πα∈∴01sin ≠+α,0cos 2≠=α∴01sin 2=-α,即21sin =α∴6πα=∴33=αtg(18)解(I )作MP ∥AB 交BC 于点P ,NQ ∥AB 交BE 于点Q ,连结PQ ,依题意可得MP ∥NQ ,且NQ MP =,即MNQP 是平行四边形。
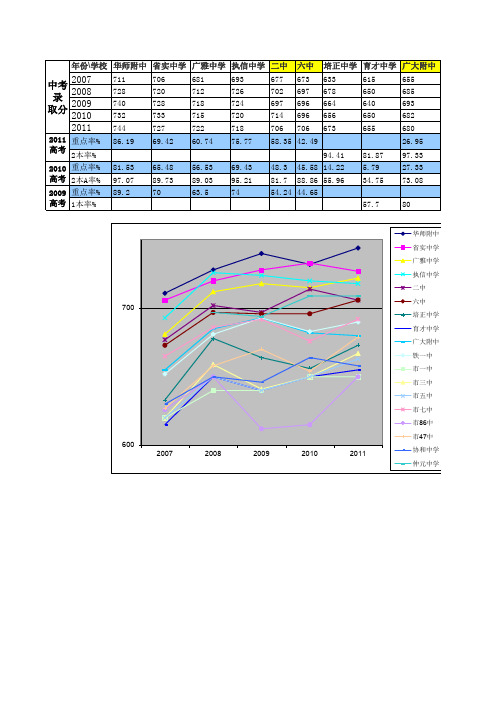
广州历届中考录取分数统计表及高中高考升学率_2012
32.5 31.47
43.32
97.33 76.16 84.98 77.74 84.62 96.58 77.1 87.76 88.63 95.73
31.94
29.55 6.16 9.68 9.39 31.25 72.35 33.16 46.24 36.79 77.76
9.77 22.84 11.15 34.28 54.6 47.6
年份\学校 华师附中 省实中学 广雅中学 执信中学 二中 六中 培正中学 育才中学 广大附中
中考 录
取分
2007 2008 2009 2010
711 728 740 732
706 720 728 733
681 712 718 715
693 726 724 720
677 673 633 702 697 678 697 696 664 714 696 656
681 640 659 650 686 684 650 658 650
697
671
693 640 641 640 692 683 612 670 646
694
673
683 650 650 650 676 689 615 654 664
709
687
690 650 667 663 692 673 650 679 658
2010
2011
华师附中 省实中学 广雅中学 执信中学 二中 六中 培正中学 育才中学 广大附中 铁一中 市一中 市三中 市五中 市七中 市86中 市47中 协和中学 仲元中学
铁一中 市一中 市三中 市五中 市七中 市16中 市86中 市47中 协和中学 仲元中学 番禺中学 石化中学
652 620 620 620 665 659 626 627 630
2002年广东省广州市中考数学试卷

2002年广东省广州市中考数学试卷一、选择题(共13小题,满分35分)1.(2分)0.000000108这个数,用科学记数法表示为()A.1.08×10﹣9B.1.08×10﹣8C.1.08×10﹣7D.1.08×10﹣62.(2分)计算0.25×所得的结果是()A.2 B.C.0 D.3.(2分)如果两圆只有一条公切线,那么这两个圆的位置关系是()A.外离B.外切C.相交D.内切4.(2分)如图,若四边形ABCD是半径为1的⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为()A.(2π﹣2)cm2B.(2π﹣1)cm2C.(π﹣2)cm2D.(π﹣1)cm2 5.(3分)函数y=中,自变量x的取值范围()A.x>﹣4 B.x>1 C.x≥﹣4 D.x≥16.(3分)y=kx+b的图象不经过第三象限,k、b的取值范围是()A.k>0且b>0 B.k>0且b<0 C.k<0且b≥0 D.k<0且b<0 7.(3分)若点(﹣2,y1)(﹣1,y2)、(1,y3)都在反比例函数y=﹣的图象上,则有()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y l>y3>y28.(3分)抛物线y=x2﹣4x+5的顶点坐标是()A.(﹣2,﹣1)B.(﹣2,﹣1)C.(2,1) D.(2,﹣1)9.(3分)某装满水的水池按一定的速度放掉水池的一半水后.停止放水并立即按一定的速度注水,水池注满后,停止注水,又立即按一定的速度放完水池的水.若水池的存水为v(立方米),放水或注水的时间为t(分钟),则v与t只能是()A.B.C.D.10.(3分)直线y=x与抛物线y=x2﹣2的两个交点的坐标分别是()A.(2,2),(1,1)B.(2,2),(﹣1,﹣1)C.(﹣2,﹣2),(1,1)D.(﹣2,﹣2),(﹣l,﹣1)11.(3分)如图,若C是线段AB的中点,D是线段AC上的任一点(端点除外),则()A.AD•DB<AC•CBB.AD•DB=AC•CBC.AD•DB>AC•CBD.AD•DB与AC•CB大小关系不确定12.(3分)在一次向“希望工程”捐款的活动中,已知小刚的捐款数比他所在学习小组中13人捐款的平均数多2元,则下列判断中,正确的是()A.小刚在小组中捐款数不可能是最多的B.小刚在小组中捐款数可能排在第12位C.小刚在小组中捐款数不可能比捐款数排在第7位的同学的少D.小刚在小组中捐款数可能是最少的13.(3分)若⊙O1、⊙O2的半径分别为1和3,且⊙O1和⊙O2外切,则平面上半径为4,且与⊙O1、⊙O2都相切的圆有()A.2个 B.3个 C.4个 D.5个二、填空题(共6小题,每小题3分,满分18分)14.(3分)如图,AB∥CD,若∠ABE=120°,∠DCE=35°,则有∠BEC=度.15.(3分)过△ABC的顶点C作边AB的垂线,如果这垂线将∠ACB分为40°和20°的两个角,那么∠A、∠B中较大的角的度数是.16.(3分)如图所示,在正方形ABCD中,AO⊥BD,OE,FG,HI都垂直于AD,EF,GH,IJ都垂直于AO,若已知S△AIJ=1,则正方形ABCD的面积为.17.(3分)方程x﹣5=的解是.18.(3分)在一次科技知识竞赛中,一组学生成绩统计如下:分数5060 7080 90 100人数2 5 10 13 14 6这组学生成绩的中位数是分.19.(3分)在平坦的草地上有A,B,C三个小球,若已知A球和B球相距3米,A球和C球相距1米,则B球和C球可能相距米.(球半径忽略不计,请填出两个符合条件的数)三、解答题(共8小题,满分97分)20.(8分)已知:如图,A是直线l外的一点.求作:(1)一个⊙A,使得它与l有两个不同的交点B、C;(2)一个等腰△BCD,使得它内接于⊙A(说明:要求写出作法)21.(9分)解方程22.(9分)在半径为27m的圆形广场中央点O的上空安装了一个照明光源S,S′射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图).求光源离地面的垂直高度SO(精确到0.1m,=1.414,=1.732,=2.236,以上数据供参考)23.(13分)在如图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).(1)在给出的直角坐标系中(或舍去该直角坐标系,在自己另建立适当的直角坐标系中),分别写出点A、B、C的坐标;(2)根据你得出的A、B、C三点的坐标,求图象经过这三点的二次函数的解析式.24.(13分)如图,⊙O的弦AB、CD的延长线相交于点E.请你根据上述条件,写出一个正确的结论(所写的结论不能自行再添加新的线段及标注其他字母),并给出证明.(证明时允许自行添加辅助线)25.(15分)当a取什么数值时,关于未知数x的方程ax2+4x﹣1=0只有正实数根.26.(15分)如图,在△ABC中,∠B=90°,AB=4,BC=3,O是AB的中点,OP ⊥AB交AC于点P.(1)证明线段AO、OB、OP中,任意两条线段长度之和大于第三条线段的长度;(2)过线段OB(包括端点)上任一点M,作MN⊥AB交AC于点N.如果要使线段AM、MB、MN中任意两条线段长度之和大于第三条线段的长度,那么请求出线段AM的长度的取值范围.27.(15分)某玩具工厂有四个车间,某周是质量检查周,现每个车间都原有a (a>0)个成品,且每个车间每天都生产b(b>0)个成品,质检科派出若干名检验员星期一、星期二检验其中两个车间原有的和这两天生产的所有成品,然后,星期三至星期五检验另两个车间原有的和本周生产的所有成品,假定每个检验员每天检验的成品数相同.(1)这若干名检验员1天检验多少个成品(用含a、b的代数式表示);(2)试求出用b表示a的关系式;(3)若1名质检员l天能检验b个成品,则质检科至少要派出多少名检验员?2002年广东省广州市中考数学试卷参考答案与试题解析一、选择题(共13小题,满分35分)1.(2分)0.000000108这个数,用科学记数法表示为()A.1.08×10﹣9B.1.08×10﹣8C.1.08×10﹣7D.1.08×10﹣6【分析】科学记数法就是将一个数字表示成(a×10的n次幂的形式),其中1≤|a|<10,n表示整数.n为整数位数减1,即从左边第一位开始,在首位非零的后面加上小数点,再乘以10的n次幂.此题n<0,n=﹣7.【解答】解:0.000 000 108=1.08×10﹣7.故选C.2.(2分)计算0.25×所得的结果是()A.2 B.C.0 D.【分析】根据负整数指数幂、零指数幂的运算法则计算.【解答】解:原式=0.25×4+1=2.故选A.3.(2分)如果两圆只有一条公切线,那么这两个圆的位置关系是()A.外离B.外切C.相交D.内切【分析】两圆内含时无公切线,两圆内切时只有一条公切线,两圆相离时有4条公切线,两圆外切时,有3条公切线,两圆相交时有2条公切线.两圆只有一条公切线,那么这两个圆的位置关系是内切.【解答】解:∵两圆只有一条公切线,∴两个圆内切.故选D.4.(2分)如图,若四边形ABCD是半径为1的⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为()A.(2π﹣2)cm2B.(2π﹣1)cm2C.(π﹣2)cm2D.(π﹣1)cm2【分析】阴影部分的面积等于圆的面积减去正方形的面积,求出圆内接正方形的边长,即可求解.【解答】解:连接AO,DO,∵ABCD是正方形,∴∠AOD=90°,AD==,圆内接正方形的边长为,所以阴影部分的面积=(π﹣2)cm2.故选C.5.(3分)函数y=中,自变量x的取值范围()A.x>﹣4 B.x>1 C.x≥﹣4 D.x≥1【分析】根据二次根式的意义可知:x+4≥0;根据分式的意义可知:x﹣1>0,列不等式组可求x的范围.【解答】解:根据题意得:,解得:x>1.故选B.6.(3分)y=kx+b的图象不经过第三象限,k、b的取值范围是()A.k>0且b>0 B.k>0且b<0 C.k<0且b≥0 D.k<0且b<0【分析】根据图象在坐标平面内的位置关系确定k,b的取值范围,从而求解.【解答】解:由题意可得,一次函数y=kx+b的图象经过第一、二、四象限,又有k<0时,直线必经过二、四象限,故知k<0.再由图象过一、四象限或原点,所以b≥0.故选C.7.(3分)若点(﹣2,y1)(﹣1,y2)、(1,y3)都在反比例函数y=﹣的图象上,则有()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y l>y3>y2【分析】根据反比例函数的增减性解答即可.【解答】解:∵k<0,∴函数图象在二,四象限,由题意可知:(﹣2,y1)(﹣1,y2)在第二象限,(1,y3)在第四象限,∵第四象限内点的纵坐标总小于第二象限内点的纵坐标,∴y3最小,在第二象限内,y随x的增大而增大,∴y2>y1.故选B.8.(3分)抛物线y=x2﹣4x+5的顶点坐标是()A.(﹣2,﹣1)B.(﹣2,﹣1)C.(2,1) D.(2,﹣1)【分析】此题既可以利用抛物线顶点坐标公式确定顶点坐标,也可以利用配方法确定顶点坐标.【解答】解:∵y=x2﹣4x+5=x2﹣4x+4﹣4+5=(x﹣2)2+1∴抛物线y=x2﹣4x+5的顶点坐标是(2,1).故选C.9.(3分)某装满水的水池按一定的速度放掉水池的一半水后.停止放水并立即按一定的速度注水,水池注满后,停止注水,又立即按一定的速度放完水池的水.若水池的存水为v(立方米),放水或注水的时间为t(分钟),则v与t只能是()A.B.C.D.【分析】理解进水,出水的几个阶段,把握几个关键语句:“放掉水池的一半水”,“立即按一定的速度注水”,“放完水池的水”.【解答】解:根据题意:装满水的水池按一定的速度放掉水池的一半水后.停止放水,排除B;并立即按一定的速度注水,排除C;水池注满后,停止注水,又立即按一定的速度放完水池的水,排除D.分析可得:存水v的变化为A.故选A.10.(3分)直线y=x与抛物线y=x2﹣2的两个交点的坐标分别是()A.(2,2),(1,1)B.(2,2),(﹣1,﹣1)C.(﹣2,﹣2),(1,1)D.(﹣2,﹣2),(﹣l,﹣1)【分析】用代入法即可.【解答】解:把直线y=x与抛物线y=x2﹣2组成方程组得:,解得或即点为(2,2),(﹣1,﹣1)故选B.11.(3分)如图,若C是线段AB的中点,D是线段AC上的任一点(端点除外),则()A.AD•DB<AC•CBB.AD•DB=AC•CBC.AD•DB>AC•CBD.AD•DB与AC•CB大小关系不确定【分析】熟练掌握线段的概念和灵活的应用,对图中各个线段进行分析即解.【解答】解:因为AB=AC+BC,BD=BC+CD,又因为AC=BC,那么可得出:AD•BD=(AC﹣CD)(BC+CD)=AC•BC﹣CD2,因此AD•DB<AC•CB,故选A.12.(3分)在一次向“希望工程”捐款的活动中,已知小刚的捐款数比他所在学习小组中13人捐款的平均数多2元,则下列判断中,正确的是()A.小刚在小组中捐款数不可能是最多的B.小刚在小组中捐款数可能排在第12位C.小刚在小组中捐款数不可能比捐款数排在第7位的同学的少D.小刚在小组中捐款数可能是最少的【分析】利用平均数的定义即可判断出:小刚的捐款数比他所在学习小组中13人捐款的平均数多2元,小刚的捐款数不会是最少的,但可能排在第12位.【解答】解:因为小刚的捐款数比他所在学习小组中13人捐款的平均数多2元,所以小刚的捐款数不会是最少的,但可能排在第12位.故选B.13.(3分)若⊙O1、⊙O2的半径分别为1和3,且⊙O1和⊙O2外切,则平面上半径为4,且与⊙O1、⊙O2都相切的圆有()A.2个 B.3个 C.4个 D.5个【分析】两圆相切,包括两圆内切或两圆外切.两圆外切,则圆心距等于两圆半径之和;两圆内切,则圆心距等于两圆半径之差.【解答】解:∵⊙O1、⊙O2的半径分别为1和3,半径为4,1+3=4,∴与⊙O1、⊙O2都相切的圆有5个;分别为有两个与这两圆外切;有两个这两圆相切于这两圆的公共点,这两圆中一个与它外切,一个与它内切;还有一个是这两圆在它的内部相切,每个与它外切.故选D.二、填空题(共6小题,每小题3分,满分18分)14.(3分)如图,AB∥CD,若∠ABE=120°,∠DCE=35°,则有∠BEC=95度.【分析】两直线平行,同旁内角互补以及内错角相等,在作辅助线后,根据这两条性质即可解答.【解答】解:如图,过点E作EF∥AB,由平行线的传递性可得EF∥CD∵EF∥AB,∵∠FEB=180°﹣∠ABE=60°,∵EF∥CD,∴∠FEC=∠DCE=35°,∴∠BEC=∠FEB+∠FEC=95°.15.(3分)过△ABC的顶点C作边AB的垂线,如果这垂线将∠ACB分为40°和20°的两个角,那么∠A、∠B中较大的角的度数是70°.【分析】根据直角三角形两锐角互余可以得到,∠A、∠B中有一个是70°,另一个是50°,因而∠A、∠B中较大的角的度数是70°.【解答】解:如图,依题意得∠ACD=40°,∠DCB=20°,而CD⊥AB于D,∴∠A=50°,∠B=70°,因而∠A、∠B中较大的角的度数是70°.故填空答案:70°.16.(3分)如图所示,在正方形ABCD中,AO⊥BD,OE,FG,HI都垂直于AD,EF,GH,IJ都垂直于AO,若已知S△AIJ=1,则正方形ABCD的面积为256.【分析】根据题意知:△AIJ,△IJH,△IHG,△GHF,△GFE,△EFO,△EOD为等腰直角三角形,根据△AIJ的面积,可将正方形ABCD的边长求出,进而可求出其面积.【解答】解:在Rt△AIJ中,∵S=(IJ)2=1△AIJ∴IJ=在Rt△IJH中,IH=IJ=2;在Rt△IHG中,GH=IH=2;在Rt△GHF中,GF=GH=4;在Rt△GFE中,EF=GF=4;在Rt△EFO中,OE=ED=EF=8;∴AD=2ED=16∴正方形ABCD的面积为:162=256故答案为256.17.(3分)方程x﹣5=的解是x=5.【分析】把方程两边平方后求解.【解答】解:把方程两边平方得(x﹣5)2=5﹣x,即x2﹣9x+20=0,解得x=4,或x=5,代入原方程:当x=4时=﹣1,无意义,当x=5时原方程成立,故原方程的解为x=5.故本题答案为:x=5.18.(3分)在一次科技知识竞赛中,一组学生成绩统计如下:分数5060 7080 90 100人数2 5 10 13 14 6这组学生成绩的中位数是80分.【分析】求中位数可将一组数据从小到大依次排列,中间数据(或中间两数据的平均数)即为所求.【解答】解:因为共有2+5+10+13+14+6=50人,所以排序后第25、26个数的平均数即为所求,这组学生成绩的中位数是(80+80)÷2=80(分).故答案为80.19.(3分)在平坦的草地上有A,B,C三个小球,若已知A球和B球相距3米,A球和C球相距1米,则B球和C球可能相距如3等(答案不惟一只需满足2米≤距离≤4米)米.(球半径忽略不计,请填出两个符合条件的数)【分析】此题注意两种情况:当A,B,C三个小球共线时,根据线段的和、差计算;当A,B,C三个小球不共线时,根据三角形的三边关系进行分析.【解答】解:当A,B,C三个小球共线时,则BC=2或4;当A,B,C三个小球不共线时,则2<BC<4.则B球和C球可能相距2米≤BC≤4米.如3等(答案不惟一只需满足2米≤距离≤4米).三、解答题(共8小题,满分97分)20.(8分)已知:如图,A是直线l外的一点.求作:(1)一个⊙A,使得它与l有两个不同的交点B、C;(2)一个等腰△BCD,使得它内接于⊙A(说明:要求写出作法)【分析】(1)一个⊙A,使得它与l有两个不同的交点B、C,即圆与直线的关系是相割,是圆的半径大于点A到直线l的距离即可;(2)作BC的垂直平分线,交⊙A于点D,连接BD和CD即可.【解答】解:(1)在l外取一点,使点与A在l的两侧;以A为圆心,两点的距离为半径作圆;交l与B,C两点,⊙A就是所求的圆.(2)作BC的垂直平分线,交⊙A于点D,连接BD和CD.△BCD就是所求的三角形.21.(9分)解方程【分析】此题是对分式方程的解答,按解分式方程的步骤进行,注意最后检验.【解答】解:去分母,得x2﹣4=3(x+1)﹣3.整理得x2﹣3x﹣4=0.解之得,x1=4,x2=﹣1.经检验,x=﹣1是増根.∴原方程的根是x=4.22.(9分)在半径为27m的圆形广场中央点O的上空安装了一个照明光源S,S′射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图).求光源离地面的垂直高度SO(精确到0.1m,=1.414,=1.732,=2.236,以上数据供参考)【分析】圆锥的高,底面上的半径,母线正好构成直角三角形,根据三角函数就可以求出.【解答】解:在△SAB中,SA=SB,∵SO⊥AB∴O是AB的中点.且∠ASO=∠BSO=60°.在直角△ASO中,OA=27m.∴tan60°=27÷SO∴SO=27÷tan60°∴SO=9≈15.6m.答:光源离地面的垂直高度SO为15.6m.23.(13分)在如图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).(1)在给出的直角坐标系中(或舍去该直角坐标系,在自己另建立适当的直角坐标系中),分别写出点A、B、C的坐标;(2)根据你得出的A、B、C三点的坐标,求图象经过这三点的二次函数的解析式.【分析】本题主要考查二次函数解析式的确定、先在题目给出的坐标系中读出A、B、C三点的坐标,然后可用待定系数法求出抛物线的解析式.【解答】解:(1)点A的坐标为(2,3),点B的坐标为(4,1),点C的坐标为(8,9).(2)设所求的二次函数解析式为:y=ax2+bx+c.把点A、B、C的坐标代入抛物线的解析式中,可得:,解得,∴所求的二次函数解析式为y=x2﹣4x+9.(答案不唯一,也可以A或B或C为原点创建新的坐标系进行求解)24.(13分)如图,⊙O的弦AB、CD的延长线相交于点E.请你根据上述条件,写出一个正确的结论(所写的结论不能自行再添加新的线段及标注其他字母),并给出证明.(证明时允许自行添加辅助线)【分析】已知中的EA,EC是圆的两条割线,因而可以满足割线定理,连接AD,BC就可以得到相似三角形,就可以写出求证的结论.【解答】可以证明的结论是EA•EB=EC•ED.证明:连接AD,BC,∵∠A=∠C,∠E=∠E,∴△AED∽△CEB.∴=.即EA•EB=EC•ED.25.(15分)当a取什么数值时,关于未知数x的方程ax2+4x﹣1=0只有正实数根.【分析】由题意可知:本题需要讨论a=0与a≠0两种情况;当a=0时,原方程变为4x﹣1=0,解得x的值即可;当a≠0时,需根据△来求得a的取值范围,再根据根与系数的关系,来确定a 的取值.【解答】解:(1)当a=0时,方程为4x﹣1=0,解得x=;(2)当a≠0时,△=42﹣4a(﹣1)=16+4a≥0,解得a≥﹣4且a≠0;又知方程有两个实根,则根据根与系数的关系可得:x1+x2=﹣>0,x1•x2=﹣>0,则a<0,所以﹣4≤a<0时,原方程有两个正的实根;答:当﹣4≤a≤0时,原方程有两个正的实根.26.(15分)如图,在△ABC中,∠B=90°,AB=4,BC=3,O是AB的中点,OP ⊥AB交AC于点P.(1)证明线段AO、OB、OP中,任意两条线段长度之和大于第三条线段的长度;(2)过线段OB(包括端点)上任一点M,作MN⊥AB交AC于点N.如果要使线段AM、MB、MN中任意两条线段长度之和大于第三条线段的长度,那么请求出线段AM的长度的取值范围.【分析】(1)利用相似三角形的性质求得个线段的长即可;(2)根据相似三角形的性质得比例式,列不等式即可求得.【解答】解:(1)∵∠B=90°,OP⊥AB,∴∠AOP=∠B=90°,∴△AOP∽△ABC.∴∵AB=4,BC=3,O是AB的中点.∴∴OP=∵OP=<AO=OB=2,且+2>2.∴OP+AB>OB即AO,BO,OP中,任意两条线段的长度之和大于第三条线段的长度.∵∠B=90°,OP⊥AB∴OP∥BC∵O是AB的中点,∴OP是△ABC的中位线.∴OP=BC∵BC=3∴OP=;(2)当M在OB上时,设AM=x(2≤x≤4)则MB=4﹣x,∵△AMN∽△ABC∴∴MN=x又MN<AM,MB<AM∴MN+MB>AM,∴x+(4﹣x)>x∴x<∴AM的取值范围为2≤AM<.27.(15分)某玩具工厂有四个车间,某周是质量检查周,现每个车间都原有a (a>0)个成品,且每个车间每天都生产b(b>0)个成品,质检科派出若干名检验员星期一、星期二检验其中两个车间原有的和这两天生产的所有成品,然后,星期三至星期五检验另两个车间原有的和本周生产的所有成品,假定每个检验员每天检验的成品数相同.(1)这若干名检验员1天检验多少个成品(用含a、b的代数式表示);(2)试求出用b表示a的关系式;(3)若1名质检员l天能检验b个成品,则质检科至少要派出多少名检验员?【分析】(1)由题意得星期一,二个车间两天的产品数为:2b×2=4b,原有2a,那么两天检查了(2a+4b),一天检查a+2b;(2)后3天检查的产品数为:原来有的2a+2个车间5天生产的.工效相同,除以3和(1)得到的代数式相等;(3)让总工作量÷一个人的工作量即可.【解答】解:(1)星期一,星期二2个车间两天的产品数为:2b×2=4b,原有2a,那么两天检查了(2a+4b),一天检查a+2b;(2)根据题意得:解得a=4b;(3)÷b===7.5.答:质检科至少要派出8名检验员.。
广东北江中学2002~2003学年初三升学模拟测试(二)

广东北江中学2002~2003学年初三升学模拟测试(二)物理试题班级_________姓名______________学号________得分______________一、单选题(每小题3分,共21分)1、用嘴对着镜子“哈气”,镜面会变得模糊,但过一段时间镜面又得清晰了,在这个过程中的物态变化是()A、先汽化后液化;B、先液化后汽化;C、只有液化;D、只有汽化2、一只鸡蛋漂浮在浓盐水的液面上,所受浮力为F1,现往盐水中缓缓加入清水,同时微微搅动盐水直至鸡蛋在盐水的水面下呈悬浮状态,此时鸡蛋所受的浮力为F2,则()A、F2>F1;B、F2<F1;C、F2=F1;D、无法确定3、当高压电线断裂落地,请不要靠近,更不要用手去拉电线,正确的做法是派人看守现场,迅速找电工师傅来处理,这是因为()A、人走近时会造成跨步电压触电;B、高压电线温度很高C、高压线的电压高,对人有巨大的推力而置人于死地;D、高压电线有巨大的吸引力,把人吸去触电而死4、从显像管尾部的热灯丝发射出来的电子,高速撞击在电视机荧光屏上,使屏发光,则在显像管内()A、电流方向从灯丝到荧屏;B、电流方向从荧屏到灯丝;C、显像管内是真空,无法通过电流;D、电视机使用的是交流电,显像管中的电流方向不断改变。
5、在下列图中,表示晶体凝固图像的是()6、一木块在水平桌面上受到水平向右的拉力为0.4N时,作匀速直线运动,若水平拉力增大到0.6N,此时木块在水平方向受到的合力大小为()A、0.4N;B、0.6N;C、0N;D、0.2N7、在相同路面的情况下,汽车在水平的公路上运行时,速度越大,紧急刹车后,前进的距离就越长,这是因为()A、汽车速度越大,受到的地球引力越小;B、汽车速度越大,摩擦力越小;C、汽车速度越大,惯性越大;D、汽车速度越大,动能越大。
二、多选题(每小题3分,共9分。
每小题有两项或两项以上的选项是正确的,全部选对的得3分,有选对但不全的得2分,有选错或全不选的得0分)8、下列关于光的现象的说法中错误..的是()A、我国古代使用的铜镜能成正立放大的实像;B、激光准直利用了光的折射性质;C、老花镜的焦距可以在太阳光下用刻度尺粗略测出;D、照相机照相时在底片上成倒立放大的虚像9、以下是我们生活中可见到的几种现象,在这些现象中物体因为受力而改变运动状态的是:()A、力揉面团,面团形状发生变化;B、篮球撞击在篮板上被弹回;C、用力握小皮球,球变瘪了;D、一阵风把地面上的灰尘吹得漫天飞舞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市2002年高中阶段学校招生考试数学(本卷满分150分,考试时间120分钟) 第Ⅰ卷(选择题, 共35分)一、选择题(每小题有四个选项,其中有且仅有一项是符合题意的,本题共有13小题,第1~4题每小题2分,第5~13题每小题3分,共35分)1.0.000 000 108这个数,用科学记数法表示为 ( )(A )91.0810-⨯ (B )81.0810-⨯ (C )71.0810-⨯ (D )61.0810-⨯2.计算)210.2512-⎛⎫⨯-+⎪⎝⎭所得的结果是 ( )(A )2 (B )54 (C )0 (D )17163.如果两圆只有一条公切线,那么这两个圆的位置关系是 ( ) (A )外离 (B )外切 (C )相交 (D )内切4.如图1,若四边形ABCD 是半径为1cm 的⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )()222cm π- (B )()221cm π-(C )()22cm π- (D )()21cm π-5.函数y =中,自变量x 的取值范围是 ( ) (A )x>-4 (B )x>1 (C )x ≥-4 (D )x ≥16.如果已知一次函数y=kx+b 的图象不经过第三象限,也不经过原点,那么k 、b 的取值范围是 ( )(A )k>0且b>0 (B )k>0且b<0 (C )k<0且b>0 (D )k<0且b<07.若点()()()1232,11,y y y --、,、都在反比例函数1y x=-的图象上,则 ( ) (A )123y y y >> (B )213y y y >> (C )312y y y >> (D )132y y y >>8.抛物线245y x x =-+的顶点坐标是 ( )(A )(-2,1) (B )(-2,-1) (C )(2,1) (D )(2,-1)9.某装满水的水池按一定的速度放掉水池的一半水后,停止放水并立即按一定的速度注水,水池注满后,停止注水,又立即按一定的速度放完水池的水。
若水池的存水量为v (立方米),放水或注水的时间t (分钟),则v 与t 的关系的大致图象只能是 ( )10.直线y x =与抛物线22y x =-的两个交点的坐标分别是 ( )(A )(2,2)(1,1) (B )(2,2)(-1,-1)(C )(-2,-2)(1,1) (D )(-2,-2)(-1,1)11.如图3,若C 是线段AB 的中点,D 是线段AC 上的任一点(端点除外),则 ( ) (A )CB AC DB AD ⋅<⋅ (B )CB AC DB AD ⋅=⋅ (C )CB AC DB AD ⋅>⋅(D )CB AC DB AD ⋅⋅与大小关系不确定12.在一次向“希望工程”捐款的活动中,若已知小明的捐款数比他所在学习小组中13个人捐款的平均数多2元,则下列的判断中,正确的是 ( )(A )小明在小组中捐款数不可能是最多的 (B )小明在小组中捐款数可能排在第12位(C )小明在小组中捐款数不可能比捐款数排在第七位的同学的少 (D )小明在小组中捐款数可能是最少的13.若12⊙⊙o o 、的半径分别为1和3,且1⊙o 和2⊙o 外切,则平面上半径为4且与12⊙⊙o o 、都相切的圆有( )(A )2个 (B )3个(C )4个 (D )5个第Ⅱ卷(非选择题,共115分)二、填空题(本题共有6小题,每小题3分,共18分)14.如图4,AB//CD ,若∠ABE=120°,∠DCE=35°,则∠BEC=_________________。
15.过△ABC 的顶点C 作边AB 的垂线,如果这垂线将∠ACB 分为40°和20°的两个角,那么∠A 、∠B 中较大的角的度数是______________。
16.如图5,在正方形ABCD 中,AO ⊥BD ,OE 、FG 、HI 都垂直于AD ,EF 、GH 、IJ 都垂直于AO ,若已知1AIJ S ∆=,则ABCD S 正方形=________________。
17.方程5x -=__________________。
18这组学生成绩的中位数是______________。
19.在平坦的草地上有A 、B 、C 三个小球,若已知A 球和B 球相距3米,A 球与C 球相距1米,则B 球与C 球可能相距______________米。
(球的半径忽略不计,只要求填出一个符合条件的数)三、(本题满分8分)20.已知:如图6,A 是直线l 外的一点。
求作:(1)一个⊙A ,使得它与l 有两个不同的交点B 、C ; (2)一个等腰△BCD ,使得它内接于⊙A 。
(说明:要求写出作法。
)四、(本题共有2个小题,每小题9分,共18分)21.解方程243311 xx x-=-++22.在半径为27m的圆形广场中央点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图7)。
求光源离地面的垂直高度SO(精确到0.1m)2.236===,以上数据供参考。
)___________五、(本题满分13分)23.在图8的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度)。
(1)在给出的直角坐标系中(或舍去该直角坐标系,在自己另建立适当的直角坐标系中)分别写出点A、B、C的坐标;(2)根据你得出的A、B、C三点的坐标,求图象经过这三点的二次函数的解析式。
六、(本题满分13分)24.如图9,⊙O的弦AB、CD的延长线相交于点E请你根据上述条件,写出一个正确的结论(所写的结论不能自行再添加新的线段及标注其它字母),并给出证明。
(证明时允许自行添加辅助线)七、(本题满分15分)25.当a 取什么数值时,关于未知数x 的方程2410ax x +-=只有正实数根?八、(本题满分15分)26.如图10,在△ABC 中,∠B=90°,AB=4,BC=3,O 是AB 的中点,OP ⊥AB 交AC 于点P 。
(1)证明线段AO 、OB 、OP 中,任意两条线段长度之和大于第三条线段的长度;(2)过线段OB (包括端点)上任一点M ,作MN ⊥AB 交AC 于点N 。
如果要使线段AM 、MB 、MN 中任意两条线段长度之和大于第三条线段的长度,那么请求出线段AM 的长度的取值范围。
九、(本题满分15分)27.某玩具工厂有四个车间,某周是质量检查周,现每个车间都原有a(a>0)个成品,且每个车间每天都生产b(b>0)个成品,质检科派出若干名检验员星期一、星期二检验其中两个车间原有的和这两天生产的所有成品,然后,星期三至星期五检验另两个车间原有的和本周生产的所有成品,假定每个检验员每天检验的成品数相同。
(1)这若干名检验员1天检验多少个成品?(用含a 、b 的代数式表示) (2)试求出用b 表示a 的关系式;(3)若1名质检员1天能检验54b 个成品,则质检科至少要派出多少名检验员?广州市2002年高中阶段学校招生考试参考答案1.C 2.A 3.D 4.C 5.B 6.C 7.B 8.C 9.A 10.B11.A 12.B 13.D 14.95° 15.70 16.256 17.x=5 18.80分 19.3 20.(1)作法:①在l 外取一点E ,使点E 、A 在l 的两侧②以点A 为圆心,AE 长为半径,作圆交l 于B 、C 两点。
则⊙A 即为所求。
(2)①以点B 为圆心,BC 长为半径画弧,交⊙A 于点D , ②连结BD 和CD 。
则△BCD 即为所求。
(其它作法只要符合要求,均视为正确)21.解:去分母,得()24313x x -=+-, 整理,得2340x x --=, 解之,得124,1x x ==-。
经检验,x=-1是增根。
∴原方程的根是x=422.解:在△SAB 中,SA=SB ,∠ASB=120° ∵SO ⊥AB ,∴O 为AB 的中点。
且∠ASO=∠BSO=60°。
在Rt △ASO 中,OA=27m,∴)(6.153933276027m ctg ASO ctg OA SO ≈=⋅=︒⋅=∠⋅=。
答:光源S 离地面的垂直高度为15.6m 。
23.解法一(在所给的直角坐标系中计算) (1)点A 的坐标是(2,3),点B 的坐标是(4,1),点C 的坐标是(8,9)。
(2)设所求的二次函数解析式为:2y ax bx c =++。
把点A 、B 、C 的坐标分别代入上式,得:423,1641,6489。
a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩ 解之,得124,9。
a b c ⎧=⎪⎪=-⎨⎪=⎪⎩∴所求的二次函数解析式为21492y x x =-+。
解法二(在以B 为原点,另建的直角坐标系中计算) (1)以B 为原点,建立如图所示的直角坐标系。
点A 的坐标是(-2,2), 点B 的坐标是(0,0), 点C 的坐标是(4,8)。
(2)设所求的二次函数解析式为:2y ax bx c =++。
把点A 、B 、C 的坐标分别代入上式,得:422,0,1648。
a b c c a b c -+=⎧⎪=⎨⎪++=⎩ 解之,得1,20,0。
a b c ⎧=⎪⎪=⎨⎪=⎪⎩∴所求的二次函数解析式为212y x =。
解法三(在以点A 为原点,另建的直角坐标系中计算) (1)以A 为原点,建立如图所示的直角坐标系, 点A 的坐标是(0,0), 点B 的坐标是(2,-2), 点C 的坐标是(6,6)。
(2)设所求的二次函数解析式为:2y ax bx c =++把点A 、B 、C 的坐标分别代入上式,得:0,422,3666。
c a b c a b c =⎧⎪++=-⎨⎪++=⎩ 解之,得1,22,0。
a b c ⎧=⎪⎪=-⎨⎪=⎪⎩∴所求的二次函数解析式为2122y x x =-。
(本答案仅列出三种解法。
)六、可以得出的结论及证明如下: (1)EA ·EB=EC ·ED 证明:连结AD 、BC 。
∵∠A=∠C ,∠E=∠E , ∴△AED ∽△CEB 。
∴AE EDCE EB=。
即 AE ·EB=CE ·ED 。
(2)AE>DE 。
证明:连结AD 、BD 、BC ,∵∠1是△BCD 的外角,∠C 是△BCD 的内角, ∴∠1>∠C 。
而∠ADE>∠1,∠C=∠A , ∴在△ADE 中,∠ADE>∠A 。
