第四章1 半导体的导电性
半导体的导电性
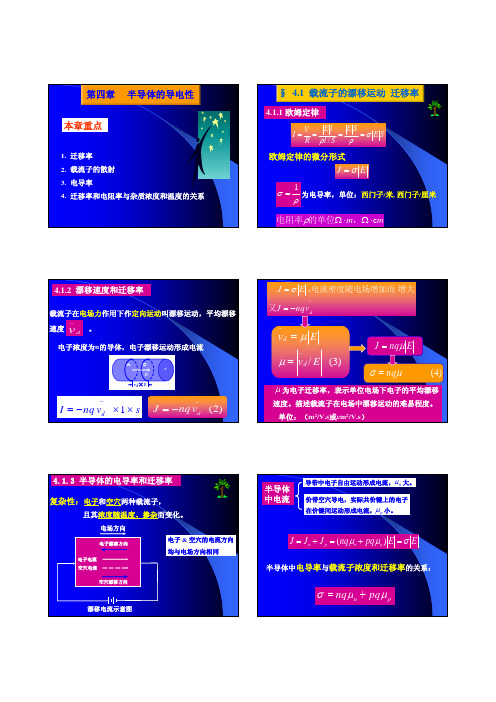
第四章半导体的导电性本章重点1.迁移率2.载流子的散射3.电导率4.迁移率和电阻率与杂质浓度和温度的关系§ 4.1 载流子的漂移运动迁移率4.1.1 欧姆定律S E S E S l l E R V I σρρ====/为电导率,单位:西门子/米, 西门子/厘米ρσ1=mm c ⋅Ω⋅Ω,的单位电阻率ρ欧姆定律的微分形式EJ σ=4.1.2 漂移速度和迁移率载流子在电场力作用下作定向运动叫漂移运动,平均漂移速度。
dv −(2)d J nq v −=−E v d ×1sAO 电子浓度为n 的导体,电子漂移运动形成电流1d I nq v s−=−××−−==dv nq J E J 又增大电流密度随电场增加而,σ/(3)d d v Ev E μμ−−==Enq J μ=)4(μσnq =为电子迁移率,表示单位电场下电子的平均漂移速度。
描述载流子在电场中漂移运动的难易程度。
单位:(m 2/V.s 或cm 2/V.s )μ漂移电流示意图电场方向4.1.3 半导体的电导率和迁移率复杂性:电子和空穴两种载流子,且其浓度随温度、掺杂而变化。
空穴漂移方向电子电流空穴电流电子漂移方向电子& 空穴的电流方向均与电场方向相同半导体中电流EE pq nq J J J p n p n σμμ=+=+=)(半导体中电导率与载流子浓度和迁移率的关系:pn pq nq μμσ+=导带中电子自由运动形成电流,大。
n μ价带空穴导电,实际共价键上的电子在价键间运动形成电流,小。
p μn nq σμ=对N 型半导体n>>pppq σμ=对P 型半导体p>>n 对本征半导体p =n =n i()i n p n q σμμ=+电子迁移率大于空穴迁移率,高速开关器件主要依靠电子导电。
电导率主要取决于多子§ 4.2 载流子的散射J E σ=,电场一定,电流密度恒定应不断增加,,载流子受电场力加速J v nq J d −−=矛盾的两方面:原因所在:载流子与晶格原子或电离杂质等发生碰撞而交换能量,从而改变载流子速度的大小和方向4.2.1 载流子散射与漂移运动1、载流子的散射——改变速度的方向和大小处在外电场中的载流子运动:散射+漂移运动。
《半导体物理》第四章

长声学波,声子数最多,作用最大。
电子和声子的碰撞
• 声子的能量为:
1 1 1 a E (n )a a 2 2 exp(a ) 1 k0T
• 电子与声子的碰撞过程:
k 'k q E ' E h
• 具有单一极值、球形等能面的半导体,对导带电子散射 的几率是
k T (m ) Ps v 4 u
2 c 0 * 2 n 2
由形变引起导带底的变化
Ec c
V V0
最后,因电子热运动速度与T1/2成正比,声学波散射几率
Ps T 3 / 2
• 对于硅、锗具有旋转椭球等能面的半导体,切变也会引 起能带极值的变化,即横声学波也参与对电子的散射。 总的散射几率依然如上式,为T3/2关系。
§4.3 迁移率与杂质浓度和温度的关系
1、平均自由时间τ和散射几率P的关系 1 P
当几种散射机构同时存在时
总散射几率: 相应的平均自由时间:
P Pj
j
1
j
1
j
τ-P关系的数学推导 用N(t)表示t时刻未遭到散射的电子数,则在 t ~ t t 被 散射的电子数
• 对于硅、锗及III-V族化合物,其原胞结构均由两套 面心立方原子套构而成,基元有2个原子,三维结构 每个波矢q共有6支格波:3支声学波和3支光学波。 • 3支声学波为2横1纵。声学波是 q = 0时,=0。 • 长声学波代表质心的振动。在长波范围内,波数q越 大,波长越短,能量越大,声子数越少。 同时,其能 量 为量子化的: (n+1/2)h 。
载流子的散射 存在破坏周期性势场的作用因素: 载流子在半导体中运动时,不断与振动 杂质 着的晶格原子或杂质离子发生碰撞,碰撞后 缺陷 载流子速度的大小及方向均发生改变,这种 晶格热振动 现象称为载流子的散射。
半导体的导电性

当前研究的不足与挑战
半导体导电性的调控机制尚不完全清楚,需要进一步深入研究。
一些高性能的半导体材料和器件仍然依赖进口,需要加强自主创新和知识产权保护。
半导体产业的发展面临着技术、环境、资金等多方面的挑战,需要积极应对。
发展智能制造和绿色制造,提高半导体产业的核心竞争力。
加强基础研究和应用研究,推动半导体材料和器件的创新发展。
实现半导体材料和器件的全链条自主可控,保障国家安全和产业安全。
未来发展的趋势与展望
THANKS
谢谢您的观看
影响因素
迁移率与材料的晶体结构、杂质和温度等因素有关。
迁移率
载流子密度是衡量半导体材料中载流子数量的参数,定义为材料的电阻率与电阻率的乘积,即n=ρσ,其中ρ为电阻率。
定义
载流子密度与材料的纯度、晶体结构和掺杂等因素有关。
影响因素
载流子密度
03
半导体导电性的测量与实验技术
四探针电阻测量技术是一种非接触式测量方法,通过施加电流和测量电压来计算电阻率。
温度依赖Hall效应
通过测量不同温度下半导体内部的霍尔电压,研究温度对载流子浓度和迁移率的影响。
Hall效应测量
深能级瞬态谱技术
利用光脉冲激发半导体中的电子,并测量电子在各个时间点的分布情况,从而了解半导体中的缺陷、杂质等特性。
时间分辨深能级瞬态谱技术
通过使用超快激光脉冲,对半导体内部电子的动态行为进行高时间分辨率的测量,研究电子在半导体中的输运过程。
半导体导电性的基本概念
半导体导电主要通过自由电子和空穴两种载流子实现。
在半导体内部,自由电子和空穴的数量受温度、光照等因素影响。
当加电压时,自由电子和空穴的数量增加,从而导致电流增加。
第四章-半导体的导电性

单位时间由于散射而失去的能量: 0v l0
单位时间由电场获得的能量: qvd | E|
稳态时两者应相等,即
qd
E
0
v l0
联立解得:v d
80
3
m n
------与电场无关
2、负微分电导
1)负微分电导
负阻效应产生条件:半导体能带结构中存在多能谷, 且能谷的曲率不同;载流子发生能谷间散射。
负微分电导的 产生机理:对GaAS而言,当电场 达到3×103 V/cm后,低能谷1 中的电子可从电 场中获得足够的能量而开始转移到高能谷2中, 发生能谷间的散射,并伴随发射或吸收一个光学 声子.进入能谷2的电子,有效质量大为增加, 迁移率大大降低,平均漂移速度减小,电导率下 降,产生负阻效应.
角频率为ωa的格波,能量是量子化的,只能是
(
n
1 2
)a
声子:晶格振动的能量量子。
根据统计计 算,格波的 平均能量为
1 2
a
exp(
1
a
)-1
a
k0T
包含平均声子 数为
晶格振动对 载流子的散 射可以看成 载流子与声 子的碰撞。
1 nq = exp( ωa )- 1
koT
k'-k q
E'-Ea
声学波散射概率:
d N t liN m t+ t- N t= P t - N
dt t 0 t
N( t)N = 0ex( p p- ) t
设N0为t=0时未遭散射的电子数。所以在t到t +dt时间内被散射的电子数为:
d= NN0Pepd t t
平均自由时间:
=1 N0
0N0Pte-pdt = t P 1
08-第四章-半导体的导电性

en
vdx1 秒
平均自由时间
弛豫时间
系统从非平衡态恢复到平衡态 所需时间
* 的统计表示 t=0时,撤除电场,有N0个电子作定向运动 N(t)为t时刻还未遭到碰撞的电子数 P为单位时间内电子被碰撞的几率 在tt+dt时间内被碰撞的电子数可表示为:
N (t ) N (t dt) N (t ) Pdt dN (t ) PN (t )
n型半导体载流子浓度随温度的变化曲线ln(n)-1/T n型半导体载流子浓度随掺杂浓度ND的变化曲线 半导体费米能级随掺杂浓度ND - NA的变化曲线
N型半导体中的电子浓度随温度的变化关系
ln(n) 斜率:Eg/2k 斜率:ED/2k
1/T
n型半导体载流子浓度随掺杂浓度ND的变化曲线
p,n
n p
C N * 临界浓度 D 的估算
非简并 弱 简并
简并
强简并
-2kT
0
5kT
Ef-Ec
Ec
ND 3 EC ED KT N D dEf Ef ln 0 ln 2 2 2 N C dT 2NN D3
1 2 1 e t 2 r vd (0)t at * 2 m 2 e
在tt+dt时间内被碰撞的电子数为 PN (t )dt
这些电子定向位移之和为 rPN (t )dt
N0个电子定向位移之总和为 S 0 rPN (t )dt
S
0
1 e 2 e N 0 e 2 t PN exp( Pt ) dt N 0 0 * * * 2 me me P2 me
* 简并的温度范围 简并时的电中性方程:n N D
半导体的导电性

第四章半导体的导电性本章主要内容载流子在外加电场作用下的漂移运动半导体的迁移率、电导率和电阻率随温度和杂质浓度的变化规律迁移率的本质-----散射4.1 载流子的漂移运动迁移率1、欧姆定律对于金属,电流I = V(电压)/R(电阻)V-I关系是直线对于半导体,流过不同截面的电流强度不一定相同,“即电流分布不均匀,而欧姆定律不能说明材料内部各处电流的分布情况。
电流密度:通过垂直于电流方向的单位面积的电流J = ∆I/∆S单位:A/cm2或A/m2欧姆定律微分形式:上式把通过导体中某一点的电流密度和该处的电导率及电场强度直接联系了起来。
S故: 半导体导电= 电子导电J = Jn + Jp = (nqu平均自由程:载流子在连续两次散射间自由运动的平均路程平均自由时间:载流子通过平均自由程所需的平均时间τ电场:载流子加速---定向运动;散射:载流子运动方向改变---杂乱无章,各个方向;半导体的主要散射机构:离化杂质散射晶格散射中性杂质散射位错散射(P为散射几率)起因:常温下,浅施主带正电• 双曲线,电离杂质处于一个焦点 • 速度小,作用时间长,偏离角θ大,τ小 • 弹性散射,不改变入射电子能量,只改变运动方向 τ ∝ T3/2/NI 杂质浓度(2)、晶格散射 晶格原子在其平衡位置附近不断进行热振动,且各个 原子的振动不是孤立的。
分析表明:晶格中原子的振动都 是由若干不同的基本波动按波的叠加原理组合而成,这些 基本波动称为格波。
q代表格波波矢, q 的方向即波的传播方向晶格散射:载流子在运动过程中遭受振动的晶格原子的散射, 失去在电场中获得的能量,失去动量。
在能带具有单一极值的半导体中 起主要散射作用的是长波。
即波 长比原子间距大很多倍的格波。
电子热运动速度~105m/s 电子波波长约10-8m 根据动量守恒要求,声子波长 范围应在同一量级,即10-8m,而 晶体中原子间距为10-10m,因而 起主要散射作用的是长波。
半导体物理:半导体的导电性

而“自由”载流子只是在连续的两次散射之间才是“自由”的。 平均自由程:连续两次散射间自由运动的平均路程 平均自由时间:连续两次散射间的平均时间
4.2.2半导体的主要散射机构
半导体中载流子遭到散射的根本原因: 在于晶格周期性势场遭到破坏而存在有附加势场。
4.2
4.2.1
F h dk dt
电离杂质对电子和空 穴的散射
电离杂质对载流子散射的问题,与α粒子被原子核散射的情形 很类似。 载流子的轨道是双曲线,电离杂质在双曲线的一个焦点上。
Zq2 V
4 ror
Z—电离杂质的电荷数
r—载流子与离子的距离
v
v
电离
施主
+
散射
V’
电离
–
受主
散射
V’
电离杂质散射示意图
为描述散射作用强弱,引入散射几率P,它定义为单位时间内 一个载流子受到散射的次数。
如果离化的杂质浓度为Ni,电离杂质散射的散射几率Pi与Ni及 其温度的关系为
上式表明:
Pi NiT 3 2
Ni越高,载流子受电离杂质散射的几率越大; 温度升高导致载流子的热运动速度增大,从而更容易掠过电离杂
质周围的库仑势场,遭电离杂质散射的几率反而越小。
个截面,这两个截面间所围成
的体积中总电子数为 N nsυd t
图4.1 平均漂移速度分析模型
这N个电子经过t时间后都将通过A面,因此按照电流强度的定义
I
Q t
qN t
nqsυd t t
nqsυd
与电流方向垂直的单位面积上所通过的电流强度定义为电流密
度,用J表示,那么
J
半导体的导电性

2、漂移速度:定向运动的速度
漂移电流
I Q q n volume
q
t n
(vt
t s)
qnvs
t
漂移电流密度
J I qnv s
3、迁移率
欧姆定律微分表达式 J
漂移电流密度
J I qnv s
v
qn
平均漂移速度的大小与电场强度成正比,其系数
合金散射是混合晶体特有的散射机制。在 原子有序排列的混合合金中,几乎不存在合金 散射效应。
练习
T=300K时,砷化镓的掺杂浓度为NA=0, ND=1016cm-3,设杂质全部电离,电子的移迁率为 7000cm2/V.s, 空穴的迁移率为320cm2/V.s,若外 加电场强度ξ=10V/cm,求漂移电流密度和电导率
§4.4 电阻率与杂质浓度和温度的关系
一、电阻率和杂质浓度的关系
nqn pq p
1
nqn
1
nqn
1
pq p
1
pq p
1
ni
q(n
p
)
n型 p型 本征
300k时,本征 Si: =2.3×105Ω·cm , 本征Ge: =47 Ω· cm 本征GaAs: =200 Ω· cm
杂质半导体:随温度T增加,有杂质电离和本 征激发,有电离杂质散射和晶格振动散射。
(1)AB段: 低温杂质电离区
1
nqn pqp
s
q m
1
3
AT 2
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 半导体的导电性
1 1 Pt N 0 Pe tdt N0 0 P
(4 39)
平均自由时间的数值等于散射概率的倒数
第四章 半导体的导电性
vd:电子的平均漂移速度
第四章 半导体的导电性
导体内做一截面A,I是一秒钟内通过截面A 的电量。在A面右方,距A面为 vd ×1 做一 面,两截面间的电子,在一秒钟内均能通 过A面。
第四章 半导体的导电性
设n为电子浓度,则两面间电子数为
nvd 1 s
乘以电子量即为电流强度,所以
I qnvd s
半导体晶格上原子也在不停地围绕 格点做热振动。 半导体掺有一定杂质,RT一般电离 了,带有电荷。
第四章 半导体的导电性
载流子在半导体中运动时,会不断地与热振动着 的晶格原子、电离杂质离子发生作用,发生碰撞。
碰撞后载流子速度的大小及方向就发生改变。
用波描述,电子波在半导体中传播遭到散射。 载流子无规则的热运动也正是由于它们不断地 遭到散射的结果。
第四章 半导体的导电性
解:须先求出本征载流子浓度
又
联立得:
第四章 半导体的导电性
故样品的电导率:
即: E=1.996V/cm
第四章 半导体的导电性
4.3 迁移率与杂质浓度 和温度的关系
第四章 半导体的导电性
4.3.1 平均自由时间和散射概率的关系
载流子在电场中作漂移运动时,只有在
连续两次散射之间的时间内才作加速运动,
第四章 半导体的导电性
例1.室温下,本征锗的电阻率为47 , 试求本征载流子浓度。 若掺入锑杂质,使每 个锗原子中有一 个杂质原子,计算室温下电子浓度和空穴 浓度并试求该掺杂锗材料的电阻率。设杂 质全部电离, 锗原子的浓度为 设 p 1700 2 / Vg , 且认 cm 为不随掺杂而变化。
第四章 半导体的导电性
J 指通过垂直于I的单位面积的电流,即 J=Δ I/ Δ S (4-4)
单位:A/m2 A/cm2
第四章 半导体的导电性
J= |E|
(4-7)
导体中某点J和该处的及E直接联系起 来—欧姆定律微分形式(微分欧姆定律)。
第四章 半导体的导电性
4.1.2
漂移速度和迁移率
外加V,导体内部自由电子受到电场力的 作用,沿电场的反方向作定向运动构成电流。 电子在电场力作用下的这种运动称为漂移 运动,定向运动的速度称为漂移速度
第四章 半导体的导电性
1.电离杂质的散射
杂质电离后是一个带电离子,施主电离后带正 电,受主电离后带负电。
在电离施主或受主周围形成一个库仑势场,局部 地破坏周期性势场,是使载流子散射的附加势场。
第四章 半导体的导电性
当载流子运动到电离杂质附近,库仑势场的作 用,使载流子运动方向改变,以速度v接近电离杂质, 而以 v 离开,类似粒子在原子核附近的散射。
第四章 半导体的导电性
解:本征半导体的电阻率表达式为:
施主杂质原子的浓度
故
第四章 半导体的导电性
其电阻率
第四章 半导体的导电性
例2. 在半导体锗材料中掺入施主杂质浓 度 ,受主杂质浓度 ; 设室温下本征锗材料的电阻率 , 假设电子和空穴的迁移率分别 为 ,若流过 样品的电流密度为 ,求所加的电 场强度。
J nq | E |
(4 12)
再与式(4-7)相比,得到
nq
(4 13)
J=E
式(4-13)为电导率和迁移率间的关系。
第四章 半导体的导电性
4.1.3 半导体的电导率和迁移率
半导体的导电机理:电子导电、空穴导电
第四章 半导体的导电性
同一电场作用,电子、空穴平均漂移速度不会 相同,导带电子平均漂移速度要大些,价带空 穴迁移率要小些。 以 n p分别代表电子和空穴迁移率; Jn Jp 分 别代表电子和空穴电流密度;n, p 分别代表电子 和空穴浓度,则半导体中总电流密度J 应为
第四章 半导体的导电性
4.2.2 半导体的主要散射机构
半导体中载流子在运动过程中被散射原因?
周期性势场的被破坏!引入附加势场
导致电子运动过程中状态不断发生改变。
第四章 半导体的导电性
主要散射机构:
电离杂质散射 晶格振动的散射 等同的能谷间散射 中性杂质散射 位错散射载流子之间的散射
当同时存在i种散射机构时:
P pi
i
总的平均自由时间:
1 P 1
P
i i
1
P i
i i
1
i
第四章 半导体的导电性
4.3.2 电导率、迁移率与平均自由时间的关系
设电子沿x方向运动
n
E qE 而 n (2) mn
(1)
注意:
第四章 半导体的导电性
外加电场: 1)载流子作定向运动 2)载流子不断遭到散射 运动轨迹:热运动 和漂移运动的叠加
散射几率:单位时 间内一个载流子被 散射的次数
第四章 半导体的导电性
由于电场作用而获得的漂移速度,便不断地 散射到各个方向上去,漂移速度不能无限积累。 载流子在电场作用下的加速运动,只在两次 散射之间才存在,经过散射后它们又失去了获得 的附加速度。 因此,在外力和散射的影响下,使载流子以一 定的平均速度沿力的方向漂移,这个平均速度是恒 定的平均漂移速度。
V I (4 1) R l R (4 2) s 1 (4 3)
其中,: cm; 西门子 / cm
第四章 半导体的导电性
欧姆定律不能说明导体内部各处电 流的分布情况. 半导体中, 一般电流分布 在截面各处并不均匀, 流过不同截面的电 流强度可能不同, 常用电流密度J.
第四章 半导体的导电性
第四章 半导体的导电性
重点:
半导体的迁移率、电导率、电阻率随温度和 杂质浓度的变化规律
载流子的散射概念,了解迁移率的本质 载流子散射的物理本质(定性结论) 电导率 弱电场情况下电导率的统计理论
第四章 半导体的导电性
4.1 载流子的漂移运动和迁移率
4.1.1 复习欧姆定律:
p
(6)
2 nq 2 n nq p 混合型: =nq n pq p (7) mn mp
第四章 半导体的导电性
4.3.3 迁移率与杂质和温度的关系
P 而
1
电离杂质散射: Pi NiT-3/2 声学波散射: Ps T3/2 光学波散射:Po [exp( hv1 ) 1]1 k0T
格波能量以ha为单元, 称为声子。 晶格与其他物质(如电子、光子)相 互作用而交换能量时,晶格原子的振动状 态就要发生变化,格波能量就改变。
第四章 半导体的导电性
格波能量变化是ha 整数倍,格波的 能量子 ha 称为声子。 把能量为(n+1/2 )ha 的格波描述 为n个属于这一格波的声子,当格波能量 减少一个ha 时,就称做放出一个声子, 增加一个 ha 就称做吸收一个声子。
m m
n
p
q n n (3) mn 同理 p q p m
n
n p
相同电场作用下,电子的速度快
(4)
第四章 半导体的导电性
各种类型材质的电导率如下:
nq 2 n n型: n nq n (5) mn P型: p pq p nq 2 p m
两种载流子的浓度相差很悬殊而迁移率差别 不太大的杂质半导体来说,它的电导率主要由 多子决定。
对n型且n》p =qn n (4-16) 对于p型半导体,p>>n,电导率为 =qp p (4-17) 对于本征半导体,n=p=ni,电导率为 =qni( n +p ) (4-18)
第四章 半导体的导电性
3 其他因素引起的散射 等同的能谷间散射—低温时谷间散射很小 对于能量极值相同的多能谷,电子可以从 一个极值附近散射到另外一个极值附近。
第四章 半导体的导电性
中性杂质散射(低温重掺杂半导体) 没有电离的中性杂质对周期性势场有一定 的微扰作用引起的散射 位错散射 位错密度很高(>104cm-2)的材料需考虑 合金散射:多元化合物半导体混晶,两种同 族原子在其晶格中相应的位置上随机排列,都 会产生对载流子产生散射作用 载流子之间的散射(强简并半导体)
显然:
(4 8)
J qnvd
(4 9)
第四章 半导体的导电性
导体内E定时,e具一恒定不变的 vd 。 E增大,J相应增大, vd 随着|E|的增大而增 大。v 的大小与|E|成正比,写为:
d
vd | E |
(4 10)
第四章 半导体的导电性
称为电子的迁移率,表示单位
第四章 半导体的导电性
所谓自由载流子,只在两次散射之间才真正 是自由运动的。 其连续两次散射间自由运动的平均路程称为 平均自由程, 平均时间称为平均自由时间。
第四章 半导体的导电性
图示意画出电子无规则热运动。无外电场时,电 子虽不停息地做热运动,但宏观上它们没有沿着一定 方向流动,所以不构成电流。
P
பைடு நூலகம்1
所以: 电离杂质散射: μi Ni-1T3/2 声学波散射: μ s T -3/2 hv1 光学波散射: o [exp( ) 1]
k0T
第四章 半导体的导电性
1 P 1
4.2 载流子的散射
外加电场E理想情况:载流子在电场力作用下作漂移运动
第四章 半导体的导电性
