第四章半导体的导电性讲解
合集下载
《半导体物理》第四章
1 nq a exp( ) 1 k0T
长声学波，声子数最多，作用最大。
电子和声子的碰撞
• 声子的能量为：
1 1 1 a E (n )a a 2 2 exp(a ) 1 k0T
• 电子与声子的碰撞过程：
k 'k q E ' E h
• 具有单一极值、球形等能面的半导体，对导带电子散射 的几率是
k T (m ) Ps v 4 u
2 c 0 * 2 n 2
由形变引起导带底的变化
Ec c
V V0
最后，因电子热运动速度与T1/2成正比，声学波散射几率
Ps T 3 / 2
• 对于硅、锗具有旋转椭球等能面的半导体，切变也会引 起能带极值的变化，即横声学波也参与对电子的散射。 总的散射几率依然如上式，为T3/2关系。
§4.3 迁移率与杂质浓度和温度的关系
1、平均自由时间τ和散射几率P的关系 1 P
当几种散射机构同时存在时
总散射几率： 相应的平均自由时间：
P Pj
j
1
j
1
j
τ-P关系的数学推导 用N(t)表示t时刻未遭到散射的电子数，则在 t ~ t t 被 散射的电子数
• 对于硅、锗及III-V族化合物，其原胞结构均由两套 面心立方原子套构而成，基元有2个原子，三维结构 每个波矢q共有6支格波：3支声学波和3支光学波。 • 3支声学波为2横1纵。声学波是 q = 0时，=0。 • 长声学波代表质心的振动。在长波范围内，波数q越 大，波长越短，能量越大，声子数越少。 同时，其能 量 为量子化的： (n+1/2)h 。
载流子的散射 存在破坏周期性势场的作用因素： 载流子在半导体中运动时，不断与振动 杂质 着的晶格原子或杂质离子发生碰撞，碰撞后 缺陷 载流子速度的大小及方向均发生改变，这种 晶格热振动 现象称为载流子的散射。
长声学波，声子数最多，作用最大。
电子和声子的碰撞
• 声子的能量为：
1 1 1 a E (n )a a 2 2 exp(a ) 1 k0T
• 电子与声子的碰撞过程：
k 'k q E ' E h
• 具有单一极值、球形等能面的半导体，对导带电子散射 的几率是
k T (m ) Ps v 4 u
2 c 0 * 2 n 2
由形变引起导带底的变化
Ec c
V V0
最后，因电子热运动速度与T1/2成正比，声学波散射几率
Ps T 3 / 2
• 对于硅、锗具有旋转椭球等能面的半导体，切变也会引 起能带极值的变化，即横声学波也参与对电子的散射。 总的散射几率依然如上式，为T3/2关系。
§4.3 迁移率与杂质浓度和温度的关系
1、平均自由时间τ和散射几率P的关系 1 P
当几种散射机构同时存在时
总散射几率： 相应的平均自由时间：
P Pj
j
1
j
1
j
τ-P关系的数学推导 用N(t)表示t时刻未遭到散射的电子数，则在 t ~ t t 被 散射的电子数
• 对于硅、锗及III-V族化合物，其原胞结构均由两套 面心立方原子套构而成，基元有2个原子，三维结构 每个波矢q共有6支格波：3支声学波和3支光学波。 • 3支声学波为2横1纵。声学波是 q = 0时，=0。 • 长声学波代表质心的振动。在长波范围内，波数q越 大，波长越短，能量越大，声子数越少。 同时，其能 量 为量子化的： (n+1/2)h 。
载流子的散射 存在破坏周期性势场的作用因素： 载流子在半导体中运动时，不断与振动 杂质 着的晶格原子或杂质离子发生碰撞，碰撞后 缺陷 载流子速度的大小及方向均发生改变，这种 晶格热振动 现象称为载流子的散射。
华南理工半导体物理—第四章
E=0 2
1 6 3 随机热运动 4
5
当一个小电场E施加于半导体时，每一个电子会从电场上 受到一个-qE的作用力，且在各次碰撞之间，沿着电场的反向 被加速。因此，一个额外的速度成分将再加至热运动的电子上 ，此额外的速度成分称为漂移速度(drift velocity) 一个电子由于随机 的热运动及漂移成分两 者所造成的位移如图所 示。 值得注意的是，电 子的净位移与施加的电 场方向相反。
电离杂质散射 • 半导体中的电离杂质形成正、负电中心， 对载流子有吸引或排斥作用，从而引起载 流子散射。
电离杂质散射几率
Pi N iT
3
2
上式表明，随着温度的降低，散射几率 增大。因此，这种散射过程在低温下是 比较重要的。
Байду номын сангаас
晶格振动散射
半导体晶体中原子的振动是引起载流子 被散射的主要原因之一。
mn n 0.26 0.911030 kg 1000104 m2 / V s c q 1.6 1019 C
1.48 1013 s 0.148 ps.
又
1 3 3kT 2 mn vth kT vth 107 cm / s 2 2 mn
所以，平均自由程则为
漂移运动，迁移率与电导率
• 漂移运动：载流子在电场力作用下的定向运动， 定向运动的速度称为漂移速度
j E
vd n E
j nqvd
jn nqn E
n nqn
J jn j p (nqn nq p ) E
(nqn nq p )
载流子散射
j E
dI dV J E ds dl
半导体中电流的大小还可以从另一个角度 来理解。
第半导体物理课件 第四章
用，对电子产生散射作用。
• 横声学波要引起一定的切变，对具有多极值、旋转椭球等 能面的锗、硅来说，也将引起能带极值的变化。
光学波散射
• 离子性半导体中，长纵光学波有重要的散射作用。 • 每个原胞内正负离子振动位移相反，正负离子形成硫密 相间的区域，造成在一半个波长区域内带正电，另一半 个波长区域内带负电，将产生微区电场，引起载流子散 射。 长声学波振动，声子的速度很小，散射前后电子能量基本不 变，－－弹性散射 光学波频率较高，声子能量较大，散射前后电子能 量有较大的改变，－－非弹性散射。
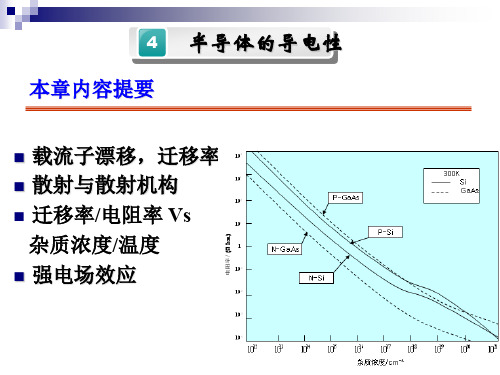
迁移率和杂质与温度关系
杂质浓度较低，迁移率随温度升高迅速减小，晶格散射起主要作用； 杂质浓度高，迁移率下降趋势不显著，说明杂质散射机构的影响为主。当 杂质浓度很高时，低温范围内，随温度升高，电子迁移率缓慢上升，直到
很高温度(约550K左右)才稍有下降，这说明杂质散射起主要作用。晶格 振动散射与前者比影响不大，所以迁移率随温度升高而增大；温度继续升 高后，又以晶格振动散射为主，故迁移随温度下降。
② 计算中假设散射后的速度完全无规则，即散射后载流子向各个方向运动 的几率相等。这只适用于各向同性的散射．对纵声学波和纵光学波的散射确 实是各向同性的．但是电离杂质的散射则偏向于小角散射。所以精确计算还 应考虑散射的方向性。
下节较精确地计算半导体的电导率，为简单起见，仍限于讨论各向同性的 散射。
5 玻耳兹曼方程· 电导率的统计理论
• 各向同性晶体特点：
a、声学波散射： Ps∝T3/2 b、光学波散射：P o∝[exphv/k0T）]-1
2）电离杂质散射：即库仑散射
散射几率Pi∝NiT-3/2（Ni：为杂质浓度总和）。
3)其它散射机构
08-第四章-半导体的导电性
e e * 2me
en
vdx1 秒
平均自由时间
弛豫时间
系统从非平衡态恢复到平衡态 所需时间
* 的统计表示 t=0时，撤除电场，有N0个电子作定向运动 N(t)为t时刻还未遭到碰撞的电子数 P为单位时间内电子被碰撞的几率 在tt+dt时间内被碰撞的电子数可表示为：
N (t ) N (t dt) N (t ) Pdt dN (t ) PN (t )
n型半导体载流子浓度随温度的变化曲线ln(n)-1/T n型半导体载流子浓度随掺杂浓度ND的变化曲线 半导体费米能级随掺杂浓度ND - NA的变化曲线
N型半导体中的电子浓度随温度的变化关系
ln(n) 斜率：Eg/2k 斜率：ED/2k
1/T
n型半导体载流子浓度随掺杂浓度ND的变化曲线
p,n
n p
C N * 临界浓度 D 的估算
非简并 弱 简并
简并
强简并
-2kT
0
5kT
Ef-Ec
Ec
ND 3 EC ED KT N D dEf Ef ln 0 ln 2 2 2 N C dT 2NN D3
1 2 1 e t 2 r vd (0)t at * 2 m 2 e
在tt+dt时间内被碰撞的电子数为 PN (t )dt
这些电子定向位移之和为 rPN (t )dt
N0个电子定向位移之总和为 S 0 rPN (t )dt
S
0
1 e 2 e N 0 e 2 t PN exp( Pt ) dt N 0 0 * * * 2 me me P2 me
* 简并的温度范围 简并时的电中性方程：n N D
en
vdx1 秒
平均自由时间
弛豫时间
系统从非平衡态恢复到平衡态 所需时间
* 的统计表示 t=0时，撤除电场，有N0个电子作定向运动 N(t)为t时刻还未遭到碰撞的电子数 P为单位时间内电子被碰撞的几率 在tt+dt时间内被碰撞的电子数可表示为：
N (t ) N (t dt) N (t ) Pdt dN (t ) PN (t )
n型半导体载流子浓度随温度的变化曲线ln(n)-1/T n型半导体载流子浓度随掺杂浓度ND的变化曲线 半导体费米能级随掺杂浓度ND - NA的变化曲线
N型半导体中的电子浓度随温度的变化关系
ln(n) 斜率：Eg/2k 斜率：ED/2k
1/T
n型半导体载流子浓度随掺杂浓度ND的变化曲线
p,n
n p
C N * 临界浓度 D 的估算
非简并 弱 简并
简并
强简并
-2kT
0
5kT
Ef-Ec
Ec
ND 3 EC ED KT N D dEf Ef ln 0 ln 2 2 2 N C dT 2NN D3
1 2 1 e t 2 r vd (0)t at * 2 m 2 e
在tt+dt时间内被碰撞的电子数为 PN (t )dt
这些电子定向位移之和为 rPN (t )dt
N0个电子定向位移之总和为 S 0 rPN (t )dt
S
0
1 e 2 e N 0 e 2 t PN exp( Pt ) dt N 0 0 * * * 2 me me P2 me
* 简并的温度范围 简并时的电中性方程：n N D
第4章.-半导体物理-半导体的导电性
p
pq2 m*p
p
一般混合型半导体:
nq2 mn*
n
pq2 m*p
p
意义：平均自由时间愈长，或说单位时间内遭受散射的次数愈少，
载流子的迁移率愈高；电子和空穴的迁移率不同，因为它们的平均
自由时间和有效质量不同。一般电子迁移率大于空穴迁移率。
The Scattering of Carriers
b、光学波散射：
Po
[exp(
1
k0T
)
1]1
举例：GaAs
小结：
半导体中的散射机构是电离杂质散射和晶格振动散射，而 晶格振动散射主要是以长纵光学波和长纵声学波为主。
散射作用的强弱用散射几率P来衡量。
电离杂质散射： P
NiT
3
2；长纵声学波：P
T
3 2
(3)其它散射机构
散射几率 Pi NiT 3/ 2
杂质浓度总和Ni越大，载流子受到散射的机会越大 T越高，载流子热运动平均速度越大，散射几率越少
电离施主杂质散射
电离受主杂质散射
电离杂质散射示意图
(2)晶格振动散射
各原子对平衡位置的位移可以分为若干不同频率位移波的迭加。 原子的平衡位置
R As exp[ i(q r t)]
（vdn和vdp分别为电子和空穴的平均漂移速度）
在本征情况下， J= Jn+ Jp
电场不太强时，漂移电流遵从欧姆定律 J E
n型半导体，n>>p，Jn>>Jp E nqvdn
vdn
nq
E
半导体的导电特性
半导体
本征半导体 杂质半导体
P型半导体(空穴型） N型半导体（电子型）
常用半导体材料硅和锗的原子结构
价电子：最外层的电子受原子核的束缚最 小，最为活跃，故称之为价电子。 最外层有几个价电子就叫几价元素， 半导体材料硅和锗都是四价元素。
Si+14 2 8 4
Ge+32 2 8 18 4
2. 半导体的内部结构及导电方式：
一是势垒电容CB 二是扩散电容CD
(1) 势垒电容CB
势垒电容是由空间电荷区的离子薄层形成的。 当外加电压使PN结上压降发生变化时，离子薄层 的厚度也相应地随之改变，这相当PN结中存储的 电荷量也随之变化，犹如电容的充放电。
图 01.09 势垒电容示意图
(2) 扩散电容CD
扩散电容是由多子扩散后，在PN结的另一侧 面积累而形成的。因PN结正偏时，由N区扩散 到P区的电子，与外电源提供的空穴相复合，形 成正向电流。刚扩散 过来的电子就堆积在P 区内紧靠PN结的附近， 形成一定的多子浓度 梯度。
vi
RL vo
vo
t
例3：设二极管的导通电压忽略，已知
vi=10sinwt(V)，E=5V，画vo的波形。
vi 10v
5v
R
t
D
vo
vi
E
vo
5v
t
例4：电路如下图，已知v=10sin(t)(V)，
E=5V，试画出vo的波形
vi
解：
t
vD
t
例5：VA=3V, VB=0V，求VF (二极管的导 通电压忽略)
根据理论推导，二极管的伏安特性曲线可用下式表示
V
I IS (e VT 1)
式中IS 为反向饱和电流，V 为二极管两端的电压降 ，VT =kT/q 称为温度的电压当量，k为玻耳兹曼常数 ，q 为电子电荷量，T 为热力学温度。对于室温（相 当T=300 K），则有VT=26 mV。
半导体的导电性
第四章半导体的导电性本章主要内容载流子在外加电场作用下的漂移运动半导体的迁移率、电导率和电阻率随温度和杂质浓度的变化规律迁移率的本质-----散射4.1 载流子的漂移运动迁移率1、欧姆定律对于金属，电流I = V(电压）/R（电阻）V-I关系是直线对于半导体，流过不同截面的电流强度不一定相同，“即电流分布不均匀，而欧姆定律不能说明材料内部各处电流的分布情况。
电流密度：通过垂直于电流方向的单位面积的电流J = ∆I/∆S单位：A/cm2或A/m2欧姆定律微分形式：上式把通过导体中某一点的电流密度和该处的电导率及电场强度直接联系了起来。
S故: 半导体导电= 电子导电J = Jn + Jp = (nqu平均自由程：载流子在连续两次散射间自由运动的平均路程平均自由时间：载流子通过平均自由程所需的平均时间τ电场：载流子加速---定向运动；散射：载流子运动方向改变---杂乱无章，各个方向；半导体的主要散射机构：离化杂质散射晶格散射中性杂质散射位错散射(P为散射几率)起因：常温下，浅施主带正电• 双曲线，电离杂质处于一个焦点 • 速度小，作用时间长，偏离角θ大，τ小 • 弹性散射，不改变入射电子能量，只改变运动方向 τ ∝ T3/2/NI 杂质浓度（2）、晶格散射 晶格原子在其平衡位置附近不断进行热振动，且各个 原子的振动不是孤立的。
分析表明：晶格中原子的振动都 是由若干不同的基本波动按波的叠加原理组合而成，这些 基本波动称为格波。
q代表格波波矢， q 的方向即波的传播方向晶格散射：载流子在运动过程中遭受振动的晶格原子的散射， 失去在电场中获得的能量，失去动量。
在能带具有单一极值的半导体中 起主要散射作用的是长波。
即波 长比原子间距大很多倍的格波。
电子热运动速度~105m/s 电子波波长约10-8m 根据动量守恒要求，声子波长 范围应在同一量级，即10-8m,而 晶体中原子间距为10-10m，因而 起主要散射作用的是长波。
半导体物理 第4章 半导体的导电性-赵老师-2012
v (k ) v (k ' )
38
物理与光电工程学院
4.2.2 载流子的散射
晶格振动 电离杂质 产生附加势场 的原因 载流子 空位 中性杂质 位错
39
物理与光电工程学院
4.2.2 载流子的散射
散射几率(Pi):描述散射的强弱，它表示单位时间内一 个载流子受到散射的次数。 1）电离杂质散射----杂质电离产生库仑场
四、三维晶格振动的一般结论
对于N个原胞组成的三维晶体，设每个原胞中有n个原 子，该晶体的晶格振动有以下三个一般结论： （1） 格波共有3n支，其中3支声频支，其余支 3(n-1)为光频支； （2） 每支格波有N个振动模；
（3） 共有3nN个振动模．
原胞内 原胞 含 数 原子 数
单原子链 双原子链 三维结构 1 2 n N N N
简谐近似下原子的运动方程 ：
设方程组的解是一振幅为A, 频率为的简谐振动:
un Ae
i ( qna t )
qna 表示第n个原子振动的初位相。若第n’和n 个原子的初位相满足：
qn' a qna l 2
代表n和n’的两个原子的振动完全同步。 显然q相当于波矢：
2 q
nqn
对于p型半导体（p>>n），电导率为：
nqp
对于本征半导体（n＝p＝ni），则电导率为：
i n i q n ＋ p
物理与光电工程学院
37
4.2.2 载流子的散射
载流子散射的根本原因：周期性势场被破坏。 晶格的周期性被破坏后，与周期性势场相比，存在一附 加势场，使能带中的电子发生不同k状态间的跃迁，即 遭到散射：
共有N个q值（振动模）： q 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i 1/ ni q( p n )
n , p
§4.1载流子的漂移运动
迁移率
表4-1：本征半导体在温度为300K时，电子的迁移 率μn和空穴的迁移率μp 半导体材料 Ge Si μn(cm2/v· s) 3800 1450 μp(cm2/v· s) 1800 500
GaAs
8000
14 n 10 n N D 1016 cm3 , p i 16 102 / cm3 0 / cm3 n 10 2
J ( qnn qp p ) qnn 1.6021019 1016 700010 112A / cm2
练习
课本习题4，17
Si
§4.1载流子的漂移运动
电子漂移电流和空穴漂移电流的总和
迁移率
J (qnn qp p )
N型半导体
qnn qp p
n 1 / qnn
n p n qnn p n p qp p
N型半导体
本征半导体
p 1/ qp p
p n ni i ni q( p n )
第四章半导体的导电性
§4.1 载流子的漂移运动
§4.2 载流子的散射
迁移率
§4.３ 迁移率与杂质浓度和温度的关系
§4.４ 电阻率与杂质浓度和温度的关系
§4.1载流子的漂移运动
本节主要内容： 一. 欧姆定律的微分表达式 二. 漂移速度和迁移率 三.半导体的电导率和迁移率
迁移率
§4.1载流子的漂移运动
I J qn v s
平均漂移速度的大小与电场强度成正比，其系数
v
qn
电子的迁移率，单位：cm2/V.s， 单位电场作用下载流子获得的平 均速度，反映了载 流子在电场 作用下输运能力。 电导率与迁移率间的关系
qn
§4.1载流子的漂移运动
ξ
电子漂移方向 空穴漂移方向 空穴电流方向
简并与并简并半导体载流子特性
以硅材料为例，掺入杂质磷，ΔED=0.044eV
石墨烯与半导体物理
2010年诺贝尔物理奖授予了俄罗斯裔科学家安德烈· 海姆和
康斯坦丁· 诺沃肖洛夫，以表彰他们在石墨烯方面的研究
Science 22 October 2004: Vol. 306. no. 5696, pp. 666 - 669
迁移率
Si Si
-
Si Si
电子电流方向
Si
P+
半导体中的导电作用应该是电 子导电和空穴导电的总和
导电的电子是在导带中，他们是脱离了 共价键可以在半导体中自由运动的电子； 导电的空穴是在价带中，空穴电流实际 上是代表了共价键上的电子在价键间运 动时所产生的电流
Si
Si
Si
Si Si
+
Si
Si Si
BSi Si
400
且迁移率随杂质浓度和温度的变化而变化
练习
T=300K时，砷化镓的掺杂浓度为NA=0， ND=1016cm-3，设杂质全部电离，电子的移迁率为 7000cm2/V.s, 空穴的迁移率为320cm2/V.s，若外 加电场强度ξ=10V/cm,求漂移电流密度
解： 室温下，砷化镓的ni=107cm-3<<ND，属强电离区
作业
课本习题5
§4.2 载流子的散射
一、载流子散射的概念:
二、半导体的主要散射机构
三、其它因素引起的散射
§4.2 载流子的散射
载流子在电场作用下做加速运动，漂移速度 是否会不
断加大，使
由
不断加大呢？
知：答案是否定的。为什么呢？ 电离杂质散射 晶格振动散射 中性杂质散射 位错散射 合金散射 等同的能谷间散射
因为载流子 在运动过程
中受到散射
§4.1载流子的漂移运动
迁移率
高纯Si,GaAs和Ge中载流子漂移速度与外加电场的关系
§4.2 载流子的散射
一、载流子散射的概念:
1. 散射：载流子与其它粒子发生弹性或非弹性碰撞，
碰撞后载流子的速度的大小和方向发生了改变。
2. 电子运动是布洛赫波，波在传播过程中周期性势场 受到破坏，由于受到附加势场作用遭到了散射，使 波的波矢
一. 欧姆定律的微分表达式
欧姆定律： I V R
l 电阻由材料特性决定： R s
迁移率
电阻率： 电导率：
单位： .cm 1/ , 单位：S/cm
§4.1载流子的漂移运动
一. 欧姆定律的微分表达式
迁移率
金属：在面积为S，长为L的导体两端，加电压V， 在导体内形成电场
V l
Q q n volum e I t t q n ( v t s ) qnv s t
漂移电流密度
I J qn v s
§4.1载流子的漂移运动
迁移率
v qn
二. 漂移速度和迁移率
欧姆定律微分表达式
漂移电流密度J ຫໍສະໝຸດ k) 于 v(态以k
发生了变化，E发生了变化，原来处 运动的电子，改变为 k' 态，以 v(k ' )
运动。
§4.2 载流子的散射
载流子的运动：定向运动和散射。
• 当有外电场时，一方面载流子沿电场方向定向运动，另一 方面，载流子仍不断地遭到散射，使载流子的运动方向不 断地改变。在外电场力和散射的双重作用下，载流子以一 定的平均速度沿力的方向漂移，形成了电流，而且在恒定 电场作用下，电流密度是恒定的。
无外加电场
有外加电场
§4.2 载流子的散射
2. 平均自由程和平均自由时间： 在连续两次散射间自由运动的平均路程叫做平均 自由程，平均时间称为平均自由时间。 3. 散射几率P： 单位时间一个电子受到散射的次数。用来描述散 射强弱
§4.2 载流子的散射
二、半导体的主要散射机构
1.电离杂质散射
施主电离杂质带正电，受主电离杂质带负电，它们 与载流子之间产生一个附加的库仑场，当载流子运 动到电离杂质附近时，由于库仑场的作用，载流子
载流子在电场ξ的作用下，定向运动形成电流I，为 描述I在导体中的分布情况，引入电流密度J，即: I V l J s Rs Rs 欧姆定律微分表达式
J
§4.1载流子的漂移运动
迁移率
二. 漂移速度和迁移率
漂移运动：电子在电场作用下做定 向运动称为漂移运动。 漂移速度：定向运动的速度平均 速度 漂移电流
n , p
§4.1载流子的漂移运动
迁移率
表4-1：本征半导体在温度为300K时，电子的迁移 率μn和空穴的迁移率μp 半导体材料 Ge Si μn(cm2/v· s) 3800 1450 μp(cm2/v· s) 1800 500
GaAs
8000
14 n 10 n N D 1016 cm3 , p i 16 102 / cm3 0 / cm3 n 10 2
J ( qnn qp p ) qnn 1.6021019 1016 700010 112A / cm2
练习
课本习题4，17
Si
§4.1载流子的漂移运动
电子漂移电流和空穴漂移电流的总和
迁移率
J (qnn qp p )
N型半导体
qnn qp p
n 1 / qnn
n p n qnn p n p qp p
N型半导体
本征半导体
p 1/ qp p
p n ni i ni q( p n )
第四章半导体的导电性
§4.1 载流子的漂移运动
§4.2 载流子的散射
迁移率
§4.３ 迁移率与杂质浓度和温度的关系
§4.４ 电阻率与杂质浓度和温度的关系
§4.1载流子的漂移运动
本节主要内容： 一. 欧姆定律的微分表达式 二. 漂移速度和迁移率 三.半导体的电导率和迁移率
迁移率
§4.1载流子的漂移运动
I J qn v s
平均漂移速度的大小与电场强度成正比，其系数
v
qn
电子的迁移率，单位：cm2/V.s， 单位电场作用下载流子获得的平 均速度，反映了载 流子在电场 作用下输运能力。 电导率与迁移率间的关系
qn
§4.1载流子的漂移运动
ξ
电子漂移方向 空穴漂移方向 空穴电流方向
简并与并简并半导体载流子特性
以硅材料为例，掺入杂质磷，ΔED=0.044eV
石墨烯与半导体物理
2010年诺贝尔物理奖授予了俄罗斯裔科学家安德烈· 海姆和
康斯坦丁· 诺沃肖洛夫，以表彰他们在石墨烯方面的研究
Science 22 October 2004: Vol. 306. no. 5696, pp. 666 - 669
迁移率
Si Si
-
Si Si
电子电流方向
Si
P+
半导体中的导电作用应该是电 子导电和空穴导电的总和
导电的电子是在导带中，他们是脱离了 共价键可以在半导体中自由运动的电子； 导电的空穴是在价带中，空穴电流实际 上是代表了共价键上的电子在价键间运 动时所产生的电流
Si
Si
Si
Si Si
+
Si
Si Si
BSi Si
400
且迁移率随杂质浓度和温度的变化而变化
练习
T=300K时，砷化镓的掺杂浓度为NA=0， ND=1016cm-3，设杂质全部电离，电子的移迁率为 7000cm2/V.s, 空穴的迁移率为320cm2/V.s，若外 加电场强度ξ=10V/cm,求漂移电流密度
解： 室温下，砷化镓的ni=107cm-3<<ND，属强电离区
作业
课本习题5
§4.2 载流子的散射
一、载流子散射的概念:
二、半导体的主要散射机构
三、其它因素引起的散射
§4.2 载流子的散射
载流子在电场作用下做加速运动，漂移速度 是否会不
断加大，使
由
不断加大呢？
知：答案是否定的。为什么呢？ 电离杂质散射 晶格振动散射 中性杂质散射 位错散射 合金散射 等同的能谷间散射
因为载流子 在运动过程
中受到散射
§4.1载流子的漂移运动
迁移率
高纯Si,GaAs和Ge中载流子漂移速度与外加电场的关系
§4.2 载流子的散射
一、载流子散射的概念:
1. 散射：载流子与其它粒子发生弹性或非弹性碰撞，
碰撞后载流子的速度的大小和方向发生了改变。
2. 电子运动是布洛赫波，波在传播过程中周期性势场 受到破坏，由于受到附加势场作用遭到了散射，使 波的波矢
一. 欧姆定律的微分表达式
欧姆定律： I V R
l 电阻由材料特性决定： R s
迁移率
电阻率： 电导率：
单位： .cm 1/ , 单位：S/cm
§4.1载流子的漂移运动
一. 欧姆定律的微分表达式
迁移率
金属：在面积为S，长为L的导体两端，加电压V， 在导体内形成电场
V l
Q q n volum e I t t q n ( v t s ) qnv s t
漂移电流密度
I J qn v s
§4.1载流子的漂移运动
迁移率
v qn
二. 漂移速度和迁移率
欧姆定律微分表达式
漂移电流密度J ຫໍສະໝຸດ k) 于 v(态以k
发生了变化，E发生了变化，原来处 运动的电子，改变为 k' 态，以 v(k ' )
运动。
§4.2 载流子的散射
载流子的运动：定向运动和散射。
• 当有外电场时，一方面载流子沿电场方向定向运动，另一 方面，载流子仍不断地遭到散射，使载流子的运动方向不 断地改变。在外电场力和散射的双重作用下，载流子以一 定的平均速度沿力的方向漂移，形成了电流，而且在恒定 电场作用下，电流密度是恒定的。
无外加电场
有外加电场
§4.2 载流子的散射
2. 平均自由程和平均自由时间： 在连续两次散射间自由运动的平均路程叫做平均 自由程，平均时间称为平均自由时间。 3. 散射几率P： 单位时间一个电子受到散射的次数。用来描述散 射强弱
§4.2 载流子的散射
二、半导体的主要散射机构
1.电离杂质散射
施主电离杂质带正电，受主电离杂质带负电，它们 与载流子之间产生一个附加的库仑场，当载流子运 动到电离杂质附近时，由于库仑场的作用，载流子
载流子在电场ξ的作用下，定向运动形成电流I，为 描述I在导体中的分布情况，引入电流密度J，即: I V l J s Rs Rs 欧姆定律微分表达式
J
§4.1载流子的漂移运动
迁移率
二. 漂移速度和迁移率
漂移运动：电子在电场作用下做定 向运动称为漂移运动。 漂移速度：定向运动的速度平均 速度 漂移电流