江苏省徐州市铜山区2017_2018学年七年级数学上学期期中抽测试题苏科 精品
苏科版数学七年级上册《期中测试卷》附答案

苏科版数学七年级上学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题(本大题共8小题,共24.0分)1.下列各式中正确的是( )A. ﹣|5|=|﹣5|B. |﹣5|=5C. |﹣5|=﹣5D. |﹣1.3|<02.在数轴上到原点距离等于3数是( )A. 3B. ﹣3C. 3或﹣3D. 不知道3.下列计算正确的是( )A. 4x﹣x=4B. 2x+3x=5xC 3xy﹣2xy=xy D. x+y=xy4. 实数a、b、c在数轴上的位置如图所示,则下列式子中一定成立的是( )A. a+b+c>0B. |a+b|<cC. |a﹣c|=|a|+cD. |b﹣c|>|c﹣a|5.若|x-2|+|y+6|=0,则x+y的值是()A. 4B. 4C.D. 86.某商场元旦促销,将某种书包每个x元,第一次降价打“八折”,第二次降价每个又减18元,经两次降价后售价为102元,则所列方程是()A. x﹣0.8x﹣18=102B. 0.08x﹣18=102C. 102﹣0.8x=18D. 0.8x﹣18=1027. 2010年5月27日,上海世博会参观人数达到37.7万人,37.7万用科学记数法表示应为A. 0.377×l06B. 3.77×l05C. 3.77×l04D. 377×1038.杨辉三角形,又称贾宪三角形帕斯卡三角形,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉所著的《详解九章算术》(1261年)一书中用如图的三角形解释二项和的乘方规律观察下列各式及其展开式:请你猜想(a+b)10展开式的第三项的系数是( )A. 36B. 45C. 55D. 66二、填空题(本大题共10小题,共30.0分)9.25-的倒数是_______.10.在下列各式:①π﹣3;②ab=ba;③x;④2m﹣1>0;⑤x yx y-+;⑥8(x2+y2)中,整式有_____.11.绝对值不大于4所有负整数的和是_____________.12.某校七年级学生乘车去郊外秋游,如果每辆汽车坐45人,那么有16人坐不上汽车;如果每辆汽车坐50人,那么有一辆汽车空出9个座位,有x辆汽车,则根据题意可列出方程为______.13.若规定[x]表示不超过x的最大整数,如[4.3]=4,[﹣2.6]=﹣3;则[5.9]+[4.9]=_____.14.已知x=1是方程3x﹣m=x+2n的解,则整式m+2n+2008的值等于_____15.下列说法:①﹣a是负数:②一个数的绝对值一定是正数:③一个有理数不是正数就是负数:④绝对值等于本身的数是非负数,其中正确的是_____.16.多项式3x|m|y2+(m+2)x2y-1是四次三项式,则m的值为______.17.已知|a|=1,|b|=2,如果a>b,那么a+b=_____.18.如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,则第2019次输出的结果为______.三、解答题(本大题共10小题,共96.0分)19.把下列各数填入表示它所在的数集的括号里 ﹣(﹣2.3),227,0,﹣42,30%,π,﹣|﹣2013|,﹣512,.0.3 (1)负整数集合[ …] (2)正有理数集合[ …] (3)分数集合[ …] 20.计算(1)0﹣(+3)+(﹣5)﹣(﹣7)﹣(﹣3)(2)48×(﹣23)﹣(﹣48)÷(﹣8) (3)﹣12×(12﹣34+112)(4)﹣12﹣(1﹣0.5)×13×[3﹣(﹣3)2]. 21.化简:(1)﹣3(2x ﹣3)+7x +8; (2)3(x 2﹣12y 2)﹣12(4x 2﹣3y 2) 22.若3x m +5y 2与x 3y n 的和是单项式,求m n ﹣mn 的值.23.若a 与b 互为相反数b 与c 互为倒数,并且m 的平方等于它本身,试求222a bm +++bc ﹣3m 的值.24.已知A=3b 2﹣2a 2+5ab,B=4ab ﹣2b 2﹣a 2. (1)化简:3A ﹣4B ;(2)当a=1,b=﹣1时,求3A ﹣4B 的值.25.如图两摞规格完全相同的课本整齐地叠放在讲台上请根据图中所给出的数据信息,回答下列问题:(1)每本课本的厚度为 cm .(2)若有一摞上述规格的课本x本整齐地叠放在讲台上请用含x的代数式表示出这摞课本的顶部距离地面的高度;(3)当x=42时,求课本的顶部距离地面的高度.26. 一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:时间7:008:009:0010:0011:0012:0013:0014:0015:00体温0C(与前升0.2降1.0降0.8降1.0降06升0.4降0.2降0.2降0一次比较)注:病人早晨进院时医生测得病人体温是40.2℃.问:(1)病人什么时候体温达到最高,最高体温是多少?(2)病人中午12点时体温多高?(3)病人几点后体温稳定正常?(正常体温是37℃)27.阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是.(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值;拓广探索:(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.28.对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.(1)计算2⊙(﹣3)的值;(2)当a,b在数轴上位置如图所示时,化简a⊙b;(3)已知(a⊙a)⊙a=8+a,求a的值.答案与解析一、选择题(本大题共8小题,共24.0分)1.下列各式中正确的是( )A. ﹣|5|=|﹣5|B. |﹣5|=5C. |﹣5|=﹣5D. |﹣1.3|<0 【答案】B【解析】【分析】正数的绝对值等于其本身,负数的绝对值等于其相反数,0的绝对值为0,据此依次判断即可. 【详解】A、∵﹣|5|=-5,|﹣5|=5,∴﹣|5|≠|﹣5|,∴选项A不符合题意;B、∵|﹣5|=5,∴选项B符合题意;B、∵|﹣5|=5,∴选项C不符合题意;D、∵|﹣1.3|=1.3>0,∴选项D不符合题意.故选:B.【点睛】本题主要考查了绝对值的代数意义,熟练掌握相关概念是解题关键.2.在数轴上到原点距离等于3的数是( )A. 3B. ﹣3C. 3或﹣3D. 不知道【答案】C【解析】分析】根据数轴上到原点距离等于3的数为绝对值是3的数即可求解.【详解】绝对值为3的数有3,-3.故答案为C.【点睛】本题考查数轴上距离的意义,解题的关键是知道数轴上的点到原点的距离为绝对值.3.下列计算正确的是( )A. 4x﹣x=4B. 2x+3x=5xC. 3xy﹣2xy=xyD. x+y=xy【答案】C【解析】【分析】合并同类项时,字母不变,系数相加(减),据此依次计算即可.【详解】A:4x2﹣x2=3x2,故A错误;B:2x2+3x2=5x2,故B错误;C: 3xy﹣2xy=xy,故C正确;D:x与y不是同类项,不能合并,故D错误;故选:C.【点睛】本题主要考查了合并同类项,熟练掌握相关法则是解题关键.4. 实数a、b、c在数轴上的位置如图所示,则下列式子中一定成立的是( )A. a+b+c>0B. |a+b|<cC. |a﹣c|=|a|+cD. |b﹣c|>|c﹣a|【答案】C【解析】试题分析:先根据数轴确定a.b,c的取值范围,再逐一对各选项判定,即可解答.解:由数轴可得:a<b<0<c,∴a+b+c<0,故A错误;|a+b|>c,故B错误;|a﹣c|=|a|+c,故C正确;|b﹣c|<|c﹣a|,故D错误;故选:C.考点:数轴.5.若|x-2|+|y+6|=0,则x+y的值是()A. 4B. 4C.D. 8【答案】B【解析】【分析】根据已知等式,利用非负数的性质求出x,y的值,即可确定出x+y的值.【详解】∵|x−2|+|y+6|=0,∴x−2=0,y+6=0,解得x=2,y=−6,则x+y=2−6=−4.故选:B.【点睛】此题考查绝对值,解题关键在于掌握绝对值的非负性.6.某商场元旦促销,将某种书包每个x元,第一次降价打“八折”,第二次降价每个又减18元,经两次降价后售价为102元,则所列方程是()A. x﹣0.8x﹣18=102B. 0.08x﹣18=102C. 102﹣0.8x=18D. 0.8x﹣18=102【答案】D【解析】【分析】根据等量关系:第一次降价后的价格−第二次降价的18元=最后的售价列出方程即可.【详解】设某种书包每个x元,可得:0.8x﹣18=102,故选:D.【点睛】本题主要考查了一元一次方程的实际运用,准确找出等量关系是解题关键.7. 2010年5月27日,上海世博会参观人数达到37.7万人,37.7万用科学记数法表示应为A. 0.377×l06B. 3.77×l05C. 3.77×l04D. 377×103【答案】B【解析】37.7万=377000=3.77×105.故答案为B.8.杨辉三角形,又称贾宪三角形帕斯卡三角形,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉所著的《详解九章算术》(1261年)一书中用如图的三角形解释二项和的乘方规律观察下列各式及其展开式:请你猜想(a+b)10展开式的第三项的系数是( )A. 36B. 45C. 55D. 66【答案】B【解析】【分析】根据题意可得出(a+b)10的展开式的系数是杨辉三角第11行的数,并且第三项的系数为第十一行的第三个数,从而进一步得出规律求解即可.【详解】依据规律可得到:(a+b)10的展开式的系数是杨辉三角第11行的数,第3行第三个数为1,第4行第三个数为3=1+2,第5行第三个数为6=1+2+3,…第11行第三个数为:1+2+3+…+9=()199452+⨯=.故选:B.【点睛】本题主要考查了整式中的规律计算,准确找出相应的规律是解题关键.二、填空题(本大题共10小题,共30.0分)9.25-的倒数是_______.【答案】-5 2【解析】【分析】根据倒数概念求解.【详解】25-的倒数是-52.故答案是:-52.【点睛】考查了求一个数的倒数,解题关键是求一个数的倒数是交换分子和分母的位置即可.10.在下列各式:①π﹣3;②ab=ba;③x;④2m﹣1>0;⑤x yx y-+;⑥8(x2+y2)中,整式有_____.【答案】①、③、⑥.【解析】【分析】单项式与多项式统称为整式,据此依次判断即可. 【详解】①π﹣3,是整式;②ab=ba,不是整式,是等式;③x,是整式;④2m﹣1>0,不是整式,是不等式;⑤x yx y-+,不是整式,是分式;⑥8(x2+y2),是整式∴整式有①、③、⑥.故答案为:①、③、⑥.【点睛】本题主要考查了整式的定义,熟练掌握相关概念是解题关键.11.绝对值不大于4的所有负整数的和是_____________.【答案】-10【解析】试题分析:根据绝对值的定义及有理数的大小比较法则即可得到结果. 绝对值不大于4的所有负整数是-4、-3、-2、-1,它们的和是-10.考点:本题考查的是绝对值,有理数的大小比较点评:本题是基础应用题,只需学生熟练掌握绝对值的定义,即可完成.12.某校七年级学生乘车去郊外秋游,如果每辆汽车坐45人,那么有16人坐不上汽车;如果每辆汽车坐50人,那么有一辆汽车空出9个座位,有x 辆汽车,则根据题意可列出方程为______. 【答案】4516509x x +=- 【解析】 【分析】设有x 辆汽车,根据去郊游的人数不变,即可得出关于x 的一元一次方程,此题得解. 【详解】解:设有x 辆汽车, 根据题意得:4516509x x +=-. 故答案为:4516509x x +=-.【点睛】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键. 13.若规定[x ]表示不超过x 的最大整数,如[4.3]=4,[﹣2.6]=﹣3;则[5.9]+[4.9]=_____. 【答案】9. 【解析】 【分析】根据给出的法则先分别确定[5.9]=5,[4.9]=4,再求出它们的和. 【详解】解:[5.9]=5,[4.9]=4, ∴[5.9]+[4.9]=5+4=9. 故答案为:9【点睛】本题主要考查的是比较有理数的大小,掌握[x]的意义是解题的关键. 14.已知x =1是方程3x ﹣m =x +2n 的解,则整式m +2n +2008的值等于_____ 【答案】2010. 【解析】 【分析】将x =1代入方程3x ﹣m =x +2n 后通过变形得出m +2n =2,然后整体代入求解即可. 【详解】把x =1代入3x ﹣m =x +2n 得:3﹣m =1+2n , ∴m +2n =2,∴m +2n +2008=2+2008=2010. 故答案为:2010.【点睛】本题主要考查了方程的解与代数式的求值,整体代入求值是解题关键.15.下列说法:①﹣a是负数:②一个数的绝对值一定是正数:③一个有理数不是正数就是负数:④绝对值等于本身的数是非负数,其中正确的是_____.【答案】④【解析】【分析】负数是比0小的数,带负号不一定是负数;绝对值具有非负性;有理数可分为正数、负数与0;绝对值等于本身的数为0和正数;据此依次判断即可.【详解】①﹣a不一定是负数.故①错误;②一个数的绝对值一定是非负数,故②错误;③一个有理数包括正数、负数、0,故③错误;④绝对值等于本身的数是非负数,故④正确;故答案为:④【点睛】本题主要考查了有理数的相关性质,熟练掌握各自概念是解题关键.16.多项式3x|m|y2+(m+2)x2y-1是四次三项式,则m的值为______.【答案】2【解析】【分析】根据四次三项式的定义可知,该多项式的最高次数为4,项数是3,所以可确定m的值.【详解】解:∵多项式3x|m|y2+(m+2)x2y-1是四次三项式,m+≠∴m+2=4,20∴m=2.故答案为:2.【点睛】本题考查了与多项式有关的概念,解题的关键理解四次三项式的概念,多项式中每个单项式叫做多项式的项,有几项叫几项式,这些单项式中的最高次数,就是这个多项式的次数.17.已知|a|=1,|b|=2,如果a>b,那么a+b=_____.【答案】–1或–3【解析】试题分析:根据绝对值的性质可得:a=,b=2,根据a b可得:a=,b=-2,则a+b=1-2=-1或a+b=-1-2=-3.18.如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,则第2019次输出的结果为______.【答案】4【解析】分析】根据设计的程序进行计算,找到循环的规律,根据规律推导计算.【详解】解:∵第1次输出的数为:100÷2=50,第2次输出的数为:50÷2=25,第3次输出的数为:25+7=32,第4次输出的数为:32÷2=16,第5次输出的数为:16÷2=8,第6次输出的数为:8÷2=4,第7次输出的数为:4÷2=2,第8次输出的数为:2÷2=1,第9次输出的数为:1+7=8,第10次输出的数为:8÷2=4,…,∴从第5次开始,输出的数分别为:8、4、2、1、8、…,每4个数一个循环;∵(2019-4)÷4=503…3,∴第2019次输出的结果为2.故答案为:2.【点睛】此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.三、解答题(本大题共10小题,共96.0分)19.把下列各数填入表示它所在的数集的括号里﹣(﹣2.3),227,0,﹣42,30%,π,﹣|﹣2013|,﹣512,.0.3(1)负整数集合[…](2)正有理数集合[…](3)分数集合[…]【答案】(1)﹣42,﹣|﹣2013|;(2)﹣(﹣2.3),227,30%,.0.3;(3)﹣(﹣2.3),227,30%,﹣512,.0.3.【解析】 【分析】(1)负整数是指小于0的整数,据此判断即可; (2)正有理数是指大于0的有理数,据此判断即可;(3)分数包括正分数与负分数,其中有限小数与无限循环小数也是分数,据此判断即可. 【详解】∵﹣(﹣2.3)=2.3,﹣|﹣2013|=﹣2013,∴负整数集合[﹣42,﹣|﹣2013|,…]; 正有理数集合[﹣(﹣2.3),227,30%,.0.3,…];分数集合[﹣(﹣2.3),227,30%,﹣512,.0.3,…].【点睛】本题主要考查了有理数的分类,熟练掌握各类数的定义是解题关键. 20.计算(1)0﹣(+3)+(﹣5)﹣(﹣7)﹣(﹣3)(2)48×(﹣23)﹣(﹣48)÷(﹣8) (3)﹣12×(12﹣34+112)(4)﹣12﹣(1﹣0.5)×13×[3﹣(﹣3)2]. 【答案】(1)2;(2)﹣38;(3)2;(4)0. 【解析】 【分析】(1)根据有理数加减混合运算法则及顺序计算即可; (2)根据有理数混合运算法则及顺序计算即可; (3)利用乘法分配律计算即可;(4)根据有理数混合运算法则及顺序计算即可. 【详解】(1)原式=0﹣3﹣5+7+3 =﹣8+10 =2;(2)原式=﹣32﹣6 =﹣38;(3)原式=﹣6+9﹣1 =﹣7+9=2;(4)原式=﹣1﹣12×13×(3﹣9)=﹣1﹣12×13×(﹣6)=﹣1+1=0.【点睛】本题主要考查了有理数的混合运算,熟练掌握运算法则是解题关键.21.化简:(1)﹣3(2x﹣3)+7x+8;(2)3(x2﹣12y2)﹣12(4x2﹣3y2)【答案】(1)x+17;(2)x2.【解析】【分析】(1)先去括号,然后合并同类项即可;(2)先去括号,然后合并同类项即可. 【详解】(1)﹣3(2x﹣3)+7x+8=﹣6x+9+7x+8=x+17;(2)3(x2﹣12y2)﹣12(4x2﹣3y2)=3x2﹣32y2﹣2x2+32y2=x2.【点睛】本题主要考查了整式的加减混合运算,熟练掌握运算法则是解题关键.22.若3x m+5y2与x3y n和是单项式,求m n﹣mn的值.【答案】m n﹣mn=8.【解析】【分析】根据3x m+5y2与x3y n的和是单项式可得二者是同类项,从而利用同类项性质求出m、n的值代入计算即可. 【详解】∵3x m+5y2与x3y n的和是单项式,∴3x m+5y2与x3y n是同类项.∴m+5=3,n=2.解得m=﹣2.∴当m=﹣2,n=2时,m n﹣mn=(﹣2)2﹣(﹣2)×2=4+4=8.【点睛】本题主要考查了代数式的求值,发现二者之间同类项的关系是解题关键.23.若a与b互为相反数b与c互为倒数,并且m的平方等于它本身,试求222a bm+++bc﹣3m的值.【答案】当m=1时,原式=﹣2;当m=0时,原式=1.【解析】【分析】根据题意可以先得知a+b=0,bc=1,m=1或0,从而进一步分类代入求值即可. 【详解】∵a与b互为相反数b与c互为倒数,并且m的平方等于它本身,∴a+b=0,bc=1,m=1或0;当m=1时,则222a bm+++bc﹣3m=0+1﹣3=﹣2;当m=0时,则222a bm+++bc﹣3m=0+1﹣0=1.【点睛】本题主要考查了代数式的求值,熟练掌握相反数、倒数的性质及乘方运算的特例是解题关键.24.已知A=3b2﹣2a2+5ab,B=4ab﹣2b2﹣a2.(1)化简:3A﹣4B;(2)当a=1,b=﹣1时,求3A﹣4B的值.【答案】(1)3A-4B=-2a2+17b2-ab;(2)16.【解析】【分析】(1)将A、B代入求解;(2)将a=1,b=-1代入(1)式求解即可.【详解】解:(1)∵A=3b2-2a2+5ab,B=4ab-2b2-a2,∴3A-4B=3(3b2-2a2+5ab)-4(4ab-2b2-a2)=9b2-6a2+15ab-16ab+8b2+4a2=-2a2+17b2-ab;(2)当a=1,b=-1时,原式=-2+17+1=16.【点睛】本题考查了整式的加减,解答本题的关键是掌握去括号法则和合并同类项法则.25.如图两摞规格完全相同的课本整齐地叠放在讲台上请根据图中所给出的数据信息,回答下列问题:(1)每本课本的厚度为cm.(2)若有一摞上述规格的课本x本整齐地叠放在讲台上请用含x的代数式表示出这摞课本的顶部距离地面的高度;(3)当x=42时,求课本的顶部距离地面的高度.【答案】(1)0.5;(2)高出地面的距离为(85+0.5x)cm;(3)余下的课本的顶部距离地面的高度106cm.【解析】【分析】(1)根据图中所画可以得出3本课本的高度为(88-86.5)cm,从而进一步求出每本高度即可;(2)首先求出课桌的高度,然后加上x本书的高度0.5xcm即可;(3)将x=42代入(2)中的代数式计算即可.【详解】(1)书的厚度为:(88﹣86.5)÷(6﹣3)=0.5cm;故答案为:0.5;(2)∵x本书的高度为0.5xcm,课桌的高度为85cm,∴高出地面的距离为(85+0.5x)cm;(3)当x=42时,85+0.5x=106.答:余下的课本的顶部距离地面的高度106cm.【点睛】本题主要考查了代数式的实际运用,准确找出文中各数之间的关系是解题关键.26.一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:注:病人早晨进院时医生测得病人体温是40.2℃. 问:(1)病人什么时候体温达到最高,最高体温是多少? (2)病人中午12点时体温多高?(3)病人几点后体温稳定正常?(正常体温是37℃)【答案】解:(1)病人7:00时体温达到最高,最高体温是40.40C(2)病人中午12点时体温达到3740C(3)病人14点后体温稳定正常(正常体温是37℃) 【解析】 【分析】此题只要在病人早晨进院时医生测得病人体温40.2℃的基础上根据表格进行加减即可求出. 【详解】(1)早上7:00,最高达40.4℃;(2)病人中午12点时体温为:40.2+0.2−1−0.8−1−0.6+0.4=37.4℃; (3)14:00以后27.阅读材料:我们知道,4x ﹣2x +x =(4﹣2+1)x =3x ,类似地,我们把(a +b )看成一个整体,则4(a +b )﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是.(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值;拓广探索:(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.【答案】(1)﹣(a﹣b)2;(2)-9;(3)8.【解析】【分析】(1)利用整体思想,把(a−b)2看成一个整体,合并3(a−b)2−6(a−b)2+2(a−b)2即可得到结果;(2)原式可化为3(x2−2y)−21,把x2−2y=4整体代入即可;(3)依据a−2b=3,2b−c=−5,c−d=10,即可得到a−c=−2,2b−d=5,整体代入进行计算即可.【详解】(1)∵3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2=(3﹣6+2)(a﹣b)2=﹣(a﹣b)2;故答案为:﹣(a﹣b)2;(2)∵x2﹣2y=4,∴原式=3(x2﹣2y)﹣21=12﹣21=﹣9;(3)∵a﹣2b=3,2b﹣c=﹣5,c﹣d=10,∴a﹣c=﹣2,2b﹣d=5,∴原式=﹣2+5﹣(﹣5)=8.【点睛】本题考查整式的加减,解决问题的关键是读懂题意,运用整体思想解题.28.对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.(1)计算2⊙(﹣3)的值;(2)当a,b在数轴上的位置如图所示时,化简a⊙b;(3)已知(a⊙a)⊙a=8+a,求a的值.【答案】(1)2⊙(﹣3)=6;(2)a⊙b=﹣2b;(3)当a≥0时, a=83;当a<0时, a=﹣85.【解析】【分析】(1)根据文中的新运算法则将2⊙(﹣3)转化为我们熟悉的计算方式进行计算即可;(2)根据文中的新运算法则将a⊙b转化为|a+b|+|a﹣b|,然后先判断出a+b与a﹣b的正负性,之后利用绝对值代数意义化简即可;(3)先根据文中的新运算法则将(a⊙a)⊙a转化为我们熟悉的计算方式,此时注意对a进行分a≥0、a<0两种情况讨论,然后得出新的方程求解即可.【详解】(1)由题意可得:2⊙(﹣3)=|2﹣3|+|2+3|=6;(2)由数轴可知,a+b<0,a﹣b>0,∴a⊙b=|a+b|+|a﹣b|=﹣a﹣b+a﹣b=﹣2b;(3)当a≥0时,(a⊙a)⊙a=2a⊙a=4a=8+a,∴a=83;当a<0时,(a⊙a)⊙a=(﹣2a)⊙a=﹣4a=8+a,∴a=85 -.综上所述,a的值为83或85-.【点睛】本题主要考查了绝对值的化简与定义新运算的综合运用,根据题意找出正确的新运算的法则是解题关键.。
苏教版2017-2018七年级初一上册期中数学试卷(精品)

一、选择题1.下列说法中,正确的是()A.0是最小的整数B.最大的负整数是﹣1C.任何有理数的绝对值都是正数D.一个有理数的平方总是正数2.某地一天的最高气温是12℃,最低气温是2℃,则该地这天的温差是()A.﹣10℃B.10℃ C.14℃ D.﹣14℃3.a的2倍与b的的差的平方,用代数式表示应为()A.2a2﹣b2 B.2a2﹣ b C.(2a﹣b)2D.2a﹣(b)24.如图是一个简单的数值运算程序,当输入的x的值为﹣1时,则输出的值为()A.1 B.﹣5 C.﹣1 D.55.马小虎做了6道题:①(﹣1)2013=﹣2013;②0﹣(﹣1)=1;③﹣+=﹣;④÷(﹣)=﹣1;⑤2×(﹣3)2=36;⑥﹣3÷×2=﹣3.那么,他做对了()题.A.1道B.2道C.3道D.4道6.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第7个图中共有点的个数是()A.46 B.85 C.72 D.667.下列各数:﹣5,,4.11212121212…,0,,3.14,其中无理数有()A.1个B.2个C.3个D.4个8.如图,在数轴上表示到原点的距离为3个单位的点有()A.D点 B.A点 C.A点和D点D.B点和C点9.下面各组数中,相等的一组是()A.﹣22与(﹣2)2B.与()3C.﹣|﹣2|与﹣(﹣2)D.(﹣3)3与﹣3310.下列说法中正确的是()A.如果两个数的绝对值相等,那么这两个数相等B.有理数分为正数和负数C.互为相反数的两个数的绝对值相等D.最小的整数是011.下列代数式:a,﹣ab,m+n,x2+y2,﹣1,ab2c,其中单项式共有()A.6个B.5个C.4个D.3个12.下面的计算正确的是()A.6a﹣5a=1 B.a+2a2=3a3 C.﹣(a﹣b)=﹣a+b D.2(a+b)=2a+b13.图中表示阴影部分面积的代数式是()A.ad+bc B.c(b﹣d)+d(a﹣c)C.ad+c(b﹣d)D.ab﹣cd二、填空题14.单项式﹣3xy3的系数是,次数是.15.江苏省的面积约为102 600km2,这个数据用科学记数法可表示为km2.16.若2x3y n+1与﹣5x m﹣2y2是同类项,则m+n=.17.如图是一个数值转换机的示意图,若输入x的值为3,y的值为﹣2,则输出结果为.18.若a﹣2b=3,则9﹣2a+4b的值为.19.若x2=9,则x=.20.下列一组是按规律排列的数:1,2,4,8,16,…,第2016个数是.21.定义一种关于“⊙”的新运算,观察下列式子:1⊙3=1×4+3=7;3⊙(﹣1)=3×4+(﹣1)=11;5⊙4=5×4+4=24;4⊙(﹣3)=4×4+(﹣3)=13.请你想一想:5⊙(﹣6)=.22.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有个三角形(用含n的代数式表示)23.七年级有x名男生,y名女生,则七年级共有名学生.24.若﹣3a5b3y﹣4与4a4x+1b2是同类项,则x=,y=.25.已知代数式2x﹣y的值是5,则代数式4x﹣2y﹣13的值是.26.定义新运算“*”为:a*b=,则当x=3时,计算2*x﹣4*x的结果为.27.有一个六位数,它乘以3后得到六位数,这个六位数是.三、解答题28.计算:(1)﹣3+5.3+7﹣5.3 (2)(﹣3+﹣)÷(﹣)(3)2﹣(﹣18)+(﹣7)﹣15 (4)(﹣48)÷8﹣(﹣25)×(﹣6)(5)﹣14﹣|2﹣5|+6×(﹣)(6)﹣36×(﹣﹣)÷(﹣2)29.化简:(1)x2y﹣3x2y﹣6xy+5xy+2x2y (2)(2x﹣7y)﹣(4x﹣10y)(3)5a2+3ab+2(a﹣ab)﹣(5a2+ab﹣b2)30.化简,求值.已知:(a+2)2+|b﹣3|=0,求(ab2﹣3)+(7a2b﹣2)+2(ab2+1)﹣2a2b的值.31.化简求值:5ab﹣7a2b2﹣8ab+5a2b2﹣ab,其中a=﹣2,b=﹣.四、解答题(共26分)31.如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π)(1)图中阴影部分的周长为cm.(2)图中阴影部分的面积为cm2.(3)当a=4时,求出阴影部分的面积.32.某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,x(x ≥20)个羽毛球,供社区居民免费借用.该社区附近A、B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价为3元,目前两家超市同时在做促销活动:A超市:所有商品均打九折(按标价的90%)销售;B超市:买一副羽毛球拍送2个羽毛球.(1)在A超市购买羽毛球拍和羽毛球的费用为,在B超市购买羽毛球拍和羽毛球的费用为.(用含x的代数式表示)(2)该活动中心决定只在一家超市购买10副球拍和100个羽毛球,你认为在哪家超市购买划算?为什么?33.记M(1)=﹣2,M(2)=(﹣2)×(﹣2),M(3)=(﹣2)×(﹣2)×(﹣2),…,M(n)=(1)填空:M(5)=,M(50)是一个数(填“正”或“负”)(2)计算:①2M(6)+M(7);②4M(7)+2M(8);(3)直接写出2016M(n)+1008M(n+1)的值为.34.根据给出的数轴及已知条件,解答下面的问题:(1)已知点A,B,C表示的数分别为1,﹣,﹣3观察数轴,与点A的距离为3的点表示的数是,B,C两点之间的距离为;(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N 点也恰好重合,则M,N两点表示的数分别是:M,N;(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P,Q(用含m,n的式子表示这两个数).35.有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b﹣c0,a+b0,c﹣a0.(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.36.已知|x﹣5|+(2y+6)2=0,A=﹣x2﹣2xy+y2,B=﹣x2﹣6xy+3y2.(1)求y﹣x的值.(2)求3A﹣[2A﹣B﹣4(A﹣B)]的值.37.实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;(2)十字框框住的5个数之和能等于2015吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.38.如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.(1)若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为cm.(2)由题(1)的启发,请你能借助“数轴”这个工具帮助小红解决下列问题:问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?。
苏教版2017-2018学年上学期七年级数学期中试卷及答案

(2)将长方形 OABC 沿数轴水平移动,移动后的长方形记为 O′A′B′C′,移动后的长方形 O′A′B′C′与原长方形 OABC 重叠部分(如图 2 中阴影部分)的面积记为 S. ①当 S 恰好等于原长方形 OABC 面积的一半时,数轴上点 A′表示的数为 ②设点 A 的移动距离 AA′=x. ⅰ.当 S=4 时,x= ; OO′,当点 D,E 所表示的 .
18.如右图,数轴上一动点 A 向左移动 2 个单位长度到达点 B,再向右移 动 5 个单位长度到达点 C,若点 C 表示的数为 1,则点 A 表示的数为 ▲ . 19.已知|m|=4,|n|=6,且 m+n=|m+n|,则 m﹣n 的值是 ▲ . 20.按下面的程序计算,若开始输入的值 x 为正数,最后输出的结果为 15,则满足条件的 x 的值分别 有 ▲ .
称为 a 的“哈利数”。如:3 的“哈利数”是
-2 的“哈利数”是
, 已知
,
是
的“哈利数”,
是
1
苏教版 2017-2018 学年上学期七年级数学期中试卷及答案
的“哈利数”, A、3
是
的“哈利数”,…,依次类推,则 C、 D、
=( ▲ )。
B、-2
▲
二、填空题(共 10 小题,每小题 2 分,共 20 分) 11.“辽宁号” 航空母舰的满载排水量为 67500 吨,将数 67500 用科学记数法表示为 . 12.“比数 x 的 3 倍小 5 的数”用代数式表示为 ▲ . 13.已知方程 14.比较大小: ▲ . 是关于 的一元一次方程,则 = ▲ .
4
苏教版 2017-2018 学年上学期七年级数学期中试卷及答案
(1)若(1,b)是“相伴数对”,求 b 的值; (2)写出一个“相伴数对”(a,b),其中 a≠0,且 a≠1; (3)若(m,n)是“相伴数对”,求代数式 m﹣ ﹣[4m﹣2(3n﹣1)]的值.
2017-2018学年七年级数学上学期期中试题苏科版

江苏省连云港市灌南县2017-2018学年七年级数学上学期期中试题一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一个是正确的,请把你认为正确的选项代号填写在括号里)1.-2的相反数是()A .2B .-2C .D .2.下列各式中,去括号正确的是()A .-(2a +b)=-2a +bB .3(a -b)=3a -bC .3x -(2y -z)=3x -2y+zD .x -(y +z)=x -y+z 3.在数-3,-2,0,3中,大小在-1和2之间的数是( ) A.-3 B. -2 C. 0 D. 3 4.下列各组数中,相等的是( ) A .与B .与C .与D .与5.下列各数:-,0,-80,,,+|-2|,-(+62),其中属于负整数的共有( )A .1个B .2个C .3个D .4个 6.下列说法正确的是() A .是二次三项式B .是单项式C .的次数是8 D .的系数是7.下列计算正确的是( )A .B .C .D .简的结果为()8.实数、在数轴上的位置如图所示,则化 A. B.C.D.二、填空题(本大题有8小题,每小题3分,共24分.将结果直接填写在横线上) 9.汽车向东行驶5千米记作+5千米,那么汽车向西行驶5千米记作千米. 10.在数轴上,表示﹣3的点与原点的距离是. 11.一个数的倒数是,这个数是.12.火星与地球的距离约为千米,这个数据用科学记数法表示为千米. 13.若与是同类项,则.14.已知多项式的值为1,则多项式的值为.15.现规定一种新运算:a △b=ab -2a -2b +1,如:3△2=3×2-2×3-2×2+1=-3,则4△5的值为.16.试写出一个含a 的代数式,使a 不论取什么值,这个代数式的值总是正数.三、解答题(本大题有10小题,共102分.解答时应写出必要的演算步骤或文字说明) 17.(每小题6分,计24分)计算: (1)(2)(3)(4)18.(每小题6分,共12分)化简:(1)(2)19.(本题满分8分)先化简,后求值:,其中,.20.(本题满分8分)已知互为相反数,是绝对值最小的有理数,求的值.21.(本题满分8分)某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):(1)生产量最多的一天比生产量最少的一天多生产多少辆?(2)本周总的生产量是多少辆?22. (本题满分6分)意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为边长值构造正方形:再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如下表所示:11231511211321④③②①…仔细观察图形,上表中的,.若按此规律继续作长方形,则序号为⑧的长方形周长是.23. (本题满分8分)一个点A 从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位;…….(1)第一次移动后这个点在数轴上表示的数是; (2)第二次移动后这个点在数轴上表示的数是;(3)第五次移动后这个点在数轴上表示的数是;(4)第n 次移动后这个点在数轴上表示的数是.24. (本题满分8分)如图:(1)用代数式表示阴影部分的面积; (2)当a=10,b=4,π的取值为3时,求阴影部分的面积.25. (本题满分8分)为了节约用水,某市决定调整居民用水收费方法,规定:如果每户每月用水不超过20吨,每吨水收费3元,如果每户每月用水超过20吨,则超过部分每吨水收费3.8元;小红看到这种收费方法后,想算算她家每月的水费,但是她不清楚家里每月的用水是否超过20吨. (1)如果小红家每月用水15吨,水费是多少?如果每月用水35吨,水费是多少?(2)如果字母x 表示小红家每月用水的吨数,那么小红家每月的水费该如何用x 的代数式表示.阅卷人 得分26.(本题满分12分)图1是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)图2中的阴影部分的正方形的边长等于.(2)请用两种不同的方法求图2中阴影部分的面积.方法1:;方法2:.(3)观察图2写出,,三个代数式之间的等量关系:.(4)根据(3)题中的等量关系,解决如下问题:若,,求的值.2017-2018学年度第一学期期中学业水平检测 七年级数学试题参考答案一、选择题(本大题共8小题,每小题3分,共24分)二、填空题(本大题共8小题,每小题3分,共24分)9.-5 10. 3 11.12.13.9 14. 7 15. 3 16.(答案不唯一)三、解答题(本大题共10题,共102分.解答应写出文字说明、证明过程或演算步骤) 17.计算:(每小题6分,计24分)(1)41;(2)4;(3)-10;(4)18.化简:(每小题6分,计12分)图1 图2。
2017-2018学年江苏省徐州市市区联考七年级(上)期中数学试卷

2017-2018学年江苏省徐州市市区联考七年级(上)期中数学试卷一、选择题(本大题共8小题,每小题3分,共24分)1.(3分)在﹣2,﹣,0,2四个数中,最大的数是()A.﹣2B.﹣C.0D.22.(3分)如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是()A.B.C.D.3.(3分)某一天的最高气温为2℃,最低气温为﹣8℃,那么这天的温差是()A.﹣10℃B.﹣6℃C.6℃D.10℃4.(3分)我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4 400 000 000人,这个数用科学记数法表示为()A.44×108B.4.4×108C.4.4×109D.4.4×1010 5.(3分)两个有理数的和是负数,那么这两个数一定()A.都是负数B.有一个为零C.绝对值不相等D.至少有一个数是负数6.(3分)绝对值不大于3的所有整数的和是()A.﹣1B.0C.1D.67.(3分)如图所示,已知数轴上两数a和b,下列关系正确的是()A.a<﹣b<b<﹣a B.﹣a<﹣b<a<bC.﹣b<﹣a<a<b D.a<b<﹣b<﹣a8.(3分)设面积为3的正方形的边长为a,下列关于a的四种说法:①a是有理数;②a是无理数;③a可以用数轴上的一个点来表示;④1<a<2,其中说法正确的是()A.①③B.②④C.①③④D.②③④二、填空题(本大题共8小题,每小题3分,共24分)9.(3分)若小明家去年收入8万元,记作+8万元,则去年支出4万元,记作万元.10.(3分)已知长方形周长为20cm,设长为xcm,则宽为cm.11.(3分)下列各数中:,﹣|﹣2|,0,π,﹣(﹣),0.,正有理数个数有个.12.(3分)设a﹣3b=5,则2(a﹣3b)2+3b﹣a﹣15的值是.13.(3分)粗心的小马在画数轴时只标了单位长度(一格表示单位长度为1)和正方向,而忘了标上原点(如图),若点B和点C点表示的两个数的绝对值相等,则点A表示的数是.14.(3分)按图中程序运算,如果输入﹣1,则输出的结果是.15.(3分)若|a|=3,b2=25,且a<b,则2a﹣b的值为.16.(3分)下列说法:①﹣的系数是﹣2;②mn2的次数是3次;③3xy2﹣4x3y+1是七次三项式;④是多项式,其中说法正确的是(写出所有正确结论的字号)三、解答题(本大题共9小题,共72分)17.(10分)计算:(1)7﹣(+2)﹣(﹣4)+(﹣5)(2)(﹣2)÷(﹣10)×(﹣3)18.(10分)计算:(1)(﹣36)×(﹣+﹣)(2)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].19.(10分)计算:(1)a2﹣3ab+5﹣a2﹣3ab﹣7 (2)5(x+y)﹣4(3x﹣2y)﹣3(2x﹣3y)20.(6分)先化简,再求值:3a2b﹣[2ab2﹣2(ab﹣a2b)+ab]+3ab2,其中a=5,b=﹣2.21.(6分)如图,正方形ABCD和正方形ECGF的边长分别为a和6.(1)写出表示阴影部分面积的代数式(结果要求化简);(2)求a=4时,阴影部分的面积.22.(7分)一辆货车从超市(O点)出发,向东走2km到达小李家(A点),继续向东走4km到达小张家(B点),然后又回头向西走10km到达小陈家(C 点),最后回到超市.(1)以超市为原点,向东方向为为正方向,以1cm表示1km,画出数轴,并在数轴上表示A,B,C,D的位置.(2)小陈家(C点)距小李家(A点)有多远?(3)若货车每千米耗油0.5升,这趟路货车共耗油多少升?23.(7分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有n张桌子时,两种摆放方式各能坐多少人?(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌为什么?24.(10分)甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为x盒时,在甲店购买需付款元;在乙店购买需付款元.(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?25.(6分)高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数,例如:[2.9]=2,[﹣1.5]=﹣2.试探索:(1)[﹣5]=,[π]=;(2)[2.7]+[2.3]=;(3)[]+[]+[]+[]+[]+[]=.2017-2018学年江苏省徐州市市区联考七年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题3分,共24分)1.(3分)在﹣2,﹣,0,2四个数中,最大的数是()A.﹣2B.﹣C.0D.2【分析】根据有理数的大小比较法得出﹣2<﹣<0<2,即可得出答案.【解答】解:∵﹣2<﹣<0<2,∴最大的数是2,故选:D.【点评】有理数的大小比较法则是:正数都大于0,负数都小于0,正数大于一切负数,两个负数比较大小,其绝对值大的反而小.2.(3分)如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是()A.B.C.D.【分析】求出每个数的绝对值,根据绝对值的大小找出绝对值最小的数即可.【解答】解:∵|﹣0.6|<|+0.7|<|+2.5|<|﹣3.5|,∴﹣0.6最接近标准,故选:C.【点评】本题考查了绝对值以及正数和负数的应用,掌握正数和负数的概念和绝对值的性质是解题的关键,主要考查学生的理解能力,题目具有一定的代表性,难度也不大.3.(3分)某一天的最高气温为2℃,最低气温为﹣8℃,那么这天的温差是()A.﹣10℃B.﹣6℃C.6℃D.10℃【分析】用最高温度减去最低温度,再根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】解:2﹣(﹣8)=2+8=10℃.故选:D.【点评】本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键.4.(3分)我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4 400 000 000人,这个数用科学记数法表示为()A.44×108B.4.4×108C.4.4×109D.4.4×1010【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥1时,n是非负数;当原数的绝对值<1时,n是负数.【解答】解:将4400000000用科学记数法表示为:4.4×109.故选:C.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n 的值.5.(3分)两个有理数的和是负数,那么这两个数一定()A.都是负数B.有一个为零C.绝对值不相等D.至少有一个数是负数【分析】根据有理数的加法法则,由和是负数,可得加数的关系,可得答案.【解答】解:负数加负数等于负数,负数加0等于负数,负数加正数,负数的绝对值大,和是负数.故选:D.【点评】本题考查了有理数的加法,一正数一负数时,负数的绝对值大,两负数,一负数与零,和都是负数.6.(3分)绝对值不大于3的所有整数的和是()A.﹣1B.0C.1D.6【分析】先求出绝对值不大于3的所有整数,再相加即可.【解答】解:绝对值不大于3的所有整数为0,±1,±2,±3,和为0+1+(﹣1)+2+(﹣2)+3+(﹣3)=0,故选:B.【点评】本题考查了有理数的大小比较和绝对值,能求出符合的所有整数是解此题的关键.7.(3分)如图所示,已知数轴上两数a和b,下列关系正确的是()A.a<﹣b<b<﹣a B.﹣a<﹣b<a<b C.﹣b<﹣a<a <b D.a<b<﹣b<﹣a【分析】根据a、b两点在数轴上的位置判断出其符号与绝对值的大小,进而可得出结论.【解答】解:∵由图可知a<0<b,﹣a>b,∴a<﹣b<b<﹣a.故选:A.【点评】本题考查的是有理数的大小比较,熟知数轴上右边的数总比左边的大是解答此题的关键.8.(3分)设面积为3的正方形的边长为a,下列关于a的四种说法:①a是有理数;②a是无理数;③a可以用数轴上的一个点来表示;④1<a<2,其中说法正确的是()A.①③B.②④C.①③④D.②③④【分析】直接利用得出正方形的边长,再利用实数的性质分析得出答案.【解答】解:∵面积为3的正方形的边长为a,∴a=,故①a是有理数,错误;②a是无理数,正确;③a可以用数轴上的一个点来表示,正确;④1<a<2,正确,则说法正确的是:②③④.故选:D.【点评】此题主要考查了实数的性质,正确掌握实数有关性质是解题关键.二、填空题(本大题共8小题,每小题3分,共24分)9.(3分)若小明家去年收入8万元,记作+8万元,则去年支出4万元,记作﹣4万元.【分析】“正”和“负”是表示互为相反意义的量,向北走记作正数,那么向北的反方向,向南走应记为负数.【解答】解:小明家去年收入8万元,记作+8万元,则去年支出4万元,记作﹣4万元,故答案为:﹣4.【点评】本题考查了正数和负数的定义.解本题的根据是掌握正数和负数是互为相反意义的量.10.(3分)已知长方形周长为20cm,设长为xcm,则宽为10﹣x cm.【分析】依据公式矩形的周长=2(长+宽),解答即可.【解答】解:矩形的宽=10﹣x,故答案为:10﹣x.【点评】此题考查列代数式问题,本题应注意矩形的周长=2(长+宽)这个知识点的变换使用.11.(3分)下列各数中:,﹣|﹣2|,0,π,﹣(﹣),0.,正有理数个数有3个.【分析】根据大于零的有理数是正有理数,可得答案.【解答】解:,﹣(﹣),0.是正有理,故答案为:3.【点评】本题考查了有理数,利用有理数的定义是解题关键,注意0既不是正数也不是负数.12.(3分)设a﹣3b=5,则2(a﹣3b)2+3b﹣a﹣15的值是30.【分析】将a﹣3b=5代入代数式2(a﹣3b)2+3b﹣a﹣15即可求得它的值.【解答】解:∵3b﹣a=﹣5,∴2(a﹣3b)2+3b﹣a﹣15=2×52﹣5﹣15=30.【点评】此题考查的是代数式的转化,通过观察可知已知与所求的式子的关系,然后将变形的式子代入即可求出答案.13.(3分)粗心的小马在画数轴时只标了单位长度(一格表示单位长度为1)和正方向,而忘了标上原点(如图),若点B和点C点表示的两个数的绝对值相等,则点A表示的数是﹣3.【分析】如果点C,B表示的数的绝对值相等,那么CB的中点即为坐标原点,即可得出A表示的数.【解答】解:如图,CB的中点即数轴的原点O,则B点表示的数为﹣2,可以得到点A表示的数是﹣3.故答案为:﹣3.【点评】此题考查了数轴有关内容,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.确定数轴的原点是解决本题的关键.14.(3分)按图中程序运算,如果输入﹣1,则输出的结果是3.【分析】把x=﹣1代入程序中计算,判断结果大于2,输出即可.【解答】解:把x=﹣1代入得:﹣1+4﹣(﹣3)﹣5=﹣1+4+3﹣5=1<2,把x=1代入得:1+4﹣(﹣3)﹣5=1+4+3﹣5=3>2,则输出的结果是3,故答案为:3【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.15.(3分)若|a|=3,b2=25,且a<b,则2a﹣b的值为﹣1或﹣11.【分析】根据绝对值的性质与有理数的乘方求出a、b,再根据a<b确定出a、b 的对应值,然后代入代数式进行计算即可得解.【解答】解:∵|a|=3,b2=25,∴a=3或﹣3,b=5或﹣5,∵a<b,∴a=3时,b=5,此时2a﹣b=2×3﹣5=﹣1,a=﹣3时,b=5,此时2a﹣b=2×(﹣3)﹣5=﹣6﹣5=﹣11,故答案为:﹣1或﹣11.【点评】本题考查了代数式求值,绝对值的性质,有理数的乘方,是基础题,准确确定出a、b的对应关系是解题的关键.16.(3分)下列说法:①﹣的系数是﹣2;②mn2的次数是3次;③3xy2﹣4x3y+1是七次三项式;④是多项式,其中说法正确的是②④(写出所有正确结论的字号)【分析】根据单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数;多项式中次数最高的项的次数叫做多项式的次数;多项式的组成元素的单项式,即多项式的每一项都是一个单项式,单项式的个数就是多项式的项数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式进行分析即可.【解答】解:①﹣的系数是﹣2,说法错误;②mn2的次数是3次,说法正确;③3xy2﹣4x3y+1是七次三项式,说法错误;④是多项式,说法正确;故答案为:②④.【点评】此题主要考查了单项式和多项式,关键是掌握单项式的相关定义,掌握多项式次数的计算方法.三、解答题(本大题共9小题,共72分)17.(10分)计算:(1)7﹣(+2)﹣(﹣4)+(﹣5)(2)(﹣2)÷(﹣10)×(﹣3)【分析】(1)根据有理数的加减混合运算法则计算;(2)根据有理数的乘除混合运算法则计算.【解答】解:(1)7﹣(+2)﹣(﹣4)+(﹣5)=7+4﹣2﹣5=11﹣7=4;(2)(﹣2)÷(﹣10)×(﹣3)=﹣2××=﹣.【点评】本题考查的是有理数的加减运算、乘除运算,掌握它们的运算法则是解题的关键.18.(10分)计算:(1)(﹣36)×(﹣+﹣)(2)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].【分析】(1)利用乘法分配律计算可得;(2)根据有理数的混合运算顺序和运算法则计算可得.【解答】解:(1)原式=16﹣30+21=7;(2)原式=﹣1﹣××(﹣7)=﹣1+=【点评】本题主要考查有理数的混合运算,熟练掌握有理数的混合运算的顺序和法则是解题的关键.19.(10分)计算:(1)a2﹣3ab+5﹣a2﹣3ab﹣7(2)5(x+y)﹣4(3x﹣2y)﹣3(2x﹣3y)【分析】(1)合并同类项可得;(2)先去括号,再合并同类项即可得.【解答】解:(1)原式=﹣6ab﹣2;(2)原式=5x+5y﹣12x+8y﹣6x+9y=﹣13x+22y【点评】本题主要考查整式的加减,解题的关键是熟练掌握去括号法则和合并同类项的能力是解题的关键.20.(6分)先化简,再求值:3a2b﹣[2ab2﹣2(ab﹣a2b)+ab]+3ab2,其中a=5,b=﹣2.【分析】原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=3a2b﹣2ab2+2ab﹣3a2b﹣ab+3ab2=ab+ab2,当a=5,b=﹣2时,原式=﹣10+20=10.【点评】此题考查了整式的加减﹣化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.21.(6分)如图,正方形ABCD和正方形ECGF的边长分别为a和6.(1)写出表示阴影部分面积的代数式(结果要求化简);(2)求a=4时,阴影部分的面积.【分析】(1)根据题意可以用代数式表示出阴影部分的面积;(2)将a=4代入(1)中的代数式即可解答本题.【解答】解:(1)由图可得,阴影部分的面积是:=,即阴影部分的面积是;(2)当a=4时,==8﹣12+18=14,即=4时,阴影部分的面积是14.【点评】本题考查列代数式、代数式求值,解答本题的关键是明确题意,列出相应的代数式.22.(7分)一辆货车从超市(O点)出发,向东走2km到达小李家(A点),继续向东走4km到达小张家(B点),然后又回头向西走10km到达小陈家(C 点),最后回到超市.(1)以超市为原点,向东方向为为正方向,以1cm表示1km,画出数轴,并在数轴上表示A,B,C,D的位置.(2)小陈家(C点)距小李家(A点)有多远?(3)若货车每千米耗油0.5升,这趟路货车共耗油多少升?【分析】(1)根据数轴与点的对应关系,可知超市在原点,小李家所在的位置表示的数是+2,小张家所在的位置表示的数是+6,小陈家所在的位置表示的数是﹣4;(2)2﹣(﹣4)=6;(3)先算这趟路一共有多少千米,再乘以货车每千米耗油的升数.【解答】解:(1)如下图:点O表示超市,点A表示小李家,点B表示小张家,点C表示小陈家.(2)从图中可看出小陈家距小李家6千米.故小陈家距小李家6千米.(3)0.5×(|+2|+|+4|+|﹣10|+|+4|)=0.5×20=10(升).故这趟路货车共耗油10升.【点评】本题考查了数轴:规定了原点、正方向、单位长度的直线叫做数轴.数轴的三要素:原点,单位长度,正方向.23.(7分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有n张桌子时,两种摆放方式各能坐多少人?(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌为什么?【分析】能够根据桌子的摆放发现规律,然后进行计算判断.【解答】解:(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人.即有n张桌子时是6+4(n﹣1)=4n+2.第二种中,有一张桌子是6人,后边多一张桌子多2人,即6+2(n﹣1)=2n+4.(2)中,分别求出两种对应的n的值,或分别求出n=25时,两种不同的摆放方式对应的人数,即可作出判断.打算用第一种摆放方式来摆放餐桌.因为,当n=25时,4×25+2=102>98当n=25时,2×25+4=54<98所以,选用第一种摆放方式.【点评】关键是通过归纳与总结,得到其中的规律.24.(10分)甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为x盒时,在甲店购买需付款(5x+60)元;在乙店购买需付款(4.5x+72)元.(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?【分析】(1)甲店需付费:4副乒乓球拍子费用+(x﹣4)盒乒乓球费用;乙店需付费:(4副乒乓球拍子费用+x盒乒乓球费用)×0.9,把相关数值代入求解即可;(2)把x=10代入(1)得到的式子计算,比较结果即可;(3)可在甲店购买乒乓球拍子,在乙店购买乒乓球.【解答】解:(1)甲店需付费:4×20+(x﹣4)×5=80+5x﹣20=(5x+60)元;乙店需付费:(4×20+x×5)×0.9=(4.5x+72)元;故答案为(5x+60);(4.5x+72);(2)当x=10时,甲店需付费5×10+60=110元;乙店需付费4.5×10+72=117元,∴到甲商店比较合算;(3)可在甲店购买4副乒乓球拍子,在乙店购买(10﹣4)盒乒乓球,所需费用为:4×20+(10﹣4)×5×0.9=80+27=107元.【点评】考查列代数式及代数式求值问题,得到两个商店付费的关系式是解决本题的关键.25.(6分)高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数,例如:[2.9]=2,[﹣1.5]=﹣2.试探索:(1)[﹣5]=﹣5,[π]=3;(2)[2.7]+[2.3]=4;(3)[]+[]+[]+[]+[]+[]= 6084.【分析】根据取整函数的定义分别计算即可.【解答】解:(1)[﹣5]=﹣5,[π]=3;(2)[2.7]+[2.3]=2+2=4;(3)[]+[]+[]+[]+[]+[]=55 0+733+916+1100+1283+1466=6048故答案分别为:﹣5,3,4,6084.【点评】本题考查有理数的混合运算、取整函数的定义,解题的关键是理解题意,灵活运用所学知识解决问题.。
江苏省徐州市铜山区七年级(上)期中数学试卷

(+3),并用“>”将它们连接起来.
22.(8 分)已知 a、b 互为倒数,e 是最大的负整数,且 c、d 满足(c﹣5)2+|d+5|
=0.
(1)求 2ab﹣(c+d)+e2 的值;
(2)求代数式(ab)2﹣
﹣e2017 的值.
23.(8 分)有 20 箱苹果,以每箱 20 千克为标准,超过或不足的千克数分别用 正、负数来表示,记录如表:
数有( )
A.1 个
B.2 个
C.3 个
D.4 个
7.(3 分)如果 x2+xy=2,y2+xy=7,那么 x2+y2+2xy 的值是( )
A.5
B.﹣2
C.﹣5
D.9
8.(3 分)下列计算正确的是( )
A.a﹣(a﹣b)=﹣b
B.3ab﹣ (ab﹣2)= ab+1
C.5a﹣(2a﹣1)=3a﹣1
D.﹣(﹣a3﹣b3)﹣a3=﹣b3
|8﹣5|;
⑤|0|+|+2|
|0+2|; ⑥|0|+|﹣8|
|0﹣8|.
(2)通过以上比较,请你分析、归纳出当 a、b 为有理数时,|a|+|b|
|a+b|.(用
“<”或“>”或“=”或“≥”或“≤”连接)
(3)根据(2)中你得出的结论,当|x|+2017=|x﹣2017|时,则 x 的取值范围
是
(1)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b);
(2)﹣3[3x2﹣2(5x2﹣1)].
19.(8 分)解方程:
(1)2(2x+1)=1﹣5(x﹣2);
苏科版七年级上期中考试数学试题(三套).docx

七年级上数学期中考试试卷(一)一、选择题(每小题2分,计20分)1、有理町的相反数是(亠)A. 2 B--C- "I D. —22、数轴上的点A到原点的距离是4,则点A表示的数为(人)A. 4B. — 4C.4 或一4D.2 或一23、下列各数中:+5、—2.5、--- 、2、一、一(一7)、3 5-+3负有理数有(丄)A. 2个B.3个C.4个D.5个4、下列各组数中,结果相等的是(亠)o3( o A3A. 一1?与(-1)2;B.—与一;C. -|-2| 与一(-2);D. (―3)'与一3\3 13丿5^若\ci\=\b\,则a与b的关系是(▲)A. a=b B・a=b C. a = h=0D・ a = b 或d=—b6、在代数式:ab,—cibc,0,—.2 15,x- y,一,一屮,单项式有(亠)33X 71A、3个 B. 4个C、5个D> 6个7、某种细菌在培养过程中,每半个小时分裂一次(由1个分裂成2个,两个裂成4个…),若这种细菌由1个分裂成128个,那么这个过程需要经过(丄)小时。
A. 2B. 3C. 3.5D. 48、多项式丄-(m-4)x + 7是关于x的四次三项式,则加的值是(亠)2A. 4B. -2C. -4D. 4 或一49、一列火车长加米,以每秒n米的速度通过一个长为〃米的桥洞,用代数式表示它刚好全部通过桥洞所需的时间为(人)二、填充(每小题2分,计20分)11、 ______________________ 最大的负整数是 •12、 ___________________________________________ 绝对值大于3小于6的所有整数是 __________________________ . 13、 ______________________________________________ “x 的4倍与一2的和除以5”列式为 _________________________ . 14、 右上图是一数值转换机,若输出的结果为一32,则输入的为 ________________ 15、靖江2008年人口普查结果显示,靖江人口已达66.5万,请你将66.5万用科学记数法表示应是 _________________________ .16> 4— (+1)+(— 6)— (— 5)写成省略加号的和的形式为______________________ . 17、 冬天某FI 上午的温度是3 °C,屮午上升了 5°C 达到最高温度,到夜间最冷时下降T 10°C,则这天的Fl 温差是 ________ °C.18、 已知关于x 的方程:ax+4=\~2x 恰为一元一次方程,那么系数G 应该满足的条件为 _____________ •19、 ________________________________________________________ 单项式-3Z 1/与单项式丄Fy"是同类项,则m-2n= ___________________________________ .20、 将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折吋每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么如 果对折五次,可以得到 _______ 条折痕,对折n 次可以得到 ____________________ 条 折痕.三、计算(16分+18分=34分)21、计算:(本题16分)p + m 工|A.-——秒B. £秒nc.吐竺秒nD.10、已知冈=3 y =4,且x>y,则2x-y 的值为A. +2B. ±2C- +10D. 一2 或+10第一次对折第二次对折 第三次对折22、化简及求值(本题8分+10分)(1). 一丄(% — 3) — 2(0 — 1)(3) 5(3咼一2脑)—4(—加+3咼),其中。
2017-2018学年苏科版七年级上期中统考数学试题含答案
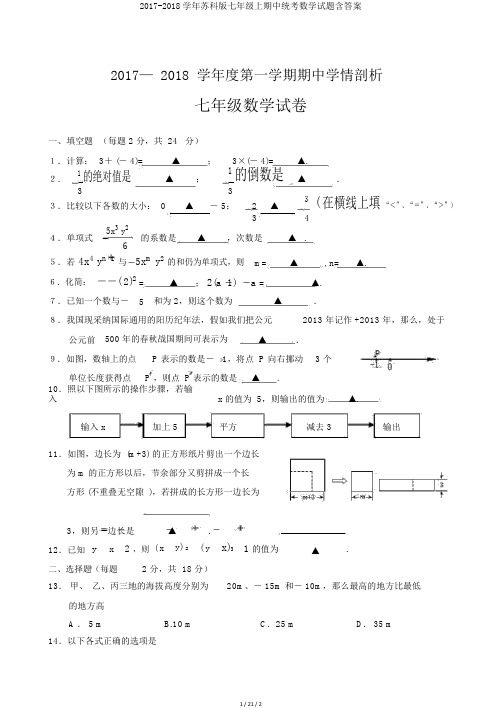
2017— 2018 学年度第一学期期中学情剖析七年级数学试卷一、填空题(每题 2 分,共 24 分)1.计算:3+ (- 4)= ▲;3×(- 4)= ▲.2.1 的绝对值是▲; 1 的倒数是▲.3 33.比较以下各数的大小: 0 ▲- 5; 2 ▲3 (在横线上填“<”、“=”、“>”)5x3 y2 3 44.单项式的系数是▲,次数是▲ .65.若 4x4 y n 1与5x m y2的和仍为单项式,则m= ▲, n= ▲.6.化简:--( 2)2 = ▲; 2(a 1) a = ▲.7.已知一个数与- 5 和为 2,则这个数为▲.8.我国现采纳国际通用的阳历纪年法,假如我们把公元2013 年记作 +2013 年,那么,处于公元前500 年的春秋战国期间可表示为▲.9.如图,数轴上的点P 表示的数是-1,将点 P 向右挪动 3 个单位长度获得点P ,则点 P 表示的数是▲.10.照以下图所示的操作步骤,若输入x 的值为 5,则输出的值为▲.输入 x 加上 5 平方减去 3 输出11.如图,边长为 (m+3) 的正方形纸片剪出一个边长为 m 的正方形以后,节余部分又剪拼成一个长方形 (不重叠无空隙 ),若拼成的长方形一边长为3,则另一边长是▲.12.已知y x 2 ,则( x y) 2 ( y x)3 1的值为▲.二、选择题(每题 2 分,共18 分)13.甲、乙、丙三地的海拔高度分别为20m、- 15m 和- 10m,那么最高的地方比最低的地方高A . 5 m B.10 m C.25 m D. 35 m14.以下各式正确的选项是A. 6 a-5a=1B. a+2a2=3 a3C.-( a- b)=- a+bD.2(a+b)=2 a+b。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省徐州市铜山区2017-2018学年七年级数学上学期期中抽测试题
七年级数学试题参考答案及评分意见
说明:1.本意见对每题给出了一种或几种解法供参考,如果考生的解法与本意见不同,可根据试题
的主要考查内容比照本意见制定相应的评分细则.
2.对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的分段分数.只给整数分数.
一、选择题(每题3分,共30分)
二、填空题(每题3分,共18分)
11. 4- 12.-2 a 2
b (答案不唯一) 13.2±
14.2
4a ⎛⎫
⎪⎝⎭
或 216a 15.19 16.1140
三.细心算一算:本大题共4小题,共32分.解答应写出文字说明、推理过程或演算步骤. 17.
()1255167671525........166771 1................20................3⎛⎫⎛⎫⎛⎫-
++-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭--++-+= =()()分
=分
分
()()()3252630051252630050........1100060................2=1060................3-⨯---÷⎡⎤⎣⎦-⨯+-÷---
=()()分=分分
18.
()()
()()()2
22
2
2222
2
22222153315512........115512...............33...............4a
b ab ab a b a b ab ab
a b a b ab ab a b a b ab ---+---+-+-=-4
=4分=4分分
()()()2
2
2
22222332519306...........29+30 6...............321 6................4x x x x x x x ⎡⎤
---⎣
⎦
⎡⎤=---⎣⎦
=--=-分分分
19.
()14+2115.....2 99.........3 1.........4x x x x =-==解:
分分分
()()()2316232.....2 97 (37)
(49)
x x x x +-=-+==解:
分分
分
20.
()()()
()()()22222216734673 4........2 6374 3 3 .. (31)
13 2 (53)
a a a a a a a a a a a a a a --------++=-+-++-+=--=-=-=- 解:分分
当时,原式分
()()()()2
22222225323453234 ........2 54323 3 ..............32423 3......5a
a a a a a a a a a a a a a a ⎡⎤---+⎣⎦-+--=-+-+-=--=-=+-=
解:分分当时,原式分
四.耐心做
一做:本大题共5小题,每小题8分,共40分.解答应写出文字说明、推理过程或演算步骤
21. ……………4分
……………8分
22.(1)根据题意ab =1, c =5, d =-5,e =-1. …………………2分 原式=()22ab c d e -++=201=3-+ …………………4分
(2)
()()()2
2017
201722017==101=101=22018
c d ab e +------+原式 ……………8分
23. 解:(1)()2.53=5.5--(千克)
答:20箱苹果中,最轻的一箱比最重的一箱少5.5千克. ……………2分 (2)3124 1.52+12+2.53= 4.5-⨯-⨯-⨯⨯⨯-(千克)
答:与标准重量比较,20箱苹果总计不足4.5千克. ……………6分 (3)()2020 4.56=2373⨯-⨯(元)
答:若苹果售价每千克6元,则这20箱苹果全部售出可以收入2373元. ……………8分
24. (解:(1)某用户10月份用水13 m³,那么该用户应缴纳水费 39 元;……………2分 (2)小明家9月份用水10 m ³,10月份用水18m³,那么9、10月小明家共需支付 86.25 元水费;
……………4分 (3)
()()3
3
153=458 3.75=3087-45-30=45126=2 15+8+2=257⨯⨯÷(元); (元); (元);米;米 ........分
答:若小明家8月份共支付水费87元,那么小明家8月份共用水25立方米. ………8分
25. (1)比较下列各式的大小 (用“<”或“>”或“=”连接)
① = ; ② = ;③ > ; ④ > ;⑤ = ; ⑥ = . ………3分
(2)|a |+|b | ≥ |a +b | ………5分
(3)x 的取值范围是 x ≤0 ; ………6分 若x >0,且|x |+|y |=10,|x+y |═2,则y = -6或-4 . ………8分。
