2014年重庆南开高2015级高三10月月考 理科数学
2015年高考重庆市理科数学真题含答案解析(超完美版)

2015年高考重庆市理科数学真题一选择题1.已知集合A={}1,2,3,B={}2,3,则( ) A .A B =B .A ⋂B=∅C .ABD .BA2.在等差数列{}n a 中,若2a =4,4a =2,则6a =( ) A .-1B .0C .1D .63.重庆市2013年各月的平均气温(o C )数据的茎叶图如下:则这组数据的中位数是( )A .19B .20C .21.5D .234.“x>1”是“12log (x+2)<0”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件5.某几何体的三视图如图所示,则该几何体的体积为( )A .13π+ B .23π+C .123π+D .223π+6.若非零向量a ,b 满足|a|=3|b|,且(a -b )⊥(3a +2b ),则a 与b 的夹角为( ) A .4π B .2πC .34πD .π7.执行如图所示的程序框图,若输入K 的值为8,则判断框图可填入的条件是( )A .s ≤34B .s ≤56C .s ≤1112D .s ≤15248.已知直线l :x+ay-1=0(a ∈R )是圆C :224210x y x y +--+=的对称轴. 过点A (-4,a )作圆C 的一条切线,切点为B ,则|AB|=( ) A .2B .C .6D .9.若tan α=2tan5π,则3cos()10sin()5παπα-=-( )A .1B .2C .3D .410.设双曲线22221x y a b-=(a>0,b>0)的右焦点为1,过F 作AF 的垂线与双曲线交于B,C 两点,过B,C 分别作AC ,AB 的垂线交于点D.若D 到直线BC 的距离小于a 范围是( ) A .(-1,0)(0,1) B .(-∞,-1)(1,+∞) C.(0)(0 D .(-∞,)+∞)二、填空题11.设复数a+bi (a ,b ∈R a+bi )(a-bi )=________.12.53x ⎛ ⎝的展开式中8x 的系数是________(用数字作答).13.在ABC 中,B=120o ,,A 的角平分线,则AC=_______.14.如图,圆O 的弦AB ,CD 相交于点E ,过点A 作圆O 的切线与DC 的延长线交于点P ,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=_______.15.已知直线l 的参数方程为11x ty t=-+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线C 的极坐标方程为235cos 24(0,)44ππρθρθ=><<,则直线l 与曲线C 的交点的极坐标为_______. 16.若函数f (x )=|x+1|+2|x-a|的最小值为5,则实数a=_______.17.端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个。
重庆南开中学2015届高三数学9月月考试题理(含解析)

重庆南开中学高2015级高三9月月考数学试题(理科)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知向量)2,1(-=→x a ,)1,2(=→b ,且→→⊥b a ,则=x ( ) A .21-B .1-C .5D .0【答案】D考点:向量垂直的条件. 2.函数234y x x =--+的定义域为( )A .(4,1)--B .(4,1)-C .(1,1)-D .(1,1]- 【答案】C 【解析】 试题分析:由1114104310430122<<-⇒⎩⎨⎧<<-->⇒⎩⎨⎧<-+->⇒⎩⎨⎧>+-->+x x x x x x x x x ,故选C . 考点:函数的定义域.3.已知命题“p ⌝或q ⌝”是假命题,则下列命题:①p 或q ;②p 且q ;③p ⌝或q ;④p ⌝且q ;其中真命题的个数为( ) A .1B .2C .3D .4【答案】C 【解析】试题分析:由命题“p ⌝或q ⌝”是假命题,知p ⌝,q ⌝两个均为假命题,从而p 、q 均是真命题,故知①p 或q ;②p 且q ;③p ⌝或q 均为真命,故选C . 考点:命题真假的判断.4.函数3()=2+2x f x x -在区间(0,1)内的零点个数是( ) A .0 B .1C .2D .3【答案】B考点:函数的零点.5.已知243.03.0,3log ,4log -===c b a ,则c b a ,,的大小关系是( )A .c b a <<B .c a b <<C .b c a <<D .b a c << 【答案】A 【解析】 试题分析:由于19.013.0,14log 3log 1log 0,01log 4log 24443.03.0>===<=<==<=-c b a ,故知c b a <<,所以选A.考点:比较大小.6. ∆ABC 中,角C B A ,,所对的边分别为c b a ,,,若15,10,60===a b A ,则cos =B ( )A .6 B .6- C .223 D .223- 【答案】A考点:正弦定理.7.函数)80(1102)(2≤≤+++=x x x x x f 的值域为( )A .]61,81[B .]10,8[C .]61,101[ D .]10,6[ 【答案】D 【解析】试题分析:由于)80(,19)1(19)1()(2≤≤+++=+++=x x x x x x f ,令]9,1[1∈=+t x ,则有2229919t t t y t t y -=-='⇒+=,知y 在[]3,1上是减函数,在[]9,3上是增函数,所以10,6max min ==y y ,故知函数的值域为]10,6[,故选D.考点:函数的值域.8.已知⎩⎨⎧>+-≤-=02602)(2x x x x xx f ,则关于x 的不等式2(3)(2)-<f x f x 的解集为( ) A .)3,3(--B .)1,3(-C .),32()32,(+∞+--∞D .),32()1,3(+∞+-【答案】D考点:1.分段函数;2.解不等式.9.已知21,x x 是关于x 的一元二次方程20++=ax bx c 的两根,若121<<x x ,则 2221212()++x x x x 的取值范围是( )A .(5,)+∞B .(1,)+∞C .1(,)2+∞ D .),41(+∞【答案】C 【解析】考点:1.一元二次不等式的根与系数的关系;2.基本不等式的性质及其变形应用.10.已知函数()3ln (1)=≥f x x x ,若将其图像绕原点逆时针旋转(0,)2πθ∈角后,所得图像仍是某函数的图像,则当角θ取最大值0θ时,0tan θ=( ) A.3 B.3 C.3 D.3【答案】C 【解析】考点:1.函数的定义;2.函数的导数.第Ⅱ卷(共100分)二、填空题(本大题共6小题,考生作答5小题,每小题5分,共25分.将答案填在答题纸上)11.已知集合}1)1(log |{21->-=x x A ,}2|{x y y B ==,则=B A C R )(___ __.【答案】),3[]1,0(+∞ 【解析】试题分析:由1)1(log 21->-x 得到31210<<⇒<-<x x ,即A=(1,3),从而),3[]1,(+∞-∞= A C R ,而B=(0,+∞),所以=B A C R )(),3[]1,0(+∞ .考点:集合的运算.12.设:21(0)+<>p x m m ,0121:>--x x q ,若p 是q 的充分不必要条件,则实数m 的取值范围为 . 【答案】(0,2]考点:充分条件和必要条件的应用 13.已知函数123()1234+++=+++++++x x x x f x x x x x ,则55(3)(3)22-++-=f f ___. 【答案】8 【解析】试题分析:由于123()1234+++=+++++++x x x x f x x x x x )41312111(4+++++++-=x x x x ,从而)231211211231(4)25(++++-+--=+-x x x x x f=+-++-+--+---=--)231211211231(4)25(x x x x x f )231211211231(4++++-+-+x x x x所以8)25()25(=--++-x f x f ,从而令3=x ,得8)325()325(=--++-f f ,故答案为:8. 考点:函数值的求法.考生注意:14、15、16为选做题,请从中任选两题作答,若三题全做,则按前两题给分. 14.如图,圆O 的直径AB 与弦CD 交于点P ,7, 5, 15CP PD AP ,则=∠DCB ______. OPDCBA【答案】45考点:与圆有关的比例线段.15.已知直线1:=+ny mx l 与曲线⎪⎪⎩⎪⎪⎨⎧==ϕϕsin 21cos 21:y x C (ϕ为参数)无公共点,则过点),(n m 的直线与曲线θθρ222sin 9cos 436+=的公共点的个数为 .【答案】2考点:1.圆的参数方程;2.根的存在性及根的个数判断;3.简单曲线的极坐标方程.16.已知函数)0(1)(>-++=a a x x x f ,若不等式6)(≥x f 的解集为(,2][4,)-∞-+∞, 则a 的值为__________. 【答案】3 【解析】试题分析:函数f (x )=|x+1|+|x-a |表示数轴上的x 对应点到-1和a 对应点的距离之和,由于不等式6)(≥x f 的解集为(,2][4,)-∞-+∞,所以数轴上的-2、4对应点到-1和a 对应点的距离之和正好等于6,故有⎩⎨⎧=-++=--++-64146212a a ,即31452=⇒⎩⎨⎧=-=+a a a ,故答案为:3. 考点:绝对值不等式的解法.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题13分)已知函数)(x f 对任意R x ∈满足0)()(=-+x f x f ,)1()1(+=-x f x f ,若当[0,1)∈x 时,b a x f x +=)((0>a 且1≠a ),且21)23(=f .(1)求实数b a ,的值;(2)求函数)()()(2x f x f x g +=的值域. 【答案】(1)1,41-==b a ;(2)]1621,41[-考点:1.函数的奇偶性;2.函数的周期性. 18.(本小题13分)如图,AB 是圆的直径,PA 垂直于圆所在的平面,C 是圆上的点. (1)求证:平面⊥PAC 平面PBC ;(2)若1,1,2===PA AC AB ,求二面角A PB C --的余弦值.【答案】(1)祥见解析;(2)46. 【解析】考点:1.平面与平面垂直的判定;2.二面角的平面角及其求法. 19.(本小题13分)在数列{}n a 中,122,511-+==-n n n a a a (*,2N n n ∈≥). (1)求23,a a 的值;(2)是否存在常数λ,使得数列}2{nn a λ+是一个等差数列?若存在,求λ的值及}{n a 的通项公式;若不存在,请说明理由.【答案】(1)132=a ,333=a ;(2)12)1(,1+⋅+=-=nn n a λ.【解析】试题分析:(1)直接把n=2,3,代入a n =2a n -1+2n-1(n ∈N *,n ≥2),再注意a 1=5,即可求出数列的前三项;考点:1.数列递推关系式的应用;2.等差关系的确定. 20.(本小题12分)设抛物线22(0)y px p =>的焦点为F ,其准线与x 轴的交点为Q ,过Q 点的直线l 交抛物 线于,A B 两点.(1)若直线l 的斜率为22,求证:0=⋅; (2)设直线,FA FB 的斜率分别为21,k k ,求21k k +的值. 【答案】(1)祥见解析;(2)0. 【解析】试题分析:(1)由点斜式写出直线l 的方程,和抛物线方程联立后化为关于x 的一元二次方程,利用根与系数关系求出A ,B 两点的横坐标的和与积,写出向量FB FA ,的坐标,展开数量积后代入根与系数关系得答案; (2)设直线l 的方程为l :x =ky −2p,和抛物线方程联立后化为关于y 的一元二次方程,写出根与系数关系,由两点式求出斜率后作和化简,代入根与系数关系即可得到答案. 试题解析:(1))2(22:p x y l += 与抛物线方程联立得04322=+-p px x 设),(),,(2211y x B y x A083)(423)2)(2(221212121=++-=+--=⋅p x x p x x y y p x p x FB FA ; (2)设直线2:p ky x l -= 与抛物线联立得0222=+-p pky y 0))((22))(()(2222122121212211221121=--⋅-=--+-=-+-=-+-=+p ky p ky pk p kp p ky p ky y y p y ky p ky y p ky y p x y p x y k k . 考点:1.直线与圆锥曲线的关系;2.抛物线的简单几何性质.21.(本小题12分)已知函数x bx ax x f ln )(2-+=,R b a ∈,.(1)若0<a 且2=-b a ,试讨论()f x 的单调性;(2)若对[2,1]∀∈--b ,总(1,)∃∈x e 使得()0<f x 成立,求实数a 的取值范围. 考点:1.二次函数的性质;2.利用导数研究函数的单调性.22.(本小题12分)已知函数()f x 满足对任意实数,x y 都有()()()1+=++f x y f x f y 成立,且当0>x 时, ()1>-f x ,(1)0=f .(1)求(5)f 的值;(2)判断()f x 在R 上的单调性,并证明;(3)若对于任意给定的正实数ε,总能找到一个正实数σ,使得当0||σ-<x x 时,0|()()|ε-<f x f x ,则称函数()f x 在0=x x 处连续。
重庆南开中学2015届高三10月月考数学(文)试题 Word版含答案

重庆南开中学高2015级高三10月月考数学试题(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟. 注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上. 4.所有题目必须在答题卡上作答,在试题卷上答题无效. 5.考试结束后,将试题卷和答题卡一并收回.第Ⅰ卷(选择题共50分)一. 选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1.已知A ,B 为两个集合,若命题:p x A ∀∈,都有2x B ∈则( ) A .:p x A ⌝∃∈使得2x B ∈ B .:p x A ⌝∃∉使得2x B ∈ C .:p x A ⌝∃∈使得2x B ∉ D .:p x A ⌝∀∉,2x B ∉ 2.已知向量(5,6)a =-,(6,5)b =,则a 与b ( )A .垂直B .不垂直也不平行C .平行且同向D .平行且反向3.设集合2{|20M x x x =--<},{|y 2,N y x x M ==∈}则集合()R C M N ⋂=( ) A .(—2,4) B .(—1,2) C .∞⋃∞(-,-1][2,+)D .(∞⋃∞(-,-2)4,+)4.已知正项等比数列{}n a 中,n S 为其前项和n ,且2431,7a a S ==则5=S ( )A .152 B .314 C .334 D .172 5.对于平面a 、b 、m 和直线a 、b 、m 、n 下列命题中真命题是( )A .若//,a a b βγ⋂=,则//a bB .若//a b b α⊂, 则//a αC .若,,,a m a n m α⊂⊥⊥则a α⊥D .,a a βα⊂⊥,则a β⊥2350x y +-≤6.若实数,x y 满足约束条件 250x y --≤,则目标函数|1|z x y =++的最小值是( )0x ≤A .0B .4C .83 D .727.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( ) A .29π B .23π C .169π D .3π8.将函数()sin f x = 的图像向右平移6π个单位,再将图象上每一点横坐 标伸长为原来的2倍后得到()y g x =图像,若在[0.2)x π∈上关于x 的方程有两个 不等的实根.1x ,2x 则12+x x 的值为( ) A .52ππ或 B .322ππ或 C .3ππ或 D .522ππ或9.已知函数()y f x =是定义在R 上的奇函数,且'()()0f x f x -> (其中'()()f x f x 是导函数)恒成立.若(ln 3)(ln 2),,(1)32f f a b c ef ===-,则,,a b c 的大小关系是( ) A .a b c >> B .c a b >> C .c b a >> D .b c a >>10.已知函数421()421x x x xk f x +⋅+=++,,若对任意的实数.123,,x x x ,不等式123()()()f x f x f x +> 恒成立,则实数k 的取值范围是( ) A .03k ≤< B .14k ≤≤ C .132k -≤≤ D .142k -≤≤第Ⅱ卷(非选择题共100分)二.填空题:本大题共5小题,每小题5分,共25分,把答案填写在答题卡相应位置上. 11.复数21i z i+=对应的复平面上的点在第 象限.12.若()f x = 则((2))f f 的值为 .12,2x e x -<33log (1),2x x -≥7212x π+13.已知正实数12,,,x a a y 成等差数列,12,,,x b b y 成等比数列,则21212()a a b b +的最小值是.14.在ABC ∆中,角,,A B C 对应的边分别为,,a b c若3,a b =且2cos cos cos a A b C c B =+ 则边c 的长为 .15.如图,已知边长为1的正方形ABCD 位于第一象限,且顶点分别在,x y 的正半轴上(含原点)滑动,则OB OC ⋅的最大值是 .三.解答题:本大题6个小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16:(本小题满分13分)某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组. (1)科研攻关小组中男、女职员的人数;(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率.17.(本小题满分13分)已知递增等差数列{}n a 首项12,n a S =为其前n 项和,且1232,23S S S 成等比数列. (1) 求{}n a 的通项公式; (2) 设14n n n b a a +=求数列{}n b 的前n 项和n T18.(本小题满分13分)如图所示,PA ⊥平面ABCD ,四边形ABCD 为正方形,且.E F G 、、分别是线段PA PD CD BC 、、、的中点.(1) 求证://BC EFG 平面 (2) 求证:DH AEG ⊥平面19.(本小题满分12分) 设函数2()2sin cos cos sin sin (02f x x x x ϕϕϕπ=+-<<)在x π=处取最小值.(1)求ϕ的值;(2)若实数α满足1()(),(,)252f f ππαααπ+-=∈试求sin 2cos 21sin cos αααα+--的值.20.(本小题满分12分)如图,底面ABCD 为菱形的直四棱柱1111ABCD A BC D =,所有棱长都为2, 60BAD ∠=,E 为1BB 的延长线上一点,11D E D AC ⊥面.(1) 求线段1B E 的长度及三棱锥1E D AC =的体积1E D AC V -(2) 设AC BD 和交于点O ,在线段1D E 上是否存在一点P ,11//EO AC P 使面?若存在,求1:D E PE 的值;若不存在,说明理由.21.(本小题满分12分)设函数2()2(4)()f x ax a x lnx a R =+++∈(1) 若15a =,求()f x 在点(1,(1))f 处的切线方程; (2) 若a 为整数,且函数()y f x =的图象与x 轴交于不同的两点,试求a 的值.。
重庆市南开中学高三数学10月月考试题 理 新人教A版
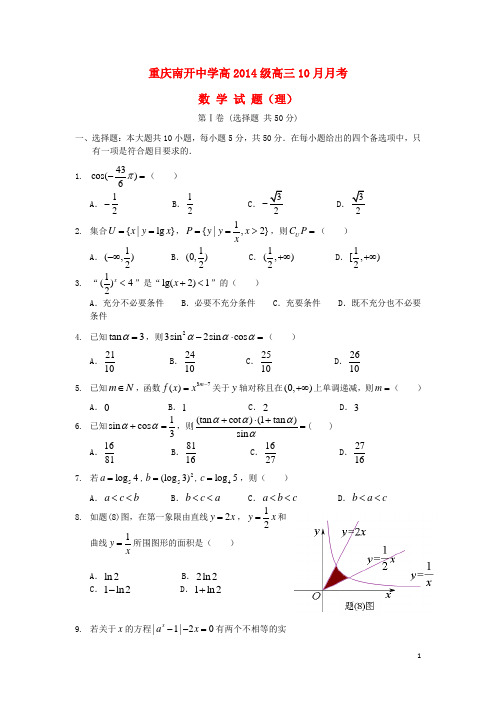
重庆南开中学高2014级高三10月月考数 学 试 题(理)第Ⅰ卷 (选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1. 43cos()6π-=( ) A .12- B .12C .3-D .32. 集合{|lg }U x y x ==,1{|,2}P y y x x==>,则U C P =( )A .1(,)2-∞B .1(0,)2C .1(,)2+∞D .1[,)2+∞3. “1()42x<”是“lg(2)1x +<”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4. 已知tan 3α=,则23sin 2sin cos ααα-⋅=( )A .2110 B .2410 C .2510D .26105. 已知m N ∈,函数37()m f x x -=关于y 轴对称且在(0,)+∞上单调递减,则m =( )A .0B .1C .2D .3 6. 已知1sin cos 3αα+=,则(tan cot )(1tan )sin αααα+⋅+=( ) A .1681 B .8116 C .1627 D .27167. 若5log 4a =,25(log 3)b =,4log 5c =,则( )A .a c b <<B .b c a <<C .a b c <<D .b a c << 8. 如题(8)图,在第一象限由直线2y x =,12y x =和曲线1y x=所围图形的面积是( )A .ln 2B .2ln 2C .1ln2-D .1ln2+9. 若关于x 的方程|1|20xa x --=有两个不相等的实题(14)图数解,则实数a 的取值范围是( )A .1(0,)(1,)e e UB .1(0,)(1,2)2e e UC .221(0,)(1,)e eU D .2(1,)e10. 已知函数()f x 在R 上可导,其导函数为()f x ',若()f x 满足:(1)[()()]0'-->x f x f x ,22(2)()--=x f x f x e ,则下列判断一定正确的是( )A .(1)(0)<f fB .(2)(0)>f efC .3(3)(0)>f e f D .4(4)(0)<f e f第Ⅱ卷 (非选择题 共100分)二、填空题:本大题共6小题,考生作答5小题,每小题5分,共25分.把答案填写在答题卡相应位置上. 11. 函数212()log (23)f x x x =--的单调递减区间为________________.12. 函数y x =+________________. 13. 若非空..集合2{|,}A x m x Z =>∈至多含有4个元素,则实数m 的取值范围是________________.考生注意:14、15、16为选做题,请从中任选两题作答,若三题全做,则按前两题给分. 14. 如题(14)图,O e 是ABC ∆的外接圆,过点C 作O e 的切线交AB 的延长线于点D ,CD =,3AB BC ==,则AC =________________.15. 在直角坐标系中,以原点O 为极点,x 轴的正半轴为极轴,建立极坐标系.若曲线1ρ=和2cos()3πρθ=+交于,A B两点,则||AB =________________.16. 若存在实数x 使|||1|3x a x -+-≤成立,则实数a 的取值范围是________________. 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分13分)已知函数22()(sin cos )2cos 2f x x x x =++-. (Ⅰ)求()f x 的单调递增区间; (Ⅱ)当3[,]44x ππ∈时,求()f x 的值域. 18. (本小题满分13分)已知函数()22x xf x -=-. (Ⅰ)判断()f x 的奇偶性并证明;(Ⅱ)若2(1)(1)0f m f m -+-<,求实数m 的取值范围.19. (本小题满分13分)已知函数73()sin()cos()44f x x x ππ=++-. (Ⅰ)求()f x 的对称轴方程; (Ⅱ)已知3sin()5αβ+=-,4cos()45πβ+=-,3,()24ππαβ∈,求()f α的值.20. (本小题满分12分)已知函数21()(1)ln 2f x x a x a x =-++()a R ∈. (Ⅰ)若()f x 在(2,)+∞上单调递增,求a 的取值范围; (Ⅱ)若()f x 在(0,)e 内有极小值12,求a 的值.21. (本小题满分12分)已知椭圆2222:1x y C a b +=(0)a b >>的离心率为12,焦点到其相应准线的距离是3.(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(4,0)A 的直线l 与椭圆C 交于不同的两点,M N ,使得81||||7AM AN ⋅=?若存在,求出直线l 的方程;若不存在,请说明理由.22. (本小题满分12分)已知()=xf x e ,24()2+-=x xg x .(Ⅰ)若关于x 的方程2[()]()40f x m f x +⋅+=有两个不相等的正根,求实数m 的取值范围;(Ⅱ)直线(1)=>y t t 与(),0,()y f x x y g x ===的图象分别交于,,M S N 三点.求证:不存在两个不同的t 使得||||SM SN 的值相等.重庆南开中学高2014级高三10月月考数学试题答案(理)一、选择题1~5 CDBAB 6~10 DDACC 二、填空题11. (3,)+∞ 12. (,1]-∞ 13. [222,45)-+ 14.37215. 3 16. [2,4]-三、解答题17.解:(I )2()12sin cos 2cos 2sin 2cos 22sin(2)4f x x x x x x x π=++-=+=+故的单调增区间为(II )∴∴当时,的最大值为1,最小值为2-18.解:(Ⅰ)()f x 定义域为R ,当x 递增时,2x递增,12x-递增,∴()f x 在R 上递增; ∵()22()xx f x f x --=-=-,∴()f x 是奇函数(Ⅱ)∵()f x 是奇函数,∴原不等式等价于22(1)(1)(1)f m f m f m -<--=- ∵()f x 在R 上递增,∴211m m -<-,解得(,2)(1,)m ∈-∞-+∞U19.解:(Ⅰ)7733()sin coscos sin cos cos sin sin4444f x x x x x ππππ=+++ 222sin()4x x x π==-令42x k πππ-=+,解得()f x 的对称轴是34x k ππ=+,k Z ∈(Ⅱ)()2sin()2sin[()()]44f ππαααββ=-=+-+2sin()cos()2cos()sin()44ππαββαββ=++-++…………(*) ∵324ππαβ<<≤ ∴3(,)2παβπ+∈,3(,)44ππβπ+∈ ∴4cos()5αβ+=-,3sin()45πβ+= 代入(*)式得∴48()25f α=20.解:(Ⅰ)∵()f x 在(2,)+∞上单调递增,∴2(1)()0x a x af x x-++'=≥在(2,)+∞恒成立即2(1)0x a x a -++≥在(2,)+∞恒成立,即2(1)0x a x x -+-≥在(2,)+∞恒成立即2(1)x a x x --≥在(2,)+∞恒成立,即a x ≤在(2,)+∞恒成立 ∴实数a 的取值范围是(,2]-∞(Ⅱ)()f x 定义域为(0,)+∞,2(1)()(1)()x a x a x a x f x x x-++--'==①当1a >时,令()0f x '>,结合()f x 定义域解得01x <<或x a > ∴()f x 在(0,1)和(,)a +∞上单调递增,在(1,)a 上单调递减此时21()()ln 2f x f a a a a a ==--+极小值 若()f x 在(0,)e 内有极小值12,则1a e <<,但此时211ln 022a a a a --+<<矛盾②当1a =时,此时()f x '恒大于等于0,不可能有极小值 ③当1a <时,不论a 是否大于0,()f x 的极小值只能是1(1)2f a =-- 令1122a --=,即1a =-,满足1a < 综上所述,1a =-21.解:(Ⅰ)由题得12c a =,23a c c -= 联立222a c b =+ 解得 2a =,1c =,23b = ∴椭圆方程为22143x y += (Ⅱ)易知直线m 斜率存在,设直线:m (4)y k x =-,11(,)M x y ,22(,)N x y 与椭圆方程联立得 2222(34)3264120k x k x k +-+-= ∴2222(32)4(34)(6412)0k k k ∆=-+->,解得1122k -<< 21223234k x x k +=+,2122641234k x x k -=+又12||||4|4|AM AN x x ⋅=--212(1)(4)(4)k x x =+--21212(1)(4()16)k x x x x =+-++22222641232(1)(416)3434k k k k k -=+-⨯+++2236(1).34k k =++∴223681(1)347k k +=+,解得k =1122k -<<∴直线m的方程为(4)4y x =±-22.解:(Ⅰ)∵2()40x x e m e +⋅+=有两个不相等的正根,令xt e =∴关于t 的方程240t m t +⋅+=有两个大于1且不相等的根∴214016012m m m ⎧⎪++>⎪∆=->⎨⎪⎪->⎩ 解得(5,4)m ∈-- (Ⅱ)联立y t =和()xf x e =,解得ln x t =,∴||ln SM t =联立y t =和()=g x 21t x t -=,∴21||t SN t-=∴2||ln ||1SM t t SN t =-,令2ln ()1t th t t =- 不存在两个不同的t (1)t >使得||||SM SN 的值相等⇔不存在两个不同的t (1)t >使()h t 的值相等2222ln ln 1()(1)t t t t h t t ---'=-令22()ln ln 1u t t t t t =--- ∴1()2ln u t t t t t '=--,21()12ln u t t t''=-- ∵当1t >时,21()12ln 0u t t t''=--< ∴()u t '在(1,)+∞上单调递减 ∴当1t >时,()(1)0u t u ''<= ∴()u t 在(1,)+∞上单调递减 ∴当1t >时,()(1)0u t u <=∴当1t >时,22()()0(1)u t h t t '=<- ∴()h t 在(1,)+∞上单调递减∴不存在两个不同的t (1)t >使()h t 的函数值相等,结论得证。
重庆南开中学2015届高三9月月考理数试题

重庆南开中学高2015级高三9月月考数学试题(理科)本试卷分第1卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟.注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用 橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上. 4.所有题目必须在答题卡上作答,在试题卷上答题无效. 5.考试结束后,将试题卷和答题卡一并收回。
第I 卷(选择题 共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知向量)2,1(-=→x a ,)1,2(=→b ,且→→⊥b a ,则=x ( ) A .21-B .1-C .5D .02.函数y =的定义域为( )A .(4,1)--B .(4,1)-C .(1,1)-D .(1,1]-3.已知命题“p ⌝或q ⌝”是假命题,则下列命题:①p 或q ;②p 且q ;③p ⌝或q ;④p ⌝且q ;其中真命题的个数为( ) A .1B .2C .3D .44.函数3()=2+2xf x x -在区间(0,1)内的零点个数是( ) A .0B .1C .2D .35.已知243.03.0,3log ,4log -===c b a ,则c b a ,,的大小关系是( ) A .c b a << B .c a b << C .b c a << D .b a c <<6.∆ABC 中,角C B A ,,所对的边分别为c b a ,,,若15,10,60===a b A ,则c o s =B ( )A B . C D . 7.函数)80(1102)(2≤≤+++=x x x x x f 的值域为( ) A .]61,81[ B .]10,8[ C .]61,101[D .]10,6[B8.已知⎩⎨⎧>+-≤-=02602)(2x x x x xx f ,则关于x 的不等式2(3)(2)-<f x f x 的解集为( ) A .)3,3(--B .)1,3(-C .),32()32,(+∞+--∞D .),32()1,3(+∞+-9.已知21,x x 是关于x 的一元二次方程20++=ax bx c 的两根,若121<<x x ,则2221212()++x x x x 的取值范围是( ) A .(5,)+∞ B .(1,)+∞ C .1(,)2+∞ D .),41(+∞10.已知函数()(1)=≥f x x x ,若将其图像绕原点逆时针旋转(0,)2πθ∈角后,所得图像仍是某函数的图像,则当角θ取最大值0θ时,0tan θ=( )ABCD 第Ⅱ卷(共100分)二、填空题(本大题共6小题,考生作答5小题,每小题5分,共25分.把答案填写在答题卡相应位置上)11.已知集合}1)1(log |{21->-=x x A ,}2|{x y y B ==,则=B A C R )(___ __.12.设:21(0)+<>p x m m ,0121:>--x x q ,若p 是q 的充分不必要条件,则实数m 的取值范围为 . 13.已知函数123()1234+++=+++++++x x x x f x x x xx,则55((22-++--=f f ___. 考生注意:14、15、16为选做题,请从中任选两题作答,若三题全做,则按前两题给分. 14.如图,圆O 的直径AB 与弦CD 交于点P ,7, 5, 5CP PD AP ===则=∠DCB ______.15.已知直线1:=+ny mx l 与曲线⎪⎪⎩⎪⎪⎨⎧==ϕϕsin 21cos 21:y x C (ϕ为参数)无公共点,则过点),(n m 的 直线与曲线θθρ222sin 9cos 436+=的公共点的个数为 .16.已知函数)0(1)(>-++=a a x x x f ,若不等式6)(≥x f 的解集为(,2][4,)-∞-+∞, 则a 的值为__________.三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题13分)已知函数)(x f 对任意R x ∈满足0)()(=-+x f x f ,)1()1(+=-x f x f ,若当[0,1)∈x 时,b a x f x +=)((0>a 且1≠a ),且21)23(=f . (1)求实数b a ,的值;(2)求函数)()()(2x f x f x g +=的值域.18.(本小题13分)如图,AB 是圆的直径,PA 垂直于圆所在的平面,C 是圆上的点. (1)求证:平面⊥PAC 平面PBC ;(2)若1,1,2===PA AC AB ,求二面角A PB C --的余弦值. 19.(本小题13分)在数列{}n a 中,122,511-+==-n n n a a a (*,2N n n ∈≥). (1)求23,a a 的值;(2)是否存在常数λ,使得数列}2{nn a λ+是一个等差数列?若存在,求λ的值及}{n a 的通项公式;若不存在,请说明理由. 20.(本小题12分)设抛物线22(0)y px p =>的焦点为F ,其准线与x 轴的交点为Q ,过Q 点的直线l 交抛物 线于,A B 两点.(1)若直线l ,求证:0=⋅FB FA ; (2)设直线,FA FB 的斜率分别为21,k k ,求21k k +的值.21.(本小题12分)已知函数x bx ax x f ln )(2-+=,R b a ∈,. (1)若0<a 且2=-b a ,试讨论()f x 的单调性;(2)若对[2,1]∀∈--b ,总(1,)∃∈x e 使得()0<f x 成立,求实数a 的取值范围. 22.(本小题12分)已知函数()f x 满足对任意实数,x y 都有()()()1+=++f x y f x f y 成立,且当0>x 时,()1>-f x ,(1)0=f .(1)求(5)f 的值;(2)判断()f x 在R 上的单调性,并证明;(3)若对于任意给定的正实数ε,总能找到一个正实数σ,使得当0||σ-<x x 时,0|()()|ε-<f x f x ,则称函数()f x 在0=x x 处连续。
重庆市南开中2014年学高三高2015级10月南开2015级10月月考试题理科

重庆南开中学高2015级高三(10月)月考数 学 试 题(理 科)考试说明:本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.(1)答题前,考生先将自己的姓名、准考证号码填写清楚;(2)选择题必须使用2B 铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,字迹清楚;(3)请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效;(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.第I 卷(选择题 共50分)一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个备选项中,只有一项是符合题目要求的。
1.复数)1(i i +=Z (i 为虚数单位)在复平面内对应的点位于 ( )A.第一象限B.第二象限C.第三象限D.第四象限2.角α终边经过点)1,1(-,则=αc o s ( )A.1B.1-C.22D.22- 3.设3log π=a ,3.02=b ,31log 2=c ,则 ( ) A.c b a >> B.bc a >> C.b a c >> D.c a b >> 4.“23s i n =x ”是“3π=x ”的 ( ) A.充要条件 B.充分不必要条件C.必要不充分条件D.既不充分又不必要条件5.函数28)(2+-=-x x x f 的一个零点所在区间为 ( )A.)2,1(B.)3,2(C.)4,3(D.)5,4(6.如果命题“非p 或非q ”是假命题,给出下列四个结论:①命题“p 且q ”是真命题 ②命题“p 且q ”是假命题③命题“p 或q ”是真命题 ④命题“p 或q ”是假命题其中正确的结论是 ( )A.①③B.②④C.②③D.①④7.将函数)sin(ϕω+=x y ),0(πϕω<>的图象向左平移3π个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为x y sin =,则)s i n (ϕω+=x y 图像上离y 轴距离最近的对称中心为 ( ) A.)0,3(πB.)0,65(π C.)0,6(π- D.)0,3(π-8.已知()f x 是定义在R 上的奇函数,对R x ∈∀恒有)2()()2(f x f x f +=-,且当)1,0(∈x 时,x x x f -=2)(则=)23(f ( ) A. 43 B.41 C.41- D.43- 9.1tan10sin 40+= ( )A. B. C.2 D.10. 已知函数)0(1032)(23>+-=m nx mx x f 有且仅有两个不同的零点,则n m 22lg lg + 的最小值为 ( ) A.71 B. 91 C. 111 D. 131第II 卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分。
重庆一中2015届高三上学期 10月月考数学试卷(理科)(解析版)

重庆一中2015届高三上学期 10月月考数学试卷(理科)一、选择题(本题共10个小题,每小题5分,共50分)1.(5分)已知集合A{1,2},B={1,2},则可以确定不同映射f:A→B的个数为()A.1B.2C.3D.42.(5分)已知集合M={x|x2﹣2x<0},N={x|x<a},若M⊆N,则实数a的取值范围是()A.[2,+∞)B.(2,+∞)C.(﹣∞,0)D.(﹣∞,0] 3.(5分)已知α,β∈(0,π),则α+β=是sinα=cosβ的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(5分)函数f(x)=Asin(ωx+θ)(A>0,ω>0)的部分图象如图所示,则f(x)=()A.sin(2x﹣)B.sin(2x﹣)C.sin(4x+) D.sin(4x+)5.(5分)一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.6.(5分)方程有解,则a的最小值为()A.2B.1C.D.7.(5分)函数f(x)=sin(2x+θ)+cos(2x+θ),(|θ|<)的图象关于点对称,则f(x)的增区间()A.B.C.D.8.(5分)﹣2sin10°(cot5°﹣tan5°)=()A.1B.C.D.29.(5分)已知函数f(x)的导函数为f′(x),且满足f′(x)<2f(x),则()A.f(2)>e2f(1) B.e2f(0)>f(1) C.9f(ln2)<4f(ln3)D.e2f(ln2)<4f (1)10.(5分)给定实数a(a≠0),f:R→R对任意实数x均满足f(f(x))=xf(x)+a,则f (x)的零点的个数()A.0B.1C.2D.3二、填空题(本大题共6小题,考生作答5小题,每小题5分,共25分)11.(5分)函数的定义域为.12.(5分)在△ABC中,A=60°,AC=4,BC=2,则△ABC的面积等于.13.(5分)已知定义在R上的函数f(x)满足:f(x)=且f(x+2)=f(x),g(x)=,则方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为.14.(5分)如图所示,已知AB,BC是⊙O的两条弦,AO⊥BC,AB=,BC=2,则⊙O的半径等于.15.(5分)以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是(t为参数),圆C的极坐标方程是ρ=4cosθ,则直线l被圆C截得的弦长为.16.若不等式|x+1|+|x﹣3|≥a+对任意的实数x恒成立,则实数a的取值范围是.三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)17.(13分)已知函数f(x)=.(1)求f(x)的值域和最小正周期;(2)方程m[f(x)+]+2=0在内有解,求实数m的取值范围.18.(13分)已知函数f(x)=ax2+bx﹣a﹣ab(a≠0),当x∈(﹣1,3)时,f(x)>0;当x∈(﹣∞,﹣1)∪(3,+∞)时,f(x)<0.(1)求f(x)在(﹣1,2)内的值域;(2)若方程f(x)=c在[0,3]有两个不等实根,求c的取值范围.19.(13分)如图,在多面体ABC﹣A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=BC.(Ⅰ)求证:AB1∥面A1C1C;(Ⅱ)求二面角C﹣A1C1﹣B的余弦值的大小.20.(12分)设函数f(x)=x3﹣ax,g(x)=bx2+2b﹣1.(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;(2)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]内的最小值.21.(12分)已知圆C:(x﹣1)2+(y﹣1)2=2经过椭圆Γ:=1(a>b>0)的右焦点F,且F到右准线的距离为2.(1)求椭圆Γ的方程;(2)如图,过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点,求的最大值.22.(12分)设函数f(x)=﹣aln(1+x),g(x)=ln(1+x)﹣bx.(1)若函数f(x)在x=0处有极值,求函数f(x)的最大值;(2)是否存在实数b,使得关于x的不等式g(x)<0在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由;(3)证明:不等式﹣1<﹣lnn≤(n=1,2.…).重庆一中2015届高三上学期10月月考数学试卷(理科)参考答案与试题解析一、选择题(本题共10个小题,每小题5分,共50分)1.(5分)已知集合A{1,2},B={1,2},则可以确定不同映射f:A→B的个数为()A.1B.2C.3D.4考点:映射.专题:计算题;函数的性质及应用.分析:由映射的定义知集合A中每一个元素在集合B中有唯一的元素和它对应,A中1在集合B中有1或2与1对应,有两种选择,同理集合A中2也有两种选择,由分步计数原理求解即可.解答:解:由映射的定义知A中1在集合B中有1或2与1对应,有两种选择,同理集合A中2也有两种选择,由分步计数原理得从集合A={1,2}到集合B={1,2}的不同映射共有2×2=4个故选D.点评:本题考查映射的概念,考查两个集合之间映射的方式,求解本题可以利用列举法,最好选用计数原理,方便快捷,可迅速得出答案.2.(5分)已知集合M={x|x2﹣2x<0},N={x|x<a},若M⊆N,则实数a的取值范围是()A.[2,+∞)B.(2,+∞)C.(﹣∞,0)D.(﹣∞,0]考点:交集及其运算.专题:集合.分析:求出M中不等式的解集确定出M,根据N以及M为N的子集,确定出a的范围即可.解答:解:由M中不等式变形得:x(x﹣2)<0,解得:0<x<2,即M=(0,2),∵N={x|x<a},且M⊆N,∴a≥2,则a的范围为[2,+∞).故选:A.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.(5分)已知α,β∈(0,π),则α+β=是sinα=cosβ的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:运用诱导公式,和充分必要条件的定义判断求解.解答:解:(1)∵α,β∈(0,π),则α+β=,∴α=﹣β,∴sinα=sin(﹣β),即sinα=cosβ成立(2)∵sinα=cosβ,∴sinα=sin(﹣β),α=﹣β+2πk,k∈z,∴α+β=不一定成立.所以α+β=是sinα=cosβ的充分不必要条件,故选;A点评:本题考查了三角函数公式,性质,充分必要条件的定义,知识点多,但是难度不大.4.(5分)函数f(x)=Asin(ωx+θ)(A>0,ω>0)的部分图象如图所示,则f(x)=()A.sin(2x﹣)B.sin(2x﹣)C.sin(4x+) D.sin(4x+)考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:由y=Asin(ωx+φ)的部分图象可求得其振幅A及最小正周期T=π,继而可得ω;再由sin(2×+θ)=可求得θ,从而可得答案.解答:解:由图知f(x)在x=π时取到最大值,且最小正周期T满足T=π+=,∴A=,T==π,ω=2;由sin(2×+θ)=,得:sin(+θ)=1,∴+θ=2kπ+,θ=2kπ﹣,k∈Z.∴f(x)=sin(2x﹣).故选:B.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求θ是难点,考查识图与运算能力,属于中档题.5.(5分)一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.考点:由三视图求面积、体积.专题:计算题.分析:由三视图可知该几何体,是过一正三棱柱的上底面一边作截面,截去的部分为三棱锥,利用间接法求出其体积.解答:解:由三视图可知该几何体,是过一正三棱柱的上底面一边作截面,截去的部分为三棱锥,而得到的几何体.原正三棱锥的底面边长为2,高为2,体积V1=Sh=×2=2.截去的三棱锥的高为1,体积V2=×1=故所求体积为V=V1﹣V2=故选A.点评:本题考查三视图求几何体的体积,考查计算能力,空间想象能力,三视图复原几何体是解题的关键6.(5分)方程有解,则a的最小值为()A.2B.1C.D.考点:函数的零点与方程根的关系.专题:函数的性质及应用.分析:若方程有解,根据将对数式化为指数式后要得+2x=a有解,根据基本不等式求出+2x的最小值,即可得到答案.解答:解:若方程有解,则=a﹣2x有解即+2x=a有解∵+2x≥1故a的最小值为1故选B点评:本题考查的知识点是函数零点与方程根的关键,指对互化,基本不等式,其中将对数式化为指数式后得到+2x=a有解,是解答的关键.7.(5分)函数f(x)=sin(2x+θ)+cos(2x+θ),(|θ|<)的图象关于点对称,则f(x)的增区间()A.B.C.D.考点:两角和与差的正弦函数;正弦函数的单调性.专题:常规题型;三角函数的图像与性质.分析:利用两角和的正弦公式化成标准形式,根据图象关于点对称,求出θ的值,然后根据正弦函数的单调增区间求函数f(x)的单调增区间.解答:解:f(x)=sin(2x+θ)+cos(2x+θ),=2sin(2x+θ+),∵图象关于点对称,∴2×+θ+=kπ,(k∈Z)∴θ=kπ,(k∈Z),∵|θ|<,∴,∴f(x)=2sin(2x+);由(k∈Z)解得:(k∈Z)∴函数f(x)的增区间为.故选D.点评:本题考查了三角函数式的化简及三角函数的图象与性质,解题的关键是把三角函数式化成标准形式,在求θ值时要注意其范围.8.(5分)﹣2sin10°(cot5°﹣tan5°)=()A.1B.C.D.2考点:三角函数的化简求值.专题:三角函数的求值.分析:由条件利用同角三角函数的基本关系把要求的式子化为=﹣4cos10°,通分后利用诱导公式、和差化积公式化为2cos30°,从而得到结果.解答:解:﹣2sin10°(cot5°﹣tan5°)=﹣2sin10°(﹣)=﹣2sin10°•=﹣4cos10°======2cos30°=,故选:C.点评:题主要考查同角三角函数的基本关系、诱导公式、和差化积公式的应用,属于中档题.9.(5分)已知函数f(x)的导函数为f′(x),且满足f′(x)<2f(x),则()A.f(2)>e2f(1) B.e2f(0)>f(1) C.9f(ln2)<4f(ln3)D.e2f(ln2)<4f (1)考点:导数的运算.专题:函数的性质及应用.分析:构造函数g(x)=,利用定义得到函数的单调性,问题得以解决.解答:解:令g(x)=,则g′(x)==<0,则g(x)=为减函数,∴g(0)>g(1),即>,即e2f(0)>f(1),故选:B点评:本题首先须结合已知条件构造函数,然后考察用导数判断函数的单调性,再由函数的单调性和函数值的大小关系,判断自变量的大小关系,属中档题10.(5分)给定实数a(a≠0),f:R→R对任意实数x均满足f(f(x))=xf(x)+a,则f (x)的零点的个数()A.0B.1C.2D.3考点:根的存在性及根的个数判断.专题:计算题;选作题;函数的性质及应用.分析:假设函数有零点,通过反复利用公式f(f(x))=xf(x)+a,最终可得a=0,与题意相矛盾,从而说明没有零点.解答:解:若f(x)有零点b,则f(b)=0,则f(f(b))=f(0)=b•f(b)+a=a,即f(0)=a,则f(f(0))=f(a)=0•f(0)+a=a,则f(a)=a,则f(f(a))=f(a)=a•f(a)+a=a2+a=a,则a2=0,解得,a=0,与题意相矛盾,故f(x)没有零点.故选A.点评:本题考查了函数的零点的定义及对于新知识的接受能力,属于难题.二、填空题(本大题共6小题,考生作答5小题,每小题5分,共25分)11.(5分)函数的定义域为(﹣1,1).考点:函数的定义域及其求法.分析:由对数函数的真数一定大于0,可以得到x+1>0,又因为偶次开方被开方数一定非负且分式中分母不能为0,可以得到﹣x3﹣3x+4>0,进而求出x的取值范围.解答:解:∵x+1>0,∴x>﹣1,又∵﹣x3﹣3x+4>0,即x3+3x﹣4=(x3﹣1)+3(x﹣1)=(x﹣1)(x2+x+4),且x2+x+4≥>0,故﹣x3﹣3x+4>0⇔x﹣1<0,解得,x<1从而,﹣1<x<1故答案为:(﹣1,1)点评:定义域是2015届高考必考题通常以选择或填空的形式出现,通常注意:①偶次开方被开方数一定非负,②分式中分母不能为0,③对数函数的真数一定要大于0,④指数和对数的底数大于0且不等于1.⑤另外还要注意正切函数的定义域.12.(5分)在△ABC中,A=60°,AC=4,BC=2,则△ABC的面积等于2.考点:正弦定理.专题:解三角形.分析:利用三角形中的正弦定理求出角B,再利用三角形的面积公式求出△ABC的面积.解答:解:∵△ABC中,A=60°,AC=4,BC=2,由正弦定理得:,∴,解得sinB=1,∴B=90°,C=30°,∴△ABC的面积=.故答案为:.点评:本题着重考查了给出三角形的两边和其中一边的对角,求它的面积.正余弦定理、解直角三角形、三角形的面积公式等知识,属于基础题.13.(5分)已知定义在R上的函数f(x)满足:f(x)=且f(x+2)=f(x),g(x)=,则方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为﹣7.考点:分段函数的应用.专题:计算题;数形结合;函数的性质及应用.分析:化简g(x)的表达式,得到g(x)的图象关于点(﹣2,1)对称,由f(x)的周期性,画出f(x),g(x)的图象,通过图象观察[﹣5,1]上的交点的横坐标的特点,求出它们的和.解答:解:由题意知,函数f(x)的周期为2,则函数f(x),g(x)在区间[﹣5,1]上的图象如下图所示:由图形可知函数f(x),g(x)在区间[﹣5,1]上的交点为A,B,C,易知点B的横坐标为﹣3,若设C的横坐标为t(0<t<1),则点A的横坐标为﹣4﹣t,所以方程f(x)=g(x)在区间[﹣5,1]上的所有实数根之和为﹣3+(﹣4﹣t)+t=﹣7.故答案为:﹣7.点评:本题考查分段函数的图象和运用,考查函数的周期性、对称性和应用,同时考查数形结合的能力,属于中档题.14.(5分)如图所示,已知AB,BC是⊙O的两条弦,AO⊥BC,AB=,BC=2,则⊙O的半径等于1.5.考点:与圆有关的比例线段.专题:计算题;立体几何.分析:设垂足为D,⊙O的半径等于R,先计算AD,再计算R即可.解答:解:设垂足为D,⊙O的半径等于R,则∵AB,BC是⊙O的两条弦,AO⊥BC,AB=,BC=2,∴AD=1,∴R2=2+(R﹣1)2,∴R=1.5.故答案为:1.5点评:本题考查垂径定理的运用,考查学生的计算能力,属于基础题.15.(5分)以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是(t为参数),圆C的极坐标方程是ρ=4cosθ,则直线l被圆C截得的弦长为.考点:参数方程化成普通方程;点的极坐标和直角坐标的互化.专题:坐标系和参数方程.分析:圆C的极坐标方程是ρ=4cosθ,利用可得直角坐标方程,可得圆心C 及其半径r.由直线l的参数方程(t为参数),消去参数可得y=x﹣4.利用点到直线的距离公式可得圆心C到直线l的距离d.再利用弦长公式l=2即可得出.解答:解:∵圆C的极坐标方程是ρ=4cosθ,∴ρ2=4ρcosθ,∴x2+y2=4x,化为(x﹣2)2+y2=4,其圆心C(2,0),半径r=2.由直线l的参数方程(t为参数),消去参数可得y=x﹣4.圆心C到直线l的距离d==.∴直线l被圆C截得的弦长=2=.故答案为:2.点评:本题考查了极坐标方程参数方程化为直角坐标方程、点到直线的距离公式、弦长公式,考查了推理能力与计算能力,属于基础题.16.若不等式|x+1|+|x﹣3|≥a+对任意的实数x恒成立,则实数a的取值范围是(﹣∞,0)∪{2}.考点:绝对值不等式的解法.专题:计算题;数形结合;转化思想.分析:不等式对任意的实数x恒成立转化为a+小于等于函数y=|x+1|+|x﹣3|的最小值,根据绝对值不等式的几何意义可知函数y=|x+1|+|x﹣3|的最小值为4,因此原不等式转化为分式不等式的求解问题.解答:解:令y=|x+1|+|x﹣3|,由绝对值不等式的几何意义可知函数y=|x+1|+|x﹣3|的最小值为4,∵不等式对任意的实数x恒成立∴原不等式可化为≤4解得a=2或a<0故答案为:(﹣∞,0)∪{2}.点评:考查绝对值不等式的几何意义,把恒成立问题转化为求函数的最值问题,体现了转化的思想方法,属中档题.三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)17.(13分)已知函数f(x)=.(1)求f(x)的值域和最小正周期;(2)方程m[f(x)+]+2=0在内有解,求实数m的取值范围.考点:两角和与差的正弦函数;三角函数的周期性及其求法.专题:常规题型;三角函数的图像与性质.分析:(1)先利用和差公式把函数解析式化成标准形式,然后结合正弦函数的值域求f(x)的值域;(2)根据x的范围求出[f(x)+]的范围,然后由m[f(x)+]+2=0知,m≠0,f(x)+=﹣,只须让≤﹣≤2即可.解答:解:(1)f(x)=2sin(2x+)﹣.∵﹣1≤sin(2x+)≤1.∴﹣2﹣≤2sin(2x+)﹣≤2﹣,T==π,即f(x)的值域为[﹣2﹣,2﹣],最小正周期为π.…(7分)(2)当x∈[0,]时,2x+∈[],故sin(2x+)∈[],此时f(x)+=2sin(2x+)∈[,2].由m[f(x)+]+2=0知,m≠0,∴f(x)+=﹣,即≤﹣≤2,即,解得﹣≤m≤﹣1.即实数m的取值范围是[﹣].点评:本题考查了三解函数式的化简及三角函数的图象与性质,解题的关键是把函数解析式化成标准形式,在求解函数的值域时注意x的取值范围.把方程有解问题转化成求函数的值域问题解决.18.(13分)已知函数f(x)=ax2+bx﹣a﹣ab(a≠0),当x∈(﹣1,3)时,f(x)>0;当x∈(﹣∞,﹣1)∪(3,+∞)时,f(x)<0.(1)求f(x)在(﹣1,2)内的值域;(2)若方程f(x)=c在[0,3]有两个不等实根,求c的取值范围.考点:二次函数在闭区间上的最值;函数的值域;函数的零点与方程根的关系.专题:函数的性质及应用.分析:(1)由题意,﹣1,3是方程ax2+bx﹣a﹣ab=0的两根,求得得a和b的值,可得二次函数f(x)的解析式,从而求得f(x)在(﹣1,2)内的值域.(2)由题意可得x2﹣2x+c﹣3=0,在[0,3]有两个不等实根,设g(x)=x2﹣2x+c﹣3,则,由此解得c的范围.解答:解:(1)由题意,﹣1,3是方程ax2+bx﹣a﹣ab=0的两根,可得a=﹣1,b=2,则f(x)=﹣x2+2x+3=﹣(x﹣1)2+4 在(﹣1,2)内的值域为(0,4].(2)方程﹣x2+2x+3=c,即x2﹣2x+c﹣3=0,在[0,3]有两个不等实根,设g(x)=x2﹣2x+c﹣3,则,解得3≤c<4.点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了转化的数学思想,属基础题.19.(13分)如图,在多面体ABC﹣A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=BC.(Ⅰ)求证:AB1∥面A1C1C;(Ⅱ)求二面角C﹣A1C1﹣B的余弦值的大小.考点:二面角的平面角及求法;直线与平面平行的判定.专题:空间位置关系与距离;空间角.分析:(Ⅰ)取BC中点E,连结AE,C1E,B1E,由已知得四边形CEB1C1是平行四边形,AEC1A1是平行四边形,由此能证明AB1∥面A1C1C.(Ⅱ)由已知得A1A=AB=AC=1,A1A⊥AB,A1A⊥AC,从而A1A⊥面ABC,以A为原点,以AC为x轴建立坐标系,利用向量法能求出二面角C﹣A1C1﹣B的余弦值的大小.解答:(Ⅰ)证明:取BC中点E,连结AE,C1E,B1E,∵B1C1∥BC,,∴,∴四边形CEB1C1是平行四边形,∴B1E∥C1C,B1E=C1C,∵C1C⊂面A1C1C,B1E不包含于平面A1C1C,∴B1E∥面A1C1C,又ABB1A1是正方形,∴A1A C1E,∴AEC1A1是平行四边形,∴AE∥A1C1∵A1C1⊂面A1C1C,AE⊄面A1C1C,∴AE∥面A1C1C,∵AE∩B1E=E,∴面B1AE∥面A1C1C,∵AB1⊂面B1AE,∴AB1∥面A1C1C.(Ⅱ)∵四边形ABB1A1为正方形,∴A1A=AB=AC=1,A1A⊥AB,∴,∵A1C=A1B,∴,由勾股定理可得:∠A1AC=90°,∴A1A⊥AC,∵AB∩AC=A,∴A1A⊥面ABC,∵A1C=A1B=BC,∴,由勾股定理,得∠BAC=90°,∴AB⊥AC,故以A为原点,以AC为x轴建立坐标系如图,C(1,0,0),A1(0,0,1),,B(0,1,0),∴=(﹣1,0,1),=(﹣1,0,1),=(0,﹣1,1),=(),设面A1C1C的法向量为=(x,y,z),由•=0,=0,∴,令z=1,则=(1,﹣1,1),设面A1C1B的法向量为,则则,令k=1,则…(10分)所以,设二面角C﹣A1C1﹣B的平面角为α,,所以.…(12分)点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.20.(12分)设函数f(x)=x3﹣ax,g(x)=bx2+2b﹣1.(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;(2)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]内的最小值.考点:利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.专题:计算题;分类讨论;导数的概念及应用;导数的综合应用.分析:(1)分别求出函数f(x),g(x)的导数,由于曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,所以f(1)=g(1),且f′(1)=g′(1),列出方程,解出即可;(2)写出h(x)的解析式,求出单调增区间和减区间,得到h(﹣2)=h(1),讨论①当t+3<1,②当﹣2≤t<1时,③当t≥1时,通过单调性,分别求出最小值即可.解答:解:(1)因为f(x)=x3﹣ax(a>0),g(x)=bx2+2b﹣1,所以f′(x)=x2﹣a,g′(x)=2bx.因为曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,所以f(1)=g(1),且f′(1)=g′(1),即﹣a=b+2b﹣1,且1﹣a=2b,解得a=,b=.(2)当a=1,b=0时,h(x)=x3﹣x﹣1,b=,则由(2)可知,函数h(x)的单调递增区间为(﹣∞,﹣1),(1,+∞),单调递减区间为(﹣1,1).因为h(﹣2)=﹣,h(1)=﹣,所以h(﹣2)=h(1).①当t+3<1,即t<﹣2时,[h(x)]min=h(t)=t3﹣t﹣1.②当﹣2≤t<1时,[h(x)]min=h(﹣2)=﹣.③当t≥1时,h(x)在区间[t,t+3]上单调递增,[h(x)]min=h(t)=t3﹣t﹣1.综上可知,函数h(x)在区间[t,t+3]上的最小值[h(x)]min=.点评:本题考查导数的运用:求切线方程和求单调区间、极值和最值,考查分类讨论的思想方法,考查运算能力,属于中档题.21.(12分)已知圆C:(x﹣1)2+(y﹣1)2=2经过椭圆Γ:=1(a>b>0)的右焦点F,且F到右准线的距离为2.(1)求椭圆Γ的方程;(2)如图,过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点,求的最大值.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)在圆(x﹣1)2+(y﹣1)2=2中,令y=0,得F(2,0),得a2=8,由此能求出椭圆方程.(2)依题意射线l的斜率存在,设l:y=kx(x>0,k>0),设P(x1,kx1),Q(x2,kx2),直线代入椭圆、圆的方程,结合向量的数量积公式,利用导数,即可求的最大值.解答:解:(1)在C:(x﹣1)2+(y﹣1)2=2中,令y=0得F(2,0),即c=2,又得a2=8,∴椭圆Γ:=1.…(4分)(2)依题意射线l的斜率存在,设l:y=kx(x>0,k>0),设P(x1,kx1),Q(x2,kx2)直线代入椭圆方程得:(1+2k2)x2=8,∴x2=.(6分)由直线代入圆的方程得:(1+k2)x2﹣(2+2k)x=0,∴x1=,∴•=(x1,kx1)•(x2,kx2)=(x1x2+k2x1x2)=2•(k>0).(9分)设φ(k)=,φ′(k)=,令φ′(k)>0,得﹣1<k<.又k>0,∴φ(k)在(0,)上单调递增,在(,+∞)上单调递减.∴当k=时,φ(k)max=,即•的最大值为2.…(12分)点评:本题考查直线、圆、椭圆、平面向量等基础知识,考查直线与圆锥曲线的位置关系,考查运算求解能力、推理论证能力,考查数形结合、化归转化及函数与方程等数学思想.22.(12分)设函数f(x)=﹣aln(1+x),g(x)=ln(1+x)﹣bx.(1)若函数f(x)在x=0处有极值,求函数f(x)的最大值;(2)是否存在实数b,使得关于x的不等式g(x)<0在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由;(3)证明:不等式﹣1<﹣lnn≤(n=1,2.…).考点:利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(1)由已知得:,且函数f(x)在x=0处有极值,得a=1,从而求出函数的表达式,找出单调区间求出最值;(2)由已知得:再对b分情况讨论:①若b≥1,②若b≤0,③若0<b <1综合得出b的取值范围是x∈[1,+∞);(3)由前两问综合得出.解答:解析:(1)由已知得:,且函数f(x)在x=0处有极值∴,∴a=1∴,∴当x∈(﹣1,0)时,f'(x)>0,f(x)单调递增;当x∈(0,+∞)时,f'(x)<0,f(x)单调递减;∴函数f(x)的最大值为f(0)=0.(2)由已知得:①若b≥1,则x∈[0,+∞)时,∴g(x)=ln(1+x)﹣bx在[0,+∞)上为减函数,∴g(x)=ln(1+x)﹣bx<g(0)=0在(0,+∞)上恒成立;②若b≤0,则x∈[0,+∞)时,∴g(x)=ln(1+x)﹣bx在[0,+∞)上为增函数,∴g(x)=ln(1+x)﹣bx>g(0)=0,不能使g(x)<0在(0,+∞)上恒成立;③若0<b<1,则时,,当时,g'(x)≥0,∴g(x)=ln(1+x)﹣bx在上为增函数,此时g(x)=ln(1+x)﹣bx>g(0)=0,∴不能使g(x)<0在(0,+∞)上恒成立;综上所述,b的取值范围是b∈[1,+∞).(3)由(1)、(2)得:取得:.令,则,.因此.又,故.点评:本题考察了函数的最值问题,函数的单调性,导数的应用,不等式的证明,渗透了分类讨论思想,是一道综合题.欢迎下载,资料仅供参考!!!。
重庆市南开中学2015届高三12月月考数学(理)试题Word版含答案

重庆南开中学高2015级高三12月月考数学试题(理科)考试说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.(1)答题前,考生先将自己的姓名、准考证号码填写清楚;(2)选择题必须使用2B 铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写, 字体工整,字迹清楚;(3)请按照题号顺序在各题目的答题区域内作答.超出答题区域书写的答案无效,在草稿 纸、试题卷上答题无效;(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.第Ⅰ卷(选择题共50分)一.选择题:本大题共l0小题,每小题5分,共50分.在每小题给出的四个备选项中,只 有一项是符合题目要求的。
1.关于x 的不等式ax +b >0的解集不可能...是( ) (A)R (B)φ (C) ⎭⎬⎫⎩⎨⎧-a b x x > (D)⎭⎬⎫⎩⎨⎧≠a b x x 2.抛物线x y 42=的焦点到准线的距离为( ) (A)41 (B)21(C)2 (D)4 3.已知⎪⎭⎫⎝⎛∈ππ,2a ,5102cos 2sin =-a a ,则=a cos ( ) (A)54-(B)53- (C)54 (D)534.等比数列{}n a 的前n 项和为n S ,且4a ,2a 2,a 3成等差数列,若a 1=1。
则S 4=( ) (A)7 (B)8 (C)15 (D)165.已知单位向量a ,b 夹角为3π,则b a -2=( )(A)2 (B)3 (C)2 (D)56.已知直线()00022>,>b a by ax =+-平分圆014222=+-++y x y x C :的圆周长,则ba 21+的最小值为( ) (A) 24 (B) 223+ (C)4 (D)67.已知定义在R 上的偶函数()x f 满足:当x ≥0时,()83-=x x f ,则关于x 的不等式:()122>-x f 的解集为( )(A){}20>或<x x x (B) {}40>或<x x x (C) {}42>或<x x x - (D) {}22>或<x x x - 8.下列说法正确的个数是( )①命题“0123≤+-∈∀x x R x ,”的否定是“0120300>,+-∈∃x x R x ”; ②“ac b =”是“三个数a ,b ,c 成等比数列”的充要条件;⑨“1-=m ”是“直线01)12(=+-+y m mx 和直线023=++my x 垂直”的充要条件: ④“复数()R b a bi a Z ∈+=,是纯虚数的充要条件是0=a ”是真命题.(A)1 (B)2 (C)3 (D)49.设21F F ,为双曲线C :()0012222>,>b a by a x =-的左、右焦点,过坐标原点O 的直线与双曲线C 在第一象限内交于点P ,若a PF PF 621=+,且21F PF ∆为锐角三角形,则直线OP 斜率的取值范围是( )(A)⎪⎪⎭⎫⎝⎛34332, (B)⎪⎭⎫ ⎝⎛334, (C)⎪⎪⎭⎫ ⎝⎛3321, (D) ⎪⎪⎭⎫⎝⎛2332, 10.存在实数a ,使得对函数()x g y =定义域内的任意x ,都有()x g a <成立,则称a 为 g(x)的下界,若a 为所有下界中最大的数,则称a 为函数()x g 的下确界.已知+∈R z y x ,,且以z y x ,,为边长可以构成三角形,则()()2z y x zxyz xy z y x f ++++=,,的下确界为( )(A)61 (B)41 (C) 31 (D) 21第Ⅱ卷(非选择置共100分)二、填空置:本大题共5小题,每小题5分,共25分.把答案填写在答题卡相应位置上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆南开中学高2015级高三10月月考
数学试题(理科)
考试说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
(1)答题前,考生先将自己的姓名、准考证号码填写清楚;
(2)选择题必须使用2B 铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工
字迹清楚;
(3)请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效;
(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷(选择题共50分)
一.选择题:本大题共l0小题,每小题5分,共50分。
在每小题给出的四个各选项中,只有一项是符合题目要求的。
1.复数(1)Z i i =+(i 为虚数单位)在复平面内对应的点位于 ( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限
2.角α终边经过点(1,1)-,则cos α= ( )
A .1
B .-l
C .
32 D .22 3.设log 3a π=,0.32b =,21log 3
c =则 A .a b c >> B .a c b >> C .c a b >> D .b a c >>
4.3sin 23
x x π==“”是“”的 ( ) A .充要条件 B .充分不必要条件
C .必要不充分条件
D .既不充分又不必要条件
5.函数2()=82f x x x --+的一个零点所在区间为 ( )
A .(1,2)
B .(2,3)
C .(0,4)
D .(4,5)
6.如果命题“非p 或非q ”是假命题,给出下列四个结论:
①题“p 且q ”是真命题 ②命题“p 且q ”是假命题
③题“p 或q ”是真命题 ④命题“p 或q ”是假命题
其中正确的结论是 ( )
A .①③
B .②④
C .②③
D .①④
7.将函数sin()(0,||)y x ωϕωϕπ=+><的图象向左平移 个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为sin y x =则sin()y x ωϕ=+图像上离y 轴距离最近的对称中心为 ( )
A .(,0)3π
B .5(,0)6π
C .(,0)6π-
D .(,0)3
π- 8.已知()f x 是定义在R 上的奇函数,对x R ∀∈恒有(2)()(2)f x f x f -=+,且当(0,1)x ∈时,2()f x x x =-,则3
()2f =
( )
A .34
B .14
C .14-
D .34
- 9.4cos10tan80-=
A .3-
B .2-
C .1-
D .3
10.已知函数32()2310(0)f x mx nx m =-+>有且仅有两个不同的零点,则2211g m g n +的最小值为 ( )
A .
17 B .19 C .111 D .111
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题5分,共25分。
把答案填写在答题卡相应位置上。
11.已知2()3f x x x =+则定积分
20()f x dx =⎰ 12.已知A =
212x x
x +< ,{|1}B x x a =-<,且A B φ⋂≠则a 的取值范围为 13.已知(
,)2
πθπ∈,1122sin(2)sin cos 3πθθθ+=-=
考生注意:14、15、16为选做题,请从中任选两题作答,若三题全做,则按前两题给分.
14.如图,PQ 为半圆O 的直径,A 为以OQ 为直径的半圆A 的圆心,圆O 的的弦PN 切圆A 于点M ,PN=8,则圆A 的半径为
15.已知曲线12C C 、的极坐标方程分别为cos cos 10ρθρθ++=
则曲线1C 上的点与曲线2C 上的点的最近距离为
16.若不等式2|3||7|3x x a a ++-≥-的解集为R ,则实数a 的取值范围是 3
π
三、解答题:本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分13分) 已知函数()sin()cos cos()2f x x x x π
π=-+-
(1) 求函数的最小正周期;
(2) 当,44x ππ⎡⎤∈-⎢⎥⎣⎦
时,求函数()f x 的最大值和最小值.
18.(本小题满分13分) 已知函数()2sin(),6f x x x R π=+
∈ (1) 已知tan 2,(
,)2πθθπ=-∈,求()f θ的值 若8,0,,()2,()35f f παβαβ⎡⎤∈==⎢⎥⎣⎦
,求(22)f βα+的值.
19.(本小题满分13分) 设函数3221()(1)()3
f x x x m x x R =++-∈ (1) 当1m =时,求函数()f x 的单调区间与极值;
(2) 若函数(sin )0,
2y f x x π⎡⎤=∈⎢⎥⎣⎦
在上单调递增,求实数m 的取值范围.
20.(本小题满分l2分)
已知函数1()sin ()3
f x x ωπ⎡⎤=+⎢⎥⎣⎦的部分图象如图所示,其中P 为函数图象的最高点,A ,B 是函数图象与x 轴的相邻两个交点,
若y 轴不是函数()f x 图象的对称轴,且1tan 2
APB ∠=
(1)求函数()f x 的解析式; (2)已知角αβθ、、满足:2
12122(
)()=333f f αβππ-⋅-且3+=tan 24παβθ=,,求sin()sin()cos 2θαθβθ++的值.
21.(本小题满分12分) 已知函数2()()x f x ax x a e -=++
(1) 若函数()y f x =在点(0,(0))f 处的切线与直线310x y -+=平行,求a 的值;
22.(本小题满分12分)
已知函数()ln f x x =
(1)若方程()f x a x +=有且只有一个实数解,求a 的值;
(2)若函数215()()()22
g x f x x mx m =+
-≥的极值点1212,()x x x x <恰好是函数2()()2h x f x x bx =--的零点,记'()h x 为函数()h x 的导函数,求1
212(()')2x x y x x h +=-的最小值.。
