集美中学导学案---高二数学
微积分基本定理

例1计算下列定积分:
(1)ʃdx;(2)ʃ(2x-)dx;(3)ʃ(cosx-ex)dx.
跟踪训练1计算下列定积分:
(1)ʃ5x4dx;(2)ʃ(+)26xdx.
探究点二 分段函数的定积分
例2已知函数f(x)=先画出函数图象,再求这个函数在[0,4]上的定积分.
【巩固练习】
1.(1+cosx)dx等于()
A.πB.2C.π-2D.π+2
2.若ʃ(2x+)dx=3+ln 2,则a的值是()
A.5B.4C.3D.2
3.ʃ(x2-x)dx=_______
4.已知f(x)=,计算ʃf(x)dx.
5.在下面所给图形的面积S及相应表达式中,正确的有()
S=ʃ[f(x)-g(x)]dxS=ʃ(2-2x+8)dx S=ʃf(x)dx-ʃf(x)dx
探究点四 求不分割型图形的面积
问题怎样利用定积分求不分割型图形的面积?
例4计算由曲线y2=x,y=x2所围图形的面积S.
跟踪训练4求由抛物线y=x2-4与直线y=-x+2所围成图形的面积.
探究点五 分割型图形面积的求解
问题由两条或两条以上的曲线围成的较为复杂的图形,在不同的区间位于上方和下方的曲线不同时,这种图形的面积如何求呢?
例5计算由直线y=x-4,曲线y=以及x轴所围图形的面积S.
跟踪训练5求由曲线y=,y=2-x,y=-x所围成图形的面积.
探究点六 定积分的综合应用
例6在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为,试求:切点A的坐标以及在切点A的切线方程.
跟踪训练6如图所示,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.
高中高二数学教案(精选6篇)

随着社会一步步向前发展,我们可以使用讲话稿的机会越来越多,讲话稿可以起到指引或总结会议,传达贯彻上级精神等作用。
那么讲话稿一般是怎么写的呢?这次漂亮的小编为您带来了高中高二数学教案(精选6篇),希望可以启发、帮助到大家。
高二数学优秀教案篇一一、学情分析本节课是在学生已学知识的基础上进行展开学习的,也是对以前所学知识的巩固和发展,但对学生的知识准备情况来看,学生对相关基础知识掌握情况是很好,所以在复习时要及时对学生相关知识进行提问,然后开展对本节课的巩固性复习。
而本节课学生会遇到的困难有:数轴、坐标的表示;平面向量的坐标表示;平面向量的坐标运算。
二、考纲要求1、会用坐标表示平面向量的加法、减法与数乘运算。
2、理解用坐标表示的平面向量共线的条件。
3、掌握数量积的坐标表达式,会进行平面向量数量积的运算。
4、能用坐标表示两个向量的夹角,理解用坐标表示的平面向量垂直的条件。
三、教学过程(一)知识梳理:1、向量坐标的求法(1)若向量的起点是坐标原点,则终点坐标即为向量的坐标。
(2)设A(x1,y1),B(x2,y2),则=xxxxxxxxxxxxxxxx_||=xxxxxxxxxxxxxx_(二)平面向量坐标运算1、向量加法、减法、数乘向量设=(x1,y1),=(x2,y2),则+=-=λ=。
2、向量平行的坐标表示设=(x1,y1),=(x2,y2),则∥?xxxxxxxxxxxxxxxx.(三)核心考点·习题演练考点1.平面向量的坐标运算例1.已知A(-2,4),B(3,-1),C(-3,-4)。
设(1)求3+-3;(2)求满足=m+n的实数m,n;练:(20xx江苏,6)已知向量=(2,1),=(1,-2),若m+n=(9,-8)(m,n∈R),则m-n的值为考点2平面向量共线的坐标表示例2:平面内给定三个向量=(3,2),=(-1,2),=(4,1)若(+k)∥(2-),求实数k的值;练:(20xx,四川,4)已知向量=(1,2),=(1,0),=(3,4)。
高二下学期数学教案5篇

高二下学期数学教案5篇高二下学期数学教案(精选篇1)目的要求:1.复习巩固求曲线的方程的基本步骤;2.通过教学,逐步提高学生求贡线的方程的能力,敏捷把握解法步骤;3.渗透“等价转化”、“数形结合”、“整体”思想,培养学生全面分析问题的能力,训练思维的深刻性、宽阔性及严密性。
教学重点、难点:方程的求法教学方法:讲练结合、讨论法教学过程:一、学点聚集:1.曲线C的方程是f(x,y)=0(或方程f(x,y)=0的曲线是C)实质是①曲线C上任一点的坐标都是方程f(x,y)=0的解②以方程f(x,y)=0的解为坐标的点都是曲线C上的点2.求曲线方程的基本步骤①建系设点;②寻等列式;③代换(坐标化);④化简;⑤证明(若第四步为恒等变形,则这一步骤可省略)二、基础训练题:221.方程x-y=0的曲线是()A.一条直线和一条双曲线B.两个点C.两条直线D.以上都不对2.如图,曲线的方程是()A.x?y?0 B.x?y?0 C.xy?1 D.x?1 y3.到原点距离为6的点的轨迹方程是。
4.到x轴的距离与其到y轴的距离之比为2的点的轨迹方程是。
三、例题讲解:例1:已知一条曲线在y轴右方,它上面的每一点到A?2,0?的距离减去它到y轴的距离的差都是2,求这条曲线的方程。
例2:已知P(1,3)过P作两条互相垂直的直线l1、l2,它们分别和x轴、y轴交于B、C两点,求线段BC的中点的轨迹方程。
2例3:已知曲线y=x+1和定点A(3,1),B为曲线上任一点,点P在线段AB上,且有BP∶PA=1∶2,当点B在曲线上运动时,求点P 的轨迹方程。
巩固练习:1.长为4的线段AB的两个端点分别在x轴和y轴上滑动,求AB中点M的轨迹方程。
22.已知△ABC中,B(-2,0),C(2,0)顶点A在抛物线y=x+1移动,求△ABC的重心G的轨迹方程。
思考题:已知B(-3,0),C(3,0)且三角形ABC中BC边上的高为3,求三角形ABC的垂心H的轨迹方程。
集美中学2015--2016学年第一学期(秋季)各科教师任课表(
下午
数学
温银榕1-2
30龚洪洋3-4
赖春葵5-6
余亮7-8
郑锐9-10
林青青11-12
省叶阿通13-14
李争童(新)
4+1
王韫雅1-2
40李华3-4
5陈玮5-6
0吴春玲7、9
11陈娟兰10-11
刘伟8、12
新杨正国13-14
4+1
1许雅红1-2
文0方超飞3-4
理0戴赛红5-6
8丁仕杰7-8
刘海江9-10
谢艺明7-8
13李想9-14
2
3梁磊1、3、7、10
0黄仪2、4、5-6
张勤勇8-9
洪伟11-14
文2+1
理3
0 2林米晴1-2
4蒋丽英3-4
4+1
黄
仪
9
周五
上午
地理
2袁洁龄1-7
010牛志杰8-14
2
1孙良书1、3、13-14
0陈绍锋2、4、11-12
马玉辉5-6
王宝国7-10
文2+1
理3
陈庆军1-2
0张艳梅3-4
4+1
张艳梅
8
周四
上午
信
息
技术
★宋红1—4(户)、新
0★张志勇5-9(户)
★黄楚涵10-14
2
宋红
张志勇
黄楚涵
周三下午第三节选修
1
宋红
3
周五
上午
通用
技术
★张恩锋1-14
1
张恩锋
1
周五
上午
心理健康与
口语
★廖潭林1-14、新
高二数学优秀教案(优秀8篇)

高二数学优秀教案(优秀8篇)篇一:高二数学优秀教案5 篇一高中数学教案:圆教学目的:掌握圆的标准方程,并能解决与之有关的。
问题教学重点:圆的标准方程及有关运用教学难点:标准方程的灵活运用教学过程:一、导入新课,探究标准方程二、掌握知识,巩固练习练习:⒈说出下列圆的方程⑴圆心(3,-2)半径为5⑵圆心(0,3)半径为3⒉指出下列圆的圆心和半径⑴(x-2)2+(y+3)2=3⑵x2+y2=2⑶x2+y2-6x+4y+12=0⒊判断3x-4y-10=0和x2+y2=4的位置关系⒋圆心为(1,3),并与3x-4y-7=0相切,求这个圆的方程三、引伸提高,讲解例题例1、圆心在y=-2x上,过p(2,-1)且与x-y=1相切求圆的方程(突出待定系数的数学方法)练习:1、某圆过(-2,1)、(2,3),圆心在x轴上,求其方程。
2、某圆过A(-10,0)、B(10,0)、C(0,4),求圆的方程。
例2:某圆拱桥的跨度为20米,拱高为4米,在建造时每隔4米加一个支柱支撑,求A2P2的长度。
例3、点M(x0,y0)在x2+y2=r2上,求过M的圆的切线方程(一题多解,训练思维)四、小结练习P771,2,3,4五、作业P811,2,3,4篇二:关于高二数学教案篇二【教学目标】1、会用语言概述棱柱、棱锥、圆柱、圆锥、棱台、圆台、球的结构特征。
2、能根据几何结构特征对空间物体进行分类。
3、提高学生的观察能力;培养学生的空间想象能力和抽象括能力。
【教学重难点】教学重点:让学生感受大量空间实物及模型、概括出柱、锥、台、球的结构特征。
教学难点:柱、锥、台、球的结构特征的概括。
【教学过程】1、情景导入教师提出问题,引导学生观察、举例和相互交流,提出本节课所学内容,出示课题。
2、展示目标、检查预习3、合作探究、交流展示(1)引导学生观察棱柱的几何物体以及棱柱的图片,说出它们各自的特点是什么?它们的共同特点是什么?(2)组织学生分组讨论,每小组选出一名同学发表本组讨论结果。
高中数学教学设计(优秀8篇)

高中数学教学设计(优秀8篇)高中数学教学设计篇一一、指导思想与理论依据数学是一门培养人的思维,发展人的思维的重要学科。
因此,在教学中,不仅要使学生“知其然”而且要使学生“知其所以然”。
所以在学生为主体,教师为主导的原则下,要充分揭示获取知识和方法的思维过程。
因此本节课我以建构主义的“创设问题情境——提出数学问题——尝试解决问题——验证解决方法”为主,主要采用观察、启发、类比、引导、探索相结合的教学方法。
在教学手段上,则采用多媒体辅助教学,将抽象问题形象化,使教学目标体现的更加完美。
二、教材分析三角函数的诱导公式是普通高中课程标准实验教科书(人教A版)数学必修四,第一章第三节的内容,其主要内容是三角函数诱导公式中的公式(二)至公式(六).本节是第一课时,教学内容为公式(二)、(三)、(四).教材要求通过学生在已经掌握的任意角的三角函数的定义和诱导公式(一)的基础上,利用对称思想发现任意角与、、终边的对称关系,发现他们与单位圆的交点坐标之间关系,进而发现他们的三角函数值的关系,即发现、掌握、应用三角函数的诱导公式公式(二)、(三)、(四).同时教材渗透了转化与化归等数学思想方法,为培养学生养成良好的学习习惯提出了要求。
为此本节内容在三角函数中占有非常重要的地位。
三、学情分析本节课的授课对象是本校高一(1)班全体同学,本班学生水平处于中等偏下,但本班学生具有善于动手的良好学习习惯,所以采用发现的教学方法应该能轻松的完成本节课的教学内容。
四、教学目标(1).基础知识目标:理解诱导公式的发现过程,掌握正弦、余弦、正切的诱导公式;(2).能力训练目标:能正确运用诱导公式求任意角的正弦、余弦、正切值,以及进行简单的三角函数求值与化简;(3).创新素质目标:通过对公式的推导和运用,提高三角恒等变形的能力和渗透化归、数形结合的数学思想,提高学生分析问题、解决问题的能力;(4).个性品质目标:通过诱导公式的学习和应用,感受事物之间的普通联系规律,运用化归等数学思想方法,揭示事物的本质属性,培养学生的唯物史观。
高二下学期数学教案

高二下学期数学教案作为一位辛劳耕耘的教育工作者,通常会被要求编写教案,编写教案有利于我们科学、公道地安排课堂时间。
那么优秀的教案是什么样的呢?以下是作者为大家整理的高二下学期数学教案,欢迎大家鉴戒与参考,期望对大家有所帮助。
高二下学期数学教案1一、指导思想在学校教学工作意见指导下,在年级部工作的框架下,认真落实学校订备课组工作的各项要求,严格实行学校的各项教育教学制度和要求,强化数学教学研究,提高全组老师的教学、教研水平,明确任务,团结协作,美满完成教学教研任务。
二、教材简析使用人教版《普通高中课程标准实验教科书·数学(A版)》,教材在坚持我国数学教育良好传统的条件下,认真处理继承、鉴戒、发展、创新之间的关系,体现基础性、时期性、典型性和可接受性等,具有亲和力、问题性、科学性、思想性、运用性、联系性等特点。
三、教学任务本学期上半期授课内容为《选修1—2》和《选修4—4》,中段考落后入第一轮复习。
四、学生基本情形及教学目标认真贯彻高中数学新课标精神,建立新的教学理念,以“双基”教学为主要内容,坚持“抓两头、带中间、整体推动”,使每个学生的数学能力都得到提高和发展。
高二文科学生共有10个班,其中尖尖班2个,8个平行重点班。
尖尖班的学生重点是数学尖子生的培养,冲刺高考数学高分为目标。
平行班学生的主要任务有两点,第一点:保证重点学生的数学成绩稳步上升,成为学生的优势科目;第二点:加强数学学习比较困难学生的辅导培养,增加其信息并逐渐缩小数学成绩差距。
五、教法分析1、选取与内容密切相干的,典型的,丰富的和学生熟悉的素材,用生动活泼的语言,创设能够体现数学的概念和结论,数学的思想和方法,以及数学运用的学习情境,使学生产生对数学的亲切感,引发学生“看个究竟”的冲动,以到达培养其爱好的目的。
2、通过“视察”,“摸索”,“探究”等栏目,引发学生的摸索和探索活动,切实改进学生的学习方式。
3、在教学中强调类比,推广,特别化,化归等数学思想方法,尽可能养成其逻辑思维的习惯。
集美中学高二年数学理科单元测试题
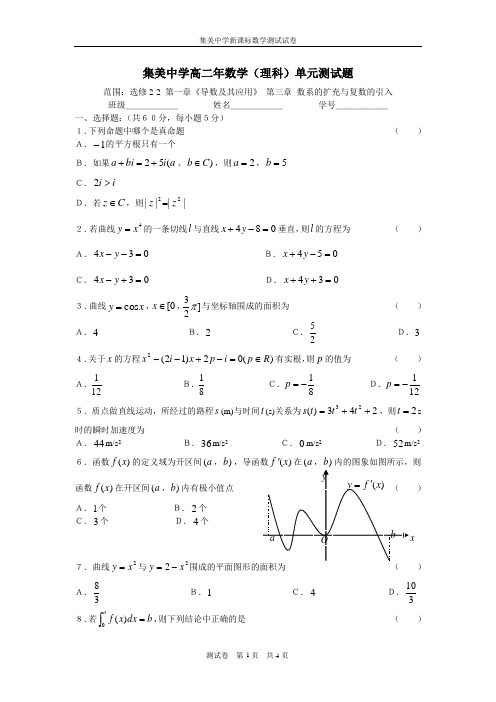
集美中学高二年数学(理科)单元测试题范围:选修2-2 第一章《导数及其应用》 第三章 数系的扩充与复数的引入 班级______ 姓名______ 学号______一、选择题:(共60分,每小题5分) 1.下列命题中哪个是真命题 ( ) A.1-的平方根只有一个B.如果a i bi a (52+=+、)C b ∈,则2=a ,5=b C.i i >2D.若C z ∈,则||||22z z =2.若曲线4x y =的一条切线l 与直线084=-+y x 垂直,则l 的方程为 ( ) A.034=--y x B.054=-+y x C.034=+-y x D.034=++y x3.曲线x y cos =,0[∈x ,]23π与坐标轴围成的面积为 ( ) A.4 B.2 C.25D.3 4.关于x 的方程)(02)12(2R p i p x i x ∈=-+--有实根,则p 的值为 ( ) A.121 B.81 C.81-=p D.121-=p 5.质点做直线运动,所经过的路程s (m)与时间t (s)关系为243)(23++=t t t s ,则2=t s时的瞬时加速度为 ( ) A.44m/s 2 B.36m/s 2 C.0m/s 2 D.52m/s 2 6.函数)(x f 的定义域为开区间a (,)b ,导函数)(x f '在a (,)b 内的图象如图所示,则函数)(x f 在开区间a (,)b 内有极小值点A.1个 B.2个C.3个 D.4个7.曲线2x y =与22x y -=围成的平面图形的面积为 ( ) A.38 B.1 C.4 D.3108.若⎰=ab dx x f 0)(,则下列结论中正确的是 ( )A.若)(x f 是R 上的偶函数,则⎰-=aa x f 0)(;B.若)(x f 是R 上的奇函数,则⎰-=aab x f 2)(;C.若0>b ,则)(x f 在0[,]a 恒有0)(>x f ;D.以上说法都不正确. 9.如果N 1力能拉长弹簧1cm ,为将弹簧拉长6cm ,所耗费的功是 ( ) A.18.0J B.26.0J C.12.0J D.28.0J 10.设1z 、C z ∈2,已知1||||21==z z ,2||21=-z z ,则||21z z +为 ( ) A.2 B.2 C.3 D.1 11.对于R 上可导的任意函数)(x f ,若满足0)()1(≥'-x f x ,则必有 ( ) A.)1(2)2()0(f f f <+ B.)1(2)2()0(f f f ≤+ C.)1(2)2()0(f f f ≥+ D.)1(2)2()0(f f f >+12.函数x ax y -=3在R 上是减函数,则 ( ) A.1=a B.0<a C.2=a D.0≤a 二、填空题:(共16分,每小题4分)13.已知ABCD 是复平面内的平行四边形,A ,B ,D 三点对应的复数分别为i 31+,i -,i 53+,则点C 所对应的复数为___________. 14.计算定积分=-⎰dx x 22|1|_______________.15.已知C z ∈,且1|21|=-+i z ,则||z 的最大值为_____________. 16.将此式++++∞→2111(lim n n n (21)+表示为定积分_____________. 三、解答题:(共74分,17题至21题12分,22题14分)17.分别计算出下列各式的值:⑴))12ln(2('+⋅x x;(其中1>x ); ⑵dx x x x )cos sin (20⎰++π; ⑶2)1(2-+i i ;18.已知复数)1(216)2(2i imm i z ----+=.当实数m 取什么值时,复数z 是 ⑴零; ⑵虚数; ⑶纯虚数; ⑷复平面内第二、四象限角平分线上的点对应的复数.19.已知函数54)(23+++=bx ax x x f 在1-=x 与23=x 处有极值.求: ⑴写出函数的解析式; ⑵求出函数的单调区间; ⑶求)(x f 在1[-,]2上的最值.20.设1z 是虚数,1121z z z +=是实数,且112≤≤-z . ⑴求||1z 的值以及1z 的实部的取值范围; ⑵若1111z z w +-=,求证w 为纯虚数.21.在曲线)0(2≥=x x y 上某一点A 处作一切线使之与曲线以及x 轴所围的面积为121,试求:⑴切点A 的坐标;⑵过切点A 的切线方程.22.(2006年福建卷)统计表明,某种型号的汽车在匀速行驶中每小时耗油量y (升)关于行驶速度x (千米/小时)的函数解析式可以表示为:880312800013+-=x x y)1200(≤<x .已知甲、乙两地相距100千米.⑴当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?⑵当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集美中学导学案---高二数学
导学案—§9.6空间向量坐标运算(一)日期
一、教材导读
1空间直角坐标系:
(1)若空间的一个基底的三个基向量互相垂直,且长为1,这个基底叫单位正交基底,用{,,}i j k 表示;
(2)在空间选定一点O 和一个单位正交基底{,,}i j k ,以点O 为原点,分别以,,i j k 的方向为正方向建立三条数轴:x 轴、y 轴、z
轴,它们都叫坐标轴.我们称建立了一个空间直角坐标系O xyz -,点O 叫原点,向量 ,,i j k 都叫坐标向量.通过每两个坐标轴的
平面叫坐标平面,分别称为xOy 平面,yOz 平面,zOx 平面;
2.空间直角坐标系中的坐标:
在空间直角坐标系O xyz -中,对空间任一点A ,存在唯一的有序实数组(,,)x y z ,使OA xi yj zk =++ ,有序实数组(,,)
x y z 叫作向量A 在空间直角坐标系O xyz -中的坐标,记作(,,)A x y z ,x 叫横坐标,y 叫纵坐标,z 叫竖坐标.
3.空间向量的直角坐标运算律:
(1)若123(,,)a a a a = ,123(,,)b b b b = ,则
①112233(,,)a b a b a b a b +=+++ ,②112233(,,)a b a b a b a b -=--- ,
③123(,,)()a a a a R λλλλλ=∈ , ④ 112233a b a b a b a b ⋅=++ ,
⑤112233//,,()a b a b a b a b R λλλλ⇔===∈ ,⑥1122330a b a b a b a b ⊥⇔++= .
(2)若111(,,)A x y z ,222(,,)B x y z ,则212121(,,)AB x x y y z z =--- .
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标
二、例题
例1 已知)5,4,3(-=,)6,1,2(--=
则=+ ;=-b a ;
32-= ;=∙ 。
例2(42p 2)
集美中学导学案---高二数学
班级 高二( )班 座号 姓名
三、作业
43p 1~6.。
