泥沙粒径与沉降速度关系表
砂子的沉降风速计算公式

砂子的沉降风速计算公式砂子的沉降风速是指在大气环境中,砂子颗粒由于重力作用而向下运动的速度。
砂子的沉降风速是地质学、气象学和环境科学等领域的重要参数,对于研究自然环境和预测自然灾害具有重要意义。
在实际工程中,准确计算砂子的沉降风速对于建筑物的设计和土壤侵蚀的预防具有重要意义。
本文将介绍砂子的沉降风速计算公式及其应用。
砂子的沉降风速与砂子颗粒的粒径、密度、形状以及大气环境中的风速等因素密切相关。
一般来说,砂子颗粒越大、密度越大,其沉降风速就越大;而风速越大,砂子的沉降风速也会增加。
根据这些因素,研究者提出了一系列砂子的沉降风速计算公式,其中最为常用的是斯托克斯定律和牛顿定律。
斯托克斯定律是最早用于描述颗粒在流体中运动的定律之一,它适用于小颗粒在粘性流体中的沉降运动。
斯托克斯定律认为,当颗粒的直径小于0.1mm时,颗粒的沉降速度与颗粒的直径的平方成正比。
斯托克斯定律的计算公式如下:V = (2/9) (r^2) g (ρ1 ρ2) / η。
其中,V为砂子的沉降风速,r为砂子颗粒的半径,g为重力加速度,ρ1为砂子颗粒的密度,ρ2为流体的密度,η为流体的粘度。
牛顿定律适用于大颗粒在流体中的沉降运动。
牛顿定律认为,当颗粒的直径大于0.1mm时,颗粒的沉降速度与颗粒的直径的平方根成正比。
牛顿定律的计算公式如下:V = (1/18) (d^2) g (ρ1 ρ2) / η。
其中,V为砂子的沉降风速,d为砂子颗粒的直径,g为重力加速度,ρ1为砂子颗粒的密度,ρ2为流体的密度,η为流体的粘度。
以上两个公式是砂子的沉降风速计算中最为常用的公式,它们可以较为准确地预测砂子在大气环境中的沉降风速。
但需要注意的是,这两个公式都是在理想情况下得出的结果,在实际应用中可能会受到一些因素的影响而产生偏差。
因此,在实际工程中,需要根据具体情况对计算结果进行修正和调整。
砂子的沉降风速计算公式的应用范围非常广泛。
在地质学领域,砂子的沉降风速可以帮助研究者了解地质构造和地层的形成过程;在气象学领域,砂子的沉降风速可以帮助预测自然灾害,如沙尘暴和风沙侵蚀;在环境科学领域,砂子的沉降风速可以帮助评估土壤侵蚀的程度,指导土地的合理利用和保护。
河流动力学第三章 泥沙特性

三、泥沙的水下休止角
– 定义:静水中、不致塌落的倾角 – 影响因素:泥沙粒径、级配及形状 – 变化范围:32º-39 º
三、泥沙的水下休止角 f tgφ
• 根据天津大学研究成果,泥沙水下休止角(°)与粒径D(mm)
有如下关系: 32.5 1.27d
抛石
➢ 0.5 <Red<1000时,由于Cd 为ω及d的函数,目 前无合适的计算公式,只能借助实验资料来计算
ω及Red。
21
22
三、泥沙的沉速
– 天然泥沙不是球体,需要考虑差异 – 基本原理、基本方法大同小异 – 相关研究较多,但所得公式结构相近 – 过渡区复杂,各家公式百花齐放 – 水电部规范综合了多家公式
– 特点
♥ 包含孔隙在内: s = s (1-e) ♥ 变幅较大:最大1.7t/m3,最小0.3t/m3 ♥ 原因:孔隙变化较大
二、泥沙的干容重与干密度
– 影响因素
♥ 泥沙粒径 ➢ 颗粒越细其值越小:
D<0.005mm0.56t/m3 ➢ 颗粒越细变幅越大:0.56-1.35t/m3 ♥ 泥沙淤积厚度 ➢ 淤积深度越深干容重越大,变幅越小
1.72 s gd 0.41 m / s
Red= D/ =0.41×3.5/1000/10-6=1432.1>1000,假定符合,
属紊流
泥沙的水力特性
四、其他影响因素
– 泥沙形状
♥ 细颗粒不重要 ♥ 砾石、卵石、块石应考虑(越扁平,沉速越小)
– 水质
♥ 絮凝的影响 ♥ 出现絮凝后,沉速增加,一般0.4-0.5mm/s
D
(
6V
)1/
3
颗粒沉降速度计算
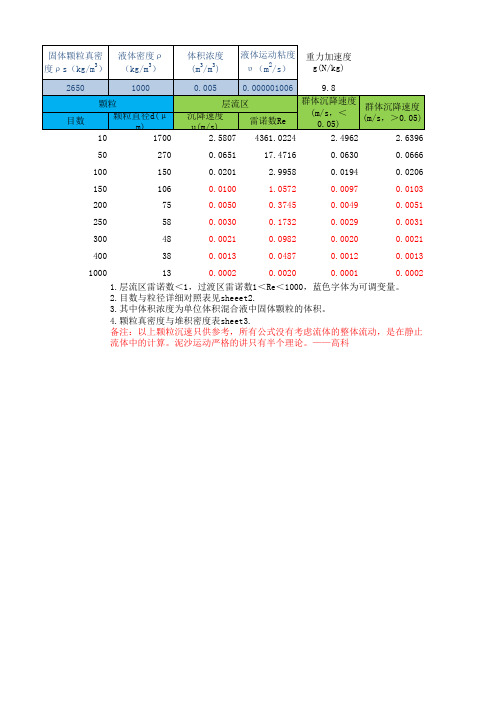
过渡区
群体沉降速度 群体沉降速度
沉降速度 u(m/s)
雷诺数Re (m/s,<0.05) (m/s,>0.05)
0.2219 32.4991
0.2147
0.2270
0.0250 2.6302
0.0242
0.0256
0.0125 1.1781
0.0121
0.0127
0.0083 0.7331
0.0080
群体沉降速度 (m/s,>0.05)
2.5807 4361.022
270
0.0651
17.4716
0.0630
0.0666
100
150
0.0201
2.9958
0.0194
0.0206
150
106
0.0100
1.0572
0.0097
0.0103
200
75
0.0050
0.3745
0.0049
0.0051
250
58
0.0030
0.1732
0.0029
0.0031
300
48
0.0021
0.0982
0.0020
0.0021
400
38
0.0013
0.0487
0.0012
0.0013
1000
13
0.0002
0.0020
0.0001
0.0002
1.层流区雷诺数<1,过渡区雷诺数1<Re<1000,蓝色字体为可调变量。 2.目数与粒径详细对照表见sheeet2. 3.其中体积浓度为单位体积混合液中固体颗粒的体积。 4.颗粒真密度与堆积密度表sheet3. 备注:以上颗粒沉速只供参考,所有公式没有考虑流体的整体流动,是在静止 流体中的计算。泥沙运动严格的讲只有半个理论。——高科
泥沙沉速实验报告

泥沙沉速实验报告引言沉积是河流、湖泊、海洋等自然水体中的重要过程之一。
沉积速度的测定对于研究水体的流动特性和沉降物的运移有着重要的意义。
本次实验旨在通过观察不同颗粒物在水体中的沉降速度,探究泥沙的沉降特性。
材料与方法材料本实验所用材料如下:- 透明的水槽- 不同粒径的泥沙样品- 显微镜- 计时器方法1. 将透明的水槽放置在水平台上,保持稳定。
2. 将待测的泥沙样品分别加入水槽中,使其悬浮于水体中。
3. 使用计时器记录每个样品开始沉降的时间,并持续观察其沉降过程。
4. 当泥沙样品完全沉降至底部,停止计时。
结果与讨论本次实验我们选取了不同颗粒粒径的泥沙样品进行测试,观察了它们的沉降速度。
以下是不同颗粒粒径泥沙样品的实验结果:泥沙粒径(mm)沉降时间(s)0.1 350.3 420.5 550.7 681.0 84根据实验结果,我们可以得出以下结论:1. 泥沙的沉降速度与颗粒粒径成反比。
粒径越小的泥沙沉降速度越快。
2. 泥沙的沉降速度受到水中颗粒浓度的影响。
当水中颗粒浓度增加时,泥沙的沉降速度会减慢。
3. 泥沙的沉降速度还与水的黏度有关。
黏度越大,泥沙的沉降速度越慢。
实验过程中,我们还观察到了泥沙样品的沉降过程。
随着时间的推移,泥沙样品逐渐从悬浮状态转为沉降状态,最终沉降到水槽的底部。
在观察过程中,我们使用了显微镜来观察微观颗粒的行为。
结论本次实验通过观察不同粒径泥沙样品的沉降过程,得出了泥沙粒径与沉降速度、水质浓度和水的黏度的关系。
这对于进一步研究河流、湖泊、海洋等自然水体中的沉积特性具有重要意义。
同时,我们也意识到在实际应用中,应根据具体情况选择合适的泥沙样品进行实验,以获得更准确的结果。
参考文献(请参考相关文献格式,将实验所涉及的文献列出)。
河流动力学2-泥沙特性

Chap1 泥沙特性本章知识要点:泥沙粒径表达形式泥沙的组成与粒配曲线比表面积的意义双电层与结合水泥沙干容重及其影响因素泥沙沉速与层流、紊流、过渡区絮凝现象● 泥沙来源:①流域地表冲蚀而来;②从原河床上冲起的。
● 土壤侵蚀最严重的黄河中游的黄土高原永定河和西辽河流域,相当于地表每年普遍冲掉0.6毫米的厚度,加上人类活动,如盲目开垦等,含沙量很高的正是黄河中游的一些干支流,年均含沙量高达300公斤/m 2以上,而南部一些省份,年均含沙量不足1公斤/m 2。
§1-1 泥沙的几何特性一、泥沙的粒径● 泥沙的不同形状与它们在水流中的运动状态有关,较粗的沿河底推移前进,碰撞机会多,动量较大易磨损;反之不易磨损而保持棱角峥嵘的外貌。
为比较不同泥沙颗粒的形状、大小的异同,必须有某些指标对它们进行对比。
泥沙的形状的表达方式● 球度系数:(因为泥沙接近于球体,所以以球体作参照物)与沙粒等体积的球体的表面积与泥沙的实际表面积之比(与球接近的程度)。
研究表明,球度系数相等的两颗泥沙,在水中的流体动力特性大致相同。
由于球度系数难以测定(V 可用排水、称重法确定,但表面积难以测定),常用泥沙的长、中、短三个轴a, b, c ,按下式近似表示:Φ=1942年克来拜因提出)● 形状系数:ab c S P = 1、 等容粒径:泥沙颗粒的大小通常用泥沙颗粒直径来表示,泥沙颗粒形状不规则,难以确定泥沙的粒径,实际中采用等容粒径来表示。
即:与泥沙颗粒体积相等的球体直径。
(泥沙体积可用称重、排水等方法测出:W V g ρ=)——对比水力学中表面粗糙度的∆确定 136V d π⎛⎫= ⎪⎝⎭ 式中:V 为泥沙颗粒的体积。
2、算术平均粒径:用长、中、短轴(a 、b 、c )的算数平均值来表征泥沙粒径1()3d a b c =++3、几何平均粒径:d =当泥沙形状为椭球体时,等容粒径与几何平均粒径相同(V=лabc/6=лd 3/6)4、中轴长度:接近而偏大于几何平均粒径(较粗天然沙测量的结果)5、筛径:仅对于单颗的卵石、砾石等可以通过称重,再除以泥沙的重率,得到体积而后求其等容粒径,或直接量测其三轴长度,再求其平均值。
城市排水沟道中泥沙运动流速分析

无机物占 (*’ , 沙粒在 物的体积中有机物占 #’ , [ !, ,] 。表 ! 中的 "++ 以下的占沉积物体积的 (&’ 数据可以说明沟道沉泥中所含沙粒大小的体积平均 百分数, 国内个别城市也曾有人作过分析, 得出近似 的结论。
表!
$’ % ! + " ’, # -・ $ % % ・ & " # & ’ 式中 ! + — — —扬动流速, . / 0; 其它符号与单位同 (%) 式。
(*)
注: 流速单位为 . / 0。
(&) 沙玉清教授提出的非球体颗粒的沉速修正 系数是必要而合理的, 其起动流速、 扬动流速、 止动 流速等计算公式是在分析大量前人研究成果的基础 上所作的概括, 与国内外排水沟道多年实用的经验 数值也比较吻合。 (#) 自然界中沙粒形状极不规则, 一般呈尖角 形, 并非球体, 过渡区内非球体颗粒的等容粒径沉速 为球体颗粒沉速的 *’3 , 过去在国内外排水工程中 都没有给予修正。相应的起动流速、 扬动流速、 止动 流速应为球体的 $$"3 4 $$’3 。 ( %) 排水沟道中的沉积物分析表明: 沉积物体积 中有机物占 #3 , 无机物占 ,*3 , 沙粒粒径在 &.. 以下 的 占 ,"3 。沟 道 自 清 目 标 的 沙 粒 粒 径 定 为 &.. 是较为合适的。 (’) 关于沟道自清流速的概念究竟应以泥沙运 动中的三种流速概念的哪一种为准, 过去在国内外 文献中都未见明确论述。认为沟道自清流速的概念 应是指起动流速而言, 它在理论上能满足沟底沉沙 ($$) ($&) 沿底部沙浪跳跃滚动随水流前进达到自清要求。扬 动流速显然要求过高, 在经济上欠合理。止动流速 不能满足已经沉积在沟底的泥沙自清要求, 在技术 上不合适。 (() 污水沟道现用的最小设计流速 " ) (. / 0 可 满足污水管道大小管径自清目标沙粒粒径为 &.. 的起动流速要求, 沟道可以达到基本自清的目的。 国内外排水沟道的实际运行情况也证实了这一流速 能满足沟道的自清功能。 ( *) 起动流速、 扬动流速、 止动流速三者与 & " 2 &
颗粒沉降速度计算

过渡区
群体沉降速度 群体沉降速度
沉降速度 u(m/s)
雷诺数Re (m/s,<0.05) (m/s,>0.05)
0.2219 32.4991
0.2147
0.2270
0.0250 2.6302
0.0242
0.0256
0.0125 1.1781
0.0121
0.0127
0.0083 0.7331
0.0080
群体沉降速度 (m/s,>0.05)
2.5807 4361.0224
2.4962
2.6396
50
270
0.0651
17.4716
0.0630
0.0666
100
150
0.0201
2.9958
0.0194
0.0206
150
106
0.0100
1.0572
0.0097
0.0103
200
75
0.0050
0.3745
0.00490Biblioteka 005125058
0.0030
0.1732
0.0029
0.0031
300
48
0.0021
0.0982
0.0020
0.0021
400
38
0.0013
0.0487
0.0012
0.0013
1000
13
0.0002
0.0020
0.0001
0.0002
1.层流区雷诺数<1,过渡区雷诺数1<Re<1000,蓝色字体为可调变量。 2.目数与粒径详细对照表见sheeet2. 3.其中体积浓度为单位体积混合液中固体颗粒的体积。 4.颗粒真密度与堆积密度表sheet3. 备注:以上颗粒沉速只供参考,所有公式没有考虑流体的整体流动,是在静止 流体中的计算。泥沙运动严格的讲只有半个理论。——高科
泥沙的沉速讲解

1/
3
s
1
/
3
1/
3
4 3
ReD CD
1/ 3
ReD
Sa
d
g1/
3
s
1/
3
1
/
3
g1/
3
s
2/3
1/ 3 d
上述公式中单位用国际单位:ω:m/s,g:m/s2,d:m
公式单位若为:ω: cm/s,g:cm/s2,d:mm
g1
/
3
s
1/ 3 d
10 2/ 3
F 3 d 3 d
(2-4)
圆球绕流阻力的一般表达式 (2-2)
F
Cd
d2
4
2
2
得
Cd
24
d
24 Red
(2-5)
8
5、层流区、紊流区和过渡区圆球沉速公式 ①、层流区圆球沉速公式( Red<0.5)源自将CD24
d
代入球体在静水中沉速的一般表达式
(2-5)
4 s gd 3Cd
得
第2章 泥沙的沉速 2.1 泥沙沉降的不同形式 1、沉速的定义
单颗粒泥沙在足够大的静止清水中等速下沉时的速度, 称为泥沙的沉速。用符号ω表示。
定义的理解,应注意的几点 ⒉ 泥沙在水中沉降时所受作用力 ⒊ 泥沙在水中沉降特点 ⒋ 研究泥沙沉降的意义
5. 泥沙在静水中下沉时的运动状态
沙粒雷诺数
Red
D
泥沙在层流区的岗恰洛夫沉速公式为
0.75 1 s gd 2 1 s gd 2 18 24
(2-21)
13
3、岗恰洛夫公式 ②紊流区沉速公式(d>1.5mm)
