清华出版社工程力学答案-第5章 杆件的内力分析与内力图
工程力学(范钦珊-蒋永莉-税国双-著)-清华大学出版社.pdf
工程力学——课后练习题讲解教师张建平第一章静力学基础课后习题：1. P32习题1-12. P32习题1-23. P33习题1-8图a和b所示分别为正交坐标系Ox解：图（）：F分力：图与解图，两种情形下受力不同，二者的1-2a解图示压路机的碾子可以在推力或拉力作用下滚过）：θ解图第二章力系的简化课后习题：1. P43习题2-12. P43习题2-23. P44习题2-4由作用线处于同一平面内的两个力F和习题图所示一平面力系对A(30)，B(0，图示的结构中，各构件的自重都略去不计。
1图2-4解习题）中的梁∑0,F0,1m习题3-3图解：根据习题3-3第三章附加习题课后习题：1. P69习题3-52. P69习题3-63. P70习题3-74. P71习题3-135. P71习题3-143-14 图示为凸轮顶杆机构，在凸轮上作用有力偶，其力偶矩确定下列结构中螺栓的指定截面Ⅰ－Ⅰ上的内力分量，，产生轴向拉伸变形。
，产生剪切变形。
如习题4-2图所示直杆A、C、B在两端A、B处固定，在C解：首先分析知，该问题属于超静定问题，受力图如图所示：试用截面法计算图示杆件各段的轴力，并画轴力图，单解：(a)题题－3一端固定另一端自由的圆轴承受四个外力偶作用，如5-3解：将轴划分为四个截面扭矩平衡方程im m 扭矩平衡方程+m3-3扭矩平衡方程5-5 试写出图中所示各梁的剪力方程、弯矩方程图3建立坐标系并确定两个控制面，如图左侧为研究对象：−=）取根据力平衡方程和弯矩平衡方程得出4ql弯矩方程：1解建立坐标系，并取两个控制面，如图ql ql1Q。
工程力学05-杆件的内力图
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
构件内力图概念、画法
杆件基本变形时内力图的表示
内力图沿杆轴线的分布规律 最大内力与危险截面的确定
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
5.2 轴力图与扭矩图
5.2.2 扭矩图 1）扭转内力分量与扭矩
作用在杆件上的外力偶矩可以向杆轴线简化， 简化的结果若力偶作用面在横截面上，该力偶矩分 量——扭矩 扭矩可以是外力简化，也可以由传递的功率计 算得到 2）功率P、转速n和外力偶矩T P (5-1) T=9549 n (N.m) 式中： P：功率（kW) n：转速（r/min)
d
D MD D
确定控制截面
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
5.2 轴力图与扭矩图
5.2.2 扭矩图 MA=1146N.m，MB=MC=350N.m，MD=446N.m。 MB MC MA 求各截面扭矩 BC段 SMx= 0 B C A
C
l l MO =2FPl
FP D B
MC C
l
FP
D B
FQC
S M C= 0
解得：
– MC + MO – FP×l =0
FQC=FP MC = MO – FP×l = 2FPl– FPl = FPl
工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象，三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳，将绳的另一端固定在点C ，在绳的点B 系另一绳BE ，将它的另一端固定在点E 。
然后在绳的点D 用力向下拉，并使绳BD 段水平，AB 段铅直；DE 段与水平线、CB 段与铅直线成等角α=0.1rad （弧度）（当α很小时，tan α≈α）。
如向下的拉力F=800N ，求绳AB 作用于桩上的拉力。
题2-4图作BD 两节点的受力图 联合解得：kN F F F A 80100tan 2=≈=α2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，，机构在图示位置平衡。
工程力学-第5章杆件内力图
截面上的弯矩等于截面任 一侧外力对截面形心力矩的代 数和。
a 5 F 3a 3 2F ME Fa 2 2 3 2
目录
§5.5.4 剪力方程和弯矩方程 剪力图和弯矩图
y
q
例题5-4(教材p84) 简支梁受均布载荷作用 B
x
A
FAY
x
C
l
试写出剪力和弯矩方程，并画 出剪力图和弯矩图。 解：1．确定约束力
受扭转变形杆件通常为轴类零件，其横 截面大都是圆形的。所以本章主要介绍圆轴 扭转。
§5.4 外力偶矩的计算 扭矩和扭矩图
4.外力偶矩
直接计算
§5.4 外力偶矩的计算 扭矩和扭矩图
按输入功率和转速计算
已知 轴转速－n 转/分钟 输出功率－P 千瓦 求：力偶矩Me
电机每秒输入功： 外力偶作功完成：
W P 1000(N m) n W M e 2 60
集中力偶作用处，弯矩图突变
目录
§5.5.5
载荷集度、剪力和弯矩间的关系
从左到右，向上（下）集中力作用处，剪力图向上（下） 突变，突变幅度为集中力的大小。弯矩图在该处为尖点。 从左到右，顺（逆）时针集中力偶作用处，弯矩图向上 （下）突变，突变幅度为集中力偶的大小。剪力图在该点没 有变化。 5、也可通过积分方法确定剪力、 弯矩图上各点处的数值。 dFS dM q FS dM FSdx d F q d x S dx dx
扭矩图
5.5
§5.5.1 §5.5.2 §5.5.3 §5.5.4
弯曲内力
弯曲的概念和实例 受弯杆件的简化 剪力和弯矩 剪力方程和弯矩方程 剪力图和弯矩图 §5.5.5 载荷集度、剪力和弯矩间的关系
工程力学习题册第五章 - 答案
第五章拉伸和压缩一、填空题1.轴向拉伸或压缩的受力特点是作用于杆件两端的外力__大小相等___和__方向相反___，作用线与__杆件轴线重合_。
其变形特点是杆件沿_轴线方向伸长或缩短__。
其构件特点是_等截面直杆_。
2.图5-1所示各杆件中受拉伸的杆件有_AB、BC、AD、DC_，受压缩的杆件有_BE、BD__。
图5-13.内力是外力作用引起的，不同的__外力__引起不同的内力，轴向拉、压变形时的内力称为_轴力__。
剪切变形时的内力称为__剪力__，扭转变形时的内力称为__扭矩__，弯曲变形时的内力称为__剪力与弯矩__。
4.构件在外力作用下，_单位面积上_的内力称为应力。
轴向拉、压时，由于应力与横截面__垂直_，故称为__正应力__；计算公式σ＝F N/A_；单位是__N/㎡__或___Pa__。
1MPa＝__106_N/m2＝_1__N/mm2。
5.杆件受拉、压时的应力，在截面上是__均匀__分布的。
6.正应力的正负号规定与__轴力__相同，__拉伸_时的应力为__拉应力__，符号为正。
__压缩_时的应力为__压应力_，符号位负。
7.为了消除杆件长度的影响，通常以_绝对变形_除以原长得到单位长度上的变形量，称为__相对变形_，又称为线应变，用符号ε表示，其表达式是ε＝ΔL/L。
8.实验证明：在杆件轴力不超过某一限度时，杆的绝对变形与_轴力__和__杆长__成正比，而与__横截面面积__成反比。
9.胡克定律的两种数学表达式为σ＝Eε和ΔL＝F N Lo/EA。
E称为材料的_弹性模量__。
它是衡量材料抵抗_弹性变形_能力的一个指标。
10.实验时通常用__低碳钢__代表塑性材料，用__灰铸铁__代表脆性材料。
11.应力变化不大，应变显著增大，从而产生明显的___塑性变形___的现象，称为__屈服___。
12.衡量材料强度的两个重要指标是__屈服极限___和__抗拉强度__。
13.采用___退火___的热处理方法可以消除冷作硬化现象。
工程力学第五章习题答案
工程力学第五章习题答案工程力学第五章习题答案工程力学是一门研究物体受力和变形的学科，它在工程实践中起着重要的作用。
第五章是工程力学课程中的重要章节，主要讲述了刚体平衡和平面力系的平衡。
在这一章中，有许多习题需要我们进行解答和分析。
下面我将为大家提供一些工程力学第五章习题的答案，希望能对大家的学习有所帮助。
1. 习题：一个悬臂梁的长度为L，梁的质量为m，质心距离支点的距离为a。
求悬臂梁在支点处的支反力和力矩。
答案：根据平衡条件，悬臂梁在支点处的支反力应该等于悬臂梁的重力，即F= mg。
而力矩可以通过计算重力的力矩和质心的力矩来求解。
重力的力矩为0，因为支点处的支反力通过支点，所以力臂为0。
质心的力矩为Ma，即力矩M = mga。
2. 习题：一个平面力系由三个力组成，分别是F1 = 10N，F2 = 5N，F3 = 8N。
已知F1与F2夹角为60度，F2与F3夹角为120度，求力系合力的大小和方向。
答案：首先，我们需要将力系中的三个力进行分解。
根据三角函数的知识，可以得到F1在x轴和y轴上的分量分别为F1x = 10N * cos60°，F1y = 10N *sin60°；F2在x轴和y轴上的分量分别为F2x = 5N * cos120°，F2y = 5N *sin120°；F3在x轴和y轴上的分量分别为F3x = 8N * cos0°，F3y = 8N * sin0°。
然后，将各个力在x轴和y轴上的分量相加得到合力的分量Fx和Fy。
最后，利用勾股定理可以求得合力的大小F和方向θ。
3. 习题：一个物体质量为m，放在一个斜面上，斜面的倾角为θ。
已知斜面的摩擦系数为μ，求物体在斜面上的静摩擦力的大小和方向。
答案：物体在斜面上的重力可以分解为垂直于斜面的分力mgcosθ和平行于斜面的分力mgsinθ。
根据静摩擦力的定义，静摩擦力的大小不超过μmgcosθ。
工程力学第5章答案
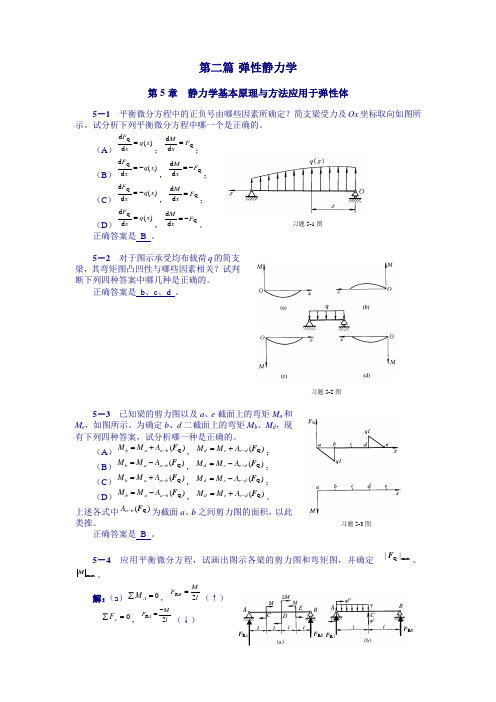
习题5-1图习题5-2图习题5-3图第二篇 弹性静力学第5章 静力学基本原理与方法应用于弹性体5－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
（A ）)(d d Qx q xF =；Q d d F x M=；（B ）)(d d Qx q xF -=，Qd d F x M-=； （C ）)(d d Qx q xF -=，Qd d F x M=；（D ）)(d d Qx q xF =，Qd d F x M-=。
正确答案是 B 。
5－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。
正确答案是 b 、c 、d 。
5－3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ，如图所示。
为确定b 、d 二截面上的弯矩M b 、M d ，现有下列四种答案，试分析哪一种是正确的。
（A ）)(Q F b a a b A M M -+=，)(Q F d e e d A M M -+=； （B ）)(Q F b a a b A M M --=，)(Q F d e e d A M M --=； （C ）)(Q F b a a b A M M -+=，)(Q F d e e d A M M --=； （D ）)(Q F b a a b A M M --=，)(Q F d e e d A M M -+=。
上述各式中)(Q F b a A -为截面a 、b 之间剪力图的面积，以此类推。
正确答案是 B 。
5－4 应用平衡微分方程，试画出图示各梁的剪力图和弯矩图，并确定 m a x Q ||F 、maxM。
解：（a ）0=∑A M ，l MF B 2R =（↑）0=∑y F ，lM F A2R -=（↓）F R AF R BF R BABABCDCEF R AF R B F R Al MF 2||m a x Q =， M M 2||max =（b ）0=∑A M022R 2=⋅+⋅+⋅--l F l ql lql ql BqlF B41R =（↑）=∑y F ，ql F A 41R -=（↓）2R 4141ql l ql l F M B C =⋅=⋅=（＋）2ql M A =ql F 45||max Q =, 2max ||ql M =（c ）0=∑y F ，ql F A =R （↑）0=∑A M ，2ql M A =0=∑D M ，022=-⋅-⋅+D M lql l ql ql223ql M D=ql F =max Q ||, 2max 23||qlM =（d ）0=∑B M 0232R =⋅-⋅⋅-⋅l ql ll q l F Aq lF A 45R =（↑）0=∑y F ，qlF B 43R =（↑）0=∑B M ，22l q M B= 0=∑D M ，23225ql M D=ql F 45||max Q =, 2max 3225||ql M =（e ）0=∑y F ，F R C = 0 0=∑C M ，0223=+⋅+⋅-C M lql l ql2ql M C =0=∑B M ，221ql M B ==∑y F ，ql F B =Qql F =max Q ||, 2max ||ql M =M ACF R ABABACF R BF R AF R CBAF R AF R CM CCABC习题5-6图（f）0=∑AM，qlF C21R=（↑）=∑y F，qlF A21R-=（↓）=∑y F，021Q=-+-BFqlqlqlF B21Q==∑DM，042221=+⋅-⋅DMllqlql，8D, 8EqlF21||maxQ=,2max81||qlM=5－5其剪力图如图所示。
工程力学习题册第五章 - 答案
第五章拉伸与压缩一、填空题1、轴向拉伸或压缩得受力特点就是作用于杆件两端得外力__大小相等___与__方向相反___,作用线与__杆件轴线重合_。
其变形特点就是杆件沿_轴线方向伸长或缩短__。
其构件特点就是_等截面直杆_。
2、图51所示各杆件中受拉伸得杆件有_AB、BC、AD、DC_,受压缩得杆件有_BE、BD__。
图513、内力就是外力作用引起得,不同得__外力__引起不同得内力,轴向拉、压变形时得内力称为_轴力__。
剪切变形时得内力称为__剪力__,扭转变形时得内力称为__扭矩__,弯曲变形时得内力称为__剪力与弯矩__。
4、构件在外力作用下,_单位面积上_得内力称为应力。
轴向拉、压时,由于应力与横截面__垂直_,故称为__正应力__;计算公式σ＝F N/A_;单位就是__N/㎡__或___Pa__。
1MPa＝__106_N/m2＝_1__N/mm2。
5、杆件受拉、压时得应力,在截面上就是__均匀__分布得。
6、正应力得正负号规定与__轴力__相同,__拉伸_时得应力为__拉应力__,符号为正。
__压缩_时得应力为__压应力_,符号位负。
7、为了消除杆件长度得影响,通常以_绝对变形_除以原长得到单位长度上得变形量,称为__相对变形_,又称为线应变,用符号ε表示,其表达式就是ε＝ΔL/L。
8、实验证明:在杆件轴力不超过某一限度时,杆得绝对变形与_轴力__与__杆长__成正比,而与__横截面面积__成反比。
9、胡克定律得两种数学表达式为σ＝Eε与ΔL＝F N Lo/EA。
E称为材料得_弹性模量__。
它就是衡量材料抵抗_弹性变形_能力得一个指标。
10、实验时通常用__低碳钢__代表塑性材料,用__灰铸铁__代表脆性材料。
11、应力变化不大,应变显著增大,从而产生明显得___塑性变形___得现象,称为__屈服___。
12、衡量材料强度得两个重要指标就是__屈服极限___与__抗拉强度__。
13、采用___退火___得热处理方法可以消除冷作硬化现象。
工程力学(材料力学)-5-杆件的内力图
工
MA＝0
MO=2FPl
D C l l
FP
B
程
A
力 FP
MA＝0
FQD FP＝ － 0
MO=2FPl
D A
FQD
MD＋MA + MO − FP ×(2l − ∆)＝ 0
D
因为D截面无限接近B截面， 因为D截面无限接近B截面，所 以式中
MD
FP
l
l
∆ →0
FQD＝FP
MD＝ 0
基本概念与基本方法
♣ 指定横截面上内力分量的确定-例题 1 指定横截面上内力分量的确定-
工程力学
工 程 力
第二篇 材料力学
工程力学
第二篇 材料力学
工 程 力
第5章 杆件的内力图
第5章 杆件的内力图
杆件在外力作用下，横截面上将产生轴力、剪力、 杆件在外力作用下 ， 横截面上将产生轴力 、 剪力 、 扭 弯矩等内力分量。在很多情形下， 矩 、 弯矩等内力分量 。 在很多情形下 ， 内力分量沿杆件的 长度方向的分布不是均匀的。研究强度问题， 长度方向的分布不是均匀的 。 研究强度问题 ， 需要知道哪 些横截面可能最先发生失效，这些横截面称为危险面。 些横截面可能最先发生失效 ， 这些横截面称为危险面 。 内 力分量最大的横截面就是首先需要考虑的危险面。 力分量最大的横截面就是首先需要考虑的危险面 。 研究刚 度问题虽然没有危险面的问题， 度问题虽然没有危险面的问题 ， 但是也必须知道内力分量 沿杆件长度方向是怎样变化的。 沿杆件长度方向是怎样变化的。 工 程 力 为了确定内力分量最大的横截面， 为了确定内力分量最大的横截面 ， 必须知道内力分量 沿着杆件的长度方向是怎样分布的。 沿着杆件的长度方向是怎样分布的 。 杆件的内力图就是表 示内力分量变化的图形。 示内力分量变化的图形。 本章首先介绍内力分量的正负号规则；然后介绍轴力 本章首先介绍内力分量的正负号规则 ； 扭矩图和剪力图与弯矩图，重点是剪力图与弯矩图； 图 、 扭矩图和剪力图与弯矩图 ， 重点是剪力图与弯矩图 ； 最后讨论载荷、剪力、 最后讨论载荷 、 剪力 、 弯矩之间的微分关系及其在绘制剪 力图和弯矩图中的应用。 力图和弯矩图中的应用。
工程力学课后习题答案第五章空间任意力系
第五章 空间任意力系解：cos 45sin 60 1.22x F F KN == cos45cos600.7y F F KN ==sin 45 1.4z F F KN == 6084.85x z M F mm KN mm ==⋅5070.71y z M F mm KN mm ==⋅ 6050108.84z x y M F mm F mm KN mm =+=⋅5.2 解：21sin cos sin x F F F αβα=- 1cos cos y F F βα=-12sin cos z F F F βα=+12sin cos x z M F a aF aF βα==+1sin y M aF β= 121cos cos sin cos sin z y x M F a F a aF aF aF βααβα=-=---解：两力F 、F ′能形成力矩1M1502M Fa KN m ==⋅ 11cos 45x M M =10y M = 11sin 45z M M =1cos 4550x M M KN m ==⋅ 11sin 4550100z z M M M M KN m =+=+=⋅22505C z x M M M KN m =+=⋅63.4α=90β= 26.56γ=5.4 如图所示，置于水平面上的网格，每格边长a = 1m ，力系如图所示，选O 点为简化中心，坐标如图所示。
已知：F 1 = 5 N ，F 2 = 4 N ，F 3 = 3 N ；M 1 = 4 N·m ，M 2 = 2 N·m ，求力系向O 点简化所得的主矢'R F 和主矩M O 。
解：'1236R F F F F N =+-=方向为Z 轴正方向21232248x M M F F F N m =++-=⋅ 1123312y M M F F F N m =--+=-⋅2214.42O y x M M M N m =+=⋅56.63α=33.9β=-90γ=5.5 解：120,cos30cos300AxBx X F F T T =+++=∑210,sin30sin300AzBz Z F F T T W =+-+-=∑120,60cos3060cos301000zBx M T T F =---=∑120,3060sin3060sin301000xBz M W T T F =-+-+=∑21110,0yMWr T r T r =+-=∑20.78,13Ax Az F KN F KN =-= 7.79, 4.5Bx Bz F KN F KN == 1210,5T KN T KN ==2a ，AB 长为2b ，列出平衡方程并求解0Bz F =100Az F N =5.7xyz BAFF 140cm60cm40cm20c m20cmBxF BzF AzF AxF解：10,0AxBx X F F F =++=∑0,0AzBz Z F F F =++=∑10,1401000zBx M F F =--=∑10,20200yM F F =-=∑ 0,401000xBz MF F =+=∑320,480Ax Az F N F N ==-1120,320Bx Bz F N F N =-=-800F N =解：G 、H 两点的位置对称于y 轴BG BH F F =0,sin 45cos60sin 45cos600BGBH Ax X F F F =-++=∑0,cos45cos60cos45cos600BGBH Ay Y F F F =--+=∑0,sin60sin600Az BG BH Z F F F W =---=∑0,5sin 45cos605sin 45cos6050xBG BH MF F W =+-=∑28.28,0,20,68.99BG BH Ax Ay Az F F KN F F KN F KN ===== 5.9。
2016工程力学（高教版）教案：第五章杆件的内力分析
第五章杆件的内力分析在进行结构设计时，为保证结构安全正常工作，要求各构件必须具有足够的强度和刚度。
解决构件的强度和刚度问题，首先需要确定危险截面的内力。
内力计算是结构设计的基础。
本章研究杆件的内力计算问题。
第一节杆件的外力与变形特点进行结构的受力分析时，只考虑力的运动效应，可以将结构看做是刚体；但进行结构的内力分析时，要考虑力的变形效应，必须把结构作为变形固体处理。
所研究杆件受到的其他构件的作用，统称为杆件的外力。
外力包括载荷（主动力）以及载荷引起的约束反力（被动力）。
广义地讲，对构件产生作用的外界因素除载荷以及载荷引起的约束反力之外，还有温度改变、支座移动、制造误差等。
杆件在外力的作用下的变形可分为四种基本变形及其组合变形。
一、轴向拉伸与压缩受力特点：杆件受到与杆件轴线重合的外力的作用。
变形特点：杆沿轴线方向的伸长或缩短。
产生轴向拉伸与压缩变形的杆件称为拉压杆。
图：5-1所示屋架中的弦杆、牵引桥的拉索和桥塔、阀门启闭机的螺杆等均为拉压杆。
图5-1二、剪切受力特点：杆件受到垂直杆件轴线方向的一组等值、反向、作用线相距极近的平行力的作用。
变形特点：二力之间的横截面产生相对的错动。
产生剪切变形的杆件通常为拉压杆的连接件。
如图5-2所示螺栓、销轴连接中的螺栓和销钉，均产生剪切变形。
图5-2三、扭转受力特点：杆件受到作用面垂直于杆轴线的力偶的作用。
变形特点：相邻横截面绕杆轴产生相对旋转变形。
产生扭转变形的杆件多为传动轴，房屋的雨蓬梁也有扭转变形，如图：5-3所示。
图5-3四、平面弯曲受力特点：杆件受到垂直于杆件轴线方向的外力或在杆轴线所在平面内作用的外力偶的作用。
变形特点：杆轴线由直变弯。
各种以弯曲为主要变形的杆件称为梁。
工程中常见梁的横截面多有一根对称轴（图5-4）各截面对称轴形成一个纵向对称面，梁的轴线也在该平面内弯成一条曲线，这样的弯曲称为平面弯曲。
如图5-4所示。
平面弯曲是最简单的弯曲变形，是一种基本变形。
清华出版社工程力学答案-第5章 杆件的内力分析与内力图
eBook工程力学习题详细解答教师用书(第5章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题5－1 习题5－2 习题5－3 习题5－4 习题5－5 习题5－6工程力学习题详细解答之五第5章 杆件的内力分析与内力图5－1 试用截面法计算图示杆件各段的轴力，并画轴力图。
5－2 圆轴上安有5个皮带轮，其中轮2为主动轮，由此输入功率80 kW ；1、3、4、5均为从动轮，它们输出功率分别为25 kW 、15 kW 、30 kW 、10 kW ，若圆轴设计成等截面的，为使设计更合理地利用材料，各轮位置可以互相调整。
1． 请判断下列布置中哪一种最好？(A) 图示位置最合理；(B) 2轮与5轮互换位置后最合理； (C) 1轮与3轮互换位置后最合理； (D) 2轮与3轮互换位置后最合理。
2． 画出带轮合理布置时轴的功率分布图。
30kN 20kN10kN20kN10kN 5kNBAD CB A DC BACBA C(a)(b)(c)(d)F NF ACBF N xDACB102030ACF N x210ADCF N -10习题5－1图解： 1. D2. 带轮合理布置时轴的扭矩图如图（b ）所示。
5－3 一端固定另一端自由的圆轴承受4个外力偶作用，如图所示。
各力偶的力偶矩数值均示于图中。
试画出圆轴的扭矩图。
固定固定(kN.m)习题5－3图P x (kW)2540(b)习题5－2图5－4 试求图示各梁中指定截面上的剪力、弯矩值。
（a）题解：取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：22222211qa qa qa a qa M M qaF Q =−=⎟⎠⎞⎜⎝⎛⋅−=−= 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：222222222qa qa qa a qa M M qaqa qa F Q =−=⎟⎠⎞⎜⎝⎛⋅−=−=−−= （b）题解：取1-1截面右段为研究对象，1-1截面处的剪力和弯矩按正方向假设：21P 12322qa a qa a qa M qa qa qa qa F F Q −=⋅−⋅−==+=+= 取2-2截面右段为研究对象，2-2截面处的剪力和弯矩按正方向假设：2222222qa qa a qa a qa M qaF Q −=+⋅−⋅−== （c）题解：（1）考虑整体平衡，可解A 、C 支座约束力0m kN 5.4124m kN 4,0)(=⋅××−×+⋅=∑C i A F F M得 kN 25.1=C F0kN 12,0=×−+=∑C A iyF F F得 kN 75.0=A F（2）取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：BB5kN1 m34AAB(b)(a)(c)(d)习题5－4图0,01=−=∑Q A iyF F F得 kN 75.01=Q F02,0)(11=+×−=∑M F F MQ i A得 m kN 5.11⋅=M(3) 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：0,02=−=∑Q A iyF F F得 kN 75.02=Q F0m kN 42,0)(22=+⋅+×−=∑M F F M Q i A得 m kN 5.22⋅−=M(4) 取3-3截面右段为研究对象，3-3截面处的剪力和弯矩按正方向假设：0kN 12,03=×−+=∑C Q iyF F F得 kN 75.03=Q F0m kN 1221,0)(23=⋅××−−=∑M F M i C得 m kN 13⋅−=M (5) 取4-4截面右段为研究对象，4-4截面处的剪力和弯矩按正方向假设：0kN 12,04=×−=∑Q iyF F得 kN 24=Q F0m kN 1221,0)(24=⋅××−−=∑M F Mi C得 m kN 14⋅−=M （d）题解：（1）考虑整体平衡，可解A 、B 支座约束力03m kN 2m kN 15,0)(=×+⋅+⋅×−=∑B i A F F M 得 kN 1=B F0kN 5,0=+−=∑B A iyF F F得 kN 4=A F（2）取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：0,01=−=∑Q A iyF F F得 kN 41=Q F01,0)(11=+×−=∑M FF M Ai得 m kN 41⋅=M(3) 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：0kN 5,02=−−=∑Q A iyF F F得 kN 12−=Q F01,0)(22=+×−=∑M F F M A i得 m kN 42⋅=M(4) 取3-3截面右段为研究对象，3-3截面处的剪力和弯矩按正方向假设：0,03=+=∑B Q iyF F F得 kN 13−=Q F1m kN 2,0)(33=×+⋅+−=∑B iF M F M得 m kN 33⋅=M(5) 取4-4截面右段为研究对象，4-4截面处的剪力和弯矩按正方向假设：0,04=+=∑B Q iyF F F得 kN 14−=Q F1,0)(44=×+−=∑B i F M F M得 m kN 14⋅=M5－5 试写出以下各梁的剪力方程、弯矩方程。
工程力学电子教案(第三版)第5章 杆件的内力
§5－2 杆件扭转时的内力
例5－2 传动轴(图5－9a)的转速n=150r/min；
A处为主动轮，输入功率PA=70kW，B、C、D处
为从动轮，其输出功率分别为PB=30kW， PC=PD=20kW。试绘制该轴的扭矩图。
图5－9
§5－2 杆件扭转时的内力
(2)计算扭矩 须将轴分为AB、AC和CD三段， 逐段计算扭矩。应用截面法，假想地沿1－1横截 面把轴截开，取左段为研究对象(图5－9b)，为保 持左段平衡，1－1横截面上的扭矩T1为
图5－2
§5－1 杆件拉(压)时的内力
3. 轴力
现以图5－3a所示拉杆为例，求其任意横截面
m－m上的内力。
应用截面法，假想地沿m－m截面把杆截开，
取左段为研究对象(图5－3b)，列出平衡方程
得
∑Fx=0，FN－F=0
FN=F 由于内力FN的作用线与杆的轴线重合，故FN 称为轴力。
§5－1 杆件拉(压)时的内力
显然，图5－7所示m－m横截面上的扭矩为
正。
§5－2 杆件扭转时的内力
图5－8
§5－2 杆件扭转时的内力
●与求轴力的方法类似，用截面法计算扭矩时， 通常先假设扭矩为正，然后根据计算结果的正负 确定扭矩的实际方向。
●若作用于轴上的外力偶矩多于两个，也与拉 伸(压缩)问题中绘制轴力图相仿，以横坐标表示 横截面的位置、纵坐标表示相应横截面上的扭矩， 用图线来表示各横截面上扭矩沿轴线变化的情况。 这样的图线称为扭矩图。
1.工程实例：钻探机的钻杆(图5－5a)、机器中的 传动轴(图5－5b)
图5－5
§5－2 杆件扭转时的内力
2. 计算简图 这些杆件都是两端作用两个大小相等、方
向相反且作用平面垂直于杆件轴线的力偶，致使 杆件的任意两个横截面之间都发生绕轴线的相对 转动，这种变形称为扭转变形。
工程力学第5章 杆件的内力分析与内力图
62
习题 5.1 试求图示杆件各段的轴力，并画轴力图。 5.2 试画下列各杆的扭矩图。 5.3 图示传动轴，转速n=350r/min，轮2为主动轮， 输入功率P2=70kW，轮1，3，4均为从动轮，输出功率 分别为P1=P3=20 kW，P4=30 kW。 （1）试画轴的扭矩图； （2）若各轮位臵可以互换，试判断怎样布臵最合 理。 5.4 试用截面法求下列梁中1-1、2-2截面上的剪力和 弯矩。
4
4.弯曲（bending） 即在一对大小相等、转向相反、位于杆的纵向平面 内的力偶作用下，杆的两相邻横截面绕垂直于杆轴线的 直线产生相对转动，截面间的夹角发生改变，如图5.1 （e）所示。 工程实际中的杆件可能同时承受不同形式的外力， 变形情况可能比较复杂。但不论怎样复杂，其变形均是 由基本变形组成的。
13
5.2.2 轴力的正负符号约定 为了研究方便，工程上习惯约定：轴力方向以使杆 件微段拉伸为正；反之，使杆件微段压缩为负，图5.4所 示为FN的正方向。
14
5.2.3 轴力图 在多个外力作用时，由于杆件不同截面的轴力可能 不同，为了形象地表明各截面的轴力的变化情况，通常 将其绘成轴力图。表示轴力沿杆件轴线方向变化的图形， 称为轴力图（diagram ofnormalforce）。作法是：沿杆轴 线方向取横坐标，称为基线，表示截面位臵，以垂直于 杆轴线方向为纵坐标，其值代表对应截面的轴力值，绘 制各截面的轴力变化曲线。拉力、压力各绘在基线的一 侧，图中在拉力区标注，压力区标注，并标注各控 制截面处 FN及单位。
20
5.3.2 扭矩与扭矩图 扭矩是扭转变形杆的内力，它是杆横截面上的分布 内力向截面形心简化后的内力主矩沿过形心的法向分量， 用MT表示。
21
沿杆轴线方向取横坐标，表示截面位臵，其垂直杆 轴线方向的坐标代表相应截面的扭矩，正、负扭矩分别 画在基线两侧，并标注、号及控制截面处MT和单 位，如图5.7（d）所示。
工程力学第5章复习杆件的内力图
M
斜直线
曲线
自左向右折角 自左向右突变
图
x
x
x
x
x 与 M2 x
特
m
征M
M
M
M
M
反 M M1
增函数 降函数 坟状 盆状 折向与P反向 M1 M2 m
18
简易作图法: 利用内力和外力的关系及特殊点的内力值来作 图的方法。
用简易作图法画下列各图示梁的内力图。
qa
q
A
解: 利用内力和外力的关系及 特殊点的内力值来作图。
q0L2
Q(
x
)
q0 6L
(L2
3x2)
3
M (x)
q0x 6L
(
L2
x2
)
x
③根据方程画内力图
16
根据剪力、弯矩、载荷集度的微分关系画弯曲内力图
q(x)
x dx
弯矩图上某点处的 切线斜率等于该点 处剪力的大小。
dM (x) dx
FQ (x)
剪力图上某点处的切线斜率 等于该点处荷载集度的大小
dFQ x qx
轮输出 P2=150kW，P3=150kW，P4=200kW，试绘制扭矩图。
m2
m3
m1
m4
解：①计算外力偶矩
m1
9.55
P1 n
9.55
500 300
A
15.9(kN m)
n
B
C
D
m2
m3
9.55
P2 n
9.55
150 300
4.78 (kN m)
m4
9.55
P4 n
9.55
200 300
工程力学课后习题答案杆类构件的内力分析答案
第六章 杆类构件的内力分析习 题6.1 试求图示结构1-1和2-2截面上的内力，指出AB 和CD 两杆的变形属于哪类基本变形，并说明依据。
解：（a ）应用截面法：对题的图取截面2-2以下部分为研究对象，受力图如图一所示：BM图一 图二 由平衡条件得：0,AM=∑ 6320N F ⨯-⨯= 解得： N F =9KNCD 杆的变形属于拉伸变形。
应用截面法，取题所示截面1-1以右及2-2以下部分作为研究对象，其受力图如图二所示，由平衡条件有：0,OM=∑ 6210N F M ⨯-⨯-= （1）0,yF=∑ 60N S F F --= （2）将N F =9KN 代入（1）-（2）式，得：M =3 kN·m S F =3 KN AB 杆属于弯曲变形。
（b ）应用截面法 ，取1-1以上部分作为研究对象，受力图如图三所示，由平衡条件有：0,Fx =∑20NF -= N F =2KN0,DM=∑ 210M -⨯= M =2KNAB 杆属于弯曲变形6.2 求图示结构中拉杆AB 的轴力。
设由AB 连接的1和2两部分均为刚体。
解：首先根据刚体系的平衡条件，求出AB 杆的内力。
刚体1的受力图如图一所示D图一图二平衡条件为：0,CM=∑104840D NF F⨯-⨯-⨯=（1）刚体2受力图如图二所示，平衡条件为：0,EM=∑240N DF F⨯-⨯=（2）解以上两式有AB杆内的轴力为：NF=5KN6.3试求图示各杆件1-1、2-2和3-3截面上的轴力，并做轴力图。
解：（a）如图所示，解除约束，代之以约束反力，做受力图，如图1a所示。
利用静力平衡条件，确定约束反力的大小和方向，并标示在图1a中，作杆左端面的外法线n，将受力图中各力标以正负号，轴力图是平行于杆轴线的直线，轴力图线在有轴向力作用处要发生突变，突变量等于该处总用力的数值，对于正的外力，轴力图向上突变，对于负的外力，轴力图向下突变，轴力图如2a所示，截面1和截面2上的轴力分别为1NF=-2KN2NF=-8KN，（a）nkN(a1)(2)C（b）CB4kNb1）（b2）（（b）解题步骤和（a）相同，杆的受力图和轴力图如（1b）（2b）所示，截面1和截面2上的轴力分别为1N F =4KN 2N F =6KN（c ）解题步骤和（a ）相同，杆的受力图和轴力图如（1c ）（2c ）所示，截面1，截面2和截面3上的轴力分别为1N F =3F 2N F =4F ，3N F =4FB C（c ）4F（c 1）（c 2）（d）A D（d 1）（d 2）（d ）解题步骤和（a ）相同，杆的受力图和轴力图如（1d ）（2d ）所示，截面1和截面2 上的轴力分别为1N F =2KN 2N F =2KN6.4 求图示各轴1-1、2-2截面上的扭矩，并做各轴的扭矩图。
工程力学课后习题答案第五章空间任意力系
工程力学课后习题答案第五章空间任意力系本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March第五章 空间任意力系解：cos 45sin 60 1.22x F F KN == cos45cos600.7y F F KN ==sin 45 1.4z F F KN == 6084.85x z M F mm KN mm ==⋅5070.71y z M F mm KN mm ==⋅ 6050108.84z x y M F mm F mm KN mm =+=⋅解：21sin cos sin x F F F αβα=- 1cos cos y F F βα=-12sin cos z F F F βα=+12sin cos x z M F a aF aF βα==+1sin y M aF β= 121cos cos sin cos sin z y x M F a F a aF aF aF βααβα=-=---解：两力F 、F ′能形成力矩1M1502M Fa KN m ==⋅ 11cos 45x M M =10y M = 11sin 45z M M =1cos 4550x M M KN m ==⋅ 11sin 4550100z z M M M M KN m =+=+=⋅22505C z x M M M KN m =+=⋅63.4α= 90β= 26.56γ=如图所示，置于水平面上的网格，每格边长a = 1m ，力系如图所示，选O 点为简化中心，坐标如图所示。
已知：F 1 = 5 N ，F 2 = 4 N ，F 3 = 3 N ；M 1 = 4 N·m ，M 2 = 2 N·m ，求力系向O 点简化所得的主矢'R F 和主矩M O 。
题图解：'1236R F F F F N =+-=方向为Z 轴正方向21232248x M M F F F N m =++-=⋅ 1123312y M M F F F N m =--+=-⋅2214.42O y x M M M N m =+=⋅56.63α= 33.9β=-90γ=解：120,cos30cos300AxBx X F F T T =+++=∑210,sin30sin300AzBz Z F F T T W =+-+-=∑120,60cos3060cos301000zBx M T T F =---=∑120,3060sin3060sin301000xBz M W T T F =-+-+=∑21110,0yMWr T r T r =+-=∑20.78,13Ax Az F KN F KN =-= 7.79, 4.5Bx Bz F KN F KN == 1210,5T KN T KN ==题图2a ，AB 长为2b ，列出平衡方程并求解0Bz F =100Az F N =xyz BAFF 140cm60cm40cm20c m20cmBxF BzF AzF AxF题图解：10,0Ax Bx X F F F =++=∑0,0AzBz Z F F F =++=∑10,1401000zBx M F F =--=∑ 10,20200yM F F =-=∑ 0,401000xBz MF F =+=∑320,480Ax Az F N F N ==- 1120,320Bx Bz F N F N =-=-800F N =题图解：G 、H 两点的位置对称于y 轴BG BH F F =0,sin 45cos60sin 45cos600BGBH Ax X F F F =-++=∑0,cos45cos60cos45cos600BGBH Ay Y F F F =--+=∑0,sin60sin600Az BG BH Z F F F W =---=∑0,5sin 45cos605sin 45cos6050xBG BH MF F W =+-=∑28.28,0,20,68.99BG BH Ax Ay Az F F KN F F KN F KN =====。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
eBook工程力学习题详细解答教师用书(第5章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题5－1 习题5－2 习题5－3 习题5－4 习题5－5 习题5－6工程力学习题详细解答之五第5章 杆件的内力分析与内力图5－1 试用截面法计算图示杆件各段的轴力，并画轴力图。
5－2 圆轴上安有5个皮带轮，其中轮2为主动轮，由此输入功率80 kW ；1、3、4、5均为从动轮，它们输出功率分别为25 kW 、15 kW 、30 kW 、10 kW ，若圆轴设计成等截面的，为使设计更合理地利用材料，各轮位置可以互相调整。
1． 请判断下列布置中哪一种最好？(A) 图示位置最合理；(B) 2轮与5轮互换位置后最合理； (C) 1轮与3轮互换位置后最合理； (D) 2轮与3轮互换位置后最合理。
2． 画出带轮合理布置时轴的功率分布图。
30kN 20kN10kN20kN10kN 5kNBAD CB A DC BACBA C(a)(b)(c)(d)F NF ACBF N xDACB102030ACF N x210ADCF N -10习题5－1图解： 1. D2. 带轮合理布置时轴的扭矩图如图（b ）所示。
5－3 一端固定另一端自由的圆轴承受4个外力偶作用，如图所示。
各力偶的力偶矩数值均示于图中。
试画出圆轴的扭矩图。
固定固定(kN.m)习题5－3图P x (kW)2540(b)习题5－2图5－4 试求图示各梁中指定截面上的剪力、弯矩值。
（a）题解：取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：22222211qa qa qa a qa M M qaF Q =−=⎟⎠⎞⎜⎝⎛⋅−=−= 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：222222222qa qa qa a qa M M qaqa qa F Q =−=⎟⎠⎞⎜⎝⎛⋅−=−=−−= （b）题解：取1-1截面右段为研究对象，1-1截面处的剪力和弯矩按正方向假设：21P 12322qa a qa a qa M qa qa qa qa F F Q −=⋅−⋅−==+=+= 取2-2截面右段为研究对象，2-2截面处的剪力和弯矩按正方向假设：2222222qa qa a qa a qa M qaF Q −=+⋅−⋅−== （c）题解：（1）考虑整体平衡，可解A 、C 支座约束力0m kN 5.4124m kN 4,0)(=⋅××−×+⋅=∑C i A F F M得 kN 25.1=C F0kN 12,0=×−+=∑C A iyF F F得 kN 75.0=A F（2）取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：BB5kN1 m34AAB(b)(a)(c)(d)习题5－4图0,01=−=∑Q A iyF F F得 kN 75.01=Q F02,0)(11=+×−=∑M F F MQ i A得 m kN 5.11⋅=M(3) 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：0,02=−=∑Q A iyF F F得 kN 75.02=Q F0m kN 42,0)(22=+⋅+×−=∑M F F M Q i A得 m kN 5.22⋅−=M(4) 取3-3截面右段为研究对象，3-3截面处的剪力和弯矩按正方向假设：0kN 12,03=×−+=∑C Q iyF F F得 kN 75.03=Q F0m kN 1221,0)(23=⋅××−−=∑M F M i C得 m kN 13⋅−=M (5) 取4-4截面右段为研究对象，4-4截面处的剪力和弯矩按正方向假设：0kN 12,04=×−=∑Q iyF F得 kN 24=Q F0m kN 1221,0)(24=⋅××−−=∑M F Mi C得 m kN 14⋅−=M （d）题解：（1）考虑整体平衡，可解A 、B 支座约束力03m kN 2m kN 15,0)(=×+⋅+⋅×−=∑B i A F F M 得 kN 1=B F0kN 5,0=+−=∑B A iyF F F得 kN 4=A F（2）取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：0,01=−=∑Q A iyF F F得 kN 41=Q F01,0)(11=+×−=∑M FF M Ai得 m kN 41⋅=M(3) 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：0kN 5,02=−−=∑Q A iyF F F得 kN 12−=Q F01,0)(22=+×−=∑M F F M A i得 m kN 42⋅=M(4) 取3-3截面右段为研究对象，3-3截面处的剪力和弯矩按正方向假设：0,03=+=∑B Q iyF F F得 kN 13−=Q F1m kN 2,0)(33=×+⋅+−=∑B iF M F M得 m kN 33⋅=M(5) 取4-4截面右段为研究对象，4-4截面处的剪力和弯矩按正方向假设：0,04=+=∑B Q iyF F F得 kN 14−=Q F1,0)(44=×+−=∑B i F M F M得 m kN 14⋅=M5－5 试写出以下各梁的剪力方程、弯矩方程。
(a)题 解：()()()()()()()()()()()()Q Q Q Q 10222222332322423422.,.,.,.,M M F x M x xx l l l MMF x M x x M l x l l l MMF x M x x M l x l l l MMF x M x x Ml x l ll=−=−≤≤=−=−+≤≤=−=−+≤≤=−=−+≤≤BAqq(b)(c)(d)(e)(f)ql 2AlACAB A习题5－5和习题5－6图(b)题 解：()()()()()()()22Q Q 111104421122244.,.,F x ql qx M x ql x l F x ql M x ql l x l x l =−−=−−≤≤=−=−≤≤(c)题解：()()()()()()22Q 2Q 110222023.,.,F x ql qx M x qlx ql qx x l F x M x ql l x l =−=+−≤≤==≤≤(d)题 解：()()()()()()()()()2Q 2Q 55110244212333232.,.,F x ql qx M x qlx qx x l F x ql q l x M x ql l x q l x l x l =−=−≤≤=−+−=−−−≤≤ (e)题解：()()()()()()()()2Q 2Q 110212222.,.,F x qx M x qx x l l F x ql q x l M x ql x q x l l x l ==≤≤⎛⎞=−−=−−−≤≤⎜⎟⎝⎠ (f)题解：()()()()()()()()()2Q 2Q 1110222122222222.,.,qlF x qx M x qlx qx x l qlql F x q l x M x l x q l x l x l =−+=−+≤≤=−+−=−−−≤≤5－6 试画出习题5－5中各梁的剪力图、弯矩图，并确定剪力和弯矩的绝对值的最大值。
题（a ）解：0=∑A M ，l MF B 2R =（↑） 0=∑y F ，lM F A2R =（↓） lM F 2||max Q =M M 2||max =题（b ）解：0=∑A M ， 022R 2=⋅+⋅+⋅−−l F l ql l ql ql B(a)BA2MF QO2M l 2M l 2Ml 2M l 2M2M (a1)(a2)习题5－6a 解图A(b)2qlO141414(b1)(b2)习题5－6b 解图ql F B 41R =（↑） 0=∑y F ， ql F A 41R =（↓） 2R 4141ql l ql l F M B C =⋅=⋅= 2ql M A =ql F 45||max Q = 2max ||ql M =题（c ）解：0=∑y F ，A R （↑）0=∑A M ，2ql M A =0=∑D M ，022=−⋅−⋅+D M l ql l ql ql223ql M D = ql F =max Q || 2max 23||ql M = 题（d ）解：0=∑B M , 02132R =⋅−⋅⋅−⋅l ql l q l F A ql F A 45R =（↑） 0=∑y F ，ql F B 43R =（↑）0=∑B M ，22l q M B = 0=∑D M ，23225ql M D=ql F 45||max Q =2max 3225||ql M =题（e ）解：0=∑y F ，F R C = 00=∑C M ，0223=+⋅+⋅−C M l ql l ql 2ql M C = 0=∑B M ，221ql M B=0=∑y F ，ql F B =Qql F =max Q ||(e)qF Q /M /ql (e1)(e2)习题5－6e 解图q(d)AOF Q /ql0.751.25(d1)(d2)习题5－6d 解图2max ||ql M = 题（f ）解：0=∑A M ，ql F B 21R =（↑） 0=∑y F ，ql F A 21R =（↓）0=∑y F ，021Q =−+−B F ql ql ql F B 21Q =0=∑DM ，042221=+⋅−⋅DM ll q l ql 281ql M D −= 281ql M E = ql F 21||max Q = 2max 81||ql M =上一章 返回总目录 下一章(f)AO (f1)(f2)F /qlM 0.5习题5－6f 解图。