A标准答案及评分细则(样本)
[2024上]手机媒体概论_答案及评分标准_A卷
![[2024上]手机媒体概论_答案及评分标准_A卷](https://img.taocdn.com/s3/m/425c1711e55c3b3567ec102de2bd960590c6d9de.png)
阳光学院考试答案及评分标准专用纸2023年—— 2024年第二学期教师姓名:洪欣课程名称:手机媒体概论(A卷)考试方式:闭卷考核对象(年级专业): 22级广告学一、选择题(共30分,每小题2分)1.【A】联合国教科文组织2.【C】彩信3.【C】哈贝马斯4.【B】同步或异步传播有机统一5.【B】3G6.【C】《即时通信工具公众信息服务发展管理暂行规定》(也称"信十条”)7.【C】《中国妇女报·彩信版》8.【A】5万个汉字9.【B】G P R S类型10.【C】基于位置的服务11.【A】《城外》12.【C】中国移动手机阅读基地13.【B】手机电视可以随身携带,能实时接收最新的信息。
14.【B】140字15.【D】中国移动多媒体广播二、名词解释题(共20分,每小题4分)1.4G:4G是第四代移动通信及技术的简称,是集3G与W L A N于一体,并能够传输高质量视频图像,且图像传输质量与高清晰度与电视不相上下的技术产品。
2.彩信:彩信的英文名是M M S,彩信意为多媒体信息服务。
支持多媒体功能,能够传递更丰富的内容和信息,这些信息包括文字、图像、声音、数据等各种多媒体格式的信息。
它与手机摄像头结合。
3.手机报:手机报是将纸质报纸的新闻内容,通过移动通信技术平台传播,使用户能通过手机阅读到报纸内容的一种信息传播业务。
4.手机媒体:手机媒体是指借助手机进行信息传播的工具。
它是以分众为传播目标,以定向为传播效果,以互动为传播应用的大众传播媒介。
手机媒体被公认为是继报刊、广播、电视、互联网之后的“第五媒体”。
5.数字电视:数字电视,又称数位电视或数码电视,是指从演播室到发射、传输、接收的所有环节都是使用数字电视信号,或对该系统所有的信号传播都是通过由0、1数字串所构成的二进制数字流来传播的电视类型。
相对于与模拟电视,其信号损失小,接收效果好。
三、简答题(共20分,每小题5分)1.请分析手机用户的特征。
口语考试评分细则
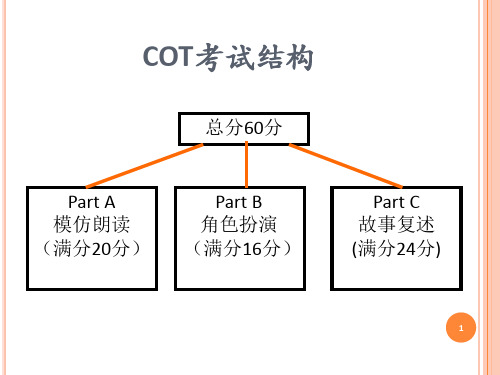
PART B 角色扮演
既考听力,也考口语。
回答机器提问的答案来自: (1)机器对生的提问的回答 (2)引子 所以考生要适当做些笔记
10
PART B 角色扮演结构
引子
Q1:您为什么决定换工作? 电脑答: Q2:这份工作很不一样,对吧?
电脑答:
Q3:您还行医吗? 电脑答: 电脑问1: A1:考生回答 电脑问2: A2:考生回答 电脑问3 A3:考生回答
6
基本按原语速,漏几个词
4
基本按原语速,漏一些词
D
0-2
0-2
不能按原语速,漏一个句 子或10个以上词
3
PART A 模仿朗读样本
4
1分钟左右,100左右单词
模仿朗读文本
The greatest mystery of them all is the Pyramids. From early times, many have tried to solve the mystery of these great monuments, representative of ancient Egyptian wisdom. In particular, the Great Pyramid on the outskirts of Cairo has long held a great fascination. Among the sixty Pyramids found in Egypt, this is the largest of them all. The great Pyramid is a gigantic stone mountain, made up of three million stones, each stone weighing two point five tons. The length of the base measures two hundred thirty metres. The height reaches one hundred and forty-seven metres, equivalent to a building forty stories high. 请给下列样本打分
安徽省普通中等专业学校办学水平评估A类指标体系及评分细则(试行)【模板】

6.学生每天至少有1小时的体育锻炼活动,近三年学生体质健康达标率、优秀率逐年提高(1分)
7.学生劳动观念普遍树立,并具备较高的劳动技能。(1分)
1.学校课程表、德育课大纲、德育课教材,传统文化进校园材料。
2.学校特色校园文化建设材料。
创新校企合作育人的方式与途径,形成运行有效的协同育人机制,每个主干专业与3个以上有较大影响力的企业建立了稳定的合作关系;所有适合的专业实施现代学徒制且成效明显,并有省级及以上现代学徒制项目;牵头组建省级行业型或跨市的区域型职教集团。
广泛运用项目教学、工作过程导向等教学模式,一体化教学深入实施。
建成2个以上省级示范专业。
3.校园体育、卫生、生活等设施齐全,开展文明校园创建。(1分)
1.学校土地证或相关土地证明材料。
2.学校校舍建筑面积统计表、房产证或建筑物竣工验收相关材料。
3.校园布局平面图,运动场实景图片、竣工验收相关材料。
4.文明校园创建相关材料。
2.2
师资队伍
★(8分)
建成一支专兼结合、结构合理、素质优良、适应需要的教师队伍。
1.专业建设规划科学,实施方案可行。(2分)
2.专业设置上,形成5个及以上适应地方主导产业和行业、企业发展要求的主干专业。(2分)
3.每个主干专业与3个以上有影响力的企业建立了稳定的合作关系。(2分)
4.牵头或参与组建职教集团,并承担省级及以上现代学徒制项目。(2分)
5.建立了政府、行业、企业、研究机构和学校共同参与的“专业建设指导委员会”,定期召开专业建设研讨会,指导专业建设。(2分)
2.建有支持移动互联网的网络学习平台,并建有在线开放课程,开展线上线下混合式教学。(1分)
2024年全国中学生数学奥林匹克竞赛(预赛)加试参考答案与评分标准(A卷)

2024年全国中学生数学奥林匹克竞赛(预赛)暨2024年全国高中数学联合竞赛加试(A 卷)参考答案及评分标准说明:1.评阅试卷时,请严格按照本评分标准的评分档次给分.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,10分为一个档次,不得增加其他中间档次.一.(本题满分40分)给定正整数r .求最大的实数C ,使得存在一个公比为r 的实数等比数列1{}n n a ,满足n a C 对所有正整数n 成立.(x 表示实数x 到与它最近整数的距离.)解:情形1:r 为奇数.对任意实数x ,显然有12x ,故满足要求的C 不超过12. 又取{}n a 的首项112a ,注意到对任意正整数n ,均有1n r 为奇数,因此1122n n r a .这意味着12C 满足要求.从而满足要求的C 的最大值为12. …………10分 情形2:r 为偶数.设*2()r m m N .对任意实数 ,我们证明1a 与2a 中必有一数不超过21m m ,从而21m C m . 事实上,设1a k ,其中k 是与1a 最近的整数(之一),且102. 注意到,对任意实数x 及任意整数k ,均有x k x ,以及x x .若021m m ,则121m a k m . 若1212m m ,则22221m m m m ,即21m m r m m ,此时 2121m a a r kr r r m . …………30分 另一方面,取121m a m ,则对任意正整数n ,有1(2)21n n m a m m ,由二项式展开可知11(211)(1)2121n n n m m a m K m m ,其中K 为整数,故21n m a m .这意味着21m C m 满足要求. 从而满足要求的C 的最大值为212(1)m r m r .综上,当r 为奇数时,所求C 的最大值为12;当r 为偶数时,所求C 的最大值为2(1)r r . …………40分二.(本题满分40分)如图,在凸四边形ABCD 中,AC 平分BAD ,点,E F 分别在边,BC CD 上,满足||EF BD .分别延长,FA EA 至点,P Q ,使得过点,,A B P 的圆1 及过点,,A D Q 的圆2 均与直线AC 相切.证明:,,,B P Q D 四点共圆.(答题时请将图画在答卷纸上)证明:由圆1 与AC 相切知180BPA BAC CAD CAF PAC ,故,BP CA 的延长线相交,记交点为L .由||EF BD 知CE CF CB CD.在线段AC 上取点K ,使得CK CE CF CA CB CD ,则||,||KE AB KF AD . …………10分由ABL PAL KAF ,180180BAL BAC CAD AKF ,可知ABL KAF ∽,所以KF AB AL KA. …………20分 同理,记,DQ CA 的延长线交于点L ,则KE AD AL KA. 又由||,||KE AB KF AD 知KE CK KF AB CA AD,即KE AD KF AB . 所以AL AL ,即L 与L 重合.由切割线定理知2LP LB LA LQ LD ,所以,,,B P Q D 四点共圆.…………40分三.(本题满分50分)给定正整数n .在一个3n ×的方格表上,由一些方格构成的集合S 称为“连通的”,如果对S 中任意两个不同的小方格,A B ,存在整数2l ≥及S 中l 个方格12,,,lA C C CB ==,满足iC 与1i C +有公共边(1,2,,1i l −).求具有下述性质的最大整数K :若将该方格表的每个小方格任意染为黑色或白色,总存在一个连通的集合S ,使得S 中的黑格个数与白格个数之差的绝对值不小于K .解:所求最大的K n =.对一个由小方格构成的集合S ,记b S 是S 中的黑格个数,w S 是S 中的白格个数. 用[,]i j 表示第i 行第j 列处的方格,这里13i ≤≤,1j n ≤≤.对于两个方格[,]A i j =,[,]B i j ′′=, 定义它们之间的距离为(,)||||d A B i i j j ′′=−+−.首先,如果将方格表按国际象棋棋盘一样黑白间隔染色,我们证明对任意连通的集合S ,均有||b w S S n −≤,这表明K n ≤.设[1,1]是黑格,并记{0,1}ε∈,满足(mod 2)n ε≡.先证b w S S n −≤.可不妨设S 包含所有黑格,这是因为若S 不包含所有黑格, 取不属于S 的黑格A 满足(,)d A S 最小,这里(,)min (,)B Sd A S d A B ∈=.易知(,)1d A S =或2.若(,)1d A S =,取{}S S A ′=,则S 仍是连通的,且b w S S ′′−更大. 若(,)2d A S =,则存在与A 相邻的白格C ,而C 与S 中某个方格B 相邻,取{,}S S A B ′= ,则S 仍是连通的,且bw S S ′′−不变. 因而可逐步扩充S ,使得S 包含所有黑格,保持S 的连通性,且b w S S −不减.考虑白格集合{[,]|}k W i j i j k =+=,3,5,,1k n ε++,每个k W 中至少有一个方格属于S ,否则不存在从黑格[1,1]A S =∈到黑格[3,1]B n ε=−+的S 中路径.故1()2w S n ε≥+,而1(3)2b S n ε=+,故b w S S n −≤. …………10分 类似可证w b S S n −≤.同上,可不妨设S 包含所有白格, 从而1(3)2w S n ε=−. 再考虑黑格集合{[,]|}k B i j i j k =+=, 4,6,,2k n ε+−,每个k B 中至少有一个黑格属于S ,否则不存在从白格[1,2]A =到白格[3,]B n ε=−的S 中路径. 从而1()2b S n ε≥−,故w b S S n −≤. …………20分 下面证明K n =具有题述性质,即对任意的染色方案,总存在连通的集合S , 使得b w S S n −≥.设表格中共有X 个黑格和Y 个白格,在第二行中有x 个黑格和y 个白格. 于是3X Y n +=, x y n +=.故()()()()2X y Y x X Y x y n −+−=+−+=.由平均值原理可知max{,}X y Y x n −−≥.不妨设X y n −≥.取S 为第二行中的y 个白格以及所有X 个黑格.由于S 包含第二行中所有方格,因而S 是连通的. 而b S X =,w S y =,b w S S X y n −=−≥.综上所述,max K n =. …………50分四.(本题满分50分)设,A B 为正整数,S 是一些正整数构成的一个集合,具有下述性质:(1) 对任意非负整数k ,有k A S ;(2) 若正整数n S ,则n 的每个正约数均属于S ;(3) 若,m n S ,且,m n 互素,则mn S ;(4) 若n S ,则An B S .证明:与B 互素的所有正整数均属于S .证明:先证明下述引理.引理:若n S ,则n B S .引理的证明:对n S ,设1n 是n 的与A 互素的最大约数,并设12n n n ,则2n 的素因子均整除A ,从而12(,)1n n .由条件(1)及(2)知,对任意素数|p A 及任意正整数k ,有k p S .因此,将11k A n 作标准分解,并利用(3)知11k A n S .又2|n n ,而n S ,故由(2)知2n S .因112(,)1k A n n ,故由(3)知112k A n n S ,即1k A n S .再由(4)知k A n B S (对任意正整数k ). ① …………10分设n B C D ,这里正整数C 的所有素因子均整除A ,正整数D 与A 互素,从而(,)1C D .由(1)及(2)知C S (见上面1k A n S 的证明). 另一方面,因(,)1D A ,故由欧拉定理知()1D D A .因此()()(1)()0(mod )D D A n B A n n B D ,但由①知()D A n B S ,故由(2)知D S .结合C S 及(,)1C D 知CD S ,即n B S .引理证毕. …………40分回到原问题.由(1),取0k 知1S ,故反复用引理知对任意正整数y ,有1By S .对任意*,(,)1n n B N ,存在正整数,x y 使得1nx By ,因此nx S ,因|n nx ,故n S .证毕. …………50分。
水文学原理试卷A答案及评分标准(2013春)

2013 年 春季 学期《水文学原理》课程考试试卷( A卷)答案一、填空题 (每空1分,共20分)1.径流深、洪峰流量模数。
2.降水、下渗、蒸发、径流3.算术平均法、泰森多边形法、等雨量线法4.大于05.吸湿水、薄膜水、毛管水、重力水6.流域蓄水容量7.使河段蓄量与下断面出流量呈单值关系的河段长度8.产流、汇流9.基质势、重力二、名词解释 (每小题3分,共15分)1、田间持水量:土壤中所能保持的最大毛管悬着水量。
2、线性系数:运算Φ[I(t)]、]满足叠加性和倍比性的系统。
3、下渗能力:充分供水条件下的下渗率。
4、单位线:在给定流域上,单位时段内均匀分布的单位地面净雨量在流域出口断面形成的地面径流过程线。
5、线性水库:蓄水量与出流量成正比关系的水库。
三、选择题(每小题2分,共10分)ACBDB四、简答题(每小题5分,共25分)1、超渗产流模式有何特征,它与蓄满产流模式有何区别?不管当地的土壤含水量是否达到田间持水量,只要降雨强度超过下渗强度就产生地面径流,称此为超渗产流。
蓄满产流则是指一次降雨过程中,仅当包气带的含水量达到田间持水量后才产流,且以后的有效降雨全部变为径流。
可见这两种产流模式的主要区别在于:蓄满产流以包气带的含水量达到田间持水量(即蓄满)作为产流的控制条件,而超渗产流则以降雨强度大过于当地的下渗能力作为产流的控制条件,而不管蓄满与否。
2、试述裸土蒸发的三个阶段及其特点?(要求结合图形进行说明,图形上应标注相应的含水量特征值)。
各阶段土壤蒸发的特点如下:第一阶段土壤含水量大于田间持水量,土壤中的水分可以充分供给土壤表面蒸发,按土壤蒸发能力蒸发,蒸发只受气象条件影响;第二阶段,土壤土壤含水量介于毛管断裂含水量与田间持水量之间,土壤蒸发率与土壤含水量大致成正比;第三阶段土壤土壤含水量降至毛管断裂含水量以下,毛管向土壤表面送水的机制完全破坏,水分只能以薄膜水或气态水的形式向地面移动,这一阶段土壤蒸发率很微小,气象条件和土壤含水量的关系已不明显。
南京信息工程大学综合英语2课程期末考试试卷A附参考答案及评分标准

南京信息⼯程⼤学综合英语2课程期末考试试卷A附参考答案及评分标准南京信息⼯程⼤学2007 ─ 2008 学年第⼆学期综合英语2 课程期末考试试卷A 注意:1、本试卷共10 页;2、考试时间120 分钟;出卷时间:2008 年6⽉;3、姓名、学号等必须写在指定地⽅;4、适⽤专业年级:07级英语及汉英⽅向本科任课教师:沈⼴湫、张⽟环、姜萍、周志浩专业年级班级学号姓名Task One Dictation (20%)Section A. Word dictation (10%)In this section, you will hear 20 words in all, each being read twice. Try to write them on the corresponding space on the ANSWER SHEET.Section B. Passage Dictation (10%)Listen to the following passage. Altogether the passage will be read four times. During the first reading, which will be read at normal speed, listen and try to understand the meaning. For the second and third readings, the passage will be read sentence by sentence, or phrase by phrase. The last reading will be read at normal speed again and during this time you should check your work.Please write the whole passage on the ANSWER SHEET.Task Two Chinese-English Translation (10%)Translate the following sentences into English with the given words or phrases. Please write your translations on the ANSWER SHEET.1.他决定不惜代价去实现他的雄⼼壮志。
2019年全国高中数学联赛A卷一试(含附加)参考答案与评分标准

为 0),则产生的不同的 8 位数的个数为
.
答案: 498 .
解:将 2, 0, 1, 9, 20, 19 的首位不为 0 的排列的全体记为 A .
一、填空题:本大题共 8 小题,每小题 8 分,满分 64 分.
1. 已知正实数 a 满足 aa = (9a)8a ,则 loga (3a) 的值为
.
答案: 9 . 16
1
解:由条件知 9a = a8 ,故 3a =
9a ⋅a
=
9
a 16
,所以 loga (3a)
=
9 16
.
2. 若实数集合{1, 2, 3, x} 的最大元素与最小元素之差等于该集合的所有元素
所以 EPF
为直角,进而 SDPEF
=
1⋅ 2
PE
⋅
PF
=1.
5. 在1, 2, 3, , 10 中随机选出一个数 a ,在-1, - 2, -3, , -10 中随机选出一
个数 b ,则 a2 + b 被 3 整除的概率为
.
答案:
37 100
.
解:数组 (a, b) 共有102 =100 种等概率的选法.
台.不妨设正方体棱长为 1,则正方体体积为 1,结合条件知棱台 ABC - KFL 的
体积V = 1 .
4
P
设
PF
=
h
,则
KF AB
=
FL BC
=
PF PB
=
h
h +1
.注意到
PB,
PF
E
H K
G L
分别是棱锥 P - ABC 与棱锥 P - KFL 的高,于是
2009年全国高中数学联赛一、二试及详细答案和评分标准(A卷)

2009年全国高中数学联合竞赛一试试题参考答案及评分标准说明:1.评阅试卷时,请依据本评分标准,填空题只设7分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不要增加其他中间档次.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中至少4分为一个档次,不要增加其他中间档次. 一、填空(共8小题,每小题7分,共56分)1. 若函数()f x ()()()n nf x f f f f x ⎡⎤=⎡⎤⎣⎦⎣⎦,则()()991f = . 【答案】 110【解析】 ()()()1f x f x ==, ()()()2f x f f x ==⎡⎤⎣⎦……()()99f x =故()()991110f =.2. 已知直线:90L x y +-=和圆22:228810M x y x y +---=,点A 在直线L 上,B ,C 为圆M 上两点,在ABC ∆中,45BAC ∠=︒,AB 过圆心M ,则点A 横坐标范围为 .【答案】 []36, 【解析】 设()9A a a -,,则圆心M 到直线AC 的距离sin 45d AM =︒,由直线AC 与圆M 相交,得d 解得36a ≤≤.3. 在坐标平面上有两个区域M 和N ,M 为02y y x y x ⎧⎪⎨⎪-⎩≥≤≤,N 是随t 变化的区域,它由不等式1t x t +≤≤所确定,t 的取值范围是01t ≤≤,则M 和N 的公共面积是函数()f t = .【答案】 212t t -++【解析】 由题意知 ()f t S =阴影部分面积A OB OCD BS S S ∆∆∆=-- ()22111122t t =---212t t =-++4. 使不等式1111200712213a n n n +++<-+++对一切正整数n 都成立的最小正整数a 的值为 .【答案】 2009【解析】 设()1111221f n n n n =++++++.显然()f n 单调递减,则由()f n 的最大值()1120073f a <-,可得2009a =.5. 椭圆22221x y a b +=()0a b >>上任意两点P ,Q ,若OP OQ ⊥,则乘积OP OQ ⋅的最小值为 .【答案】 22222a ba b+【解析】 设()cos sin P OP OP θθ,,ππcos sin 22Q OQ OQ θθ⎛⎫⎛⎫⎛⎫±± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,.由P ,Q 在椭圆上,有 222221cos sin a b OP θθ=+ ① 222221sin cos a b OQ θθ=+ ② ①+②得22221111a b OP OQ+=+.于是当OP OQ ==OP OQ 达到最小值22222a b a b+.6. 若方程()lg 2lg 1kx x =+仅有一个实根,那么k 的取值范围是 . 【答案】 0k <或4k = 【解析】 ()20101kx x kx x ⎧>⎪⎪+>⎨⎪=+⎪⎩当且仅当0kx > ① 10x +>② ()2210x k x +-+=③对③由求根公式得1x,2122x k ⎡=-⎣ ④2400k k k ∆=-⇒≥≤或4k ≥.(ⅰ)当0k <时,由③得 12122010x x k x x +=-<⎧⎨=>⎩ 所以1x ,2x 同为负根. 又由④知121010x x +>⎧⎨+<⎩所以原方程有一个解1x .(ⅱ)当4k =时,原方程有一个解112kx =-=. (ⅲ)当4k >时,由③得12122010x x k x x +=->⎧⎨=>⎩所以1x ,2x 同为正根,且12x x ≠,不合题意,舍去. 综上可得0k <或4k =为所求.7. 一个由若干行数字组成的数表,从第二行起每一行中的数字均等于其肩上的两个数之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是 (可以用指数表示)【答案】 981012⨯ 【解析】 易知:(ⅰ)该数表共有100行;(ⅱ)每一行构成一个等差数列,且公差依次为11d =,22d =,232d =,…,98992d =(ⅲ)100a 为所求.设第()2n n ≥行的第一个数为n a ,则 ()22111222n n n n n n a a a a -----=++=+3222222n n n a ---⎡⎤=++⎣⎦24223222222n n n n a ----⎡⎤=++⨯+⎣⎦323232n n a --=+⨯……()121212n n a n --=+-⨯ ()212n n -=+故981001012a =⨯.8. 某车站每天800~900∶∶,900~1000∶∶都恰有一辆客车到站,但到站的时刻是随机的,且两者到站一旅客820∶到车站,则它候车时间的数学期望为 (精确到分)【答案】 27 【解析】 旅客候车的分布列为候车时间的数学期望为1111110305070902723361218⨯+⨯+⨯+⨯+⨯=二、解答题1. (本小题满分14分)设直线:l y kx m =+(其中k ,m 为整数)与椭圆2211612x y +=交于不同两点A ,B ,与双曲线221412x y -=交于不同两点C ,D ,问是否存在直线l ,使得向量0AC BD +=,若存在,指出这样的直线有多少条?若不存在,请说明理由. 【解析】 由2211612y kx m x y =+⎧⎪⎨+=⎪⎩消去y 化简整理得()2223484480k xkmx m +++-=设()11A x y ,,()22B x y ,,则122834kmx x k +=-+()()()222184344480km k m ∆=-+-> ① ………………………………………………4分由221412y kx m x y =+⎧⎪⎨-=⎪⎩消去y 化简整理得()22232120k xkmx m ----=设()34C x y ,,()44D x y ,,则34223kmx x k+=- ()()()2222243120km k m ∆=-+-+> ② ………………………………………………8分因为0AC BD +=,所以()()42310x x x x -+-=,此时()()42310y y y y -+-=.由1234x x x x +=+得2282343km kmk k -=+-. 所以20km =或2241343k k -=+-.由上式解得0k =或0m =.当0k =时,由①和②得m -<m 是整数,所以m 的值为3-,2-,1-,0,1,2,3.当0m =,由①和②得k .因k 是整数,所以1k =-,0,1.于是满足条件的直线共有9条.………14分2. (本小题15分)已知p ,()0q q ≠是实数,方程20x px q -+=有两个实根α,β,数列{}n a 满足1a p =,22a p q =-,()1234n n n a pa qa n --=-=,,(Ⅰ)求数列{}n a 的通项公式(用α,β表示);(Ⅱ)若1p =,14q =,求{}n a 的前n 项和.【解析】 方法一:(Ⅰ)由韦达定理知0q αβ⋅=≠,又p αβ+=,所以()1212n n n n n a px qx a a αβαβ------=+-,()345n =,,,整理得()112n n n n a a a a βαβ----=- 令1n n n b a a β+=-,则()112n n b b n α+==,,.所以{}n b 是公比为α的等比数列.数列{}n b 的首项为:()()222121b a a p q p ββαβαββαβα=-=--=+--+=.所以211n n n b ααα-+=⋅=,即11n n n a a βα++-=()12n =,,.所以11n n n a a βα++=+()12n =,,.①当240p q ∆=-=时,0αβ=≠,12a p ααα==+=,11n n n a a βα++=+()12n =,,变为11n n n a a αα++=+()12n =,,.整理得,111n nn na a αα++-=,()12n =,,.所以,数列n n a α⎧⎫⎨⎬⎩⎭成公差为1的等差数列,其首项为122a ααα==.所以()2111nna n n α=+-=+.于是数列{}n a 的通项公式为()1n n a n α=+;……………………………………………………………………………5分②当240p q ∆=->时,αβ≠, 11n n n a a βα++=+1n n a βαβαβα+-=+-11n n n a βαβααβαβα++=+---()12n =,,.整理得211n n n n a a ααββαβα+++⎛⎫+=+ ⎪--⎝⎭,()12n =,,.所以,数列1n n a αβα+⎧⎫+⎨⎬-⎩⎭成公比为β的等比数列,其首项为2221a ααβαββαβαβα+=++=---.所以121n n n a αβββαβα+-+=--.于是数列{}n a 的通项公式为11n n n a βαβα++-=-.………………………………………………10分(Ⅱ)若1p =,14q =,则240p q ∆=-=,此时12αβ==.由第(Ⅰ)步的结果得,数列{}n a 的通项公式为()11122nn n n a n +⎛⎫=+= ⎪⎝⎭,所以,{}n a 的前n 项和为231234122222n n n n n s -+=+++++234112341222222n n n n s n ++=+++++以上两式相减,整理得1133222n n n s ++=-所以332n n n s +=-.……………………………………………………………………………15分方法二:(Ⅰ)由韦达定理知0q αβ⋅=≠,又p αβ+=,所以1a αβ=+,222a αβαβ=++.特征方程20p q λλ-+=的两个根为α,β. ①当0αβ=≠时,通项()()1212n n a A A n n α=+=,,由12a α=,223a α=得()()122212223A A A A αααα+=⎧⎪⎨+=⎪⎩ 解得121A A ==.故 ()1n n a n α=+.……………………………………………………5分 ②当αβ≠时,通项()1212n n n a A A n αβ=+=,,.由1a αβ=+,222a αβαβ=++得12222212A A A A αβαβαβαβαβ+=+⎧⎪⎨+=++⎪⎩ 解得1A αβα-=-,2A ββα=-.故1111n n n n n a αββαβαβαβα++++--=+=---.…………………………………………………………10分 (Ⅱ)同方法一.3. (本小题满分15分)求函数y=【解析】函数的定义域为[]013,.因为y=当0x =时等号成立.故y的最小值为.……………………………………………5分 又由柯西不等式得 22y =()()()11122731312123x x x ⎛⎫+++++-= ⎪⎝⎭≤所以11y ≤. ………………………………………………………………………………10分 由柯西不等式等号成立的条件,得()491327x x x =-=+,解得9x =.故当9x =时等号成立.因此y 的最大值为11.…………………………………………………………………………………15分2009年全国高中数学联合竞赛加试试题参考答案及评分标准(A 卷)说明:1.评阅试卷时,请严格按照本评分标准的评分档次给分.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,10分为一个档次,不要增加其他中间档次. 一、填空(共4小题,每小题50分,共200分)9. 如图,M ,N 分别为锐角三角形ABC ∆(A B ∠<∠)的外接圆Γ上弧BC 、AC 的中点.过点C 作PC MN ∥交圆Γ于P 点,I 为ABC ∆的内心,连接PI 并延长交圆Γ于T . ⑴求证:MP MT NP NT ⋅=⋅;⑵在弧AB (不含点C )上任取一点Q (Q A ≠,T ,B ),记AQC ∆,QCB △的内心分别为1I ,2I ,B求证:Q ,1I ,2I ,T 四点共圆.【解析】 ⑴连NI ,MI .由于PC MN ∥,P ,C ,M ,N 共圆,故PCMN 是等腰梯形.因此NP MC =,PM NC =.ABCMNPTI连AM ,CI ,则AM 与CI 交于I ,因为MIC MAC ACI MCB BCI MCI ∠=∠+∠=∠+∠=∠,所以MC MI =.同理NC NI =.于是NP MI =,PM NI =.故四边形MPNI 为平行四边形.因此PMT PNT S S =△△(同底,等高). 又P ,N ,T ,M 四点共圆,故180TNP PMT ∠+∠=︒,由三角形面积公式1sin 2PMT S PM MT PMT =⋅∠△1s i n 2PNT S PN NT PNT ==⋅∠△1s i n 2P N N T P MT =⋅∠ 于是PM MT PN NT ⋅=⋅.⑵因为1111NCI NCA ACI NQC QCI CI N ∠=∠+∠=∠+∠=∠,B所以1NC NI =,同理2MC MI =.由MP MT NP NT ⋅=⋅得NT MTMP NP=. 由⑴所证MP NC =,NP MC =,故 12NT MTNI MI =. 又因12I NT QNT QMT I MT ∠=∠=∠=∠,有12I NT I MT ∆∆∽.故12NTI MTI ∠=∠,从而1212I QI NQM NTM I TI ∠=∠=∠=∠.因此Q ,1I ,2I ,T 四点共圆. 10. 求证不等式:2111ln 12n k k n k =⎛⎫-<- ⎪+⎝⎭∑≤,1n =,2,… 【解析】 证明:首先证明一个不等式: ⑴ln(1)1x x x x<+<+,0x >. 事实上,令()ln(1)h x x x =-+,()ln(1)1xg x x x=+-+. 则对0x >,1()101h x x '=->+,2211()01(1)(1)x g x x x x '=-=>+++. 于是()(0)0h x h >=,()(0)0g x g >=.在⑴中取1x n=得⑵111ln 11n n n⎛⎫<+< ⎪+⎝⎭. 令21ln 1nn k k x n k ==-+∑,则112x =,121ln 111n n n x x n n -⎛⎫-=-+ ⎪+-⎝⎭ 211n n n<-+210(1)n n=-<+因此1112n n x x x -<<<=.又因为111ln (ln ln(1))(ln(1)ln(2))(ln 2ln1)ln1ln 1n k n n n n n k -=⎛⎫=--+---++-+=+ ⎪⎝⎭∑.从而12111ln 11nn n k k k x k k -==⎛⎫=-+ ⎪+⎝⎭∑∑12211ln 111n k k n k k n -=⎛⎫⎛⎫=-++ ⎪ ⎪++⎝⎭⎝⎭∑12111n k kk k -=⎛⎫>- ⎪+⎝⎭∑1211(1)n k k k -==-+∑111(1)n k k k -=-+∑≥111n=-+>-.11. 设k ,l 是给定的两个正整数.证明:有无穷多个正整数m k ≥,使得C k m 与l 互素.【解析】 证法一:对任意正整数t ,令(!)m k t l k =+⋅⋅.我们证明()C 1k m l =,. 设p 是l 的任一素因子,只要证明:C k m p Œ.若!p k Œ,则由 1!C ()kkmi k m k i ==-+∏1[((!)]k i i t l k =≡+∏ 1ki i =≡∏()1!m o d k p α+≡.及|!p k α,且1!p k α+Œ,知|!C k m p k α且1!C k m p k α+Œ.从而C k m p Œ.证法二:对任意正整数t ,令2(!)m k t l k =+⋅⋅,我们证明()C 1k m l =,. 设p 是l 的任一素因子,只要证明:C k m p Œ.若!p k Œ,则由1!C ()kkmi k m k i ==-+∏21[((!)]ki i t l k =≡+∏ 1ki i =≡∏()!m o dk p ≡. 即p 不整除上式,故C k m p Œ.若|!p k ,设1α≥使|!p k α,但1!p k α+Œ.12|(!)p k α+.故由 11!C ()k kmi k m k i -==-+∏21[((!)]ki i t l k =≡+∏ 1ki i =≡∏()1!mod k p α+≡及|!p k α,且1!p k α+Œ,知|!C k m p k α且1!C k m p k α+Œ.从而C k m p Œ.12. 在非负数构成的39⨯数表111213141516171212223242526272829313233343536373839x x x x x x x x x P x x x x x x x x x x x x x x x x x x⎛⎫ ⎪= ⎪ ⎪⎝⎭ 中每行的数互不相同,前6列中每列的三数之和为1,1728390x x x ===,27x ,37x ,18x ,38x ,19x ,29x 均大于.如果P 的前三列构成的数表111213212223313233x x x S x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭满足下面的性质()O :对于数表P 中的任意一列123k k k x x x ⎛⎫ ⎪⎪ ⎪⎝⎭(1k =,2,…,9)均存在某个{}123i ∈,,使得⑶{}123min ik i i i i x u x x x =≤,,.求证:(ⅰ)最小值{}123min i i i i u x x x =,,,1i =,2,3一定自数表S 的不同列. (ⅱ)存在数表P 中唯一的一列***123k k k x x x ⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭,*1k ≠,2,3使得33⨯数表***111212122231323k k k x x x S x x x x x x ⎛⎫ ⎪'= ⎪ ⎪ ⎪⎝⎭ 仍然具有性质()O .【解析】 (ⅰ)假设最小值{}123min i i i i u x x x =,,,1i =,2,3不是取自数表S 的不同列.则存在一列不含任何i u .不妨设2i i u x ≠,1i =,2,3.由于数表P 中同一行中的任何两个元素都不等,于是2i i u x <,1i =,2,3.另一方面,由于数表S 具有性质()O ,在⑶中取2k =,则存在某个{}0123i ∈,,使得002i i x u ≤.矛盾.(ⅱ)由抽届原理知{}1112min x x ,,{}2122min x x ,,{}3132min x x , 中至少有两个值取在同一列.不妨设 {}212222min x x x =,,{}313232min x x x =,.由前面的结论知数表S 的第一列一定含有某个i u ,所以只能是111x u =.同样,第二列中也必含某个i u ,1i =,2.不妨设222x u =.于是333u x =,即i u 是数表S 中的对角线上数字.111213212223313233x x x S x x x x x x ⎛⎫⎪= ⎪ ⎪⎝⎭记{}129M =,,,,令集合 {}{}12|min 13ik i i I k M x x x i =∈>=,,,.显然{}111332|k k I k M x x x x =∈>>,且1,23I ∉.因为18x ,38111x x >≥,32x ,所以8I ∈. 故I ∅≠.于是存在*k I ∈使得{}*22max |k k x x k I =∈.显然,*1k ≠,2,3. 下面证明33⨯数表 ***111212122231323k k k x x x S x x x x x x ⎛⎫ ⎪'= ⎪ ⎪ ⎪⎝⎭具有性质()O .从上面的选法可知{}{}*1212:min min i i i i i ik u x x x x x '==,,,,(13)i =,.这说明 {}*111211min k x x x u >,≥,{}*313233min k x x x u >,≥.又由S 满足性质()O .在⑶中取*k k =,推得*22k x u ≤,于是{}**2212222min k k u x x x x '==,,.下证对任意的k M ∈,存在某个1i =,2,3使得i ik u x '≥.假若不然,则{}12min ik i i x x x >,,1i =,3且*22k k x x >.这与*2k x 的最大性矛盾.因此,数表S '满足性质()O .下证唯一性.设有k M ∈使得数表 111212122231323k k k x x x S x x x x x x ⎛⎫⎪= ⎪ ⎪⎝⎭具有性质()O ,不失一般性,我们假定 {}111121311m i n u x x x x ==,, ⑷{}221222322min u x x x x ==,,{}331323333m i n u x x xx ==,,3231x x <.由于3231x x <,2221x x <及(ⅰ),有{}11112111min k u x x x x ==,,.又由(ⅰ)知:或者()a {}3313233min k k u x x x x ==,,,或者{}2212222()min k k b u x x x x ==,,.如果()a 成立,由数表S 具有性质()O ,则 {}11112111m i n ku x x x x ==,,, ⑸{}22122222min k u x x x x ==,,, {}3313233m i n k k u x x x x ==,,.由数表S 满足性质()O ,则对于3M ∈至少存在一个{}123i ∈,,使得*i ik u x ≥.由*k I ∈及⑷和⑹式知,*1111k x x u >=,*3323k x x u >=.于是只能有*222k k x u x =≤.类似地,由S '满足性质()O 及k M ∈可推得*222k k x u x '=≤.从而*k k =.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图6.12 湖南城市学院20 —20 学年第 学期 专业 年级期末/补考/重修课程
数据结构 考核试题标准答案及评分细则
考核方式:闭卷 考试时量:120分钟 试卷类型:A/B/C
一、判断题(共10分,每小题1分)
1-5 X X X X X 6-10 √√√√√
二、填空题(共20分,每空1分) 1 关系
2 有穷性、确定性、可行性、输入、输出
3 任意多个
4 前驱、1、后续、任意多个
5 n-1
6 移动栈顶指针 存入元素
7 不包含任何字符(长度为0)的串 由一个或多个空格(仅由空格符)组成的串
8 n
9 一个结点可能有若干个前驱,也可能有若干个后继 10、顺序存储结构、有序的
三、选择题(共30分,每小题2分)
1-5 BCBBD 6-10 CBBBC 11-15 CCBBD
四、简答题(共32分,每小题8分)
1、已知如图所示的有向图,请给出该图的:
如图6.10所示
2、.试比较顺序存储结构和链式存储结构的优缺点。
在什么情况下用顺序表比链表好? 答:① 顺序存储时,相邻数据元素的存放地址也相邻(逻辑与物理统一);要求内存中可用存储单元的地址必须是连续的。
优点:存储密度大(=1?),存储空间利用率高。
缺点:插入或删除元素时不方便。
2分
②链式存储时,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针2分
优点:插入或删除元素时很方便,使用灵活。
缺点:存储密度小(<1),存储空间利用率低。
4分 顺序表适宜于做查找这样的静态操作;链表宜于做插入、删除这样的动态操作。
若线性表的长度变化不大,且其主要操作是查找,则采用顺序表;
若线性表的长度变化较大,且其主要操作是插入、删除操作,则采用链表。
3、给定二叉树的两种遍历序列,分别是:
前序遍历序列:D ,A ,C ,E ,B ,H ,F ,G ,I ; 中序遍历序列:
D ,C ,B ,
E ,H ,A ,G
,I ,F ,
试画出二叉树B ,并简述由任意二叉树B 的前序遍历序列和中序遍历序列求二叉树B 的思想方法。
解:方法是:由前序先确定root
,由中序可确定root 的左、右子树。
然后由其左子树的元素集合和右子树的集合对应前序遍历序列中的元素集合,可继续确定root 的左右孩子。
将他们分别作为
新的root ,不断递归,则所有元素都将被唯一确定,问题得解。
4分3分 画图3分 4、画出下列网络的最小生成树。
答:
h
图1 对应的森林
i
f
五、综合题(共16分,每小题8分)
1、中序线索二叉树如图1(左)所示;后序线索二叉树如图1(右)所示;
该二叉树转换后的的森林如图1所示。
2、某通讯系统只可能有A、B、C、D、E、F 6种字符,其出现的概率分别是0.1、0.4、0.04、0.16、0.19、0.11,试画出相应的哈夫曼树,并设计哈夫曼编码。
(8分)
解:
(4分)
编码:A:1011 B:0 C:1010 D:110 E:111 F:100(4分)。
