整式的乘除20141010
整式的乘除知识点

整式的乘除知识点整式的乘法运算是指对两个或多个整式进行相乘的运算。
整式的除法运算是指对一个整式除以另一个整式的运算。
整式的乘除运算是代数学中的基本运算,它在代数方程的解法、因式分解等应用中起着重要作用。
一、整式的乘法运算整式的乘法是指对两个或多个整式进行相乘的运算,其规则如下:1.单项式相乘:两个单项式相乘时,按照数字相乘,字母相乘,再将相同字母的指数相加的原则进行运算。
例如:(3x^2)(-2xy)=-6x^3y2.整式相乘:将一个整式中的每一项与另一个整式中的每一项进行相乘,然后将所得的结果相加。
例如:(x+5)(x-3)=x^2-x(3)+5(x)-15=x^2-3x+5x-15=x^2+2x-153.公式相乘:根据一些常见公式和特殊公式,可以通过整式的乘法运算简化计算。
例如:(a+b)(a-b)=a^2-(b)^2=a^2-b^2二、整式的除法运算整式的除法是指对一个整式除以另一个整式的运算,其规则如下:1.简单整式的除法:当被除式是单项式,除式也是单项式,并且除式不为零时,可以进行简单整式的除法运算。
例如:12x^3/4x=x^32.整式长除法:当被除式是一个整式,除式也是一个整式,并且除式不为零时,可以进行整式长除法运算。
例如:(3x^3-2x^2+4x-6)/(x+2)=3x^2-8x+20余-463.分式的除法:分式的除法可以利用倒数的概念进行处理,将除法问题转化为乘法问题。
例如:(a/b)÷(c/d)=(a/b)×(d/c)=(ad)/(bc)三、整式乘除运算的性质和应用1.乘法交换律:整式的乘法满足交换律,即a×b=b×a。
这个性质可以简化计算,使得整式的乘法更加灵活。
2.乘法结合律:整式的乘法满足结合律,即(a×b)×c=a×(b×c)。
这个性质可以改变运算次序,简化计算过程。
3.乘法分配律:整式的乘法满足分配律,即a×(b+c)=a×b+a×c。
整式的乘除课件

详细描述
分配律是整式乘除中的基本运算规则,即 $a(b+c) = ab + ac$。通过分配律,可以 将复杂的整式乘法或除法转化为简单的代数 运算。例如,利用分配律计算整式 $(x+y)^2$,可以得出结果$x^2 + 2xy + y^2$。同样地,在整式除法中,也可以利 用分配律进行简化计算。
05
THANKS
感谢观看
单项式相除,系数相除,同底数的幂 相减。
如果两个单项式相除,可以直接将它 们的系数相除,同时将同底数的幂相 减。例如,$frac{3x^2}{5x} = frac{3}{5}x^{2-1} = frac{3}{5}x$。
单项式除以多项式
将多项式拆分成单项式,分别与被除式相除。
如果单项式除以多项式,可以将多项式拆分成若干个单项式,然后分别与被除式 相除。例如,$frac{x}{x+1} = frac{x}{x+1}$。
在数学教育中,整式的乘除是培养学生逻辑思维和数学素养 的重要内容之一。通过整式的乘除训练,可以提高学生的数 学思维能力,增强学生的数学应用能力。
02
整式乘法规则
单项式乘单项式
总结词
这是整式乘法中最简单的形式,只需 将两个单项式的系数相乘,并将相同 的字母的幂相加。
详细描述
例如,$2x^3 times 3x^2 = 6x^{3+2} = 6x^5$。
单项式乘多项式
总结词
将一个单项式与一个多项式中的每一项分别相乘,然后合并同类项。
详细描述
例如,$(2x - 3y) times 3x = 6x^2 - 9xy$。
多项式乘多项式
总结词
将两个多项式的每一对相应项分别相乘,然后合并同类项。
整式的乘除
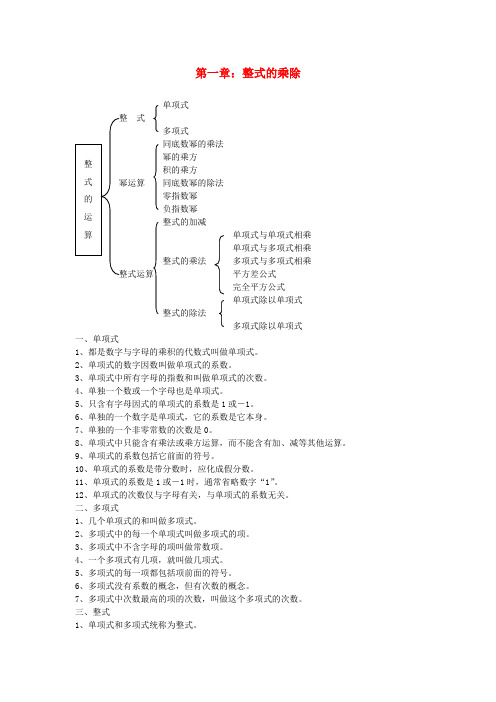
第一章:整式的乘除单项式式多项式同底数幂的乘法 幂的乘方 积的乘方同底数幂的除法 零指数幂 负指数幂 整式的加减单项式与单项式相乘 单项式与多项式相乘 整式的乘法 多项式与多项式相乘 整式运算 平方差公式 完全平方公式 单项式除以单项式 整式的除法多项式除以单项式 一、单项式1、都是数字与字母的乘积的代数式叫做单项式。
2、单项式的数字因数叫做单项式的系数。
3、单项式中所有字母的指数和叫做单项式的次数。
4、单独一个数或一个字母也是单项式。
5、只含有字母因式的单项式的系数是1或―1。
6、单独的一个数字是单项式,它的系数是它本身。
7、单独的一个非零常数的次数是0。
8、单项式中只能含有乘法或乘方运算,而不能含有加、减等其他运算。
9、单项式的系数包括它前面的符号。
10、单项式的系数是带分数时,应化成假分数。
11、单项式的系数是1或―1时,通常省略数字“1”。
12、单项式的次数仅与字母有关,与单项式的系数无关。
二、多项式1、几个单项式的和叫做多项式。
2、多项式中的每一个单项式叫做多项式的项。
3、多项式中不含字母的项叫做常数项。
4、一个多项式有几项,就叫做几项式。
5、多项式的每一项都包括项前面的符号。
6、多项式没有系数的概念,但有次数的概念。
7、多项式中次数最高的项的次数,叫做这个多项式的次数。
三、整式1、单项式和多项式统称为整式。
2、单项式或多项式都是整式。
3、整式不一定是单项式。
4、整式不一定是多项式。
5、分母中含有字母的代数式不是整式;而是今后将要学习的分式。
四、整式的加减1、整式加减的理论根据是:去括号法则,合并同类项法则,以及乘法分配率。
2、几个整式相加减,关键是正确地运用去括号法则,然后准确合并同类项。
3、几个整式相加减的一般步骤:(1)列出代数式:用括号把每个整式括起来,再用加减号连接。
(2)按去括号法则去括号。
(3)合并同类项。
4、代数式求值的一般步骤:(1)代数式化简。
(2)代入计算(3)对于某些特殊的代数式,可采用“整体代入”进行计算。
整式的乘除

整式的乘除整式是指由常数、变量及它们的乘、除运算符号经有限次组合而成的代数表达式。
整式是代数学中一个重要的概念,掌握整式的乘除运算是解决代数问题的关键。
一、整式的乘法整式的乘法是指将两个或多个整式相乘的运算。
在整式的乘法中,我们需要遵循如下规则:1.同底数的幂相乘,底数不变,指数相加。
例如:am* an = am+n2.乘法满足交换律和结合律。
3.不同底数幂相乘时,可以将其视为两个不同的因数。
例如:am * bn = abn下面是一个整式乘法的示例:假设有整式 a = 2ab2,b = 3a2b,c = 4a2b2。
要求计算整式 d = a * (b + c) 的值。
根据乘法分配律,我们可以将乘法转化为加法运算,即:d = a * b + a * c。
将 a、b、c 的值代入计算,有:d = 2ab2 * 3a2b + 2ab2 * 4a2b2化简上式,将幂相加,并化简系数,得到:d = 6a3b3 + 8a3b4因此,整式 d 的值为 6a3b3 + 8a3b4。
二、整式的除法整式的除法是指将一个整式除以另一个整式的运算。
在整式的除法中,我们需要遵循如下规则:1.除法满足结合律,但不满足交换律。
2.同底数的幂相除,底数不变,指数相减。
例如:am/ an = am-n3.除法中,除数不为零。
下面是一个整式除法的示例:假设有整式 p = 5a3b2c 和 q = 10a2c2。
要求计算整式 r = p / q 的值。
根据整式除法的规则,我们需要将p 和q 化简到最简形式,然后进行除法运算。
首先,我们将 p 和 q 化简,并将指数按照从大到小的顺序排列:p = 5a3b2c,q = 10a2c2进行除法运算,将 p 中每一项除以 q 中的对应项,并将指数进行相减:r = (5a3b2c) / (10a2c2)再化简这个分式,我们可以将分子和分母都除以其最大公因式 5ac,得到最简形式:r = (a2b2) / (2c)因此,整式 r 的值为 (a2b2) / (2c)。
整式的乘除的法则及公式

整式的乘除的法则及公
式
公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]
整式的乘除的法则及公式
1、同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
(、为正整数)
2、幂的乘方法则:幂的乘方,底数不变,指数相乘。
(为正整数)
3、积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,在把所得的幂相乘。
(、为正整数)
4、单项式与单项式相乘的法则;单项式与单项式相乘,把它们的系数、同底
数幂分别相乘,其余字母连同它的指数不变,作
为积的因式。
5、单项式与多项式相乘法则:单项式与多项式相乘,就是用单项式去乘多项
式的每一项,再把所得的积相加。
a(b-2a)=ab-2am
6、多项式与多项式相乘法则:多项式与多项式相乘,先用一个多项式的每一
项乘另一个多项式的每一项,再把所得的积相
加,如果有同类项要合并同类项。
(a+n)(b+m)=ab+an+nb+nm
7、平方差公式:两数和与这两数差的积等于这两数的平方差。
8、两数和(差)完全平方公式:两数和(差)的平方,等于这两数的平方和
(差),加上(减去)这两数积的2倍。
9、整式化简:应遵循先乘方,再乘除,最后算加减的顺序,能运用乘法公式
的则运用乘法公式。
整式的乘除知识点整理

知识点1:幂的运算(1)同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
即,n m n m a a a +=⋅(2)幂的乘方法则:幂的乘方,底数不变,指数相乘。
即,mn n m a a =)((3)积的乘方法则:积的乘方,等于把积中每一个因式分别乘方,再把所得的幂相乘。
即,nn n b a ab =)((4)同底数幂的除法法则:同底数幂相除,底数不变,指数相减。
即,n m n m a a a -=÷知识点2:整式的乘法运算(1)单项式与单项式相乘法则:单项式与单项式相乘,只要将系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式(2)单项式与多项式相乘法则:单项式与多项式相乘,先用单项式分别乘以多项式的每一项,再把所得的积相加。
(3)多项式与多项式相乘法则:多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
知识点3:整式的除法运算(1)单项式与单项式相除法则:单项式除以单项式,只要将系数、相同字母的幂分别相除,对于只在一个被除式中出现的字母,则连同它的指数一起作为商的一个因式(2)多项式除以单项式法则:多项式除以单项式,先用多项式的每一项分别除以单项式,再把所得的商相加。
知识点4:乘法公式(1)两数和乘以这两数的差公式(又叫做:平方差公式):22))((b a b a b a -=-+(2)两数和的平方公式(又叫做:完全平方和公式):2222)(b ab a b a ++=+(3)两数差的平方公式(又叫做:完全平方差公式):2222)(b ab a b a +-=-知识点5:因式分解因式分解是指把一个多项式化成几个整式的积的形式,也叫分解因式。
因式分解最终结果特别注意以下几点:第一,必须分解成积的形式;第二,分解成的各因式必须是整式;第三,必须分解到不能再分解为止。
整式的乘除经典讲义(可直接用)

整式的乘除经典讲义(可直接用)整式的乘法讲义同底数幂的乘法同底数幂的乘法法则如下:1.幂的底数相同且相乘时,底数a可以是一个具体的数字或字母,也可以是一个单项或多项式。
2.指数是1时,不要误以为没有指数。
3.对乘法,只要底数相同指数就可以相加;而对于加法,不仅底数相同,还要求指数相同才能相加。
4.当三个或三个以上同底数幂相乘时,法则可推广为a^m * a^n = a^(m+n) (其中m、n均为正数)。
5.公式还可以逆用:a^m * a^n = a^(m+n)(m、n都是正数);a^m * a^-n = a^(m-n)(m为正数,n为负数)。
幂的乘方与积的乘方1.幂的乘法法则为基础推导出幂的乘方法则:(a^m)^n = a^(mn)(m、n都是正数)。
2.幂的乘方法则可以逆向运用:a^(mn) = (a^m)^n(m、n 都为正数)。
3.积的乘方,等于把积每一个因式分别乘方,再把所得的幂相乘,即(ab)^n = a^n * b^n(n为正整数)。
底数有负号时的运算1.底数是a与(-a)时不是同底,但可以利用乘法法则化成同底。
2.一般地,(-a)^n = a^n(当n为偶数时),(-a)^n = -a^n(当n为奇数时)。
3.底数有时形式不同,但可以化成相同。
4.要注意区别(ab)^n与(a+b)^n意义是不同的,不要误以为(a+b)^n= a^n + b^n(a、b均不为零)。
幂的除法同底数幂相除,底数不变,指数相减,即a^m ÷ a^n =a^(m-n)(a≠0,m、n都是正数,且m。
n)。
在应用时需要注意以下几点:1.法则使用的前提条件是“同底数幂相除”而且不能做除数,所以法则中a≠0.2.任何不等于0的数的次幂等于1,即a^0 = 1,(-2.5)^0 = 1,则无意义。
3.任何不等于0的数的负p次幂(p是正整数),等于这个数的p的次幂的倒数,即a^-p = 1/a^p(a≠0,p是正整数),而-1、0、-3都是无意义的;当a>0时,a^-p的值一定是正的;当a<0时,a^-p的值可能是正也可能是负的,如(-2)^-2 = 1/(-2)^2 = 1/4.4.运算要注意运算顺序。
第九讲 整式的乘除

第九讲 整式的乘除考试目标解读1.同底数幂的乘法法则:n m n m a a a +=•(n m ,都是正整数)同底数幂相乘,底数不变,指数相加。
注意底数可以是多项式或单项式。
2.幂的乘方法则:mn n m a a =)((n m ,都是正整数)幂的乘方,底数不变,指数相乘。
幂的乘方法则可以逆用:即m n n m mn a a a )()(==3.积的乘方法则: n n n b a ab =)((n 是正整数)。
积的乘方,等于各因数乘方的积。
4.同底数幂的除法法则:n m n m a a a -=÷(n m a ,,0≠都是正整数,且)n m同底数幂相除,底数不变,指数相减。
5.零指数和负指数;10=a ,即任何不等于零的数的零次方等于1。
p p a a 1=-(p a ,0≠是正整数),即一个不等于零的数的p -次方等于这个数的p 次方的倒数1.典型例题考点一:同底数幂的乘法例1:若53=a ,63=b ,求b a +3的值。
例2:若125512=+x ,求()x x +-20092的值。
练习:1、计算32)(x x ⋅-所得的结果是( )A.5xB.5x -C.6xD.6x -2、下列计算正确的是( )A.822b b b =⨯B.642x x x =+C.933a a a =⨯D.98a a a =3、下面计算正确的是( )A.4533=-a aB.n m n m +=⋅632C.109222=⨯D.10552a a a =⋅4、=-⋅-23)()(a b b a , ()=-⋅-⋅-62)()(a a a 。
5、计算:(1)=⨯461010 (2)=⎪⎭⎫⎝⎛-⨯-6231)31((3)=⋅⋅b b b 32 (4)-2y ⋅ 5y =6、已知:5 ,3==n m a a ,求2++n m a 的值7、若62=-a m ,115=+b m ,求3++b a m 的值考点二:幂的乘方例1:若52=n ,求n 28的值。
