高三三模考试数学试题(理科)2017.6
2017年河南省郑州市高考数学三模试卷(理科)(解析版)

2017年河南省郑州市高考数学三模试卷(理科)(解析版)2017年河南省郑州市高考数学三模试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.设命题p:∀x>,log2x<2x+3,则¬p为()A。
∀x>,log2x≥2x+3B。
∃x>,log2x≥2x+3C。
∃x>,log2x<2x+3D。
∀x<,log2x≥2x+32.已知复数m=4﹣xi,n=3+2i,若复数m+n∈R,则实数x的值为()A。
﹣6B。
6C。
7D。
53.已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$,焦点在y 轴上,若焦距为4,则a等于()A。
$\sqrt{13}$B。
$\sqrt{15}$C。
5D。
$\sqrt{17}$4.已知$\frac{x}{a}+\frac{y}{b}=1$,$\frac{x}{b}+\frac{y}{a}=1$,则$\frac{x^2}{a^2}+\frac{y^2}{b^2}$的值等于()A。
2B。
1C。
$\frac{1}{2}$D。
05.设集合A={x1,x2,x3,x4},$x_i∈\{-1,1\}$,$i\in\{1,2,3,4\}$,那么集合A中满足条件“$x_1^2+x_2^2+x_3^2+x_4^2≤3$”的元素个数为()A。
60B。
65C。
80D。
816.如图是某个几何体的三视图,则这个几何体体积是()A。
48B。
72C。
96D。
1207.设实数x,y满足$x^2+y^2=25$,$xy=12$,则$x+y$的最大值为()A。
25B。
49C。
12D。
248.已知等比数列{an},且$a_6+a_8=\frac{\pi^2}{2}$,则2xy的最大值为()A。
$\pi^2$B。
$4\pi^2$C。
$8\pi^2$D。
$16\pi^2$9.若实数$a$、$b$、$c∈R^+$,且$ab+ac+bc+2\sqrt{(abc)^2}=1$,则$2a+b+c$的最小值为()A。
2017年高考全国三卷理科数学试卷.doc

2017年普通高等学校招生全国统一考试(III卷)2017.6理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
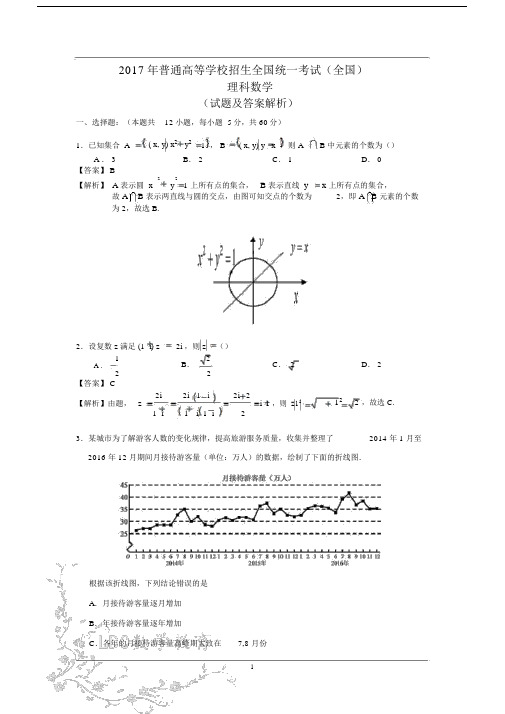
2 y2 B x y y x1. 已知集合 A {( x, y) | x 1},{( , ) | } ,则A∩B 中元素的个数为A. 3B. 2C. 1D. 02. 设复数z 满足(1 + i) z = 2i,则| z | =A. 12B.22C. 2D. 23. 某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年1 月至2016 年12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图。
根据该折线图,下列结论错误的是A. 月接待游客量逐月增加B. 年接待游客量逐年增加C. 各年的月接待游客量高峰期大致在7、8 月D. 各年 1 月至6 月的月接待游客量相对于7 月至12 月,波动性更小,变化比较平稳5 3 3的展开式中x4. (x + y)(2x - y)y 的系数为A. -80B. -40C. 40D. 802 2x y5. 已知曲线C:1(a 0,b 0)2 2a b5的一条渐近线方程为y x22 y 2x,且与椭圆1有公共焦点,则12 3C 的方程为2 y2xA. 18 102 y2x1B.4 52 y2xC. 15 42 y2xD. 14 36. 设函数 f (x) cos(x ) ,则下列结论错误的是3A. f (x) 的一个周期为 2B. y f ( x) 的图象关于直线8x 对称3C. f (x) 的一个零点为xD. f ( x) 在( , ) 单调递减6 2理科数学第 1 页(共 4 页)7. 执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A. 5B. 4C. 3D. 28. 已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为A. B. 3 4C. D.2 49. 等差数列{a n} 的首项为1,公差不为0,若a2、a3、a6 成等比数列,则{a n} 前6 项的和为A. -24B. -3C. 3D. 82 2x y10. 已知椭圆C:1(a b 0)2 2a b的左、右顶点分别为A1、A2,且以线段A1A2 为直径的圆与直线bx ay 2ab 0相切,则 C 的离心率为A.63B.33C.23D.132 x a x 1 x 111. 已知函数 f (x) x 2 (e e ) 有唯一零点,则 a =A. 12B.13C.12D. 112. 在矩形ABCD 中,AB = 1,AD = 2,动点P 在以点 C 为圆心且与BD 相切的圆上,若AP AB AD,则的最大值为A. 3B. 2 2C. 5D. 2二、填空题:本题共4小题,每小题5分,共20分。
2017高考全国3卷理科数学试题与答案
2017年普通高等学校招生全国统一考试(全国)理科数学(试题及答案解析)一、选择题:(本题共12小题,每小题 5分,共 60分)1.已知集合 A ( x, y) x 2 y 2 1 , B( x, y) y x ,则 AB 中元素的个数为()A . 3B . 2C . 1D . 0【答案】 B221 上所有点的集合, B 表示直线 yx 上所有点的集合,【解析】 A 表示圆 x y 故 A B 表示两直线与圆的交点,由图可知交点的个数为2,即 A B 元素的个数为2,故选 B.2.设复数 z 满足 (1 i) z 2i ,则 z ()1 B .2 C . 2D . 2A .22【答案】 C2i 2i 1 i 2i 2 122 ,故选 C.【解析】由题, z1 i 1 ii 1 ,则 z 121 i23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年 1 月至2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A .月接待游客量逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在 7,8 月份D .各年 1 月至 6 月的月接待游客量相对 7 月至 12 月,波动性更小,变化比较平稳【答案】 A【解析】由题图可知, 2014年8月到 9月的月接待游客量在减少,则 A 选项错误,故选 A.4. ( x y)(2 x y)5 的展开式中 x 3 y 3 的系数为()A .B .C . 40D . 80【答案】 C【解析】由二项式定理可得,原式展开中含x 3 y3的项为x 22 x 23y 33240x 333 3C 5y C 5 2xyy,则 x y 的系数为 40,故选 C.225x ,且与椭圆5.已知双曲线C :x2y 2 1( a 0 , b 0 )的一条渐近线方程为 yx 2 y 2ab21 有公共焦点.则 C 的方程为()123A . x 2 y 2 1B . x 2 y 21C . x 2 y 21D . x 2 y 218104 55443【答案】 B【解析】 ∵双曲线的一条渐近线方程为y5 x ,则 b5 ① 又∵ 椭圆x 2y 22 a21 与双曲线有公共焦点,易知 c 3 ,则 a 2b 2 c29 ②123x2y2由①② 解得 a 2,b5 ,则双曲线 C 的方程为1,故选 B.456.设函数 f ( x)πcos(x) ,则下列结论错误的是()38πA . f (x) 的一个周期为2πB . y f ( x) 的图像关于直线 x对称3C . f ( xπ π ) 的一个零点为 xD . f (x) 在 ( , π) 单调递减【答案】 D 62【解析】函数 fx cos xπ的图象可由 y cosx 向左平移π个单位得到,3 3 如图可知, f x在 π, π 上先递减后递增, D 选项错误,故选 D.2y- Ox67.执行右图的程序框图,为使输出S 的值小于 91,则输入的正整数N的最小值为() A . 5 B .4 C .3 D . 2【答案】 D【解析】程序运行过程如下表所示:SM t 初始状态 0 100 1 第1次循环结束 100 10 2 第2次循环结束 90 1 3此时 S 90 91 首次满足条件,程序需在 t 3 时跳出循环,即 N2 为满足条件的最小值,故选 D.8.已知圆柱的高为 1,它的两个底面的圆周在直径为 2的同一个球的球面上,则该圆柱的体积为()A .πB .3π ππ4C .D .【答案】 B241 2【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径23 , r122则圆柱体体积 Vπ 23πrh,故选 B.49.等差数列 a n 的首项为 1,公差不为 0.若 a 2 , a 3 , a 6 成等比数列,则a n前 6项的和为()A . 24B . 3C . 3D . 8【答案】 A【解析】 ∵ a n为等差数列,且 a 2 , a 3 , a 6 成等比数列,设公差为 d .则 a 32 a 2 a 6 ,即 a 12d 2a 1 d a 15d又∵ a 1 1 ,代入上式可得 d 2 2d 0又∵ d 0 ,则 d 2∴ S 66a 1 6 5 d 1 6 6 5 224 ,故选 A.2 222xya b 0A 1A 2A 1 A 210.已知椭圆 C : a 2 b 21( )的左、右顶点分别为, ,且以线段 为直径的圆与直线 bx ay 2ab 0 相切,则 C 的离心率为()A .6B .3C .21 33D .33【答案】 A【解析】 ∵ 以 A 1 A 2 为直径为圆与直线 bx ay2ab 0 相切,∴圆心到直线距离d 等于半径,∴ d2aba22又∵ a0,b0 ,则上式可化简为 a 2 3b 2 ∵ b 2 a 2c 2,可得 a 23 a2c2,即 c22a 23∴ ec 6,故选Aa311.已知函数 f ( x) x 2 2xa(e x 1e x 1 ) 有唯一零点,则a()1 1 1A . 2B . 3C . 2D . 1【答案】 C【解析】由条件,f ( x) 22xx 1e x 1x a(e) ,得:f (2x) (2 x) 2 2(2x) a(e 2 x 1e (2 x ) 1 )x 2 4 x 4 42x a(e 1 x e x 1 )22 x x 1e x 1x a(e ) ∴ f (2x) f (x) ,即 x 1 为 f (x) 的对称轴,由题意, f (x) 有唯一零点,∴ f ( x) 的零点只能为 x 1 ,即 f (1) 12 2 1 a(e 1 1e 1 1) 0 ,解得 a 1.212.在矩形 ABCD 中, AB 1, AD2 ,动点 P 在以点 C 为圆心且与 BD 相切的圆上.若APABAD ,则的最大值为()yA . 3B . 2 2P gC . 5D . 2BC【答案】 A【解析】由题意,画出右图.设 BD 与 C 切于点 E ,连接 CE .E以 A 为原点, AD 为 x 轴正半轴,xA(O)DAB 为y轴正半轴建立直角坐标系,则 C 点坐标为 (2,1) . ∵|CD| 1,|BC | 2.22.∴BD 1 25 ∵ BD 切 C 于点 E .∴CE ⊥BD .∴ CE 是 Rt △ BCD 中斜边 BD 上的高 .1 |BC| |CD|2 S △ BCD 22 2 2|EC ||BD | 5 5|BD |5即 C 的半径为 25 .5∵P 在 C 上.∴ P 点的轨迹方程为 ( x 2)2( y 1)245 .设 P 点坐标(x 0, y 0),可以设出 P 点坐标满足的参数方程如下:2x 0 2 5 cos 2y 0 15 sin而 AP (x 0 , y 0 ) , AB (0,1) , AD (2,0) .∵ AP AB AD (0,1) (2,0) (2 , )∴115,y 01 2 5 sin .x 05cos52两式相加得:1 2 5sin15cos552( 2 5 )2 ( 5 )2 sin( )5 5 2 sin( ) ≤ 3(其中 sin5, cos2 5 )55当且仅当π2 k π, kZ 时,取得最大值 3.2二、填空题:(本题共4小题,每小题 5分,共 20分)x y ≥ 0,13.若 x , y 满足约束条件xy 2 ≤ 0, 则 z 3x 4 y 的最小值为 ________.y ≥ 0,【答案】 1【解析】由题,画出可行域如图:目标函数为 z 3 x 4 y ,则直线 3 zz 值越小.yx 纵截距越大, 由图可知: z 在 A 1,1 4 4处取最小值,故 z min 3 1 4 1 1 .x y 2 0yA(1,1)B x(2,0)x y 014.设等比数列 a n满足 a 1 a 21 , a 1 a 33 ,则 a4 ________.【答案】 8【解析】a n 为等比数列,设公比为 q .a 1 a 2 1a 1 a 1 q 1 ① a 1 a 33 ,即 a 1 a 1 q 2 3 ② , 显然 q 1, a 1 0 ,②得 1 q3 ,即 q2 ,代入 ① 式可得 a 1 1 ,①a 4 a 1q 3 138 .2f (x)x 1,x ≤ 0, f ( x1115.设函数 2x , x 0,则满足 f (x))的 x 的取值范围是 ________.2【答案】1 ,4【解析】fxx 1,x ≤ 0, f x f x1 1 1 1 f x2 x , x 02,即 f x2由图象变换可画出yf x1 与 y1 fx的图象如下:2yyf (x 1)2( 1,1)4 4x1 122y 1 f (x)由图可知,满足 f x1 1 1 f x 的解为,.2416. a , b 为空间中两条互相垂直的直线,等腰直角三角形 ABC 的直角边 AC 所在直线与a ,b 都垂直,斜边①当直线 AB 与 a 成②当直线 AB 与 a 成AB 以直线 AC 为旋转轴旋转,有下列结论: 60 角时, AB 与 b 成 30 角;60 角时, AB 与 b 成 60 角;③直线 AB 与 a 所成角的最小值为45 ; ④直线 AB 与 a 所成角的最大值为60 .其中正确的是 ________(填写所有正确结论的编号)【答案】 ②③【解析】由题意知, a 、 b 、AC 三条直线两两相互垂直,画出图 形如图 .不妨设图中所示正方体边长为 1,故|AC| 1, AB2,斜边 AB 以直线 AC 为旋转轴旋转,则A 点保持不变,B 点的运动轨迹是以C 为圆心, 1为半径的圆 .以 C 为坐标原点,以 CD 为 x 轴正方向, CB 为 y 轴正方向,CA 为 z 轴正方向建立空间直角坐标系.则 D(1,0,0) , A(0,0,1) ,直线 a 的方向单位向量 a(0,1,0) , | a | 1 .B 点起始坐标为 (0,1,0) ,直线 b 的方向单位向量 b (1,0,0) , | b | 1 .设 B 点在运动过程中的坐标B (cos ,sin,0) , 其中 为 BC 与CD 的夹角, [0,2 π) . 那么 AB '在运动过程中的向量 AB ( cos, sin ,1) , | AB | 2 .设 AB 与 a 所成夹角为[0, π] ,2则cos 故设AB( cos , sin ,1) (0,1,0)2| sin| [0,2] .a AB22π π[ ,] ,所以③正确,④错误.4 2与 b 所成夹角为π[0, ],2AB bcosb AB(cos,sin,1) (1,0,0) .b AB2| cos |2当AB与 a 夹角为60π时,即3,sin2cos 2 cos 2 12 .∵ cos2sin 2322 1,∴ | cos| 2 .2∴ cos2| cos| 1 .22π∵[0, ]. 2π∴=,此时AB与b夹角为60.3∴② 正确,①错误.三、解答题:(共70分.第 17-20题为必考题,每个试题考生都必须作答.第22, 23题为选考题,考生根据要求作答)(一)必考题:共60分.17.( 12分)ABC 的内角A,B,C的对边分别为a,b,c,已知sin A 3 cos A 0 ,a 2 7 ,b 2.( 1)求 c;( 2)设D为 BC 边上一点,且AD AC ,求△ ABD 的面积.【解析】(1)由 sin A 3 cos A0 得2sin A π0 ,3即 A πkπk Z ,又A0, π,3∴ A ππ,得A2π33.1由余弦定理222.又∵a 27, b 2,cosAa b c 2 bc cos A代入并整理22得 c25 ,故c 4 .1(2)∵ AC2, BC27, AB 4 ,2 2 22 7 .由余弦定理 cosCab c2ab 7∵ AC AD ,即 △ACD 为直角三角形,则 ACCD cosC ,得 CD 7 .由勾股定理 AD CD 223 .AC 又 A2π DAB2π π π,则32 ,36 S △ ABD1AD AB sinπ3 .2618.( 12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶 4元,售价每瓶 6元,未售出的酸奶降价处理, 以每瓶 2元的价格当天全部处理完. 根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为 500 瓶;如果最高气温位于区间 20 ,25 ,需求量为 300瓶;如果最高气温低于 20,需求量为 200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温 10 ,1515 ,2020 ,25 25 ,3030 ,3535 ,40天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率.( 1)求六月份这种酸奶一天的需求量 X (单位:瓶)的分布列; ( 2)设六月份一天销售这种酸奶的利润为 Y (单位:元).当六月份这种酸奶一天的进货量 n (单位:瓶)为多少时, Y 的数学期望达到最大值?【解析】 ⑴易知需求量 x 可取 200,300,500P X 2 16 1200 3 530 P X 36 2300 3 530 P X 25 7 4 2500 3 .30 5则分布列为:X 200 300 500P122555⑵① 当 n ≤ 200 时: Y n 6 4 2n ,此时 Y max 400 ,当 n 200 时取到 .②当 2004 2n 1 2 n 200 2 n ≤ 300 时: Y 2005 58 800 2n 6n 800n5 55此时 Y max 520 ,当 n 300 时取到 .③当 300n ≤ 500 时,Y1200 2n200223002n 30022n 25553200 2n5此时 Y 520.④当 n ≥ 500 时,易知 Y 一定小于 ③ 的情况 .综上所述:当 n 300 时, Y 取到最大值为 520 .19.(12分)如图,四面体 ABCD 中,△ABC 形.?ABD ?CBD ,AB= BD.(1)证明:平面 ACD ^ 平面 ABC ;(2)过 AC 的平面交BD于点E,若平面 AEC 把四面体 ABCD 分成体积相等的两部分.求二面角D- AE- C的余弦值.是正三角形,△ACD 是直角三角DECB【解析】⑴取 AC 中点为 O ,连接 BO , DO ;A DABC 为等边三角形∴ BO AC E∴ AB BC CAB BCOBD BD ABDCBD .B ABDDBC∴ AD CD ,即ACD 为等腰直角三角形,ADC A为直角又 O 为底边 AC 中点∴DO AC令 AB a ,则 AB AC BC BD a易得:OD 2, OB3 a a22222∴ OD OB BD由勾股定理的逆定理可得DOB2即OD OBOD ACOD OB z AC OBO OD平面 ABC D AC平面 ABCOB平面 ABC又∵OD 平面ADC平面 ADC C E由面面垂直的判定定理可得平面 ABC ⑵由题意可知V D ACE V B ACE即B , D 到平面ACE的距离相等即E为 BD中点以 O 为原点, OA 为x轴正方向,OB 为y轴正方向, OD 为 z 轴正方向,设 AC a ,建立空间直角坐标系,则O 0,0,0 , Aa a3,0,0 , D 0,0,,B 0,a,0222OB yAx3 a,E 0, a,44a3a a a a易得: AE,a,, AD,0, , OA,0,0244222设平面 AED的法向量为 n1,平面 AEC 的法向量为n2,AE n 1 03,1, 3则n 1 ,解得 n 1 ADAE n 2 0 0,1, 3OA n 2,解得 n 2若二面角 D AE C 为,易知为锐角,则 cosn 1 n 27n 1 n 272lC于 A ,B 两点,圆 M 是以2012分)已知抛物线 C : y = 2x2 0)的直线 交 .(,过点( , 线段 AB 为直径的圆.( 1)证明:坐标原点 O 在圆 M 上;( 2)设圆 M 过点 P ( 4, - 2 ),求直线 l 与圆 M 的方程.【解析】 ⑴显然,当直线斜率为 0 时,直线与抛物线交于一点,不符合题意.设 l : x my 2 , A( x 1 , y 1 ) , B( x 2 , y 2 ) , 联立:y 22 x得 y 22my 40 ,x my24 m216 恒大于 0 , y 1 y 22m , y 1 y 24 .uuruuurOA OBx 1 x 2 y 1 y 2(my 1 2)( my 2 2)(m 2 1)y 1 y 2 2m( y 1 y 2 ) 4 uur uuur 4( m 2 1) 2 m(2 m) 4∴ OA OB ,即O 在圆 M 上.uuur uur⑵若圆 M 过点 P ,则 AP BP(x 1 4)( x 2 4) ( y 1 2)( y 2 2) 0(my 1 2)( my 2 2) ( y 1 2)( y 2 2) 0(m 2 1)y 1 y 2 (2 m 2)( y 1y 2 ) 8 02m 10 解得 m 1或 1化简得 2m21①当 m时, l : 2xy4 0 圆心为 Q(x 0 , y 0 ) ,2y 0y 1y 2 1, x 01y 0 29 ,22249 22半径 r|OQ |142则圆 M : ( x 9 )2 ( y 1 )2 854 2 16②当 m 1 时, l : x y 2 0 圆心为 Q(x 0 , y 0 ) ,y 0 y 1 y 2 1 , x 0 y 0 2 3 , 2半径 r|OQ |32 12则圆 M : ( x 3)2 ( y 1)21021.( 12分)已知函数 f (x)x 1 a ln x .( 1)若 f (x) ≥ 0 ,求 a 的值;( 2)设 m 为整数,且对于任意正整数 n , (1 + 1 1 1m ,求 m 的最)(1 + 2 ) 鬃?(1 n ) <2 2 2小值.【解析】 ⑴ f (x) x 1 a ln x , x 0则 f ( x)1 a xa,且 f (1) 0当 a ≤ 0 x x上单调增, 所以 0x 1时, f x 0 , f x 在 0 , 时, f x0 ,不满足题意;当 a 0 时,当 0 x a 时, f (x) 0 ,则 f (x) 在 (0, a) 上单调递减;当 x a 时, f ( x) 0 ,则 f (x) 在 (a,) 上单调递增.①若 a 1 , f (x) 在 (a,1) 上单调递增 ∴ 当 x (a,1) 时 f ( x) f (1) 0 矛盾 ②若 a 1 , f (x) 在 (1,a) 上单调递减 ∴ 当 x (1,a) 时 f ( x)f (1) 0 矛盾③若 a1 , f ( x) 在 (0,1) 上单调递减, 在 (1,) 上单调递增 ∴ f (x) ≥ f (1)0 满足题意综上所述 a 1 .⑵ 当 a 1 时 f ( x) x 1 ln x ≥ 0 即 ln x ≤ x 1则有 ln( x 1) ≤ x 当且仅当 x0 时等号成立∴ ln(11 1 , kN *k)k22一方面: ln(11 ) ln(11 ... ln(11 1 1 ...1 1 ,2 2 )n )22n 1n 122222即 (111 1e .)(122 )...(12 n)2另一方面: (11 11 (1 1 1 )(1 1 1352)(1 2 )...(1 2 n ) )(1 2 2 3 ) 642 2 2 2 当 n ≥3 时, (1 1 1 1 (2,e))(1 2 2 )...(12 n )2 ∵ m *(1 1 1 1 m ,N , )(1 2 )...(1 2 n )2 2∴ m 的最小值为 3 .22. [选修 4-4:坐标系与参数方程 ] ( 10分)在直角坐标系 xOy 中,直线 l的参数方程为x t ,( t 为参数),直线l的参数方程ykt,xm,为m( m 为参数),设 l 与 l 的交点为 P ,当 k 变化时, P 的轨迹为曲线 C .y,k( 1)写出 C 的普通方程:( 2)以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 设 l : cos( nis ) ,M 为 l 与 C 的交点,求 M 的极径.【解析】 ⑴将参数方程转化为一般方程l 1 : y k x 2⋯⋯ ① l 2 : y1 x2 ⋯⋯ ②k① ② 消 k 可得: x 2y 24即 P 的轨迹方程为 x 2 y 2 4 ; ⑵将参数方程转化为一般方程l 3 : x y 2 0⋯⋯ ③联立曲线 C 和 l 3x y2x2y24x3 22解得2y2x cos5 由sin 解得y即 M 的极半径是 5 .23. [选修 4-5:不等式选讲 ](10分)已知函数 f ( x) | x | | x | .( 1)求不等式 f ( x) 的解集;( 2)若不等式 f ( x) x x m 的解集非空,求 m 的取值范围.3, x ≤ 1【解析】 ⑴ f x| x1| | x2| 可等价为 f x2x 1, 1x 2 .由 f x ≥ 1 可得:3,x ≥ 2①当 x ≤ 1 时显然不满足题意; ②当 1 x 2时, 2x 1≥1 ,解得 x ≥1 ;③当 x ≥ 2 时, f x 3 ≥ 1 恒成立 .综上, f x1的解集为 x | x ≥ 1 .⑵不等式 f x ≥ x 2x m 等价为 f xx 2x ≥ m ,令 g xf xx 2 x ,则 g x ≥ m 解集非空只需要g xmax ≥ m .x 2 x 3, x ≤ 1而 g xx 2 3 x 1, 1 x 2 .2x 3, x ≥ 2x①当 x ≤ 1 时, gxmaxg13 1 15 ;2②当 1 x 2 时, g xmaxg 333 3 1 5 ;222 4③当 x ≥ 2 时, g x maxg 22 22 3 1 .综上, g xmax5,故 m5 .44。
山东省青岛市2017届高三第三次模拟考试数学理试题含答案

2017年青岛市高三自主检测数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分。
考试时间120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔和0。
5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.3.第Ⅱ卷必须用0。
5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|110,N},{|}A x x x B x x a A =<<∈==∈,则A B = A .{1,2,3} B .{|13}x x << C .{2,3} D.{|1x x <2.若复数z 满足24z=-,则复数z 的实部为A .2C .2- D .0 3.某高校调查了2000.1制成了如图所示的频率分布直 方图,其中自习时间的范围是[17.530],,样本数据分组为 [17.520),,[2022.5),, [) 22.5,25,[2527.5),, [27.530],。
则这200名学生中每周的自习时间不低于25小时的人数为A .30B .60C .80D .1204.如图,某几何体的三视图是三个半径相等的圆 及每个圆中两条相互垂直的半径,若该几何体的体 积是283π,则三视图中圆的半径为A .2B .3C .4D .65.在边长为4的正三角形ABC 中,12AD DB =,M 是BC 的中点,则AM CD ⋅=A .16B . C.- D .8- 6.已知函数()f x 满足()()f x f x π-=,当02x π≤≤时,()cos 1f x x =-,则当0x π≤≤时,()f x 的图象与x 轴所围成图形的面积为 A.2π-B 。
哈尔滨2017年高三第三次模拟考试数学试题(理)含答案

______(其中 VP ABE 、 VP CDF 分别为四面体 P — ABE 、 P — CDF 的体积).
15.已知数列
an 满足 an n2 4n cos nπ ,则 an 的前 50 项的和为______.
2 2 M 2,3 16.已知圆 C : x y 25 ,过点 作直线 l 交圆 C 于 A , B 两点,分别过 A , B 两
(Ⅰ)求 m 值和
2017 年高三第三次模拟考试
理科数学试卷 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150 分,考试时间 120 分钟。考试结束后,将本试卷和答题卡一并交回。 注意事项: 1.答题前,考生务必先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条 形码区域内。 2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米黑色字迹的签字笔书写, 字体工整、笔记清楚。 3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草 稿纸、试题卷上答题无效。 4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。 5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 第Ⅰ卷(选择题共 60 分) 一、选择题(本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的.)
的离心率 e2 的范围是(
3 5 , A. 2 3 5 ,2 B. 3
)
2,3 C.
3 ,3 D. 2
ABC
2 , P 在面 ABC 的射影为
11.三棱锥 P ABC 中,底面 ABC 满足 BA BC ,
9 AC 的中点,且该三棱锥的体积为 2 ,当其外接球的表面积最小时, P 到面 ABC 的距离为 ( )
2017年高考仿真试题(三)数学理科试题(含答案)word版

2017年普通高考理科数学仿真试题(三)本试卷分第I 卷和第Ⅱ卷两部分,共5页,满分150分,考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回.第I 卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题“Z x ∈∃使022≤++m x x ”的否定是A.Z x ∈∃使m x x ++22>0B.不存在Z x ∈使m x x ++22>0C.对Z x ∈∀使022≤++m x xD.对Z x ∈∀使m x x ++22>02.已知集合(){}{x y y B x x y x A x ,2,2lg 2==-==>}0,R 是实数集,则A.[]1,0B.(]1,0C.(]0,∞-D.以上都不对 3.设i 为虚数单位,则1+i+i 2+i 3+…+i 10=A.iB.—iC.2iD.—2i4.若某程序框图如右图所示,则该程序运行后输出的B 等于A.7B.15C.31D.635.已知直线⊥l 平面α,直线⊂m 平面β,给出下列命题:①;//m l ⊥⇒βα②;//m l ⇒⊥βα ③βα⊥⇒m l // ④.//βα⇒⊥m l其中正确命题的序号是A.①②③B.②③④C.①③D.②④6.ABC ∆的三个内角A 、B 、C 的对边分别为a 、b 、c ,已知1sin =B ,向量()().2,1,,==q b a p 若q p //,则C ∠的大小为 A.6π B.3π C.2π D.32π 7.将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大.当3,4固定在图中的位置时,填写空格的方法为A.6种B.12种C.18种D.24种8.一个几何体按比例绘制的三视图如图所示:(单位:m )则该几何体的体积为 A.337m B.329m C.327m D.349m 9.函数())(⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛≤≤≤-+=20cos ,011πx x x x x f 的图象与x 轴所围成的封闭图形的面积为 A.23 B.1 C.2 D.21 10.已知数列{}n a 各项均为正数.若对于任意的正整数p 、q 总有q p q p a a a ⋅=+且8a =16,则=10aA.16B.32C.48D.6411.已知双曲线12222=-by a x (a >b >0),直线t x y l +=:交双曲线于A 、B 两点,△OAB 的面积为S (O 为原点),则函数()t f S =的奇偶性为A.奇函数B.偶函数C.不是奇函数也不是偶函数D.奇偶性与a 、b 有关 12.定义一种运算:⎩⎨⎧≤=⊗ab b a a b a ,,,令()()45sin cos 2⊗+=x x x f ,且⎥⎦⎤⎢⎣⎡∈2,0πx ,则函数⎪⎭⎫ ⎝⎛-2πx f 的最大值是 A.45 B.1 C.—1 D.45-第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.为了解一片经济林的生长情况,随机测量了其中100株树林的底部周长(单位:cm ).根据所得数据画出样本的频率分布直方图(如右图),那么在这100株树林中,底部周长小于110cm 的株数是___________.< >b.14.从抛物线x y 42=上一点P 引抛物线准备线的垂线,垂足为M ,且5=PM ,设抛物线的焦点为F ,则△MPF 的面积为_______.15.若不等式组⎪⎩⎪⎨⎧≥--≤≤-≤-01,21,042y x y x x 表示的平面区域为()14,22≤+-y x M 表示的平面区域为N ,现随机向区域M 内抛一点,则该点落在平面区域N 内的概率是________.16.请阅读下列材料:若两个正实数21,a a 满足12221=+a a ,那么.221≤+a a证明:构造函数()()()()1222122221++-=-+-=x a a x a x a x x f ,因为对一切实数x ,恒有()0≥x f ,所以0≤∆,从而得()084221≤-+a a ,所以.221≤+a a 根据上述证明方法,若n 个正实数满足122221=+⋅⋅⋅++n a a a 时,你能得到的结论为_______________.三、解答题:本大题共6小题,共74分.17.(本小题满分12分)在△ABC 中,a ,b ,c 分别是角A 、B 、C 的对边,()(),cos ,cos ,2,C B n c a b m =-=且m//n.(I )求角B 的大小;(II )设()(ωωωx B x x f sin 2cos +⎪⎭⎫ ⎝⎛-=>)0,且()x f 的最小正周期为π,求()x f 在区间⎥⎦⎤⎢⎣⎡2,0π上的最大值和最小值.18.(本小题满分12分)在一次食品卫生大检查中,执法人员从抽样中得知,目前投放某市的甲、乙两种食品的合格率分别为90%和80%.(I )今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.(II )若某消费者从两种食品中任意各购一件,设ξ的分布列,并求其数学期望.19.(本小题满分12分)如图所示的多面体,它的正视图为直角三角形,侧视图为矩形,俯视图为直角梯形(尺寸如图所示)(I )求证:AE//平面DCF ;(II )当AB 的长为29,。
2017年高考全国三卷理科数学试卷

B. -40
C. 40
D. 80
理科数学 第 1 页(共 4 页)
5.
已知曲线 C:
x2 a2
y2 b2
1(a
0, b
0) 的一条渐近线方程为
y
5 x ,且与椭圆 x2 y2 1有公共焦点,
2
12 3
则 C 的方程为
A. x2 y2 1 8 10
B. x2 y2 1 45
22. [选修 4—4:坐标系与参数方程](10 分)
x 2 t,
在直角坐标系
xOy
中,直线
l1
的参数方程为
y
kt,
(t为参数) ,直线 l2 的参数方程为
x 2 m,
y
m k
,
(m为参数) ,设 l1 与 l2 的交点为 P,当 k 变化时,P 的轨迹为曲线 C。
根据该折线图,下列结论错误的是
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在 7、8 月
D. 各年 1 月至 6 月的月接待游客量相对于 7 月至 12 月,波动性更小,变化比较平稳
4. (x + y)(2x - y)5 的展开式中 x3y3 的系数为
A. -80
已知函数 f (x) x 1 a ln x 。
(1)若 f (x) 0 ,求 a 的值;
(2)设
m
为整数,且对于任意正整数
n,
(1
1 2
)(1
1 22
)L
(1
1 2n
)
河北省2017届高考第三次模拟考试数学试题(理)有答案

唐山市2016-2017学年度高三年级第三次模拟考试理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则( ){}220A x x x =-<(){}log 1B x y x ==-A B = A. B. C. D.()0,+∞()1,2()2,+∞(),0-∞2.已知为虚数单位,,则复数的共轭复数为( )i ()211z i i -=+z A. B. C. D. 1355i--1355i +1355i-+1355i -3.总体由编号为01,02,03,…,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的4个个体的编号为( )A.05B.09C.11D.204.已知双曲线的一条渐近线方程为,则的离心率为( )()2222:10,0x y C a b a b -=>>20x y +=CC.25555.执行下图程序框图,若输出,则输入的为( )4y =xA.或或1B.C.3-2-2-或1D.12-6.数列是首项,对于任意,有,则前5项和( ){}n a 11a =*,m n N ∈3n m n a a m +=+{}n a 5S =A.121 B.25C.31D.357.某三棱锥的三视图如图所示,则其体积为( )A.4B.8C.D.43838.函数(其中为自然对数的底数)的图象大致为( )()()11x x e f x x e +=-eAB C D9.若,则( )()92901291x a a x a x a x -=++++…1239a a a a ++++=…A.1B.513C.512D.51110.函数()在内的值域为,则的取值范围是( )()cos 6f x x πω⎛⎫=+ ⎪⎝⎭0ω>[]0,π3⎡-⎢⎣ωA. B. C. D.35,23⎡⎤⎢⎥⎣⎦53,62⎡⎤⎢⎣⎦5,6⎡⎫+∞⎪⎢⎣⎭55,63⎡⎤⎢⎥⎣⎦11.抛物线的焦点为,为准线上一点,为轴上一点,为直角,若线段的中点2:4C y x =F N M y MNF ∠MF 在抛物线上,则的面积为( )E C MNF △D.2323212.已知函数有两个极值点,()32f x x ax bx =++12,x x且,若,函数,则( )12x x <10223x x x +=()()()0g x f x f x =-()g x A.恰有一个零点 B.恰有两个零点C.恰有三个零点D.至多两个零点第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量,,则在方向上的投影为 .()3,1=-a ()2,1=b a b 14.直线的三个顶点都在球的球面上,,若三棱锥的体积为2,则该球的表ABC △O 2AB AC ==O ABC -面积为 .15.已知变量满足约束条件,目标函数的最小值为,则实数.,x y 102100x y x y x y a -+≥⎧⎪--≤⎨⎪+-≥⎩2z x y =+5-a =16.数列的前项和为,若,则 .{}n a n n S ()*2142n n n S a n N -+=-∈na=三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在中,角,,所对应的边分别为,,,.ABC △A B C a b c cos a b b C -=(1)求证:;sin tan C B =(2)若,为锐角,求的取值范围.1a =C c 18.某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:t[)0,15[)15,30[)30,45[)45,60[)60,75[)75,90男同学人数711151221女同学人数89171332若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.(i )求抽取的4位同学中既有男同学又有女同学的概率;(ii )记抽取的“读书迷”中男生人数为,求的分布列和数学期望.X X 19.如图,平行四边形中,,ABCD 24BC AB ==,,,分别为,的中点,60ABC ∠=︒PA AD ⊥E F BC PE 平面.AF ⊥PED(1)求证:平面;PA ⊥ABCD (2)求直线与平面所成角的正弦值.BF AFD 20.已知椭圆经过点.()2222:10x y a b a b Γ+=>>13,2E ⎫⎪⎭3(1)求椭圆的方程;Γ(2)直线与圆相切于点,且与椭圆相交于不同的两点,,求的最大值.l 222:O x y b +=M ΓA B AB 21.已知函数,.()()2ln 1f x x ax =++0a >(1)讨论函数的单调性;()f x (2)若函数在区间有唯一零点,证明:.()f x ()1,0-0x 2101e x e --<+<22.点是曲线上的动点,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,以P ()221:24C x y -+=O x 极点为中心,将点逆时针旋转得到点,设点的轨迹方程为曲线.O P 90︒Q Q 2C (1)求曲线,的极坐标方程;1C 2C (2)射线与曲线,分别交于,两点,定点,求的面积.()03πθρ=>1C 2C A B ()2,0M MAB △23.已知函数.()21f x x a x =++-(1)若,解不等式;1a =()5f x ≤(2)当时,,求满足的的取值范围.0a ≠()1g a f a ⎛⎫= ⎪⎝⎭()4g a ≤a唐山市2016—2017学年度高三年级第三次模拟考试理科数学参考答案一.选择题:BACCD DBDAC BA 二.填空题:(13(14)(15)(16)544π3-12n n -三.解答题:(17)解:(Ⅰ)由根据正弦定理得,cos a b b C -=sin sin sin cos A B B C -=即,()sin sin sin cos B C B B C +=+,sin cos cos sin sin sin cos B C B C B B C +=+,sin cos sin C B B =得.sin tan C B =(Ⅱ)由余弦定理得,()222222cos 4428c a b ab C b b b =+-=+-=+-由知,cos a b b C -=21cos 1cos a b C C==++由为锐角,得,所以.C 0cos 1C <<12b <<从而有.218c <<所以的取值范围是.c (1,22(18)解:(Ⅰ)设该校4000名学生中“读书迷”有人,则,解得.x 81004000x=320x =所以该校4000名学生中“读书迷”约有320人.(Ⅱ)(ⅰ)抽取的4名同学既有男同学,又有女同学的概率:.454813114C P C =-=(ⅱ)可取0,1,2,3.X ,,()45481014C P X C ===()133548317C C P X C ===,,()223548327C C P X C ===()3155481314C C P X C ===的分布列为:X X 0123P1143737114.()1331301231477142E X =⨯+⨯+⨯+⨯=(19)解:(1)连接,因为平面,平面,所以,AE AF ⊥PED ED ⊂PED AF ED ⊥PF EDCBA在平行四边形中,,,ABCD 24BC AB ==60ABC ∠=︒所以,,2AE =23ED =从而有,222AE ED AD +=所以,AE ED ⊥又因为,AF AE A = 所以平面,平面,ED ⊥PAE PA ⊂PAE 从而有,ED PA ⊥又因为,,PA AD ⊥AD ED D = 所以平面.PA ⊥ABCD (2)以为坐标原点,建立如图所示的空间直角坐标系,E则,,,()0,2,0A ()23,0,0D ()3,1,0B -因为平面,所以,AF ⊥PED AF PE ⊥又因为为中点,所以,F PE 2PA AE ==所以,,()0,2,2P ()0,1,1F ,,,()0,1,1AF =- ()3,2,0AD =- ()3,0,1BF =设平面的法向量为,AFD (),,n x y z =由,得,,0AF n ⋅= 0AD n ⋅= 0320y z y -+=⎧⎪⎨-=⎪⎩令,得.1x =(3,3n =设直线与平面所成的角为,则:BF AFD θ,2321sin cos ,27BF n BF n BF n θ⋅=<>==⨯ 即直线与平面.BF AFD 21(20)解:(Ⅰ)由已知可得,解得,,223114a b+=223a b -=2a =1b =所以椭圆Γ的方程为.2214x y +=(Ⅱ)当直线垂直于轴时,由直线与圆:相切,l x l O 221x y +=可知直线的方程为,易求l 1x =±3AB =当直线不垂直于轴时,设直线的方程为,l x l y kx m =+由直线与圆,即l 22:1O x y +=211m k =+,221m k =+将代入,整理得,y kx m =+2214x y +=()222148440k x kmx m +++-=设,,则,,()11,A x y ()22,B x y 122814kmx x k -+=+21224414m x x k -=+()222121214AB x k x x x x =-=++-2222144114k m k k +-==++又因为,221m k =+所以,()2222231431214k k kk AB k +++=≤=+,即231k k =+2k =综上所述,的最大值为2.AB (21)解:(Ⅰ),,()21221'211ax ax f x ax x x ++=+=++1x >-令,,()2221g x ax ax =++()24842a a a a ∆=-=-若,即,则,0∆<02a <<()0g x >当时,,单调递增,()1,x ∈-+∞()'0f x >()f x 若,即,则,仅当时,等号成立,0∆=2a =()0g x ≥12x =-当时,,单调递增.()1,x ∈-+∞()'0f x ≥()f x 若,即,则有两个零点0∆>2a >()g x ()12a a a x ---=()22a a a x -+-=由,得,()()1010g g -==>102g ⎛⎫-< ⎪⎝⎭121102x x -<<-<<当时,,,单调递增;()11,x x ∈-()0g x >()'0f x >()f x 当时,,,单调递减;()12,x x x ∈()0g x <()'0f x <()f x 当时,,,单调递增.()2,x x ∈+∞()0g x >()'0f x >()f x 综上所述,当时,在上单调递增;02a <≤()f x ()1,-+∞当时,在和上单调递增,2a >()f x ()2a a a ⎛--- - ⎝()2a a a ⎫-+-⎪+∞⎪⎭在上单调递减.()2a a a -+-(Ⅱ)由(1)及可知:仅当极大值等于零,即时,符合要求.()00f =()10f x =此时,就是函数在区间的唯一零点.1x ()f x ()1,0-0x 所以,从而有,202210ax ax ++=()00121a x x =-+又因为,所以,()()2000ln 10f x x ax =++=()()00ln 1021x x x +-=+令,则,01x t +=1ln 02t t t--=设,则,()11ln 22h t t t =+-()221'2t h t t-=再由(1)知:,,单调递减,102t <<()'0h t <()h t 又因为,,()22502e h e --=>()1302e h e --=<所以,即.21e t e --<<2101e x e --<+<(22)解:(Ⅰ)曲线的极坐标方程为.1C 4cos ρθ=设,则,则有.(),Q ρθ,2P πρθ⎛⎫- ⎪⎝⎭4cos 4sin 2πρθθ⎛⎫=-= ⎪⎝⎭所以,曲线的极坐标方程为. 2C 4sin ρθ=(Ⅱ)到射线的距离为M 3πθ=2sin33d π==,()4sin cos 23133B A AB ππρρ⎛⎫=-=-= ⎪⎝⎭则1332S AB d =⨯=(23)解:(Ⅰ),()21f x x x =++-所以表示数轴上的点到和1的距离之和,x 2-因为或2时,3x =-()5f x =依据绝对值的几何意义可得的解集为. ()5f x ≤{}32x x -≤≤(Ⅱ),()1121g a a a a=++-当时,,等号当且仅当时成立,所以无解;0a <()2215g a a a=--+≥1a =-()4g a ≤当时,,01a <≤()221g a a a=+-由得,解得,又因为,所以;()4g a ≤22520a a -+≤122a ≤≤01a <≤112a ≤≤当时,,解得,1a >()214g a a =+≤312a <≤综上,的取值范围是.a 13,22⎡⎤⎢⎥⎣⎦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保密★启用并使用完毕前
部分学校高三仿真试题
理 科 数 学
本试卷,分第Ⅰ卷和第Ⅱ卷两部分.共4页,满分150分.考试用时120分钟.考试结束后,将本试卷和答题卡一并交回. 注意事项:
1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、区县和科类填写在答题卡和试卷规定的位置上.
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号.
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤.
第Ⅰ卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若
i i
ai
212-=-,则=a A .5 B .5- C .5i D .5i -
2.已知集合{}
2
|0=-<A x x x ,{}|=<B x x a ,若A B A = ,则实数a 的取值范
围是
A .(]1-∞,
B .()1-∞,
C .[)1+∞,
D .()1+∞, 3.已知等比数列{}n a 满足14=a ,2641
4
a a a =-,则2a = A .2 B .1 C .
12 D .1
8
4.直线3y kx =+与圆22(2)(3)4x y -+-=相交于,M N 两点,若MN ≥则k 的取值范围是
A .3
[,0]4
- B .[ C .[ D .2[,0]3
-
5.下列四个结论中错误的个数是
①若0.40.433,log 0.5,log 0.4===a b c ,则>>a b c
②“命题p 和命题q 都是假命题”是“命题∧p q 是假命题”的充分不必要条件 ③若平面α内存在一条直线a 垂直于平面β内无数条直线,则平面α与平面β垂直 ④已知数据12,,, n x x x 的方差为3,若数据()121,1,1,0,R n ax ax ax a a +++>∈ 的方差为12,则a 的值为2
A .0
B .1
C .2
D .3 6.某几何体的三视图如图所示,则该几何体的表面积为
A .8(4)π+
B .8(8)π+
C .16(
π+ D .
7.
B D k 值是
A .4
B .5
C .6
D .7 9.若直线)2(+=x k y 上存在点(),x y 满足
011-≥⎧⎪
+≤⎨⎪≥-⎩
x y x y y ,则实数k 的取值范围是 A .⎥⎦⎤
⎢⎣
⎡--41,1 B .⎥⎦⎤
⎢⎣
⎡-51,1 C .(]⎪⎭⎫⎢⎣⎡∞+-∞-,,511 D .⎥⎦
⎤
⎢⎣⎡-5
1,41
10.已知函数()f x 的导函数为()f x ',且满足2()2()=--f x x f x .当(,0)
x ∈-∞时,()2'<f x x ;若(2)()44+--≤+f
m
f m m ,则实数m 的取值范围是
A .(]1,
-∞- B .(]2,-∞- C .[1,)-+∞ D .[2,)-+∞
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题5分,共25分.
11.在区间[]
0,1上随机选取两个数x 和y ,则满足20-<x y 的概率为 . 12.观察下列各式:3
1=1,3321+2=3,33321+2+3=6,333321+2+3+4=10,…,由此推得:33331+2+3+n = .
13.6个人站成一排,若甲、乙两人之间恰有2人,则不同的站法种数为 . 14.已知()lg
2x f x x =-,若()()0f a f b +=,则41
a b
+的最小值是 . 15.设双曲线22
221(0,0)x y a b a b
-=>>的右焦点是F ,左、右顶点分别是12,A A ,过
F 做x 轴的垂线交双曲线于,B C 两点,若12A B A C ⊥,则双曲线的离心率为 .
三、解答题:本大题共6小题,共75分. 16.(本小题满分12分)
如图,在ABC ∆中,M 是边BC
的中点,cos BAM ∠=
, tan AMC ∠=. (Ⅰ)求角B 的大小; (Ⅱ)若角6
BAC π
∠=
,BC 边上的中线AM
ABC ∆的面积.
17.(本小题满分12分)
如图,已知三棱锥O ABC -的三条侧棱OA ,OB ,OC 两两垂直,ABC ∆为等边三角形, M 为ABC ∆内部一点,点P 在OM 的延长线上,且PA PB =. (Ⅰ)证明:OB OA =; (Ⅱ)证明:AB OP ⊥;
(Ⅲ)
若::AP PO OC =,求二面角B OA P --的余弦值.
18.(本小题满分12分)
在标有“甲”的袋中有4个红球和3个白球,这些球除颜色外
完全相同. (Ⅰ)若从袋中依次取出3个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
(Ⅱ)现从甲袋中取出个2红球,1个白球,装入标有“乙”的空袋.若从甲袋中任取2球,乙袋中任取1球,记取出的红球的个数为X ,求X 的分布列和数学期望EX .
O
B
C
P
M
∙
19.(本小题满分12分)
已知数列{}n a 和{}n b 满足1232(N*)n b
n a a a a n =∈ .若{}n a 是各项为正数的等比数
列,且14a =,326b b =+. (Ⅰ)求n a 与n b ; (Ⅱ)设1
n n
c b =
-,记数列{}n c 的前n 项和为n S . ①求n S ;②求正整数k ,使得对任意N *n ∈,均有n k S S ≥. 20.(本小题满分13分)
已知抛物线2:4C y x =,点M 与抛物线C 的焦点F 关于原点对称,过点M 且斜率为k 的直线l 与抛物线C 交于不同两点B ,A ,线段AB 的中点为P ,直线PF 与抛物线C 交于两点D ,E .
(Ⅰ)判断是否存在实数k 使得四边形AEBD 为平行四边形.若存在,求出k 的值;若不存在,说明理由; (Ⅱ)求
2
2PM
PF 的取值范围.
21.(本小题满分14分)
已知λ∈R ,函数()ln x
f x e x x λ=-( 2.71828e = 是自然对数的底数).
(Ⅰ)若()10f =,证明:曲线()y f x =没有经过点2
,03M ⎛⎫ ⎪⎝⎭
的切线; (Ⅱ)若函数()f x 在其定义域上不单调,求λ的取值范围; (Ⅲ)是否存在正整数n ,当1
1,n n ne λ++⎡⎫
∈+∞⎪⎢
⎣⎭
时,函数()f x 的图象在x 轴的上方,若存在,求n 的值;若不存在,说明理由.。
