圆幂定理练习题.docx
2-3-4圆幂定理

141+ = 第四讲 圆幂定理在圆锥曲线中的应用圆幂定理在圆中的应用【例 1】如图,在平面直角坐标系 xOy 中,已知点 A (-1 ,0),点 P 是圆O : x 2 + y 2 = 4上的任意一点,过点B (1 ,0)作直线 BT 垂直于 AP ,垂足为T ,则2PA + 3PT 的最小值是.【例 2】(2015 全国 1 文)已知过点 A (0 ,1)且斜率为 k 的直线l 与圆C : (x - 2)2 + ( y - 3)2 = 1交于 M 、N .(1) 求 k 的取值范围;(2) OM ⋅ ON = 12,其中O 为坐标原点,求| MN |.圆幂定理在椭圆上的推广x 2 y 2 1 【例 3】(2019•陆良县月考)已知椭圆C : a 2 + b 2 = 1(a > b > 0)的左右焦点分别为 F 1, F 2,离心率为 2, 椭圆C 上的点 M (1 , 3)到点 F , F 的距离之和等于 4. 2 1 2(1)求椭圆C 的标准方程;2 (2)是否存在过点 P (2 ,1)的直线l 与椭圆C 相交于不同的两点 A , B ,满足 PA ⋅ PB = PM?若存在,求出直线l 的方程;若不存在,请说明理由.【例 4】(2017•南京二模)在平面直角坐标系中,焦点在 x 轴上的椭圆C : x 8 y 2 b 21经过点(b ,2e ),其中 2142 AP TBe 为椭圆C 的离心率.过点T (1 ,0)作斜率为 k (k > 0)的直线l 交椭圆C 于 A , B 两点( A 在 x 轴下方).(Ⅰ)求椭圆C 的方程;(Ⅱ)过原点O 且平行于l 的直线交椭圆C 于点 M , N ,求 AT ⋅ BT 的值;MN 2(Ⅲ)记直线l 与 y 轴的交点为 P ,若 = 2 ,求直线l 的斜率 k .5。
《幂的运算法则》热点专题高分特训(含答案)

幂的运算法则(人教版)一、单选题(共15道,每道6分)1.下列计算正确的有( )①;②;③;④.A.0个B.1个C.2个D.3个答案:A解题思路:①中:,①错误;②中:,②错误;③中:,③错误;④中:,④错误.所以正确的有0个.故选A.试题难度:三颗星知识点:幂的乘方2.有一句谚语说:“捡了芝麻,丢了西瓜”,意思是说有些人办事只抓一些无关紧要的小事,却忽略了具有重大意义的大事.据测算,25万粒芝麻才1000克,那么1粒芝麻有( )A. B.C. D.答案:C解题思路:根据题意,得故选C.试题难度:三颗星知识点:同底数幂的除法3.计算的结果是( )A.-10B.9C. D.-9答案:D解题思路:观察式子结构划部分,按照法则进行运算.故选D.试题难度:三颗星知识点:幂的混合运算4.计算的结果为( )A. B.C. D.答案:C解题思路:可以把当作底数,首先化为同底数幂,然后利用同底数幂的乘除法则进行计算.故选C.试题难度:三颗星知识点:同底数幂的乘除混合运算5.计算的结果是( )A. B.C. D.答案:B解题思路:观察式子结构划部分,按照法则进行运算.观察式子底数不同,可以把当作底数,首先化为同底数幂,然后利用同底数幂的除法法则进行计算.故选B.试题难度:三颗星知识点:幂的混合运算6.若,则的值为( )A.4B.3C.-2D.-3答案:A解题思路:观察式子,等式右边底数是6,左边底数是2,3,2×3=6,根据可得,所以,解得.故选A.试题难度:三颗星知识点:积的乘方7.若,,则的值为( )A.1B.16C.4D.8答案:D解题思路:观察式子,,又因为,,所以.故选D.试题难度:三颗星知识点:整体代入8.若,,则的结果是( )A.7B.12C.81D.64答案:B解题思路:观察式子,根据可得,又因为,,所以.故选B.试题难度:三颗星知识点:整体代入9.计算的结果为( )A. B.C. D.答案:C解题思路:观察式子结构划部分,按照法则进行运算.观察式子底数不同,可以把n当作底数,首先化为同底数幂,然后利用同底数幂的乘法法则进行计算.故选C.试题难度:三颗星知识点:幂的混合运算10.计算的结果为( )A. B.C. D.答案:C解题思路:观察式子结构划部分,按照法则进行运算.观察式子底数不同,可以把x当作底数,首先化为同底数幂,然后利用同底数幂的乘法法则进行计算.故选C.试题难度:三颗星知识点:幂的混合运算11.计算的结果为( )A. B.C. D.答案:C解题思路:观察式子结构划部分,按照法则进行运算.观察式子底数不同,可以把m当作底数,首先化为同底数幂,然后利用同底数幂的乘除法则进行计算.故选C.试题难度:三颗星知识点:幂的混合运算12.计算的结果是( )A. B.C. D.答案:D解题思路:观察式子结构划部分,按照法则进行运算.观察式子底数不同,可以把a当作底数,首先化为同底数幂,然后利用同底数幂的乘除法则进行计算.故选D.试题难度:三颗星知识点:幂的混合运算13.计算的结果为( )A.8B.C. D.0答案:B解题思路:观察式子结构划部分,按照法则进行运算.故选B.试题难度:三颗星知识点:幂的混合运算14.已知,,则的值为( )A.41B.42C.251D.401答案:B解题思路:观察式子,根据可得,又因为,所以.所以.故选B.试题难度:三颗星知识点:整体代入15.已知,,,则的值为( )A.3B.1C. D.答案:C解题思路:观察式子,根据可得,又因为,,,所以.故选C.试题难度:三颗星知识点:整体代入。
人教B版高中数学选修4-1创新设计练习1.3.1圆幂定理(含答案详析)

1.3 圆幂定理与圆内接四边形1.3.1 圆幂定理基础达标1.圆内两条相交弦,其中一弦长为8 cm ,且被交点平分,另一条弦被交点 分成1∶4两部分,则这条弦长是( )A .2 cmB .8 cmC .10 cmD .12 cm 解析:由相交弦推论,即可得.设另一条弦被分成x cm ,4x cm.则⎝ ⎛⎭⎪⎫822=x ·4x ,所以x =2 cm. 所以弦长为10 cm.答案:C2.如图所示,PC 切⊙O 于A ,PO 的延长线交⊙O 于B ,BC 切⊙O 于B , 若AC ∶CP =1∶2,则PO ∶OB 等于( )A .2∶1B .1∶1C .1∶2D .1∶4解析:连接OA ,则OA ⊥PC ,∴△P AO ∽△PBC ,∴PO PC =OA BC ,即PO OA =PC BC ,又∵OA =OB ,AC ∶CP =1∶2,设AC =x ,则CP =2x ,∴CA =x =BC ,∴PO OA =2x x =2,∴PO ∶OB =2∶1.答案:A3.如图所示,在⊙O 中,弦AB 与半径OC 相交于点M,且OM=MC,AM=1.5,BM=4,则OC等于()A.2 6 B. 6C.2 3 D.2 2解析:延长CO交⊙O于D,则DM=3CM,CM·MD=MA·MB,所以1.5×4=3CM2,CM=2,OC=2 2.答案:D4.如图所示,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为________.解析:由相交弦定理知EA·EB=EC·ED.①又∵E为AB中点,AB=4,DE=CE+3,∴②式可化为22=EC(CE+3)=CE2+3CE,∴CE=-4(舍去)或CE=1.∴CD=DE+CE=2CE+3=2+3=5.答案:55.如图所示,P A、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于点C,图中互相垂直的线段有________⊥________(只要求写出一对线段).解析:如题图所示,由于P A、PB均为⊙O切线,∴P A⊥OA,PB⊥OB.又由切线长定理知P A=PB,OP为∠APB的角平分线,∴AB⊥OP,故应填P A⊥OA或PB ⊥OB或AB⊥OP.答案:AB OP6.如图,已知在⊙O中,P是弦AB的中点,过点P作半径OA的垂线分别交⊙O于C、D两点,垂足是点E.求证:PC·PD=AE·AO.证明:连接OP,∵P为AB的中点,∴OP⊥AB,AP=PB.∵PE⊥OA,∴AP2=AE·AO.∵PD·PC=P A·PB=AP2,∴PD·PC=AE·AO.综合提高7.如图所示,P A、PB是⊙O的两条切线,A、B为切点,连接OP交AB于C,连接OA、OB,则图中等腰三角形、直角三角形个数分别为()A.1,2 B.2,2C.2,6 D.1,6解析:∵P A、PB为⊙O切线,∴OA⊥AP,OB⊥PB,P A=PB,OP平分∠APB,∴OP⊥AB.∴直角三角形有6个,等腰三角形有2个.即直角三角形有:△OAP,△OBP,△OCA,△OCB,△ACP,△CBP;等腰三角形有:△OAB,△ABP.答案:C8.如图所示,P A切⊙O于A,PBC是⊙O的割线,且PB=BC,P A=32,那么BC的长为()A. 3 B.2 3C.3 D.3 3解析:根据切割线定理P A2=PB·PC,所以(32)2=2PB2.所以PB=3=BC.答案:C9.如图,⊙O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE=________;CE=________.解析:由圆的割线定理知:AB·AC=AD·AE,∴AE=8,∴DE=5.连接EB,∵∠EDB=90°.∴EB为直径.∴∠ECB=90°.由勾股定理,得EB2=DB2+ED2=AB2-AD2+ED2=16-9+25=32.在Rt△ECB中,EB2=BC2+CE2=4+CE2,∴CE2=28,∴CE=27.答案:52710.如图,P AB、PCD是⊙O的两条割线,PC=AB,P A=20,CD=11,则AB的长为________.解析:设PC=AB=x,则x(x+11)=20×(20+x),解得x=25.所以AB的长为25.答案:2511.如图所示,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.猜想:四边形ABCD的四边有何关系?解:AB+CD=AD+BC.理由:因为AB、BC、CD、DA都与⊙O相切,L、M、N、P为切点,所以AL=AP,LB=MB,DN=DP,NC=MC.所以AB+CD=AL+LB+DN+NC=AP+MB+DP+MC=AD+BC.即AB+CD=AD+BC.12.(创新拓展)已知⊙O与⊙O′外切于P点,AB为两圆的一条外公切线,A、B为切点,AC为⊙O的直径,CD切⊙O′于D,如图所示.求证:AC=CD.证明:方法一:作两圆的公切线MN.再连接P A、PB和PC,如图所示,易得∠APB=90°.∵AC为⊙O直径,∴∠APC=90°.∴C、P、B三点共线.在Rt△ACB中利用射影定理得AC2=CP·CB.又∵CD2=CP·CB,∴CD2=AC2.∴AC=CD.方法二:如图所示,作线段OO′.则OO′必过P点,连接O′B、O′C、O′D,并作O′M⊥AC于M.设⊙O半径为R,⊙O′半径为r.∵MO′2=OO′2-OM2,∴MO′=(R+r)2-(R-r)2=2Rr.∵CO′2=CM2+MO′2,∴CO′2=(2R-r)2+4Rr=4R2+r2.∴CD2=CO′2-O′D2=4R2+r2-r2=4R2. ∴CD=2R=AC.。
圆幂定理及运用

D
D
圆幂定理及运用
一、圆幂定理研究与证明
1、如图,AB 、CD 是⊙O 两条弦,相交于点P 。
求证:P A ·PB =PC ·PD
2、PT 是⊙O 的切线,PAB 是⊙O 的割线。
求证:PT 2=P A ·PB
3、PAB 、PCD 是⊙O 的割线。
求证:P A ·PB =PC ·PD
二、圆幂定理的运用
1、已知:如图,⊙O 的弦AB 与CD 相交于点P ,AP =6,BP =3,CP =2,求CD 的长。
变式1:若AP =6,BP =3,CD =11,求CP 的长
变式2:已知P 为⊙O 内一点,OP =2,过P 作任一弦AB ,若PA =2,PB =。
求⊙O 的半径
2、已知:如图,AB =4,BP =2,CP =4。
求CD 的长
变式1:AB =4,BP =2,CD =1。
求CP 的长
变式2:若PT 是⊙O 的切线。
求PT 的长
变式3:连结PO ,若PO =5,求⊙O 的半径
3、如图,若⊙O 的半径OA =5,P 在OA 上,PA =2,MN 过点P ,MP :PN =1:2.求弦心距OQ 的长
4、过⊙O 外一点P 的一条割线PAB 交⊙O 于A 、B 两点,PO 交⊙O 于C ,AB =7,PA =4,⊙O 的半径为10,求PO 的长。
A
P。
(建议下载)圆幂定理练习题

C.3个是半圆的三等分点,则∠C.145°.如图,以等腰三角形的腰为直径作圆,交底边于D,连结B.∠BAD>∠D.∠BAD<∠AD⊥BC于D,AB=2,DB为斜边上的高,S△ABC=4S△ABD,则ABC在半圆上,CD⊥AB于点百度文库爱是看得见萨科技的沃尔克我去额咳咳,省得麻烦迫.8.如图,AB是⊙O的直径,CB切⊙O与B,CD切⊙O与D,交BA的延长线于E.若AB=3,ED=2,则BC的长为______.9.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点,(Ⅰ)求∠AOD的度数;(Ⅱ)若AO=8 cm,DO=6 cm,求OE的长.10.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.(1)求证:BC是⊙O切线;(2)若BD=5,DC=3,求AC的长.11.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连结AC、OC、BC.(1)求证:∠ACO=∠BCD;(2)若BE=2,CD=8,求AB和AC的长.8cm ,DO =6cm ,.cm 102=DO .有∠AEO =90°,∴∠AEO =∠AEO ∽△AOD ..cm 8.4=ADOD平分∠BAC ,的直径,CD ⊥AB ,∴=.∴∠.又∵OA =OC A .∴∠1=∠2.即:∠ACO ,∠AEC =∠CEB ..∴CE 2=BE ·CEAE=.=8022=+CE AE ,为圆周上一5C 的切线,过点作l A ___________.CD =的切线,切点为,交圆于A PO O B ,.C ∠=、如图所示,过⊙O外一点AP.已知AC=4,AB。
(完整word版)圆幂定理和托勒密定理.docx

板块 1. 圆幂定理例 1.如图, AB 为圆 O 的直径, PA 为圆 O 的切线,PB与圆O相交于 D.若PA= 3, PD ∶ DB = 9∶16,则 PD = ________; AB= ________.例 2 如图, PT 切⊙ O 于点 T ,PA 交⊙ O 于 A、 B 两点,且与直径 CT 交于点 D, CD=2 ,AD=3 , BD=6 ,求 PB 的值.例 3 自圆 O 外一点 P 引圆的一条切线 PA,切点为 A, M 为 PA 的中点,过点 M 引圆的割线交圆于B, C 两点,且∠ BMP =100°,∠ BPC= 40°.求∠ MPB 的大小.例4 如图,在平行四边形 ABCD 中,过 A 、 B、 C 三点的圆交 AD 于点 E,且与 CD 相切,若AB=4 , BE=5 ,求 DE 的长例 5如图所示,已知PA 与⊙ O 相切, A 为切点, PBC 为割线,弦CD∥ AP,AD 、BC 相交于E 点, F 为 CE 上一点,且 DE 2= EF ·EC.(1)求证:∠ P=∠ EDF ;(2) 求证: CE·EB= EF ·EP;(3)若 CE∶ BE= 3∶ 2, DE= 6, EF= 4,求 PA 的长.例6 如图,△ ABC 内接于⊙于E, CD 的延长线交 PA 于O,AB 是∠ O 的直径, PA 是过 A 点⊙ O 的切线,弦 CD 交 AB F,AC=8 ,CE :ED=6 : 5,,AE : BE=2 : 3,求 AB 的长.练习:1.如图, PT 是⊙ O 的切线, T 为切点, PB 是⊙ O 的割线,交⊙ O 于 A 、B 两点,交弦CD 于点M ,已知CM=10 ,MD=2 , PA=MB=4,则PT的长为.2.如图,PAB 、PCD为⊙ O 的两条割线,若PA=5 ,AB=7 , CD=11 ,则AC : BD=.3.如图,AB是⊙ O 的直径, C 是AB延长线上的一点,CD是⊙ O 的切线, D 为切点,过点 B 作⊙ O的切线交CD于点F,若AB=CD=2,则CE=.4. 如图,AB是⊙O 的直径,弦 CD AB ,垂足为E, P 是 BA延长线上C F的点,连结 PC 交⊙O 于F,如果 PF7 ,FC 13 ,且 PA AE: EB:2:4:1,PO EB A那么 CD 的长是.DBC 于点F,BF5 .已知点A在 CEA5. 如图, BC 是半圆⊙O 的直径, EF D EFC的延长线上, AB 与半圆交于 D ,且AB 8,AE 2 ,则AD的长为 __________.BOC F6.如图,⊙ O 的弦 AB 平分半径 OC,交 OC 于 P 点,已知 PA、 PB 的长分别为方程 x212x 240 的两根,则此圆的直径为 ()A .8 2B.6 2C.4 2 D .2 27.如图, BC 是半圆的直径, O 为圆心, P 是 BC 延长线上一点, PA 切半圆于点 A , AD ⊥BC 于点 D.(1) 若∠ B=30 °,问 AB 与 AP 是否相等 ?请说明理由;(2) 求证: PD · PO=PC·PB ;(3) 若 BD : DC=4 : l,且 BC =10,求 PC 的长.8.如图,△ ABC 中,∠ C=90°, O 为 AB 上一点,以 O 为圆心, OB 为半径的圆与 AB 相交于点 E,与 AC 相切于点 D,已知 AD=2 , AE=1 ,那么BC=.9.如图,已知 A 、 B、 C、 D 在同一个圆上,BC=CD , AC 与 BD 交于 E,若AC=8 , CD=4 ,且线段BE、 ED 为正整数,则BD=.10.如图, P 是半圆 O 的直径 BC 延长线上一点,PA 切半圆于点A,AH ⊥BC 于 H,若 PA=1, PB+PC= a ( a >2) ,则 PH=()2 B .1a D.aA .C.a a23 11.如图,△ ABC 是⊙ O 的内接正三角形,弦EF 经过 BC 的中点 D,且EF∥ AB ,若 AB=2 ,则 DE 的长为 ()151C.3D. 1A .B.22212.如图, PA、PB 是⊙ O 的两条切线, PEC 是一条割线, D 是 AB 与 PC 的交点,若 PE=2,CD=1 ,求 DE 的长.板块 2. 托勒密定理托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.设四边形 ABCD 内接于圆,则有:即:AB CD AD BC AC BD ;定理:在四边形 ABCD中,有: AB CD AD BC AC BD并且当且仅当四边形 ABCD内接于圆时,等式成立;例1.如图,在△ ABC 中,∠ A 的平分线交外接∠圆于 D,连结 BD ,求证:AD· BC=BD(AB + AC) .例 2.已知 a、 b、 c 是△ ABC 的三边,且 a2=b(b +c),求证:∠ A=2 ∠B.例 3 在△ ABC 中,已知∠ A∶∠ B∶∠ C=1∶2∶4,例 4 若a、 b 、x、 y 是实数,且a2 b 2 1 , x2y 21.求证: ax by 1 .2.过圆外一点 P作圆的两条切线和一条割线,切点为A, B。
圆幂定理试题及答案

圆幂定理试题及答案一、选择题1. 圆幂定理指的是()A. 圆上任意两点的距离等于它们到圆心的距离之和B. 圆上任意两点的距离等于它们到圆心的距离之差C. 圆上任意一点到圆心的距离等于该点到圆上其他点的距离之和D. 圆上任意一点到圆心的距离等于该点到圆上其他点的距离之差2. 在圆幂定理中,如果圆上一点P到圆心O的距离为OP,点P到圆上另一点A的距离为PA,则以下哪个表达式是正确的?()A. OP = PAB. OP + PA = 2RC. OP - PA = RD. OP × PA = R^2二、填空题3. 若圆的半径为5cm,圆上一点到圆心的距离为3cm,则该点到圆上任意一点的距离之和为_________。
4. 已知圆幂定理中的OP = 8cm,PA = 6cm,且点A在圆上,则圆的半径R为_________。
三、解答题5. 如图所示,圆O的半径为10cm,点P在圆上,OP(点P到圆心O的距离)为12cm。
求点P到圆上另一点B的距离PB。
6. 在一个半径为7cm的圆中,有两点A和B,已知OA(点A到圆心O 的距离)为5cm,求AB的长度。
四、证明题7. 证明圆幂定理:在一个给定的圆中,圆上任意一点到圆心的距离与该点到圆上其他点的距离之和等于圆的直径。
答案一、选择题1. 正确答案:D2. 正确答案:B二、填空题3. 该点到圆上任意一点的距离之和为10cm + 10cm = 20cm。
4. 圆的半径R可以通过勾股定理计算得出:R^2 = OP^2 - OA^2,所以R^2 = 8^2 - 6^2 = 64 - 36 = 28,因此R = √28 ≈ 5.29cm。
三、解答题5. 由于OP > OA,根据圆幂定理,PB = 2R - OP = 2 * 10 - 12 = 20 - 12 = 8cm。
6. 同样使用圆幂定理,AB = 2R - OA - OB,但是OB = OA = 5cm,所以AB = 2 * 7 - 5 - 5 = 14 - 10 = 4cm。
《弦切角定理》《圆幂定理》练习题及答案
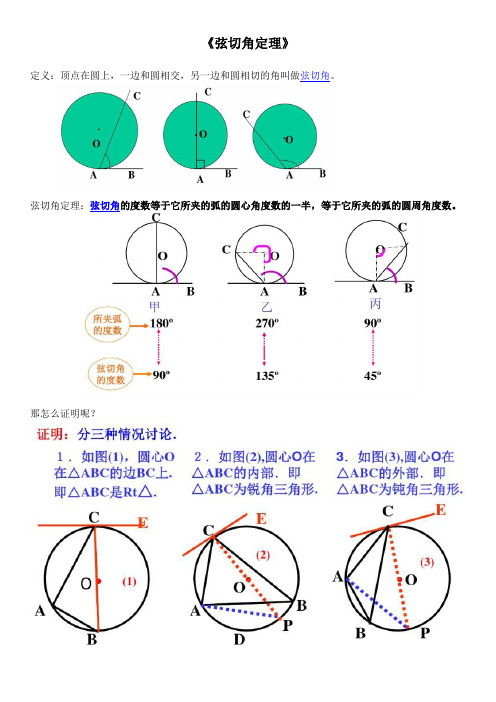
《弦切角定理》定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
弦切角定理:弦切角的度数等于它所夹的弧的圆心角度数的一半,等于它所夹的弧的圆周角度数。
那怎么证明呢?《圆幂定理》(1)相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在⊙O 中,∵弦AB 、CD 相交于点P ,∴PA PB PC PD ⋅=⋅(2)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在⊙O 中,∵直径AB CD ⊥, ∴2CE AE BE =⋅(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在⊙O 中,∵PA 是切线,PB 是割线∴ 2PA PC PB =⋅(4)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如上图)。
即:在⊙O 中,∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅【精典例题】1、如图,PA 、PB 是⊙O 的切线,AC 是⊙O 的直径,∠P=50°,则∠BOC 的度数为( ) A .50°B .25°C .40°D .60°2、如图,BD 为圆O 的直径,直线ED 为圆O 的切线,A .C 两点在圆上,AC 平分∠BAD 且交BD 于F 点.若∠ADE =19°,则∠AFB 的度数为何?( ) A .97°B .104°C .116°D .142°解答:解:∵PA 、PB 是⊙O 的切线, ∴∠OAP =∠OBP =90°, 而∠P =50°,∴∠AOB =360°﹣90°﹣90°﹣50°= 130°, 又∵AC 是⊙O 的直径,∴∠BOC =180°﹣130°=50°. 故选A .BADB3、如图,AB 为⊙O 的直径,PD 切⊙O 于点C ,交AB 的延长线于D ,且CO=CD ,则∠PCA=( )A 、30°B 、45°C 、60°D 、67.5°4、已知⊙O 的半径为1,圆心O 到直线l 的距离为2,过l 上任一点A 作⊙O 的切线,切点为B ,则 线段AB 长度的最小值为( )A 、1B 、2C 、3D 、2解答:如右图所示,OA ⊥l ,AB 是切线,连接OB , ∵OA ⊥l ,∴OA=2, 又∵AB 是切线, ∴OB ⊥AB ,在Rt △AOB 中,AB =22OB OA -=2212-=3.故选C .5、如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形, 两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管 道,则O 到三条支路的管道总长(计算时视管道为线,中心O 为点) 是( )A.2mB.3mC.6mD.9m解答:在Rt △ABC 中,BC =8m,AC =6m,AB =22BC AC +=2286+=10. ∵中心O 到三条支路的距离相等,设距离是r .△ABC 的面积=△AOB 的面积+△BOC 的面积+△AOC 的面积 即:12AC •BC =12AB •r+12BC •r+12AC •r 即:6×8=10r+8r+6r ∴r=4824=2. 故O 到三条支路的管道总长是2×3=6m .故选C .解答:解:∵BD 是圆O 的直径, ∴∠BAD =90°, 又∵AC 平分∠BAD ,∴∠BAF =∠DAF =45°, ∵直线ED 为圆O 的切线, ∴∠ADE =∠ABD =19°,∴∠AFB =180°-∠BAF -∠ABD =180°-45°-19°=116°. 故选C .解答:解:如图:∵PD 切⊙O 于点C , ∴OC ⊥PD , 又∵OC=CD , ∴∠COD=45°, 连接AC ,∵AO=CO , ∴∠ACO=22.5°,∴∠PCA=90°-22.5°=67.5°. 故选D .O(第5题图)6、如图,AB 是⊙O 的直径,BC 交⊙O 于点D ,DE ⊥AC 于点E ,要使DE 是⊙O 的切线,还需补充一个条件,则补充的条件不正确...的是( ) A. DE =DO B. AB =AC C. CD =DB D. AC ∥OD7、已知AB 是⊙O 的直径,点P 是AB 延长线上的一个动点,过P 作⊙O 的切线,切点为C ,∠APC 的平分线交AC 于点D ,则∠CDP 等于( )A 、30°B 、60°C 、45°D 、50°解答:连接OC ,∵OC=OA ,,PD 平分∠APC ,∴∠CPD=∠DPA ,∠A=∠ACO , ∵PC 为⊙O 的切线,∴OC ⊥PC ,∵∠CPD+∠DPA+∠A+∠ACO=90°,∴∠DPA+∠A=45°,即∠CDP=45°. 故选C .8、如图,CB 切⊙O 于点B ,CA 交⊙O 于点D 且AB 为⊙O 的直径,点E 是ABD 上异于点A 、D 的一点.若∠C =40°,则∠E 的度数为 .9、已知:如图,三个半圆以此相外切,它们的圆心都在x 轴的正半轴上并与直线y =x 相切,设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3,则当r 1=1时,r 3=解答:由三个半圆依次与直线y =x 相切并且圆心都在x 轴上,∴y =x 倾斜角是30°,∴得,OO 1=2r 1,OO 1=2r 2,001=2r 3,r 1=1,∴r3=9.故答案为9.333333解答:当AB=AC 时,连接AD ,∵AB 是⊙O 的直径,∴AD ⊥BC ,∴CD=BD , ∵AO=BO ,∴OD 是△ABC 的中位线,∴OD ∥AC ,∵DE ⊥AC ,∴DE ⊥OD ,∴DE 是⊙O 的切线.所以B 正确. 当CD=BD 时,AO=BO ,∴OD 是△ABC 的中位线,∴OD ∥AC ∵DE ⊥AC ∴DE ⊥OD ∴DE 是⊙O 的切线.所以C 正确.当AC ∥OD 时,∵DE ⊥AC ,∴DE ⊥OD .∴DE 是⊙O 的切线.所以D 正确. 故选A .ABCD P· OE解答:如图:连接BD ,∵AB 是直径,∴∠ADB =90°,∵BC 切⊙O 于点B ,∴∠ABC =90°, ∵∠C =40°,∴∠BAC =50°,∴∠ABD =40°,∴∠E =∠ABD =40°. 故答案为:40°.10、如图,在Rt △ABC 中,∠ABC 是直角,AB=3,BC=4,P 是BC 边上的动点,设BP=x ,若能在AC 边上找到一点Q ,使∠BQP=90°,则x 的取值范围是 .解答:解:过BP 中点以BP 为直径作圆,连接QO ,当QO ⊥AC 时,QO 最短,即BP 最短, ∵∠OQC=∠ABC=90°,∠C=∠C ,∴△ABC ∽△OQC ,∴=,∵AB=3,BC=4,∴AC=5, ∵BP=x ,∴QO=x ,CO=4﹣x ,∴=,解得:x=3,当P 与C 重合时,BP=4,∴BP=x 的取值范围是:3≤x ≤4, 故答案为:3≤x ≤4.11、如图,AD 是⊙O 的弦,AB 经过圆心O ,交⊙O 于点C ,∠DAB=∠B=30°. (1)直线BD 是否与⊙O 相切?为什么? (2)连接CD ,若CD=5,求AB 的长.解答:(1)直线BD 与⊙O 相切.如图连接OD ,CD , ∵∠DAB=∠B=30°,∴∠ADB=120°, ∵OA=OD ,∴∠ODA=∠OAD=30°,∴∠ODB=∠ADB ﹣∠ODA=120°﹣30°=90°. 所以直线BD 与⊙O 相切.(2)连接CD ,∠COD=∠OAD+∠ODA=30°+30°=60°, 又OC=OD ,∴△OCD 是等边三角形,即:OC=OD=CD=5=OA ,∵∠ODB=90°,∠B=30°,∴OB=10,∴AB=AO+OB=5+10=15.12、已知:如图,AB 为⊙O 的直径,⊙O 过AC 的中点D ,DE ⊥BC 于点E . (1)求证:DE 为⊙O 的切线;(2)若DE =2,tan C =12,求⊙O 的直径.【解析】(1)证明:联结OD . ∵ D 为AC 中点, O 为AB 中点,∴ OD 为△ABC 的中位线. ∴OD ∥BC . ∵ DE ⊥BC , ∴∠DEC=90°.∴∠ODE=∠DEC=90°. ∴OD ⊥DE 于点D. ∴ DE 为⊙O 的切线.(2)解:联结DB . ∵AB 为⊙O 的直径, ∴∠ADB=90°. ∴DB ⊥AC . ∴∠CDB=90°. ∵ D 为AC 中点, ∴AB=AC .在Rt △DEC 中,∵DE=2 ,tanC=12, ∴EC=4tan DEC=. 由勾股定理得:DC=在Rt △DCB 中, BD=tan DC C ⋅ BC=5. ∴AB=BC=5. ∴⊙O 的直径为5.【巩固练习】1.已知⊙O 的半径为10cm ,如果一条直线和圆心O 的距离为10cm ,那么这条直线和这个圆的位置关系为( )A. 相离B. 相切C. 相交D. 相交或相离2.如右图,A 、B 是⊙O 上的两点,AC 是⊙O 的切线,∠B=70°,则∠BAC 等于( )A. 70°B. 35°C. 20°D. 10°(第2题) (第3题) (第4题) (第5题)3.如图,PA 切⊙O 于A ,PB 切⊙O 于B ,OP 交⊙O 于C ,下列结论中,错误的是( )A. ∠1=∠2B. PA=PBC. AB ⊥OPD. 2PA PC ·PO4.如图,已知⊙O 的直径AB 与弦AC 的夹角为30°,过C 点的切线PC 与AB 的延长线交于P ,PC=5,则⊙O 的半径为( )A.335 B. 635 C. 10 D. 55.如图已知AB 是⊙O 的直径,弦AD 、BC 相交于点P ,那么AB ︰CD 等于∠BPD 的( )A. 正弦B. 余弦C. 正切D. 余切6.如图A 、B 、C 是⊙O 上三点,AB ⌒的度数是50°,∠OBC=40°,则∠OAC 等于( )A. 15°B. 25°C. 30°D. 40°(第6题) (第7题) (第8题) (第9题)7.如图AB 为⊙O 的一条固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C ,作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当C 点在半圆(不包括A 、B 两点)上移动时,点P ( )A. 到CD 的距离不变B. 位置不变C. 等分DB ⌒D. 随C 点的移动而移动8.如图AD 、AE 和BC 分别切⊙O 于D 、E 、F ,如果AD=20,则△ABC 的周长为( ) A. 20 B. 30 C. 40 D. 21359.如图在⊙O 中,直径AB 、CD 互相垂直,BE 切⊙O 于B ,且BE=BC ,CE 交AB 于F ,交⊙O 于M ,连结MO 并延长,交⊙O 于N ,则下列结论中,正确的是( )A. CF=FMB. OF=FBC. BM⌒的度数是22.5° D. BC ∥MN 10.如图⊙O 的两条弦AB 、CD 相交于点P ,已知AP=2cm ,BP=6cm ,CP ︰PD =1︰3,则DP=_________.(第10题) (第11题) (第12题) (第13题)11.如图AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,P 是BA 的延长线上的点,连结PC ,交⊙O 于F ,如果PF=7,FC=13,且PA ︰AE ︰EB = 2︰4︰1,则CD =_________.12.从圆外一点P 引圆的切线PA ,点A 为切点,割线PDB 交⊙O 于点D 、B ,已知PA=12,PD=8,则=∆∆DAP ABP S S :__________.13.⊙O 的直径AB=10cm ,C 是⊙O 上的一点,点D 平分BC ⌒,DE=2cm ,则AC=_____. 14.如图,AB 是⊙O 的直径,∠E=25°,∠DBC=50°,则∠CBE=________.(第14题) (第15题) (第17题) (第18题)15.点A 、B 、C 、D 在同一圆上,AD 、BC 延长线相交于点Q ,AB 、DC 延长线相交于点P ,若∠A=50°,∠P=35°,则∠Q=________.16.在Rt △ABC 中,∠C=90°,AC=12cm ,BC=5cm ,以点C 为圆心,6cm 的长为半径的圆与直线AB 的位置关系是________.17.如图,在△ABC 中,AB=AC,∠BAC=120°,⊙A 与BC 相切于点D,与AB 相交于点E,则∠ADE 等于___度. 18.如图,PA 、PB 是⊙O 的两条切线,A 、B 为切点,直线OP 交⊙A 于点D 、E,交AB 于C.图中互相垂直的线段有_________(只要写出一对线段即可).19.已知⊙O 的半径为4cm,直线L 与⊙O 相交,则圆心O 到直线L 的距离d 的取值范围是____.E A PO EC D BA20.如图,PA 、PB 是⊙O 的切线,切点分别为A 、B,且∠APB=50°,点C 是优弧AB 上的一点,则∠ACB 的度数为________.(第20题) (第21题) (第22题) (第23题)21.如图,⊙O 为△ABC 的内切圆,D 、E 、F 为切点,∠DOB=73°,∠DOE=120°, 则∠DOF=_______度,∠C=______度,∠A=_______度.22.如图,AB 、AC 为⊙O 的切线,B 、C 是切点,延长OB 到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ ADO 等于_______23.如图AB 是⊙O 的直径,AC 是⊙O 的切线,,A 为切点,连结BC 交圆0于点D,连结AD,若∠ABC =45°,则下列结论正确的是( )A.AD =BCB.AD =ACC.AC >ABD.AD >DC24.如图,在平面直角坐标系中,⊙P 与x 轴相切于原点O ,平行于y 轴的直线交⊙P 于M,N 两点.若点M 的坐标是(2,-1),则点N 的坐标是( )A .(2,-4) B. (2,-4.5) C.(2,-5) D.(2,-5.5)(第24题) (第25题) (第26题) (第27题)25、如图,AB 是⊙O 的直径,AD 是⊙O 的切线,点C 在⊙O 上,BC ∥OD ,AB =2,OD =3,则BC 的长为( )A .B . CD26、已知圆O 的半径为R ,AB是圆O 的直径,D 是AB 延长线上一点,DC是圆O 的切线,C 是切点,连结AC ,若∠CAB =30°,则BD 的长为( )A .BC .D 27、如图,在平面直角坐标系中,⊙A 与y 轴相切于原点O ,平行于x 轴的直线交⊙A 于M 、M 两点,若点M 的坐标是(-4,-2),则点N 的坐标为( )A .(-1,-2)B .(1,2)C .(-1.5,-2)D .(1.5,-2)PO C BA212123322R R R28、如图,AB 是圆O 的直径,AC 是圆O 的切线,A 为切点,连结BC 交圆于点D ,连结AD ,若∠ABC =45°,则下列结论正确的是( )A .B .C .D .(第28题) (第29题) (第30题) (第31题)29、如图,AB 是⊙O 的直径,⊙O 交BC 的中点于D,DE ⊥AC 于E,连接AD,则下列结论正确的个数是( )①AD ⊥BC ②∠EDA =∠B ③OA =AC ④DE 是⊙O 的切线A .1 个B .2个C .3 个D .4个30、一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN =60︒,则OP =( )A .50 cmB .25cm C .cm D .50cm 31、如图,DB 为半圆的直径,A 为BD 延长线上一点,AC 切半圆于点E ,BC ⊥AC 于点C ,交半圆于点 F .已知BD =2,设AD =x ,CF =y ,则y 关于x 的函数解析式是 .32、如图, AB 与⊙O 相切于点B ,线段OA 与弦BC 垂直于点D ,∠AOB =60°,BC =4cm ,则切线AB = cm.(第32题) (第33题) (第34题) (第35题)33、如图,直线AB 切⊙O 于C 点,D 是⊙O 上一点,∠EDC =30º,弦EF ∥AB ,连结OC 交EF 于H 点,连结CF ,且CF =2,则HE 的长为_________.34、如图,点A 、B 、C 在⊙O 上,切线CD 与OB 的延长线交于点D ,若∠A =30°,CD =,则⊙O 的半径长为 .35、如图,在中,,与相切于点,且交于两点,则图中阴影部分的面积是 (保留).O 12AD BC =12AD AC =AC AB >AD DC >12333503第19题图ABC DO32ABC △120AB AC A BC =∠==,°,A ⊙BC D AB AC 、M N 、π36、如图,⊙O 内切于△ABC ,切点分别为D ,E ,F .∠B =50°,∠C =60°,连结OE ,OF ,DE ,DF ,则∠EDF 等于( )A .40°B .55°C .65°D .70°(第36题) (第73题) (第38题)37、如图,一个边长为4 cm 的等边三角形ABC 的高与⊙O 的直径相等.⊙O 与BC 相切于点C ,与AC 相交于点E ,则CE 的长为________cm.38、如图,直线l 与半径为4的⊙O 相切于点A ,P 是⊙O 上的一个动点(不与点A 重合),过点P 作PB ⊥l ,垂足为B ,连结PA .设PA =x ,PB =y ,则x -y 的最大值是________.39、如图,AB 是半圆O 的直径,C 为半圆上一点,过C 作半圆的切线,连接AC, 作直线AD ,使∠DAC=∠CAB ,AD 交半圆于E,交过C 点的切线于点D. (1)试判断AD 与CD 有何位置关系,并说明理由; (2)若AB=10,AD=8,求AC 的长.40、如图,点A ,B ,C 在半径为8的⊙O 上,过点B 作BD ∥AC ,交OA 延长线于点D ,连结BC ,且∠BCA =∠OAC =30°.(1)求证:BD 是⊙O 的切线; (2)求图中阴影部分的面积.答案:8、据切线长定理有AD=AE,BE=BF,CD=CF;则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40.故选C.9、解:A错,F显然不是弦的平分点;B错,F不是半径的中点;C错,M点平分应为45°;D对,∵BE为圆O的切线,∴BE⊥AB,∵CD⊥AB,∴BE∥CD,∴∠BEF=∠DCF,∵BC=BE,∴∠BCE=∠BEF,∴∠BCE=∠DCF,∵OC=OM,∴∠DCF=∠CMN,∴∠BCE=∠CMN,∴BC∥MN.故选D.10、解:如图利用相交弦定理可知:11、根据割线定理,PF*PC=PA*PB,设EB=X则PA=2X,AE=4X,PB=7X7*(7+13)=2X*7X,X2=10在三角形PCE中,CE2=PC2-PE2=400-360=40,CD=2CE=10412、由切割线定理可得PA2=PD×PB,∵PA=12,PD=8 ∴PB=18.由弦切角和公共角易知△PAD∽△PBA.∴S△PAD:S△PBA=PA2:PB2=4:9.⌒,∴OD平分BC,∴OE为△ABC的中位线,13、∵点D平分BC又∵⊙O的直径AB=10cm,∴OD=5cm,DE=2cm,∴0E=3cm,则弦AC=6cm.故答案为6cm.14、连接AC,∵∠DBA和∠DCA都为AD所对的圆周角,∴∠DBA=∠DCA,∵AB为⊙O的直径,∴∠BCA=90°,∴∠CBA+∠CAB=90°,∵∠CAB=∠E+∠DCA,∴∠CBD+∠DBA+∠E+∠DBA=90°,∵∠E=25°,∠DBC=50°,∴∠DBA=7.5°,∴∠CBE=∠DBA+∠DBC=57.5°15、∠A=50°,故∠BCD=130°(因为是圆,同弧的角互补),由P=35°计得∠CDQ=85°,故可以计出∠Q=45°.16.相交 17.60 18.如OA⊥PA,OB⊥PB,AB⊥OP等. 19.0≤d<4. 20.65°21. 146°,60°,86° 22.64°23、【答案】A 24、【答案】A 25、【答案】A 26、【答案】C27、【答案】C 28、【答案】A 29、【答案】D 30、【答案】A31、 32、【答案】433、【答案】34、【答案】2.3536、B 由∠B =50°,∠C =60°可求出∠A =70°,则易求得∠EOF =110°,∴∠EDF =12∠EOF =55°.37、过O 作OF ⊥AC 于F ,连结OC ,如图.则CE =2CF .根据△ABC 为等边三角形,且边长为4 cm ,易求得它的高为2 3 cm ,即OC = 3 cm.∵BC 与⊙O 相切,∴∠OCB =90°.又∠ACB =60°,∴∠OCF =30°.3π3在Rt△OFC中,可得CF=OC·cos 30°=3×32=32(cm),故CE=2CF=3 cm.38、如图,连结OA,过点O作OC⊥AP于点C,所以∠ACO=90°,AC=12AP.易证△OAC∽△APB,所以OA AP =ACPB,即4x=x2y,所以y=x28.所以x-y=x-x28=-18(x-4)2+2,所以x-y的最大值是2.39.(1)AD⊥CD.理由:连接OC,则OC⊥CD.∵OA=OC,∴∠OAC=∠OCA,又∠OAC= ∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,又∠DAC=∠CAB.∴△ACD∽△ABC,∴AC ADAB AC=,即AC2=AD·AB=80,故40、22.(1)证明:如图,连结OB,交CA于点E.∵∠C=30°,∠C=12∠BOA,∴∠BOA=60°.∵∠OAC=30°,∴∠AEO=90°.∵BD∥AC,∴∠DBE=∠AEO=90°.∴OB⊥BD.∴BD是⊙O的切线.(2)解:∵AC∥BD,∴∠D=∠OAC=30°.∵∠OBD=90°,OB=8,∴BD=3OB=8 3.∴S阴影=S△BDO-S扇形AOB=12×8×83-60·π×82360=323-32π3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.在△ ABC中,∠ A∶∠ B∶∠ C=1∶ 2∶ 3, CD⊥ AB 于 D,AB= a,则 DB=()
a a a3a
A.B.C.D.
4324
2.如图, AD 是△ ABC高线, DE⊥ AB 于 E,DF⊥ AC于 F,则 (1)AD2= BD·CD(2)AD2= AE·AB(3)AD2=AF· AC(4)AD2= AC2- AC· CF 中正确的有 ()
A. 1 个B. 2 个C.3 个D.4 个
3.如图, AB 是⊙ O 的直径, C, D 是半圆的三等分点,则∠C+∠ E+∠ D=()
A. 135°B. 110°C.145°D.120°
4.如图,以等腰三角形的腰为直径作圆,交底边于D,连结 AD,那么 ()
A.∠ BAD+∠ CAD= 90°B.∠ BAD>∠ CAD
C.∠ BAD=∠ CAD D.∠ BAD<∠ CAD
二、填空题
5.在 Rt△ABC中,∠ BAC= 90°, AD⊥ BC于 D, AB= 2, DB= 1,则 DC= ______, AD=______.6.在 Rt△ABC中, AD 为斜边上的高,S△ABC=4S△ABD,则 AB∶ BC=______.
7.如图, AB 是半圆 O 的直径,点 C 在半圆上, CD⊥ AB 于点 D,且 AD= 3DB,设∠ COD=,则
tan 2______.
2
8.如图, AB 是⊙ O 的直径, CB 切⊙ O 与 B,CD 切⊙ O 与 D,交 BA 的延长线于E.若 AB= 3,ED =2,则 BC的长为 ______.
9.如图,在梯形ABCD中, AB∥ CD,⊙ O 为内切圆, E 为切点,
(Ⅰ)求∠ AOD的度数;
(Ⅱ)若 AO=8 cm, DO= 6 cm,求 OE的长.
10.如图,在△ ABC中,∠ C= 90°, AD 是∠ BAC的平分线, O 是 AB 上一点,以OA 为半径的⊙ O 经过点 D.
(1)求证: BC是⊙ O 切线;
(2)若 BD= 5, DC=3 ,求 AC的长.
11.如图, AB 是⊙ O 的直径, CD 是⊙ O 的一条弦,且CD⊥ AB 于 E,连结 AC、 OC、BC.
(1)求证:∠ ACO=∠ BCD;
(2)若 BE= 2, CD=8,求 AB 和 AC 的长.
专题十三 相似三角形定理与圆幂定理参考答案
习题 13
一、选择题: 1. A
2. C
3. D
4. C
二、填空题
1 5. 3, 3
6. 1∶2
7.
8. 3
3
三、解答题
9. (Ⅰ)∵ AB ∥CD ,
∴∠ BAD +∠ ADC = 180°.∵⊙ O 内切于梯形 ABCD , ∴AO 平分∠ BAD ,有∠ DAO = 1
∠ BAD ,
2
又 DO 平分∠ ADC ,有∠ ADO = 1
∠ ADC .
2
1
∴∠ DAO +∠ ADO = (∠ BAD +∠ ADC)= 90°,∴∠ AOD = 180°- (∠ DAO +∠ ADO)=
90°.
(Ⅱ)∵在 Rt △ AOD 中, AO = 8cm , DO = 6cm ,
∴由勾股定理,得
AO 2 DO 2 10cm.
∵E 为切点,∴ OE ⊥ AD .有∠ AEO =90°,∴∠ AEO =∠ AOD .
又∠ CAD 为公共角,∴△ AEO ∽△ AOD . ∴ OE
AO
, OE
AO OD
4.8cm .
OD AD
AD
10. (1)连接 OD .∵ OA =OD , AD 平分∠ BAC ,
∴∠ ODA =∠ OAD ,∠ OAD =∠ CAD .∴∠ ODA =∠ CAD . ∴OD ∥ AC .∴∠ ODB =∠ C =90°.∴ BC 是⊙ O 的切线. (2)过 D 作 DE ⊥ AB 于 E .∴∠ AED =∠ C = 90°.
又∵ AD = AD ,∠ EAD =∠ CAD ,∴△ AED ≌△ ACD . ∴AE = AC , DE = DC = 3.
在 Rt △ BED 中,∠ BED = 90°,由勾股定理,得
BE
BD 2 DE 2
4 ,设 AC =x(x >0),则 AE = x .
在 Rt △ ABC 中,∠ C = 90°, BC = BD + DC = 8, AB = x + 4,由勾股定理,得x 2+8 2= (x + 4)2.解得 x = 6.即 AC = 6.
11. (1)连结 BD ,∵ AB 是⊙ O 的直径, CD ⊥ AB ,
∴
=
.∴∠ 1=∠ 2.
又∵ OA =OC ,∴∠ 1=∠ A .∴∠ 1=∠ 2. 即:∠ ACO =∠ BCD .
(2)由 (1)问可知,∠ A =∠ 2,∠ AEC =∠ CEB .
∴△ ACE ∽△ CBE .∴
CE
AE
.∴ CE 2= BE ·
AE .
BE CE
又 CD = 8,∴ CE = DE = 4.
∴ AE = 8.∴ AB = 10.∴ AC = AE 2
CE 2
80
4 5.
模拟题集锦:
l
C
1、 如图,已知⊙ O 的直径 AB 5 , C 为圆周上一
D
点, BC 4 ,过点 C 作⊙ O 的切线 l ,过点 A 作
B
O
A
l 的垂线 AD ,垂足为 D ,则 CD ___________.
2、如图,已知 PA 是圆 O 的切线,切点为
A , PO 交圆 O 于 B, C 两点, PA
3, PB 1 ,
则圆 O 的半径为
, C .
A
C
P B O
3、如图, PAB 、 PC 分别是圆 O 的割线和切线( C 为切点),若 PA
AB 3 ,则 PC 的长为
A . 6
2
B . 6
C
C . 3 2
D . 3 O
P
A
B
4、如图,PC切e O于点C,割线PAB经过圆心O,弦CD AB
C
于点 E ,已知 e O 的半径为 3 , PA 2 ,则 PC_________ ,
OE _________.B·
O EAP
D
5、如图,圆O 和圆O相交于 A, B 两点, AC 是圆O的切线, AD 是
圆 O 的切线,若BC= 2, AB=4,则BD_.A
O .
.O '
C B
D
6 、如右图 : PA切e O 于点 A , PA 4 , PBC 过圆心 O ,且与圆相交于 B 、 C 两点,
AB : AC 1: 2,则 e O 的半径为.
C
O
7、如下图,在圆内接四边形ABCD 中,对角线 AC, BD 相交于B
点 E .已知BC CD 2 3 ,AE2EC ,CBD 30o
P
,A
则 CAB30o, AC 的长是6.
8、如图所示,过⊙O 外一点 A 作一条直线与⊙O 交于 C, D 两点, AB 切⊙ O 于 B,弦 MN 过 CD
的中点 P.已知 AC=4,AB=6,则 MP· NP=25
.
4
A
M C
D
P
B N O。
