完整版相交线平行线培优讲义
七年级数学培优提高讲义：相交线与平行线(一) (1)
七年级数学竞赛讲座：相交线与平行线一、知识要点：1.平面上两条不重合的直线，位置关系只有两种：相交和平行。
2.两条不同的直线，若它们只有一个公共点，就说它们相交。
即，两条直线相交有且只有一个交点。
3.垂直是相交的特殊情况。
有关两直线垂直，有两个重要的结论：（1）过一点有且只有一条直线与已知直线垂直；（2）直线外一点与直线上所有点的连线中，垂线段最短。
4．两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ ；⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做____________ ；⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_______________.5．平行公理：经过直线外一点，有且只有一条直线与这条直线______.推论：如果两条直线都与第三条直线平行，那么_____________________.6．平行线的判定：⑴两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：_______________________.⑵两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单说成：___________________________.⑶两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：_______________________. 7．在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线_______ .8．平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等.简单说成：＿＿＿＿＿＿＿＿＿＿.⑵两条平行直线被第三条直线所截，内错角相等.简单说成：__________.⑶两条平行直线被第三条直线所截，同旁内角互补.简单说成：__________________。
培优提高讲义：相交线与平行线(一)
七年级数学：相交线与平行线一、知识要点：1.平面上两条不重合的直线，位置关系只有两种：相交和平行。
2.两条不同的直线，若它们只有一个公共点，就说它们相交。
即，两条直线相交有且只有一个交点。
3.垂直是相交的特殊情况。
有关两直线垂直，有两个重要的结论：（1）过一点有且只有一条直线与已知直线垂直；（2）直线外一点与直线上所有点的连线中，垂线段最短。
4．两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ ；⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做____________ ；⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_______________.5．平行公理：经过直线外一点，有且只有一条直线与这条直线______.推论：如果两条直线都与第三条直线平行，那么_____________________.6．平行线的判定：⑴两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：_______________________.⑵两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单说成：___________________________.⑶两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：_______________________. 7．在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线_______ .8．平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等.简单说成：＿＿＿＿＿＿＿＿＿＿.⑵两条平行直线被第三条直线所截，内错角相等.简单说成：__________.⑶两条平行直线被第三条直线所截，同旁内角互补.简单说成：__________________。
著名机构数学讲义寒假07-七年级培优版-相交线与平行线综合--教师版
教师姓名冯娜娜学生姓名年级初一上课时间单击此处输入日期。
学科数学课题名称相交线与平行线综合知识模块Ⅰ：相交线的性质定理（一）概念：1、.邻补角有一条公共边，另一边互为反向延长线的两个角，叫做互为邻补角．2.、对顶角一个角的两边分别为另一个角两边的反向延长线，这样的两个角叫做对顶角．3、垂线相交线与平行线综合两条直线相交所成四个角中，如果有一个角是直角，我们就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．4、垂线段过直线外一点，作已知直线的垂线，这点和垂足之间的线段．5.、点到直线的距离直线外一点到这条直线的垂线段的长度．（二）性质：1、对顶角的性质：对顶角相等．2.、邻补角的性质：互为邻补角的两个角和为180°．3、垂线的基本性质：（1）经过一点有且只有一条直线垂直于已知直线；（2）垂线段最短．【例1】下列语句中，正确的个数是（）①相等的角为对顶角；②不相等的角一点不是对顶角；③不是对顶角的角都不相等；④有公共定点且和为180︒的两个角为邻补角.A、1B、2C、3D、4【答案】A【例2】以下结论中正确的个数是（）①如果两条直线相交所成的两个角都相等，那么这两条直线互相垂直；②如果两条直线相交所成的三个角都相等，那么这两条直线互相垂直；③如果两条直线相交所成的四个角都相等，那么这两条直线互相垂直；④如果两条直线相交，若有一组邻补角相等，那么这两条直线互相垂直.A、1B、2C、3D、4【答案】C【例3】如图1，下列说法中错误的是（）A、∠1与∠5是直线AD、CD被直线AC所截成的同位角；B、∠2与∠4是直线AB、BC被直线AC所截成的同旁内角；C、∠1与∠3是直线AD、BC被直线AB所截成的内错角；D、∠1与∠4是直线AD、BC被直线AC所截成的内错角；【答案】D知识模块Ⅱ：平行线的性质与判定1、平行线的基本性质经过直线外一点，有且只有一条直线与已知直线平行．推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．平行公理及推论是整个初中平面几何的基石，是其它公理、定理的基础．平行公理及其推论在说明直线平行时，经常用到． 注意：这条性质与垂线的性质很相似，但过任意一点都可以画垂线，而画平行线，只能是过直线外一点才可以．2、平行线的三种判定方法：（1）两条直线被第三条直线所截，如果同位角相等，那么两条直线平行，简单地说，同位角相等，两直线平行．（2）两条直线被第三条直线所截，如果内错角相等，那么两条直线平行，简单地说，内错角相等，两直线平行．（3）两条直线被第三条直线所截，如果同旁内角互补，那么两条直线平行，简单地说，同旁内角互补，两直线平行．【例4】已知：如图∠1=∠2，∠C =∠D ，∠A =∠F 相等吗？试说明理由【答案】∵ ∠1=∠DGF (对顶角相等)，∠1=∠2∴ ∠DGF =∠2∴ DB ∥EC （同位角相等，两直线平行） ∴∠DBA =∠C （两直线平行，同位角相等） 又∵∠C =∠D ∴∠DBA =∠D∴ DF ∥AC （内错角相等，两直线平行） ∴∠A =∠F （两直线平行，内错角相等）【例5】如图6所示，B 、E 分别是线段AC 、DF 上的点，AF 交BD 于G ，交EC 于H ，且∠1=∠2，∠HG21FEDCBAD =∠C.请说明AC//DF.【答案】∵∠1=∠2，∠1=∠3（对顶角相等）∴∠3 =∠2（等量代换）∴DB∥EC（同位角相等，两直线平行）∴∠D=∠FEH（两直线平行，同位角相等∵∠C=∠D∴∠C=∠FEH（等量代换）∴AC∥DF【例6】如图，在六边形ABCDEF中，AF∥CD，∠A=∠D，∠B=∠E，请说明BC∥EF. 【答案】联结BE、AD∵AF∥CD∴∠ADC=∠DAF（两直线平行，内错角相等）∵∠A=∠D∴∠A－∠DAF =∠D－∠ADC（等量减等量，差相等）即∠ADE=∠BAD∴AB∥DE（内错角相等，两直线平行）∴∠ABE=∠BED（两直线平行，内错角相等）同理∠CBE=∠BEF∴BC∥EF（内错角相等，两直线平行）【例7】如图所示，已知∠E+∠G=∠B+∠F+∠D，请说明AB∥CD.【答案】分别过点E、F、G作EH∥FM∥GN∥AB的平行线，则∠B=∠BEH，∠HEF=∠EFM，∠GFM=∠FGN，∠DGN=∠D∵∠E+∠G=∠B+∠F+∠D∴∠BEH+∠HEF+∠FGN+∠DGN=∠B+∠EFM+∠GFM +∠D∴∠DGN=∠D∴GN∥CD（内错角相等，两直线平行）∴AB∥CD（平行线的传递性）【习题1】如图，∠DAB和∠B是直线DE和BC被直线所截而成的角．【答案】AB；内错【习题2】两条直线相交于一点时有____对对顶角，三条直线相交于一点时有____对对顶角．【答案】2；6【习题3】如图3，已知：a∥b，∠3＝l37°，则∠1＝____，∠2＝____．【答案】137；43【习题4】在同一平面内，若直线a∥c，b∥c．则a b．【答案】∥【习题5】∠1和∠2互为补角，又是对顶角，则它们的两边所在的直线．【答案】互相垂直【习题6】如图，已知：AB∥CD，AC平分∠DAB．∠D：∠DAB＝2：1，则∠ACD的度数是．【答案】30°【习题7】如图，已知：AB∥DE，∠ABC＝80°，∠CDE＝140°，则∠BCD＝．【答案】40°【习题8】已知：∠1＝60°，另一个角∠2的两边与∠1的两边互相平行，且∠2是钝角，则∠2＝．【答案】120°【习题9】如图，因修筑公路需要在某处开凿一条隧道AB，为了加快进度，决定在A、B两处同时开工．如果在A地测得隧道方向为北偏东62°，那么在B地应按方向施工，就能保证隧道准确接通．【答案】南偏西62°【习题10】下列四个图中，么l和/2是对顶角的图的个数是( )A．0个B．1个C．2个D．3个【答案】A【习题11】下列说法中错误的是( )A．内错角相等，两直线平行B．两直线平行，同旁内角互补C．同角的补角相等D．相等的角是对顶角【答案】D【习题12】如图，AB⊥BC，BC⊥CD，∠EBC＝∠BCF，则∠ABE与∠FCD的关系是( ) A．是同位角且相等B．不是同位角但相等C．是同位角但不相等D．不是同位角也不相等【答案】B【习题13】如图，由∠1＝∠2，则可得出( )A．AD∥BC B．AB∥CDC．AD∥BC且AB∥CD D．∠3＝∠4【答案】B【习题14】点P为直线l外一点，点A、B、C为l上三点．P A＝5厘米，PB＝6厘米，PC＝6厘米，则点P到直线l的距离是( )厘米A．5B．小于5C．不大于5D．7【答案】C【习题15】如图，OB⊥OD，OC⊥OA，∠BOC=32°，那么∠AOD等于( )A．148°B．132°C．128°D．90°【答案】A【习题16】如图，已知∠l＝∠2，∠B＝∠C，说明AB∥CD．理由如下：解：∵∠1＝∠2（已知），又∵∠1＝ ( )，∴∠2＝ ( )，∴∥BF( )∴∠＝∠3 ( )又∵∠B＝∠C(已知)，∴∠B＝（等量代换）．∴AB∥CD( )【答案】∠4；对顶角相等；∠4；等量代换；CE；同位角相等，两直线平行；∠C；两直线平行，同位角相等；∠3；内错角相等，两直线平行【习题17】如图，AB∥CD，AD∥BE．试说明∠ABE＝∠D．【答案】提示：由AB∥CD得∠ABE＝∠BEC，由AD∥BE得∠D＝∠BEC，故∠ABE＝∠D【习题18】如图，MN、EF是两面互相平行的镜面，一束光线AB照射到镜面MN上，反射光线为BC，则∠1＝∠(1)作出光线BC经镜面EF反射后的反射光线CD；(2)试判断AB与CD的位置关系．【答案】(1)略 (2)AB∥CD【习题19】在△ABC中，CD平分∠ACB，DE∥AC交BC于E，EF∥CD交AB于F．说明：EF平分∠DEB．【答案】提示：先说明∠EDC＝∠ACD，∠DCE＝∠BEF，∠EDC＝∠DEF，再由∠ACD＝∠DCE得∠DEF＝∠BEF，即EF平分∠DEB【习题20】如图，已知AB∥CD，猜想图1、图2、图3中∠B，∠BED，∠D之间有什么关系？(1)请用等式表示出它们的关系；(2)说明其中的一个等式．①；②；③．【答案】(1) ①∠BED＝∠B+∠D②∠B＝∠BED+∠D⑧∠D＝∠BED+∠B (2)略。
七年级数学培优提高讲义：相交线与平行线(一)
七年级数学：相交线与平行线 一、知识要点： 1•平面上两条不重合的直线，位置关系只有两种：相交和平行。 2•两条不同的直线，若它们只有一个公共点，就说它们相交。即，两条直线相交有且只有一 个交点。 3•垂直是相交的特殊情况。有关两直线垂直，有两个重要的结论： （1） 过一点有且只有一条直线与已知直线垂直； （2） 直线外一点与直线上所有点的连线中，垂线段最短。
4 •两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角 分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做 ___________ ;⑵如果两个角都在两直线之间， 并且分别在第三条直线的两侧， 具有这种关 系的一对角叫做 :⑶如果两个角都在两直线之间，但它们在第三条直线的同 一旁，具有这种关系的一对角叫做 __________________ • 5.平行公理：经过直线外一点，有且只有一条直线与这条直线 _______ . 推论：如果两条直线都与第三条直线平行，那么 __________________________ . 6•平行线的判定：⑴两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行 简单说成： _________________________ •⑵两条直线被第三条直线所截，如果内错角相等，那 么这两条直线平行.简单说成： _______________________________ •⑶两条直线被第三条直线所 截，如果同旁内角互补，那么这两条直线平行 •简单说成： ________________________ • 7.在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线 ______ • &平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等 .简单说成： __________ ___________ .⑵两条平行直线被第三条直线所截，内错角相等 .简单说成： ___________ .⑶两条平行直线被第三条直线所截，同旁内角互补 .简单说成： ___________________ 。• 方法指导：平行线中要理解平行公理， 能熟练地找出“三线八角”图形中的同位角、内错角、 同旁内角，并会运用与“三线八角” 有关的平行线的判定定理和性质定理， 利用平行公理及 其推论证明或求解。例1.如图 ⑴，直线a与b平行，/ 1 = （3x+70） 求/ 3的度数。 ,/ 2=(5x+22)
(完整版)相交线与平行线讲义OK
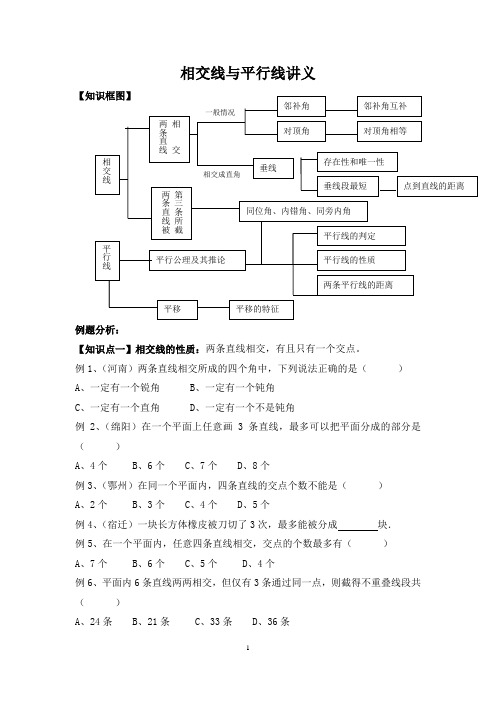
相交线与平行线讲义例题分析：【知识点一】相交线的性质：两条直线相交，有且只有一个交点。
例1、（河南）两条直线相交所成的四个角中，下列说法正确的是（）A、一定有一个锐角 B、一定有一个钝角C、一定有一个直角D、一定有一个不是钝角例2、（绵阳）在一个平面上任意画3条直线，最多可以把平面分成的部分是（）A、4个B、6个C、7个D、8个例3、（鄂州）在同一个平面内，四条直线的交点个数不能是（）A、2个B、3个C、4个D、5个例4、（宿迁）一块长方体橡皮被刀切了3次，最多能被分成块．例5、在一个平面内，任意四条直线相交，交点的个数最多有（）A、7个B、6个C、5个D、4个例6、平面内6条直线两两相交，但仅有3条通过同一点，则截得不重叠线段共（）A、24条B、21条C、33条D、36条例7、如右图，两条非平行的直线AB ，CD 被第三条直线EF 所截，交点为PQ ，那么这3条直线将所在平面分成（ ）A 、5个部分B 、6个部分C 、7个部分D 、8个部分【知识点二】对顶角、邻补角： 对顶角定义：两个角有一个公共的顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种关系的两个角互为对顶角。
邻补角定义：两个角有一个公共边，它们的另一条边互为反向延长线，具有这种关系的两个角互为邻补角。
对顶角的性质：对顶角相等。
邻补角的性质：邻补角互补。
例1、（漳州）如右图，直线b a 、相交于点o ，若∠1等于40°，则∠2等于（ ）A 、50°B 、60°C 、140°D 、160°例2、（辽宁）如图，已知直线AB ，CD 相交于点O ，OA 平分∠EOC ，∠EOC=100°， 则∠BOD 的度数是（ ）A 、20°B 、40°C 、50°D 、80°例3、（湘西州）如图，直线AB ，CD 相交于O 点，若∠1=30°，则∠2，∠3的度数分别为（ ）A 、120°，60°B 、130°，50°C 、140°，40°D 、150°，30° 例4、如右图，图中有 对对顶角．例5、（1）延长射线OM ；（2）平角是一条射线；（3）线段、射线都是直线的一部分；（4）锐角一定小于它的余角；（5）大于直角的角是钝角；（6）一个锐角的补角与这个锐角的余角的差是90°；（7）相等的两个角是对顶角；（8）若∠A+∠B+∠C=180°，则这三个角互补；（9）互为邻补角的两个角的平分线互相垂直．以上说法正确的有（ ）例7例1例2 例3例4A 、2个B 、3个C 、4个D 、5个例6、命题①邻补角互补；②对顶角相等；③同旁内角互补；④两点之间线段最短；⑤直线都相等；⑥任何数都有倒数；⑦如果22b a =，那么b a =；⑧如果∠A+∠B=90°，那么∠A 与∠B 互余．其中真命题有（ ）A 、3个B 、4个C 、5个D 、6个【知识点三】垂线：垂线的定义：当两条直线相交所成的四个角中有一个角为90°时，这两条直线互相垂直，其中一条直线叫做另一条直线的垂线。
七年级数学培优提高讲义：相交线与平行线(一)
七年级数学：相交线与平行线ﻩ一、知识要点：1.平面上两条不重合的直线，位置关系只有两种:相交和平行。
2.两条不同的直线,若它们只有一个公共点,就说它们相交。
即，两条直线相交有且只有一个交点。
３.垂直是相交的特殊情况。
有关两直线垂直,有两个重要的结论:（1)过一点有且只有一条直线与已知直线垂直;（2)直线外一点与直线上所有点的连线中，垂线段最短。
4.两条直线被第三条直线所截,构成八个角，在那些没有公共顶点的角中，⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧,具有这种关系的一对角叫做＿＿＿________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧，具有这种关系的一对角叫做＿_______＿_＿_ ;⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_＿__＿_____＿____.5.平行公理:经过直线外一点,有且只有一条直线与这条直线______.推论：如果两条直线都与第三条直线平行,那么＿＿____＿＿__＿＿_＿_______.6.平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等，那么这两条直线平行.简单说成：__＿_＿_＿_＿＿_____＿__＿____．⑵两条直线被第三条直线所截,如果内错角相等，那么这两条直线平行.简单说成:___＿___＿_____＿__＿_＿__＿＿____．⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:_________＿_______＿_＿＿__.７.在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线_______ .８．平行线的性质:⑴两条平行直线被第三条直线所截,同位角相等．简单说成: ＿＿_＿＿＿＿_＿＿.⑵两条平行直线被第三条直线所截，内错角相等．简单说成:__＿_＿___＿_.⑶两条平行直线被第三条直线所截，同旁内角互补．简单说成:＿__＿__＿__________＿。
七年级数学培优提高讲义：相交线与平行线
七年级数学：相交线与平行线一、知识要点：1 .平面上两条不重合的直线,位置关系只有两种：相交和平行.2 .两条不同的直线,假设它们只有一个公共点,就说它们相交.即,两条直线相交有且只有一个交点.3 .垂直是相交的特殊情况.有关两直线垂直,有两个重要的结论：〔1〕过一点有且只有一条直线与直线垂直；〔2〕直线外一点与直线上所有点的连线中,垂线段最短.4 .两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做；⑵如果两个角都在两直线之间, 并且分别在第三条直线的两侧, 具有这种关系的一对角叫做；⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做 .5 .平行公理：经过直线外一点,有且只有一条直线与这条直线 .推论：如果两条直线都与第三条直线平行,那么 .6 .平行线的判定：⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行简单说成：.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成：.⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成： .7 .在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线 .8 .平行线的性质：⑴两条平行直线被第三条直线所截,同位角相等.简单说成：.⑵两条平行直线被第三条直线所截,内错角相等.简单说成：.⑶两条平行直线被第三条直线所截,同旁内角互补.简单说成： ..方法指导：平行线中要理解平行公理, 能熟练地找出“三线八角〞图形中的同位角、内错角、同旁内角,并会运用与“三线八角〞有关的平行线的判定定理和性质定理, 利用平行公理及其推论证实或求解.、例题精讲例 1.如图(1),直线a与b 平行,/ 1 = (3x+70)° , /2=(5x+22)求/ 3的度数.解：: all b,/3=/4 〔两直线平行,内错角相等〕Z1 + Z3=Z2+Z4=180°〔平角的定义〕Z1 = Z 2 〔等式性质〕那么3x+70 = 5x+22 解得x=24即/ 1= 14273= 180° -/1 = 38°图〔1〕评注：建立角度之间的关系,即建立方程〔组〕,是几何计算常用的方法.例 2.：如图〔2〕, AB // EF// CD, EG 平分/ BEF, / B+ /B-/D=24° ,求/ GEF 的度数.解：••• AB // EF // CD,/B=/BEF, /DEF=/D 〔两直线平行,内错角相等〕/ B+/ BED+ / D =192° 〔〕 即/ B+ / BEF+ / DEF+ Z D=192 ° .•-2 〔/B+/D 〕 =192° 〔等量代换〕 那么/ B+/D=96° 〔等式性质〕8- Z D=24 ° 〔〕,/B=60° 〔等式性质〕即/BEF=60° 〔等量代换〕 EG 平分/ BEF 〔〕/ GEF= 1 / BEF=30 ° 〔角平分线定义〕2例 3.如图〔3〕, AB II CD,且/ B=40° , / D=70 ° ,求/ DEB 的度数. 解：过E 作EF // AB ••• AB // CD 〔〕EF// CD 〔平行公理〕 / BEF= / B=40°/ DEF= / D=70 ° 〔两直线平行,内错角相等〕/ DEB= / DEF- / BEF / DEB = / D- / B=30°评注：证实或解有关直线平行的问题时,如果不构成“三线八角 图〔3〕例4.锐角三角形 ABC 的三边长为a, b, c, 求证：h a +h b +h cV a+b+c分析：对应边上的高看作垂线段,而邻边看作斜线段 证实：由垂线段最短知,h a< c , h b 〈a, h c< b 以上三式相加得 h a +h b +h cv a+b+c研究垂直关系应掌握好垂线的性质. 1 .以过一点有且只有一条直线垂直于直线. 2 .垂线段最短.例5.如图〔4〕,直线 AB 与CD 相交于 O, EF AB 于F, GH CD 于H, 求证EF 与GH 必相交. 分析：欲证EF 与GH 相交,直接证很困难,可考虑用反证 法. 证实：假设EF 与GH 不相交. ••• EF 、GH 是两条不同的直线图〔2〕/ BED+ / D =192,那么应添出辅助而h a, h b, h c 分别为对应边上的高线长,AE GHFDCOBEF//GH EF AB GH AB 又因GH CD 故AB //CD (垂直于同一直线的两直线平行)图(4) 这与AB和CD相交矛盾.所以EF与GH不平行,即EF与GH必相交评注：此题应用结论：(1)垂直于同一条直线的两直线平行.(2)两条平行线中的一条直线垂直于第三条直线,那么另一条直线也平行于第三条直线；例6.平面上n条直线两两相交且无3条或3条以上直线共点,有多少个不同交点？解：2条直线产生1个交点,第3条直线与前面2条均相交,增加2个交点,这时平面上3条直线共有1+2=3个交点；第4条直线与前面3条均相交,增加3个交点,这时平面上4条直线共有1+2+3=6个交点；那么n条直线共有交点个数：1+2+3+…+ (n-1)= 1n(n-1)2评注：此题是平面上n条直线交点个数最多的情形,需要仔细观察,由简及繁,深入思考,从中发现规律.例7. 6个不同的点,其中只有3点在同一条直线上,2点确定一条直线,问能确定多少条直线？解：6条不同的直线最多确定：5+4+3+2+1=15条直线,除去共线的3点中重合多算的2条直线,即能确定的直线为15-2=13条.另法：3点所在的直线外的3点间最多能确定3条直线,这3点与直线上的3点最多有3X 3=9条直线,加上3点所在的直线共有：3+9+1=13条评注：一般地,平面上n个点最多可确定直线的条数为：1+2+3+ •••+(n-1)= — n(n-1)2例8. 10条直线两两相交,最多将平面分成多少块不同的区域?3条直线中的第3条直线与另两条直线相交,最多有两个交点,此直线被这两点分成3段, 每一段将它所在的区域一分为二,那么区域增加3个,即最多分成2+2+3=7个不同区域；同理：4条直线最多分成2+2+3+4=11个不同区域；10条直线最多分成2+2+3+4+5+6+7+8+9+10=56 个不同区域推广：n条直线两两相交,最多将平面分成2+2+3+4+…+n=1+°n(n+1)= ° (n2+n+2)块不同2 2的区域思考：平面内n 个圆两两相交,最多将平面分成多少块不同的区域?例9.平面上n 条直线两两相交,求证所成得的角中至少有一个角不大于 证实：平面上n 条直线两两相交最多得对顶角n(n° X2=n(n-1)对,即2n(n-1)个角2平面上任取一点 O,将这n 条直线均平行移动过点 O, 成为交于一点O 的n 条直线,这n 条直线将以O 为顶点的圆周角分为 2n 个(共n 对) 互不重叠的角：1、 2、 3、 (2)由平行线的性质知,这 2n 个角中每一个都和原来 n 条 直线中的某两条直线的交角中的一个角相等,即这 2n 个角 均是原2n(n-1)个角中的角.18001+ 2+ 3+ -+ 2n >2nX =360评注：通过平移,可以把原来分散的直线集中交于同一点,从而解决问题.例10. (a)请你在平面上画出 6条直线(没有三条共点),使得它们中的每条直线都恰与另3条直线相交,并简单说明画法.(b)能否在平面上画出 7条直线(任意3条都不共点),使得它们中的每条直线都恰与另3条直线相交,如果能请画出一例,如果不能请简述理由.解：(a)在平面上任取一点 Ao过A 作两直线 m 1与n 1.在n 1上取两点B, C,在 m1上取两点 D, G .过B 作m2 // m1,过C 作m3 // m1,过 D 作 n 2 // n 1,过 G 作 n 3 // m,这时 m 2、m 3、n 2、n 3 交得 E 、 F 、H 、I 四点,如下图.由于彼此平行的直线不相交, 所以,图中每条直线都恰与另 3条直线相交.(b)在平面上不能画出没有 3线共点的7条直线,使得 其中每条直线都恰与另外 3条直线相交.理由如下：假设平面上可以画出 7条直线,其中每一条都恰与其它 个交点,又没有3条直线共点,所以每条直线上恰有与另3条直线交得的3个不同的交点.根据直线去计数这些交点,共有3X7=21个交点,但每个交点分属两条直线,被重复180 n假设这2n 个角均大于世,那么n1+ 2+ 3+--- + 2n =360,产生矛盾1、 2、 3、2n 中至少有一■个小于180°n即原来的2n(n-1)中至少有一个角不小于18003条相交,因两直线相交只有计数一次,所以这 7条直线交点总数为 21=10.5个,由于交点个数应为整数,矛盾.三、稳固练习1 .平面上有5个点,其中仅有3点在同一直线上,过每 2点作一条直线,一共可以作直线 ()条A. 6B. 7C. 8 D . 92 .平面上三条直线相互间的交点个数是()A. 3B.1 或3C. 1 或 2或 3D.不一定是 1, 2, 33 .平面上6条直线两两相交,其中仅有 3条直线过一点,那么截得不重叠线段共有( )A. 36 条B. 33 条C. 24 条 D . 21 条4 .平面中有n 个点A, B,C 三个点在一条直线上, A,D, F, E 四个点也在一条直线上,除些之外,再没有三点共线或四点共线,以这 n 个点作一条直线,那么一共可以画出38条不同的直线,这时 n 等于() (A) 9(B) 10(C) 11(D) 125 .假设平行直线AB 、CD 与相交直线EF 、GH 相交成如图示的图形, A. 4 对 B. 8 对 C. 12 对 D. 16对6 .如图, FD//BE,贝U/ 1 + /2-/3=( )A. 90° B, 135°C. 150° D, 180°27条直线是画不出来的.所以,满足题设条件的 那么共得同旁内角()7 .如图, AB //CD, / 1 = 72,那么/ E 与/ F 的大小关系 8 .平面上有5个点,每两点都连一条直线,问除了原有的 5点之外这些直线最多还有 交点9 .平面上3条直线最多可分平面为 个局部.10 .如图, AB // CD // EF, PS GH 于 P, / FRG=110 那么/ PSQ=.11 .A 、B 是直线L 外的两点,那么线段 AB 的垂直平分 线与直线的交点个数是.12 .平面内有4条直线,无论其关系如何,它们的交点个数不会超过 个. 13 .：如图, DE//CB ,求证：/ AED=/A+/B14,：如图, AB//CD,求证：/ B+/D+/F=/E+/G5.直线EF 、GH 分别“截〞平行直线 AB 、CD,各得2对同旁内角,共4对；直线AB 、 CD 分别“截〞相交直线 EF 、GH,各得6对同旁内角,共12对.因此图中共有同旁内角 4+6= 16 对第13题15 .如图, CB AB , CE 平分/ BCD , DE 平分/ CDA , /EDC+/ECD=90 ° , 求证：DA AB16 .平面上两个圆三条直线,最多有多少不同的交点？17 .平面上5个圆两两相交,最多有多少个不同的交点？最多将平面 分成多少块区域？18 . 一直线上 少条不同直线? 19 .平面上有20 .平面上有 到？画出图形.5点与直线外3点,每两点确定一条直线, 最多确定多 8条直线两两相交,试证实在所有的交角中至少有一个角小于10条直线,无任何三条交于一点,欲使它们出现 答案31个交点, 23 .怎样安排才能办1 . 5个点中任取2点,可以作4+3+2+1 = 10条直线,在一直线上的 3个点中任取2点,可作2+1 =3条,共可作10-3+1 =8 〔条〕应选 C 2 .平面上3条直线可能平行或重合.应选 D 3 .对于3条共点的直线, 条不重叠的线段 对于3条不共点的直线, 每条直线上有4个交点,截彳#3条不重叠的线段,3条直线共有9 每条直线上有5个交点,截彳#4条不重叠的线段,3条直线共有12条不重叠的线段.故共有21条不重叠的线段.应选 D 4 .由n 个点中每次选取两个点连直线,可以画出n 〔n 0条直线,假设ABC 三点不在一条2''直线上,可以画出3条直线,假设 A, D,E,F 四点不在一条直线上,可以画出6条直线,n(n 1) 3 26 2 38.整理得 n 2 n 90 0,(n 10)(n 90) 0. ••• n+9 >0 n10, •二选 B o6. ••• FD // BE2=/AGF・. / AGC= / 1-/3. •/ 1+ Z2-Z3= / AGC+ / AGF=180 °,/BAD=/CDA 〔两直线平行,•・•选B7,解：••• AB //CD内错角相等〕〔〕〔〕BAD+ / 1 = / CDA+ Z2 〔等式性质〕即/ EAD= / FDA••.AE // FD/ E= / F8.解：每两点可确定一条直线, 这5点最多可组成10条直线,又每两条直线只有一个交点,所以共有交点个数为9+8+7+6+5+4+3+2+1 =45 〔个〕又因平面上这5个点与其余4个点均有4条连线,这四条直线共有3+2+1 = 6个交点与平面上这一点重合应去掉,共应去掉应为45-30= 15个9,可分7个局部10.解•「AB II CD II EF / APQ= / DQG= / FRG=110 °同理/ PSQ=/APS・•. / PSQ=/ APQ- / SPQ= / DQG- / SPQ5X 6=30个交点,所以有交点的个数=110° -90° =20°11. 0个、1个或无数个1〕假设线段AB的垂直平分线就是L,那么公共点的个数应是无数个；2〕假设AB L,但L不是AB的垂直平分线,那么此时AB的垂直平分线与L是平行的关系,所以它们没有公共点,即公共点个数为0个；3〕假设AB与L不垂直,那么AB的垂直平分线与直线L 一定相交,所以此时公共点的个数为1个12 . 4条直线两两相交最多有1+2+3 = 6个交点13 .证实：过E作EF // BA/ 2=Z A 〔两直线平行,内错角相等〕DE // CB ,EF // BA.•./ 1 = /B 〔两个角的两边分别平行,这两个角相等〕1+/2=/B+/ A 〔等式性质〕即/ AED= ZA+ZB14 .证实：分别过点E、F、G作AB的平行线EH、PF、贝UAB // EH // PF // GQ 〔平行公理〕・ . AB // EHGQ,/ABE=/BEH 〔两直线平行,内错角相等〕同理：/ HEF = Z EFP/ PFG=/ FGQ/ QGD = / GDC/ ABE+ / EFP+ / PFG+ / GDC = / BEH+ / HEF+/FGQ+/QGD 〔等式性质〕即/ B+ / D+ / EFG= / BEF+ / GFD15.证实：••• DE 平分/ CDA CE 平分/ BCD,/ EDC= / ADE /ECD = / BCE 〔角平分线定义〕・・・ / CDA + / BCD= / EDC+ / ADE+ / ECD+ / BCE=2 〔/ EDC+ / ECD〕 = 180° DA // CB又「CB ABDA AB第15题16 .两个圆最多有两个交点,每条直线与两个圆最多有4个交点,三条直线最多有3个不同的交点,即最多交点个数为：2+4X3+3=1717 . (1) 2个圆相交有交点2X1=1个,第3个圆与前两个圆相交最多增加2X2=4个交点,这时共有交点2+2 X 2 = 6个第4个圆与前3个圆相交最多增加2X3=6个交点,这时共有交点2+2x2+2x3= 12个第5个圆与前4个圆相交最多增加2X4=8个交点5个圆两两相交最多交点个数为：2+2 X 2+2X 3+2 X 4=20(2) 2个圆相交将平面分成2个区域3个圆相看作第3个圆与前2个圆相交,最多有2X2 = 4个不同的交点,这4个点将第3个圆分成4段弧,每一段弧将它所在的区域一分为二, 故增加2X2=4块区域,这时平面共有区域：2+2X2= 6块4个圆相看作第4个圆与前3个圆相交,最多有2X3 = 6个不同的交点,这6个点将第4个圆分成6段弧,每一段弧将它所在的区域一分为二, 故增加2X3=6块区域,这时平面共有区域：2+2x2+2x3=12块5个圆相看作第5个圆与前4个圆相交,最多有2X4 = 8个不同的交点,这8个点将第5个圆分成8段弧,每一段弧将它所在的区域一分为二, 故增加2X4=8块区域,这时平面最多共有区域：2+2X 2+2 X 3+2x4=20块18 .二直线上每一点与直线外3点最多确定3X5=15条直线；直线外3点间最多能确定3 条直线,最多能确定15+3+1=19条直线19 .将这8条直线平移到共点后,构成8对互不重叠的^•顶角,这8个角的和为180°假设这8个角没有一个小于23° ,那么这8个角的和至少为：23° X 8=184° ,这是不可能的.因此这8个角中至少有一个小于23.,•••在所有的交角中至少有一个角小于2320.平面上有10条直线,假设两两相交,最多可出现45个交点,题目要求只出现31个交点, 就要减少14个交点,那么必须出现平行线,假设某一方向上有5条直线互相平行,那么可减少10 个交点；假设有6条直线互相平行,那么可减少15个交点；故在这个方向上最多可取5条平行线,这日^还有4个交点需要减去,转一个方向取3条平行线,即可减少3个交点,这时还剩下2条直线和一个需要减去的点,只须让这2条直线在第三个方向上互相平行即可. 如图这三组平行线即为所求.。
七年级数学培优提高讲义相交线与平行线
七年级数学：相交线及平行线一、学问要点：1.平面上两条不重合的直线，位置关系只有两种：相交和平行。
2.两条不同的直线，若它们只有一个公共点，就说它们相交。
即，两条直线相交有且只有一个交点。
3.垂直是相交的特别状况。
有关两直线垂直，有两个重要的结论：（1）过一点有且只有一条直线及已知直线垂直；（2）直线外一点及直线上全部点的连线中，垂线段最短。
4．两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴假如两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ ；⑵假如两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做____________ ；⑶假如两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_______________.5．平行公理：经过直线外一点，有且只有一条直线及这条直线______.推论：假如两条直线都及第三条直线平行，那么_____________________.6．平行线的断定：⑴两条直线被第三条直线所截，假如同位角相等，那么这两条直线平行.简洁说成：_______________________.⑵两条直线被第三条直线所截，假如内错角相等，那么这两条直线平行.简洁说成：___________________________.⑶两条直线被第三条直线所截，假如同旁内角互补，那么这两条直线平行.简洁说成：_______________________. 7．在同一平面内，假如两条直线都垂直于同一条直线，那么这两条直线_______ .8．平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等.简洁说成：＿＿＿＿＿＿＿＿＿＿.⑵两条平行直线被第三条直线所截，内错角相等.简洁说成：__________.⑶两条平行直线被第三条直线所截，同旁内角互补.简洁说成：__________________。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相交线与平行线
一、知识框架
二、典型例题
1. 下列说法正确的有（B ）
①对顶角相等；②相等的角是对顶角；③若两个角不相等，则这两个角一定不是对顶角
2. 如图所示,下列说法不正确的是（D
3. 下列说法正确的有（C ）
①在平面内，过直线上一点有且只有一条直线垂直于已知直线
④若两个角不是对顶角，则这两个角不相等
.
A.1 个 B.2 个 C.3 个 D.4 个 A.点B到AC的垂线段是线段 AB; B. 点C到AB的垂线段是线段 AC C.线段AD是点D到BC的垂线段；D. 线段BD是点B到AD的垂线段 D
13交于0点，图中出现了几对对顶角，若 n
条直线相交呢?
答案：3对，
n（n +1）
9.
如图，在4 4的正方形网格中， 1, 2, 3的大小关系是
②在平面内，过直线外一点有且只有一条直线垂直于已知直线
③在平面内，过一点可以任意画一条直线垂直于已知直线
④在平面内，有且只有一条直线垂直于已知直线
A.1 个 B.2 个 C.3 个 D.4
个
4
•一学员驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同,
这两次拐弯的角度可能是（ A ）
A.第一次向左拐30°第二次向右拐30° B. 第一次向右拐 50 C.第一次向右拐50°第二次向右拐130 ° D. 第一次向左拐 50 第二次向左拐 5 .如图，若 AC丄BC于C, CEU AB于D,则下列结论必定成立 的是（ A. CD>AD B.ACvBC C. BC>BD D. CD
B
1
(1)
(1)
分析:
过点P作
P E//AB
/ APE+ / A+ / C=360 °
P=/A+ / C
P=/ C-/ A,
P=/A- / C
12.如图，若 AB//EF , / C= 90 ，求 分析：如图，添加辅助线 A *C x+y-z
度数。
M
如图所示丄1丄2丄3交于点0,/仁/2, / 3: / 1=8:1,求/ 4的度数.（方程思想
） I 1 如图所示,已知AB// CD,分别探索下列四个图形中/ P与/ A, / C的关系,?请你从所 得的四个关系中任选一个加以说明 证出：x+y-z=90答案: / 仁/2>/ 3 10.
答案：36°
l
2
1
B
.5
求证：
E
所以
EAP= APF
所以
AE//FP
所以
E F
13
.已知：如图,
BAP APD
分析：法
N
法二：由 AB//CD 证明 PAB= APC,