北京大学数学科学学院双学位课程介绍-(4)
高等代数——课程介绍

《高等代数》是北京大学数学科学学院(由数学、概率统计、科学与工程计算、信息科学、金融数学五个系组成)本科一年级的三门最重要的基础课之一,为期一学年,教学时间30周,复习、考试4周,总共10学分(每学期5学分)。
每年学生约260人(包括本院学生、元培班学生和重修的学生),分成两个大班,由两个主讲教师依照同样的教学计划(包括进度、内容、习题和作业的的安排)同步授课(每周4学时),同时配备有四位助教上习题课(每周2学时)和批改作业。
主讲教师负责安排习题课内容以及指导助教的工作。
每学期期中、期末考试各一次,采用统一的考题和统一的评分标准。
考试分数为百分制。
期末总成绩为期中成绩的40%加上期末成绩的60%再减去学生未交作业的次数。
课程目前采用的教材是蓝以中编著的《高等代数简明教程》(上、下册)(北京大学出版社2002年出版,北京大学数学教学系列丛书,该书为普通高等教育“十五”国家级规划教材及2002年北京市教育精品教材重点项目)。
主要教学参考书是北大几何与代数教研室代数小组编《高等代数》(高等教育出版社,1991年,第二版,曾获国家优秀教材一等奖);丘维声编著的《高等代数》(上、下册)(高等教育出版社1996年出版,国家“九五”重点教材)。
本课程的内容包括:线性方程组,矩阵,行列式,双线性型与二次型,线性空间,线性变换,具有度量的线性空间(欧氏空间、酉空间、四维时空空间、辛空间),Jordan标准形,有理整数环,一元和多元多项式环,多线性代数(张量积、张量、外代数)的初步理论等。
本课程不仅注重讲授代数学的基本知识,更强调对于学生的“三个基本训练”和“一个初步训练”,即、代数学基本思想的训练、代数学基本方法的训练、线性代数基本计算的训练以及综合运用分析、几何、代数方法处理问题的初步训练。
北大双学位12-13(1)课程表
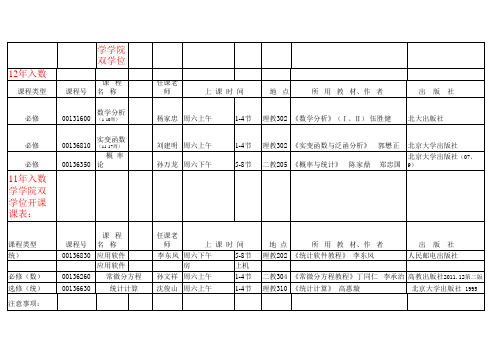
课程类型 必修 必修 必修 上 课 时 间 课程号 课 程 名 称 任课老师 00131600 数学分析(1-10周) 杨家忠 周六上午 1-4节 00136810 实变函数(11-17周) 刘建明 周六上午 1-4节 00136350 概 率 论 孙万龙 周六下午 5-8节 地 点 所 用 教 材、作 者 出 版 社 理教302 《数学分析》(Ⅰ、Ⅱ) 伍胜健 北大出版社 理教302 《实变函数与泛函分析》 郭懋正 北京大学出版社 二教205 《概率与统计》 陈家鼎 郑忠国 北京大学出版社(07、9) 出 版 社 人民邮电出版社
二教304 《常微分方程教程》丁同仁 李承治 高教出版社2011.12第二版 北京大学出版社 1995
9)
11年入数学学院双学位开课课表:
课程类型 课程号 必修(数、统) 00136830 必修(数) 选修(统) 注意事项: 1,12、11年入学的同学网上自动生成选课名单,本学期预计退课者,必须于学期开学后前两周内到教务办登记;未登记者,视为选课。 2,凡以前退过课本学期需要重新选课、缓考、重修者需在学期开学后前两周内到教务办登记。 3,2012年9月15日开始上课,2013年1月5日最后一次课考试。 4,教务联系电话:62763111 2012.4.25 00136260 00136630 上 课 时 间 课 程 名 称 任课老师 地 点 所 用 教 材、作 者 数学应用软件 李东风 周六下午 5-8节 理教202 《统计软件教程》 李东风 数学应用软件 周六4、5号机房 11-12节上机 常微分方程 统计计算 孙文祥 周六上午 沈俊山 周六上午 1-4节 1-4节 理教310 《统计计算》 高惠璇
数学学院双学位教学计划及管理细则-北京大学数学科学学院

北京大学数学科学学院数学与应用数学专业双学位/辅修一,报名1,报名条件:(1)拥护中国共产党的领导,品德良好,遵纪守法。
(2)没有不及格课程且已修课程的GPA在2.0以上。
(3)每人只能选修一个辅修或双学位专业。
2,报名办法:(1)时间: 5月(2)地点:数学科学学院教学科研办公室(理科一号楼1295E室)(3)报名程序:凡申请报名的同学需先登陆北京大学校内信息门户网上提交并打印报名表,同时附已修课程成绩单并加盖院系教务章,一并交到数学科学学院教务办。
二,录取1,本双学位专业计划录取100人。
2,录取办法:根据申请人已修相关课程成绩和总GPA择优录取,数学成绩优秀者优先考虑。
3,初步录取名单,将于5月底在数学科学学院网页双学位一栏(/)公布;最终录取结果请查看“北京大学学生综合信息管理系统”。
三,学分和收费:1,修读双学位的学生应完成44学分;2,修读辅修的学生应完成35学分;3,双学位按学分收费,每学分150元。
若中途退课,所交学费一律不退。
每学期开学后前两周办理退双手续,请先登录校内门户提交申请,申请表签字后到数院教务办公室办理。
四,课程设置及学分:双学位课程:43学分补充说明:若学生在主修专业已经修读本双学位教学计划中某门课程或内容相近课程,则不可重复修读,应选修以下课程替代,重复修读成绩无效。
一门课程如在主修专业和本双学位教学计划中均有要求,只能计算一次学分。
辅修课程:35学分补充说明:若学生在主修专业已经修读本辅修专业教学计划中某门课程或内容相近课程,则不可重复修读,应选修以下课程替代,重复修读成绩无效。
一门课程如在主修专业和本双学位教学计划中均有要求,只能计算一次学分。
说明:双学位与数院本科生一起选课、上课、考试,同质化管理,每学期课表可到数院主页双学位一栏查看。
缓考课程再次选课不需要缴费,不及格课程重修需要在学期开学后第二周内到教务办公室办理缴费手续。
五,毕业及学位授予资格审定1,同时符合以下条件者,将根据北京大学的有关规定授予北京大学数学与应用数学专业(双学位)理学学士证书:(1)完成主修专业学习,正常毕业并获得主修专业学士学位;(2)在主修专业学业结束时修完双学位教学计划规定的课程及学分,成绩合格;(3)在大四第二学期开学五周内提出证书资格申请。
北京大学数学系课程表

1-16
3-4
7-8单周
20111228
00131420
数据结构 Data Structures
1
全校必修
3.0
51.0
3.0
孙猛
本科(公费)
180
1-16
1-2单周
3-4
20120106
00131420
数据结构 Data Structures
2
全校必修
3.0
51.0
3.0
牟克典
本科(公费)
90
1
专业必修
5.0
102.0
6.0
伍胜健
本科(公费)
132
1-16
3-4
1-2
20111230
00132301
数学分析(I) Mathematical Analysis (I)
2
专业必修
5.0
102.0
6.0
张 宁
本科(公费)
130
1-16
3-4
1-2
20111230
00132304
数学分析 (III) Mathematical Analysis (III)
任选
3.0
54.0
3.0
夏壁灿
本科(公费)
20
1-16
7-9
00113840
临床试验设计与分析 Clinical trial design and analysis
1
任选
3.0
51.0
3.0
本科(公费)
20
1-16
10-12
00113850
临床试验SAS高级编程 SAS Programming in Clinical Trials
北京大学数学科学学院双学位课程介绍---

北京大学数学科学学院*双学位课程介绍*---------------课程编号:00131600 课程名称:数学分析课程类型:数、统/必修课每周3学时,3学分先修要求:高等数学(两学期)基本目的:1.实数与极限的理论、函数的可积性、函数列与函数级数一致收敛性的基本知识。
2.培养学生的抽象思维和推理能力,加深学生对微积分的理论基础的了解,为进一步学习后续数学课程作必要的理论准备。
内容提要:一. 实数与极限的理论1.实数理论初步。
2.确界存在定理,区间套定理,聚点。
3.紧性定理(序列紧,有限覆盖,一致连续)。
4.完备性(哥西基本列,实数的另一种定义)。
5.上极限与下极限。
二.连续函数1. 连续函数的基本性质2. 闭区间上连续函数的性质3.一致连续。
三. 函数的可积性1.达布和,上积分与下积分。
2.函数可积分的充要条件。
四. 函数列与函数级数的一致收敛性北京大学数学科学学院*双学位课程介绍*---------------1.一致收敛性及其判别法。
2.一致收敛函数列极限函数的性质。
教学方式:课堂讲授教材或参考书:1.教材:«数学分析»(双学位)讲义伍胜健2.参考书:«数学分析简明教程»邓东皋等高等教育出版社课程编号:00136810课程名称:实变函数课程类型:数、统/必修课每周2学时,2学分先修要求:高等数学,线性代数基本目的:1.熟悉欧氏空间中Lebesgue 测度,Lebesgue 积分的基本理论。
2.掌握L2(R n)空间理论。
3.熟悉Hilbert空间,Banach空间的基本理论。
内容提要:1.Lebesgue测度与Lebesgue 积分:Lebesgue 可测集,可测函数,Lebesgue 积分,Lebesgue积分的极限定理。
2.L2(R n)空间:L2空间的基本理论教学方式:课堂讲授教材:《实变函数与泛函分析》郭懋正北京大学出版学生成绩评定:平时作业15分,期中考试25分,期末考试60分。
北京大学第二学士学位

北京大学第二学士学位1. 北京大学第二学士学位的概况北京大学第二学士学位是一种非常特殊的学位,它是由北京大学为了满足特殊社会需求而推出的一种学位。
它的申请者必须具备一定的学历和经验,并通过北京大学的审核才能获得。
申请者必须提交个人简历、学习成绩单、学术论文等材料,并参加学术论文答辩,最终通过学术评审才能获得第二学士学位。
获得第二学士学位的人可以在政府机构、企业和科研院所中担任技术性职位,也可以在教育机构担任教学职位。
2. 北京大学第二学士学位的申请要求申请北京大学第二学士学位需要满足以下要求:1. 具有本科学历,且已获得本科学位;2. 年龄不超过35周岁;3. 具有较强的英语水平,可以提供有效的英语成绩证明;4. 具有较强的学术能力和科研能力,可以提供有效的学术成果和科研成果;5. 具有良好的学习习惯和职业操守;6. 具有良好的个人背景和社会责任感;7. 具有良好的健康状况;8. 具有较强的职业发展潜力。
3. 北京大学第二学士学位的申请流程申请者需要提供有效的身份证明文件、本科学历证书及成绩单,以及两封推荐信,并填写《北京大学第二学士学位申请表》。
申请者还需要提交本科毕业论文或研究论文,以及其他有关材料。
提交申请材料后,申请者需要参加学科专业考试,考试内容包括专业基础理论知识、专业技术知识及相关能力。
考试成绩达到规定标准后,申请者需要参加面试,面试内容包括学术能力、综合素质及学习计划等。
通过学科考试和面试后,申请者需要提交《北京大学第二学士学位申请审核表》,并缴纳相关费用。
审核通过后,申请者需要参加学位获得宣誓仪式,宣誓仪式结束后,申请者可以获得北京大学第二学士学位证书。
4. 北京大学第二学士学位的考试内容北京大学第二学士学位考试的内容主要包括学科考试、英语考试和综合考试三部分。
学科考试是第二学士学位考试的主要内容,考生需要根据自己的专业准备考试,考试内容包括理论知识和实践技能。
英语考试是考试的必备科目,考生需要掌握语法、词汇和翻译等基础知识,并能够进行英语书面表达。
双学位课程

理论与实践结合
双学位课程注重理论与实践相结合,通过实践课 程和项目,培养学生的实际操作能力和问题解决 能力。
培养目标
01
培养复合型人才
双学位课程旨在培养具有跨学科 知识和技能的复合型人才,以适 应社会发展的多元化需求。
双学位课程毕业生具备两个专业的知识和技能,能够更好地适应 复杂的工作环境。
综合素质
双学位课程注重培养学生的综合素质,包括沟通能力、团队合作 、领导力等,使毕业生在职场上更具竞争力。
适应能力
双学位课程毕业生能够更快地适应新环境和新工作,具备更强的 适应能力。
05
双学位课程注意事项
学习压力
课程数量增加
考虑奖学金和助学金
学生可以了解学校关于双学位课程的奖学金和助学金政策,以减轻经济负担。
感谢观看
THANKS
提交申请
按照学校规定的截止日期前提 交申请材料,并缴纳申请费用 。
接受录取通知
如果申请成功,学校会发出录 取通知书,申请者需要按照通 知书要求进行注册和缴费。
03
双学位课程学习内容
课程设置
1 2 3
跨学科课程
双学位课程通常包括来自两个不同学科的课程, 旨在培养学生掌握两个领域的综合知识和技能。
必修与选修
双学位课程
汇报人:可编辑 2024-01-06
目 录
• 双学位课程介绍 • 双学位课程申请流程 • 双学位课程学习内容 • 双学位课程与就业前景 • 双学位课程注意事项
01
双学位课程介绍
双学位的定义
定义
双学位课程是指学生在攻读本专 业的同时,兼修另外一个专业, 通过规定的课程和学分要求后, 同时获得两个学位的课程项目。
北京大学数学系课程设置

北京⼤学数学系课程设置本科⽣1)公共与基础课程:44-50学分⼤学英语系列课程(2-8学分),政治系列课程、军事理论以及军训等课程(18学分)、计算机系列课程(6学分),体育系列课程(4学分),数学分析(14学分)2)核⼼课程:29学分⾼等代数Ⅰ(5学分),⾼等代数Ⅱ(4学分),⼏何学(5学分),抽象代数(3学分),复变函数(3学分),常微分⽅程(3学分),数学模型(3学分),概率论(3分)3)数学系限选课程32学分a) 21学分选⾃下⾯9门课: 数论基础(3学分),群与表⽰(3学分),基础代数⼏何(3学分),拓扑学(3学分),微分⼏何(3学分),微分流形(3学分),实变函数(3学分),泛函分析(3学分),偏微分⽅程(3学分)。
b) 理学部的⾮数学学院课程8学分(其中4学分物理).c) 毕业论⽂3学分4) 数学系通识与⾃主选修课程:27学分A.理学部课程:12学分,可以选⾃理学部中的任何院系,包括数学学院。
B. 通选课:12学分,其中社会科学类⾄少2学分;哲学与⼼理学类⾄少2学分;历史学类⾄少2学分;语⾔学、⽂学、艺术与美育类⾄少4学分,其中⼤学国⽂必选,另⼀门是艺术与教育类课程;数学与⾃然科学类和社会可持续发展类⾄少2学分。
C. 在全校课程中选择其余3学分。
研究⽣中级课程分析学与偏微分⽅程中级课程《实分析》(包含初步的⼏何测度论知识)+《调和分析》:上下学期开设,作为整体⼀年的课程。
《复分析》:与复⼏何课程衔接。
《泛函分析II》。
《⼆阶椭圆型⽅程》+《双曲⽅程》:上下学期轮流开设。
每两年开设⼀次《⾮线性分析基础》;《变分学》:轮流开设,有区分度。
《多复变函数论》。
资格考试课程:分析类:1) 泛函分析II, 2) 调和分析, 3)复分析; 偏微类:4) ⼆阶椭圆型⽅程,5)双曲⽅程另:偏微分⽅程概论(各类偏微分⽅程,拟微分算⼦)列为初级课程,在本科⽣开设。
常微分⽅程与动⼒系统类课程《常微分⽅程定性理论》。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京大学数学科学学院*双学位课程介绍*---------------课程编号:00131600 课程名称:数学分析课程类型:数、统/必修课每周3学时,3学分先修要求:高等数学(两学期)基本目的:1.实数与极限的理论、函数的可积性、函数列与函数级数一致收敛性的基本知识。
2.培养学生的抽象思维和推理能力,加深学生对微积分的理论基础的了解,为进一步学习后续数学课程作必要的理论准备。
内容提要:一. 实数与极限的理论1.实数理论初步。
2.确界存在定理,区间套定理,聚点。
3.紧性定理(序列紧,有限覆盖,一致连续)。
4.完备性(哥西基本列,实数的另一种定义)。
5.上极限与下极限。
二.连续函数1. 连续函数的基本性质2. 闭区间上连续函数的性质3.一致连续。
三. 函数的可积性1.达布和,上积分与下积分。
2.函数可积分的充要条件。
四. 函数列与函数级数的一致收敛性北京大学数学科学学院*双学位课程介绍*---------------1.一致收敛性及其判别法。
2.一致收敛函数列极限函数的性质。
教学方式:课堂讲授教材或参考书:1.教材:«数学分析»(双学位)讲义伍胜健2.参考书:«数学分析简明教程»邓东皋等高等教育出版社课程编号:00136810课程名称:实变函数课程类型:数、统/必修课每周2学时,2学分先修要求:高等数学,线性代数基本目的:1.熟悉欧氏空间中Lebesgue 测度,Lebesgue 积分的基本理论。
2.掌握L2(R n)空间理论。
3.熟悉Hilbert空间,Banach空间的基本理论。
内容提要:1.Lebesgue测度与Lebesgue 积分:Lebesgue 可测集,可测函数,Lebesgue 积分,Lebesgue积分的极限定理。
2.L2(R n)空间:L2空间的基本理论教学方式:课堂讲授教材:《实变函数与泛函分析》郭懋正北京大学出版学生成绩评定:平时作业15分,期中考试25分,期末考试60分。
北京大学数学科学学院*双学位课程介绍*---------------课程编号:00136350 课程名称:概率论课程类型:数、统/必修课每周4+1学时,5学分先修要求:微积分,线性代数(或相当高等数学)基本目的:1. 本课程的目的是引导学生学习用数学的语言,来刻划、表达与抽象随机现象,着重在随机现象的“建模”。
同时,这一课程也使学生对已学过的集合论、微积分、高等代数等数学知识有运用的机会,在提高学生分析问题,解决问题的能力方面是一个很好操练机会。
2. 重点放在随机现象的刻划,形成概率空间的概念。
例如在概率空间这一部份,重在由等可能性分析过到一般的概率空间。
对随机变量,重点也在要学生掌握它的统计特征的刻划方法。
对于古典概型不宜过多陷于排列组合的计算技巧。
内容提要:1. 随机事件及其概率1) 概率的素朴定义。
2) 古典概型。
3) 事件的集合表达,事件运算与集合运算的对应。
4) 概率的加法公式。
5) 概率的公理化定义及概率的主要性质。
6) 条件概率(对正概率事件的条件概率)与全概公式。
7) 独立性。
2.随机变量1) 离散型随机变量及其取值机会的描述。
北京大学数学科学学院*双学位课程介绍*---------------2) 连续型随机变量及其取值机会的描述。
3) 分布函数。
4) 随机变量函数的分布(简单情形)。
5) 随机变量定义的抽象。
3.n维随机变量(向量)1) n维随机向量统计特征的刻划。
2) 联合分布与边缘分布。
3) 独立性。
4) 随机变量函数的分布(多维)。
5) n维正态分布。
6) 条件分布。
7) 次序统计量。
4.随机变量和随机向量的数字特征1) 期望(概率加权平均概念的抽象)。
2) 随机变量函数的期望公式。
3) 方差、协方差与相关系数。
4) 条件期望。
5.概率极限定理1) 大数定律与切比雪夫不等式,强大数律(结果与概念)。
2) 中心极限定理。
6.随机过程1)独立增量过程。
2)马尔可夫链。
北京大学数学科学学院*双学位课程介绍*---------------3)分支过程。
4)平稳过程。
教学方式:课堂教学教材:《概率与统计》陈家鼎郑忠国北京大学出版社(07、8)参考书: 《概率统计讲义》陈家鼎等编高等教育出版社《概率论基础教程》S﹒M﹒Ross著,郑忠国等译人民邮电出版社2007学生成绩评定:期末考试为主,期中考试与平时作业为辅。
课程编号:00131610 课程名称:高等代数课程类型:数、统/必修课每周2学时,2学分先修要求:线性代数基本目的:1.高等代数是学习和研究近代数学的重要基础,在自然科学、社会科学、经济领域都有重要应用。
本课程使学生学习和了解多项式、线性空间和线性变换等基本知识。
2.培养学生具有数学的思维方式、创新精神,以及解决实际问题的初步能力。
内容提要:一.多项式环1.基本概念。
2.整除性,带余除法,最大公因式。
3.不可约多顶式,唯一因式分解定理。
4.重因式。
北京大学数学科学学院*双学位课程介绍*---------------二.线性空间1.基本概念。
2.子空间及其交与和,维数公式。
3.子空间的直和。
4.商空间。
三.线性变换1.基本概念。
2.线性映射的核和象。
3.线性变换可对角化的条件。
4.不变子空间。
教学方式:课堂讲授教材:«高等代数» (上、下册第二版)丘维声高等教育出版社2003年学生成绩评定:作业成绩(20%)期末考试成绩(80%)课程编号:00136820 课程名称:近世代数课程类型:数、统/必修课每周3学时,3学分先修课要求:线性代数基本目的:本课程的目的是引导学生掌握近世代数的基本概念,主要是群、环、域的概念,以及有关群、环、域的基本理论,从而达到对近世代数的语言与理论有所了解的目的,为学习现代数学、物理或其他科学提供基础。
北京大学数学科学学院*双学位课程介绍*---------内容提要:一、引论1.本课程的研究对象2.域、环、群的定义与简单性质二、群1.群的例子2.子群,同构,同态3.群在集合上的作用,定义与例子4.群作用的轨道与不变量5.陪集,Lagrange定理,稳定化子,轨道长6.循环群与交换群7.正规子群和商群8.同态基本定理三、域和环1.域的例子,复数域及二元域的构造2.域的扩张,扩张次数,单扩张的构造3.环的例子,几个基本概念4.整数模n的剩余类环,素数p个元的域5.F[x]模某个理想的剩余类环,添加一个多项式的根的扩域教学方式:课堂讲授教材:《近世代数初步》(第二版)石生明高等教育出版社2006年学生成绩评定:作业成绩(20%)期末考试成绩(80%)北京大学数学科学学院*双学位课程介绍*---------------课程编号:课程名称:统计学课程类型:数、统/必修课每周4+1学时5学分先修要求:概率论基本目的:数理统计学是研究如何有效地收集数据,如何对数据进行推理,以便对问题进行推断或预测,从而对决策和行动提供依据和建议。
数理统计学是应用广泛的基础性学科。
通过教学,使学生掌握这门科学的基本概念和基本思想。
基本的统计方法及有关的理论。
使学生了解大量实际问题的类型及与数理统计学的联系。
还要求学生能正确进行计算和使用统计表。
内容提要:1.数理统计的研究对象。
数理统计的基本概念。
2.参数估计的方法(最大似然估计,矩估计)。
3.估计的优良性标准(均方误差,UMVU估计)。
4.估计的相合性和渐近正态性。
5.置信区间。
6.假设检验的提法与两类错误,N-P引理及似然比检验。
7.广义似然比检验和关于正态总体的检验。
8.拟合优度检验。
9.一元线性回归,多元线性回归(参数估计和检验)。
10.预测和控制。
11.变量选择和方差分析。
12.统计决策与贝叶斯分析简介。
北京大学数学科学学院*双学位课程介绍*---------------教学方式:课堂教学教材:《概率与统计》陈家鼎郑忠国北京大学出版社(07、8)参考书:《概率统计讲义》陈家鼎刘婉如汪仁官高等教育出版社学生成绩评定:期末考试为主,期中考试与平时作业为辅。
课程编号:00136830 课程名称:数学应用软件课程类型:统、数/必修课每周4+1学时5学分(包括讲授、习题、上机实习)先修要求:统计学,计算机基础基本目的:本课程力图让统计和数学双学位的同学在一个学期时间内掌握统计和数学中常用的专用软件的基本知识,能够学会用这些专用软件解决问题。
在学习软件同时,巩固学生对概率统计和数学中有关概念的掌握,加深理解。
内容提要:本课程讲授统计专业和数学专业用到的专用软件。
统计软件讲授SAS系统的使用。
SAS系统是国际公认的权威性大型数据管理、分析、开发系统,可以完成大部分实际的统计数据分析任务。
数学软件讲授LaTeX排版系统和Matlab 矩阵计算系统。
LaTeX是数学界乃至自然科学界撰写论文的最常用工具软件,用好LaTeX对科研工作是一大帮助。
Matlab是流行的矩阵计算系统,在科学工程计算中有很多应用。
北京大学数学科学学院*双学位课程介绍*---------------课程内容包括:1.SAS系统入门和SAS/INSIGHT的探索性数据分析;2.SAS语言及数据管理;3.SAS报表和图形功能;4.常用统计问题如何在SAS中处理,如假设检验,回归分析,方差分析等;TeX排版常识,如基本文章结构、公式、制表、插图、幻灯演示;6.Matlab矩阵计算介绍,包括矩阵计算、数据输入输出、程序控制结构、子程序。
教学方式:课堂教学,上机教材或参考书:《统计软件教程》李东风人民邮电出版社学生成绩评定:闭卷考试加平时成绩。
课程编号:课程名称:常微分方程课程类型:数/必修课每周4+1学时5学分先修要求:高等数学线性代数基本目的:1.掌握几类一阶微分方程的初等解法。
2.掌握高阶线性方程及线性方程组的基本理论及常系数高阶线性方程和线性方程组的解法。
3.掌握微分方程的基本理论,如解的存在唯一性、解的延伸和对初值及参数的连续依赖性。
北京大学数学科学学院*双学位课程介绍*---------------4.掌握二阶微分方程的斯托姆--刘维尔边值问题的理论。
内容提要:1.微分方程的初等积分法。
2.解的存在唯一性、解的延伸及解对初值和参数的连续依赖性。
3.常系数线性微分方程组。
4.方程的幂级数解法。
5.二阶线性微分方程的边值问题。
6.首次积分与一阶偏微分方程。
教学方式:课堂讲授教材或参考书:1.《常微分方程》王高雄周之铭朱思铭王寿松高教出版社2.《常微分方程教程》丁同仁李承治高教出版社3. 《常微分方程》V.I.Arnold (有中译本)学生成绩评定方法:平时作业和期中考试成绩(40%)期末考试成绩(60%)课程编号:课程名称:应用多元统计分析课程类型:统/必修课每周4+1学时5学分先修要求:概率论,统计学基本目的:多元分析是一门应用性很强的课程。
