北京大学数学科学学院硕士研究生入学考试
北京大学数学科学学院研究生培养方案.doc

北京大学数学科学学院研究生培养方案二〇一八年九月谢谢观赏北京大学数学科学学院研究生培养方案2018.9(适用于数学学院2018年入学的研究生)目录硕士研究生培养方案一硕士研究生培养目标二关于硕士研究生的学制、选课、教学实习、参加学术报告会等规定三数学学院各系对硕士研究生选课的具体要求四硕士研究生学位论文及其评议博士研究生培养方案五博士研究生培养目标六博士生学制及学分的要求七博士生资格考试八博士生综合考试九博士生的培养计划十博士毕业生发表论文的要求十一博士生预答辩十二博士论文的评议和答辩十三博士研究生学业奖学金评定暂行办法十四硕士研究生学业奖学金评定暂行办法十五参考文件一硕士研究生培养目标培养热爱祖国、遵纪守法、学风严谨、品行端正的专业人才,使之有较强的事业心和献身科学的精神,并具有较坚实宽广的数学理论基础,及在基础数学、概率统计、大规模工程与科学计算、信息科学和金融数学等学科的某个方向上掌握较系统的专门理论知识、技术与方法,能够运用所掌握的基础理论与专门知识解决科学研究或实际工作中的问题,掌握一门外国语。
二数学科学学院关于硕士研究生的学制、选课、教学实习、参加学术报告会等规定(不含金融数学与精算学方向金融硕士和应用统计专业硕士)1 学制3年2 硕士生修课学分要求:总学分32学分, 其中政治 3 学分英语 2 学分(英文项目的留学生选修《基础汉语》)专业必修课9 学分专业选修课18 学分注:政治包括中国特色社会主义理论与实践研究2学分马克思主义与社会科学方法论和自然辩证法概论二选一1学分留学生(研究生)和港澳台学生:《中国概况》(61410008)2学分另外1学分可选修专业选修课、或马克思主义与社会科学方法论或自然辩证法概论来替代。
3本院的所有研究生课程都可供本科生选修。
硕士研究生(仅针对本院学生)在入学前的两年内选修的数学学院研究生课程,学分没有计入本科毕业学分的,可以计为研究生阶段成绩,获得相应学分。
_北京大学数学科学学院考博参考书和考试要求博士

报考北京大学数学科学学院的考生请注意,在报考前要与所要报考方向的博士生导师取得联系。
招生人数:48人。
其中拟招收本科起点直博生20人,本校硕博连读生20人。
应试生复试权重为50%。
一、招生研究方向及考试科目1 有限群及其模表示论张继平 1.英语 2.抽象代数 3.拓扑学2 置换群及代数组合论方新贵、冯荣权1.英语 2.抽象代数 3.拓扑学、代数组合论任选一门3 球堆积与密码;数的几何宗传明1.英语 2.离散数学 3.实分析、复分析任选一门4 拓扑学姜伯驹、丁帆 1.英语 2.抽象代数 3.拓扑学5 低维拓扑王诗宬同上6 微分几何及其应用莫小欢 1.英语 2.微分几何 3.拓扑学7 小波及其在图像处理中的应用刘和平 1.英语 2.泛函分析 3.实分析8 调和分析与小波分析刘和平同上9 微分几何王长平 1.英语 2.微分几何 3.拓扑学10 多复分析谭小江 1.英语 2.微分几何 3.复分析11 非线性分析张恭庆、蒋美跃 1.英语 2.泛函分析 3.偏微分方程12 几何分析丁伟岳、史宇光 1.英语 2.微分几何 3.偏微分方程13 微分几何与PDE 田刚、朱小华1.英语 2.微分几何 3.偏微分方程、拓扑学任选一门14 常微分方程与动力系统李伟固、柳彬、杨家忠1.英语2.常微分方程3.偏微分方程、实分析、复分析任选一门15 动力系统与复杂性理论郑志明1.英语 2.常微分方程 3.偏微分方程、高等概率论任选一门16 复分析伍胜健 1.英语 2.泛函分析 3.复分析17 微分动力系统文兰、甘少波 1.英语 2.常微分方程 3.拓扑学18 微分遍历论孙文祥同上19 动力系统和哈密顿系统夏志宏同上20 非线性偏微分方程王保祥 1.英语 2.泛函分析 3.偏微分方程21 代数几何蔡金星同上22 偏微分方程及其应用王冠香、周蜀林 1.英语 2.泛函分析 3.偏微分方程23 密码学与信息安全理论冯荣权1.英语 2.抽象代数 3.计算机软件和理论、密码学任选一门24 数论:算术几何,p-进上同调田青春1.英语 2.抽象代数、微分几何任选一门 3.拓扑学25 调和分析及应用王保祥 1.英语 2.泛函分析 3.实分析1 多尺度模型与计算及自适应方法张平文 1.英语 2.计算方法 3.偏微分方程2 科学计算与随机PDE 鄂维南1.英语 2.随机过程、计算方法任选一门 3.偏微分方程3 偏微分方程数值解王鸣、许进超 1.英语 2.计算方法 3.偏微分方程4 矩阵计算及其应用徐树方 1.英语 2.计算方法 3.最优化方法5 微分方程数值解与计算流体力学汤华中、李若 1.英语 2.计算方法 3.偏微分方程6 最优化方法及其应用高立 1.英语 2.计算方法 3.最优化方法7 随机模型、算法及应用李铁军1.英语 2.计算方法 3.偏微分方程、高等概率论任选一门8 计算机图形学郭百宁 1.英语 2.计算方法 3.信号处理9 图像处理与图像重建周铁 1.英语 2.计算方法 3.偏微分方程1 概率论与随机分析,随机图与随机复杂网络马志明 1.英语、2.随机过程、3.高等概率论2 马氏过程与相互作用粒子系统陈大岳同上3 测度值马氏过程与非线性偏微分方程任艳霞同上4 生存分析、时间序列分析何书元 1.英语 2.高等统计学 3.高等概率论5 生物信息学与统计学刘军同上6 因果推断及生物医学统计耿直同上7 统计推断、机器学习、遥感郁彬同上8 生存分析刘力平同上9 可靠性、质量检测与控制、生物医学数据分析房祥忠同上10 统计机器学习、互联网搜索李航、沈向洋同上11 实验设计与分析、应用统计艾明要同上12 随机过程及其应用、非平衡统计物理、系统生物学蒋达权 1.英语 2.随机过程 3.高等概率论13 生物信息学邓明华 1.英语 2.高等统计学 3.高等概率论1 图像重建与图像分析张恭庆、姜明 1.英语 2.计算方法 3.偏微分方程2 李群表示论及其应用王正栋 1.英语 2.泛函分析 3.拓扑学3 数学物理刘旭峰 1.英语 2.抽象代数 3.实分析4 辛几何与可积系统刘张炬1.英语 2.微分几何 3.偏微分方程、拓扑学任选一门5 随机动力系统与光滑遍历论刘培东 1.英语 2.常微分方程 3.微分流形6 人工智能与智能软件林作铨1.英语 2.离散数学 3.计算机软件和理论7 程序理论、软件形式化方法裘宗燕同上8 随机数理方程、计算机科学的数学基础李未 1.英语 2.抽象代数 3.偏微分方程9 统计学习与智能信息处理马尽文 1.英语 2.模式识别 3.信号处理10 密码学与信息安全理论杨义先、徐茂智 1.英语 2.抽象代数 3.密码学11 信息安全工程杨义先、徐茂智1.英语 2.离散数学 3.计算机软件和理论12 符号计算与自动推理夏壁灿1.英语 2.抽象代数、离散数学任选一门 3.计算机软件和理论13 精算学与信用风险管理扬静平1.英语 2.随机过程、高等统计学任选一门 3.高等概率论二、初试参考书0 英语或法语1 抽象代数《代数学引论》聂灵沼、丁石孙著第二版高等教育出版社2000《抽象代数》II 徐明曜、赵春来,北京大学出版社,2007年第一版2 微分几何《黎曼几何初步》伍鸿熙、沈纯理、虞言林著北京大学出版社 1989《黎曼几何引论》陈维桓、李兴校著,北京大学出版社 2002年,第1章、2 、3 、4章《黎曼几何初步》伍鸿熙、沈纯理、虞言林著北京大学出版社 19893 拓扑学Munkres, J.R. Elements of Algebraic Topology, Addison-Wesley, Menlo Park, California, 1984 Guillemin, V. and Pollack, A., Differential Topology, Prentice-Hall, New Jersey, 1974Hu, Sze-Tsen, Homotopy Theory (Chapters 1-6>, AcademicPress, New York, 19594 实分析《实变函数论》周民强《实分析》陆善镇等5 复分析Ahlfors, Complex Analysis《复分析引论》李忠北京大学出版社6 泛函分析《泛函分析讲义》上册张恭庆、林源渠北京大学出版社7 常微分方程《常微分方程》丁同仁,李承治《微分方程定性理论》第6 、7章张芷芬等8 偏微分方程《数学物理方程讲义》姜礼尚等《偏微分方程》周蜀林北京大学出版社《二阶椭圆型方程与椭圆型方程组》陈亚浙、吴兰成9 高等概率论K.L.Chung, A Course in Probability Theory, Second Edition, Academic Press, New York, 1974R.T.Durrett, Probability, Theory and Examples, SecondEdition, Duxbury Press, 199610 高等统计学《高等统计学》郑忠国,北京大学出版社,199811 随机过程《随机过程论》第二版,钱敏平、龚光鲁,北京大学出版社《应用随机过程》,钱敏平、龚光鲁,北京大学出版社R.N.Bhattacharya and W.C.Waimire, Stochastic Processes with Applications, John Wiley & Sons, 199012 计算方法Michael T. Heath, (Scientific Computing: An Introductory Survey, Second Edition, McGraw-Hill Companies, Inc.> 科学计算导论,清华大学出版社影印13 模式识别《模式识别》,边肇祺,清华大学出版社, 1988 或 200014 离散数学<含数理逻辑,集合论与图论,代数结构)《离散数学教程》屈婉铃等,北京大学出版社, 2002 《数理逻辑基础上下册》胡世华,陆钟万科学出版社1983《Discrete Mathematics and Its Applications》,K. Rosen,McGraw-Hill,1998;影印版,机械工业出版社,199915 最优化方法《最优化方法》,孙文瑜,徐成贤,朱德通,高等教育出版社16 密码学D. R. Stinson, Cryptography, Theory and Practice, 2ndEdition.中译本,冯登国译,密码学原理与实践<第二版),电子工业出版社,2003O. Goldreich, Foundations of Cryptography, Basic Tools, 电子工业出版社,2003 <此书也有中译本)17 微分流形陈维桓,微分流形初步,高教出版社,第二版,2001 William M. Boothby, An introduction to differential manifolds and Riemannian geometry, Second Edition, Academic Press,Inc., 1986.18 计算机软件与理论<含数据结构,算法与程序设计,计算理论)《算法与数据结构— C 语言描述》,张乃孝,高等教育出版社,2002《Data Structure and Programming Design in C》<2e), R. Kruse 等,Prentice Hall,1997;影印版,清华大学出版社,1998《Introduction to Algorithm C》(2e>,T. Cormen 等;影印版,高等教育出版社,2002《 C++ Programming LanguageC》, B. Stroustrup,Addison-Wesley, 1999;影印版,高教出版社,2000;中译本,机械工业出版社,2002 或者 2005《 C Programming LanguageC》 (2e>, B. W. Kernighan and D. M. Ritchie, 影印版:清华出版社,中译本:机械工业出版社《 Introduction to Automata Theory, Languages, andComputation》<2e),J. Hopcroft, R. Motwani,J. Ullman,Addison-Wesley,2001;影印版,清华大学出版社,2002《可计算性与计算复杂性导引C》,张立昂,北京大学出版社,199619 信号处理《数字信号处理》,程乾生,北京大学出版社,200320 代数组合论N. Biggs, Algebraic Graph Theory, second edition, CambridgeUniversity Press, 1993.C. Godsil, Algebraic Combinatorics, Chapman & Hall, 1993.C. Godsil and G. Royle, Algebraic Graph Theory, GTM 207,Springer, 2001.以上考试是初试,初试通过后,有关导师可以再按照自己的要求进行专业课的笔试<这时以硕士生课程的水平为准),参考书见下。
权威辅导-2016年北京大学数学科学学院金融硕士考研拟录取名单整理

第四部分:考研经验
你以为你真的了解北京大学数学科学学院的金融硕士吗? 关于北京大学金融硕士, 就得提到四大院: 光华管理学院、 经济学院、
资料来源:育明考研考博
数学科学学院、汇丰商学院,至于哪个学院更好一些,只能说光华是 最好的也是最难的, 但是其他的学院确实不好评判, 经院现在的地位 确实不如以前了,14 年改革成专硕后也没见得有太大的改变,但是 如果能考上经院的金融硕士那可以说以后就业是非常有保障的, 数学 科学学院也是最近专业课改革, 专业一改成了数学三, 相对来说比以 前简单一些,但是由于招的人不多,五六个,而且特别坚持自己的特 色--数学,所以关注的人不如经院和光华多,至于汇丰商学院,这是 在深圳,而且大部分都是联合项目,对英语***的要求以及高昂的学 费让很多学生生畏,15 年专业课改革,加上了金融学部分,难度无 疑增大很多。接下来一一讲解: 数学科学学院: 北京大学数学科学学院的金融硕士很多考生估计都不 是很了解,毕竟名气不如光华和经院、汇丰,而且对考生的要求是比 较独特的, 一般报考的也大多数是数学专业的, 学院的方向基本就是 数学和金融的结合, 以后这也是金融发展的一个趋势, 大家不要担心 就业的问题好伐, 能考上北大的金融就业就是没问题的, 而且毕竟数 科的难度也是很大的。以前的专业课难度更大,专一不是考数三,所 以很多考生去找历年真题发现根本就找不到, 更别提答案了, 我们整 理 2014 年-2016 年的,虽都是回忆版,但是也是很珍贵的。 关于难度很多考生没概念,大家看难度的时候不要单纯的去看分数, 分数的话北大数科 360 分甚至都不如中财, 但是难度可不是中财能比 的,大家要结合专业课难度、报录比等各方面的因素,而且北大数科 专业课是比较难拿分的,2016 年前十五名的学生专业课过 130 的就
硕士研究生入学考试、复试、同等学力加试参考书目
《现代管理理论与方法》周三多,复旦大学出版社,1995年
817工程经济
《工程经济》黄愈祥,同济大学出版社,1994年
818机械设计
《机械设计》濮良贵,高等教育出版社,2001年,第7版
819机械控制工程基础
《控制工程基础》左建民,机械工业出版社2001年
820汽车理论基础
《汽车理论》余志生,机械工业出版社,2000年,第3版
502专业综合
《工程测量学》张正禄,武汉大学出版社,2005年
《GPS测量原理及应用》徐绍铨等,武汉大学出版社,2004年
503路基路面工程
《路基路面工程》邓学钧,人民交通出版社,2005年
《公路沥青路面设计规范》(JTG D50-2006),人民交通出版社
《公路水泥混凝土路面设计规范》(JTG D40-2002),人民交通出版社
复试科目
主要参考书目
529产业经济学
《产业经济学》苏东水,高等教育出版社,2000年
530统计学
《统计学原理》黄良文,中国统计出版社,2000年
531专业综合
《管理信息系统》薛华成,清华大学出版社,2003年
《物流管理》刘刚,中国人民大学出版社,2005年
532专业综合
《中级财务管理》宋献中,东北财经大学出版社,2002年
《计算机控制技术》于海生,机械工业出版社
522专业综合
《计算机控制技术》于海生,机械工业出版社
《模拟电子技术基础》童诗白,高等教育出版社,第3版
《数字电子技术基础》阎石,高等教育出版社,第5版
523锅炉原理
《锅炉原理》叶江明,中国电力出版社,2004年,第1版
524换热器原理
《换热器原理与设计》余建祖,北京航空航天大学出版社,2006年,第1版
2015北京大学计算数学专业考研(数学科学学院)专业目录招生人数参考书目历年真题复试分数线答题方法
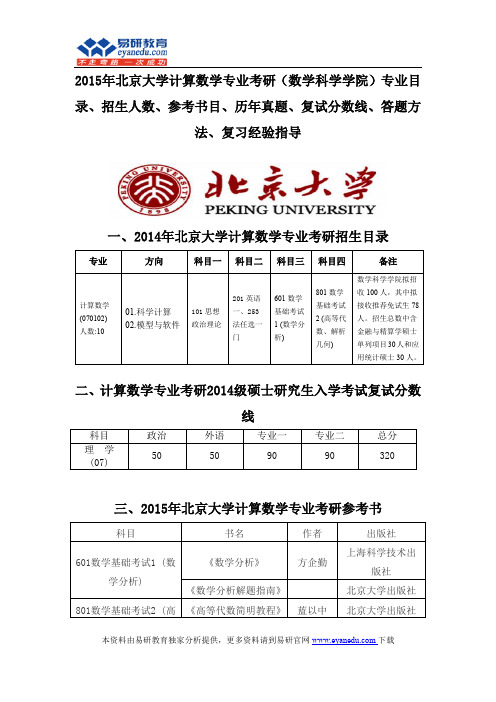
E 是单位变换)
7、(12 分)、V 是内积空间, , 是 V 中两个长度相等的向量,证明必存在某个正交变换, 将 变到 。 8、(12 分)、A 是复矩阵,B 是幂零矩阵,且 AB=BA,证明|A+2010B|=|A|。 9、(11 分)、求过 z 轴且与平面 x 2 y 3z 1 夹角为 60 的平面的方程。
三、2015年北京大学计算数学专业考研参考书
科目 601数学基础考试1 (数 学分析) 书名 《数学分析》 《数学分析解题指南》 蓝以中 作者 方企勤 出版社 上海科学技术出 版社 北京大学出版社 北京大学出版社
801数学基础考试2 (高 《高等代数简明教程》
本资料由易研教育独家分析提供,更多资料请到易研官网 下载
(2)以两条不变直线为坐标轴建立仿射坐标系 X’O’Y’,求在此坐标系中 f 的变换公式。 12、(12 分)、用不过圆锥顶点的平面切割圆锥,证明所截的曲线只可能为椭圆、双曲线和抛 物线。并说明曲线类型随切割角度的变换规律。
本资料由易研教育独家分析提供,更多资料请到易研官网 下载
0
xf ( x)dx 与
0
f ( x) dx 均收敛 x
0
x t f ( x)dx 在 (1,1) 上有定义,并且有连续导函数。
其中 为 x xdy ydz zdx ,
2
8、 (15 分)、 计算曲线积分 I
y 2 z 2 1与 x y z 0
本资料由易研教育独家分析提供,更多资料请到易研官网 下载
简答题采用“定义+框架+总结”答题法。 首先把题干中涉及到的最重要的名词(也叫大概念)进行阐述, 就像解答名词解释一样。这一环节不能省略,否则无意中丢失很多的 分数,这是很多考生容易忽视的一点。 读懂题意,列要点进行回答。回答要点一般 3-5 点,每条 150-200 字。 进行简单的总结,总结多为简单评析或引申。 【答题示范】 : 例如“简答公共财政的职能。 ” 第一,公共财政的定义。(不能缺少) 第二,公共财政的 3 大职能。(主体部分) 第三,总结评析。 【简答题答题注意事项】 : 第一,在回答简答题的时候,要采取“总-分-总”答题结构。即 在回答要点 之前进行核心名词含义的阐释,最后写几句起总结的话,这样不会给 人一种太突兀的感觉。 第二,在回答的时候字数一般在 600-800 为佳,时间为 15-20 分钟。通常字数应该是本题分值的至少 30 倍,即, 1 分至少 30 个字。 第三,如果课本没有明确答案,那你也不能拍脑门乱写,好的策 略是向课本靠拢, 将相关的你能够想到的内容往 4×150 里套就行了。
001_北京大学数学科学学院考博参考书和考试要求-博士.doc

同上
8
生存分析
刘力平
同上
可靠性、质景检测与控制、生物医学
房祥忠
同上
9
数据分析
10
统计机器学习、互联网搜索
李航、沈向洋
同上
11
试软设计与分析、应用统计
艾明要
同上
随机过程及戒应用、非平衡统计物理、
蒋达权
1.英语2.随机过程3.高等概率论
12
系统生物学
生物信息学
邓明华
1.英语2.高等统计学3.高等概率
宗传明
1.英语2.离散数学3.实分析、复分 析任选一门
4
拓扑学
姜伯驹、丁帆
1.英语2.抽象代数3.拓扑学
5
低维拓扑
王诗成
同上
6
微分几何及其应用
莫小欢
1.英语2.微分几何3.拓扑学
7
小波及其在图像处理中的应用
刘和平
1.英语2.泛函分析3.实分析
8
调和分析与小波分析
刘和平
同上
9
微分几何
王长平
1.英语2.微分几何3.拓扑学
2000
《抽象代数》II徐明曜、赵春来,北京大学出版社,2007年 第一版
《黎曼儿何初步》伍鸿熙、沈纯理、虞宣林著北京大学出版
社1989
《黎曼几何引论》陈维桓、李兴校将,北京大学出版社2002年,第1章、2、3、4章
社1989
Munkres, J. R. Elements of Algebraic Topology,
10
多复分析
谭小江
1.英语2.微分几何3.复分析
11
非线性分析
张恭庆、蒋美跃
1.英语2.泛函分析3.偏微分方程
2020-2021年中国科学院大学(数学科学学院)计算数学考研招生情况、分数线、参考书目、录取名单

一、数学科学学院简介中国科学院大学(简称国科大)数学科学学院前身为1978年成立的中国科技大学研究生院(北京)数学教学部,2002年9月更名为中国科学院研究生院数学系,2006年6月与中国科学院数学与系统科学研究院联合组建成立中国科学院研究生院数学科学学院,院长和副院长分别由数学与系统科学研究院的院长和分管教育的副院长担任。
2014年由数学与系统科学研究院承办科教融合数学科学学院,现任院长为席南华院士。
数学科学学院下设6个教研室,分别为分析数学教研室、几何与拓扑教研室、代数与数论教研室、计算数学与计算机数学教研室、概率论与数理统计教研室、运筹学与控制论教研室。
国科大数学科学学院的专任教师每年招收硕士研究生20名左右(含推免生),培养方向有分析、代数、几何、概率论、数理统计、应用数学、运筹学与控制论、应用统计专业学位硕士以及一些交叉学科的若干个研究方向。
2019年数学科学学院为中国科学院虚拟经济与数据科学研究中心代招运筹学与控制论专业学术型硕士研究生。
二、中国科学院大学计算数学专业招生情况、考试科目三、中国科学院大学计算数学专业分数线2018年硕士研究生招生复试分数线2017年硕士研究生招生复试分数线四、中国科学院大学计算数学专业考研参考书目616数学分析现行(公开发行)综合性大学(师范大学)数学系用数学分析教程。
801高等代数[1] 北京大学编《高等代数》,高等教育出版社,1978年3月第1版,2003年7月第3版,2003年9月第2次印刷.[2] 复旦大学蒋尔雄等编《线性代数》,人民教育出版社,1988.[3] 张禾瑞,郝鈵新,《高等代数》,高等教育出版社,1997.五、中国科学院大学计算数学专业复试原则最后的复试成绩综合考虑以上“业务能力、英语听力和口语、综合素质和思想品德”四个方面的成绩,复试成绩满分100分,其中业务能力占50%,英语听力和口语占30%,综合素质和思想品德占20%。
(一)业务能力面试1. 考核形式:问答2. 考核目的:主要考核考生掌握专业知识的广度、深度与扎实程度,运用专业知识的能力,思维能力,应变能力,表达能力,研究兴趣,科研能力与发展潜力。
北京大学数学科学学院考博参考书和考试要求博士

博士研究生招生信息报考北京大学数学科学学院的考生请注意,在报考前要与所要报考方向的博士生导师取得联系。
人。
应试生20人。
其中拟招收本科起点直博生20人,本校硕博连读生招生人数:48 %。
复试权重为50 招生研究方向及考试科目一、拓扑学 1.英语2.抽象代数3.有限群及其模表示论张继平1拓扑学、代数3.1.英语2.抽象代数方新贵、冯荣权置换群及代数组合论 2组合论任选一门实分析、复分3.1.英语2.离散数学宗传明球堆积与密码;数的几何3 析任选一门1.英语2.抽象代数3.拓扑学拓扑学姜伯驹、丁帆4王诗宬低维拓扑同上5莫小欢 2.微分几何3.拓扑学微分几何及其应用1.英语6小波及其在图像处理中的应用泛函分析1.英语2. 3.实分析刘和平7刘和平调和分析与小波分析同上8王长平 3.拓扑学微分几何2.1.英语微分几何9谭小江 3.复分析多复分析微分几何英语1. 2.101.英语张恭庆、蒋美跃偏微分方程非线性分析3.2.泛函分析11丁伟岳、史宇光几何分析偏微分方程微分几何英语1. 2. 3.12偏微分方程、2.英语微分几何3.1. PDE微分几何与田刚、朱小华13拓扑学任选一门偏微分方2.1.英语常微分方程3.李伟固、柳彬、杨常微分方程与动力系统14 家忠程、实分析、复分析任选一门偏微分方2.1.英语3.常微分方程动力系统与复杂性理论郑志明15 程、高等概率论任选一门1.英语复分析3.泛函分析2.复分析伍胜健161 / 83.拓扑学英语2.常微分方程1.微分动力系统文兰、甘少波17同上孙文祥微分遍历论18夏志宏动力系统和哈密顿系统同上193. 非线性偏微分方程王保祥偏微分方程英语2.泛函分析1.20代数几何同上蔡金星213.偏微分方程英语偏微分方程及其应用 2.泛函分析1.王冠香、周蜀林22计算机软件和3.英语2.抽象代数1. 冯荣权密码学与信息安全理论23理论、密码学任选一门抽象代数、微分几何任选2.1.英语田青春进上同调数论:算术几何,p-24 一门3.拓扑学王保祥调和分析及应用1.英语2.泛函分析3.实分析253.偏微分方程英语2.计算方法1.张平文多尺度模型与计算及自适应方法 1随机过程、计算方法任选英语2.1. 科学计算与随机PDE 鄂维南2 偏微分方程一门3. 偏微分方程2.计算方法3.1.偏微分方程数值解王鸣、许进超英语3最优化方法2.计算方法3. 矩阵计算及其应用1.英语徐树方 4偏微分方程计算方法3.微分方程数值解与计算流体力学 1.英语汤华中、李若2.5最优化方法最优化方法及其应用计算方法3.1.英语高立 2.6偏微分方程、计算方法3.1.英语2. 随机模型、算法及应用李铁军7 高等概率论任选一门 3.信号处理郭百宁英语计算机图形学2.计算方法1.83. 图像处理与图像重建偏微分方程英语1. 2. 周铁计算方法9概率论与随机分析,随机图与随机复1 高等概率论2.随机过程、3.英语、马志明 1. 杂网络同上马氏过程与相互作用粒子系统陈大岳 2测度值马氏过程与非线性偏微分方程任艳霞同上33.何书元生存分析、时间序列分析 2.1.英语高等统计学高等概率论42 / 8同上军刘生物信息学与统计学 5同上耿直因果推断及生物医学统计6郁彬同上统计推断、机器学习、遥感7同上刘力平生存分析8可靠性、质量检测与控制、生物医学9 同上房祥忠数据分析同上李航、沈向洋统计机器学习、互联网搜索10 同上实验设计与分析、应用统计艾明要11随机过程及其应用、非平衡统计物12 高等概率论随机过程3.蒋达权1.英语2. 理、系统生物学高等概率论生物信息学1.英语2.高等统计学3.邓明华133.偏微分方程英语2.计算方法1.张恭庆、姜明图像重建与图像分析 1拓扑学2.泛函分析3.1.英语李群表示论及其应用王正栋 2实分析2.抽象代数3.1.数学物理刘旭峰英语3偏微分方程、3. 2.微分几何英语1. 刘张炬辛几何与可积系统4 拓扑学任选一门微分流形随机动力系统与光滑遍历论常微分方程刘培东 3.1.英语2.5计算机软件和离散数学3. 2.1.英语林作铨人工智能与智能软件6 理论程序理论、软件形式化方法同上裘宗燕7随机数理方程、计算机科学的数学基8 偏微分方程3.英语2.抽象代数李未 1. 础信号处理统计学习与智能信息处理模式识别3.英语马尽文 1. 2.93.密码学杨义先、徐茂智 2.1.密码学与信息安全理论英语抽象代数10计算机软件和3.离散数学1.英语2. 杨义先、徐茂智信息安全工程11 理论抽象代数、离散数学任选1.英语2. 符号计算与自动推理夏壁灿12 3.一门计算机软件和理论3 / 8随机过程、高等统计学任英语2.1. 扬静平精算学与信用风险管理13 3.高等概率论选一门初试参考书二、英语或法语0高等教育出版社《代数学引论》聂灵沼、丁石孙著第二版2000抽象代数1年徐明曜、赵春来,北京大学出版社,2007《抽象代数》II第一版北京大学出版《黎曼几何初步》伍鸿熙、沈纯理、虞言林著1989社2002陈维桓、李兴校著,北京大学出版社《黎曼几何引论》微分几何2章3 、4年,第1章、2 、北京大学出版《黎曼几何初步》伍鸿熙、沈纯理、虞言林著1989社Munkres, J.R. Elements of Algebraic Topology, Addison-Wesley, Menlo Park, California, 1984Guillemin, V. and Pollack, A., Differential Topology, Prentice- 拓扑学3Hall, New Jersey, 1974Hu, Sze-Tsen, Homotopy Theory (Chapters 1-6>, AcademicPress, New York, 1959《实变函数论》周民强实分析4陆善镇等《实分析》Ahlfors, Complex Analysis 复分析5 北京大学出版社《复分析引论》李忠泛函分析《泛函分析讲义》上册张恭庆、林源渠北京大学出版社6《常微分方程》丁同仁,李承治常微分方程7《微分方程定性理论》第章张芷芬等76 、《数学物理方程讲义》姜礼尚等偏微分方程8北京大学出版社《偏微分方程》周蜀林《二阶椭圆型方程与椭圆型方程组》陈亚浙、吴兰成K.L.Chung, A Course in Probability Theory, Second Edition, Academic Press, New York, 1974高等概率论9R.T.Durrett, Probability, Theory and Examples, SecondEdition, Duxbury Press, 19961998高等统计学《高等统计学》郑忠国,北京大学出版社,104 / 8北京大学出版社《随机过程论》第二版,钱敏平、龚光鲁,北京大学出版社钱敏平、龚光鲁,《应用随机过程》,随机过程11R.N.Bhattacharya and W.C.Waimire, Stochastic Processeswith Applications, John Wiley & Sons, 1990Michael T. Heath, (Scientific Computing: An Introductory计算方法Survey, Second Edition, McGraw-Hill Companies, Inc.>12科学计算导论,清华大学出版社影印20001988 或模式识别《模式识别》,边肇祺,清华大学出版社,13<含数理逻辑,集合论与图论,代数结构)2002《离散数学教程》屈婉铃等,北京大学出版社,科学出版社《数理逻辑基础上下册》胡世华,陆钟万离散数学14 1983,》,K. Rosen《Discrete Mathematics and Its Applications1999;影印版,机械工业出版社,,McGraw-Hill1998 《最优化方法》,孙文瑜,徐成贤,朱德通,高等教育出版社最优化方法15D. R. Stinson, Cryptography, Theory and Practice, 2ndEdition.第二版),电子工业<中译本,冯登国译,密码学原理与实践密码学162003出版社,电子O. Goldreich, Foundations of Cryptography, Basic Tools,此书也有中译本)工业出版社,2003 <2001陈维桓,微分流形初步,高教出版社,第二版,William M. Boothby, An introduction to differential manifolds 微分流形17and Riemannian geometry, Second Edition, Academic Press,Inc., 1986.<含数据结构,算法与程序设计,计算理论)语言描述》,张乃孝,高等教育出版—C 《算法与数据结构2002社,, R. <2e)《Data Structure and Programming Design in C》;影印版,清华大学出版社,Prentice Hall,1997Kruse 等,1998等;影印T. Cormen (2e>,》《Introduction to Algorithm C 计算机软件与理论182002版,高等教育出版社,,》, B. Stroustrup《C++ Programming LanguageC译教出版社,2000;中;影印版,高Addison-Wesley, 199920052002 本,机械工业出版社,或者(2e>, B. W. Kernighan and 》C Programming LanguageC《清华出版社,中译本:机械工业出版影印版:D. M. Ritchie,社Introduction to Automata Theory, Languages, and《5 / 8,J. Ullman<2e),J. Hopcroft, R. Motwani,Computation》2002 社,,2001;影印版,清华大学出版Addison-Wesley》,张立昂,北京大学出版C《可计算性与计算复杂性导引1996社,2003 《数字信号处理》,程乾生,北京大学出版社,信号处理19N. Biggs, Algebraic Graph Theory, second edition, CambridgeUniversity Press, 1993.代数组合论C. Godsil, Algebraic Combinatorics, Chapman & Hall, 1993. 20C. Godsil and G. Royle, Algebraic Graph Theory, GTM 207,Springer, 2001.这时以上考试是初试,初试通过后,有关导师可以再按照自己的要求进行专业课的笔试< 以硕士生课程的水平为准),参考书见下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考试科目编号:
01 数学分析02 高等代数
03 解析几何04 实变函数
05 复变函数06 泛函分析
07 常微分方程08 偏微分方程
09 微分几何10 抽象代数
11 拓扑学12 概率论
13 数理统计14 数值分析
15 数值代数16 信号处理
17 离散数学18 数据结构与算法
01 数学分析(150 分)
考试参考书:
1. 方企勤等,数学分析(一、二、三册)高教出版社。
2. 陈纪修、於崇华、金路,数学分析(上、下册),高教出版社。
02 高等代数(100 分)
考试参考书:
1. 丘维声,高等代数(第二版) 上册、下册,高等教育出版社,2002年, 2003年。
高等代数学习指导书(上册),清华大学出版社,2005年。
高等代数学习指导书(下册),清华大学出版社,2009年。
2. 蓝以中,高等代数简明教程(上、下册),北京大学出版社,2003年(第一版第二次印刷)。
03 解析几何(50 分)
考试参考书:
1. 丘维声,解析几何(第二版),北京大学出版社,(其中第七章不考)。
2. 吴光磊,田畴,解析几何简明教程,高等教育出版社,2003年。
04 实变函数(50 分)
考试参考书:
1. 周民强,实变函数论,北京大学出版社,2001年。
05 复变函数(50 分)
考试参考书:
1. 方企勤,复变函数教程,北京大学出版社。
06 泛函分析(50 分)
考试参考书:
1. 张恭庆、林源渠,泛函分析讲义(上册),北京大学出版社。
07 常微分方程(50 分)
考试参考书:
1. 丁同仁、李承治,常微分方程教程,高等教育出版社。
2. 王高雄、周之铭、朱思铭、王寿松,常微分方程(第二版),高等教育出版社。
3. 叶彦谦,常微分方程讲义(第二版)人民教育出版社。
08 偏微分方程(50 分)
考试参考书:
1. 姜礼尚、陈亚浙,数学物理方程讲义(第二版),高等教育出版。
2. 周蜀林,偏微分方程,北京大学出版社。
09 微分几何(50 分)
考试参考书:
1. 陈维桓,微分几何初步,北京大学出版社(考该书第1-6章)。
2. 王幼宁、刘继志,微分几何讲义,北京师范大学出版社。
10 抽象代数(50 分)
考试参考书:
1. 丘维声, 抽象代数基础,高等教育出版社,2003年。
2. 聂灵昭、丁石孙,代数学引论(第一、二、三、四、七章,第八章第1、2、3节),高等教育出版社,2000年第二版。
11 拓扑学(50 分)
考试参考书:
1. 尤承业,基础拓扑学讲义,北京大学出版社,1997年(考该书第1-3章)。
12 概率论(50 分)
考试参考书:
1. 何书元,概率论北京大学出版社, 2006年。
2. 汪仁官,概率论引论北京大学出版社, 1994年。
13 数理统计(50 分)
考试参考书:
1. 陈家鼎、孙山泽、李东风、刘力平编,数理统计学讲义(第二版),高等教育出版社,2006年。
14 数值分析(50 分)
考试参考书:
1. 关治、陈景良,数值计算方法,清华大学出版社。
2. 蒋尔熊等,数值逼近,复旦大学出版社。
3. 王仁宏,数值逼近,高教出版社。
4. 周铁、徐树方、张平文、李铁军计算方法,清华大学出版社出版。
15 数值代数(50 分)
考试参考书:
1. 徐树方、高立、张平文,数值线性代数,北京大学出版社,2000年。
2. G. W. Stewart, Introduction to Matrix Computation, Academic Press, New York , 197
3.(有中译本)
16 信号处理(50 分)
考试参考书:
1. 程乾生,数字信号处理,北京大学出版社,2003年。
2. 奥米海姆R.W. 谢费,数字信号处理,科学出版社,1980年。
17 离散数学(50 分)
考试参考书:
1. 屈婉铃等,离散数学教程,北京大学出版社,2002年。
18 数据结构与算法(50 分)
考试参考书:
1.张乃孝主编,算法与数据结构—— C 语言描述,高等教育出版社2002年。
2. 张乃孝、裘宗燕,数据结构— C++ 与面向对象程序设计,高教出版社1998年。
3. 严蔚敏、吴伟民,数据结构(C语言版),清华大学出版社1996年。
4. 裘宗燕,从问题到程序,机械工业出版社,2005年。
5. B. Stroustrup,C++ 程序设计语言,中译本:机械工业出版社,2002年。
说明
算法与数据结构是信息科学和计算机理论的核心内容,是一门理论和实际紧密结合的课程。
通过考试主要目的是检查学生是否较全面地理解算法和数据结构的概念、掌握各种数据结构与算法的实现方式,能够分析和比较不同数据结构和算法的特点。
同时检查学生使用学习的知识解决问题的能力和程序设计的能力。
主要考试形式:
考概念——是非题、选择题、填空题、简答题形式
考存储表示——定义类型和变量、画存储示意图、根据要求选择并构造存储表示
考算法思想——问答题、画算法执行示意图
考算法设计——算法理解、填充、改错;编程序
考算法分析——计算题或证明题
考程序设计与应用——与考算法思想、设计、分析形式类似。
