高考三视图(含解析)理试题汇总(精编文档).doc
专题08 三视图-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)

专题08 三视图1.(2021年全国高考甲卷数学试题)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方 后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()体截去三棱锥A EFGA.B.C.D.【答案】D【分析】由题意及正视图可得几何体的直观图,如图所示,所以其侧视图为故选:D二、填空题2.(2021年全国高考乙卷数学(文)试题)以图①为正视图,在图①①①①中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).【答案】①①(答案不唯一)【分析】选择侧视图为①,俯视图为①,如图所示,长方体1111ABCD A B C D -中,12,1AB BC BB ===,,E F 分别为棱11,B C BC 的中点,则正视图①,侧视图①,俯视图①对应的几何体为三棱锥E ADF -.故答案为:①①.1.(2020年全国统一高考数学试卷(理科)(新课标①))下图为某几何体的三视图,则该几何体的表面积是( )A .B .C .D .【答案】C 【分析】根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得:AB AD DB === ∴ADB △是边长为根据三角形面积公式可得:211sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是:632=⨯++故选:C.2.(2019年全国统一高考数学试卷)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A.B.C.3D.2【答案】B【分析】根据圆柱的三视图以及其本身的特征,将圆柱的侧面展开图平铺,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,= B.3.(2018年全国卷①文数高考试题)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A.B.C.D.【答案】A【详解】:由题意知,题干中所给的是榫头,是凸出的几何体,求得是卯眼的俯视图,卯眼是凹进去的,即俯视图中应有一不可见的长方形,且俯视图应为对称图形故俯视图为故选A.4.(2018年全国卷高考试题)-2021年新高考数学一轮复习讲练测)如图,在下列四个正方体中,A 、B 为正方体的两个顶点,M 、N 、Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面 MNQ 不平行的是( )A .B .C .D .【答案】D【分析】对于A 选项,如下图所示,连接CD ,在正方体中,//AD BC 且AD BC =,所以,四边形ABCD 为平行四边形,则//AB CD , N 、Q 分别为DE 、CE 的中点,则//NQ CD ,//AB NQ ∴,AB ⊄平面MNQ ,NQ ⊂平面MNQ ,//AB ∴平面MNQ ;对于B 选项,连接CD ,如下图所示:在正方体中,//AD BC 且AD BC =,所以,四边形ABCD 为平行四边形,则//AB CD , M 、Q 分别为DE 、CE 的中点,则//MQ CD ,//AB MQ ∴,AB ⊄平面MNQ ,MQ 平面MNQ ,//AB ∴平面MNQ ;对于C 选项,连接CD ,如下图所示:在正方体中,//AD BC 且AD BC =,所以,四边形ABCD 为平行四边形,则//AB CD , M 、Q 分别为DE 、CE 的中点,则//MQ CD ,//AB MQ ∴,AB ⊄平面MNQ ,MQ 平面MNQ ,//AB ∴平面MNQ ;对于D 选项,如下图所示,连接BE 交MN 于点F ,连接QF ,连接CD 交BE 于点O ,若//AB 平面MNQ ,AB ⊂平面ABE ,平面ABE 平面MNQ FQ =,则//FQ AB ,则EF EQ BE AE=, 由于四边形BCED 为正方形,对角线交于点O ,则O 为BE 的中点, M 、N 分别为DE 、CE 的中点,则//MN CD ,且MNBE F =, 则12EF EN EO CE ==,1124EF OE BE ∴==, 则14EF BE =,又12EQ AE =,则EF EQ BE AE≠,所以,AB 与平面MNQ 不平行; 故选:D.5.(2017年全国普通高等学校招生统一考试理科数学(新课标1卷))某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .16【答案】B【解析】 由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为12(24)2122⨯+⨯⨯=,故选B.点睛:三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合,解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.6.(2017年全国普通高等学校招生统一考试文科数学(新课标2))如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A .90πB .63πC .42πD .36π【答案】B【详解】 由题意,该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱,故其体积为2213634632V πππ=⋅⋅⋅+⋅⋅=,故选B. 7.(2017年全国普通高等学校招生统一考试文科数学)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是283π,则它的表面积是A.17πB.18πC.20πD.28π【答案】A【详解】:由三视图知,该几何体的直观图如图所示:是一个球被切掉左上角的18,即该几何体是78个球,设球的半径为R,则37428R833Vππ=⨯=,解得R2=,所以它的表面积是78的球面面积和三个扇形面积之和,即22734221784πππ⨯⨯+⨯⨯=,故选A.8.(2016年全国普通高等学校招生统一考试理科数学(全国2卷))如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A.20πB.24πC.28πD.32π【答案】C【详解】析:由三视图分析可知,该几何体的表面积为圆锥的表面积与圆柱的侧面积之和.,,所以几何体的表面积为.考点:三视图与表面积.9.(2016年全国普通高等学校招生统一考试文科数学(全国3卷))如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为A.18+B.54+C.90D.81【答案】B【详解】:由已知中的三视图可得:该几何体是一个以俯视图为底面的斜四棱柱,其底面面积为:3×6=18,前后侧面的面积为:3×6×2=36,左右侧面的面积为:32=,++=+.故棱柱的表面积为:183654故选B.10.(2015年全国普通高等学校招生统一考试理科数学(新课标①))圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r=A .1B .2C .4D .8【答案】B 【分析】由几何体三视图中的正视图和俯视图可知,截圆柱的平面过圆柱的轴线,该几何体是一个半球拼接半个圆柱,①其表面积为:22222111142222542222r r r r r r r r r πππππ⨯+⨯+⨯⨯+⨯+⨯=+ , 又①该几何体的表面积为16+20π,①22541620r r ππ+=+ ,解得r=2,本题选择B 选项.11.(2015年全国普通高等学校招生统一考试理科数学(新课标①))一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为A.B.C.D.【答案】D【详解】:设正方体的棱长为1,由三视图判断,正方体被切掉的部分为三棱锥,①正方体切掉部分的体积为111111326⨯⨯⨯⨯=,①剩余部分体积为15166-=,①截去部分体积与剩余部分体积的比值为15.故选D.12.(2014年全国普通高等学校招生统一考试文科数学(新课标①)如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【详解】试题分析:由三视图中的正视图可知,由一个面为直角三角形,左视图和俯视图可知其它的面为长方形.综合可判断为三棱柱.13.(2014年全国普通高等学校招生统一考试理科数学(全国①卷))如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A .1727B .59C .1027D .13【答案】C【详解】因为加工前的零件半径为3,高为6,所以体积154V π=,又因为加工后的零件,左半部为小圆柱,半径为2,高4,右半部为大圆柱,半径为3,高为2,所以体积2161834V πππ=+=,所以削掉部分的体积与原体积之比为5434105427πππ-=,故选C.14.(2013年全国普通高等学校招生统一考试理科数学(新课标1卷))某几何体的三视图如图所示,则该几何的体积为A .16+8πB .8+8πC .16+16πD .8+16π【答案】A【详解】:由已知中的三视图可得该几何体是一个半圆柱和正方体的组合体,半圆柱的底面半径为2,故半圆柱的底面积212=22S ππ=⨯⨯,半圆柱的高4h =. 故半圆柱的体积为8π,长方体的长宽高分别为422,,,故长方体的体积为42216⨯⨯=, 故该几何体的体积为168+π,选A15.(2013年全国普通高等学校招生统一考试理科数学(新课标2))一个四面体的顶点在空间直角坐标系O -xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为A .B .C .D .【答案】A【详解】:因为一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),几何体的直观图如图,是正方体的顶点为顶点的一个正四面体,所以以zOx平面为投影面,则得到正视图为:故选A.16.(2012年全国普通高等学校招生统一考试理科数学(课标卷)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18【答案】B【详解】13V Sh =,1163332=⨯⨯⨯⨯,9=.选B.二、填空题17.(2021年全国高考乙卷数学(文)试题)以图①为正视图,在图①①①①中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).【答案】①①(答案不唯一)【分析】选择侧视图为①,俯视图为①,如图所示,长方体1111ABCD A B C D -中,12,1AB BC BB ===,,E F分别为棱11,B C BC的中点,则正视图①,侧视图①,俯视图①对应的几何体为三棱锥E ADF.故答案为:①①.。
【三视图高考题】高考数学【理科】综合整理三视图部分

高考数学【理科】综合整理三视图部分
【全国新课标卷】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()
()A6()B9()C12()D18
【北京卷】某三棱锥的三视图如图所示,该三梭锥的表面积是()
A. 28+65
B. 30+65
C. 56+ 125
D. 60+125
【湖南卷】某几何体的正视图和侧视图均如图1所示,则该几何体的
俯视图不可能
...是
A B C D
【福建卷】一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
A .球
B .三棱锥
C .正方体
D .圆柱
【广东】6. 某几何体的三视图如图1
) A. 12π B. 45π C. 57π D. 81π
图1
正视图
俯视图
侧视图
俯视图
侧视图
正视图
4
【湖北】4.已知某几何体的三视图如图所示,则该几何体的体积为 A .8π3
B .3π
C .10π3
D .6π
【天津】―个几何体的三视图如图所示(单位:m ),则该几何体的
体积为 3
m .
6 3
3
1.5
【安徽】某几何体的三视图如图所示,该几何体的表面积是______。
【浙江】已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于___________cm 3.
4
4
2
5
答案
【全国新课标】B
【北京卷】B
【湖南卷】D
【福建卷】D
【广东】C
【湖北】B
【天津】18+9
【安徽】92
【浙江】1。
高考三视图强化训练题.doc

高考三视图强化训练30 题三视图之间的关系。
正视图的是几何体的高,长;侧视图的是几何体的高,宽。
俯视图的是几何体的长,宽;23 47A. 3 . B 6 C.6D.73. (2014 重庆, 5 分) 某几何体的三视图如图所示,则该几何体的体积为() A.12 B .18 C.24 D . 304.【2015高考新课标2,理 6】一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为()D.1A .1B.1C.15 8 7 65.( 2014 重庆, 5 分)某几何体的三视图如图所示,则该几何体的表面积为()1. ( 2014 新课标全国卷Ⅰ, 5 分)如图,网格纸上小正方形的边长为1,粗实线画A. 54 B. 6 0出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为() C. 66 D. 7 2A.6 2 B.4 2 C.6D.42.(2014安徽,5分)一个多面体的三视图如图所示,则该多面体的体积为()6. (2014 辽宁, 5 分) 某几何体三视图如图所示,则该几何体的体积为()A. 8-πB .8-πC . 8-πD . 8-2π4 27. (2014 四川, 5 分 ) 某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是()A.3 B .2D . 18.( 2014 浙江, 5 分)某几何体的三视图( 单位: cm)如图所示,则此几何体的表面积是()A. 90 cm 2 B.129 cm 2C. 132 cm 2 D . 138 cm29.( 2013 浙江, 5 分)已知某几何体的三视图( 单位: cm)如图所示,则该几何体的体积是 ()3 3A. 108 cm B . 100 cmC. 92 cm3D.84 cm 310.( 2013 新课标全国Ⅰ ,5分)某几何体的三视图如图所示,则该几何体的体积为 ()A. 16+8πB . 8+8πC . 16+16πD . 8+16π11.【 2015 高考新课标 1,文理 11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为16 20 ,则 r ( )(A)1 (B)2(C)4 (D)812.【 2015 高考新课标 2,理 9】已知 A,B 是球 O的球面上两点,∠ AOB=90,C 为该球面上的动点,若三棱锥 O-ABC体积的最大值为 36,则球 O的表面积为 ( )A.36ππππ13.( 2015? 北京)某三棱锥的三视图如图所示,则该三棱锥的表面积是()A. 2+B. 4+C. 2+2 D. 514.( 2015? 重庆)某几何体的三视图如图所示,则该几何体的体积为()A.1B.C.D.A. B .20.( 2015? 西宁校级模拟)某几何体的三视图如图所示,且该几何体的体积是,C.D.则正视图中的x 的值是()A.2B. C . D.315.( 2015? 北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A. 1B. C . D. 221.( 2015? 金华一模)某三棱锥的三视图如图所示,该三棱锥的体积为()16.( 2015? 安徽)一个四面体的三视图如图所示,则该四面体的表面积是()A.80B.40C. D.A.1+ B . 1+2C.2+ D .222. ( 201 1 ( 2016 文理) . 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是2,体积是3.cm cm17.( 2015? 重庆)某几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.23. ( 2016 年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为()18.( 2015? 泉州模拟)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于() A. B.3 3 3 3C. D.A. 10cmB. 20cm C. 30cm D. 40cm19.( 2015? 衢州一模)如图是某几何体的三视图,则该几何体的体积为()24.( 2016 年山东高考)有一个半球和四棱锥组成的几何体,其三视图如右图所示,则该几何体的体积为( A)1+2π(B)1+ 2 π3 3 3 3(C)1+ 2 π(D)1+ 2 π3 6 625.( 2016年四川高考)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________ .26.(2016 年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位: m),则该四棱锥的体积为 _______m3.27.( 2016 年全国 II 高考)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A)20π( B)24π( C)28π( D)32π28.. ( 2016 年全国III高考)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为29.[ 2014·湖北卷 ]在如图1- 1 所示的空间直角坐标系O -xyz 中,一个四面体的顶点坐标分别是(0 ,0, 2) ,(2 ,2,0) ,(1, 2,1) ,(2 ,2,2) .给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为()图1- 1A.①和② B .①和③ C .③和② D .④和②30.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的左视图为()(A)(B)(C)(D)( A)(B)(C)90(D)81。
专题16 三视图-备战2022年高考数学(理)母题题源解密(全国乙卷)(解析版)
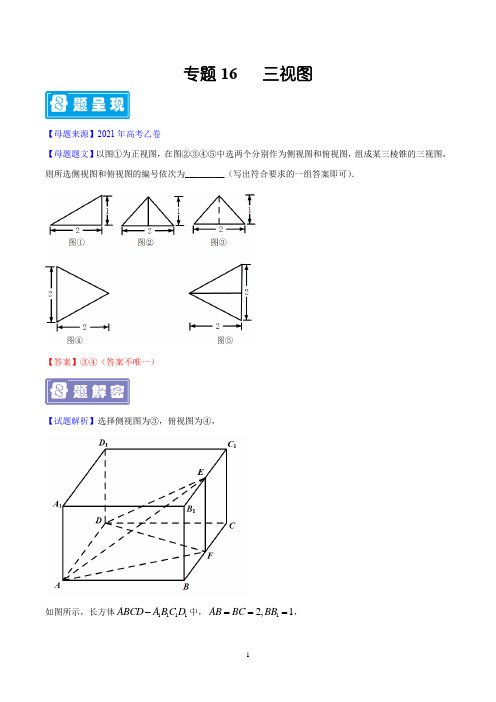
专题16 三视图【母题来源】2021年高考乙卷【母题题文】以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).【答案】③④(答案不唯一)【试题解析】选择侧视图为③,俯视图为④,如图所示,长方体1111ABCD A BC D -中,12,1AB BC BB ===,,E F分别为棱11,BC BC的中点,则正视图①,侧视图③,俯视图④对应的几何体为三棱锥E ADF.故答案为:③④.三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.【命题意图】1.认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二测法画出它们的直观图.3.会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.4.会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).5.了解球、棱柱、棱锥、台的表面积和体积的计算公式.【命题方向】空间几何体的结构是每年高考的热点之一,主要涉及空间几何体的表面积与体积的计算、三视图等内容.命题形式以选择题或填空题为主,要求考生要有较强的空间想象能力和计算能力,广泛应用转化与化归思想【得分要点】1.三视图问题的常见类型及解题策略(1)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.(2)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线,不能看到的部分用虚线表示.(3)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.2.已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.3.多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理,以确保不重复、不遗漏.4.求多面体的侧面积时,应对每一个侧面分别求解后再相加;求旋转体的侧面积时,一般要将旋转体展开为平面图形后再求面积.5.求柱体、锥体、台体体积的一般方法(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用等体积法、割补法等方法进行求解.①等体积法:一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积.②割补法:运用割补法处理不规则的空间几何体或不易求解的空间几何体的体积计算问题,关键是能根据几何体中的线面关系合理选择截面进行切割或者补成规则的几何体.要弄清切割后或补形后的几何体的体积是否与原几何体的体积之间有明显的确定关系,如果是由几个规则的几何体堆积而成的,其体积就等于这几个规则的几何体的体积之和;如果是由一个规则的几何体挖去几个规则的几何体而形成的,其体积就等于这个规则的几何体的体积减去被挖去的几个几何体的体积.因此,从一定意义上说,用割补法求几何体的体积,就是求体积的“加、减”法.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.6.求解空间几何体表面积和体积的最值问题有两个思路(1)根据几何体的结构特征和体积、表面积的计算公式,将体积或表面积的最值转化为平面图形中的有关最值,根据平面图形的有关结论直接进行判断;(2)利用基本不等式或是建立关于表面积和体积的函数关系式,然后利用函数的方法或者利用导数方法解决.7.三视图的概念①光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图;②光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图;③光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图.几何体的正视图、侧视图和俯视图统称为几何体的三视图.如图.8.三视图的画法规则(1)正视图与俯视图的长度一致,即“长对正”;(2)侧视图和正视图的高度一致,即“高平齐”;(3)俯视图与侧视图的宽度一致,即“宽相等”.注意:能看见的轮廓线用实线表示;不能看见的轮廓线用虚线表示.9.常见几何体的三视图一、单选题1.(2021·全国高三其他模拟(理))若空间某几何体的三视图如图所示,则该几何体外接球的表面积是()A.16-B.C.24πD.6+【答案】C【分析】根据三视图,可在长方体中利用构造法还原几何体,利用长方体的对角线计算外接球的直径,进而计算表面积.【详解】据三视图分析知,该几何体是由长方体截得如下图所示几何体ABCDE ,=即为外接球的直径,外接球的表面积4624S ππ=⨯=.故选C .2.(2021·全国高三其他模拟(理))某几何体的三视图如图所示,则该几何体的表面积为()A .48+B .24+C .48+D .24+【答案】C【分析】由三视图画出几何体的直观图,然后结合已知的数据求解即可【详解】由三视图可知该几何体为如图所示的四棱锥,所以该几何体的表面积为11142646548222⨯⨯+⨯+⨯⨯⨯=+故选:C.3.(2021·四川成都市·成都七中高一月考)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:3cm)是()A.43B.73C.53D.83【答案】B【分析】由几何体的三视图可知该几何体由一个长方体和一个三棱锥组成,分别求出体积即可.【详解】如图,由几何体的三视图可知该几何体由一个长方体和一个三棱锥组成,1122V =⨯⨯=长方体,111112323V =⨯⨯⨯⨯=三棱锥, 故体积17233V =+=, 故选:B.4.(2021·北京高考真题)某四面体的三视图如图所示,该四面体的表面积为( )A B .4 C .3D .2【答案】A【分析】根据三视图可得如图所示的几何体(三棱锥),根据三视图中的数据可计算该几何体的表面积.【详解】根据三视图可得如图所示的几何体-正三棱锥O ABC -,其侧面为等腰直角三角形,底面等边三角形,由三视图可得该正三棱锥的侧棱长为1,故其表面积为213112⨯⨯⨯= 故选:A.5.(2021·河南高三其他模拟(理))某个由四棱柱和三棱柱组成的组合体的三视图如图所示,则该组合体的表面积为( )A .20+B .22+C .18+D .223【答案】A【分析】 作出几何体的直观图,结合三视图中的数据可求得几何体的表面积.【详解】该组合体的直观图如图所示,其中下底面是边长为2的正方形,所以该组合体的表面积(2421224120S =⨯⨯+⨯++⨯=+故选:A.6.(2021·宜宾市翠屏区天立学校高三其他模拟(文))我国古代《九章算术》将上、下两面为平行矩形的六面体称为刍童.如图是一个刍童的三视图,其中正视图及侧视图均为等腰梯形,两底的长分别为2和4,高为2,则该刍童的表面积为()A.B.40C.16+D.16+【答案】D【分析】根据三视图,还原几何体的直观图可得,该几何体的表面由两个全等的矩形,与四个全等的等腰梯形组成,根据三视图所给数据,求出矩形与梯形的面积,求和即可.【详解】由三视图可知,该刍童的直观图是如图所示的六面体1111A B C D ABCD -,图中正方体棱长为4, 1111,,,,,,,B C D A B C A D 分别是所在正方体棱的四等分点,其表面由两个全等的矩形,与四个全等的等腰梯形组成,矩形面积为248⨯=,梯形的上下底分别为2,4,梯形的高为FG =()1242⨯+=,所以该刍童的表面积为284⨯+⨯=16+ 故选:D.【点睛】观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.7.(2019·吉林高三其他模拟(理))某几何体的三视图如图所示,则该几何体的表面积为( )A .94πB .66π+C .962π+ D .362π+ 【答案】B【分析】【详解】解:根据几何体的三视图转换为直观图为:该几何体为底面半径为1,高为3的圆柱的34. 故:233213212136644S πππ=⨯⋅⋅⋅+⨯⋅⋅+⨯⨯=+表.故选:B .8.(2019·吉林高三其他模拟(文))某几何体的三视图如图所示,则该几何体的体积为()A .94π B .66π+ C .3π D .34π【答案】A【分析】【详解】根据几何体的三视图转换为直观图为:该几何体为底面半径为1,高为3的圆柱体的34. 故239V 1344ππ=⨯⋅⋅=. 故选:A .9.(2021·浙江杭州市·杭州高级中学高三其他模拟)某空间几何体的三视图如图所示,则该几何体的体积为( )A .83B .163C .8D .16【答案】B【分析】根据三视图知该几何体是三棱锥且一个侧面与底面垂直,再根据椎体的体积公式,即可求出该几何体的体积.【详解】由三视图可知,该几何体为如图所示的三棱锥,其高为2,底面三角形的高为该几何体的体积为11162323⨯⨯=. 故选:B【点睛】 方法点睛:由三视图还原几何体,要弄清楚几何体的特征,把三视图中的数据、图形特点准确地转化为对应几何体中的线段长度、图形特点,再进行计算.10.(2019·安徽高三其他模拟(理))一个几何体的三视图及其尺寸如图所示,则该几何体的表面积为()A .16B .8C .8D .8【答案】D【分析】首先把三视图转换为几何体的直观图,进一步求出几何体的表面积.【详解】根据几何体的三视图转换为直观图为:该几何体为底面为边长为2的正方形,高为2的四棱锥体,几何体的直观图如图所示:故:A BCDE BCDE ABE ABC ACD ADE S S S S S S -=++++11222822=⨯⨯+⨯⨯=+故选:D .【点睛】本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的表面积公式的应用,主要考查运算能力和数学思维能力.11.(2021·浙江高二期末)某几何体的三视图如图,正视图和侧视图是两个全等的半圆,俯视图中圆的半径为1,则该几何体的体积为( )A .43πB .23πC .4πD .2π【分析】由三视图可知,该几何体是半径为1的半球,即可求出体积.【详解】由三视图可知,该几何体是半径为1的半球,如图, 则该几何体的体积为31421233ππ⨯⨯=. 故选:B.12.(2021·浙江金华市·高三三模)若某多面体的三视图(单位∶cm )如图所示,则此多面体的体积是( )A 3B .38cm 3 C 3 D .34cm 3【答案】D【分析】根据三视图可得该几何体为一个四棱锥,如图,即可求出体积.【详解】根据三视图还原几何体,可得该几何体为一个四棱锥,且顶点可都为一个正方体的顶点,如图粗线所示, 此多面体可看作半个正方体去掉一个三棱锥, 则此多面体的体积是334c 11222323m 2⨯-⨯⨯⨯=.13.(2020·安徽高三其他模拟)某三棱锥的三视图如图所示,该三棱锥表面上的点M、N、P、Q在三视图上对应的点分别为A、B、C、D,且A、B、C、D均在网格线上,图中网格上的小正方形的边长为1,则几何体MNPQ 的体积为()A.14B.13C.12D.23【答案】C 【分析】根据三视图可得如图三棱锥MNPQ,确定,P N位置,可得1324N MPQ F MEQV V--=⨯,即可得解.【详解】由三视图得,几何体MNPQ是一个三棱锥,且N是QF的中点,QP=34 EQ,如图,所以13331114248832 N MPQ F MEQ Q MEFV V V---=⨯==⨯⨯⨯=.故选:C.14.(2021·全国高三其他模拟(理))如图所示是某几何体的三视图,图中的四边形都是边长为a的正方形,侧视图和俯视图中的两条虚线都互相垂直,已知几何体的体积为203,则a=()A.3B C.2D【答案】C【分析】首先把三视图转换为几何体的直观图,进一步利用割补法的应用求出几何体的体积.【详解】根据几何体的三视图转换为直观图为:该几何体为一个棱长为a的正方体挖去一个底面为边长为a的长方形,高为2a 的四棱锥构成的几何体P ABCD -; 如图所示:故33215326a a V a a =-⨯-==203, 解得a =2,故选:C.二、填空题15.(2021·四川省绵阳南山中学高三其他模拟(理))一个空间几何体的主视图,侧视图是周长为8,一个内角为60︒的菱形,俯视图是圆及其圆心(如图),那么这个几何体的表面积为__________.【答案】4π【分析】由三视图还原几何体,该几何体由两个有公共底面且全等的圆锥构成,圆锥的底面直径为2,母线长度为2,可得答案.【详解】由三视图可知,该几何体由两个有公共底面且全等的圆锥构成,由主视图,侧视图是周长为8,一个内角为60︒的菱形可得,这两个圆锥的底面半径为2,母线长为2, 所以每个圆锥的底面圆的周长为2π 每个圆锥的侧面积为:12222ππ⨯⨯= 所以该几何体的表面积为224ππ⨯=故答案为:4π16.(2021·河南商丘市·高三月考(理))某三棱锥的三视图如图所示,则该三棱锥的最短棱长为___________.【分析】根据三视图还原几何体,然后计算即可.【详解】BC BD Array由图可知该三棱锥的最短棱为底面三角形的直角边即,。
高考三视图题汇编定稿版

15.(2012年高考(天津理))―个几何体的三视图如图所示(单位: ),则该几何体的体积为______ .
16.(2012年高考(辽宁理))一个几何体的三视图如图所示,则该几何体的表面积为______________.
17.(2012年高考(安徽理))某几何体的三视图如图所示,该几何体的表面积是 .
1、(2012?天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为????m3
【解析】由三视图可知几何体是组合体,下部是长方体,底面边长为3和4,高为2,
上部是放倒的四棱柱,底面为直角梯形,底面直角边长为2和1,高为1,棱柱的高为4,
所以几何体看作是放倒的棱柱,底面是5边形,
27.(天津理10)一个几何体的三视图如右图所示(单位: ),则该几何体的体积为__________
28.某长方体的三视图如右图,长度为 的体对角线在正视图中的长度为 ,在侧视图中的长度为 ,则该长方体的全面积为________________.
29.如图所示,一个三棱锥的三视图是三个直角三角形(单位:cm),则该三棱锥的外接球的表面积为____________cm2.
A. B. C.
D.
5.(2013年普通高等学校招生统一考试广东省数学(理)某四棱台的三视图如图所 示,则该四棱台的体积是
( )
A. B. C. D.
6.(2013年普通高等学校招生统一考试重庆数学(理)某几何体的三视图如题 图所示,则该几何体的体积为( )
A. B. C. D.
7.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)一个四面体的顶点在空间直角坐标系 中的坐标分别是 ,画该四面体三视图中的正视图时,以 平面为投.
三视图高考题
三视图
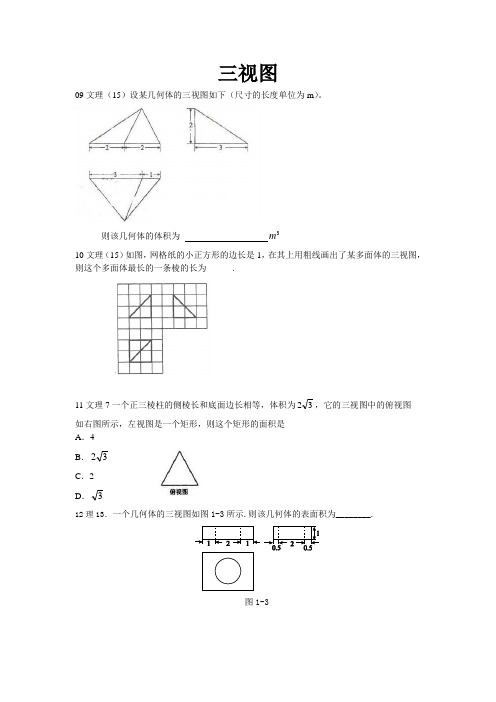
09文理(15)设某几何体的三视图如下(尺寸的长度单位为m)。
m
则该几何体的体积为3
10文理(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
2,它的三视图中的俯视图
11文理7一个正三棱柱的侧棱长和底面边长相等,体积为3
如右图所示,左视图是一个矩形,则这个矩形的面积是
A.4
2
B.3
C.2
D.3
12理13.一个几何体的三视图如图1-3所示.则该几何体的表面积为________.
图1-3
12文13.一个几何体的三视图如图所示,则该几何体的体积为__________.
13文理13)某几何体的三视图如图所示,则该几何体的体积是.。
立体几何三视图(高考题精选)
三视图强化练习(13北京)10.某四棱锥的三视图如图所示,则该四棱锥的体积为。
(12北京)7.某三棱锥的三视图如图所示,该三梭锥的表面积是()A. 28+65B. 30+65C. 56+ 125D. 60+125(11北京理)7.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A.8 B.62C.10 D.82(11北京文)5.某四棱锥的三视图如图所示,该四棱锥的表面积是A.32 B.16+162C.48 D.16+322(13辽宁)(13)某几何体的三视图如图所示,则该几何体的体积是 .(13重庆)5、某几何体的三视图如题5图所示,则该几何体的体积为()A 、5603B 、5803C 、200D 、240(13湖北)8、一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有()A. 1243V V V V B. 1324V V V V C.2134V V V V D.2314V V V V(13全国新课标1)8、某几何体的三视图如图所示,则该几何体的体积为(A )8π16(B )8π8(C )π6116(D )16π8(13全国新课标2)7、一个四面体的顶点在空间直角坐标系O xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为()(A) (B) (C) (D)(12天津)(10)一个几何体的三视图如图所示(单位:m ),则该几何体的体积3m.(11东城二模)(4)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么这个几何体的体积为(A )43(B )83(C )4(D )8(11海淀)11. 一个几何体的三视图如图所示,则这个几何体的体积为____________.(12辽宁)(13)一个几何体的三视图如图所示,则该几何体的表面积为______________。
高考数学试题分类汇编-立体几何三视图和几何证明
高考真题理科数学解析汇编:立体几何-三视图和几何证明一、选择题1 .已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为A.6B.6C.3D.22 .如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 A . 6 B .9 C .12 D .183.已知某几何体的三视图如图所示,则该几何体的体积为 ()A .8π3 B .3π C .10π3D .6π 4.某几何体的三视图如图1所示,它的体积为A .12πB .45πC .57πD .81π5.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是A .球B .三棱柱C .正方形D .圆柱6.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+B .30+C .56+D .60+二、填空题7.―个几何体的三视图如图所示(单位:m ),则该几何体的体积为______3m .8.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于___________cm 3.侧视图 正视图 俯视图9.(2012年高考(辽宁理))一个几何体的三视图如图所示,则该几何体的表面积为______________.10.某几何体的三视图如图所示,该几何体的表面积是_____.三、解答题11.如图,在四棱锥P ABCD -中,PA 丄平面A B C D,AC 丄AD ,AB 丄BC ,0=45ABC ∠,==2PA AD ,=1AC .(Ⅰ)证明PC 丄AD ;12.(2012年高考(新课标理))如图,直三棱柱111ABC A B C -中,112ACBC AA ==,D 是棱1AA 的中点,BD DC ⊥1(1)证明:BC DC ⊥113.如图,在四棱锥P —ABCD 中,底面是边长为的菱形,且∠BAD =120°,且PA ⊥平面ABCD ,PA=M ,N 分别为PB ,PD 的中点.(Ⅰ)证明:MN ∥平面ABCD ;14如图所示的几何体中,四边形A B C D是等腰梯形AB∥CD,60,DAB FC ∠=⊥平面,,ABCD AE BD CB CD CF ⊥==.DCBAP(Ⅰ)求证:BD ⊥平面AED ;15如图,直三棱柱///ABC A B C -,90BAC ∠=,/,AB AC AA λ==点M ,N 分别为/AB 和//B C 的中点.(Ⅰ)证明:MN ∥平面//A ACC ;16.如图,在直三棱柱111ABC A B C -中,1111A B AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),AD DE F⊥,为11B C 的中点.求证:(1)平面ADE ⊥平面11BCC B ;(2)直线1//A F 平面ADE .17.如图5,在四棱锥P-ABCD 中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E 是CD的中点.(Ⅰ)证明:CD⊥平面PAE;18.如图5所示,在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,点E 在线段PC 上,PC ⊥平面BDE .(Ⅰ)证明:BD ⊥平面PAC ;19.(2012年高考(大纲理))(注意:在试题卷上作答无效.........)如图,四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥底ABCD,AC =2,PA E =是PC 上的一点,2PE EC =.(1)证明:PC ⊥平面BED;ABC DPE 图5D一、选择题1. 【解析】选AABC ∆的外接圆的半径3r =,点O 到面ABC 的距离3d ==SC 为球O 的直径⇒点S 到面ABC 的距离为2d =此棱锥的体积为11233ABC V S d ∆=⨯==另:123ABC V S R ∆<⨯=排除,,B C D 2. 【解析】选B 该几何体是三棱锥,底面是俯视图,高为3此几何体的体积为11633932V =⨯⨯⨯⨯= 3.考点分析:本题考察空间几何体的三视图.解析:显然有三视图我们易知原几何体为 一个圆柱体的一部分,并且有正视图知是一个1/2的圆柱体,底面圆的半径为1,圆柱体的高为6,则知所求几何体体积为原体积的一半为3π.选B.4.解析:C.该几何体下部分是半径为3,高为5的圆柱,体积为23545V ππ=⨯⨯=,上部分是半径为3,高为4的圆锥,体积为2134123V ππ=⨯⨯⨯=,所以体积为57π.5. 【答案】D【解析】分别比较ABC 的三视图不符合条件,D 符合.【考点定位】考查空间几何体的三视图与直观图,考查空间想象能力、逻辑推理能力. 6. 【答案】B【解析】从所给的三视图可以得到该几何体为三棱锥,本题所求表面积为三棱锥四个面的面积之和.利用垂直关系和三角形面积公式,可得:10,10,10,S S S S ====后右左底因此该几何体表面积30S =+,故选B. 【考点定位】本小题主要考查的是三棱锥的三视图问题,原来考查的是棱锥或棱柱的体积而今年者的是表面积,因此考查了学生的计算基本功和空间想象能力.二、填空题7. 【答案】18+9π【解析】由三视图可该几何体为两个相切的球上方了一个长方体组成的组合体,所以其体积为:343=361+2()32V π⨯⨯⨯⨯=18+9π3m . 8. 【答案】1 【解析】观察三视图知该三棱锥的底面为一直角三角 形,右侧面也是一直角三角形.故体积等于11312123⨯⨯⨯⨯=.9. 【答案】38 【解析】由三视图可知该几何体为一个长方体在中间挖去了一个等高的圆柱,其中长方体的长、宽、高分别为4、3、1,圆柱的底面直径为2,所以该几何体的表面积为长方体的表面积加圆柱的侧面积再减去圆柱的底面积,即为2(344131)211ππ⨯+⨯+⨯+⨯⨯-=10. 【答案】92【解析】由三视图可知,原几何体是一个底面是直角梯形,高为4的直四棱柱,其底面积为(25)42282+⨯=,侧面积为(4255)464+++⨯=,故表面积为92. 三、解答题11.(1)证明,由PA ⊥平面A B C D,可得PA AD ⊥,又由,A D A C P A A C A ⊥⋂=,故AD ⊥平面PAC ,又PC ⊂平面PAC ,所以PC AD ⊥.12. 【解析】(1)在Rt DAC ∆中,AD AC =得:45ADC ︒∠=同理:1114590A DC CDC ︒︒∠=⇒∠=得:111,DC DC DC BD DC ⊥⊥⇒⊥面1BCD DC BC ⇒⊥13. (Ⅰ)如图连接BD .∵M ,N 分别为PB ,PD 的中点, ∴在∆PBD 中,MN ∥BD . 又MN ⊄平面ABCD , ∴MN ∥平面ABCD ;14. 解析:(Ⅰ)在等腰梯形ABCD 中,AB∥CD,∠DAB=60°,CB=CD,由余弦定理可知202223)180cos(2CD DAB CB CD CB CD BD =∠-⋅⋅-+=,即AD CD BD 33==,在ABD ∆中,∠DAB=60°,AD BD 3=,则ABD ∆为直角三角形,且DB AD ⊥.又AE⊥BD,⊂AD 平面AED,⊂AE 平面AED,且A AE AD = ,故BD⊥平面AED;15. (1) 证明:取''A B 中点P,连结MP,NP,而M,N 分别是A 'B 与'B 'C 的中点,所以,MP∥A 'A ,PN∥'A 'C ,所以,MP∥平面'A AC 'C ,PN∥平面'A AC 'C ,又MP NP p ⋂=,因此平面MPN∥平面'A AC 'C ,而MN ⊂平面MPN,所以,MN∥平面'A AC 'C ,16. 【答案】证明:(1)∵111ABC A B C -是直三棱柱,∴1CC ⊥平面ABC .又∵AD ⊂平面ABC ,∴1CC AD ⊥.又∵1AD DE CC DE ⊥⊂,,平面111BCC B CC DE E =,,∴AD ⊥平面11BCC B .又∵AD ⊂平面ADE ,∴平面ADE ⊥平面11BCC B .(2)∵1111A B AC =,F 为11B C 的中点,∴111A F B C ⊥.又∵1CC ⊥平面111A B C ,且1A F ⊂平面111A B C ,∴11CC A F ⊥. 又∵111 CC B C ⊂,平面11BCC B ,1111CC B C C =,∴1A F ⊥平面111A B C .由(1)知,AD ⊥平面11BCC B ,∴1A F ∥AD .又∵AD ⊂平面1, ADE A F ∉平面ADE ,∴直线1//A F 平面ADE17. 连接AC,由AB=4,3BC=,90 5.ABC AC ∠==,得5,AD =又E 是CD 的中点,所以.CD AE ⊥,,PA ABCD CD ABCD ⊥⊂平面平面所以.PA CD ⊥而,PA AE 是平面PAE 内的两条相交直线,所以CD⊥平面PAE.18. 解析:(Ⅰ)因为PC ⊥平面BDE ,BD ⊂平面BDE ,所以PC BD ⊥.又因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以PA BD ⊥.而PC PA P =,PC ⊂平面PAC ,PA ⊂平面PAC ,所以BD ⊥平面PAC .19. 解:(1)CD DE ⊥,1A E DE ⊥ ∴DE ⊥平面1ACD , 又1A C ⊂平面1ACD , ∴1A C ⊥DE 又1AC CD ⊥, ∴1A C ⊥平面BCDE 20. 【解析】(I)取11,BC B C 的中点为点1,O O ,连接1111,,,AO OO AO AO则AB AC AO BC =⇒⊥,面ABC ⊥面11BB C C AO ⇒⊥面11BB C C 同理:11A O ⊥面11BB C C 得:1111//,,,AO AO A O A O ⇒共面 又11,OO BC OO AO O ⊥=⇒BC ⊥面111AOO A AA BC ⇒⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【最新整理,下载后即可编辑】
专题21 三视图
1.某几何体的三视图如图所示,则其表面积为()
A.2π B.3π C.4π D.5π
【答案】B
点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;
2、观察正视图和侧视图找到几何体前、后、左、右的高度;
3、画出整体,然后再根据三视图进行调整.
2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )
A.B.C.
D.
【答案】B
【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2
⊥平面时,BC=2,
===,当BC ABD
AB BD AD
∆的边AB上的高为3,只有B选项符合,当BC不垂直平面ABD ABD
时,没有符合条件的选项,故选B.
点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.
2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,
可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据
3.某个长方体被一个平面所截,得到几何体的三视图
如图所示,则这个几何体的体积为( )
A . 4
B . 22
C .
203 D . 8
【答案】D
4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则
此正三棱柱的左视图的面积为( )
A . 16
B . 23
C . 43
D . 83
【答案】D
点睛:三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合. (3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.
5.某几何体的三视图如图所示,则该几何体的体积为 ( )
(A) 168π+ (B) 88π+ (C) 1616π+
(D) 816π+
【答案】A
【解析】
将三视图还原为原来的几何体,再利用体积公式求解.
原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21
422241682V ππ=⨯⨯+⨯⨯=+.故选A;
6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )
(A) 62 (B) 42 (C) 6 (D)4
【答案】C
【解析】如图所示
点睛:对于小方格中的三视图,可以放到长方体,或者正方体里
面去找到原图,这样比较好找;
7.某几何体的三视图如图所示,则该几何体的表面积为( )
A.24π-B.24π+C.20π-D.20π+
【答案】A
8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()
A.B.C.D.
【答案】A
【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,
,,
,∴,∴, ,
,,
∴,故选A .
9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
A .1π+
B .2π+
C .21π+
D .3522π++
【答案】A
【解析】
考点:由三视图求体积.
10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )
A .263π+
B .83
π+ C .243π+ D .43
π+ 【答案】C
【解析】
试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.
考点:三视图.
11.一个几何体的三视图如图所示,则该几何体的体积为( )
A . 143
B . 5
C . 163
D .6
【答案】A
【解析】
考点:三视图.
12.一个几何体的三视图如图所示,则该几何体的体积为____.
【答案】1
3
【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的
四棱锥,故其体积为11
111
V=⨯⨯⨯=.
33。
