统计学(第三版课后习题答案
《统计学基础》第三版习题答案
各位老师读者好：《统计学基础》（王瑞卿主编，北京大学出版社，2016年8月第3版）每个项目后面设置了技能训练题库，由于统计学教材很多，不同的老师在编写时内容描述会有些许差异，所以有些习题答案可能有差异，答案以本教材为准。
祝各位工作、学习顺利。
真诚欢迎各位提出您的宝贵意见！王瑞卿2016年9月12日项目1 统计概论一、填空题1．现代统计的含义包括三个方面： 、 和 。
2．一个完整的统计工作过程可以划分为 、 、 、 四个阶段。
3．总体是由许多具有 的个别事物组成的整体；总体单位是 的组成单位。
4．标志是说明总体单位的特征的名称，按表现形式不同分为 和 两种。
5．统计指标按其所说明的总体现象内容的不同，可分为 和 。
参考答案1.统计工作统计资料统计学2. 统计设计统计调查统计整理统计分析3.共同属性总体4.数量标志品质标志5.数量指标质量指标二、单项选择题1．统计总体的同质性是指（B ）。
A．总体各单位具有某一共同的品质标志或数量标志B．总体各单位具有某一共同的品质标志属性或数量标志值C．总体各单位具有若干互不相同的品质标志或数量标志D．总体各单位具有若干互不相同的品质标志属性或数量标志值2．某地区有800家工业企业，要研究这些企业的产品生产情况，总体是（ A ），总体单位是（ B ）。
A．全部工业企业B．每一家工业企业C．每一件产品D．800家工业企业的全部工业产品3．要了解某班50名学生的学习情况，则总体是（ A ），总体单位是（ C ）。
A．50名学生B．50个学生的学习成绩C．每一个学生D．每一个学生的学习成绩4．一个统计总体（ B ）。
A．只能有一个标志B．可以有多个标志C．只能有一个指标D．可以有多个指标5．张明的月工资为4560元，工资是（ B ），4550是（ C ）。
A．品质标志B．数量标志C．变量值D．指标6．在调查设计时，学校作为总体，每个班作为总体单位，各班学生人数是（ A ）。
统计学(第三版)课后习题答案
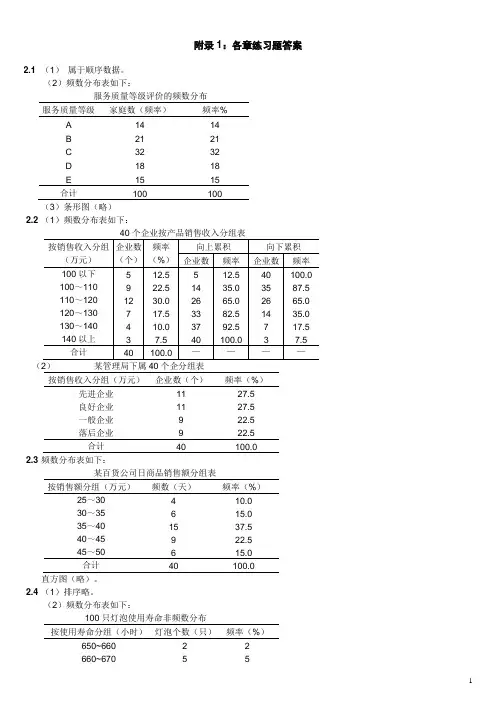
附录1：各章练习题答案2.1 （1）属于顺序数据。
（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频率）频率%A1414B2121C3232D1818E1515合计100100（3）条形图（略）2.2 （1）频数分布表如下：（2）某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.0 2.3 频数分布表如下：某百货公司日商品销售额分组表按销售额分组（万元）频数（天）频率（%）25～30 30～35 35～40 40～45 45～5046159610.015.037.522.515.0合计40 100.0 直方图（略）。
2.4 （1）排序略。
（2）频数分布表如下：100只灯泡使用寿命非频数分布按使用寿命分组（小时）灯泡个数（只）频率（%）650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100直方图（略）。
2.5 （1）属于数值型数据。
（2）分组结果如下：分组天数（天）-25~-20 6-20~-15 8-15~-10 10-10~-5 13-5~0 120~5 45~10 7合计60（3）直方图（略）。
2.6 （1）直方图（略）。
（2）自学考试人员年龄的分布为右偏。
2.7 （1（2）A班考试成绩的分布比较集中，且平均分数较高；B班考试成绩的分布比A班分散，且平均成绩较A班低。
2.8 箱线图如下：（特征请读者自己分析）2.9 （1）x =274.1（万元）；Me=272.5 ；Q L =260.25；Q U =291.25。
（2）17.21=s （万元）。
2.10 （1）甲企业平均成本＝19.41（元），乙企业平均成本＝18.29（元）；原因：尽管两个企业的单位成本相同，但单位成本较低的产品在乙企业的产量中所占比重较大，因此拉低了总平均成本。
统计学课后答案(第3版)第6章抽样分布与参数估计习题答案
第六章 抽样分布与参数估计习题答案一、单选1.B ；2.D ；3.D ；4.C ；5.A ；6.B ；7.C ；8.D ；9.A ；10.A 二、多选1.ADE ；2.ACDE ；3.ABCD ；4.ADE ；5.BCE6.ACD ；7.ACDE ；8.ACE ；9.BCE ；10.ABD 三、计算分析题1、解：n=10，小样本，由EXCEL 计算有：11.6498==S x ； （1）方差已知，由10596.14982⨯±=±nz x σα得，（494.9，501.1）（2）方差未知，由1011.62622.2498)1(2⨯±=-±nS n t x α得，（493.63，502.37）2、n=500为大样本，p=80/500=16%，则置信区间为 016.096.1%16500)16.01(16.096.1%16)1(2⨯±=-⨯±=-±n p p z p α=（14.4%，17.6%） 3、nx σσ=，由于大国抽取的样本容量大，则抽样平均误差小。
4、（1）3.10100103===nS x σ（小时）；=-=-=100)95.01(95.0)1(n p p p σ 2.18%（2）=⨯±=±3.10211202x z x σα（1099.4,1140.6） ⨯±=±2%952p z p σα2.18%=（90.64,99.36）5、为简化起见，按照重复抽样形式计算 （1）∑∑=ff s Si22=22.292； 472.010072.4===nS x σ（2）93.0691472.096.1100691002±=⨯±=±nSz x α=（690.07,691.93） 6、由于总体标准差已知，则用标准状态分布统计量估计nz x σα2=∆（1）10160170102022=-===∆αασz nz x则58.12=αz ，有%29.94)58.1(=F α=1-94.29%=5.71%，则概率%58.88%71.5%29.941=-=-=α （2）=⇒⨯=⇒⨯=∆n n nz x 2096.142σα97（个）（3）=⇒⨯=⇒⨯=∆n nnz x 2096.122σα385（个）允许误差缩小一半，样本容量则为原来的4倍。
统计学教材课后答案 第三版 袁卫 庞皓 曾五一 贾俊平主编
第四章、参数估计1．简述评价估计量好坏的标准答：评价估计量好坏的标准主要有：无偏性、有效性和相合性。
设总体参数θ的估计量有1ˆθ和2ˆθ，如果()1ˆE θθ=，称1ˆθ是无偏估计量；如果1ˆθ和2ˆθ是无偏估计量，且()1ˆD θ小于()2ˆD θ，则1ˆθ比2ˆθ更有效；如果当样本容量n →∞，1ˆθθ→，则1ˆθ是相合估计量。
2.说明区间估计的基本原理答：总体参数的区间估计是在一定的置信水平下，根据样本统计量的抽样分布计算出用样本统计量加减抽样误差表示的估计区间，使该区间包含总体参数的概率为置信水平。
置信水平反映估计的可信度，而区间的长度反映估计的精确度。
3．解释置信水平为95％的置信区间的含义答：总体参数是固定的，未知的，置信区间是一个随机区间。
置信水平为95％的置信区间的含义是指，在相同条件下多次抽样下，在所有构造的置信区间里大约有95％包含总体参数的真值。
4．简述样本容量与置信水平、总体方差、允许误差的关系答：以估计总体均值时样本容量的确定公式为例：()22/22z n E ασ= 样本容量与置信水平成正比、与总体方差成正比、与允许误差成反比。
练习题：●1.解：已知总体标准差σ=5，样本容量n =40，为大样本，样本均值x =25，（1）样本均值的抽样标准差σ5=0.7906 （2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E =α/2Z 6×0.7906=1.5496。
●2.解：（1）已假定总体标准差为σ=15元，则样本均值的抽样标准误差为x σ15=2.1429（2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E=α/2Z 6×2.1429=4.2000。
（3）已知样本均值为x =120元，置信水平1－α=95%，得 α/2Z =1.96，这时总体均值的置信区间为±α/2x Z 0±4.2=124.2115.8 可知，如果样本均值为120元，总体均值95%的置信区间为（115.8，124.2）元。
《统计学基础》第三版习题答案
各位老师读者好：《统计学基础》（王瑞卿主编，北京大学出版社，2016年8月第3版）每个项目后面设置了技能训练题库，由于统计学教材很多，不同的老师在编写时内容描述会有些许差异，所以有些习题答案可能有差异，答案以本教材为准。
祝各位工作、学习顺利。
真诚欢迎各位提出您的宝贵意见！王瑞卿2016年9月12日项目1 统计概论一、填空题1．现代统计的含义包括三个方面： 、 和 。
2．一个完整的统计工作过程可以划分为 、 、 、 四个阶段。
3．总体是由许多具有 的个别事物组成的整体；总体单位是 的组成单位。
4．标志是说明总体单位的特征的名称，按表现形式不同分为 和 两种。
5．统计指标按其所说明的总体现象内容的不同，可分为 和 。
参考答案1.统计工作统计资料统计学2. 统计设计统计调查统计整理统计分析3.共同属性总体4.数量标志品质标志5.数量指标质量指标二、单项选择题1．统计总体的同质性是指（B ）。
A．总体各单位具有某一共同的品质标志或数量标志B．总体各单位具有某一共同的品质标志属性或数量标志值C．总体各单位具有若干互不相同的品质标志或数量标志D．总体各单位具有若干互不相同的品质标志属性或数量标志值2．某地区有800家工业企业，要研究这些企业的产品生产情况，总体是（ A ），总体单位是（ B ）。
A．全部工业企业B．每一家工业企业C．每一件产品D．800家工业企业的全部工业产品3．要了解某班50名学生的学习情况，则总体是（ A ），总体单位是（ C ）。
A．50名学生B．50个学生的学习成绩C．每一个学生D．每一个学生的学习成绩4．一个统计总体（ B ）。
A．只能有一个标志B．可以有多个标志C．只能有一个指标D．可以有多个指标5．张明的月工资为4560元，工资是（ B ），4550是（ C ）。
A．品质标志B．数量标志C．变量值D．指标6．在调查设计时，学校作为总体，每个班作为总体单位，各班学生人数是（ A ）。
《统计学》课后练习题答案
A．透视表B.合并计算C.单变量求解D.分类汇总
5.小张收集了1957-2007年中国GDP的数据，如果要反映这50年我国生产发展的趋势，用什么图形最为合适？（）（知识点3.5答案：D）
A.直方图B.散点图C.饼图D.折线图
37
பைடு நூலகம்33.6
130-140
12
10.9
103
93.6
19
17.3
140-150
5
4.5
108
98.2
7
6.4
150-160
2
1.8
110
100.0
2
1.8
合计
110
100
—
—
—
—
A.树苗高度低于110厘米的占总数的39.1%B.树苗高度低于110厘米的占总数的84.5%
C.树苗高度高于130厘米的有19棵D.树苗高度高于130厘米的有103棵
第二章数据的收集与整理
2.1数据的来源
2.2统计调查方案设计
2.3调查方法
2.4调查的组织方式：普查、抽样调查、重点调查、典型调查
2.5抽样的组织方式：简单随机抽样、系统抽样、分层抽样、整群抽样
2.6数据的审定：误差
2.7数据的分组
2.8.编制次数分布表：频数（次数）、频率
习题
一、单项选择题
1．小吴为写毕业论文去收集数据资料，（）是次级数据。(知识点：2.1答案：C)
A.指标B.标志C.变量D.标志值
8.以一、二、三等品来衡量产品质地的优劣，那么该产品等级是（）。(知识点：1.7答案：A)
A.品质标志B.数量标志C.质量指标D.数量指标
统计学(第三版)课后答案 袁卫等主编
统计学第一章1.什么是统计学？怎样理解统计学与统计数据的关系？答：统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系，统计学阐述的统计方法来源于对统计数据的研究，目的也在于对统计数据的研究，离开了统计数据，统计方法以致于统计学就失去了其存在意义。
2．简要说明统计数据的来源答：统计数据来源于两个方面：直接的数据：源于直接组织的调查、观察和科学实验，在社会经济管理领域，主要通过统计调查方式来获得，如普查和抽样调查。
间接的数据：从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答：统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的，从理论上看，这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差，它是不可避免的，但可以控制的。
4.答：（1）有两个总体：A品牌所有产品、B品牌所有产品（2）变量：口味（如可用10分制表示）（3）匹配样本：从两品牌产品中各抽取1000瓶，由1000名消费者分别打分，形成匹配样本。
（4）从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答：分二个步骤：（1）按照统计研究的目的，将数据按分组标志进行分组。
按品质标志进行分组时，可将其每个具体的表现作为一个组，或者几个表现合并成一个组，这取决于分组的粗细。
按数量标志进行分组，可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组；组距式分组将变量的取值范围（区间）作为一个组。
统计分组应遵循“不重不漏”原则（2）将数据分配到各个组，统计各组的次数，编制次数分配表。
2．解释洛伦兹曲线及其用途答：洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
3. 一组数据的分布特征可以从哪几个方面进行测度？答：数据分布特征一般可从集中趋势、离散程度、偏态和峰度几方面来测度。
《统计学基础》第三版习题答案
各位老师读者好：《统计学基础》（王瑞卿主编，北京大学出版社，2016年8月第3版）每个项目后面设置了技能训练题库，由于统计学教材很多，不同的老师在编写时内容描述会有些许差异，所以有些习题答案可能有差异，答案以本教材为准。
祝各位工作、学习顺利。
真诚欢迎各位提出您的宝贵意见！王瑞卿2016年9月12日项目1 统计概论一、填空题1．现代统计的含义包括三个方面： 、 和 。
2．一个完整的统计工作过程可以划分为 、 、 、 四个阶段。
3．总体是由许多具有 的个别事物组成的整体；总体单位是 的组成单位。
4．标志是说明总体单位的特征的名称，按表现形式不同分为 和 两种。
5．统计指标按其所说明的总体现象内容的不同，可分为 和 。
参考答案1.统计工作统计资料统计学2. 统计设计统计调查统计整理统计分析3.共同属性总体4.数量标志品质标志5.数量指标质量指标二、单项选择题1．统计总体的同质性是指（B ）。
A．总体各单位具有某一共同的品质标志或数量标志B．总体各单位具有某一共同的品质标志属性或数量标志值C．总体各单位具有若干互不相同的品质标志或数量标志D．总体各单位具有若干互不相同的品质标志属性或数量标志值2．某地区有800家工业企业，要研究这些企业的产品生产情况，总体是（ A ），总体单位是（ B ）。
A．全部工业企业B．每一家工业企业C．每一件产品D．800家工业企业的全部工业产品3．要了解某班50名学生的学习情况，则总体是（ A ），总体单位是（ C ）。
A．50名学生B．50个学生的学习成绩C．每一个学生D．每一个学生的学习成绩4．一个统计总体（ B ）。
A．只能有一个标志B．可以有多个标志C．只能有一个指标D．可以有多个指标5．张明的月工资为4560元，工资是（ B ），4550是（ C ）。
A．品质标志B．数量标志C．变量值D．指标6．在调查设计时，学校作为总体，每个班作为总体单位，各班学生人数是（ A ）。
统计学课后习题答案(统计学 第三版
第1章1．什么是统计学?怎样理解统计学与统计数据的关系?2．试举出日常生活或工作中统计数据及其规律性的例子。
3．．一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此，他们开始检查供货商的集装箱，有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆，每一罐的质量精确到4位小数。
装满的油漆罐应为4.536 kg。
要求：(1)描述总体；(2)描述研究变量；(3)描述样本；(4)描述推断。
答：(1)总体：最近的一个集装箱内的全部油漆；(2)研究变量：装满的油漆罐的质量；(3)样本：最近的一个集装箱内的50罐油漆；(4)推断：50罐油漆的质量应为4.536×50＝226.8 kg。
4．“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分，选择了1000名消费者进行匿名性质的品尝试验(即在品尝试验中，两个品牌不做外观标记)，请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求：(1)描述总体；(2)描述研究变量；(3)描述样本；(4)一描述推断。
答：(1)总体：市场上的“可口可乐”与“百事可乐”(2)研究变量：更好口味的品牌名称；(3)样本：1000名消费者品尝的两个品牌(4)推断：两个品牌中哪个口味更好。
第2章统计数据的描述——练习题(1) 指出上面的数据属于什么类型；(2)用Excel制作一张频数分布表；(3) 绘制一张条形图，反映评价等级的分布。
解：（1）由于表2.21中的数据为服务质量的等级，可以进行优劣等级比较，但不能计算差异大小，属于顺序数据。
（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频数）频率%A1414B2121C 32 32D 18 18E 15 15 合计100100（3）条形图的制作：将上表(包含总标题，去掉合计栏)复制到Excel 表中，点击：图表向导→条形图→选择子图表类型→完成(见Excel 练习题2.1)。
生物统计学(第3版)杜荣骞 课后习题答案 第七章 拟合优度检验
第七章拟合优度检验7.12000年在5 760 295名成年人群中和1 596 734名儿童群体中严重CDH（先天性心脏病）和其他程度CDH的流行病学患者数如下表[36]：尚存活的成年人 2 205 21 358 23 563尚存活的儿童 2 316 16 663 18 979 合计 4 521 38 021 42 542检验在尚存活的成年人和儿童中受损害的程度，差异是否显著？答：这是2×2列联表χ2检验，使用程序如下：options linesize=76 nodate;data;do a=1 to 2;do b=1 to 2;input case @@;output;end;end;cards;2205 213582316 16663;proc freq formchar(1,2,7)='|-+';weight case;tables a*b/cellchi2 expected nocol norow nopercent chisq;title '2*2 Contingency Table Test';run;程序运行结果见下表：2*2 Contingency Table TestTABLE OF A BY BA BFrequency |Expected |Cell Chi-Square| 1| 2| Total---------------+--------+--------+1 | 2205 | 21358 | 23563| 2504.1 | 21059 || 35.72 | 4.2474 |---------------+--------+--------+2 | 2316 | 16663 | 18979| 2016.9 | 16962 || 44.347 | 5.2733 |---------------+--------+--------+Total 4521 38021 42542STATISTICS FOR TABLE OF A BY BStatistic DF Value Prob------------------------------------------------------Chi-Square 1 89.588 0.001Likelihood Ratio Chi-Square 1 89.070 0.001Continuity Adj. Chi-Square 1 89.289 0.001Mantel-Haenszel Chi-Square 1 89.586 0.001Fisher's Exact Test (Left) 2.21E-21(Right) 1.000(2-Tail) 4.20E-21Phi Coefficient -0.046Contingency Coefficient 0.046Cramer's V -0.046Sample Size = 42542从“A×B列联表的统计量”部分可以得出，连续性矫正的χ2显著性概率P＝0.001，P <0.01，故拒绝H0，在尚存活的成年人和儿童中受损害的程度差异极显著。
(完整版)孙振球第三版研究生医学统计学课后习题答案
医学统计学作业答案（二～四章）第二章三、计算分析题 1.（1） 均数=1.156 （2）标准差=0.2044（3）)5566.1~7554.0(96.1=±s x（4）0.8mmol/L 以下者占4.09%； 1.5 mmol/L 以下者占95.35%2. 平均抗体滴度：1:36.833. 08.15=x ；M=14；M 代表性好；95%的参考值范围：<(P 95) 36第三章1.（1）女性血红蛋白的变异程度（CV=0.087）> 红细胞的变异程度（CV=0.069） （2）男性血红蛋白的标准误=0.374；红细胞的标准误=0.0306 （3）健康成年女性红细胞均数95%C.I.为4.144～4.216 （4）成年男女血红蛋白含量不同，t=24.03, P =0.0001（5）男性两项指标均低于标准值，红细胞与标准值比较， t=5.89,P =0.0001 血红蛋白与标准值比较，t=15.23, P =0.00012. 该批药有效成分平均含量为95%C.I.=(101.41～104.59)3. t=1.1429， P =0.1355, 还没有足够证据认为当地现在20岁男子比以往的高。
4. t=3.71, P =0.001，新药和标准药的疗效差别有统计学意义。
5. （1）对数转换；（2）方差齐性检验，F=3.69, P =0.038， 转换后两总体方差仍不齐；（3）用welch 法校正t 检验：t=3.35, ν=17, P =0.0039 标准株和水生株平均效价差别有统计学意义。
6.（1）两药平均退热天数之差的95% C.I.为：1.0～1.8天（2）t=6.96, P =0.0001, 两药平均退热天数差别有统计学意义 （3）上述两种方法中（1）因95%C.I.不包括H 0（μ1-μ2=0），也可以说明两药退热天数不同（α=0.05）；（2）的检验中可以看出两药退热天数不同，并说明其概率非常小。
高等教育出版社《统计学》第三版答案
第1章绪论1什么是统计学怎样理解统计学与统计数据的关系2试举出日常生活或工作中统计数据及其规律性的例子。
3一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此他们开始检查供货商的集装箱有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆每一罐的质量精确到4位小数。
装满的油漆罐应为4.536 kg。
要求1描述总体2描述研究变量3描述样本4描述推断。
答1总体最近的一个集装箱内的全部油漆2研究变量装满的油漆罐的质量3样本最近的一个集装箱内的50罐油漆4推断50罐油漆的质量应为4.536×50226.8 kg。
4“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分选择了1000名消费者进行匿名性质的品尝试验即在品尝试验中两个品牌不做外观标记请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求1描述总体2描述研究变量3描述样本4一描述推断。
答1总体市场上的“可口可乐”与“百事可乐” 2研究变量更好口味的品牌名称3样本1000名消费者品尝的两个品牌4推断两个品牌中哪个口味更好。
第2章统计数据的描述——练习题●1. 解1由于表2.21中的数据为服务质量的等级可以进行优劣等级比较但不能计算差异大小属于顺序数据。
2频数分布表如下服务质量等级评价的频数分布服务质量等级家庭数频数频率 A 14 14 B 21 21 C 32 32 D 18 18 E 15 15 合计100 100 3条形图的制作将上表包含总标题去掉合计栏复制到Excel表中点击图表向导→条形图→选择子图表类型→完成见Excel练习题2.1。
即得到如下的条形图02040ABCDE服务质量等级评价的频数分布频率服务质量等级评价的频数分布家庭数频数●2. 解1要求对销售收入的数据进行分组全部数据中最大的为152最小的为87知数据全距为1528765 为便于计算和分析确定将数据分为6组各组组距为10组限以整10划分为使数据的分布满足穷尽和互斥的要求注意到按上面的分组方式最小值87可能落在最小组之下最大值152可能落在最大组之上将最小组和最大组设计成开口形式按照“上限不在组内”的原则用划记法统计各组内数据的个数——企业数也可以用Excel 进行排序统计见Excel练习题2.2将结果填入表内得到频数分布表如下表中的左两列将各组企业数除以企业总数40得到各组频率填入表中第三列在向上的数轴中标出频数的分布由下至上逐组计算企业数的向上累积及频率的向上累积由上至下逐组计算企业数的向下累积及频率的向下累积。
统计学第三版课后答案
统计学第三版答案第一章1.什么是统计学？怎样理解统计学与统计数据的关系？答：统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系，统计学阐述的统计方法来源于对统计数据的研究，目的也在于对统计数据的研究，离开了统计数据，统计方法以致于统计学就失去了其存在意义。
2．简要说明统计数据的来源答：统计数据来源于两个方面：直接的数据：源于直接组织的调查、观察和科学实验，在社会经济管理领域，主要通过统计调查方式来获得，如普查和抽样调查。
间接的数据：从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答：统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的，从理论上看，这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差，它是不可避免的，但可以控制的。
4.答：（1）有两个总体：A品牌所有产品、B品牌所有产品（2）变量：口味（如可用10分制表示）（3）匹配样本：从两品牌产品中各抽取1000瓶，由1000名消费者分别打分，形成匹配样本。
（4）从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答：分二个步骤：（1）按照统计研究的目的，将数据按分组标志进行分组。
按品质标志进行分组时，可将其每个具体的表现作为一个组，或者几个表现合并成一个组，这取决于分组的粗细。
按数量标志进行分组，可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组；组距式分组将变量的取值范围（区间）作为一个组。
统计分组应遵循“不重不漏”原则（2）将数据分配到各个组，统计各组的次数，编制次数分配表。
2．解释洛伦兹曲线及其用途答：洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
统计学第三版答案
第1章统计和统计数据第2章 1.1 指出下面的变量类型。
（1）年龄。
（2）性别。
（3）汽车产量。
（4）员工对企业某项改革措施的态度（赞成、中立、反对）。
（5）购买商品时的支付方式（现金、信用卡、支票）。
详细答案：（1）数值变量。
（2）分类变量。
（3）数值变量。
（4）顺序变量。
（5）分类变量。
1.2 一家研究机构从IT从业者中随机抽取1000人作为样本进行调查，其中60%回答他们的月收入在5000元以上，50%的人回答他们的消费支付方式是用信用卡。
（1）这一研究的总体是什么？样本是什么？样本量是多少？（2）“月收入”是分类变量、顺序变量还是数值变量？（3）“消费支付方式”是分类变量、顺序变量还是数值变量？详细答案：（1）总体是“所有IT从业者”，样本是“所抽取的1000名IT从业者”，样本量是1000。
（2）数值变量。
（3）分类变量。
1.3 一项调查表明，消费者每月在网上购物的平均花费是200元，他们选择在网上购物的主要原因是“价格便宜”。
（1）这一研究的总体是什么？（2）“消费者在网上购物的原因”是分类变量、顺序变量还是数值变量？详细答案：（1）总体是“所有的网上购物者”。
（2）分类变量。
1.4 某大学的商学院为了解毕业生的就业倾向，分别在会计专业抽取50人、市场营销专业抽取30、企业管理20人进行调查。
（1）这种抽样方式是分层抽样、系统抽样还是整群抽样？（2）样本量是多少？详细答案：（1）分层抽样。
（2）100。
第2章用图表展示数据（3）帕累托图如下：（4）饼图如下：2.2 为确定灯泡的使用寿命（单位：小时），在一批灯泡中随机抽取100只进行测试，所得数据如下：710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100（2）直方图如下：从直方图可以看出，灯泡使用寿命的分布基本上是对称的。
（3）茎叶图如下茎叶数据个数65 1 8 266 1 4 5 6 8 567 1 3 4 6 7 9 668 1 1 2 3 3 3 4 5 5 5 8 8 9 9 14 690 0 1 1 1 1 2 2 2 3 3 4 4 5 5 6 6 6 7 7 8 8 8 8 9 9 26（2 ）雷达图如下：从雷达图可以看出，甲班成绩为优良的人数高于乙班，说明甲班的考试成绩好于乙班。
统计学-基于R第3版习题答案(第一章)2095920)
第1章数据与R习题1.11. 存为R数据> zhibiao<-c("低收入户","中等偏下户","中等收入户","中等偏上户","高收入户")> y2008<-c(1500,2935,4200,5900,11000)> y2009<-c(1500,3100,4500,6400,12000)> y2010<-c(1870,3600,5222,7440,14000)> y2011<-c(2000,4200,6200,8800,16000)> y2012<-c(2300,4800,7000,10000,19000)> table1_1<-data.frame("指标"=zhibiao,"2008年"=y2008,"2009年"=y2009,"2010年"=y2010,"201 1年"=y2011,"2012年"=y2012)> table1_1指标 X2008年 X2009年 X2010年 X2011年 X2012年1 低收入户 1500 1500 1870 2000 23002 中等偏下户 2935 3100 3600 4200 48003 中等收入户 4200 4500 5222 6200 70004 中等偏上户 5900 6400 7440 8800 100005 高收入户 11000 12000 14000 16000 19000> save(table1_1,file="D:/table1.RData")2. 转化成矩阵> matrix1<-as.matrix(table1_1);matrix1指标 X2008年 X2009年 X2010年 X2011年 X2012年[1,] "低收入户" " 1500" " 1500" " 1870" " 2000" " 2300"[2,] "中等偏下户" " 2935" " 3100" " 3600" " 4200" " 4800"[3,] "中等收入户" " 4200" " 4500" " 5222" " 6200" " 7000"[4,] "中等偏上户" " 5900" " 6400" " 7440" " 8800" "10000"[5,] "高收入户" "11000" "12000" "14000" "16000" "19000"1.21. 排序工作总结人大\\R语言《统计学—基于R》（第3版）—例题和习题数据（公开资源）\\exercis e\\ch1\\exercise1_2.RData")> exercise1_2[order(-exercise1_2$地区生产总值),]地区地区生产总值19 广东省 67809.8510 江苏省 65088.3215 山东省 59426.5911 浙江省 40173.03。
医学统计学第三版第四章课后习题答案
2.ANOVA实验结果Sum of Squares df Mean Square F Sig. Between Groups 43.194 3 14.398 13.697 .000 Within Groups 37.842 36 1.051Total 81.036 39Multiple ComparisonsDependent Variable: 实验结果Dunnett t (2-sided)a(I) 分组(J) 分组Mean Difference(I-J) Std. Error Sig. 95% Confidence IntervalLower Bound Upper Bound0.5 对照组-2.15000*.45851 .000 -3.2743 -1.02571.0 对照组-2.27000*.45851 .000 -3.3943 -1.1457 1.5 对照组-2.66000*.45851 .000 -3.7843 -1.5357F=13.697 P=0.000004P A=0.000113 P B=0.000051 P C=0.000004均小于0.001根据完全随机资料的方差分析，按α=0.05水准，拒绝H0，接受H1，认为四组治疗组小白鼠的肿瘤重量总体均数不全相等，即不同剂量药物注射液的抑癌作用有差别。
3.Tests of Between-Subjects EffectsDependent Variable: 重量Source Type III Sum ofSquaresdf Mean Square F Sig.Hypothesis 99736.333 1 99736.333 58.489 .005Error 5115.667 3 1705.222a治疗Hypothesis 6503.167 2 3251.583 44.867 .000Error 434.833 6 72.472b分组Hypothesis 5115.667 3 1705.222 23.529 .001Error 434.833 6 72.472bF：44.867 23.529P：0.000246 0.001020<0.01根据随机区组资料的方差分析，按α=0.05水准，拒绝H0，接受H1，三组注射不同剂量雌激素的大白鼠子宫重量总体均数不全相等，即注射不同剂量的雌激素对大白鼠子宫重量有影响5.Tests of Between-Subjects EffectsDependent Variable: 脉搏次数df Mean Square F Sig. Source Type III Sum ofSquaresHypothesis 348005.606 1 348005.606 436.868 .000Error 3845.883 4.828 796.592aHypothesis 218.026 4 54.506 1.243 .344防护服Error 526.141 12 43.845bHypothesis 2853.674 4 713.418 16.271 .000受试者Error 526.141 12 43.845bHypothesis 508.074 4 127.018 2.897 .068试验日期Error 526.141 12 43.845bF：1.243 16.271 2.897P：0.344 0.000086 0.068根据拉丁方设计资料的方差分析，0.344>0.05，按α=0.05水准，接受H0，拒接H1，认为穿五种防护服时的脉搏数总体均数相等，即尚不能认为五种防护服对脉搏数有不同影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Hah 和网速是无形的1：各章练习题答案2.1 （1）属于顺序数据。
（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频率）频率%A1414B2121C3232D1818E1515合计100100（3）条形图（略）2.2 （1）频数分布表如下：（2）某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.02.3 频数分布表如下：某百货公司日商品销售额分组表按销售额分组（万元）频数（天）频率（%）25～30 30～35 35～40 40～45 45～5046159610.015.037.522.515.0合计40 100.0 直方图（略）。
2.4 （1）排序略。
（2）频数分布表如下：100只灯泡使用寿命非频数分布按使用寿命分组（小时）灯泡个数（只）频率（%）650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100 直方图（略）。
2.5 （1）属于数值型数据。
（2）分组结果如下：分组 天数（天）-25~-20 6 -20~-15 8 -15~-10 10 -10~-5 13 -5~0 12 0~5 4 5~10 7 合计60（3）直方图（略）。
2.6 （1）直方图（略）。
（2）自学考试人员年龄的分布为右偏。
（2）A 班考试成绩的分布比较集中，且平均分数较高；B 班考试成绩的分布比A 班分散，且平均成绩较A 班低。
2.82.9 L U 。
（2）17.21 s （万元）。
2.10 （1）甲企业平均成本＝19.41（元），乙企业平均成本＝18.29（元）；原因：尽管两个企业的单位成本相同，但单位成本较低的产品在乙企业的产量中所占比重较大，因此拉低了总平均成本。
2.11 x =426.67（万元）；48.116=s （万元）。
2.12 （1）（2）两位调查人员所得到的平均身高和标准差应该差不多相同，因为均值和标准差的大小基本上不受样本大小的影响。
（3）具有较大样本的调查人员有更大的机会取到最高或最低者，因为样本越大，变化的范围就可能越大。
2.13 （1）女生的体重差异大，因为女生其中的离散系数为0.1大于男生体重的离散系数0.08。
（2） 男生：x =27.27（磅），27.2=s （磅）； 女生：x =22.73（磅），27.2=s （磅）； （3）68%；（4）95%。
2.14 （1）离散系数，因为它消除了不同组数据水平高地的影响。
（2）成年组身高的离散系数：024.01.1722.4==s v ； 幼儿组身高的离散系数：032.03.713.2==s v ；由于幼儿组身高的离散系数大于成年组身高的离散系数，说明幼儿组身高的离散程度相对较大。
2.152.16 （1）方差或标准差；（2）商业类股票；（3）（略）。
2.17 （略）。
第3章 概率与概率分布3.1设A ＝女性，B ＝工程师，AB ＝女工程师，A+B ＝女性或工程师 （1）P(A)＝4/12＝1/3 （2）P(B)＝4/12＝1/3 （3）P(AB)＝2/12＝1/6（4）P(A+B)＝P(A)＋P(B)－P(AB)＝1/3＋1/3－1/6＝1/23.2求这种零件的次品率，等于计算“任取一个零件为次品”（记为A ）的概率()P A 。
考虑逆事件A =“任取一个零件为正品”，表示通过三道工序都合格。
据题意，有：()(10.2)(10.1)(10.1)0.648P A =---=于是 ()1()10.6480.352P A P A =-=-=3.3设A 表示“合格”，B 表示“优秀”。
由于B ＝AB ，于是)|()()(A B P A P B P ＝＝0.8×0.15＝0.123.4 设A ＝第1发命中。
B ＝命中碟靶。
求命中概率是一个全概率的计算问题。
再利用对立事件的概率即可求得脱靶的概率。
)|()()|()()(A B P A P A B P A P B P +＝ ＝0.8×1＋0.2×0.5＝0.9 脱靶的概率＝1－0.9＝0.1或（解法二）：P (脱靶)＝P (第1次脱靶)×P(第2次脱靶)＝0.2×0.5＝0.1 3.5 设A ＝活到55岁，B ＝活到70岁。
所求概率为：()()0.63(|)0.75()()0.84P AB P B P B A P A P A ＝＝＝＝ 3.6这是一个计算后验概率的问题。
设A ＝优质率达95％，A ＝优质率为80％，B ＝试验所生产的5件全部优质。
P(A)＝0.4，P (A )＝0.6，P (B|A )=0.955， P(B |A )=0.85，所求概率为：6115.050612.030951.0)|()()|()()|()()|(＝＝＝A B P A P A B P A P A B P A P B A P +决策者会倾向于采用新的生产管理流程。
3.7 令A 1、A 2、A 3分别代表从甲、乙、丙企业采购产品，B 表示次品。
由题意得：P (A 1)＝0.25，P (A 2)＝0.30， P (A 3)＝0.45；P (B |A 1)＝0.04，P (B |A 2)＝0.05，P (B |A 3)＝0.03；因此，所求概率分别为：（1）)|()()|()()|()()(332211A B P A P A B P A P A B P A P B P ++＝ ＝0.25×0.04＋0.30×0.05＋0.45×0.03＝0.0385 （2）3506.00385.00135.00.030.450.050.300.040.2503.045.0)|(3＝＝＋＋＝⨯⨯⨯⨯B A P3.8据题意，在每个路口遇到红灯的概率是p ＝24/(24+36)＝0.4。
设途中遇到红灯的次数＝X ，因此，X ～B(3，0.4)。
其概率分布如下表：3.9 设被保险人死亡数＝X ，X ～B (20000，0.0005)。
（1）收入＝20000×50（元）＝100万元。
要获利至少50万元，则赔付保险金额应该不超过50万元，等价于被保险人死亡数不超过10人。
所求概率为：P(X ≤10)＝0.58304。
（2）当被保险人死亡数超过20人时，保险公司就要亏本。
所求概率为： P(X >20)＝1－P(X ≤20)＝1－0.99842＝0.00158 （3）支付保险金额的均值＝50000×E (X ) ＝50000×20000×0.0005（元）＝50（万元） 支付保险金额的标准差＝50000×σ(X )＝50000×(20000×0.0005×0.9995)1/2＝158074（元）3.10 （1）可以。
当n 很大而p 很小时，二项分布可以利用泊松分布来近似计算。
本例中，λ= np =20000×0.0005=10，即有X ～P (10)。
计算结果与二项分布所得结果几乎完全一致。
（2）也可以。
尽管p 很小，但由于n 非常大，np 和np(1-p)都大于5，二项分布也可以利用正态分布来近似计算。
本例中，np=20000×0.0005=10，np(1-p)=20000×0.0005×(1-0.0005)=9.995， 即有X ～N (10,9.995)。
相应的概率为： P (X ≤10.5)＝0.51995，P(X ≤20.5)＝0.853262。
可见误差比较大（这是由于P 太小，二项分布偏斜太严重）。
【注】由于二项分布是离散型分布，而正态分布是连续性分布，所以，用正态分布来近似计算二项分布的概率时，通常在二项分布的变量值基础上加减0.5作为正态分布对应的区间点，这就是所谓的“连续性校正”。
（3）由于p ＝0.0005，假如n =5000，则np ＝2.5<5，二项分布呈明显的偏态，用正态分布来计算就会出现非常大的误差。
此时宜用泊松分布去近似。
3.11（1）)6667.1()30200150()150(-<-<=<Z P Z P X P ＝＝0.04779 合格率为1-0.04779＝0.95221或95.221％。
(2) 设所求值为K ，满足电池寿命在200±K 小时范围内的概率不小于0.9，即有：|200|(|200|){||}0.93030X KP X K P Z --<=<≥＝即：{}0.9530KP Z <≥，K /30≥1.64485,故K ≥49.3456。
3.12设X ＝同一时刻需用咨询服务的商品种数，由题意有X ～B(6,0.2)（1）X 的最可能值为：X 0＝[(n+1)p]＝[7×0.2]＝1 （取整数） （2）∑=--=≤-=>2668.02.01)2(1)2(k k k k C X P X P＝1-0.9011＝0.0989第4章 抽样与抽样分布4.1 a. 20, 2 b. 近似正态 c. -2.25 d. 1.504.2 a. 0.0228 b. 0.0668 c. 0.0062 d. 0.8185 e. 0.0013 4.3 a. 0.8944 b. 0.0228 c. 0.1292 d. 0.9699 4.4 a. 101, 99 b. 1 c. 不必 4.5 趋向正态4.6. a. 正态分布, 213, 4.5918 b. 0.5, 0.031, 0.9384.7. a. 406, 1.68, 正态分布 b. 0.001 c. 是，因为小概率出现了 4.8. a. 增加 b. 减少4.9. a. 正态 b. 约等于0 c. 不正常 d. 正态, 0.06 4.10 a. 0.015 b. 0.0026 c. 0.15874.11. a. (0.012, 0.028) b. 0.6553, 0.7278 4.12. a. 0.05 b. 1 c. 0.000625第5章 参数估计5.1 （1）79.0=x σ。
（2）E =1.55。
5.2 （1）14.2=x σ。
（2）E =4.2。
（3）（115.8,124.2）。
5.3 （2.88,3.76）；(2.80,3.84)；(2.63,4.01)。
5.4 （7.1,12.9）。
5.5 （7.18,11.57）。