单筋矩形截面承载能力计算
单筋矩形截面受弯构件正截面承载力计算
60
第三章 受弯构件正截面承载力计算
翼缘计算宽度bf′取下表所列各项中的最小值。
翼缘计算宽度bf′
项 次
考虑情况
1
按计算跨度l0考虑
2
按梁(纵肋)净距sn考虑
3
按翼缘高度
hf'考虑
hf'/h0≥0.1
0.1>
hf'/h0≥0.05
x xb bh0
防止超筋脆性破坏:
b
As bh0
max
b
1 fc
fy
防止少筋脆性破坏: min AS AS,min minbh
单筋矩形截面所能承受的最大弯矩(极限弯矩):
Mu,max 1 fcbh02b (1 0.5b )
3.3 受弯构件正截面承载力计算
第三章 受弯构件正截面承载力计算
一、基本公式及适用条件 1.基本公式
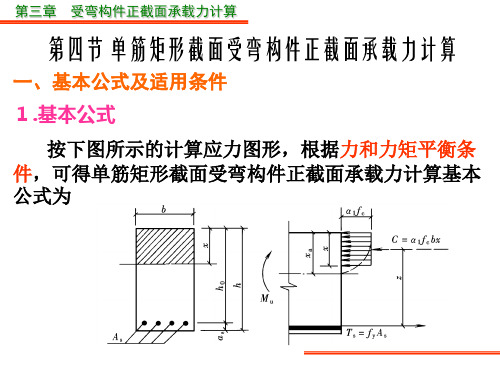
按下图所示的计算应力图形,根据力和力矩平衡条 件,可得单筋矩形截面受弯构件正截面承载力计算基本 公式为
第三章 受弯构件正截面承载力计算
1 fcbx fy As
M Mu 1 fcbxh0 x 2
M M u f y As h0 x 2
1 fcb
②若x≤ξbho,且x≥2as′,则将x值代入第二个基本 公式 求Mu;
56
第三章 受弯构件正截面承载力计算
③若x>ξ bho,说明属超筋梁,此时应取x=ξ bho代 入第二个基本公式求Mu;
④若x<2as′,则
Mu AS f y h0 as'
⑤若Mu≥M则截面安全,否则截面不安全。
04 单筋矩形截面正截面承载能力计算

在梁的正截面强度计算中 用等效矩形应力图代替受压 区抛物线应力图,x为等效矩 形应力图的高度,h0为截面 有效高度,它们的比 值:ξ=x/h0, ξ称为相对受压区 高度。
相对受压区高度ξ不仅反映了钢筋与混凝土的面积比(配筋率ρ), 也反映了钢筋与混凝土的材料强度比,是反映构件中两种材料配比 本质的参数。
钢筋混凝土构件在按承载能力极限状态计算时,引入下列假定: ①构件弯曲后,其截面仍保持平面,受压区混凝土平均应变和 钢筋的应变沿截面高度符合线性分布。平截面假定 ②正截面破坏时,构件受压区混凝士应力取抗压强度设计值fcd fcd,应力计算图形为矩形。等效矩形应力图 ③正截面破坏时,受弯、大偏心受压、大偏心受拉构件的受拉 主筋达到抗拉强度设计值fsd ,受拉区混凝土不参与工作(抗剪计算除外)。
2 正截面承载力计算的基本假定
以IIIa阶段作为承载力极限状态的计算依据
(l)上图为钢筋混凝土梁对应三个工作阶段的应变图。由图可见, 梁在第I阶段受压与受拉应变图呈直线分布,说明混凝土与钢筋应 变的变化规律符合平截面假定。随着弯矩的增加,当梁进入第II 阶段时,受压区混凝土压应变与受拉区钢筋拉应变的实测值均不 断增长,但应变图基本上仍是上、下两个三角形,平均应变仍符 合平截面假定。这种状况一直延续至第Ⅲ阶段,即梁破坏前。最 后,当梁破坏时,受压区混凝土边缘纤维压应变达到(或接近)混 凝上受弯时极限压应变,这标志着梁已开始破坏。
(4)由公式fsdAs=fcdbx或fsdAs(h0-x/2)=γ0Md 计算钢筋截面面积As;
(5)根据计算所得和构造要求选择钢筋直径、根数并布置,确定实际的As 实 ;实际采用的钢筋宜为计算所需钢筋截面面积的0.95~1.05倍。
(6)检查假定as是否接近实际,如误差大,重新计算(因为若as假<as实,则
单筋矩形截面正截面承载力计算方法

单筋矩形截面正截面承载力计算方法
在计算单筋矩形截面的承载力时,我们需要考虑两种主要的受力情况:剪力和弯矩。
以下是单筋矩形截面承载力计算的详细方法。
1.剪力承载力计算:
首先,计算纵向筋的贡献:
Vr = φ × As × fy /γs
其中,Vr为纵向筋的承载力,φ为抗剪强度折减系数,一般取0.75,As为纵向筋的截面面积,fy为纵向筋的抗拉强度设计值,γs为安全系数,一般取1.15
然后,计算混凝土的贡献:
Vc = φ × b × x × fcd /γc
其中,Vc为混凝土的承载力,b为矩形截面的宽度,x为截面混凝土
受剪应力点至受拉纵筋的距离,fcd为混凝土的抗压强度设计值,γc为
混凝土安全系数,一般取1.5
最终,剪力承载力为:
V=Vr+Vc
2.弯矩承载力计算:
首先,计算纵向筋的承载力:
Mr = φ × (As × fy) × (d - a/2) / γs
其中,Mr为纵向筋的弯矩承载力,d为矩形截面的有效高度,a为纵向筋至受压边缘的距离,As为纵向筋的截面面积,fy为纵向筋的抗拉强度设计值,γs为安全系数。
3.组合效应计算:
在实际情况中,剪力和弯矩通常是同时作用于单筋矩形截面的。
根据极限状态设计原则,剪力和弯矩的组合效应需要考虑。
计算组合效应时,可以根据相应的超信度进行组合,采用相应的抗风定额规定即可。
综上所述,单筋矩形截面的承载力计算主要包括剪力承载力和弯矩承载力的计算,并根据实际受力情况考虑组合效应。
详细的计算公式和参数需要根据具体情况进行设计和选择,以确保梁的安全可靠性。
单筋矩形截面受弯构件正截面承载力计算

单筋矩形截面受弯构件正截面承载力计算单筋矩形截面受弯构件是指具有一个纵向钢筋(单筋)和一个矩形截面的构件。
在受弯时,矩形截面受到压力,而钢筋受到拉力,通过计算正截面承载力可以确定该构件的安全性能。
下面将介绍单筋矩形截面受弯构件正截面承载力的计算方法。
首先,计算正截面的受压区高度h和内力矩M。
假设构件受弯时的截面高度为h,宽度为b,截面厚度为d。
根据等截面原则,构件的正截面宽度和截面高度相等,即b=h。
构件的弯矩M由下式计算得出:M=Rd·Z,其中Rd为设计弯矩,Z为正截面抵抗矩。
然后,计算正截面抵抗矩Z。
在单筋矩形截面中,正截面抵抗矩由钢筋和混凝土组成。
钢筋的抵抗矩可由以下公式计算得出:Zs=As·fy·(h-d/2),其中As为钢筋截面面积,fy为钢筋的抗拉强度。
混凝土的抵抗矩可由以下公式计算得出:Zc=0.85·fck·(b·h-(As+Asc)·(h/2-d/2)),其中fck为混凝土的抗压强度,Asc为纵向钢筋表面积。
正截面的抵抗矩由钢筋的抵抗矩和混凝土的抵抗矩之和得出:Z=Zs+Zc。
接下来,计算正截面的承载力。
正截面受弯构件的承载力由以下条件中的最不利情况决定:1.混凝土达到极限压应力或者钢筋达到屈服应力;2. 混凝土达到达到破坏应变时,即混凝土压应力达到0.45fck或者钢筋达到屈服应变。
计算混凝土达到极限压应力的情况下的承载力,可以得到下式:Nc=0.85·fcd0·A+(Rd-Zs)/Rd·fctd0·A,其中fcd0为混凝土的设计强度,fctd0为混凝土的设计抗拉强度,A为截面面积。
计算钢筋达到屈服应力的情况下的承载力,可以得到下式:Ns=(Zs/0.9zτs)·fsd,其中z为混凝土的截面中和高度,τs为混凝土的应力分布系数,fsd为钢筋的设计抗拉强度。
综合两种情况,正截面受弯构件的正截面承载力Fc为较小值:Fc=min{Nc,Ns}。
单筋矩形正截面受弯承载力计算公式

单筋矩形正截面受弯承载力计算公式根据图1和截面内力平衡条件,并满足承载能力极限状态计算表达式的要求,可得出如下基本计算公式:图1 单筋矩形截面梁板正截面受弯承载力计算简图∑x=0 f c bx=f y A s(1)∑M=0 KM≤f c bx(h0−)(2)式中M——弯矩设计值(N·mm);f c——混凝土轴心抗压强度设计值(N/mm2),按附表1–2取用;b——矩形截面宽度(mm);x——混凝土受压区计算高度(mm);h0——截面有效高度(mm);f y——受拉钢筋的强度设计值(N/mm2),按附表1–5取用;A s——受拉钢筋的截面面积(mm2);K——承载力安全系数, 按表1–7取用。
利用基本公式进行截面计算时,必须求解方程组,比较麻烦。
为简化计算,将式(1)、(2)改写如下:将ξ=x/h0代入公式(1)、(2),并引入截面抵抗矩系数αs,令αs =ξ(1–ξ)(3)则基本公式改写为:f c bξh0=f y A s(4)KM≤αs f c bh02(5)由式(4)可得:ρ= ξf c/f y基本公式是根据适筋破坏的情况推导出来的。
因此,它的适用条件为:(1)ρ≤ρmax或x ≤ξb h0或ξ≤ξb,以防止发生超筋破坏,ρmax=ξb f c/f y;基本公式是依据适筋构件破坏时的应力图形情况推导的,当受拉钢筋屈服的同时,受压区混凝土也达到极限压应变εcu,梁发生的临界破坏状态,就是适筋梁与超筋梁的界限。
但为了结构的安全,更有效地防止发生超筋破坏,,应用基本公式和由它派生出来的公式计算时,必须符合此条件。
(2)ρ≥ρmin,以防止发生少筋破坏钢筋混凝土梁板构件破坏时承担的弯矩等于同截面素混凝土梁板构件所能承担的弯矩时的受力状态,为适筋破坏与少筋破坏的分界。
这时梁板的配筋率应是适筋梁板的最小配筋率。
《规范》不仅考虑了这种“等承载力”原则,而且还考虑了混凝土的性质和工程经验等。
因此,基本公式应符合此条件。
单筋矩形截面受弯构件正截面承载能力计算
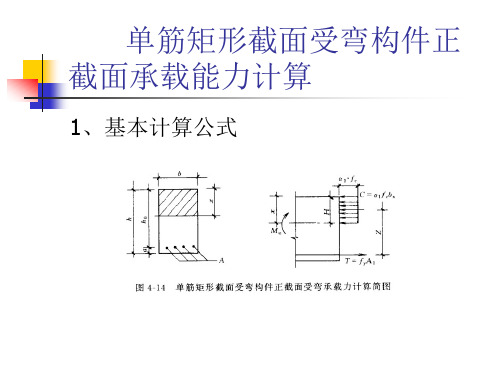
两种T型截面梁
受压区在翼缘内 受压区在翼缘外 受压区在翼缘内同矩形梁(已经解决, b 'f ) 受压区在翼缘外,把它分解成T型梁计算 关键问题: 如何判别 如何分解
截面校核 给定条件:截面配筋、截面尺寸、材料强 度 求:截面能抵抗的最大弯矩(与已知的截 面最大弯矩比较) 过程: 1)根据给定条件,分析截面适用条件。 2)如果截面适用条件满足,直接用弯矩 平衡方程求最大弯矩。 3)如果截面平衡方程不满足要求,重新 按截面设计问题进行计算。
正截面承载能力计算系数与 计算方法
x
如 满足适用条件,根据弯矩 平衡方程求弯矩
x
如不满足适用条件
向受压区钢筋取矩求弯矩 或 按最大受压区高度求弯矩
主要公式
M u1 f y' As' h0 a '
x M u 2 M M u1 1 f c bx h0 2 1 f c bx M u2 As 2 x fy f y h0 2 f y' ' As1 As fy As As1 As 2 f y' fy A
M u M ui M u 2
几个注意的问题
求出相对受压区高度大于界限受压区高 度如何处理; 求出受压区高度小于2a,如何求As 是否存在按单筋计算比按向受压区受压 钢筋合力点计算,求出的受拉钢筋还小 的情况
As , A
' s
单筋矩形梁正截面受弯承载力计算实例
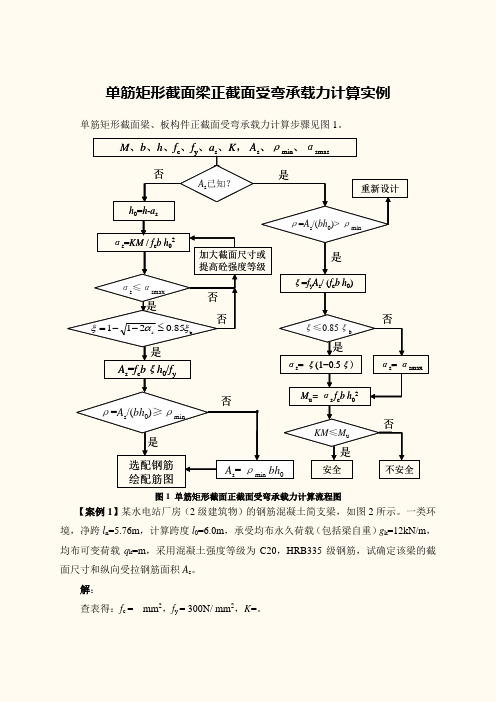
单筋矩形截面梁正截面受弯承载力计算实例单筋矩形截面梁、板构件正截面受弯承载力计算步骤见图1。
选配钢筋加大截面尺寸或是M 、b 、h 、f c 、f y 、a s 、K ,A s 、ρmin 、αsmasαs =KM / f c b h 02A s =f c b ξh 0/f ybs 85.0211ξαξ≤--=h 0=h -a s否A s = ρmin bh 0绘配筋图是是A s 已知?αs ≤αsmax提高砼强度等级ρ=A s /(bh 0)≥ρmin是ξ=f y A s / (f c b h 0)ξ≤0.85ξbαs = ξ(1−0.5ξ)M u = αs f c b h 02KM ≤M u是是安全αs = αsmax否否不安全否否否ρ=A s /(bh 0)> ρmin是重新设计图1 单筋矩形截面正截面受弯承载力计算流程图【案例1】某水电站厂房(2级建筑物)的钢筋混凝土简支梁,如图2所示。
一类环境,净跨l n =5.76m ,计算跨度l 0=6.0m ,承受均布永久荷载(包括梁自重)g k =12kN/m ,均布可变荷载q k =m ,采用混凝土强度等级为C20,HRB335级钢筋,试确定该梁的截面尺寸和纵向受拉钢筋面积A s 。
解:查表得:f c = mm 2,f y = 300N/ mm 2,K =。
(1)确定截面尺寸 由构造要求取:h =(1/8~1/12)l 0 =(1/8~1/12)×6000=750~500,取h =500mm b =(1/2~1/3)h =(1/2~1/3)×500=250~167,取b =250mm (2)内力计算M =(+ )l 02/8=(×12+×)×62 /8 = ·m (3)配筋计算取a s =40mm ,则h 0=h –a s =500–40=460mm==2c s bh f KMα248.04602506.91076.10420.126=⨯⨯⨯⨯ 290.0248.0211211s =⨯--=--=αξ<ξb =×=A s =f c bξh 0/f y =×250××460/300=1067mm 2 ρ= 1067/(250×460)=﹪>ρmin =﹪(4)选配钢筋,绘制配筋图选受拉纵筋为322(A s =1140 mm 2),需要最小梁宽b min =2c +3d +2e =2×30+ 3×22+2×25=176(mm )<250mm ,符合构造要求。
单筋矩形梁正截面承载力计算

基本构件计算:单筋矩形梁正截面承载力计算一、计算简图二、基本公式1.公式法的三个基本公式:单筋矩形梁正截面受弯承载力计算的三个基本公式:s y c A f bx f =1α⎪⎭⎫ ⎝⎛-=≤201x h bx f M M c u α⎪⎭⎫ ⎝⎛-=≤20x h A f M M s y u式中 M —— 弯矩设计值;M u —— 受弯承载力设计值,即破坏弯矩设计值;c f 1α—— 混凝土等效矩形应力图的应力值; y f —— 钢筋抗拉强度设计值; s A —— 受拉钢筋截面面积; b —— 梁截面宽度; x —— 混凝土受压区高度;h 0 —— 截面有效高度,即截面受压边缘到受拉钢筋合力点的距离,h 0=h-a ; a —— 受拉钢筋合力点到梁受拉边缘的距离,当受拉钢筋为一排时,a =c+d/2; c —— 混凝土保护层厚度; d —— 受拉钢筋直径。
2.系数法的基本公式(1)系数的公式).(s ξ-ξ=α501(4-21)s αξ211--= (4-25)ξ-=α-+=γ5012211.ss (4-26)(2)基本公式 21201)5.01(bh f bh f M c s c ααξξα=-=0h A f M s s y γ=三、基本公式的适用条件1)防止超筋破坏b ξξ≤ 或 b ρρ≤ 或 0h x b ξ≤2)防止少筋破坏bh A A s s min min ,ρ=≥四、计算方法1.截面选择(设计题)按已知的荷载设计值作用下的弯矩M 设计截面时,常遇到下列两种情形: 情形1 : 已知:M 、混凝土强度等级及钢筋等级;构件截面尺寸b 及h 。
求:所需的受拉钢筋截面面积A s 。
[解](1)确定基本数据c f ;y f ;a h h -=0(2)计算有关系数21bh f Mc s αα=s αξ211--=ξ-=α-+=γ5012211.ss(3)计算受拉钢筋 0h f MA s y s γ=或 01bh f f A ycs αξ=(4)根据求得的受拉钢筋A s ,按照有关构造要求从附表20中选用钢筋直径和根数 (5)验算适用条件1)适用条件:b ξ≤ξ;2)若b ξ>ξ:需加大截面,或提高混凝土强度等级,或改用双筋矩形截面 3)验算bh A A m in m in ,s s ρ=≥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3.2 单筋矩形截面承载能力计算矩形截面通常分为单筋矩形截面和双筋矩截面两种形式。
只在截面的受拉区配有纵向受力钢筋的矩形截面,称为单筋矩形截面(图4-10)。
不但在截面的受拉区,而且在截面的受压区同时配有纵向受力钢筋的矩形截面,称为双筋矩形截面。
需要说明的是,为了构造上的原因(例如为了形成钢筋骨架),受压区通常也需要配置纵向钢筋。
这种纵向钢筋称为架立钢筋。
架立钢筋与受力钢筋的区别是:架立钢筋是根据构造要求设置,通常直径较细、根数较少;而受力钢筋则是根据受力要求按计算设置,通常直径较粗、根数较多。
受压区配有架立钢筋的截面,不是双筋截面。
图4-10 单筋矩形截面根据4.3.1的基本假定,单筋矩形截面的计算简图如图4-11所示。
图4-11 单筋矩形截面计算简图为了简化计算,受压区混凝土的应力图形可进一步用一个等效的矩形应力图代替。
矩形应力图的应力取为α1f c(图4-12),f c为混凝土轴心抗压强度设计值。
所谓“等效”,是指这两个图不但压应力合力的大小相等,而且合力的作用位置完全相同。
图4-12 受压区混凝土等效矩形应力图按等效矩形应力计算的受压区高度x与按平截面假定确定的受压区高度x o之间的关系为:(4-7)系数α1和β1的取值见表4-2。
系数α1和β1的取值表表4-2◆基本计算公式由于截面在破坏前的一瞬间处于静力平衡状态,所以,对于图4-12 的受力状态可建立两个平衡方程:一个是所有各力的水平轴方向上的合力为零,即(4-8)式中b——矩形截面宽度;A s——受拉区纵向受力钢筋的截面面积。
另一个是所有各力对截面上任何一点的合力矩为零,当对受拉区纵向受力钢筋的合力作用点取矩时,有:(4-9a)当对受压区混凝土压应力合力的作用点取矩时,有:(4-9b)式中M——荷载在该截面上产生的弯矩设计值;h o——截面的有效高度,按下计算h o=h-a s。
h为截面高度,a s为受拉区边缘到受拉钢筋合力作用点的距离。
按构造要求,对于处于室内正常使用环境的梁和板,当混凝土的强度等级不低于C20时,梁内钢筋的混凝土保护层最小厚度(指从构件边缘至钢筋边缘的距离)不得小于25mm,板内钢筋的混凝土保护层不得小于15mm(当混凝土的强度等级小于和等于C20时,梁和板的混凝保护层最小厚度分别为30mm和20mm)。
因此,截面的有效高度在构件设计时一般可按下面方法估算(图4-13)。
图4-13 梁板的计算高度梁的纵向受力钢筋按一排布置时,h o=h-35 mm ;梁的纵向受力钢筋按两排布置时,h o=h-60 mm ;板的截面有效高度h o=h-20mm。
对于处于其它使用环境的梁和板,保护层的厚度见表4-8。
式(4-8)和式(4-9)是单筋矩形截面受弯构件正截面承载力的基本计算公式。
但是应该注意,图4-12b 的受力情况只能列两个独立方程,式(4-9a )和式(4-9b )不是相互独立的,只能任意选用其中一个与式(4-8)一起进行计算。
◆基本计算公式的适用条件式(4-8)和式(4-9)是根据筋构件的破坏简图推导出的。
它们只适用于适筋构件计算,不适用于少筋构件和超筋构件计算。
在前面的讨论中已经指出,少筋构件和超筋构件的破坏都属于脆性破坏,设计时应避免将构件设计成这两类构件。
为此,任何设计的受弯构件必须满足下列两个适用条件:▲为了防止将构件设计成少筋构件,要求构件的配筋率不得低于其最小配筋率最小配率是少筋构件与适筋构件的界限配筋率,它是根据受弯构件的破坏弯矩等于其开裂弯矩确定的。
受弯构件的最小配筋率ρmin 按构件全截面面积扣除位于受压边的翼缘面积(b f '-b )h f ' 后的截面面积计算,即(4-10)式中 A —— 构件全截面面积;b f ',h f ' ---- 分别为截面受压边缘的宽度和翼缘高度; A s,min —— 按最小配筋率计算的钢筋面积。
ρmin 取0.2%和45f t /f y (%)中的较大值。
ρmin (%)的值如表4-3所示。
建筑工程受弯构件最小配筋率ρmin 值(%) 表4-3▲为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相对界限受压区高度ξb 即(4-11)相对界限受压区高度ξb 是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb 的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y 与钢筋弹性量E s 之比值,即ξs =f y /E s ,由受压区边缘混凝土的应变为ξcu 与受拉钢筋应变ξs 的几何关系(图4-14)。
可推得其相对界限受压区高度ξb 的计算公式为(4-12)图4-14 截面应变分布为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400和RRB400钢筋,将其抗拉强度设计值f y和弹性模量E s代入式(4-12)中,可算得它们的相对界限受压区高度ξb如表4-4所示,设计时可直接查用。
当ξ≤ξb时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb值表4-4※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的钢筋,取对应于残余应变为0.2%时的应力σ0.2作为条件屈服点,并以此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点σ0.2时的钢筋应变为(图4-15):图4-15 无明显屈服点钢筋的应力—应变曲线(4-13)式中f y——无明显屈服点钢筋的抗拉强度设计值;E s——无明显屈服点钢筋的弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度ξb 的计算公式为:(4-14)截面相对受压区高度ξ与截面配筋率ρ之间存在对应关系。
ξb 求出后,可以求出适筋受弯构件截面最大配筋率的计算公式。
由式(4-8)可写出:(4-15)(4-16)式(4-16)即为受弯构件最大配筋率的计算公式。
为了使用上的方便起见,将常用的具有明显屈服点钢筋配筋的普通钢筋混凝土受弯构件的最大配筋率ρmax 列在表4-5中。
建筑工程受弯构件的截面最大配筋率ρmax (%) 表4-5当构件按最大配筋率配筋时,由(4-9a )可以求出适筋受弯构件所能承受的最大弯矩为:(4-17)式中 αsb ——截面最大的抵抗矩系数,αsb =ξb (1-ξb /2) 。
对于具有明显屈服点钢筋配筋的受弯构件,其截面最大的抵抗矩系数见表4-6。
建筑工程受弯构件截面最大的抵抗矩系数αsb 表4-6由上面的讨论可知,为了防止将构件设计成超筋构件,既可以用式(4-11)进行控制,也可以用:(4-18)(4-19)进行控制。
式(4-11 )、式(4-18)和式(4-19)对应于同一配筋和受力状况,因而三者是等效的。
设计经验表明,当梁、板的配筋率为:实心板:ρ=0.4%~0.8%矩形梁:ρ=0.6%~1.5%T形梁: ρ=0.9%~1.8%时,构件的用钢量和造价都较经济,施工比较方便,受力性能也比较好。
因此,常将梁、板的配筋率设计在上述范围之内。
梁、板的上述配筋率称为常用配筋率,也有人称它们为经济配筋率。
由于不考虑混凝土抵抗拉力的作用,因此,只要受压区为矩形而受拉区为其它形状的受弯构件(如倒T形受弯构件),均可按矩形截面计算。
◆计算例题在受弯构件设计中,通常会遇见下列两类问题:一类是截面选择问题,即假定构件的截面尺寸、混凝土的强度等级、钢筋的品种以及构件上作用的荷载或截面上的内力等都是已知的(或各种因素虽然暂时未知,但可根据实际情况和设计经验假定),要求计算受拉区纵向受力钢筋所需的面积,并且参照构造要求,选择钢筋的根数和直径。
另一类是承载能力校核问题,即构件的尺寸、混凝土的强度等级、钢筋的品种、数量和配筋方式等都已确定,要求验算截面是否能够承受某一已知的荷载或内力设计值。
利用式(4-8)、式(4-9)以及它们的适用条件式,便可以求得上述两类问题的答案。
例[4-1]现浇简支板计算例[4-2]矩形简支梁计算例[4-3]预制走道板计算◆计算表格的制作及使用▲计算表格的制作由上面的例题可见,利用计算公式进行截面选择时,需要解算二次方程式和联立方程式,还要验算适用条件,颇为麻烦。
如果将计算公式制成表格,便可以使计算工作得到简化。
计算表格的形式有两种:一种是对于各种混凝土强度等级以及各种钢筋配筋的梁板都适用的表格,另一种是对某种混凝土强度等级和某种钢筋的梁板专门制作的表格。
前一种表格通用性好,后一种表格使用上较简便。
下面只介绍通用表格的制作及使用方法。
式(4-9a)可写成:(4-20)令(4-21)则式(4-20)可写成:(4-22)式中,αs bh2o可以认为是截面在极限状态时的抵抗矩,因此可以将αs称为截面抵抗矩系数。
同样,式(4-9b)可写成:(4-23)令(4-24)则式(4-23)可写成:(4-25)式中γs——内力臂系数。
由式(4-21)可得:(4-26)代入式(4-24)可得:(4-27)因此,单筋矩形截面受弯构件正截面的配筋计算可以按照图4-16的框图进行。
图4-16 单筋矩形截面受弯构件正截面配筋计算框图式(4-26)和式(4-27)表明,ξ和γs与αs之间存在一一对应的关系,给定一个αs值,便有一个ξ值和一个γs值与之对应。
因此,可以事先给出一串αs值,算出与它们对应的ξ值和γs值,并且将它们列成表格(见附表4-1和附表4-2),设计时查用这个表格,既可以避免解算二次方程式和联立方程式,又不必按式(4-26)或(4-27)计算ξ或γs,一般情况下还不必验算构件是少筋还是超筋,因而使计算工作得到简化。
单筋矩形截面受弯构件的截面选择和承载力校核还可以用图4-17的框图表示。
对于学习过算法语言的读者来说,按照这个框图,不难编写出相应的计算机程序。
▲计算表格的使用下面通过一个例题来说明计算表格的使用方法。
例[4-4]上一页下一页。
